Generation of Data-Driven Expected Energy Models for Photovoltaic Systems
Abstract
:1. Introduction
2. Methodology
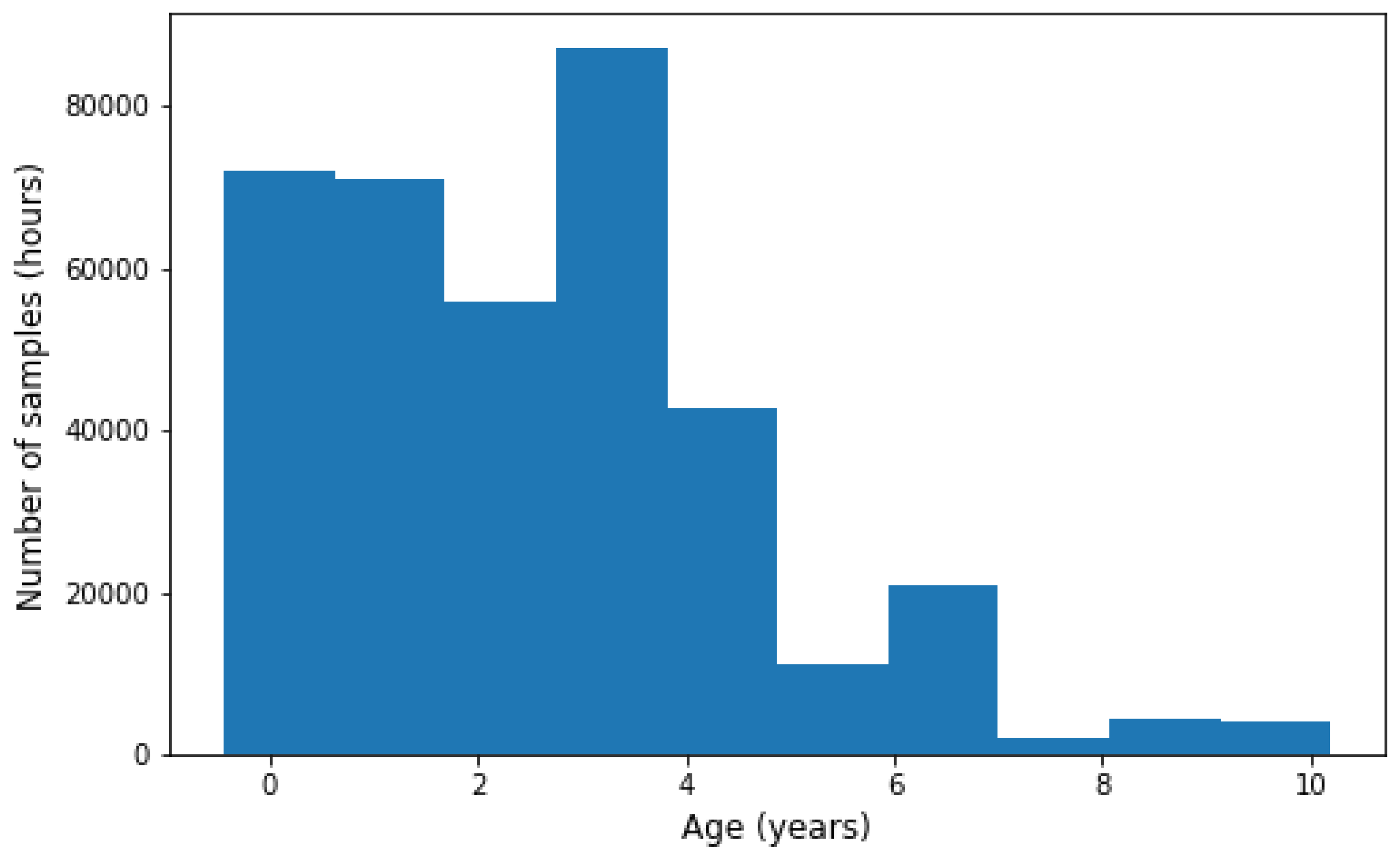
2.1. Data
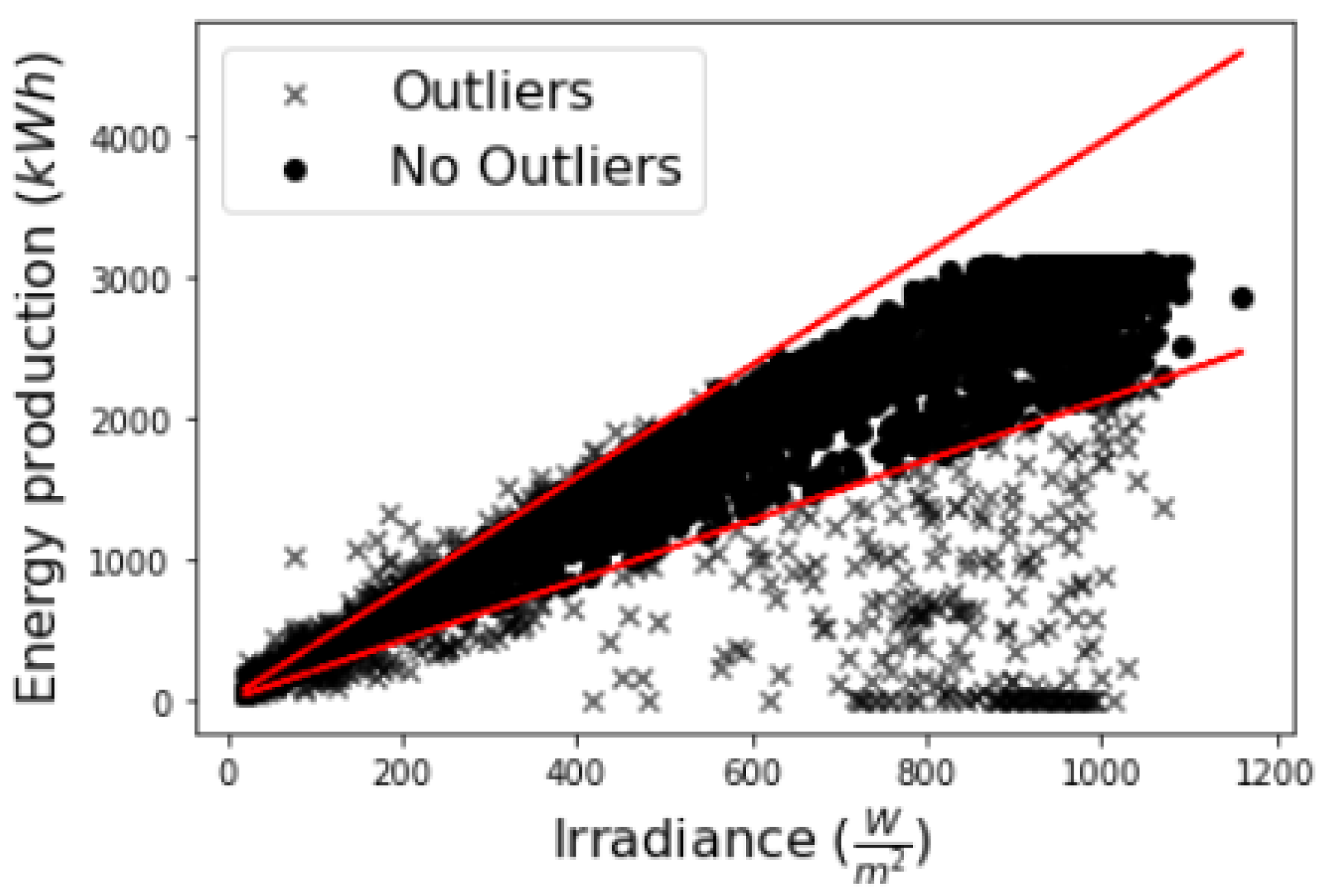
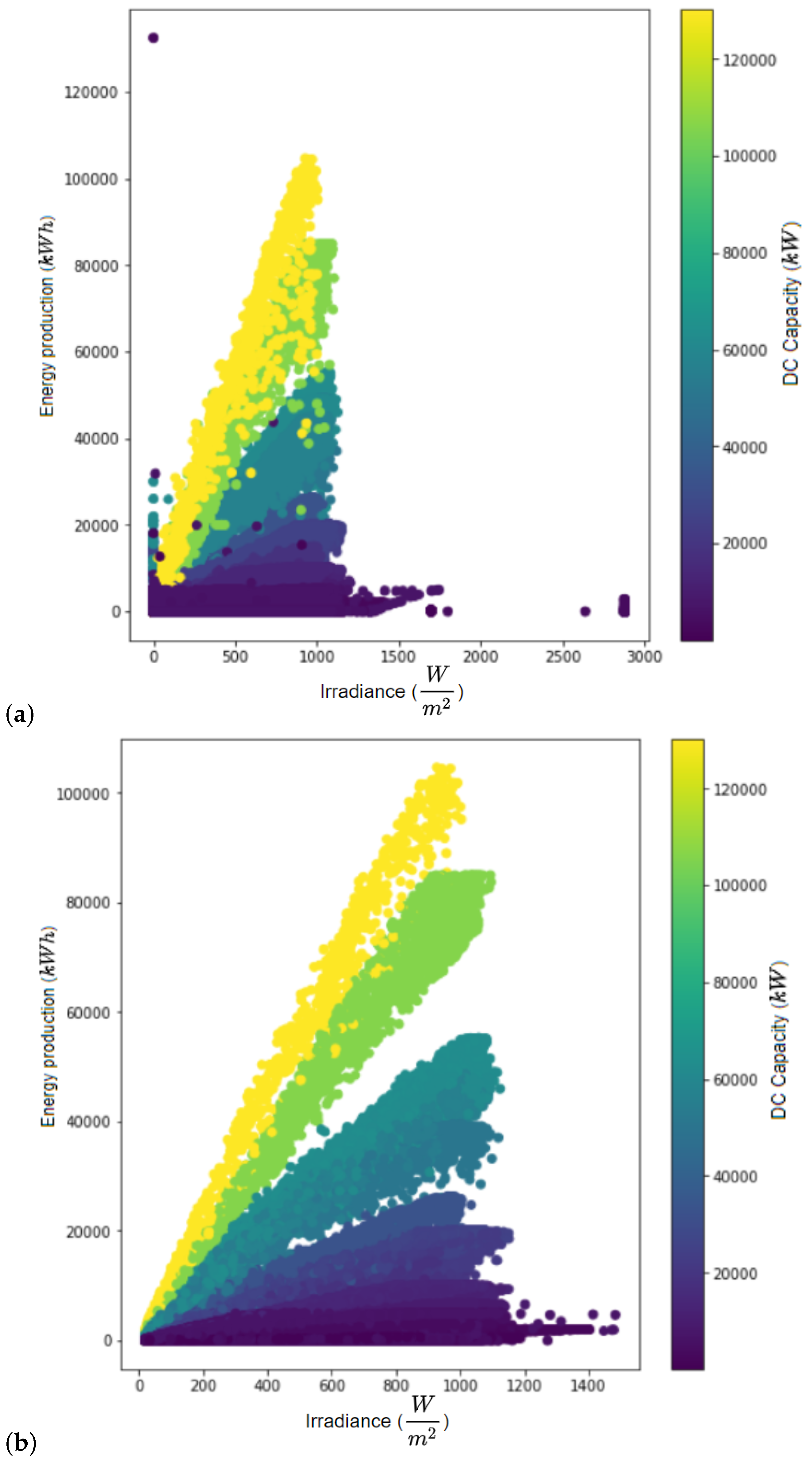
2.2. Preprocessing
- 20 ≤ Irradiance (I) ≤ 1500 ;
- Energy (E) > 0 kWh;
- Ambient temperature () ≤ 50 C and module temperature () ≤ 90 C.
2.3. Variable Standardization
2.4. Model Design and Training
2.5. Model Evaluation
3. Results and Discussion
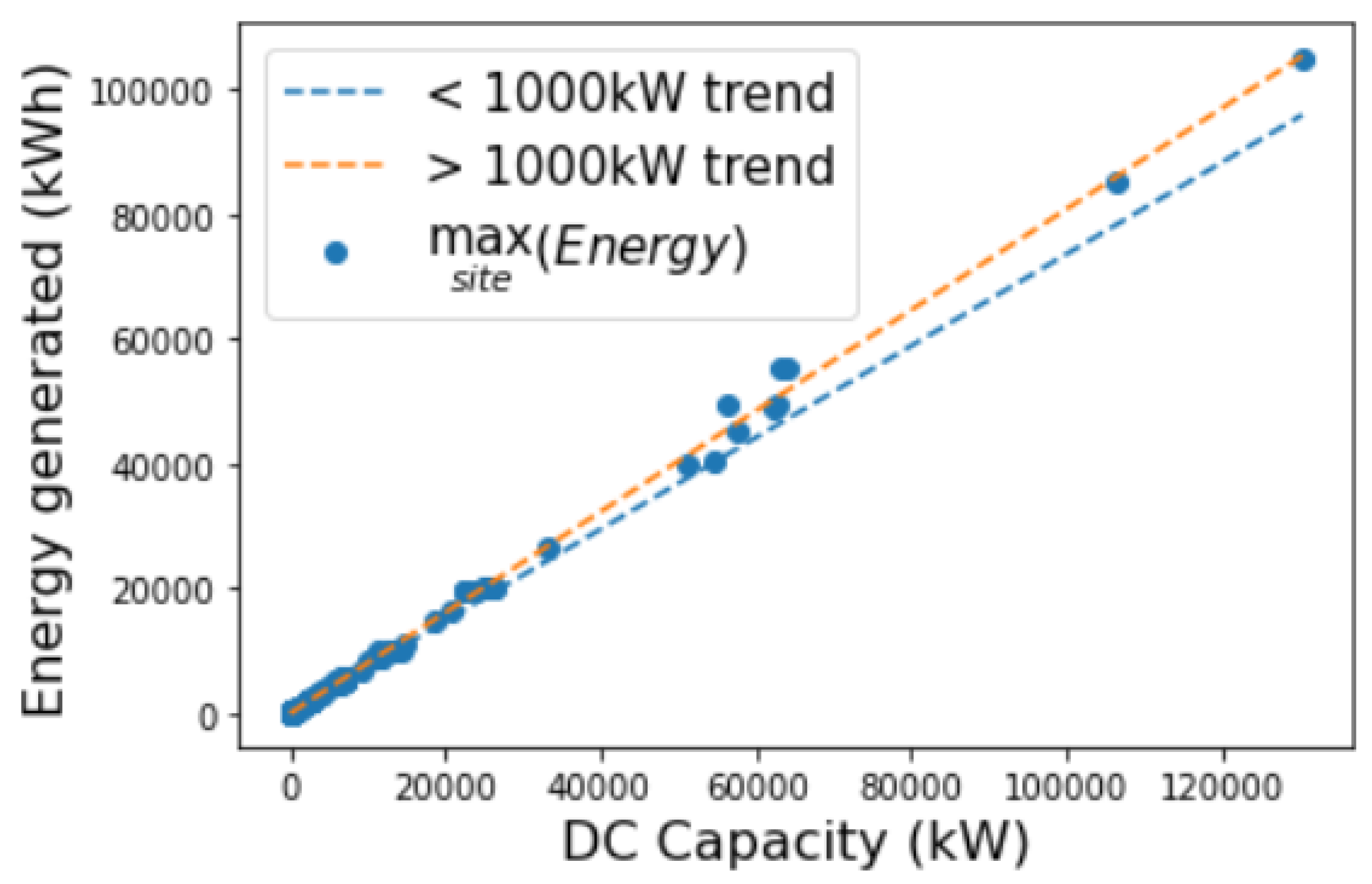
3.1. High-Capacity Systems
3.2. Low-Capacity Systems
3.3. Limitations and Future Work
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| E | Energy (kWh) |
| Expected energy (kWh) | |
| I | irradiance () |
| DC capacity (kW) | |
| ambient temperature (C) | |
| module temperature (C) | |
| e | standardized E (see Table 1) |
| i | standardized I (see Table 1) |
| c | standardized C (see Table 1) |
| Root mean squared error | |
| n | number of samples |
| p | number of predictors |
Appendix A
Appendix A.1. Tables & Figures
| Data Subsets | |||
|---|---|---|---|
| Parameters | Raw | Post-Data Quality Filters | Post-System Anomaly Filters |
| Irradiance (I) | 0.46 | 0.41 | 0.40 |
| Capacity () | 0.55 | 0.85 | 0.89 |
| Average Percent Error | ||
|---|---|---|
| >1000 kW Systems | ≤1000 kW Systems | |
| Third-order interactions | 0.03 | 0.23 |
| Second-order interactions | 0.03 | 0.21 |
| Third-order seasonal | 0.05 | 0.20 |
| Second-order seasonal | 0.04 | 0.16 |
| Third-order month | 0.12 | 0.27 |
| Second-order month | 0.08 | 0.27 |
| Third-order hour | 0.13 | 0.15 |
| Second-order hour | 0.10 | 0.05 |
| Additive interaction | 0.03 | 0.00 |
| simple additive | 0.36 | 1.44 |
| IEC | 0.39 | 1.75 |
| hour | 0.28 | 1.01 |
| month | 0.32 | 1.30 |
| seasonal | 0.32 | 1.55 |

Appendix A.2. Top-Performing Trained Models
References
- Golnas, A. PV system reliability: An operator’s perspective. In Proceedings of the 2012 IEEE 38th Photovoltaic Specialists Conference (PVSC) PART 2, Austin, TX, USA, 3–8 June 2012; pp. 1–6. [Google Scholar]
- Feng, M.; Bashir, N.; Shenoy, P.; Irwin, D.; Kosanovic, D. SunDown: Model-driven Per-Panel Solar Anomaly Detection for Residential Arrays. In Proceedings of the 3rd ACM SIGCAS Conference on Computing and Sustainable Societies, Guayaquil, Ecuador, 15–17 June 2020; pp. 291–295. [Google Scholar]
- Dyamond, W.; Rix, A. Detecting Anomalous Events for a Grid Connected PV Power Plant Using Sensor Data. In Proceedings of the 2019 Southern African Universities Power Engineering Conference/Robotics and Mechatronics/Pattern Recognition Association of South Africa (SAUPEC/RobMech/PRASA), Bloemfontein, South Africa, 29–31 January 2019; pp. 287–292. [Google Scholar]
- Harrou, F.; Sun, Y.; Taghezouit, B.; Saidi, A.; Hamlati, M.E. Reliable fault detection and diagnosis of photovoltaic systems based on statistical monitoring approaches. Renew. Energy 2018, 116, 22–37. [Google Scholar] [CrossRef] [Green Version]
- Platon, R.; Martel, J.; Woodruff, N.; Chau, T.Y. Online fault detection in PV systems. IEEE Trans. Sustain. Energy 2015, 6, 1200–1207. [Google Scholar] [CrossRef]
- Blair, N.; Dobos, A.P.; Freeman, J.; Neises, T.; Wagner, M.; Ferguson, T.; Gilman, P.; Janzou, S. System Advisor Model, Sam 2014.1. 14: General Description; Technical Report; National Renewable Energy Lab.: Golden, CO, USA, 2014. [Google Scholar]
- Deline, C.; Anderson, K.; Jordan, D.; Walker, A.; Desai, J.; Perry, K.; Muller, M.; Marion, B.; White, R. PV Fleet Performance Data Initiative: Performance Index-Based Analysis; Technical Report; National Renewable Energy Lab.: Golden, CO, USA, 2021. [Google Scholar]
- Gilletly, S.; Jackson, N.; Staid, A. Quantifying Wildfire-Induced Impacts to Photovoltaic Energy Production in the western United States. In Proceedings of the 2021 IEEE 48th Photovoltaic Specialists Conference (PVSC), Online, 20–25 June 2021. [Google Scholar]
- Klise, G.T.; Stein, J.S. Models Used to Assess the Performance of Photovoltaic Systems; Sandia National Laboratories: Albuquerque, NM, USA, 2009. [Google Scholar]
- De Soto, W.; Klein, S.A.; Beckman, W.A. Improvement and validation of a model for photovoltaic array performance. Sol. Energy 2006, 80, 78–88. [Google Scholar] [CrossRef]
- Arab, A.H.; Taghezouit, B.; Abdeladim, K.; Semaoui, S.; Razagui, A.; Gherbi, A.; Boulahchiche, S.; Mahammed, I.H. Maximum power output performance modeling of solar photovoltaic modules. Energy Rep. 2020, 6, 680–686. [Google Scholar] [CrossRef]
- King, D.L.; Kratochvil, J.A.; Boyson, W.E. Photovoltaic Array Performance Model; Sandia National Laboratories: Albuquerque, NM, USA, 2004. [Google Scholar]
- Boyson, W.E.; Galbraith, G.M.; King, D.L.; Gonzalez, S. Performance Model for Grid-Connected Photovoltaic Inverters; Technical Report; Sandia National Laboratories: Albuquerque, NM, USA, 2007. [Google Scholar]
- Dobos, A.P. PVWatts Version 5 Manual; Technical Report; National Renewable Energy Lab.: Golden, CO, USA, 2014. [Google Scholar]
- ISO/IEC TR 29110-1:2016; Photovoltaic System Performance—Part 1: Monitoring. International Electrotechnical Commission: Geneva, CH, USA, 2017.
- Myers, D. Evaluation of the Performance of the Pvusa Rating Methodology Applied to Dual Junction pv Technology: Preprint (Revised); Technical Report; National Renewable Energy Lab.: Golden, CO, USA, 2009. [Google Scholar]
- DNV GL. Narrowing the Performance Gap: Reconciling Predicted and Actual Energy Production; Technical Report; DNV GL: Oakland, CA, USA, 2019. [Google Scholar]
- Hanawalt, S. The Challenge of Perfect Operating Data; Technical Report; Power Factors: San Francisco, CA, USA, 2020. [Google Scholar]
- Livera, A.; Theristis, M.; Makrides, G.; Sutterlueti, J.; Ransome, S.; Georghiou, G.E. Performance Analysis of Mechanistic and Machine Learning models for Photovoltaic energy yield prediction. In Proceedings of the 36th European Photovoltaic Solar Energy Conference and Exhibition, Marseille, France, 9–13 September 2019; pp. 9–13. [Google Scholar]
- Ascencio-Vásquez, J.; Bevc, J.; Reba, K.; Brecl, K.; Jankovec, M.; Topič, M. Advanced PV Performance Modelling Based on Different Levels of Irradiance Data Accuracy. Energies 2020, 13, 2166. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, Y.; Zhang, C.; Yang, M. Improved artificial neural network method for predicting photovoltaic output performance. Glob. Energy Interconnect. 2020, 3, 553–561. [Google Scholar] [CrossRef]
- Bertsimas, D.; Delarue, A.; Jaillet, P.; Martin, S. The price of interpretability. arXiv 2019, arXiv:1907.03419. [Google Scholar]
- Klise, G.T. PV Reliability Operations Maintenance (PVROM) Database: Data Collection & Analysis Insights; Technical Report; Sandia National Lab.: Albuquerque, NM, USA, 2015. [Google Scholar]
- Klise, K.A.; Stein, J.S.; Cunningham, J. Application of IEC 61724 Standards to Analyze PV System Performance in Different Climates. In Proceedings of the 2017 IEEE 44th Photovoltaic Specialist Conference (PVSC), Washington, DC, USA, 25–30 June 2017; pp. 3161–3166. [Google Scholar]
- Klise, K.A. Performance Monitoring Using Pecos; Technical Report; Sandia National Lab.: Albuquerque, NM, USA, 2016. [Google Scholar]
- IEC TS 61724-3:2016; Photovoltaic System Performance—Part 3: Energy Evaluation Method. International Electrotechnical Commission: Geneva, CH, USA, 2016.
- Vining, W.; Hansen, C. PVAnalytics. 2021. Available online: https://github.com/pvlib/pvanalytics (accessed on 22 December 2021).
- Malik, S.; Dassler, D.; Fröbel, J.; Schneider, J.; Ebert, M. Outdoor data evaluation of half-/full-cell modules with regard to measurement uncertainties and the application of statistical methods. In Proceedings of the 29th European Photovoltaic Solar Energy Conference and Exhibition, Amsterdam, The Netherlands, 22–26 September 2014; pp. 3269–3273. [Google Scholar]
- Theil, H. A rank-invariant method of linear and polynomial regression analysis. Indag. Math. 1950, 12, 173. [Google Scholar]
- Tibshirani, R. Regression shrinkage and selection via the lasso: A retrospective. J. R. Stat. Soc. Ser. B 2011, 73, 273–282. [Google Scholar] [CrossRef]
- Geman, S.; Bienenstock, E.; Doursat, R. Neural networks and the bias/variance dilemma. Neural Comput. 1992, 4, 1–58. [Google Scholar] [CrossRef]
- Dirnberger, D.; Blackburn, G.; Müller, B.; Reise, C. On the impact of solar spectral irradiance on the yield of different PV technologies. Sol. Energy Mater. Sol. Cells 2015, 132, 431–442. [Google Scholar] [CrossRef]
- Eke, R.; Betts, T.R. Spectral irradiance effects on the outdoor performance of photovoltaic modules. Renew. Sustain. Energy Rev. 2017, 69, 429–434. [Google Scholar] [CrossRef] [Green Version]
- Arias, A.L. R-Squared, Adjusted R-Squared, the F Test, and Multicollinearity. In Understanding Regression Analysis; Chapman and Hall/CRC: Boca Raton, FL, USA, 2020; pp. 185–200. [Google Scholar]
- Jordan, D.C.; Deline, C.; Kurtz, S.R.; Kimball, G.M.; Anderson, M. Robust PV degradation methodology and application. IEEE J. Photovolt. 2017, 8, 525–531. [Google Scholar] [CrossRef]


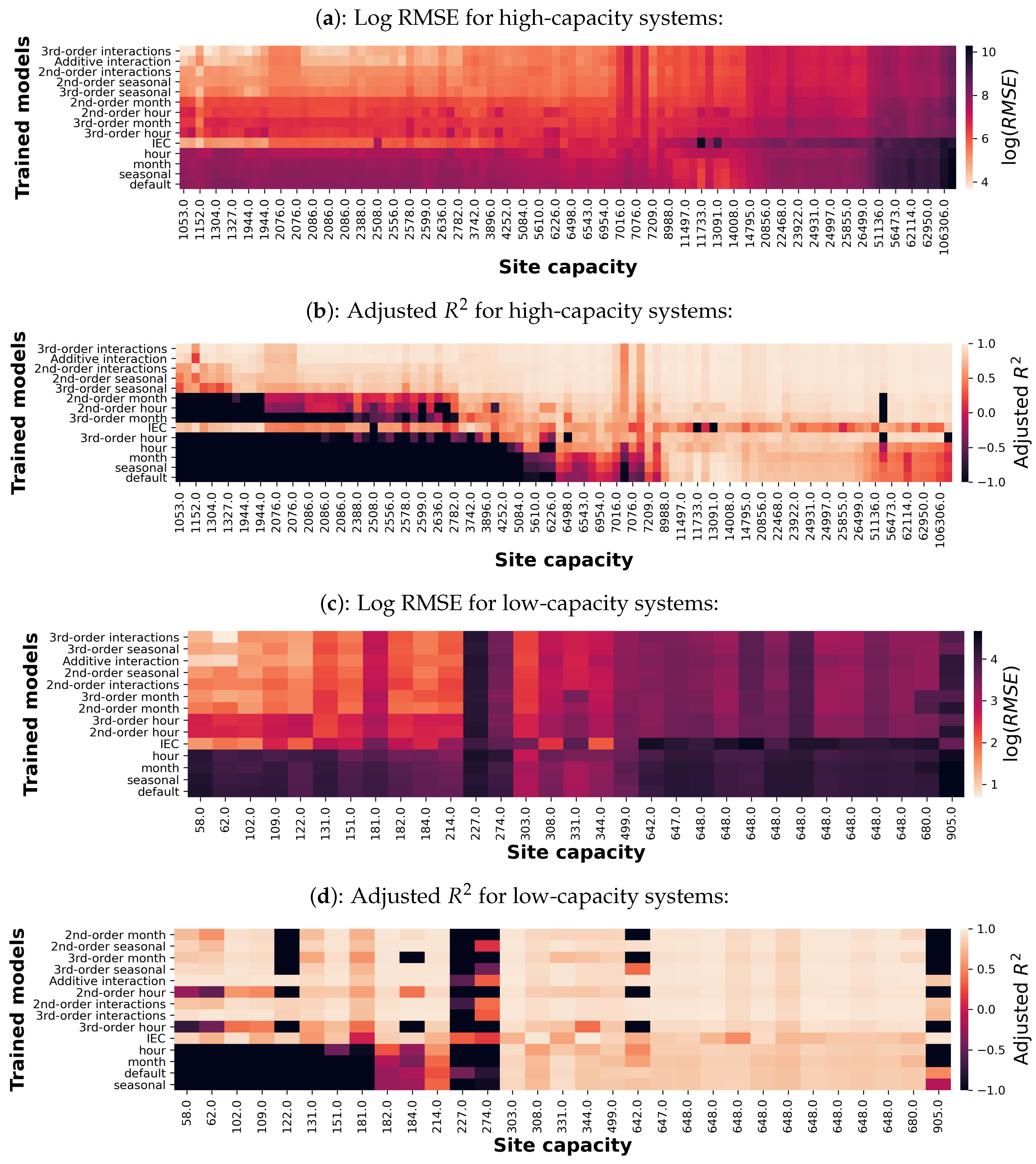
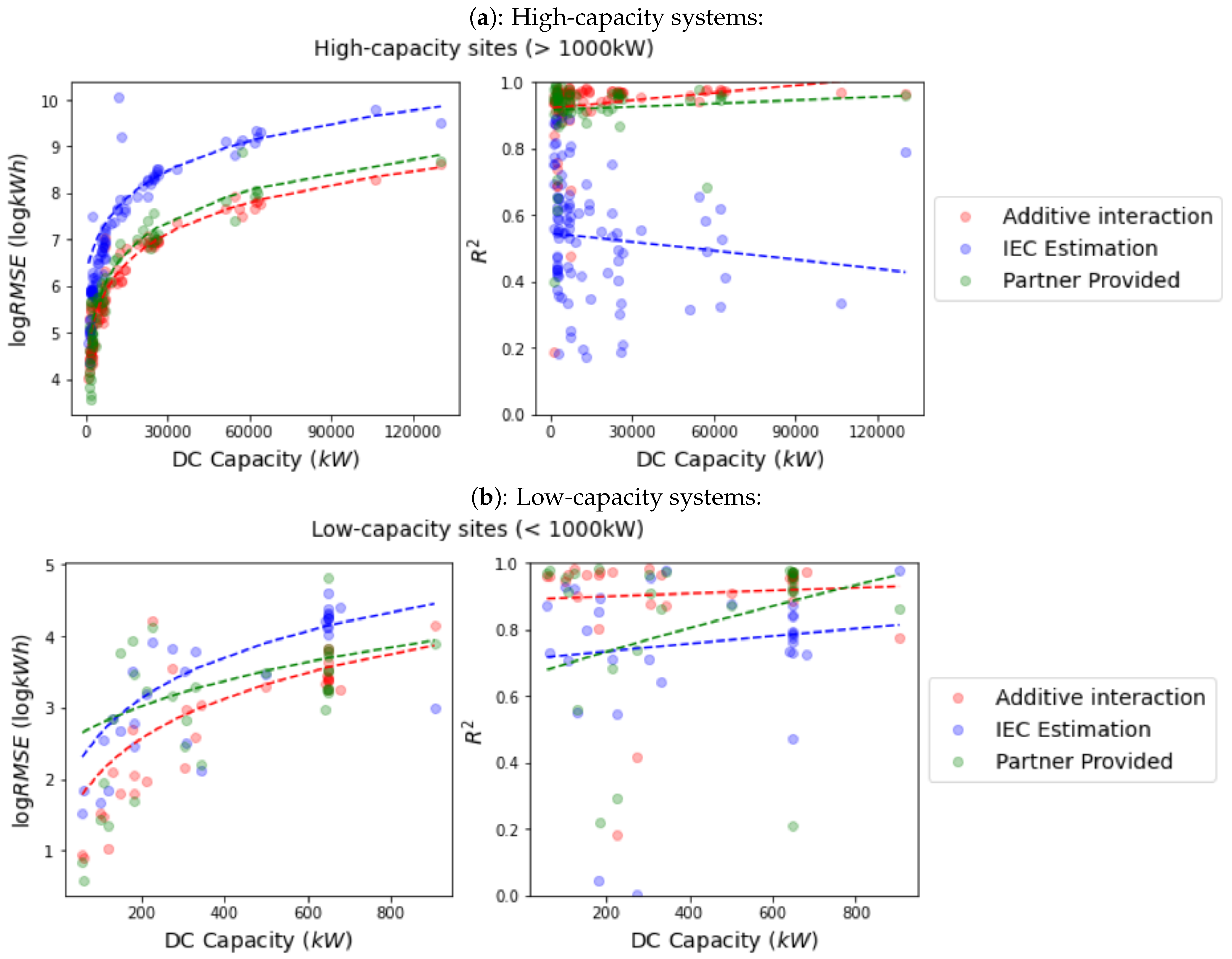

| >1000 kW Systems | <1000 kW Systems | |||
|---|---|---|---|---|
| Parameter | Mean | StDev | Mean | StDev |
| Irradiance | 571.459 | 324.199 | 413.533 | 286.110 |
| Capacity | 14,916.234 | 20,030.000 | 375.919 | 234.151 |
| Energy | 7449.152 | 12,054.525 | 119.008 | 119.829 |
| Model Category | Time Variables (t) | Interaction Degree (d) | Number Parameters for M Inputs | Number Parameters for 2 Inputs | ||
|---|---|---|---|---|---|---|
| Additive | 3 | |||||
| Additive with interaction | 2nd-order (d = 2) | M + 2 | 4 | |||
| Additive with Time-weighted | Season (t = 4) | 9 | ||||
| Month (t = 12) | 25 | |||||
| Hour (t = 15 *) | 31 | |||||
| Polynomial | 2nd-order (d = 2) | 6 | ||||
| 3rd-order (d = 3) | 10 | |||||
| d = 2 | d = 3 | |||||
| Polynomial with Time-weighted | Season (t = 4) | 2nd-order (d = 2) | t = 4 | 25 | 41 | |
| Month (t = 12) | 3rd-order (d = 3) | t = 12 | 73 | 121 | ||
| Hour (t = 15 *) | t = 15 | 90 | 151 | |||
| >1000 kW Systems | <1000 kW Systems | |||||||
|---|---|---|---|---|---|---|---|---|
| Models | Time Variable | Interaction Degree | Number Parameters Pre-Lasso | Number Parameters Post-Lasso | Wins: Adj. R | Wins: logRMSE | Wins: Adj. R | Wins: logRMSE |
| Third-order interactions | 3 | 10 | 9 | 47.9 | 49.0 | 38.7 | 38.7 | |
| Additive interaction | 1 | 4 | 4 | 22.9 | 17.7 | 32.3 | 29.0 | |
| Second-order interactions | 2 | 6 | 5 | 15.6 | 10.4 | 6.5 | 0.0 | |
| Second-order seasonal | season | 2 | 25 | 18 | 9.4 | 15.6 | 3.2 | 3.2 |
| Third-order seasonal | season | 3 | 41 | 27 | 1.0 | 4.2 | 3.2 | 3.2 |
| Second-order month | month | 2 | 73 | 43 | 0.0 | 0.0 | 3.2 | 3.2 |
| Second-order hour | hour | 2 | 90 | 44 | 0.0 | 0.0 | 0.0 | 0.0 |
| Third-order month | month | 3 | 121 | 68 | 0.0 | 0.0 | 0.0 | 3.2 |
| Third-order hour | hour | 3 | 151 | 81 | 1.0 | 1.0 | 0.0 | 6.5 |
| IEC | 1.0 | 1.0 | 12.9 | 12.9 | ||||
| hour | hour | 1 | 31 | 26 | 0.0 | 0.0 | 0.0 | 0.0 |
| month | month | 1 | 25 | 25 | 0.0 | 0.0 | 0.0 | 0.0 |
| seasonal | season | 1 | 9 | 9 | 1.0 | 1.0 | 0.0 | 0.0 |
| simple additive | 1 | 3 | 3 | 0.0 | 0.0 | 0.0 | 0.0 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hopwood, M.W.; Gunda, T. Generation of Data-Driven Expected Energy Models for Photovoltaic Systems. Appl. Sci. 2022, 12, 1872. https://doi.org/10.3390/app12041872
Hopwood MW, Gunda T. Generation of Data-Driven Expected Energy Models for Photovoltaic Systems. Applied Sciences. 2022; 12(4):1872. https://doi.org/10.3390/app12041872
Chicago/Turabian StyleHopwood, Michael W., and Thushara Gunda. 2022. "Generation of Data-Driven Expected Energy Models for Photovoltaic Systems" Applied Sciences 12, no. 4: 1872. https://doi.org/10.3390/app12041872
APA StyleHopwood, M. W., & Gunda, T. (2022). Generation of Data-Driven Expected Energy Models for Photovoltaic Systems. Applied Sciences, 12(4), 1872. https://doi.org/10.3390/app12041872






