Moving Surface Boundary-Layer Control on the Wake of Flow around a Square Cylinder
Abstract
:1. Introduction
2. Numerical Calculation Model
2.1. Governing Equations of the Fluid Flow
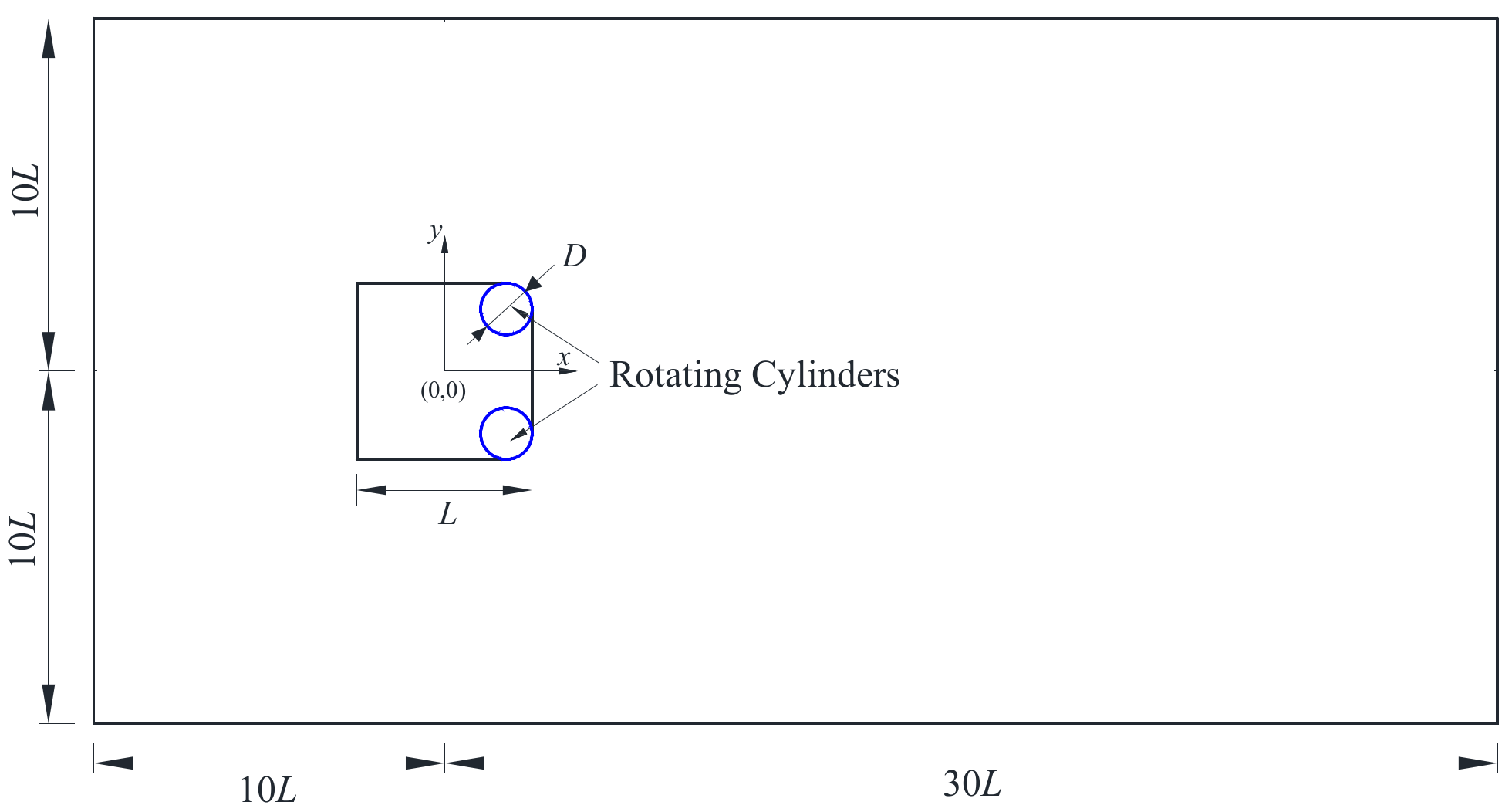
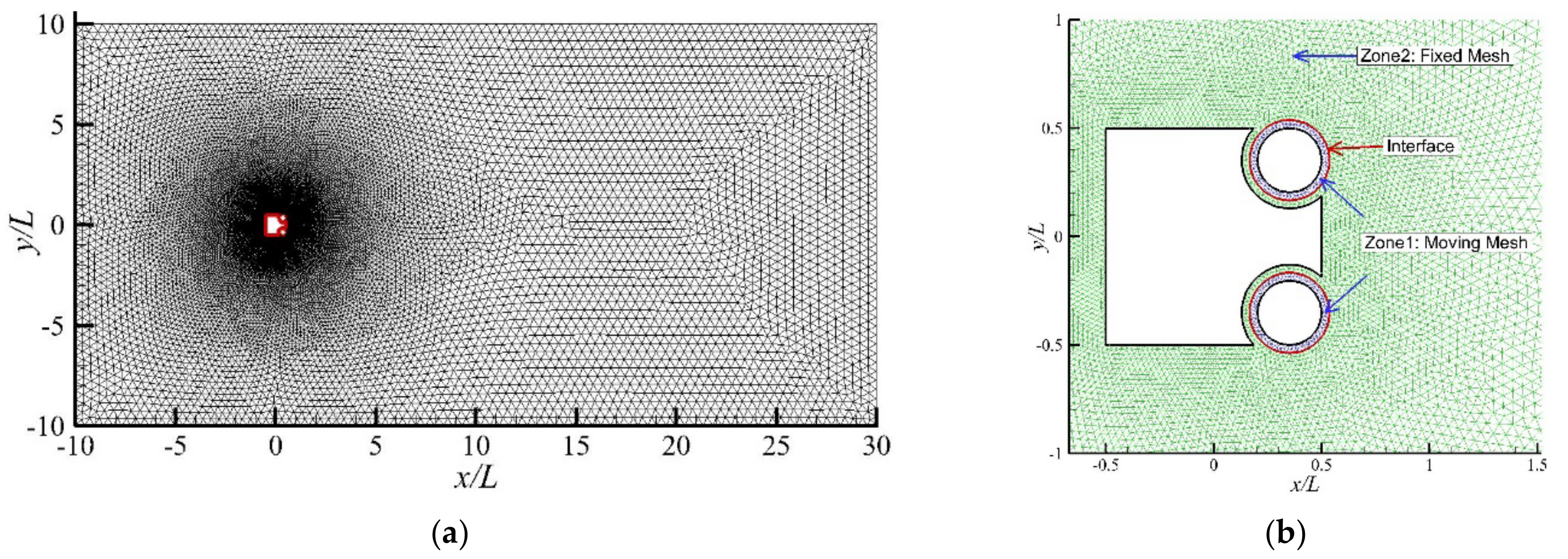
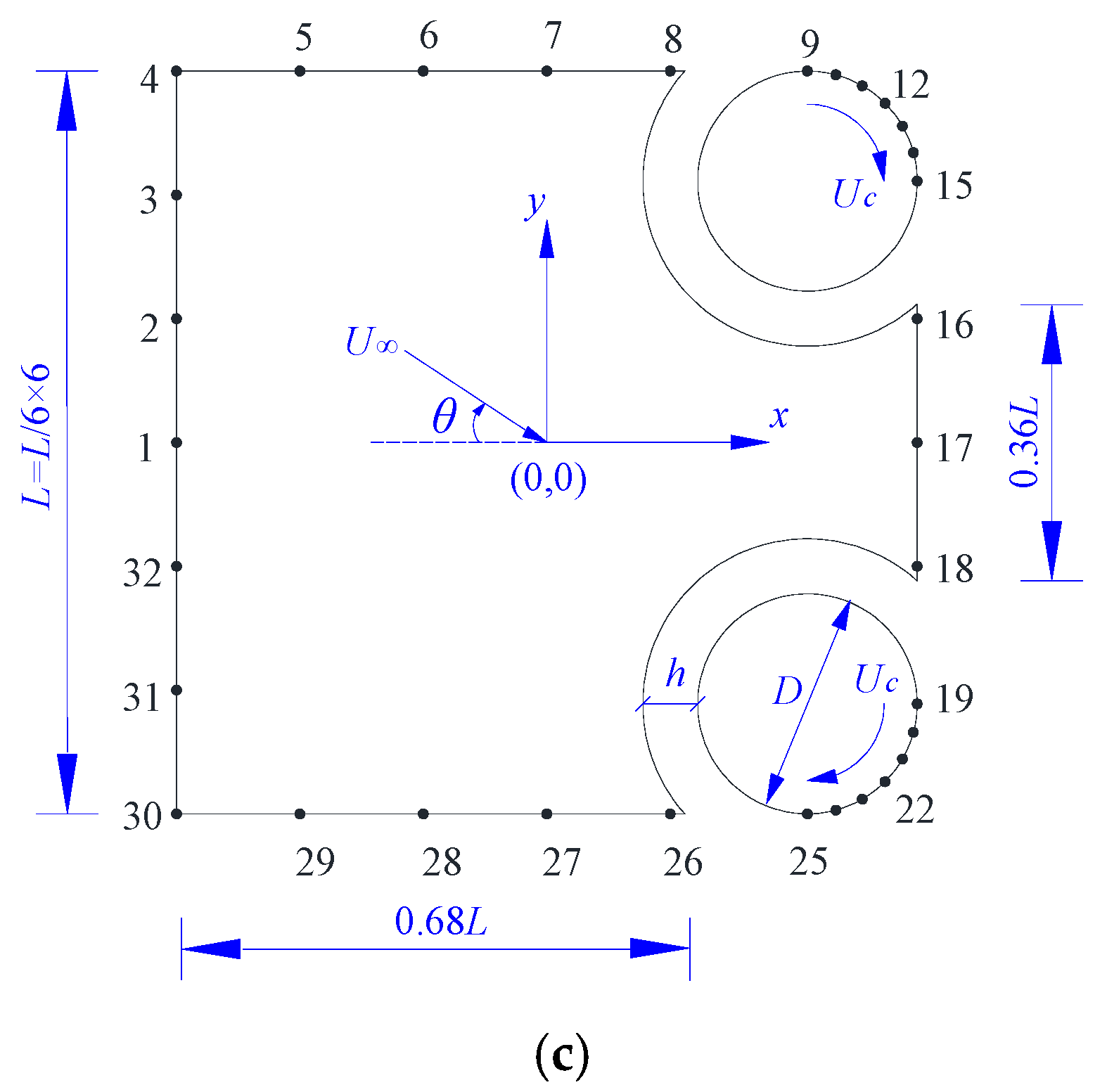
2.2. Numerical Model and Solution Setting
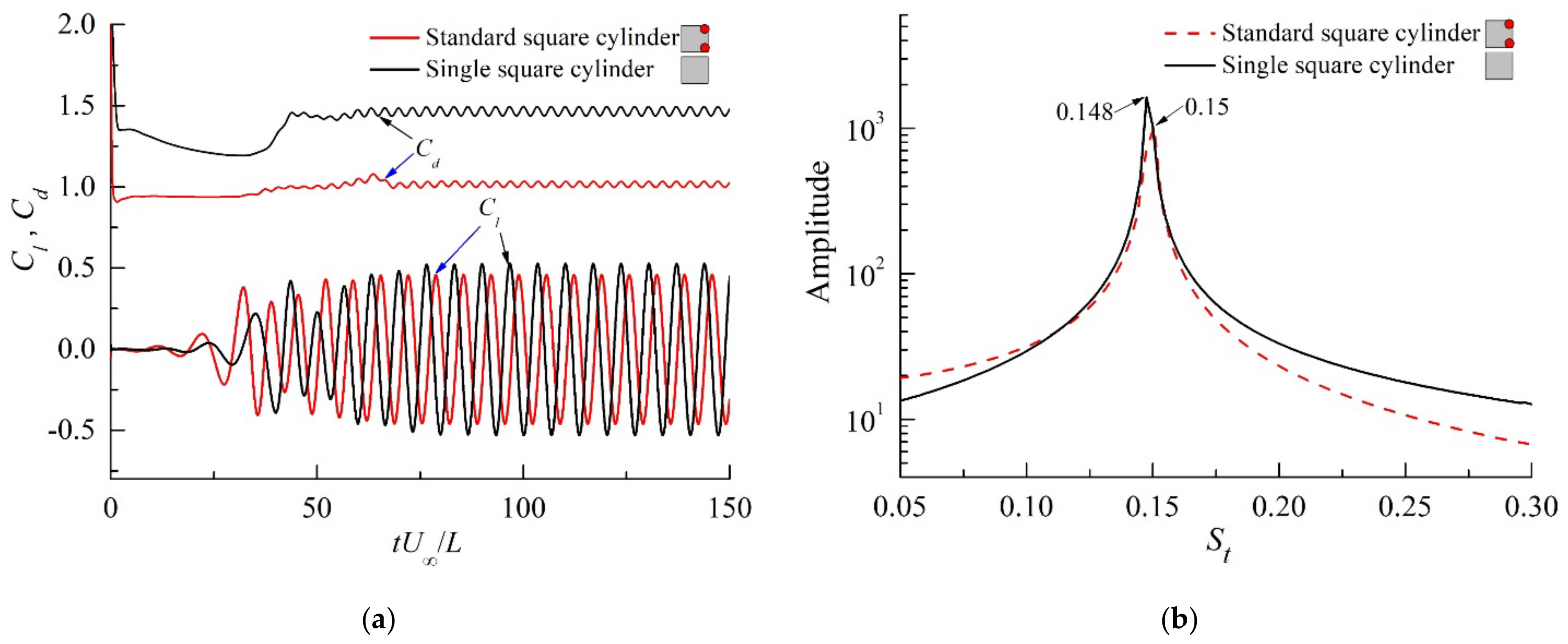
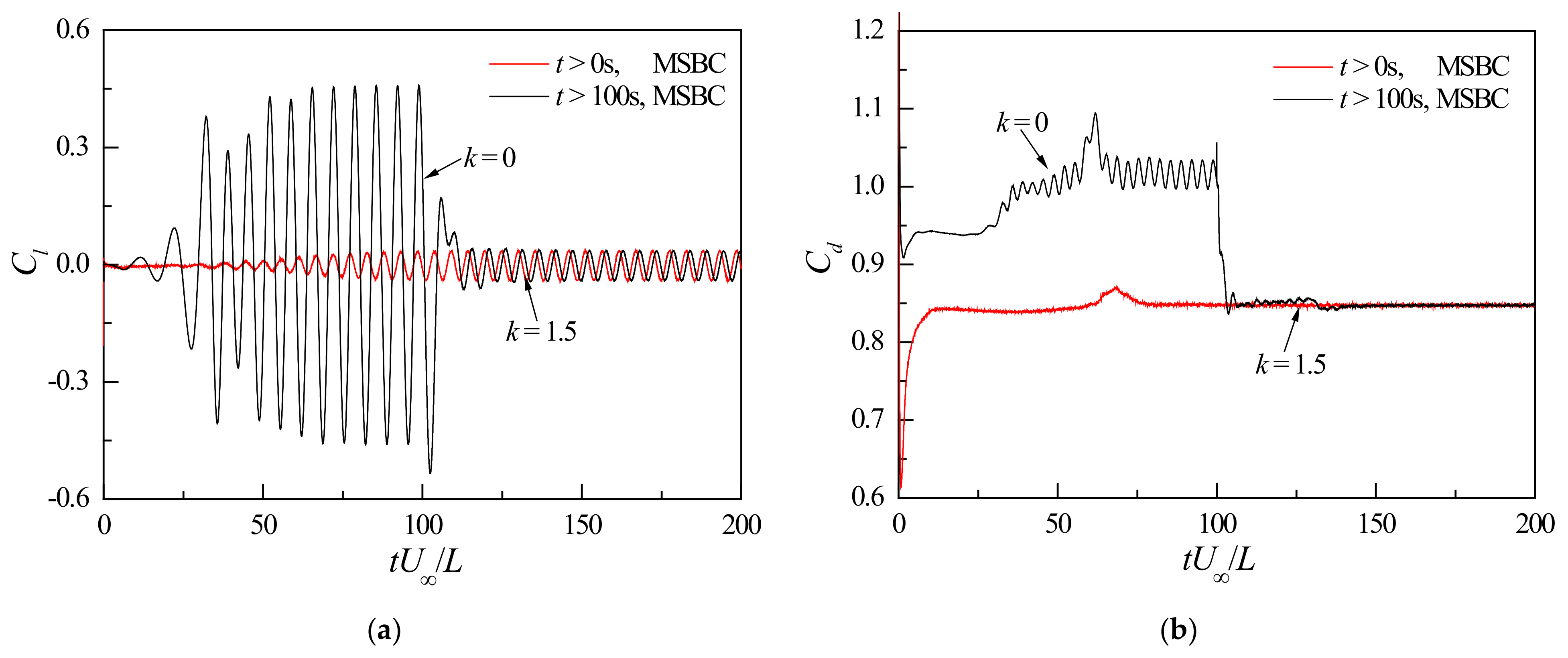
2.3. Validity Investigation
3. Results and Discussion
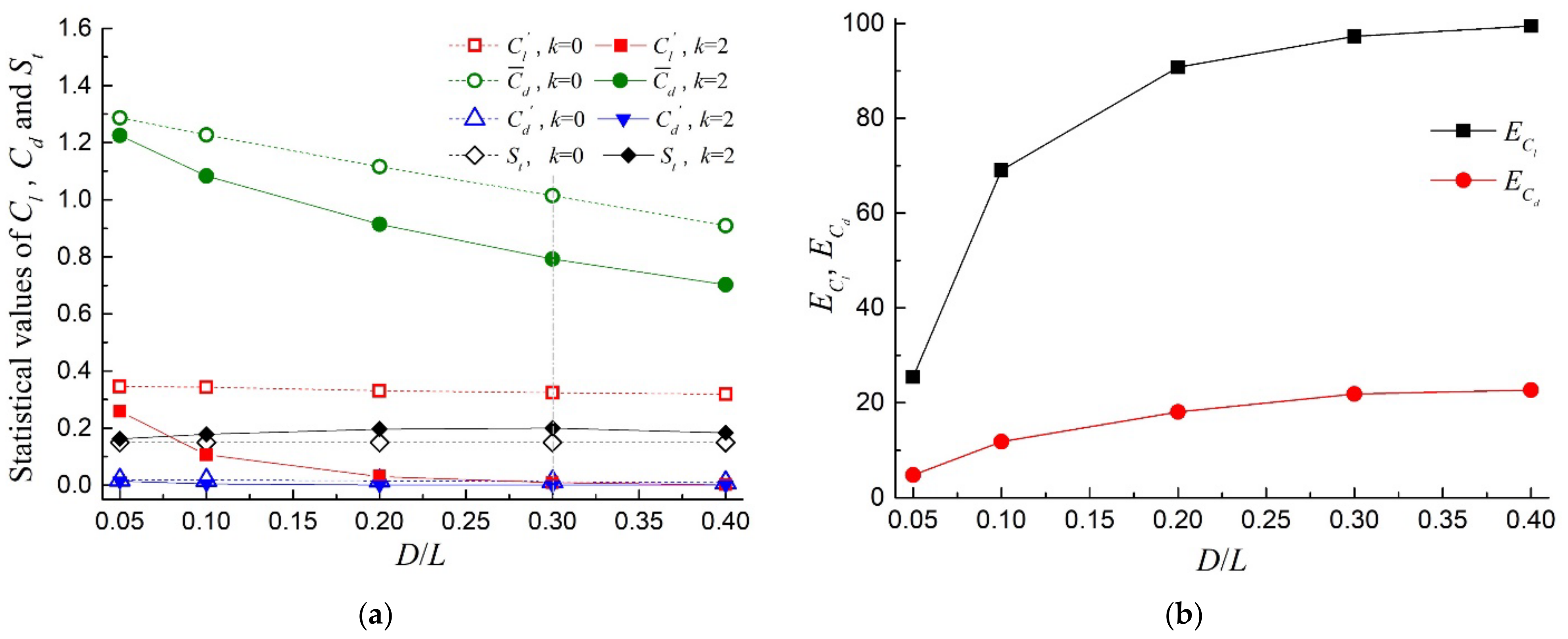
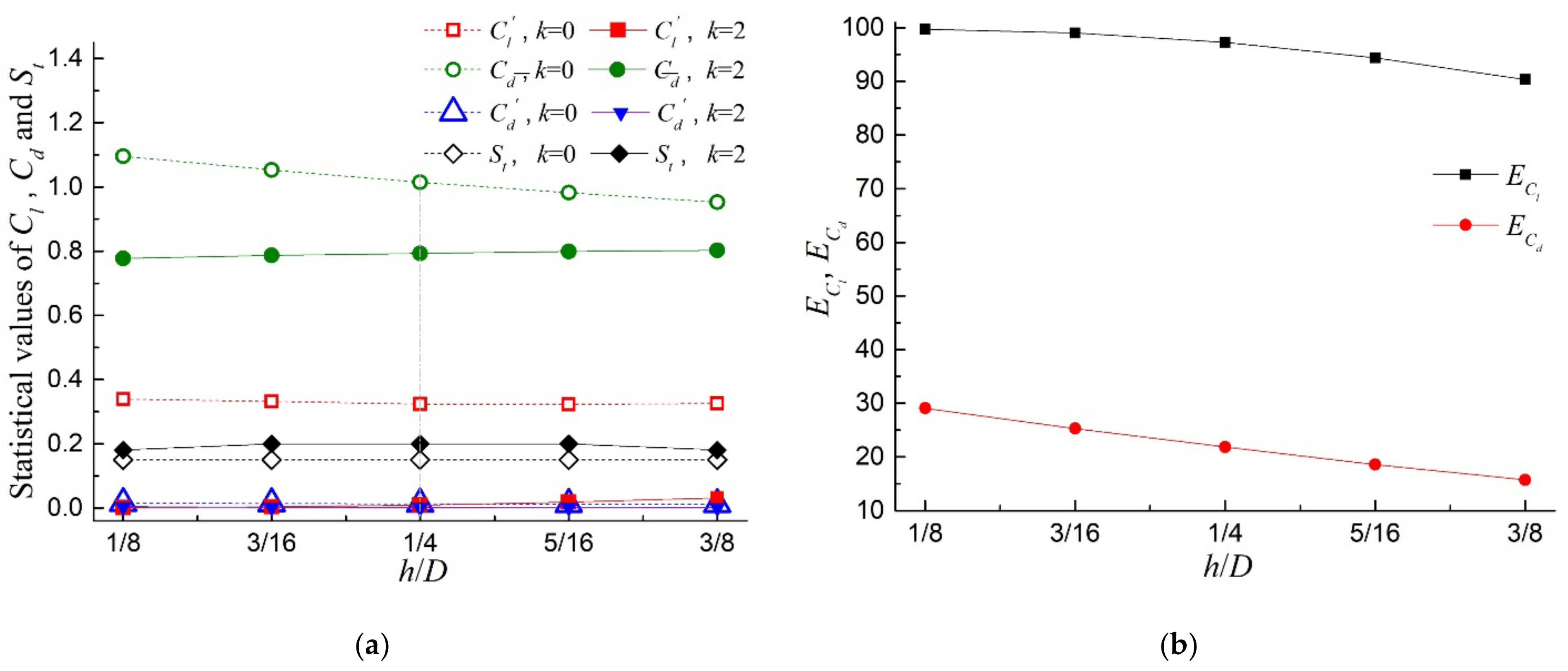
3.1. Analysis of Influence of and Parameters
3.2. Detailed Results and Analysis of and
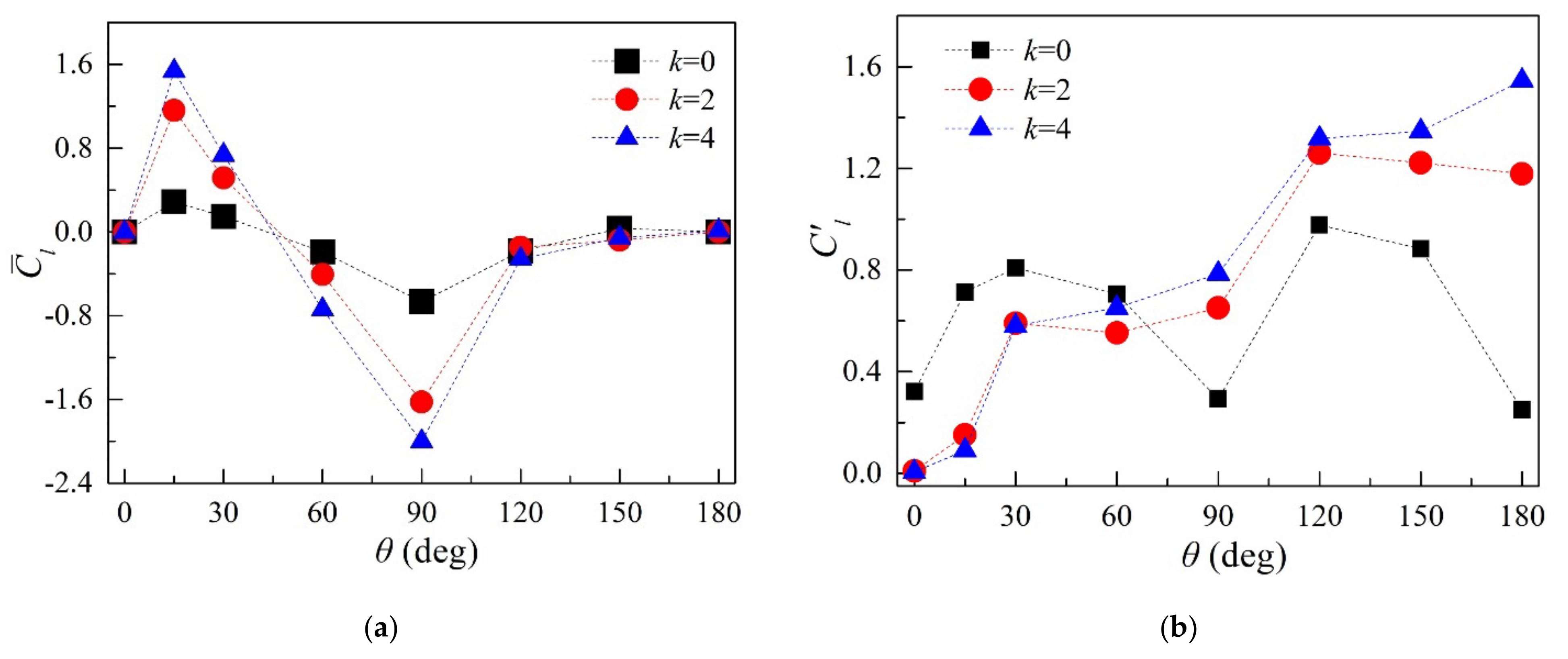
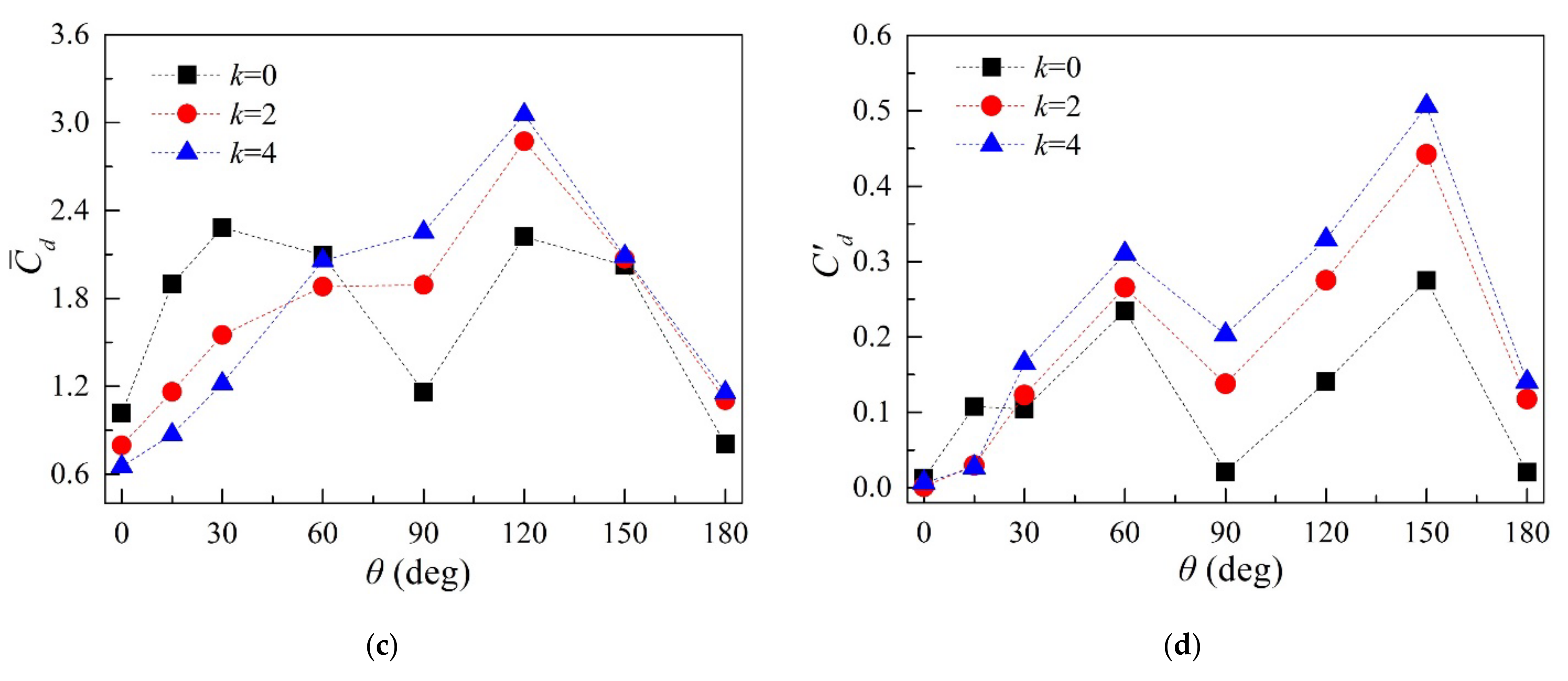
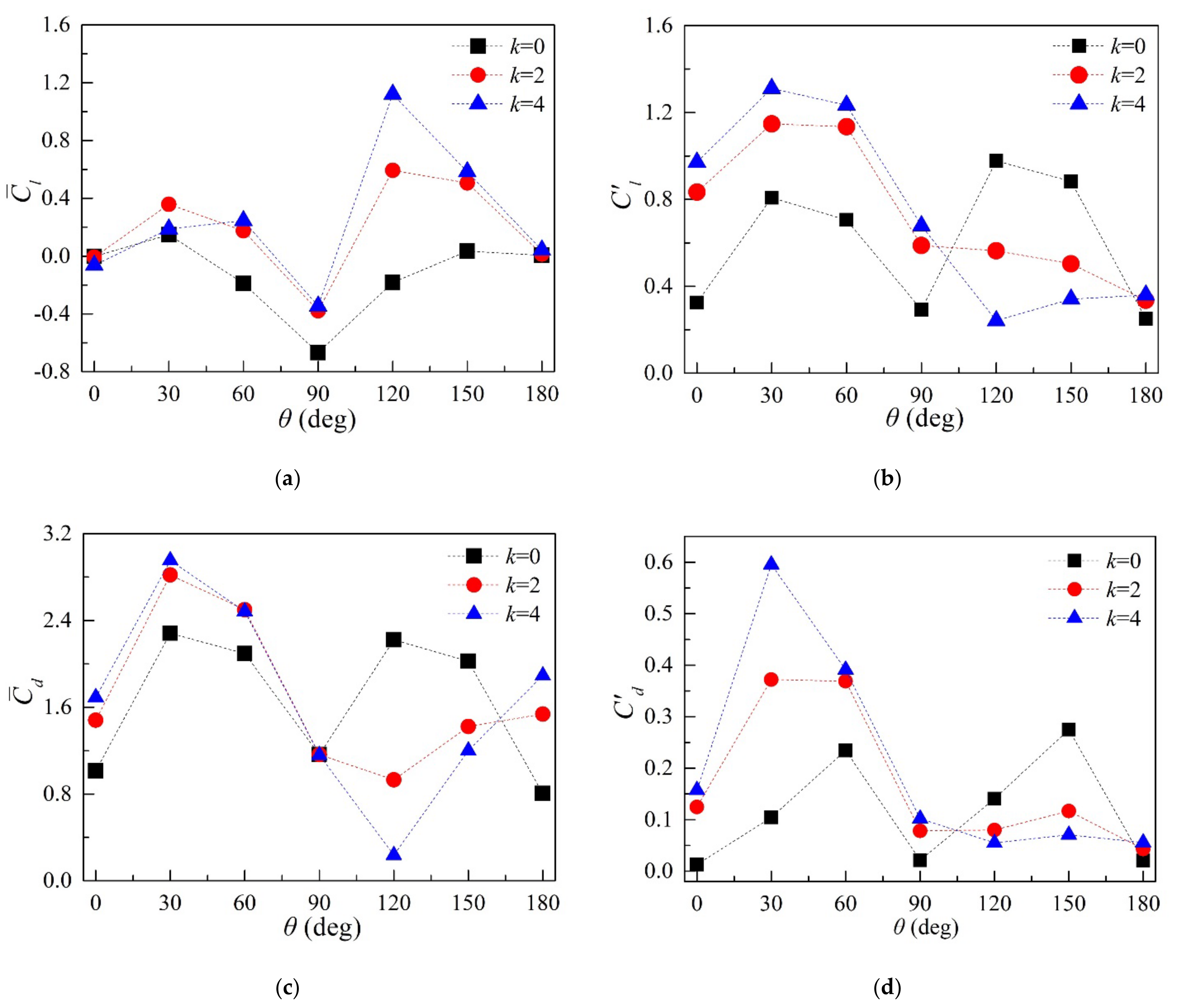
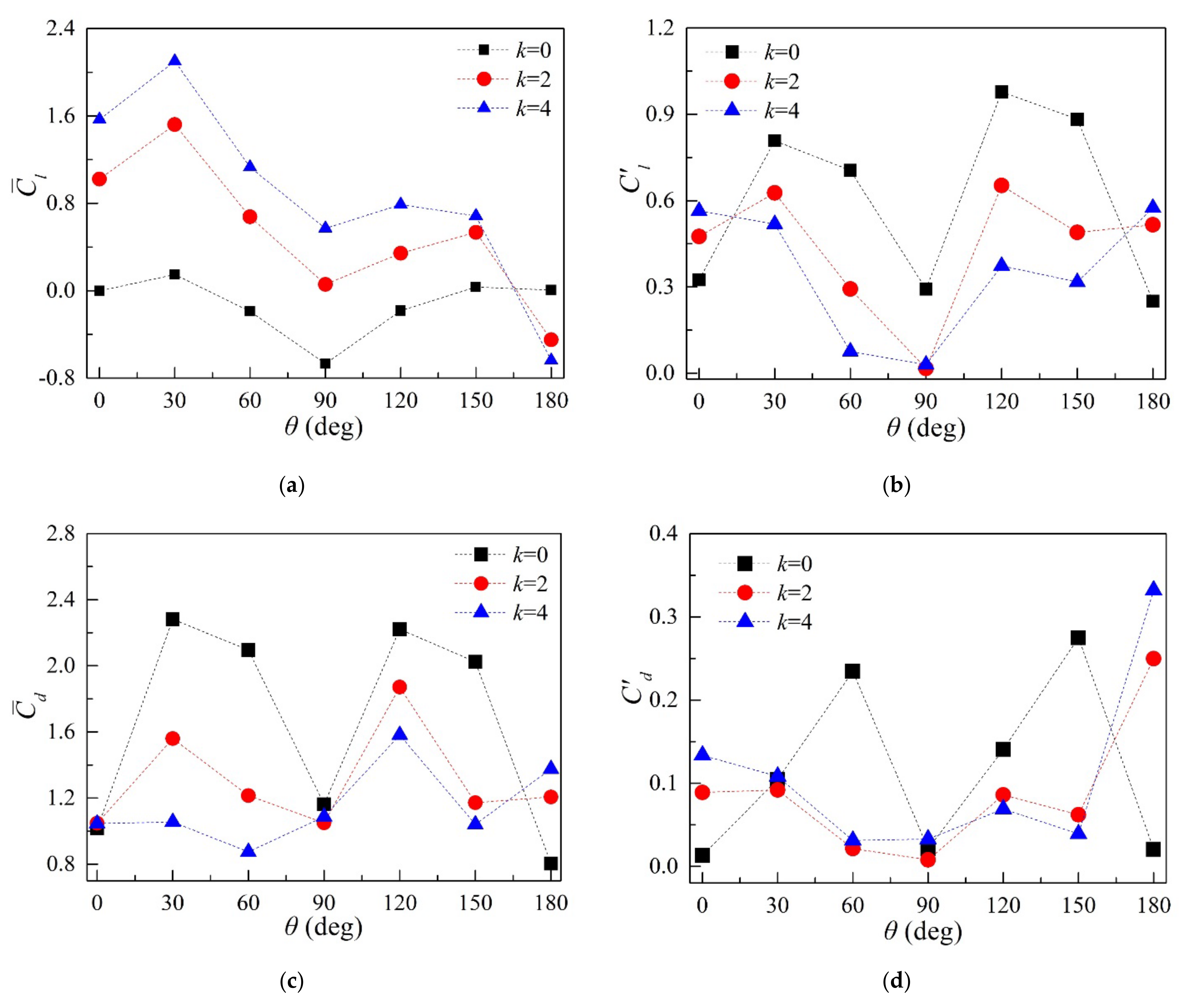
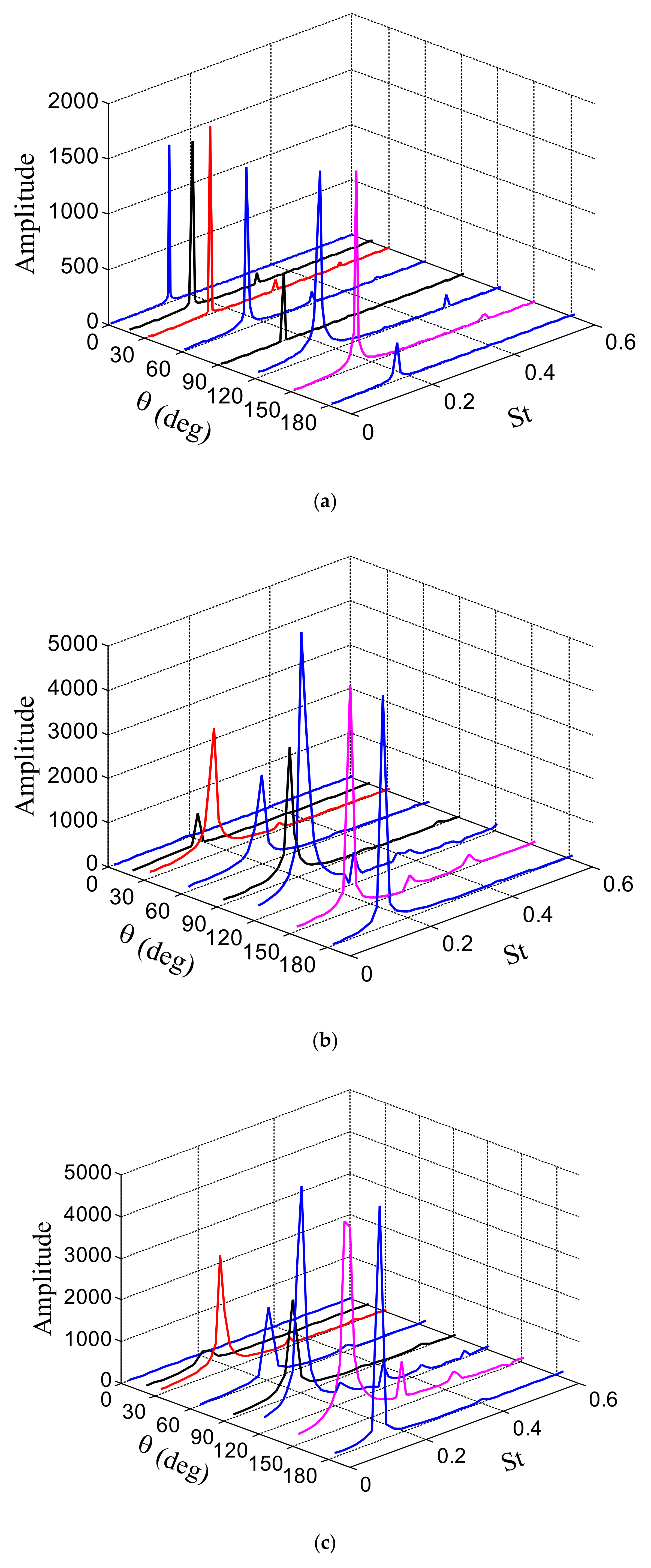
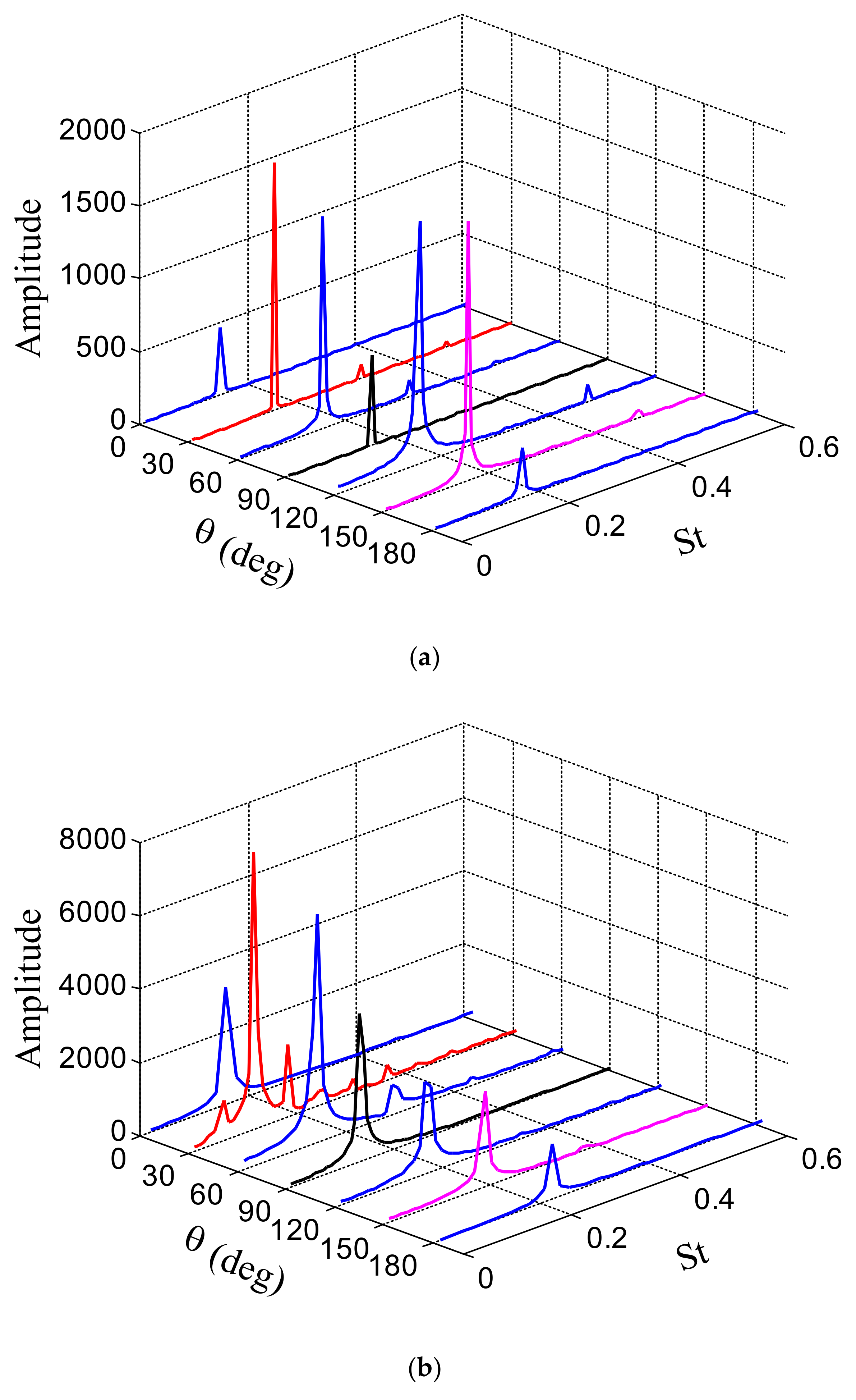
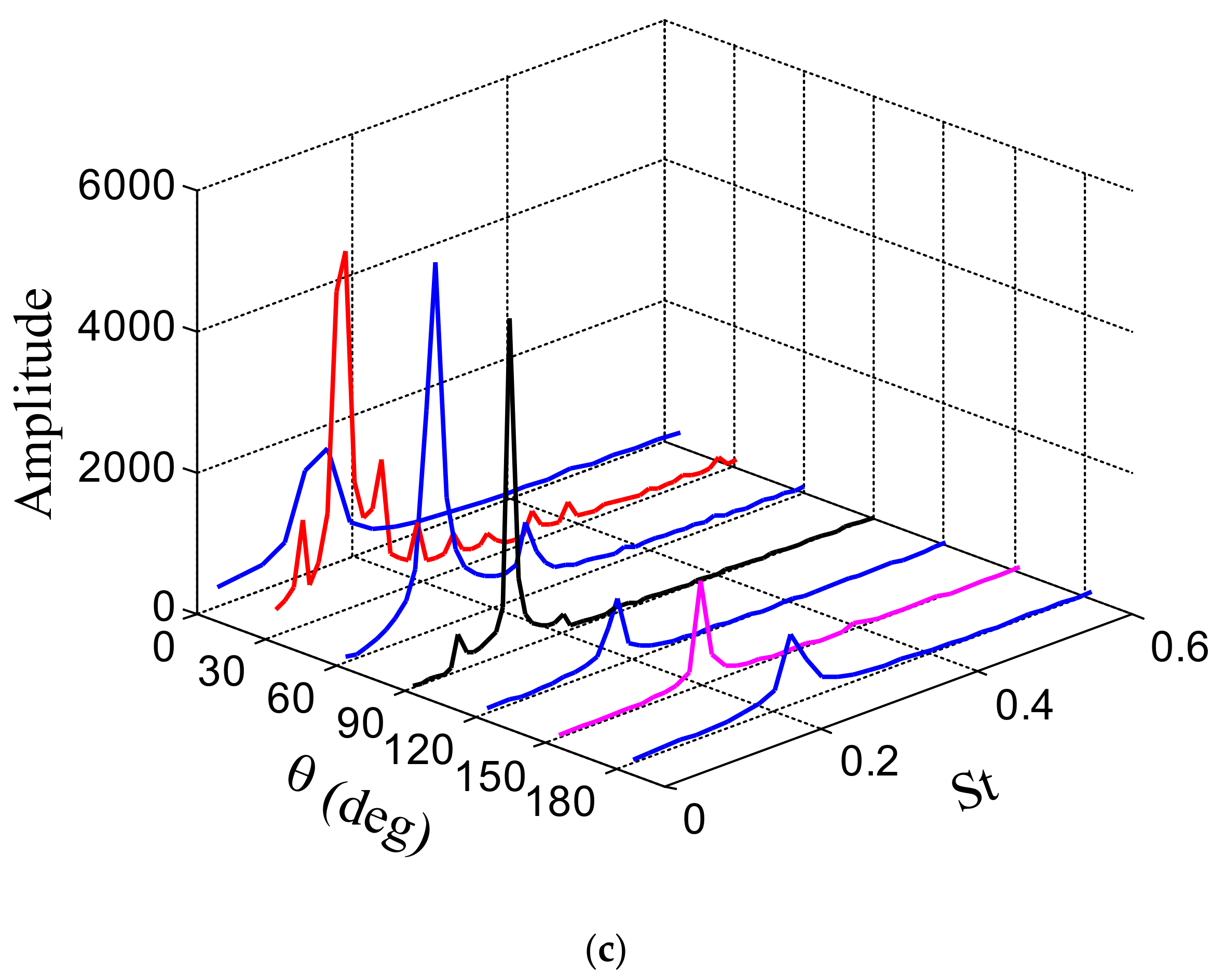
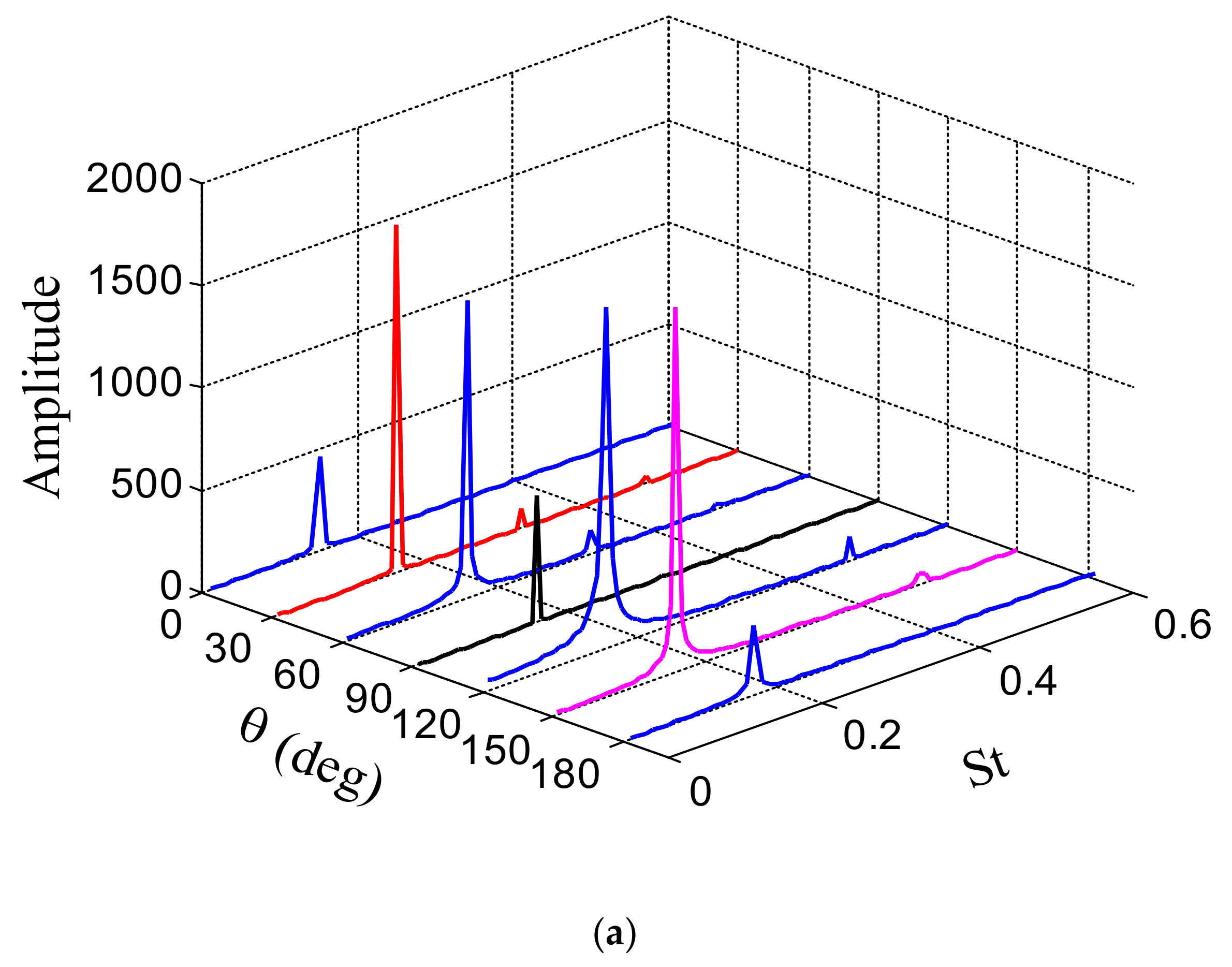
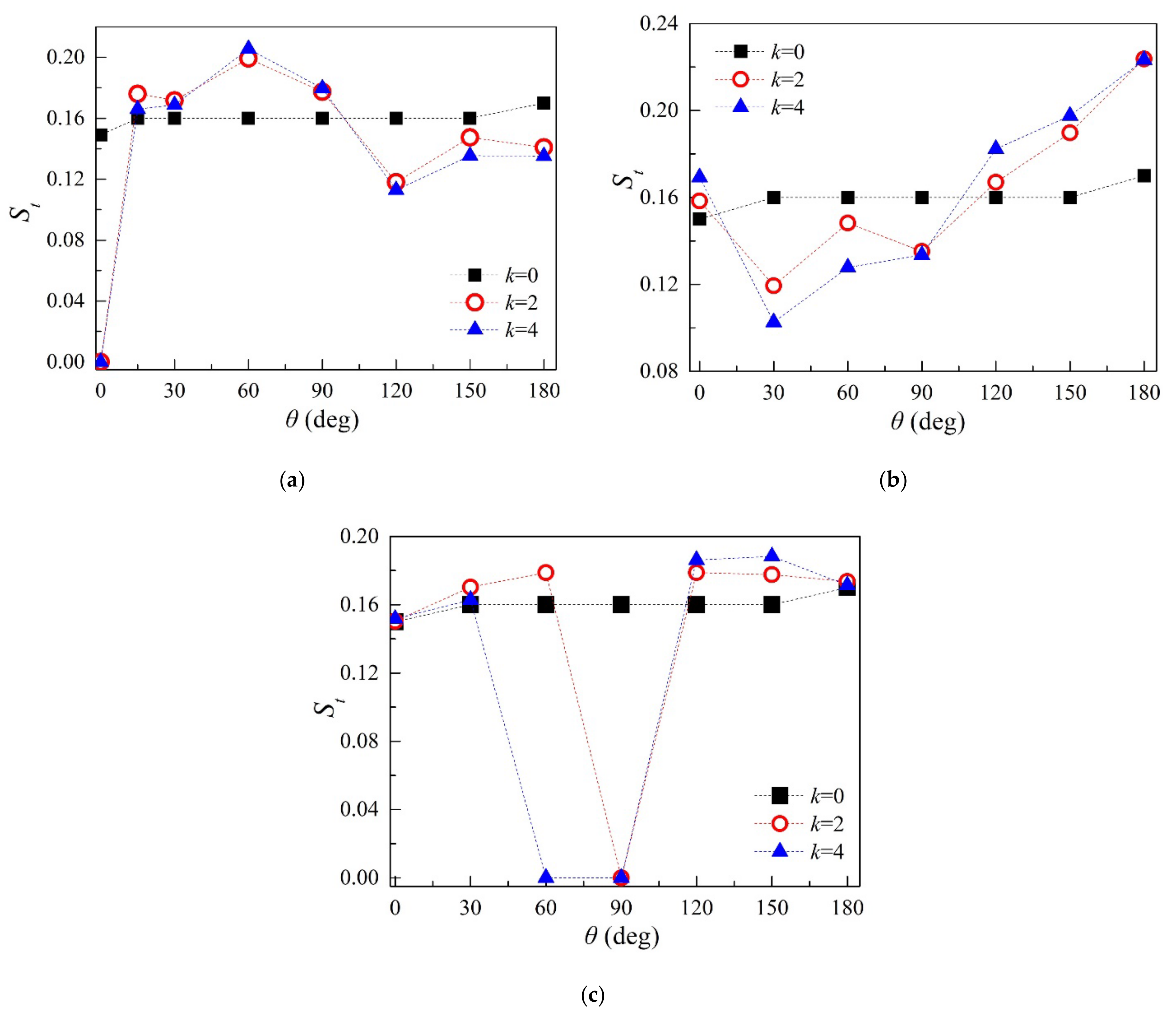
3.2.1. Aerodynamic Statistics and Frequency Characteristics
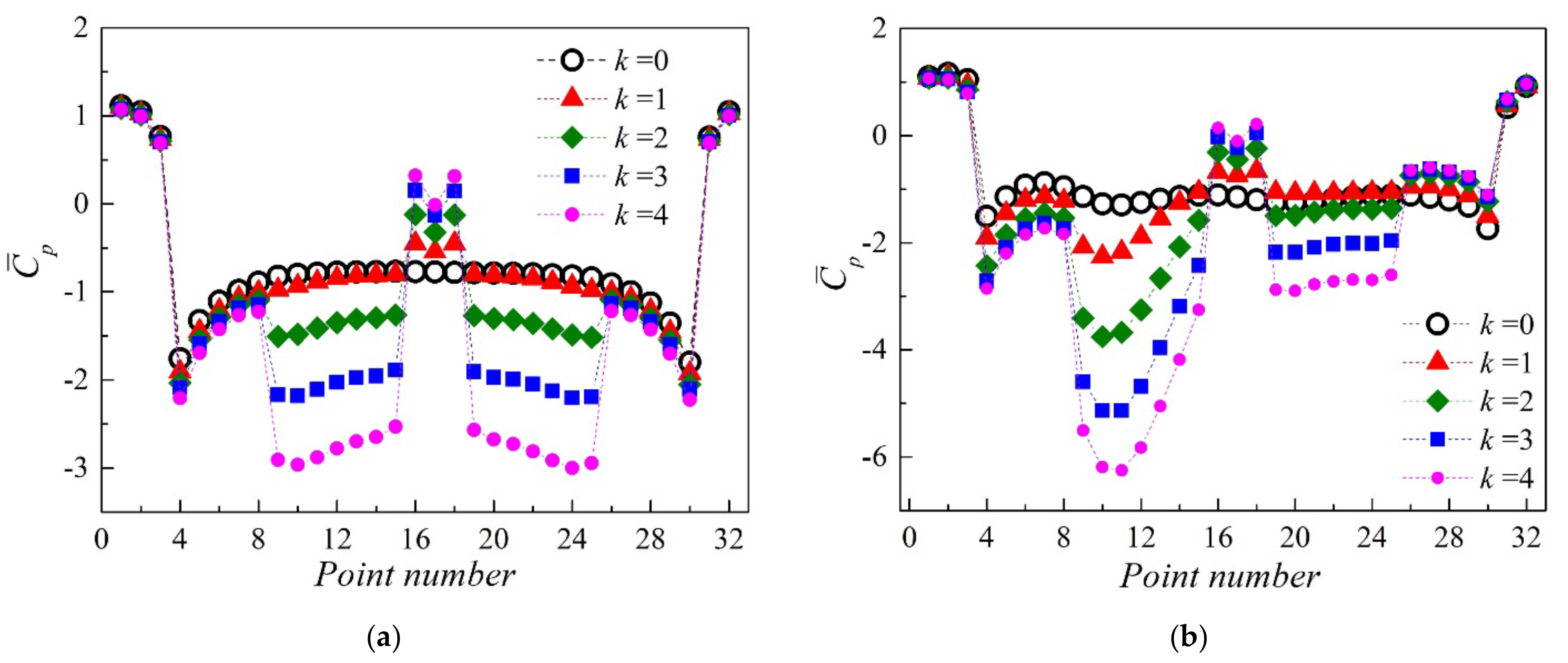
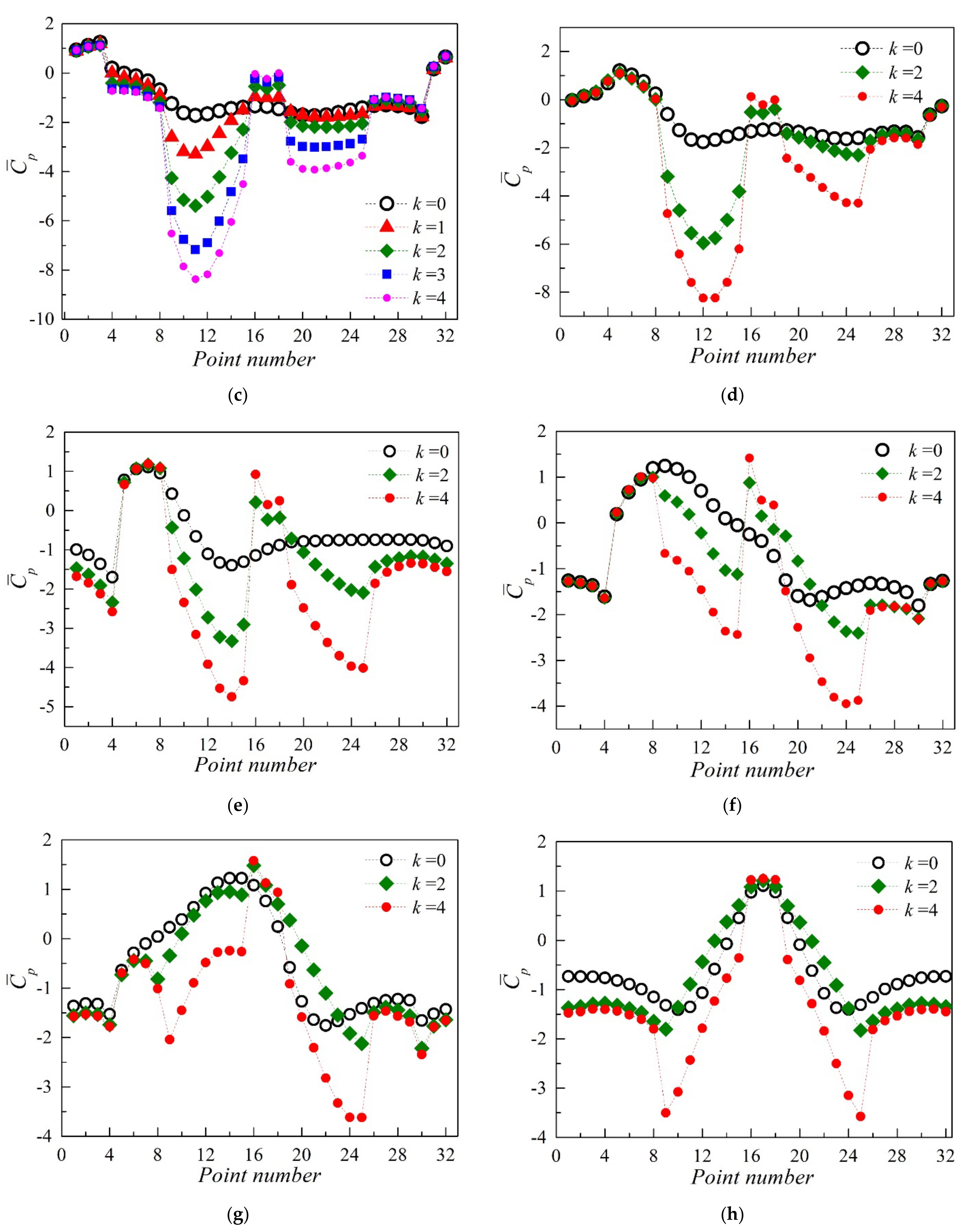
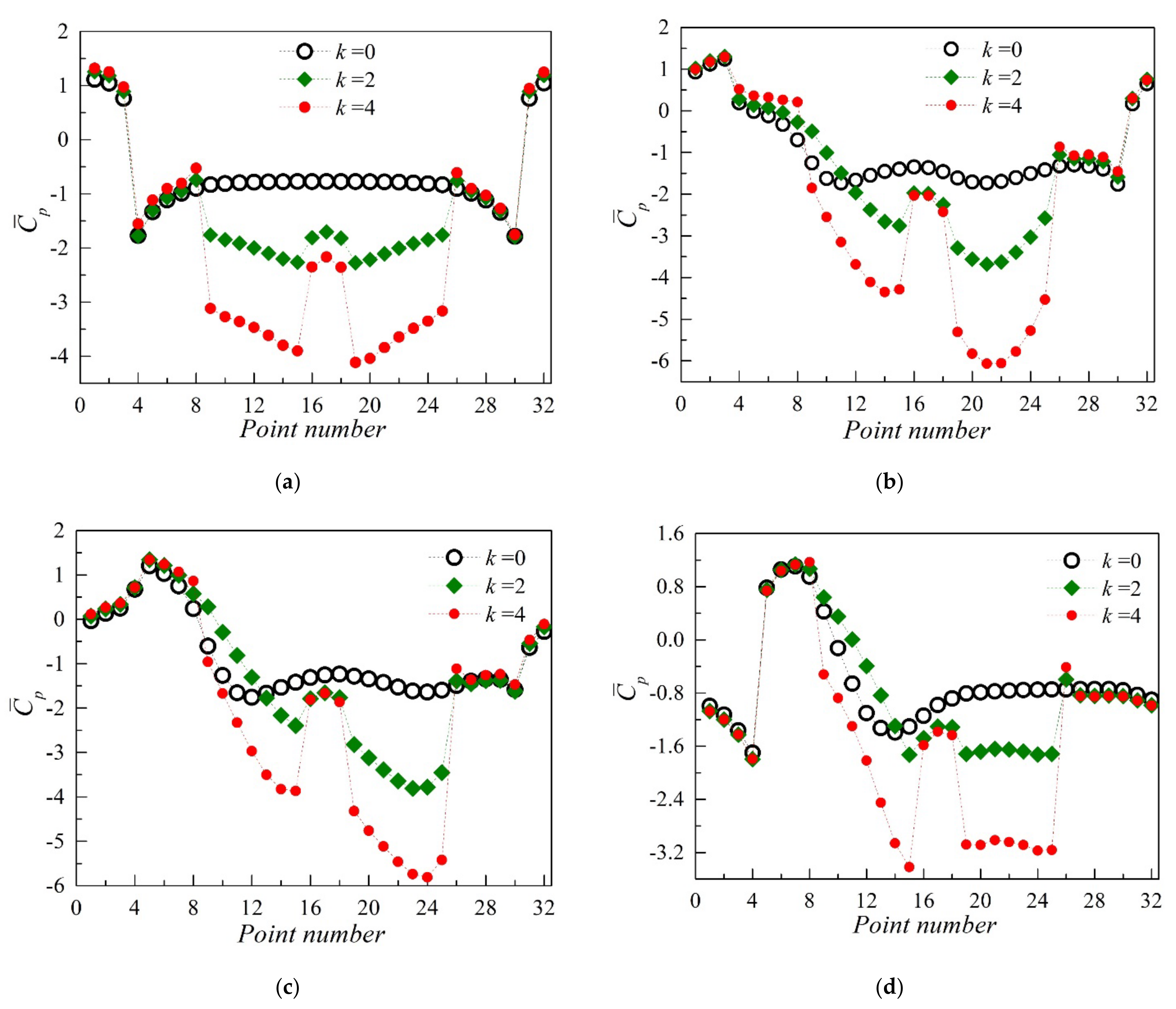
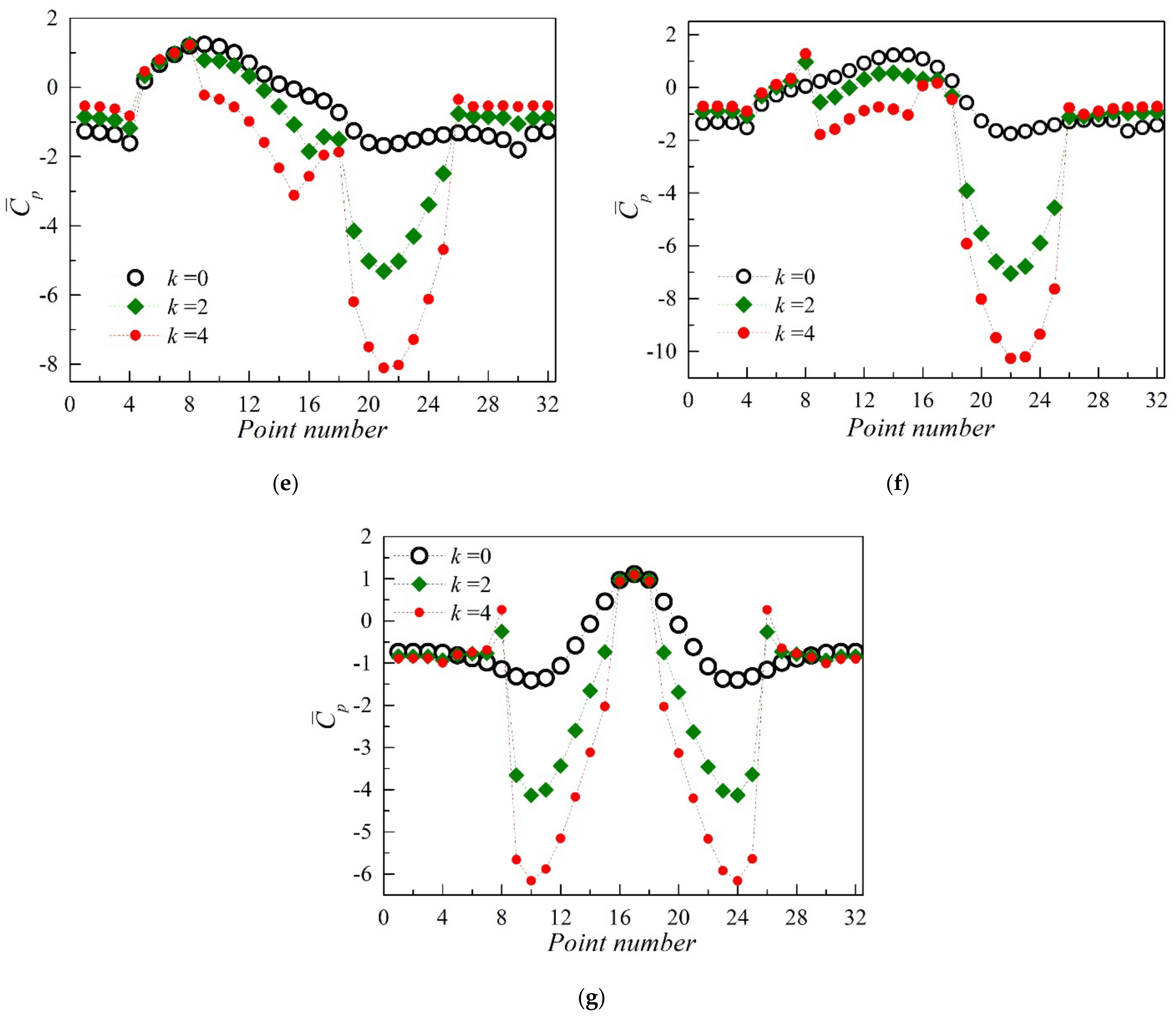
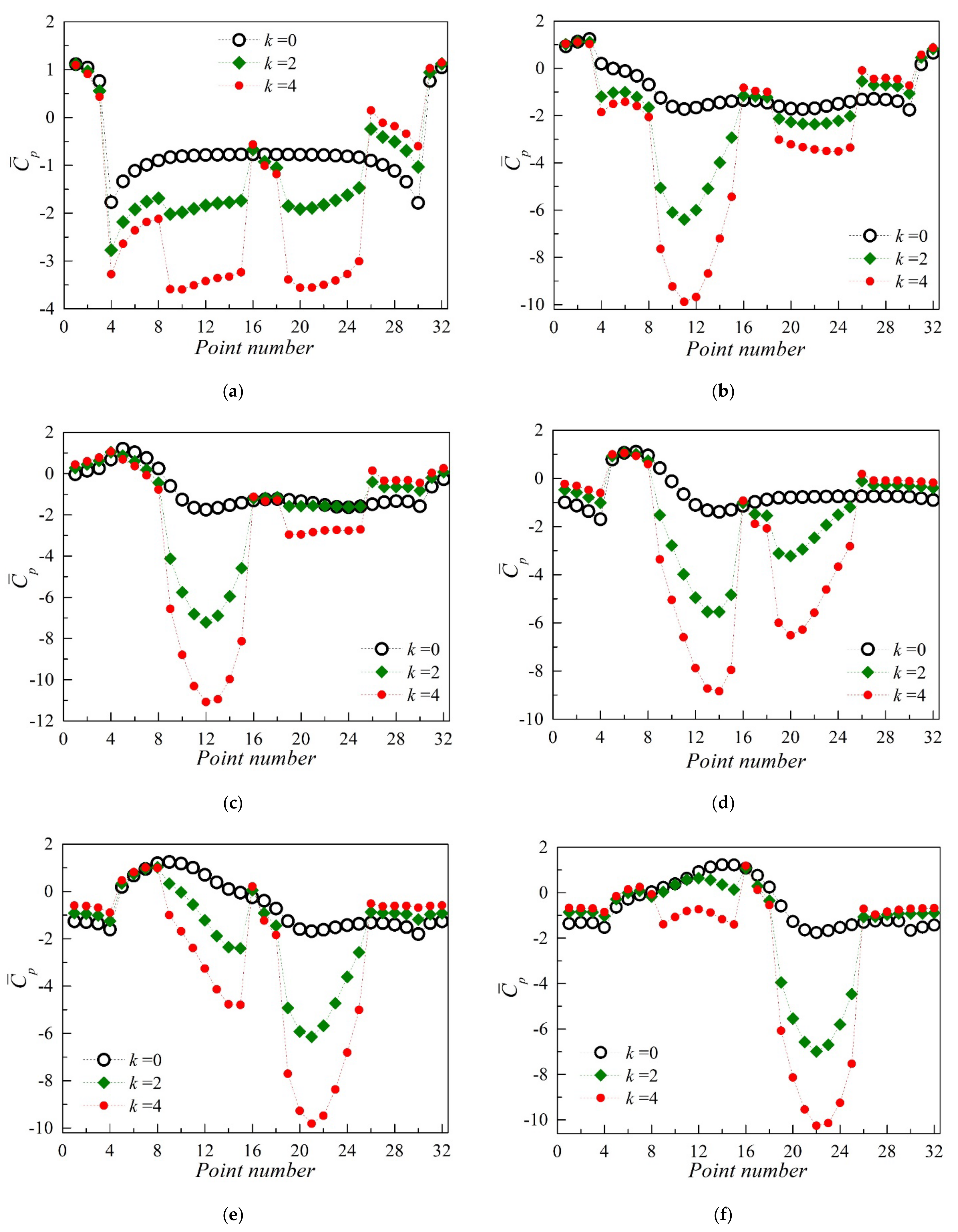
3.2.2. The Mean Pressure Distribution Characteristics
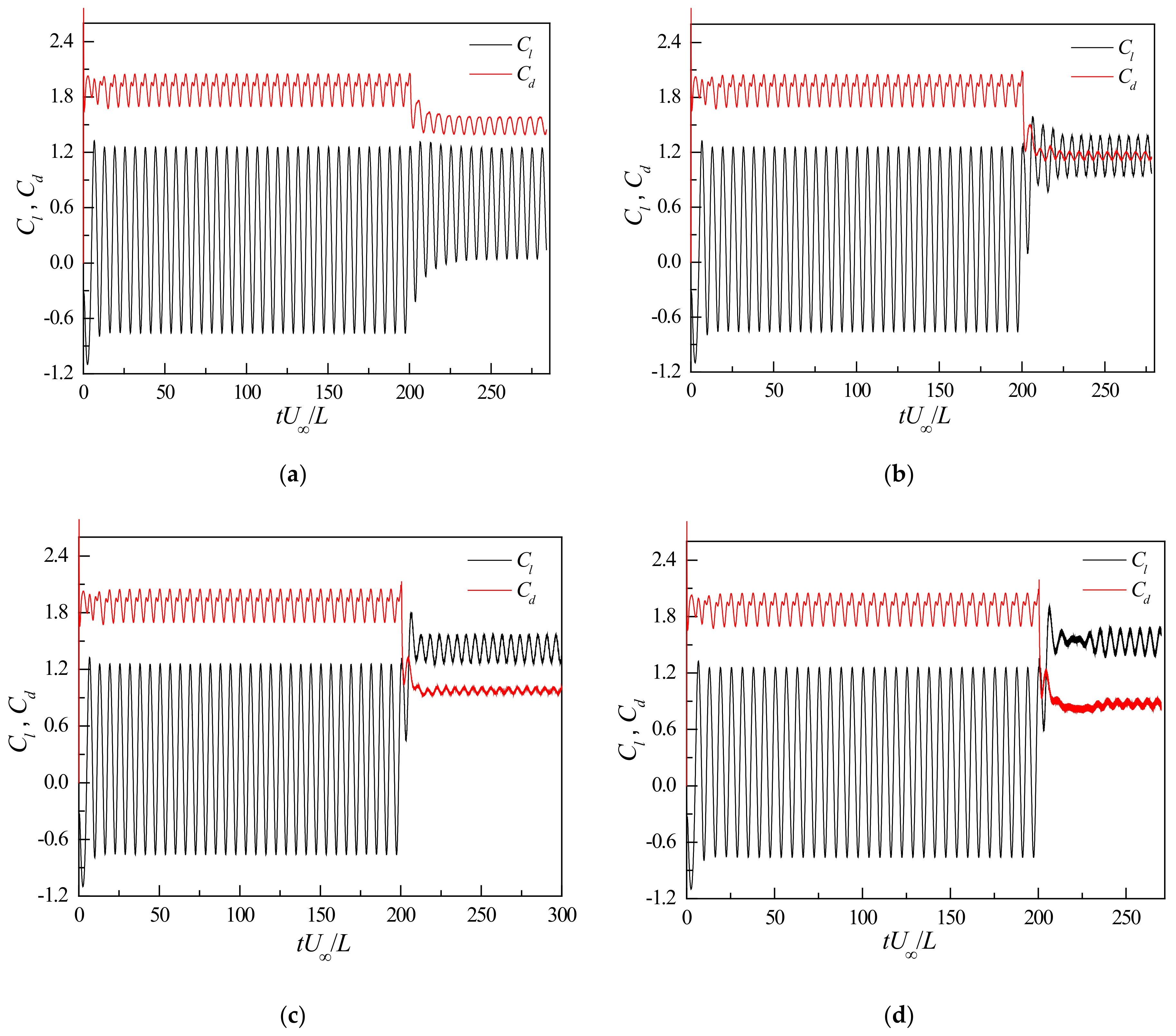
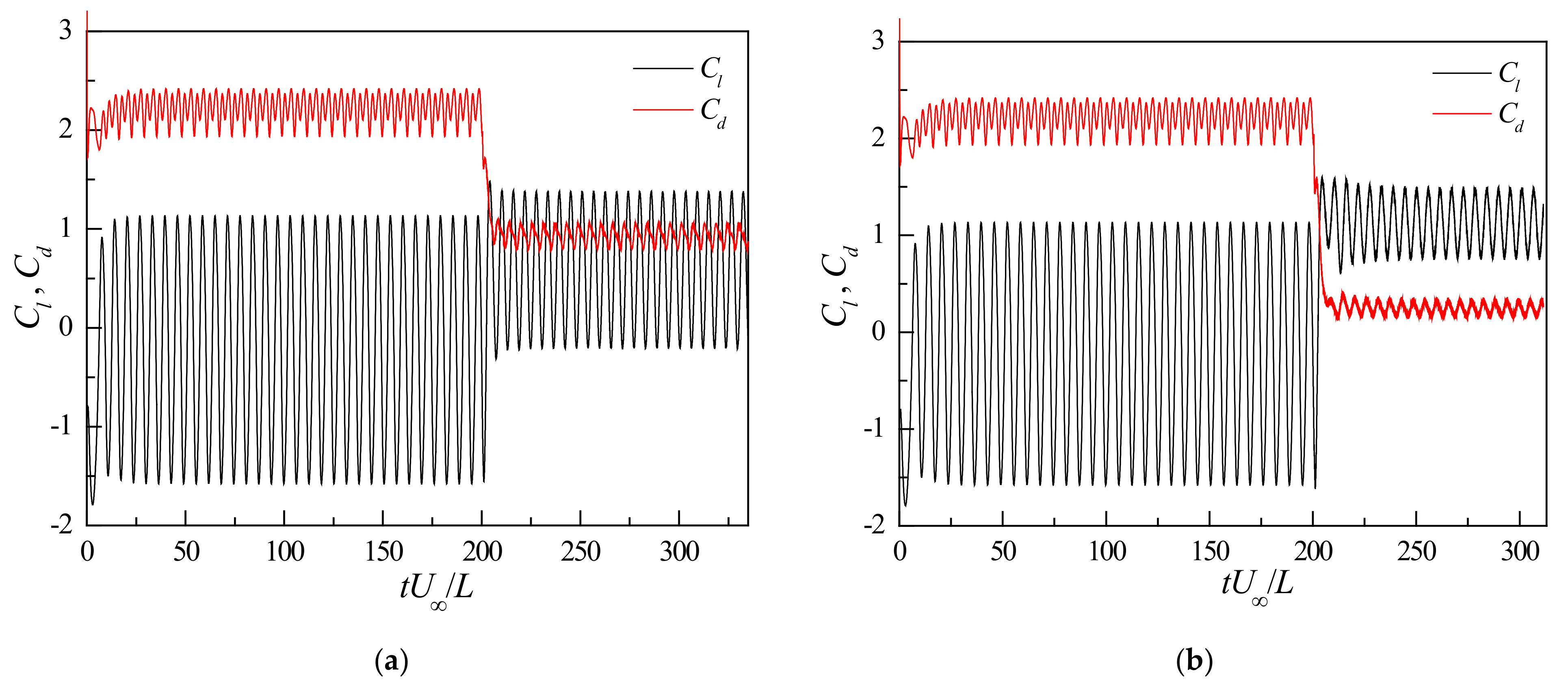
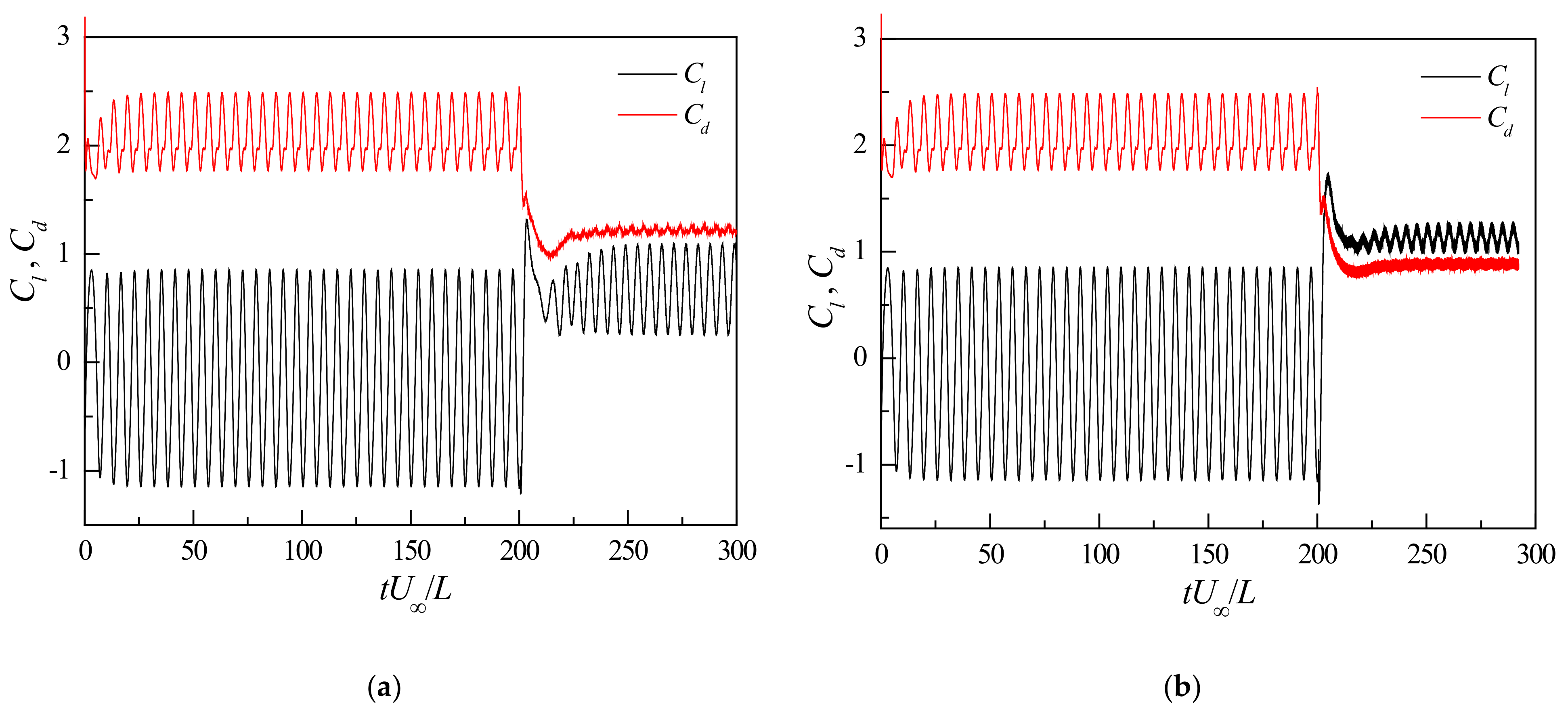
3.2.3. Aerodynamic Time History Analysis
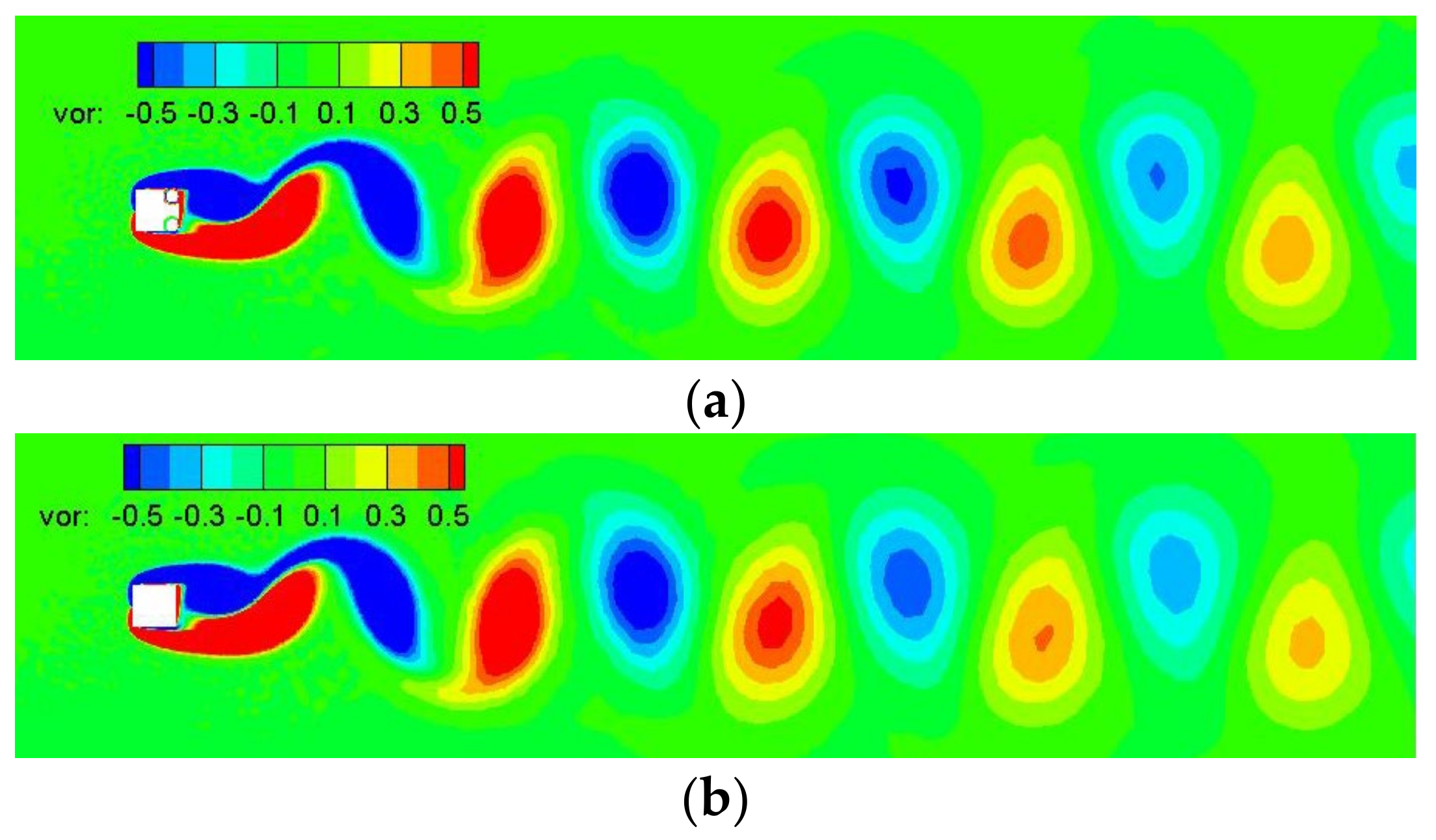
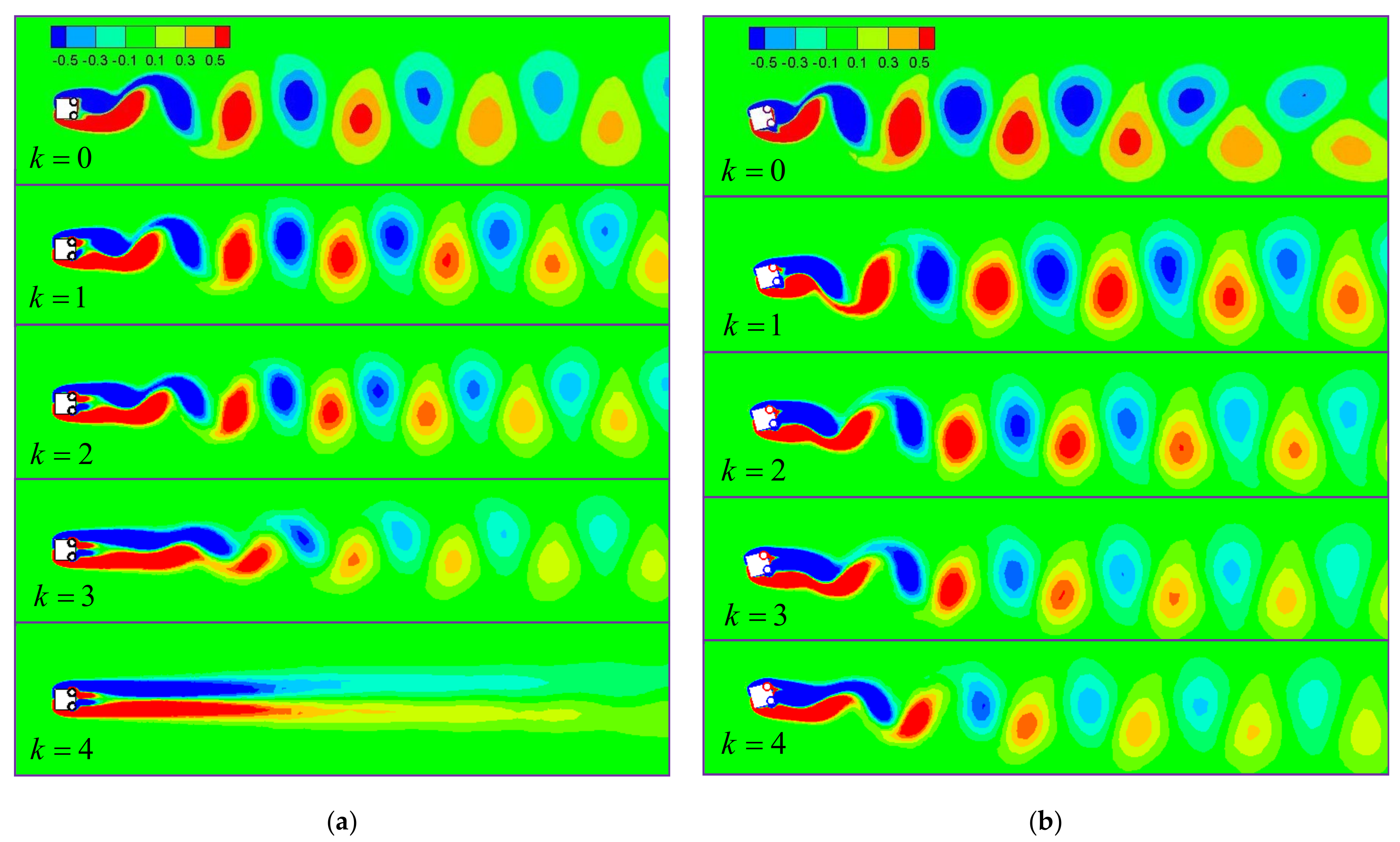
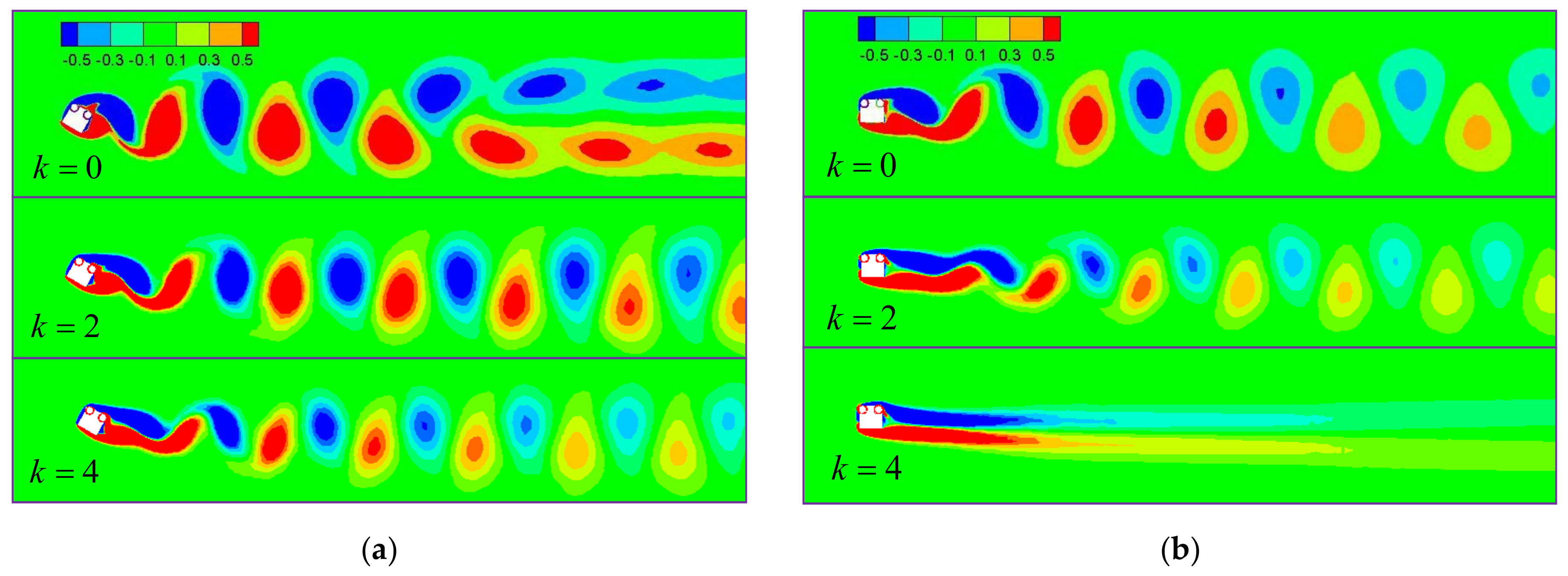
3.2.4. Wake Vortex Structure
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Choi, K.S. Near-wall structures of a turbulent boundary layer with riblets. J. Fluid Mech. 1989, 208, 417–458. [Google Scholar] [CrossRef]
- Bearman, P.W.; Owen, J.C. Reduction of bluff-body drag and suppression of vortex shedding by the introduction of wavy separation lines. J. Fluids Struct. 1998, 12, 123–130. [Google Scholar] [CrossRef]
- Bearman, P.W.; Brankovic, M. Experimental studies of passive control of vortex-induced vibration. Eur. J. Mech. B/Fluids 2004, 23, 9–15. [Google Scholar] [CrossRef]
- Lee, S.J.; Jang, Y.G. Control of flow around a NACA 0012 airfoil with a micro-riblet film. J. Fluids Struct. 2005, 20, 659–672. [Google Scholar] [CrossRef]
- Laima, S.; Li, H.; Chen, W.; Li, F. Investigation and control of vortex-induced vibration of twin box girders. J. Fluids Struct. 2013, 39, 205–221. [Google Scholar] [CrossRef]
- Chen, W.L.; Li, H.; Hu, H. An experimental study on the unsteady vortices and turbulent flow structures around twin-box-girder bridge deck models with different gap ratios. J. Wind Eng. Ind. Aerodyn. 2014, 132, 27–36. [Google Scholar] [CrossRef]
- Gao, D.L.; Deng, Z.; Yang, W.H.; Chen, W.L. Review of the excitation mechanism and aerodynamic flow control of vortex-induced vibration of the main girder for long-span bridges: A vortex-dynamics approach. J. Fluids Struct. 2021, 105, 103348. [Google Scholar] [CrossRef]
- Li, H.; Chen, W.L.; Xu, F.; Li, F.C.; Ou, J.P. A numerical and experimental hybrid approach for the investigation of aerodynamic forces on stay cables suffering from rain-wind induced vibration. J. Fluids Struct. 2010, 26, 1195–1215. [Google Scholar] [CrossRef]
- Chen, W.L.; Zhang, Q.Q.; Li, H.; Hu, H. An experimental investigation on vortex induced vibration of a flexible inclined cable under a shear flow. J. Fluids Struct. 2015, 54, 297–311. [Google Scholar] [CrossRef]
- Chen, W.L.; Xin, D.B.; Xu, F.; Li, H.; Ou, J.P.; Hu, H. Suppression of vortex-induced vibration of a circular cylinder using suction based flow control. J. Fluids Struct. 2013, 42, 25–39. [Google Scholar] [CrossRef]
- Gao, D.L.; Chen, G.B.; Chen, W.L.; Li, H. Active control of circular cylinder flow with windward suction and leeward blowing. Exp. Fluids 2019, 60, 26. [Google Scholar] [CrossRef]
- Gao, D.L.; Meng, H.; Huang, Y.W.; Chen, G.B.; Chen, W.L. Active flow control of the dynamic wake behind a square cylinder using combined jets at the front and rear stagnation points. Phys. Fluids 2021, 33, 047101. [Google Scholar] [CrossRef]
- Wu, C.J.; Wang, L.; Wu, J.Z. Suppression of the von Karman vortex street behind a circular cylinder by a travelling wave generated by a flexible surface. J. Fluid Mech. 2007, 574, 365–391. [Google Scholar] [CrossRef]
- Xu, F.; Chen, W.L.; Xiao, Y.Q.; Li, H.; Ou, J.P. Numerical study on the suppression of the vortex-induced vibration of an elastically mounted cylinder by a traveling wave wall. J. Fluids Struct. 2014, 44, 145–165. [Google Scholar] [CrossRef]
- Xu, F.; Chen, W.L.; Bai, W.F.; Xiao, Y.Q.; Ou, J.P. Flow control of the wake vortex street of a circular cylinder by using a traveling wave wall at low Reynolds number. Comput. Fluids 2017, 145, 52–67. [Google Scholar] [CrossRef]
- Kubo, C.H.; Chiou, L.C.; Chen, C.C. Wake flow pattern modified by small control cylinders at low Reynolds number. J. Fluids Struct. 2007, 23, 938–956. [Google Scholar]
- Hwang, J.Y.; Yang, K.S. Drag reduction on a circular cylinder using dual detached splitter plates. J. Wind Eng. Ind. Aerodyn. 2007, 95, 551–564. [Google Scholar] [CrossRef]
- Assi, G.R.S.; Bearman, P.W.; Kitney, N. Low drag solutions for suppressing vortex-induced vibration of circular cylinders. J. Fluids Struct. 2009, 25, 666–675. [Google Scholar] [CrossRef]
- Koca, K.; Genç, M.S.; Açıkel, H.H.; Çagdas, M.; Bodur, T.M. Identification of flow phenomena over NACA 4412 wind turbine airfoil at low Reynolds numbers and role of laminar separation bubble on flow evolution. Energy 2018, 144, 750–764. [Google Scholar] [CrossRef]
- Koca, K.; Genç, M.S.; Ozkan, R. Mapping of laminar separation bubble and bubble-induced vibrations over a turbine blade at low Reynolds numbers. Ocean Eng. 2021, 239, 109867. [Google Scholar] [CrossRef]
- Genç, M.S.; Koca, K.; Açikel, H.H. Investigation of pre-stall flow control on wind turbine blade airfoil using roughness element. Energy 2019, 176, 320–334. [Google Scholar] [CrossRef]
- Genç, M.S.; Açikel, H.H.; Koca, K. Effect of partial flexibility over both upper and lower surfaces to flow over wind turbine airfoil. Energy Convers. Manag. 2020, 219, 113042. [Google Scholar] [CrossRef]
- Koca, K.; Genç, M.S.; Bayır, E.; Soguksu, F.K. Experimental study of the wind turbine airfoil with the local flexibility at different locations for more energy output. Energy 2022, 239, 121887. [Google Scholar] [CrossRef]
- Bayramoğlu, N.; Genç, M.S.; Koca, K.; Altunal, A. Electricity production from piezoelectric patches mounted over flexible membrane wing at low Reynolds numbers. Sigma J. Eng. Nat. Sci. 2021, 39, 70–79. [Google Scholar]
- Malekzadeh, S.; Sohankar, A. Reduction of fluid forces and heat transfer on a square cylinder in a laminar flow regime using a control plate. Int. J. Heat Fluid Flow 2012, 34, 15–27. [Google Scholar] [CrossRef]
- Turhal, A.Ö.; Çuhadaroğlu, B. The effects of surface injection through a perforated square cylinder on some aerodynamic parameters. Exp. Therm. Fluid Sci. 2010, 34, 725–735. [Google Scholar] [CrossRef]
- Sohankar, A.; Khodadadi, M.; Rangraz, E. Control of fluid flow and heat transfer around a square cylinder by uniform suction and blowing at low Reynolds numbers. Comput. Fluids 2015, 109, 155–167. [Google Scholar] [CrossRef]
- Chen, W.L.; Gao, D.L.; Li, H.; Hu, H. Passive jet control of flow around a circular cylinder. Exp. Fluids 2015, 56, 201. [Google Scholar] [CrossRef]
- Gao, D.L.; Chen, W.L.; Li, H.; Hu, H. Flow around a circular cylinder with slit. Exp. Therm. Fluid Sci. 2017, 82, 287–301. [Google Scholar] [CrossRef]
- Munshi, S.R.; Modi, V.J.; Yokomizo, T. Aerodynamics and dynamics of rectangular prisms with momentum injection. J. Wind Eng. Ind. Aerodyn. 1997, 11, 873–892. [Google Scholar] [CrossRef]
- Munshi, S.R.; Modi, V.J.; Yokomizo, T. Fluid dynamics of flat plates and rectangular prisms in the presence of moving surface boundary-layer control. J. Wind Eng. Ind. Aerodyn. 1999, 79, 37–60. [Google Scholar] [CrossRef]
- Kubo, Y.; Modi, V.J.; Kotsubo, C.; Hayashida, K.; Kato, K. Suppression of wind-induced vibrations of tall structures through moving surface boundary-layer control. J. Wind Eng. Ind. Aerodyn. 1996, 61, 181–194. [Google Scholar] [CrossRef]
- Kubo, Y.; Yukoku, E.; Modi, V.J.; Yamaguchi, E.; Kato, K.; Kawamura, S.I. Control of flow separation from leading edge of a shallow rectangular cylinder through momentum injection. J. Wind Eng. Ind. Aerodyn. 1999, 83, 503–514. [Google Scholar] [CrossRef]
- Modi, V.J.; Deshpande, V.S. Fluid dynamics of a cubic structure as affected by momentum injection and height. J. Wind Eng. Ind. Aerodyn. 2000, 89, 445–470. [Google Scholar] [CrossRef]
- Patnaik, B.S.V.; Wei, G.W. Controlling wake turbulence. Phys. Rev. Lett. 2002, 88, 054502. [Google Scholar] [CrossRef] [Green Version]
- Muddada, S.; Patnaik, B.S.V. An assessment of turbulence models for the prediction of flow past a circular cylinder with momentum injection. J. Wind Eng. Ind. Aerodyn. 2010, 98, 575–591. [Google Scholar] [CrossRef]
- Mittal, S. Control of flow past bluff bodies using rotating control cylinders. J. Fluids Struct. 2001, 15, 291–326. [Google Scholar] [CrossRef]
- Korkischko, I.; Meneghini, J.R. Suppression of vortex-induced vibration using moving surface boundary-layer control. J. Fluids Struct. 2012, 34, 259–270. [Google Scholar] [CrossRef]
- Sohankar, A.; Norberg, C.; Davidson, L. Low-Reynolds number flow around a square cylinder at incidence: Study of blockage, onset of vortex shedding and outlet boundary condition. Int. J. Numer. Methods Fluids 1998, 26, 39–56. [Google Scholar] [CrossRef]
- Cheng, M.; Whyte, D.S.; Lou, J. Numerical simulation of flow around a square cylinder in uniform-shear flow. J. Fluids Struct. 2007, 23, 207–226. [Google Scholar] [CrossRef]
- Okajima, A. Strouhal number of rectangular cylinders. J. Fluids Struct. 1982, 123, 379–398. [Google Scholar] [CrossRef] [Green Version]
- Jan, Y.J.; Sheu, W.H. A numerical configuration of the dual body vortex flowmeter design. Comput. Fluids 2004, 33, 1157–1174. [Google Scholar] [CrossRef]
- Abograis, A.S.; Alshayji, A.E. Reduction of fluid forces on a square cylinder in a laminar flow using passive control methods. In Proceedings of the COMSOL Conference, Boston, MA, USA, 9–11 November 2013. [Google Scholar]








| Mesh Density | |||||||
|---|---|---|---|---|---|---|---|
| Scheme 1, coarsest | 40 | 30,344 | 15,387 | 1.523 | 0.024 | 0.446 | 0.146 |
| Scheme 2, coarse | 55 | 36,208 | 18,349 | 1.489 | 0.022 | 0.404 | 0.148 |
| Scheme 3, normal | 70 | 42,092 | 21,323 | 1.465 | 0.020 | 0.373 | 0.148 |
| Scheme 4, dense | 85 | 48,590 | 24,602 | 1.456 | 0.019 | 0.358 | 0.149 |
| Investigation | ||||
|---|---|---|---|---|
| Okajima [41], Experimental | 1.45 | - | - | 0.14~0.148 |
| Sohankar et al. [39], Numerical, 2D | 1.462 | - | 0.377 | 0.15 |
| Cheng et al. [40], Numerical, 2D | 1.45 | - | 0.372 | 0.15 |
| Jan and Sheu [42], Numerical, 2D | - | - | - | 0.148 |
| Abograis and Alshayji [43], Numerical, 2D | 1.488 | 0.027 | 0.332 | 0.153 |
| Present, Numerical, 2D () | 1.465 | 0.020 | 0.373 | 0.148 |
| 0.05 | 0.3466 | 1.2873 | 0.0186 | 0.15 | 0.2584 | 1.2255 | 0.0141 | 0.1625 | 25.45 | 4.80 |
| 0.1 | 0.3433 | 1.2274 | 0.0180 | 0.15 | 0.1063 | 1.0828 | 0.0051 | 0.1786 | 69.04 | 11.78 |
| 0.2 | 0.3309 | 1.1159 | 0.0155 | 0.15 | 0.0306 | 0.9144 | 0.0012 | 0.1961 | 90.75 | 18.06 |
| 0.3 | 0.3238 | 1.0145 | 0.0128 | 0.15 | 0.0089 | 0.7927 | 0.0008 | 0.2000 | 97.25 | 21.86 |
| 0.4 | 0.3189 | 0.9091 | 0.0093 | 0.15 | 0.0018 | 0.7027 | 0.0011 | 0.1832 | 99.44 | 22.70 |
| 0.3388 | 1.0956 | 0.0150 | 0.15 | 0.0009 | 0.7770 | 0.0039 | 0.18 | 99.73 | 29.08 | |
| 0.3318 | 1.0534 | 0.0140 | 0.15 | 0.0032 | 0.7870 | 0.0020 | 0.20 | 99.04 | 25.29 | |
| 0.3238 | 1.0145 | 0.0128 | 0.15 | 0.0089 | 0.7927 | 0.0008 | 0.20 | 97.25 | 21.86 | |
| 0.3226 | 0.9821 | 0.0121 | 0.15 | 0.0181 | 0.7996 | 0.0013 | 0.20 | 94.39 | 18.58 | |
| 0.3254 | 0.9524 | 0.0115 | 0.15 | 0.0314 | 0.8026 | 0.0006 | 0.18 | 90.35 | 15.73 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, T.; Liu, X.; Xu, F. Moving Surface Boundary-Layer Control on the Wake of Flow around a Square Cylinder. Appl. Sci. 2022, 12, 1632. https://doi.org/10.3390/app12031632
Song T, Liu X, Xu F. Moving Surface Boundary-Layer Control on the Wake of Flow around a Square Cylinder. Applied Sciences. 2022; 12(3):1632. https://doi.org/10.3390/app12031632
Chicago/Turabian StyleSong, Te, Xin Liu, and Feng Xu. 2022. "Moving Surface Boundary-Layer Control on the Wake of Flow around a Square Cylinder" Applied Sciences 12, no. 3: 1632. https://doi.org/10.3390/app12031632
APA StyleSong, T., Liu, X., & Xu, F. (2022). Moving Surface Boundary-Layer Control on the Wake of Flow around a Square Cylinder. Applied Sciences, 12(3), 1632. https://doi.org/10.3390/app12031632







