System Invariant Method for Ultrasonic Flaw Classification in Weldments Using Residual Neural Network
Abstract
:1. Introduction
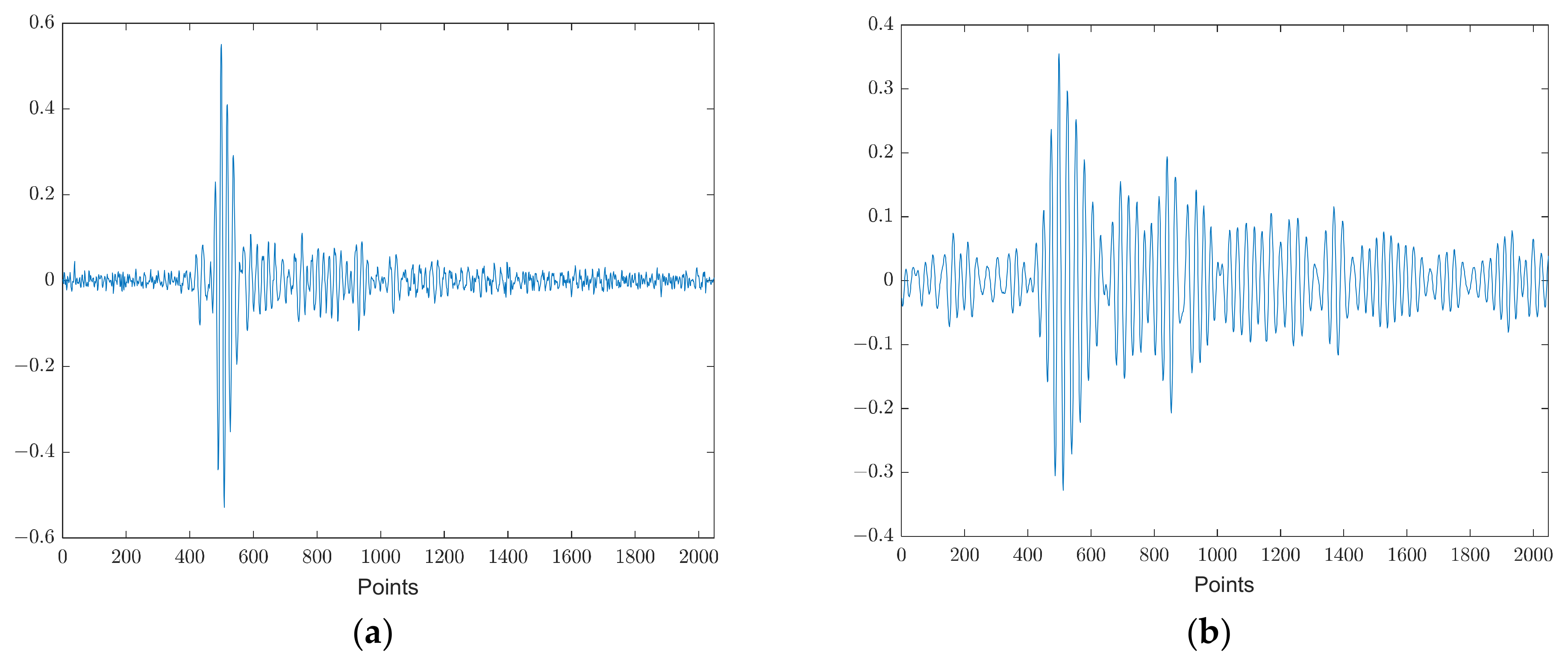
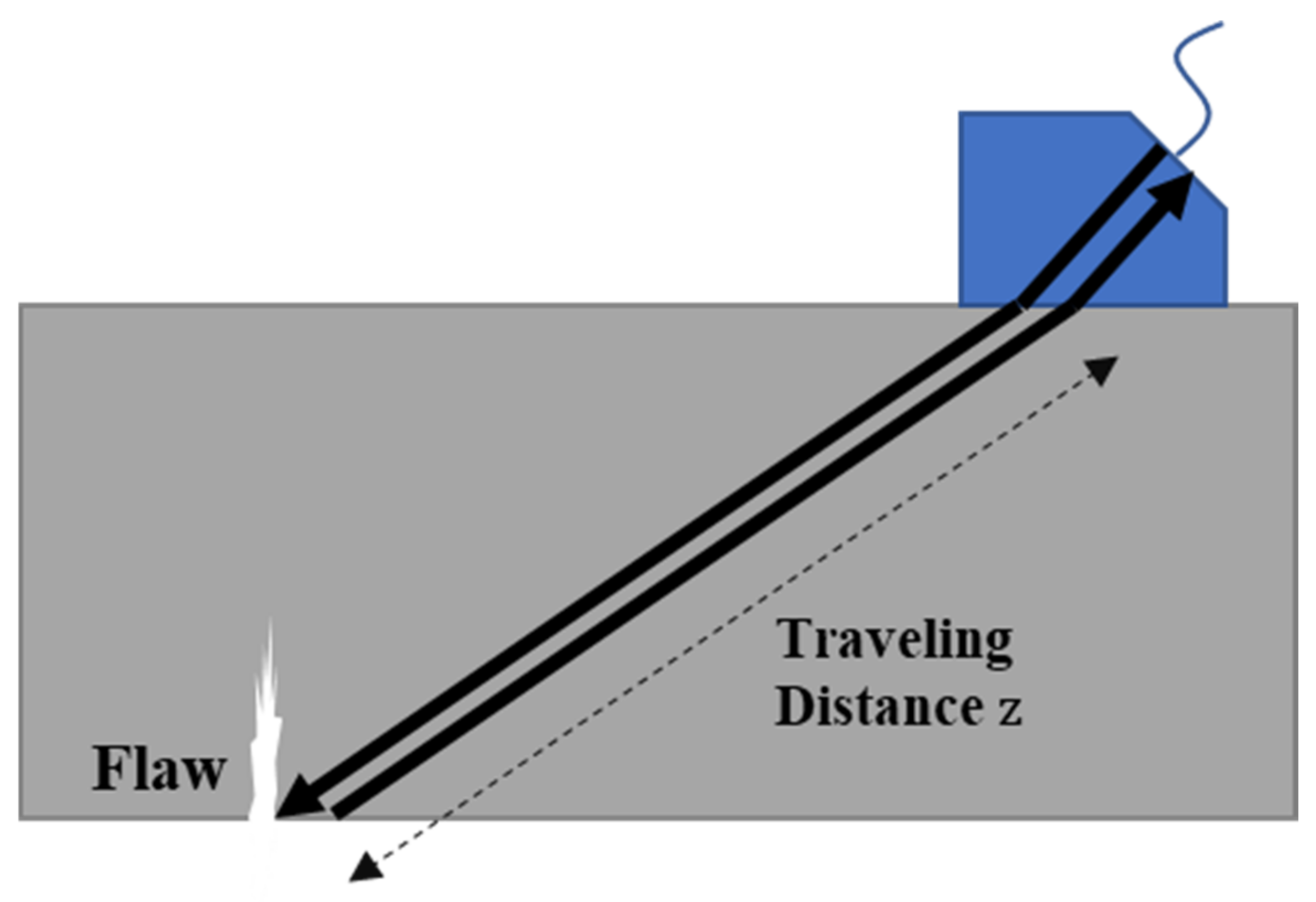
2. Ultrasonic Weldments Flaw Databases
3. Database Augmentation
4. Artificial Neural Networks
4.1. Convolutional Neural Network
4.2. Residual Neural Network
4.3. Residual Neural Network Architecture
4.4. ResNet Performance Evaluation
5. System Invariant Method
5.1. Principle of System Invariant Method
5.2. Applying System Invariant Method to Original Database
5.3. ResNet Performance Evaluation with Invariant Database
5.4. Performance Comparison
6. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| WGN | White Gaussian noise |
| ANN | Artificial neural network |
| FCNN | Fully connected neural network |
| CNN | Convolutional neural network |
| ResNet | Residual neural network |
References
- Song, S.J.; Schmerr, L.W. Ultrasonic flaw classification in weldments using probabilistic neural networks. J. Nondestruct. Eval. 1992, 11, 69–77. [Google Scholar] [CrossRef]
- Masnata, A.; Sunseri, M. Neural network classification of flaws detected by ultrasonic means. NDT E Int. 1996, 29, 87–93. [Google Scholar] [CrossRef]
- Polikar, R.; Udpa, L.; Udpa, S.S.; Taylor, T. Frequency invariant classification of ultrasonic weld inspection signals. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1998, 45, 614–625. [Google Scholar] [CrossRef] [PubMed]
- Margrave, F.W.; Rigas, K.; Bradley, D.A.; Barrowcliffe, P. The use of neural networks in ultrasonic flaw detection. Measurement 1999, 25, 143–154. [Google Scholar] [CrossRef]
- Song, S.J.; Kim, H.J.; Cho, H. Development of an intelligent system for ultrasonic flaw classification in weldments. Nucl. Eng. Des. 2002, 212, 307–320. [Google Scholar] [CrossRef] [Green Version]
- Simas Filho, E.F.; Silva, M.M.; Farias, P.C.; Albuquerque, M.C.; Silva, I.C.; Farias, C.T. Flexible decision support system for ultrasound evaluation of fiber–metal laminates implemented in a DSP. NDT E Int. 2016, 79, 38–45. [Google Scholar] [CrossRef]
- Cruz, F.C.; Simas Filho, E.F.; Albuquerque, M.C.; Silva, I.C.; Farias, C.T.; Gouvêa, L.L. Efficient feature selection for neural network based detection of flaws in steel welded joints using ultrasound testing. Ultrasonics 2017, 73, 1–8. [Google Scholar] [CrossRef]
- Meng, M.; Chua, Y.J.; Wouterson, E.; Ong, C.P.K. Ultrasonic signal classification and imaging system for composite materials via deep convolutional neural networks. Neurocomputing 2017, 257, 128–135. [Google Scholar] [CrossRef]
- Munir, N.; Kim, H.J.; Song, S.J.; Kang, S.S. Investigation of deep neural network with drop out for ultrasonic flaw classification in weldments. J. Mech. Sci. Technol. 2018, 32, 3073–3080. [Google Scholar] [CrossRef]
- Munir, N.; Kim, H.J.; Park, J.; Song, S.J.; Kang, S.S. Convolutional neural network for ultrasonic weldment flaw classification in noisy conditions. Ultrasonics 2019, 94, 74–81. [Google Scholar] [CrossRef]
- Munir, N.; Park, J.; Kim, H.J.; Song, S.J.; Kang, S.S. Performance enhancement of convolutional neural network for ultrasonic flaw classification by adopting autoencoder. NDT E Int. 2020, 111, 102218. [Google Scholar] [CrossRef]
- Rimoldi, B. Principles of Digital Communication: A Top-Down Approach; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Gallager, R.G. Principles of Digital Communication; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning Internal Representations by Error Propagation; California University San Diego La Jolla Inst for Cognitive Science (ICS-8506): San Diego, CA, USA, 1985. [Google Scholar]
- Rosenblatt, F. Principles of Neurodynamics: Perceptrons and the Theory of Brain Mechanisms; Spartan Books: Washington, DC, USA, 1961. [Google Scholar]
- Géron, A. Hands on Machine Learning with Scikit-Learn and Tensorflow: Concepts, Tools, and Techniques to Build Intelligent Systems; O’Reilly Media Inc.: Newton, MA, USA, 2017. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Nielsen, M.A. Neural Networks and Deep Learning; Determination Press: San Francisco, CA, USA, 2015. [Google Scholar]
- Li, F.F.; Karpathy, A.; Johnson, J.; Yeung, S. CS231n: Convolutional Neural Networks for Visual Recognition, Stanford University: Stanford, CA, USA, 2016.
- Lecun, Y.; Bottou, L.; Benjio, Y.; Haffner, P. Gradient-based Learning Applied to Document Recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef] [Green Version]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Springenberg, J.T.; Dosovitskiy, A.; Brox, T.; Riedmiller, M. Striving for simplicity: The all convolutional net. arXiv, 2014; arXiv:1412.6806. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Krizhevsky, A.; Hinton, G. Learning Multiple Layers of Features from Tiny Images; Technical Report No. TR-2009; Computer Science Department, University of Toronto: Toronto, ON, Canada, 2009; Available online: https://www.cs.toronto.edu/~kriz/learning-features-2009-TR.pdf (accessed on 11 January 2022).
- Wu, S.; Zhong, S.; Liu, Y. Deep residual learning for image steganalysis. Multimed. Tool. Appl. 2018, 77, 10437–10453. [Google Scholar] [CrossRef]
- Shibata, N.; Tanito, M.; Mitsuhashi, K.; Fujino, Y.; Matsuura, M.; Murata, H.; Asaoka, R. Development of a deep residual learning algorithm to screen for glaucoma from fundus photography. Sci. Rep. 2018, 8, 14665. [Google Scholar] [CrossRef] [Green Version]
- Cheng, X.; Zhang, Y.; Chen, Y.; Wu, Y.; Yue, Y. Pest identification via deep residual learning in complex background. Comput. Electron. Agric. 2017, 141, 351–356. [Google Scholar] [CrossRef]
- Zhang, W.; Li, C.; Peng, G.; Chen, Y.; Zhang, Z. A deep convolutional neural network with new training methods for bearing fault diagnosis under noisy environment and different working load. Mech. Syst. Signal Process. 2018, 100, 439–453. [Google Scholar] [CrossRef]
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted Boltzmann machines. In Proceedings of the 27th International Conference on Machine Learning (ICML-10), Haifa, Israel, 21–24 June 2010. [Google Scholar]
- Maas, A.L.; Hannun, A.Y.; Ng, A.Y. Rectifier nonlinearities improve neural network acoustic models. Proc. icml 2013, 30, 3. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv, 2014; arXiv:1412.6980. [Google Scholar]
- Schmerr, L.W. Fundamentals of Ultrasonic Nondestructive Evaluation; Springer: New York, NY, USA, 2016; pp. 650–681. [Google Scholar]
- McGillem, C.D.; Cooper, G.R. Continuous and Discrete Signal and System Analysis, 2nd ed.; Holt, Rinehart & Winston: New York, NY, USA, 1984; p. 118. ISBN 0030617030. [Google Scholar]
- Weisstein, E.W. Convolution Theorem. From MathWorld—A Wolfram Web Resource. Available online: https://mathworld.wolfram.com/ConvolutionTheorem.html (accessed on 11 January 2022).









| Manufacturer | KrautKramer | GE | Olympus | TKS | |||
|---|---|---|---|---|---|---|---|
| MWB 45-2 | WB 45-2 | WB 45-4 | MWB 45-4 | SWB 45-5 | A430S (45, 2 MHz) | 4C14 X 14A45 | |
| MWB 60-2 | WB 60-2 | WB 60-4 | MWB 60-4 | SWB 60-5 | A430S (60, 2 MHz) | 4C14 X 14A60 | |
| MWB 70-2 | WB 70-2 | WB 70-4 | MWB 70-4 | SWB 70-5 | A430S (70, 2 MHz) | 4C14 X 14A70 | |
| Title 1 | Flaws | No. of Signals |
|---|---|---|
| 1 | Crack | 2899 |
| 2 | Lack of Fusion | 1196 |
| 3 | Slag Inclusion | 634 |
| 4 | Porosity | 493 |
| 5 | Incomplete Penetration | 617 |
| Total | 5839 |
| Weldment Flaw Database | |||
|---|---|---|---|
| Training Database | Testing Database | ||
| Crack | 1740 | Crack | 1159 |
| Lack of Fusion | 1076 | Lack of Fusion | 120 |
| Slag Inclusion | 571 | Slag Inclusion | 63 |
| Porosity | 444 | Porosity | 49 |
| Incomplete Penetration | 555 | Incomplete Penetration | 62 |
| Total | 4386 | Total | 1453 |
| Original Database | |||
|---|---|---|---|
| Training Database | Testing Database | ||
| Crack | 26,100 | Crack | 1159 |
| Lack of Fusion | 16,140 | Lack of Fusion | 120 |
| Slag Inclusion | 8565 | Slag Inclusion | 63 |
| Porosity | 6660 | Porosity | 49 |
| Incomplete Penetration | 8325 | Incomplete Penetration | 62 |
| Total | 65,790 | Total | 1453 |
| Adopted ResNet Stage | |||||
|---|---|---|---|---|---|
| Layer Type | Kernel Size/Stride | Feature Maps | Activation Function | Description | |
| 1 | Input layer | - | - | - | x |
| 2 | Conv 1 | ) | FM | Relu | y = Conv 1 (x) |
| 3 | Dropout | 0.5 | - | - | y = Dropout(y) |
| 4 | Conv 2 | ) | FM | Relu | y = Conv 2 (y) |
| 5 | Dropout | 0.5 | - | - | y = Dropout (y) |
| 6 | Shortcut | - | - | - | x = x |
| 7 | Conv s | ) | FM | Relu | x = Conv s (x) |
| 8 | Add shortcut | - | - | Relu | x = x + y |
| 9 | Conv 3 | ) | FM | Relu | y = Conv 3 (x) |
| 10 | Dropout | 0.5 | - | - | y = Dropout (y) |
| 11 | Conv 4 | ) | FM | Relu | y = Conv 4 (y) |
| 12 | Dropout | 0.5 | - | - | y = Dropout (y) |
| 13 | Shortcut | - | - | - | x = x |
| 14 | Add shortcut | - | - | Relu | x = x + y |
| 15 | Conv 5 | ) | FM | Relu | y = Conv 5 (x) |
| 16 | Dropout | 0.5 | - | - | y = Dropout (y) |
| 17 | Conv 6 | ) | FM | Relu | y = Conv 6 (y) |
| 18 | Dropout | 0.5 | - | - | y = Dropout (y) |
| 19 | Shortcut | - | - | - | x = x |
| 20 | Add shortcut | - | - | Relu | x = x + y |
| Adopted ResNet Architecture | ||||
|---|---|---|---|---|
| Layer Type | Kernel Size/Stride | Feature Maps | Output Size | |
| 1 | Input Layer | - | - | 2048 |
| 2 | Conv 1 | ) | 64 | ) |
| 3 | Dropout | 0.5 | - | ) |
| 4 | Activation | Relu | - | ) |
| 5 | Max Pool | ) | - | ) |
| 6 | Stage 1 | - | 64 | ) |
| 7 | Max Pool | ) | - | ) |
| 8 | Stage 2 | - | 128 | ) |
| 9 | Max Pool | ) | - | ) |
| 10 | Stage 3 | - | 256 | ) |
| 11 | Dense Layer | 300 | - | 300 |
| 12 | Dropout | 0.5 | - | - |
| 13 | Output Layer | 5 | - | 5 |
| Original Database | Invariant Database | |||
|---|---|---|---|---|
| (Epoch > 100) | Training | Testing | Training | Testing |
| Average Accuracy (%) | 92.63 | 62.17 | 92.15 | 91.45 |
| Standard Deviation (%) | 0.64 | 4.13 | 0.43 | 1.77 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, J.; Lee, S.-E.; Kim, H.-J.; Song, S.-J.; Kang, S.-S. System Invariant Method for Ultrasonic Flaw Classification in Weldments Using Residual Neural Network. Appl. Sci. 2022, 12, 1477. https://doi.org/10.3390/app12031477
Park J, Lee S-E, Kim H-J, Song S-J, Kang S-S. System Invariant Method for Ultrasonic Flaw Classification in Weldments Using Residual Neural Network. Applied Sciences. 2022; 12(3):1477. https://doi.org/10.3390/app12031477
Chicago/Turabian StylePark, Jinhyun, Seung-Eun Lee, Hak-Joon Kim, Sung-Jin Song, and Sung-Sik Kang. 2022. "System Invariant Method for Ultrasonic Flaw Classification in Weldments Using Residual Neural Network" Applied Sciences 12, no. 3: 1477. https://doi.org/10.3390/app12031477
APA StylePark, J., Lee, S.-E., Kim, H.-J., Song, S.-J., & Kang, S.-S. (2022). System Invariant Method for Ultrasonic Flaw Classification in Weldments Using Residual Neural Network. Applied Sciences, 12(3), 1477. https://doi.org/10.3390/app12031477






