Abstract
The run-off road crash (RORC) is a representative type of lethal crash. The severity of RORC has increased owing to a combination of factors, such as roadside geometry, traffic conditions, and weather/climatic conditions. In this study, a model for estimating the RORC severity was developed based on various factors, including fixed objects, roadway geometry, traffic conditions, and road traffic environment. To develop the model, the accident data of crashes with roadside fixed objects on highways, as well as information on fixed object-related variables and roadway geometry-related variables, were collected. To improve the model in terms of implementing a close reflection of the real world, a learning method with tree augmented naïve Bayes (TAN), which takes into account the causal links between variables, was applied. The results of the analysis showed that the severity of crashes with roadside fixed objects increased sharply when the vertical slope was ≥4%, the radius of the curve was ≥250 m, the distance between the fixed object and the roadway was less than 3 m, or the density of fixed objects installation was greater than 2 for every 10 m. The proposed model allows for an analysis of sections with a high RORC severity on the roadways in operation and provides improvement measures to reduce the severity of RORC.
1. Introduction
Traffic accidents involve one or more road users, and a crash involving only one vehicle is referred to as a single vehicle crash (SVC). SVC on highways accounts for 60% of all fatal vehicle crashes [1]. SVCs can be classified into two groups, on road crashes (ORCs) and run-off road crashes (RORC), among which RORC is mostly related to a single vehicle. RORC occurs in the roadway departure of a vehicle, causing 70% of the total fatal SVC [2]. The factors that contribute to RORC can be classified into three categories—environmental factors, driver-related factors, and roadway-related factors. The environmental factors, such as weather and traffic, affect the RORC [3], and the driver-related factors, such as driver condition, inattention, and speeding, also increase roadway departures and the speed of crashes in curved sections [4,5]. The roadway factors such as lane width and clear zone distance, side slope, fixed object density, and offset from fixed objects also have a direct impact on the road departure of the vehicle [6,7,8,9,10,11].
Among the three factors described above, the roadway factors play an important role in determining if the crashes are caused by human error [12,13]. With regard to the roadway cross-section elements and road facility installation, as the shoulder width of the roadside increases, the probability of RORC decreases [6], and the crash severity decreases [7]. The vertical slope [8] and radius of the curve [9,10] affect the roadway departure of a vehicle, and the roadside fixed objects (e.g., guard rails, utility poles, piers, and trees) cause RORC [11].
To reduce the high accident severity of RORC, an external protective fence and the shock absorber have been installed and operated. It should be installed and operated only on dangerous road sections where fatal traffic accidents can occur according to precise guidelines. However, inefficient road safety facilities are being installed because the RORC contribution factors for each road section cannot be identified. In other words, an analysis of the contributing factors and preventive measures in consideration of the characteristics of each road section has not been established.
In this study, a model for RORC severity prediction was developed by applying TAN, and the prediction power of the proposed model was analyzed through comparison with the severity of actual accidents. The sensitivity analysis was performed for each variable, and the improvement priorities and measures were presented according to the degree of impact of each RORC contributing factor, which has not been investigated in previous studies.
2. Related Work
In terms of methodologies, a considerable number of studies have investigated several factors that contribute to RORC based on the collection of a variety of data and data analysis methods. In the 1980s, a lognormal regression model was developed to examine the relationship between the ROR crash frequency and a number of variables such as AADT, shoulder width, and lane width [14]. Since 1990, to address the problems of the increasing variety of variables and the errors in model accuracy, several logit/probit models and structural equations have been widely employed. The logit/probit model was developed to overcome the serious error that arises when the regression model is used in cases where the dependent variables are not continuous variables (quantitative variables) [15]. In social sciences, there are numerous cases where dependent variables are qualitative and discontinuous variables rather than quantitative variables, and to analyze such variables, binomial logit, ordered probit, and ordered logit models are applied. However, the drawback of the logit/probit model is that it cannot consider the correlation between the variables [16]. In addition, the limitations of the structural equation model is that the regression analysis can only investigate the relationship between the dependent variables and the independent variables, and that it cannot clearly determine the type of relationship [17,18].
Subsequently, the logit/probit model and structural equation model used for RORC prediction also have a few limitations in their application to road safety diagnosis. In addition, only a few studies have investigated the quantitative analysis of accident occurrence and severity. RORC often leads to fatal crashes, and identifying the factors contributing to its severity and the application of data mining techniques will enhance the utility of the research results. Furthermore, the model accuracy of existing logit/probit models and structural equations should be improved.
To enhance the accuracy of the prediction power of the RORC severity with regard to the aforementioned requirements, the adoption of a new methodology is essential. Given a set of discrete random variables that can be observed and measured, a Bayesian network is a tool that allows for the expression of the joint probability distribution between variables, while providing explanations in both quantitative and qualitative terms.
As traffic accident prediction research changes from single-factor analysis to multi-factor analysis, analysis and prevention studies of road transport [19,20,21] and maritime transport accidents [22,23,24] applying the Bayesian network are being applied.
Among all Bayesian network types, the significant advantage of the tree augmented naive Bayes (TAN) is that it involves the most natural expression of the probabilistic causal relationship or interdependence between multiple variables. TAN is expected to improve the predictive power for ROR severity, which has not been accomplished in existing prediction models. To quantify the range of influence of each factor in the field of marine transportation, TAN was applied to suggest a causal relationship for each factor [24].
3. Data Preparation
This section focuses on selecting materials for use in predicting RORC severity. As there are various variables in severity, it is necessary to classify the variables and define the collection method. This process is closely related to the explanatory power and accuracy of the model.
3.1. Target of Data Collection
The scope of the study was the section of highway in Korea where a traffic accident occurred. In the last five years, there were 223 roads where RORC occurred. All of these sections are rural roads, and the right guard rail was not installed. There were no RORC on roads with more than five lanes. This is because median barriers and guard rails are installed and operated on roads with more than five lanes. As of 2017, the ratio of installation of protective fences on highways with more than five lanes was 93.7%, but the ratio of installation of protective fences on highways with less than four lanes was only 30.6% [25]. Accordingly, the selected section is 167 sections for a two-lane road and 56 sections for a four-lane road; the intersection and junction were excluded. RORC is very unlikely to occur at intersections and junctions with SVC. In this section, vehicle-to-vehicle accidents and vehicle-to-person accidents occur due to conflicts between vehicles rather than SVC [26]. The section was also excluded from past studies and recent studies [27,28].
The contributing factors of the RORC were collected for a total of 223 sections where RORC accidents occurred. Based on the existing research, the factors were categorized into roadside fixed objects, roadway geometry, traffic conditions, and road traffic environments [3,4,5,6,7,8,9,10,11].
As shown in Figure 1, the collected variables for each factor were as follows: eight variables of the object for roadside fixed objects, six variables of the RORC section for roadway geometry, three variables of traffic conditions, and three variables of road environmental factors. Fixed objects is a characteristic of the characteristics and location of fixed obstacles, and additionally, since it collides with fixed obstacles due to the accident characteristics of RORC, the collision location is included. Roadway geometry includes the flat linearity of the road, the vertical alignment, the harmony of the alignment, and whether the design criteria were satisfied. Road environmental factors include the weather environment and the date and time of the accident. Traffic condition includes factors for traffic flow operation conditions.
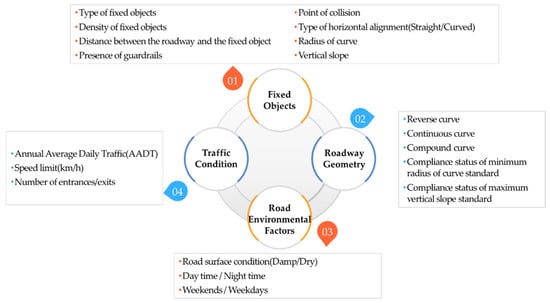
Figure 1.
Categorization of independent variables by contributing factors for RORC.
3.2. Road Segmentation for Data Collection
The segmentation of road sections is the process of classifying large and complex datasets into homogeneous groups with similar characteristics [29]. Considering that traffic accident data are heterogeneous, the data segmentation is generally regarded as the first and most important step in the prediction of accident events and the severity of accidents [30].
It has been reported that using an appropriate segmentation method can significantly reduce false positives and negatives, while determining the best sub-tree [31]. A representative segmentation method divides sections that are judged to have the same geometric factors regardless of the length [32,33]. Although the segmentation into homogeneous sections is a common approach that is used in several accident prediction studies [34,35,36], because this study aims to estimate accident severity, modified homogeneity determination criteria from the existing methods were applied. As shown in Figure 2, the homogeneous section was defined as a section that is located 100 m in the front and back of the location of the RORC. In Korea, the interval between intersections of national roads is at least 500 m. In order to minimize the effect of intersections, the length of the homogeneous section was reduced to 100 m in the front and rear [37].
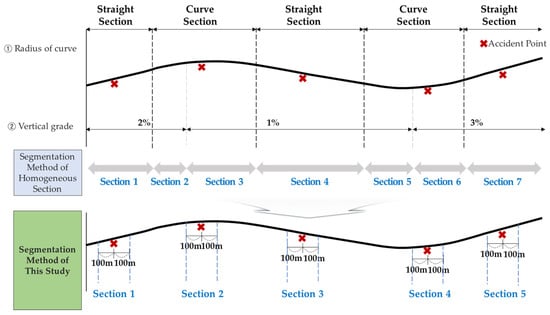
Figure 2.
Road segmentation method applied in the study.
In the segmentation method of the homogeneous section, the length of the section is increased by including both longitudinal and planar curve coincidence sections, and changes in other factors within the section occur significantly. This is because the characteristic is averaged over all “fixed objects” in the interval. However, the segmentation method of this study can minimize the factor change for “fixed objects” while reflecting the characteristics of the homogeneous section. In addition, within the same section, further classification was made according to factors such as the horizontal alignment (whether straight/curved), the radius of the curve and the vertical slope, and the combination status of reverse curve/continuous curve/compound curve, plane curve, and the vertical slope.
3.3. Data Collection Method
The detailed data on the variables are different from the collecting institutions and methods. They are based on national database data, and variables that are not aggregated are manually investigated and collected by researchers.
3.3.1. Traffic Accident Data
In this study, for the traffic accident data and severity data for road sections, five-year (2014–2018) data of 443 cases of accidents from the Traffic Accident Analysis System (TAAS), which is a database managed by the Korea Road Traffic Authority (KOROAD), were used. The severity of traffic accidents of a crash between a fixed obstacle and a vehicle alone were classified into fatal/serious/slight accidents for a two-way highway with four to six lanes, and from the collected data, the data with an unknown point of collision with the roadside fixed object were excluded. The criteria for fatal/serious/slight accidents were defined as follows:
- Fatal accident: Death within 30 days of the accident
- Serious accident: Injuries that require treatment for more than three weeks due to a traffic accident
- Slight accident: Injuries that require treatment for the period between five days or longer and less than three weeks due to a traffic accident
3.3.2. Data on Fixed Objects and Road Geometry
The TAAS database provides information on the point of collision, time, severity, violation of associated regulations, and weather, but does not provide information on the road cross-sectional characteristics, curve type of road, and AADT. In particular, because the cross-sectional characteristics of the road (type of fixed objects, distance between the roadway and the fixed object, and fixed object density) primarily contribute to crashes [11], the research team made extensive efforts to identify the characteristics that were not provided in the TAAS database. We used the KakaoMap Street View application to identify roadside elements, and this application provides images and street views of the surrounding environment of most roads in Korea from 2009 to 2021. For the road alignment characteristics, the type of horizontal alignment, radius of the curve, vertical slope, and the number of entrances/exits were identified for the four to six lane highways where the RORC events occurred using the digital topographic map (scale = 1/1000) of the Land Information Platform (LIP), which is a database managed by the National Geographic Information Institute (NGII).
3.3.3. Traffic Condition Data
For traffic condition, the average value of annual average daily traffic (AADT) was collected over five years from the Traffic Monitoring System (TMS), which is a database maintained by the Korea Institute of Civil Engineering and Building Technology, and the speed limit was identified. The distribution of each variable in these segments is presented in Table 1.

Table 1.
Descriptive statistics of target segments.
4. Methodology for Model Construction
Before implementing the model, it was necessary to review the types of BN structural learning methods, after which the optimal learning method was selected for the study, and the learning procedure was defined.
4.1. Type of Learning Method Based on a Baysian Network
A Bayesian network is a tool that allows for the expression of the joint probability distribution between variables, while providing explanations in both quantitative and qualitative terms for a given set of discrete random variables that can be observed and measured [38].
In quantitative terms, the Bayesian network explains the parts where the conditional probabilities between variables are specified, and in qualitative terms, it explains the parts expressing conditional independence or dependence between the variables [39].
A Bayesian network can be described using a model that helps determine the relationship between the variables and the data given for a specific variable and the probability that the relationship occurs. The Bayesian network consists of two parts: BN = f(G,D), where G indicates a directed acyclic graph composed of nodes and arcs. The nodes are the variables X1, …, Xn in the data set, whereas the arcs indicate direct dependencies between the variables. The graph G then encodes the independence relationships in the domain under investigation. The first task when learning a Bayesian network is to find the structure G of the network. G is estimated through iterative structural design learning. The second part, D, represents the probability distribution. In the probability distribution, , the value of the variable , which indicates the parameter in the form of , can be given when the combination of the variable and the direct parameter variable is given, where represents the set of direct parents of the variable in G. Thus, a joint distribution is obtained as follows:
where,
: Combined random variable of random variable X
: Conditional probability distribution of random variable X.
The naive Bayesian network (NBN), which is the most general form, was developed as a popular network construction algorithm. Given that parametric learning of the model does not require complex iterative processes and effectively avoids the subjectivity of expert judgment, it can reduce the complexity of the composition. However, assumptions regarding NBN construction are sometimes too hypothetical to be realistic. To improve the performance of the NBN, the structure is augmented with links between attributes or factors. This type of structure that does not require independence between attributes is called an augmented BN (ABN). In addition, if a class variable has no parent, each attribute has a class variable and a maximum of one other attribute as a parent. The ABN under this condition is called the tree augmented naïve Bayes (TAN). TAN is a Bayesian network with the assumption that there is a tree-type relationship between child nodes in order to relax the assumption of NBN with sweeping independence between the child nodes [40]. Compared to NBN and data-driven network construction approaches, TAN has is more competitive and accurate [40,41]. Thus, TAN has a wide range of applications in various risk studies [22,42] in the field of transportation.
4.2. TAN Learning Method for RORC Severity Prediction
When examining the research purpose of predicting the severity of accidents and the amount and scope of the collected data, the advantages of TAN learning are great. The TAN learning procedure is applied based on the existing research results.
4.2.1. Reasons for TAN Learning Application
The TAN learning method was employed in this study to learn the Bayesian network structure. TAN learning is a semi-naïve Bayesian learning method. The assumption of the attributes of naïve Bayes is relaxed using a tree structure, wherein each attribute is dependent on a class and one other attribute. Compared to the NBN method, where local optimization problems occur, TAN learning is more efficient and accurate for generating most BN structures. TAN learning also maintains the robustness and computational complexity of NBN training [43]. Another reason behind the use of TAN learning is that a class variable in a BN model always has at least one parent node. As shown in Figure 3, the TAN approach allows for movement in any direction to ensure that the link is appropriate for a real practical environment. This indicates that the link direction of the TAN model can be appropriately adjusted to suit the requirements of this study for RORC severity.
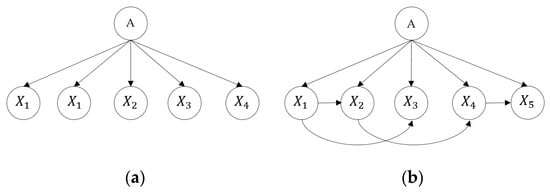
Figure 3.
Typical structures of (a) NBN and (b) TAN.
4.2.2. TAN Learning Procedure
Pearson correlation coefficients were analyzed using IBM SPSS Statistics Ver.24 (International Business Machines Corporation, New York, NY, USA) for correlation between variables using 403 out of 443 RORC data. Variables with high correlations as a result of basic analysis, such as “radius of curve” and “horizontal alignment”, were set as the top priority when designing the TAN structure.
In the case of TAN learning, the most important part is to design the learning structure after analyzing the correlation between variables. Prior to the learning procedure, a basic analysis of correlations by factors was performed. After basic analysis, for RORC severity analysis and prediction, TAN learning proceeded in five steps. The procedure was based on general learning procedures [44] and the case of application to RORC severity [45]. It is a differentiated method from the general accident event count prediction, wherein the three classes of RORC severity use conditional mutual information (severity impact variable). When this is defined in terms of a function, it can be expressed as Equation (2). This function is an approximation of the information that Xj provides about Xi (and vice versa) when the value of C is known:
where,
: Conditional mutual information
: ith state of severity impact variable
: ith state of severity impact variable
: ith state of RORC severity class variable .
- (i)
- Compute between each pair of severity impact variables.
- (ii)
- Create a maximum weighted spanning tree.
- (iii)
- The resulting undirected tree is transformed to a directed tree by choosing a root variable from the attribute variables and setting the direction of all edges to be outward from it.
- (iv)
- Construct a TAN model by adding a vertex labeled by the class variable C and adding an arc from C to each .
- (v)
- Estimate the conditional probability of each variable/node through a gradient descent approach [22].
5. Results and Verification
In TAN learning, the structure of the model is the final product of the model and represents the logical explanation. The performance of the model is presented through the shape of the learned structure and the prediction results.
5.1. Model Structure
TAN learning was conducted using MATLAB code for the 403 cases of data out of the collected 443 cases of RORC event data. The vertical alignment, vertical slope, and the compound curve showed a relatively high correlation with the RORC severity, and the horizontal alignment, the radius of the curve, and compliance with the minimum radius of the curve design criteria showed some correlation with severity. The causal relationships between the variables and the independent variables were connected by links. The vertical slope and radius of the curve have a causal relationship with the compound curve variable, and the radius of the curve is the variable that has a causal relationship with the variables of the reverse curve, continuous curve, and compliance with the minimum radius of the curve design criteria.
In summary, as shown in Figure 4, the structure of the BN model for predicting the RORC severity was developed through the TAN learning process.
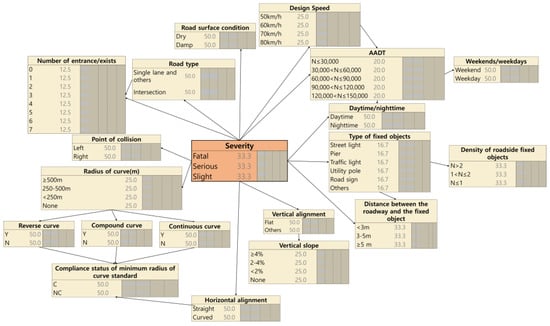
Figure 4.
BN structure for RORC severity prediction.
5.2. Modeling Result
The probability of being classified into one of the three RORC severity categories in the situation of individual data was calculated. Among the calculated values, the category with the largest probability value was selected as the predicted value. The main function of the existing regression model is to select factors that influence RORC severity, whereas machine-learning techniques, such as the Bayesian network, focus on predicting the category that the data will fall into among the three categories of RORC severity. For example, as shown in Figure 5, in case of a crash with a pier that is 2.5 m away from the roadside while driving on a road composed of a vertical slope of 4.5%, design speed of 80 km/h, damped road surface, weekdays, AADT is 33,000 vehicle/day, single lane, two entrance, weekdays, nighttime, a radius of the curve of 300 m, and with the presence of a compound curve, the probability of a fatal accident is 69.0%
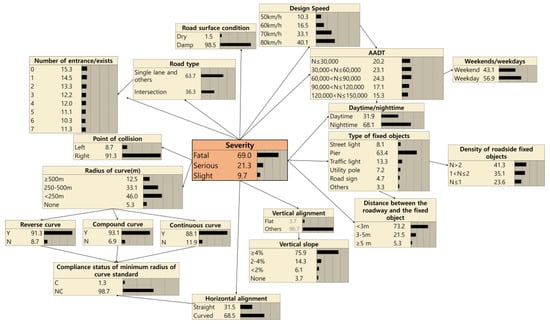
Figure 5.
RORC severity prediction model.
Table 2 shows the results of RORC severity prediction when applying road information and 403 traffic accident events that were collected using the constructed model. The severity representing the highest probability in the total 100% RORC severity distribution is presented as the severity of the corresponding interval. In the case of category 1, the probability of slight accident is 48.3%, which is higher than that of serious and fatal accidents, so the section is predicted as a slight accident section. The predicted severity was compared with the actual RORC severity, and a total agreement of 91.5% (369/403) was obtained.

Table 2.
RORC severity prediction model construction.
5.3. Model Verification
To verify the developed model, two verification methods were applied. First, there was a method of comparing the measured value with the predicted value, and the second was a method of calculating and analyzing the sensitivity and specificity.
5.3.1. Validation through Comparison between Measured Values and Predicted Values Using the Confusion Matrix
The prediction accuracy of the RORC severity prediction model was determined using data from 40 cases for validation, excluding 403 cases used for development out of the 443 collected cases in total. The result of the decision can be expressed as a confusion matrix that can compare the measured and predicted values, as presented in Table 3. The prediction power was high at 90% (13 + 16 + 9)/40). From TAN learning, it is seen that the prediction power was improved by linking the variables with a causal relationship between independent variables.

Table 3.
Results of prediction power verification for the proposed RORC severity prediction model.
However, as the 40 data used for verification may not show a distribution that can represent the total accident rate of the entire dataset, we cannot be sure that the model accuracy is high using the chaos matrix alone. In the case of comparative verification with other models, the predictive performance of the model can be comparatively verified through the likelihood ratio test (LRT), root mean square error (RMSE), and the mean absolute error (MAE) [46,47]. However, it is difficult to verify the predictive performance of a single model. When judging the predictive performance of a single TAN model, it is possible to judge more visually and easily through ROC analysis [46].
5.3.2. Exploration of Prediction Power Using Receiver Operating Characteristic (ROC) Curve
The ROC curve is a useful graphical method for exploring the prediction power in a classification model. In this study, the differentiated prediction power was evaluated by comparing the probability of predicting an actual fatal accident as a serious or a slight accident with the probability of predicting a serious accident as a fatal accident.
The ROC curve can be drawn by calculating the sensitivity and specificity of the classification model. If the result of an actual positive case is predicted as positive by a certain model, this ratio (true positive rate) is referred to as sensitivity. On the other hand, when the result of an actual negative case is predicted as negative by a certain model, this rate is referred to as specificity [48]. The results are listed in Table 4.

Table 4.
Concept of sensitivity and specificity.
The higher the values of the sensitivity and specificity, the better the prediction performance. Thus, the ROC curve is expressed as a graph by defining the sensitivity on the y-axis and (1-specificity) on the x-axis. In the ROC curve, the area under the curve is called the area under the ROC curve (AUC), and this curve serves as a measure to evaluate the prediction power according to classification. When this value is close to 0.5, it indicates a low classification prediction power, and when this value is close to 1, it indicates a high classification prediction power [49].
Figure 6 shows the results of plotting the ROC curve with the Tree Augmented Naïve Bayes (TAN) model. Because of the area under the ROC curve calculation, the AUC value was 0.763 for slight accidents, 0.797 for serious accidents, and 0.917 for fatal accidents. This shows that the classification prediction power for fatal accidents is the best. Generally, when AUC is less than or equal to 0.5, the result is not considered suitable, and the AUC from 0.9 to 1.0 can be interpreted as very accurate, while that from 0.7 to 0.9 is interpreted as relatively accurate.
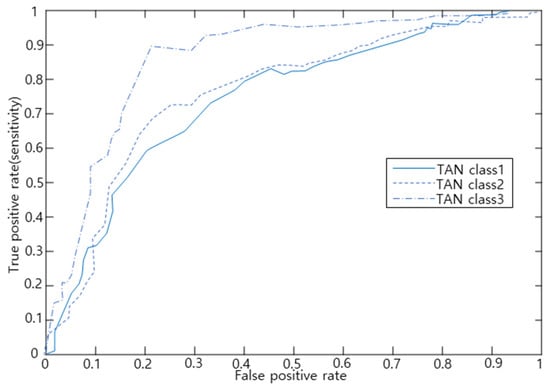
Figure 6.
ROC curve of RORC severity prediction model.
Therefore, the TAN model has a highly accurate classification prediction power for fatal accidents. The classification prediction power for serious and slight accidents is lower than that for fatal accidents, but these are still judged to be relatively accurate.
6. Discussion
It is best to calculate the severity by applying the predictive model in all situations, but there are many situations in which data collection is difficult. When it is difficult to collect data on all variables, the critical point is used to present standards for safe processing.
6.1. Calculation of RORC Severity Change Threshold
To reduce the severity of RORC, we aimed to derive threshold values that serve as criteria for the safety process. The threshold refers to the size of a variable at which the RORC severity increases sharply when the size of the variable is above or below a certain level. The CoO method was used to calculate these thresholds. CoO is analyzed based on the Kullback−Leibler divergence, which is used in information theory and probability theory. The Kullback−Leibler divergence is used to find the distance between two probability distributions and is expressed by Equation (3) below [50]:
where
: The cross-entropy of and which expresses the overall difference between two distributions
: The entropy of , which is a measure of how much information P carries (0 to ).
Here, CoO is the measurement that replaces with and with . Using this measurement, we can analyze the impact of the omitted evidence, , on the problem variable . Let be a problem variable and let be a set of evidence. Given this, the CoO of is expressed by Equation (4):
where
: CoO(Cost-of-Omission) of .
If the calculated probabilities are the same with or without evidence, the evidence is considered to be insignificant. On the contrary, if the calculated probabilities are significantly affected by the omission of evidence, the evidence is considered significant [51].
6.2. Result of Threshold Calculation
By comparing the critical point calculation results for each variable, each safety measure is suggested.
6.2.1. Road Geometry
As shown in Table 5, the threshold values for the vertical slope, the radius of the curve, and compliance with the minimum radius of the curve design criteria were calculated. In road conditions with a vertical slope ≥ 4%, the number of serious accidents and fatal accidents sharply increased (the number of slight accidents decreased), and the detailed threshold value was 4.3%. On the other hand, when the vertical slope was less than 4% or there was no vertical slope, the probability of a slight accident was higher than that of serious or fatal accidents. When the vertical slope was less than 2%, the probability of a slight accident further increased.

Table 5.
Result of the road geometry variable threshold calculation.
It can be seen that the ratio of slight accidents was highest on roads with a radius of curve ≥500 m, and the probability of fatal accidents increased on roads wherein 250 ≤ radius of curve < 500 m. In particular, because the radius of the curve was applied as a continuous variable, the probability of a fatal accident was very high in the radius range of the radius at 250–370 m. On a road with a radius of curve smaller than 250 m, the probability of a fatal accident was reduced. This is related to the tendency of drivers to reduce the driving speed and focus on safe driving by increasing the level of attention in the case of driving on curved sections with a small radius of the curve.
It can be seen that the ratio of fatal accidents decreased when there was a non-compliance with the minimum radius of curve design criteria, and the ratio of fatal accidents increased in the case of compliance with the design criteria. Similar to the analysis results that are based on the size of the radius of the curve, it is inferred that the level of driver’s attention increased in the curved road section with a curve radius smaller than the minimum design criterion of 280 m, which resulted in safe driving and helped maintain a low driving speed.
6.2.2. Curve Type of Road Variable
As shown in Table 6, from the results of calculating the RORC severity threshold according to the type of curved section, as shown in Table 6, the compound curve showed the greatest change in probability with a total CoO of 1.9. For roads with compound curves, the proportion of serious accidents and fatal accidents was high, and on the road sections without reverse and continuous curves, the proportion of fatal accidents was actually high.

Table 6.
Results of curve type of road variable threshold calculation.
The reasons for the above result can be interpreted as follows.
- (1)
- In the schematic diagram of the TAN structure, the compound curve is linked as a variable that is correlated with the radius of the curve and the vertical slope.
- (2)
- The effect of the vertical slope is greater than that of the radius of the curve.
- (3)
- The roads with compound curves involve a high proportion of serious accidents.
- (4)
- Because the reverse and continuous curves are greatly affected by the radius of the curve, a result similar to the threshold calculation result of the radius of the curve is obtained.
- (5)
- Most sections with reverse and continuous curves have a small radius of the curve, which reduces the driving speed. This subsequently causes a decrease in the probability of fatal accidents and affects only serious accidents.
6.2.3. Roadside Fixed Object Variable
Table 7 shows the threshold calculation results for the variables related to fixed objects. The total CoO of the variable of horizontal distance between the road and the fixed object was 7.3, indicating the largest impact, followed by the fixed object density variable with a CoO value of 5.8. In the sections where the horizontal distance between the road and the fixed object was less than 3 m, the probability of a fatal accident was high, especially when the fixed object was installed at a distance than 1.5 m; there was a sharp increase in the probability of a serious accident. Even when the horizontal distance between the road and the fixed object was 3–5 m, the probability of a slight accident and a fatal accident was high, but the distribution of severity varied depending on the type of the fixed object. The values in the results of the existing research are similar to those with the range of recovery distance (the width at which the roadway departure of a vehicle can be recovered) at 3 to 4.6 m [52].

Table 7.
Results of the roadside fixed object variable threshold calculation.
When the horizontal distance between the road and the fixed object and the type of fixed object in the crash were considered together, the results showed that the probability of a fatal accident greatly increased when utility poles were installed at a distance of less than 3 m. The New York State Department of Transportation (NYSDOT) recommends installing utility poles inside rather than outside of the curved road, and recommends that utility poles installed close to the road should be at a distance of 3 m or more from the outer edge of the road [53].
When the density of fixed objects exceeds two objects every 10 m, the probability of a fatal accident is high, and when the density is 1 or less, the probability of a fatal accident decreases. The results show a similar trend to the results of a previous study, and indicates that the higher the number of poles every 10 m, the higher the number of events and severity of roadside crashes [54].
Among the types of fixed obstacles, streetlights were found to have the greatest influence on serious injury accidents than other types of fixed objects. Utility poles had the greatest impact on fatalities. This is because about 9 million utility poles and 1.68 million streetlights among the fixed objects on the roadside are frequently installed [55], as well as not installing additional shock-absorbing facilities. It is most effective to separate the facility from the road by more than 3 m, but if there is not enough space, it is necessary to change it to a material that can absorb shock [56].
7. Conclusions and Outlook
In this study, the factors affecting the severity of crashes with roadside fixed objects and the degree of impact were analyzed using a Bayesian network model. In the existing studies, the drawback of a poor fit of the model still persists because the correlation of independent variables was not reflected in the model. However, when the tree augmented naïve Bayes (TAN) model was applied, this limitation was overcome and the model fit was over 90%, which confirmed the possibility of model applicability and utilization.
However, using the same data, predictive power could not be compared with the negative binomial probability distribution, binary logit, ordinal probit, and ordinal logit models used in previous studies. Due to the lack of a dataset, the validation rate was not sufficiently representative of all severity of RORC. In the future, the effectiveness of research results can be improved through the expansion of datasets and variables and the comparison of predictive power with existing models.
To minimize the influence of intersections and junctions in the road segment division method, it was limited to 200 m around the accident location. Even in an undivided section, RORC can be affected, but there is a limit that excludes influencing factors. This is because the database for road information is limited. In the future, it will be possible to divide road sections that reflect road characteristics through accurate data collection through the promotion of digitization of road information.
If there is information on road characteristics, it is possible to easily predict the RORC severity of the currently operated or planned road using the model, and to establish reasonable safety measures for the section with a high severity. When there is no information on road characteristics, it is recommended to install road safety facilities that can lower the severity in the order of the density of fixed obstacles, the horizontal distance between the road and the collision obstacles, the longitudinal slope, and the piers based on the threshold analysis results.
As a result of the application of the model, the factors affecting the RORC severity were in the order of the density of fixed objects, the horizontal distance between the roadway and the fixed object in the crash, vertical slope, and pier, when these factors either exceeded or fell short of the set threshold values. Among all types of fixed objects, piers had the largest impact.
In the development of the model, the automatic collection of information on the accident sites was not possible. Thus, the information on the accident sites was collected manually. For this reason, only the data from the sections 100 m front and behind the crash point, and not the entire road sections, were used. Because traffic accidents can be affected by changes in conditions in the sections before the accident point, further improvement in the explanatory power of the model is required by expanding the range of investigation and expanding the setting of the range of the causal relationship with the crash site. In terms of setting the variables, the continuous variables were converted into categorical variables to increase the fit of the model. An increase in the number of cumulative traffic accident data increases could open up the potential for the application of continuous variables in the future. With the application of continuous variables, it is expected that the process of deriving the threshold values of the impact variables that determine the severity of traffic accidents will become easier with improved accuracy.
Author Contributions
Conceptualization, H.K.; Data curation, J.-T.K., S.S. and H.L.; Investigation, J.-T.K.; Methodology, H.K. and J.L.; Project administration, H.K. and J.L.; Software, S.S.; Supervision, J.-T.K.; Validation, J.-T.K. and H.L.; Writing—original draft, H.K.; Writing—review & editing, J.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Road Traffic Authority grant funded by the Korea government (KNPA) (No. POLICE-00003-03-406, Development of information Provision Technology with IoT-based Traffic Control Devices and its Operation Management).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data included in this study are available upon request by contact with the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- LeRoy, A.A.; Morse, M.L.; Iatrogen, L.L.C. Multiple Medications and Vehicle Crashes: Analysis of Databases; National Highway Traffic Safety Administration: Washington, DC, USA, 2008; pp. 117–129.
- Liu, C.; Subramanian, R. Factors Related to Fatal Single-Vehicle Run-Off-Road Crashes; National Highway Traffic Safety Administration: Washington, DC, USA, 2008; pp. 71–80.
- Alruwaished, A.F. Characteristics of Drivers Who Cause Run-Off-Road-Crashes on Ohio Roadways. Ph.D. Thesis, University of Dayton, Dayton, OH, USA, August 2013. [Google Scholar]
- Chen, F.; Chen, S. Injury severities of truck drivers in single- and multivehicle accidents on rural highways. Accid. Anal. Prev. 2011, 43, 1677–1688. [Google Scholar] [CrossRef] [PubMed]
- Xie, Y.C.; Zhao, K.G.; Huynh, N. Analysis of driver injury severity in rural single-vehicle crashes. Accid. Anal. Prev. 2012, 47, 36–44. [Google Scholar] [CrossRef]
- Roque, C.; Jalayer, M. Improving roadside design policies for safety enhancement using hazard-based duration modeling. Accid. Anal. Prev. 2018, 120, 165–173. [Google Scholar] [CrossRef]
- Shaheed, M.S.; Gkritza, K. A latent class analysis of single-vehicle motorcycle crash severity outcomes. Anal. Method Accid. 2014, 2, 30–38. [Google Scholar] [CrossRef]
- McLaughlin, S.B.; Hankey, J.M.; Klauer, S.G.; Dingus, T.A. Contributing Factors to Run-Off-Road Crashes and Near-Crashes; National Highway Traffic Safety: Washington, DC, USA, 2009; pp. 59–71.
- Lord, D.; Brewer, M.A.; Fitzpatrick, K. Analysis of Roadway Departure Crashes on Two Lane Rural Roads in Texas; Texas Transportation Institute: College Station, TX, USA, 2011; pp. 143–150.
- Roque, C.; Moura, F.; Cardoso, J.L. Detecting unforgiving roadside contributors through the severity analysis of ran-off-road crashes. Accid. Anal. Prev. 2015, 80, 262–273. [Google Scholar] [CrossRef]
- Hussein, M.H.A.; Sayed, T.; Ismail, K.; Espen, A.V. Calibrating road design guides using risk-based reliability analysis. J. Transp. Eng. 2013, 140, 04014041. [Google Scholar] [CrossRef]
- Li, H.; Pang, F.; Chen, H.; Du, Y. Vibration analysis of functionally graded porous cylindrical shell with arbitrary boundary restraints by using a semi analytical method. Compos. Part B Eng. 2019, 164, 249–264. [Google Scholar] [CrossRef]
- Amiria, A.M.; Sadrib, A.; Nadimic, N.; Shamsd, M. A comparison between Artificial Neural Network and Hybrid Intelligent Genetic Algorithm in predicting the severity of fixed object crashes among elderly drivers. Accid. Anal. Prev. 2020, 138, 105468. [Google Scholar] [CrossRef]
- Good, M.C.; Fox, J.C.; Joubert, P.N. An in-depth study of accidents involving collisions with utility poles. Accid. Anal. Prev. 1987, 19, 397–413. [Google Scholar] [CrossRef]
- Ju, M.Y. Probit and ordered probit analysis and its application. J. Gov. Stud. 2000, 6, 24–49. [Google Scholar]
- Park, J.H.; Yun, D.G. Analysis of road cross section component affecting traffic accident severity on national highway. J. Korean Soc. Saf. 2017, 32, 143–149. [Google Scholar]
- Hamdar, S.H.; Mahmassani, H.S.; Chen, R.B. Aggressiveness propensity index for driving behavior at signalized intersectiions. Accid. Anal. Prev. 2008, 50, 315–326. [Google Scholar] [CrossRef] [PubMed]
- Rundmo, T.; Hale, A.R. Manager’s attitudes towards safety and accident prevention. Saf. Sci. 2003, 41, 557–574. [Google Scholar] [CrossRef]
- De Oña, J.; Mujalli, R.O.; Mujalli, R.O.; Calvo, F.J. Analysis of traffic accident injury severity on Spanish rural highways using Bayesian networks. Accid. Anal. Prev. 2011, 43, 402–411. [Google Scholar] [CrossRef] [PubMed]
- Cong, C.; Guohui, Z.; Tarefder, R.; Jianming, M.; Heng, W.; Hongzhi, G. A multinomial logit model-Bayesian network hybrid approach for driver injury severity analyses in rear-end crashes. Accid. Anal. Prev. 2015, 80, 76–88. [Google Scholar]
- Hänninen, M. Bayesian networks for maritime traffic accident prevention: Benefits and challenges. Accid. Anal. Prev. 2014, 73, 305–312. [Google Scholar] [CrossRef]
- Yang, Z.S.; Yang, Z.L.; Yin, J. Realising advanced risk-based port state control inspection using data-driven Bayesian networks. Transp. Res. Part A Pol. Pract. 2018, 110, 38–56. [Google Scholar] [CrossRef]
- Castaldo, F.; Palmieri, F.A.N.; Regazzoni, C.S. Bayesian analysis of behaviors and interactions for situation awareness in transportation systems. IEEE Trans. Intell. Transp. Syst. 2016, 17, 313–322. [Google Scholar] [CrossRef]
- Fan, S.; Blanco-Davis, E.; Yang, Z.; Zhang, J.; Yan, X. Incorporation of human factors into maritime accident analysis using a data-driven Bayesian network. Reliab. Eng. Syst. Saf. 2020, 203, 107070. [Google Scholar] [CrossRef]
- Kim, J.M.; Kim, D.S.; Ahn, J.H. Research on the Establishment of Reinforcement Plans for Vehicle Protection Fences on National Roads; Ministry of Land, Infrastructure, and Transport: Sejong, Korea, 2014; pp. 151–170.
- Park, M.; Lee, D. A random parameter negative binomial model for signalized intersection accidents in Seoul, Korea. Int. J. Inj. Control. Saf. Promot. 2021, 28, 201–207. [Google Scholar] [CrossRef]
- Lee, J.; Mannering, F. Impact of roadside features on the frequency and severity of run-off-roadway accidents: An empirical analysis. Accid. Anal. Prev. 2002, 34, 149–161. [Google Scholar] [CrossRef]
- Al-Bdairi, N.S.S.; Hernandez, S. Comparison of contributing factors for injury severity of large truck drivers in run-off-road crashes on rural and urban roadways: Accounting for unobserved heterogeneity. Int. J. Transp. Sci. Technol. 2020, 9, 116–127. [Google Scholar] [CrossRef]
- Ghadi, M.; Török, Á. A comparative analysis of black spot identification methods and road accident segmentation methods. Accid. Anal. Prev. 2019, 128, 1–7. [Google Scholar] [CrossRef]
- Cafiso, S.; D’Agostino, C.; Persaud, B. Investigating the influence of segmentation in estimating safety performance functions for roadway sections. In Proceedings of the TRB 92nd Annual Meeting, Washington, DC, USA, 13–17 January 2013; Volume 15. [Google Scholar]
- Koorey, G. Road data aggregation and sectioning considerations for crash analysis. J. Transp. Res. Board 2009, 2103, 61–68. [Google Scholar] [CrossRef] [Green Version]
- Misra, R.; Das, A. Identification of Homogeneous Sections from Road Data. Int. J. Pavement Eng. 2003, 4, 229–233. [Google Scholar] [CrossRef]
- Cafiso, S.; Graziano, A.D.; Silvestro, G.D.; Cava, G.L.; Persaud, B. Development of comprehensive accident models for two-lane rural highways using exposure, geometry, consistency and context variables. Accid. Anal. Prev. 2010, 42, 1072–1079. [Google Scholar] [CrossRef]
- Depaire, B.; Wets, G.; Vanhoof, K. Traffic accident segmentation by means of latent class clustering. Accid. Anal. Prev. 2008, 40, 1257–1266. [Google Scholar] [CrossRef] [Green Version]
- Luca, M.R.; Mauro, R.; Lamberti, R.; Dell’Acqua, G. Road safety management using bayesian and cluster analysis. Procedia Soc. Behav. Sci. 2012, 54, 1260–1269. [Google Scholar] [CrossRef] [Green Version]
- Ghadi, M.; Török, Á.; Tánczos, K. Integration of probability and clustering based approaches in the field of black spot identification. Period. Polytech. Civ. Eng. 2019, 63, 46–52. [Google Scholar] [CrossRef]
- Ministry of Land, Infrastructure, and Transport, Intersection Design Guidelines; MOLIT: Sejong, Korea, 2015; pp. 37–38.
- Baesens, B.G. Bayesian Network Classifiers for Identifying the Slope of the Customer Life Cycle of Longlife Customers. Eur. J. Oper. Res. 2004, 156, 508–523. [Google Scholar] [CrossRef] [Green Version]
- Cheng, J. Comparing bayesian network classifiers. In Proceedings of the 15th Conference on Uncertainty in Artificial Intelligence, Stockholm, Sweden, 30 July–1 August 1999; Morgan Kaufmann Publishers: Burlington, VT, USA, 1999; pp. 101–107. [Google Scholar]
- Langley, P.; Iba, W.; Thompson, K. An analysis of bayesian classifiers. In Proceedings of the Tenth National Conference on Artificial Intelligence, San Jose, CA, USA, 12–16 July 1992; Volume 92, pp. 223–228. [Google Scholar]
- Salzberg, S.L. C4.5: Programs for Machine Learning by J. Ross Quinlan; Morgan Kaufmann Publishers: Baltimore, MD, USA, 1994; pp. 235–240. [Google Scholar]
- Wang, L.K.; Yang, Z.L. Bayesian network modelling and analysis of accident severity in waterborne transportation: A case study in China. Reliab. Eng. Syst. Saf. 2018, 180, 277–289. [Google Scholar] [CrossRef]
- Friedman, N.; Geiger, D.; Goldszmitd, M. Bayesian network classifiers. Mach. Learn. 1997, 29, 131–163. [Google Scholar] [CrossRef] [Green Version]
- Chow, C.K.; Liu, C.N. Approximating discrete probability distributions with dependence trees. IEEE Trans. Inf. Theory 1968, 14, 462–467. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.; Yang, Z.; Smith, J.; Robert, B.A.P. Risk analysis of bicycle accidents: A Bayesian approach. Reliab. Eng. Syst. Saf. 2021, 209, 107460. [Google Scholar] [CrossRef]
- Wegman, F. Analyzing road design risk factors for run-off-road crashes in the Netherlands with crash prediction models. J. Saf. Res. 2014, 49, 121.e1-127. [Google Scholar]
- Martinez, P.; Mohamed, E.; Mohsen, O.; Mohamed, Y. Comparative study of data mining models for prediction of bridge future conditions. J. Perform. Constr. Facil. 2020, 34, 04019108. [Google Scholar] [CrossRef]
- Huang, Y.; Pepe, M.S. A parametric ROC model-based approach for evaluating the predictiveness of continuous markers in case-control studies. Biometrics 2009, 65, 1133–1144. [Google Scholar] [CrossRef] [Green Version]
- Hwaton, K.; Heeringen, K. The International Handbook of Suicide and Attempted Suicide; Wiley Online Library: Somerset, NJ, USA, 2000; pp. 335–412. [Google Scholar]
- Kjaerulff, U.B.; Madsen, A.L. Bayesian Networks and Influence Diagrams: A Guide to Construction and Analysis; Springer: New York, NY, USA, 2008; pp. 107–139. [Google Scholar]
- Park, H.C.; Kim, D.K.; Kho, S.Y. Bayesian Network for Freeway Traffic State Prediction. Transp. Res. Rec. 2018, 2672, 124–135. [Google Scholar] [CrossRef]
- Zegeer, C.V.; Council, F.M. Safety relationships associated with cross-sectional roadway elements. Transp. Res. Rec. 1995, 1512, 29–36. [Google Scholar]
- Zegeer, C.V.; Michael, J.C. Determination of cost-effective roadway treatments for utility pole accidents. Transp. Res. Rec. 1982, 970, 52–64. [Google Scholar]
- Ivey, D.; Zegeer, C.V. Utilities and Roadside Safety; Transportation Research Board: Washington, DC, USA, 2012; pp. 1–81. [Google Scholar]
- TAAS. Traffic Accident Analysis System. Available online: http://taas.koroad.co.kr (accessed on 13 January 2022).
- Elmarakbi, A.; Sennah, K.; Samaan, M.; Siriya, P. Crashworthiness of motor vehicle and traffic light pole in frontal collisions. J. Transp. Eng. 2006, 132, 722–733. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).