Heat Conduction and Cracking of Functionally Graded Materials Using an FDEM-Based Thermo-Mechanical Coupling Model

Abstract

In this paper, the steady-state and transient heat transfer processes of functionally graded materials (FGMs) are analyzed using a coupled thermo-mechanical model in a GPU parallel multiphysics finite–discrete element software, namely MultiFracS. First, the coupled model to handle the heat transfer problem of heterogeneous materials is verified. Then, the advantages and disadvantages of FGMs and composite materials in response to thermal shock loads are compared and the results indicate that FGMs can overcome extreme environments better than composite materials. Finally, the influence of the geometric distribution characteristics of the double-edge cracks in the gradient material plate on the crack propagation is analyzed. The simulation results show that the interaction between the cracks affects the crack propagation path under the thermal load. The inclination angle and spacing of double-edge cracks greatly influence crack propagation. Specifically, a larger inclination angle and spacing can lead to a smaller crack propagation angle. The approach in this paper provides a new quantitative tool for investigating the thermal, elastic, and cracking of functionally graded materials.

1. Introduction

The Japanese materials that scientists proposed for the functionally gradient materials (FGMs) were used to enhance the mechanical properties of heat-resistant materials and reduce the uneven thermal expansion, thermal stress, and residual stress of the material in a high-temperature environment [1]. FGMs are heterogeneous materials with a similar application environment to ceramic materials but a more prominent functional structure. In FGMs, the composition of the material changes continuously, and there is no obvious interface so that the performance of the material changes smoothly and continuously. The characteristics of microstructure and composition transition can increase thermodynamic properties, making it a promising prospect for deep geological drilling. For example, gradient cutting tools with a hard outside and tough inside have higher cutting efficiency, wear resistance, and service life compared with cemented carbide cutting tools. Therefore, the thermal response analysis of FGMs is very important for material design, optimization, and engineering applications. The modeling of FGMs and their response in a thermal environment has always been a hot topic for scholars.

Many analytical methods are used to solve the thermo-mechanical coupling problem of FGMs. For example, Tang [2] derived an analytical solution for the temperature field distribution in a functionally graded plate with a central crack under the action of two different directions of heat flow. Li et al. [3] studied the temperature distribution and the transient response of stress and displacement of functionally graded beams under one-dimensional thermal shock through Timoshenko beam theory and indicated that FGMs could effectively slow down the internal stress extremes. Obata and Noda [4] discussed the steady-state thermal stress in hollow cylindrical and hollow spherical FGMs shells, revealing the influence of radius on the stress and temperature field. Tanigawa et al. [5] studied the macro-response of an FGM plate under thermal load as a linear function and evaluated the magnitude of thermal stress by considering the change of material parameters as a linear function. Lanhe [6] used first-order shear deformation theory to derive the equilibrium equation and stability equation of an FGM rectangular plate, assuming that the material parameters change as a power function with thickness. Shodja and Gghahermaninejad [7] considered that the physical and mechanical parameters of FGM coatings vary exponentially with thickness and studied the influence of coating thickness on the internal temperature and stress of FGM coatings under thermal load. Similarly, Alibeiglool [8] studied the effect of the gradient index, aspect ratio, and thickness-to-length ratio on FGM panels under the thermo-mechanical coupling based on the exponential change of the physical and mechanical parameters. Zenkour and Sobhy [9] assumed that the thermal expansion coefficient and elastic modulus of the FGM plate are distributed in the form of a power function volume fraction and further studied the influence of the loading type on the thermal buckling behavior in the sandwich FGM plate. Zhou et al. used ABAQUS software to study the load distribution in the threads of porous ZrO2/(ZrO2 + Ni) FGM bolt connection thermal protection system [10].

The above analytical methods are mainly based on simple geometrical shapes, such as plates and beams, and only consider the heat conduction in a single direction, or the material parameters that change in the form of simple functions (power functions, exponents, etc.) Additionally, the analytical solutions of steady-state and transient temperature fields and thermal stress distribution are derived. However, analytical methods are difficult to solve complex geometric shapes and boundary conditions and cannot fully reflect the spatial distribution of various parameters of FGMs.

The numerical methods are widely used for the parameter analysis and material design of FGMs due to their low computation cost and strong applicability to boundary conditions. Traditional numerical methods such as the finite element method (FEM), the boundary element method (BEM), the meshless method, and the extended finite element method (XFEM) are widely used in the study of the thermal response of complex FGMs. For example, Zhang et al. [11] analyzed the functional gradient plate with cracks under thermal load based on the FEM and indicated that the spatial distribution of material components has a significant influence on the thermal stress intensity factor (TSIF). Peng and Chen [12] also used the FEM to study the thermal fracture of an FGM thick-walled cylinder with cracks under thermal shock load. Moghaddam and Alfano [13] performed a thermo-elastic analysis of FGM hollow cylinders with surface cracks based on the FEM. Dai et al. [14] studied the temperature distribution of the FGM plate under thermo-mechanical coupling and considered the influence of gradient parameters using the meshless Galerkin method. Sutradhar et al. [15] used Galerkin the BEM to simulate the FEG heat conduction process, and the simulation results agree with the analytical solution. Ashrafi et al. [16] investigated the thermo-elasticity of a three-dimensional FGM hollow cylinder based on the BEM and analyzed the temperature and stress changes inside the material. Yu et al. [17] studied the effect of circular holes on the heat conduction of FGM plates through the BEM and compared them with the results of various numerical methods. Zheng [18] studied the thermo-elasticity of FGMs based on the combination of the radial integration method and the BEM and applied it to analyze the dynamic fracture of materials. Garg and Pant [19] studied the influence of edge crack length on the TSIF in FGM plates under thermal load based on the element-free Galerkin method. Wang and Qin [20,21] used the meshless method to simulate the steady-state heat conduction and thermal stress distribution in a two-dimensional FGM plate. Based on aerodynamics, Wang et al. [22] studied the effects of the spatial distribution of material components, porosity, and boundary temperature on the transient thermal response of FGMs. Hu et al. [23] used the numerical manifold method (NMM) to study the steady-state heat transfer of FGMs and compared it with the existing analytical solution. They concluded that this method can simulate the steady-state heat conduction problem of FGMs. However, most of these numerical methods are limited to studying the stress intensity factor at the crack tip when dealing with the fracture of FGMs under thermal shock loading. These methods cannot consider the propagation and extension of the crack. The reason is that these numerical methods are mostly continuous, and it is difficult to simulate crack initiation, propagation, and interaction.

To this end, we studied FGM thermal-mechanical coupling and thermal cracking behavior using a GPU parallel multiphysics finite–discrete element software, namely MultiFracS, developed by Yan [24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53]. A heterogeneous material evaluation function module is added in the continuous–discontinuous thermo-mechanical coupling model to consider the variation of material parameters with space position. Thus, the heat transfer and thermo-mechanical coupling behavior of FGMs can be studied. It should be pointed out that the difference between the coupled thermo-mechanical model in this paper and in the literature [34] is that the heat conduction model in this paper can consider the hindering effect of cracks on heat transfer and can dynamically update the sharing relationship of triangular element nodes on both sides of the cracks during the crack propagation. However, in the heat conduction model in the literature [34], the adjacent triangular element always shares nodes during heat transfer calculation, Therefore, it is impossible to consider the hindering effect of cracks on heat transfer. Therefore, the heat conduction model in this paper is better than that in the literature [34]. This paper mainly includes the following aspects. First, the heat transfer models for FGMs are validated, including steady-state and transient heat conduction. Second, we analyze the steady-state thermal stress of the composite material and FGMs to verify the performance of the gradient material. Finally, the effect of geometrical parameters of pre-set cracks on crack propagation in FGMs is discussed.

2. Fundamentals of the Continuous–Discontinuous Thermo-Mechanical Coupling Model

2.1. The Continuous–Discontinuous Heat Conduction Model

As shown in Figure 1, the entire continuous–discontinuous medium is divided into triangular elements. The adjacent triangular elements on both sides of the crack do not share nodes, while the remaining adjacent triangular elements share nodes. The temperature distribution within a triangular element is represented by linear interpolation of the temperature at the three nodes of the triangular element. In addition, heat conduction inside the triangular element and heat transfer between adjacent triangular elements may occur through the crack. Therefore, we can obtain the temperature distribution of the entire continuum region.

For any given mass M, the temperature change is expressed as follows:

$$\frac{\partial T}{\partial t}=\frac{Q_{total}}{C_{p}M}$$

(1)

where $Q_{total}$ is the net heat flux flowing into the mass M per unit time, $C_p$ is the specific heat capacity, and M is the mass.

Figure 1a shows that the continuous–discontinuous medium is divided into finite element meshes of triangular elements. Then, the nodes at the cracks are separated, as shown in Figure 1b. The entire continuous–discontinuous medium is discretized into triangular elements composed of nodes. The temperature distribution of the entire continuous–discontinuous medium can be roughly estimated from the temperature at the nodes of these triangle elements. The temperature distribution in each triangular element can be obtained by linear interpolation based on the element’s three nodes. The mass of the triangle element is distributed evenly among the three nodes of the triangular element. The mass of each node is equal to 1/3 of the mass of all the triangular elements that share the node. Based on the relationship between the elements and nodes illustrated in Figure 1b, we will explain how to calculate the temperature field for the entire continuous–discontinuous medium.

Taking node 4 in Figure 1b as an example, the triangular elements sharing node 4 are Δ345, Δ456, and Δ134. Since the temperature of node 4 may be different from the temperature of nodes 1, 3, 5, and 6, heat conduction may occur in these triangular elements that share node 4. Take the triangular element Δ345 as an example. We assume that the temperature field distribution in the triangular element follows a linear distribution. The temperature gradient at any point in the same triangular element is constant, which can be expressed as:

$$\frac{\partial T}{\partial x_i}=\frac{1}{A}{\displaystyle \underset{A}{\int }\frac{\partial T}{\partial x_i}dA}=\frac{1}{A}{\displaystyle \underset{s}{\int }T{n}_{i}ds}=\frac{1}{A}{\displaystyle \sum _{m=1}^3{\overline{T}}^m}{\in }_{ij}\mathsf{\Delta }{x}_j^m$$

(2)

where $A$ is the area of the triangular element, $n_i$ is the outer normal vector, ${\overline{T}}^m$ is the average temperature of the edge m, $\mathsf{\Delta }{x}_j^m$ is the difference between the coordinate components of the two vertices of the edge m side, and ${\in }_{ij}$ is the two-dimensional permutation tensor $\in =\left(\begin{array}{cc}0& 1\\ -1& 0\end{array}\right)$.

Based on Fourier’s law of heat conduction, the heat flow rate per unit cross-sectional area in the i direction is given by:

$$q_i=-k_{ij}\frac{\partial T}{\partial x_j}$$

(3)

where k_ij is the thermal conductivity tensor, T is the temperature, and x_j is the position vector.

The temperature of node 4 in the next time step Δt is as follows:

$$T_4^{t+\mathsf{\Delta }t}=T_4^t+\frac{Q_{total\to 4}}{C_{p}M}\mathsf{\Delta }t$$

(4)

The temperature of the other nodes can be obtained similarly according to the above step. Based on this, we can obtain the evolution of the temperature field in the entire solution domain.

In addition, the continuous–discontinuous heat conduction model can also dynamically update the node-sharing relationship of adjacent triangular elements at the cracks and consider the effect of cracks caused by thermal cracking on heat transfer. For details, please refer to the literature [27].

2.2. Thermal Stress Calculation

The change in the temperature field leads to a change in the stress field. The thermal stress caused by the temperature change $\mathsf{\Delta }{\sigma }_{ij}$ is given by:

$$\mathsf{\Delta }{\sigma }_{ij}=-{\delta }_{ij}3K^{*}\alpha \mathsf{\Delta }T$$

(5)

where $\alpha$ is the thermal expansion coefficient, in the plane strain problem $K^{*}=K$, and in the plane stress problem, $K^{*}=6KG/\left(3K+4G\right)$ ($K$ is the bulk modulus and $G$ is the shear modulus) [27].

The thermal stress is applied to the triangular element as a body load, and the equivalent nodal force of the thermal stress is given by:

$$f_n=-\frac{1}{2}{\delta }_{ij}3K^{*}\alpha \mathsf{\Delta }T{n}_{j}L$$

(6)

where $n_j$ is the external normal vector of the triangle element edge and L is the edge length of the triangle element [27].

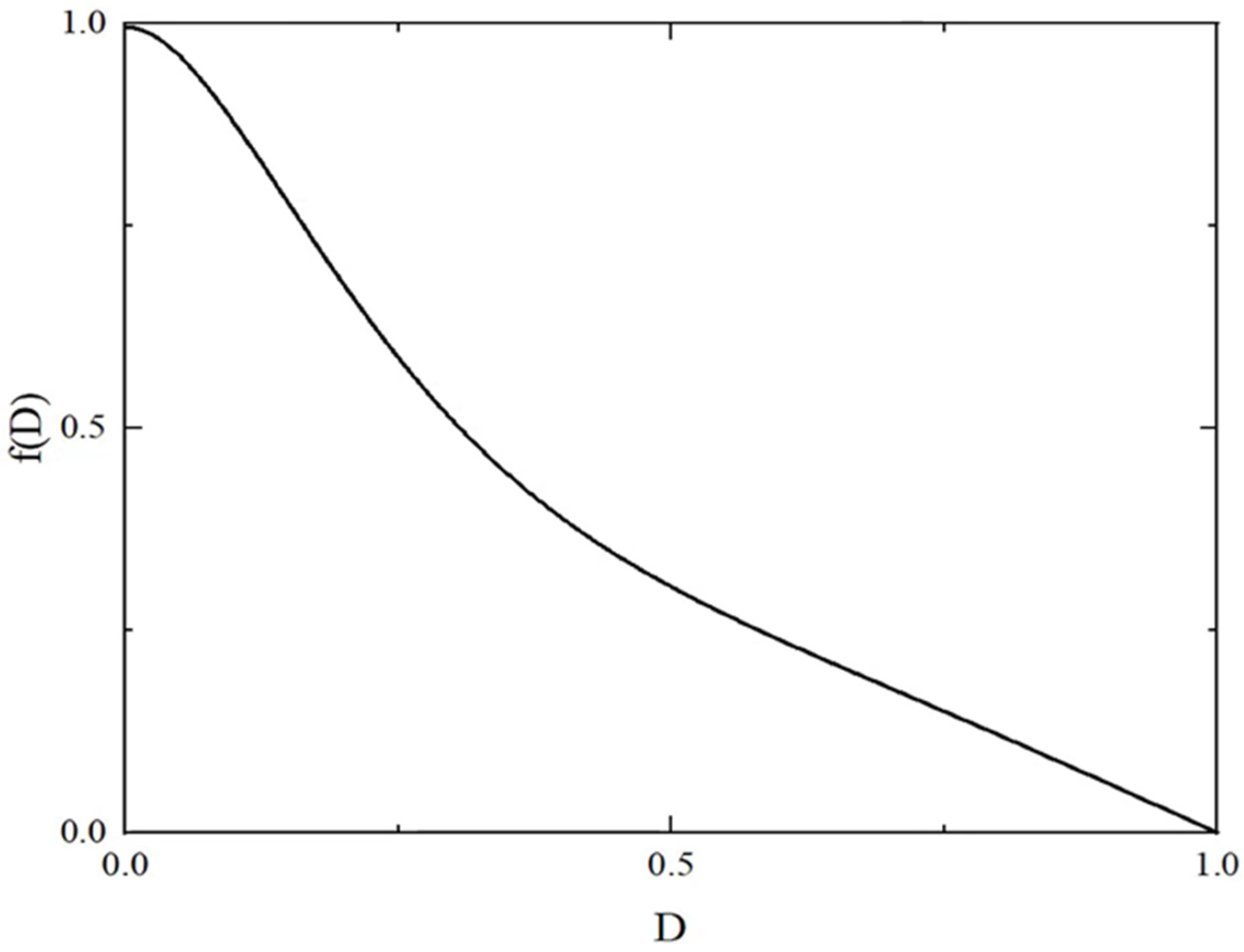
2.3. FDEM Mechanical Fracture Calculation

The equivalent nodal force of the thermal stress calculated in the previous section is input as a point load, and the FDEM mechanical fracture calculation is performed. In the FDEM, the solution domain is divided into finite element meshes of triangular elements, and initial thicknesses of joint elements, are inserted on the common edge of adjacent triangular elements (Figure 2). In this way, the triangular elements do not share nodes. The initiation, propagation, and intersection of cracks in the continuum are modeled by the breakage of joint elements. The deformation of the continuum is simulated by the bonding of the constant strain triangular element and the joint element before the joint elements are broken. The masses and forces of all triangular elements are equivalent to the nodes of the element. The motion of the nodes is determined according to Newton’s second law. After obtaining the displacement of the node, the displacement of the element is also determined.

2.3.1. FDEM Control Equation

Based on Newton’s second law, the dynamic equation of nodes in FDEM is:

$$M\ddot{x}+C\dot{x}=F$$

(7)

where M and C are the diagonal mass matrix and damping matrix of the nodes in the system, respectively, and F represents nodal force.

According to Equation (12), the coordinates and velocities of the triangular element nodes are updated at each time step using Euler’s method:

$$\begin{array}{l}{v}_i^{(t+\mathsf{\Delta }t)}=v_i^{(t)}+{\displaystyle \sum F_i^{(t)}\frac{\mathsf{\Delta }t}{m_n}}\\ x_i^{(t+\mathsf{\Delta }t)}=x_i^{(t)}+v_i^{(t)}\mathsf{\Delta }t\end{array}$$

(8)

where $F_i^{(t)}$ represents the total nodal force, $\mathsf{\Delta }t$ is the time step, and $m_n$ is the mass of the nodal, which is equal to one-third of the mass of the triangular element.

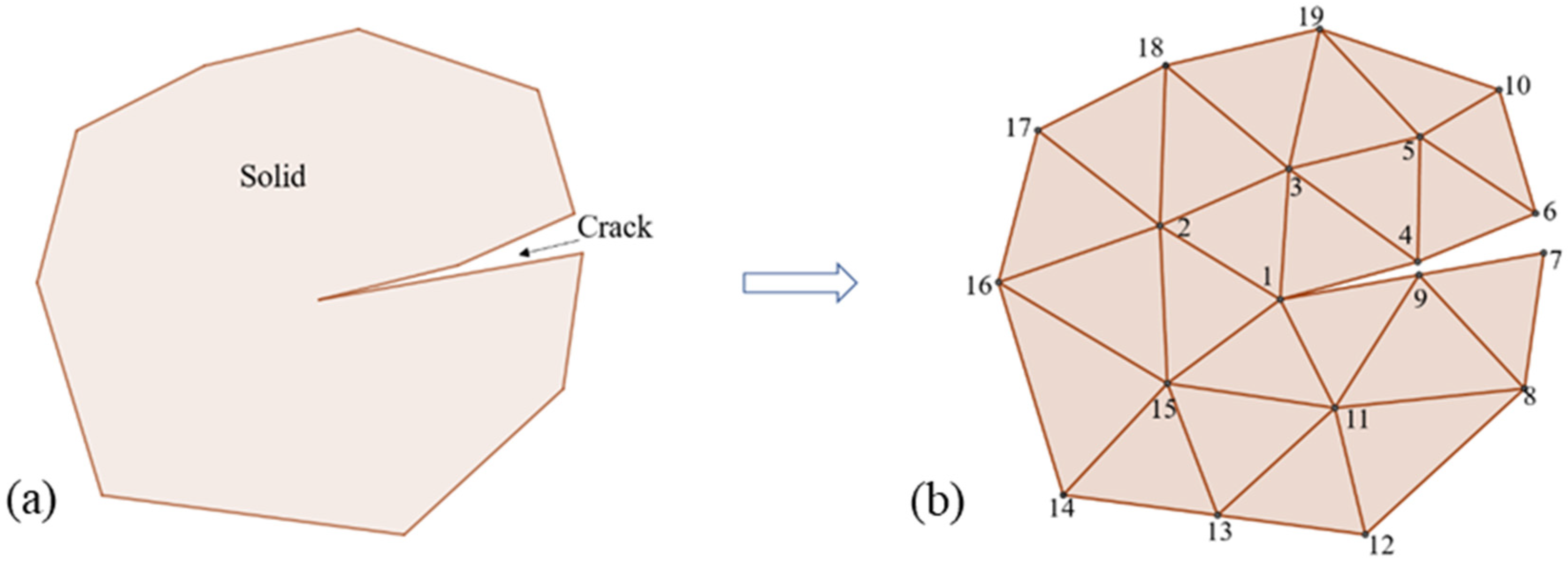
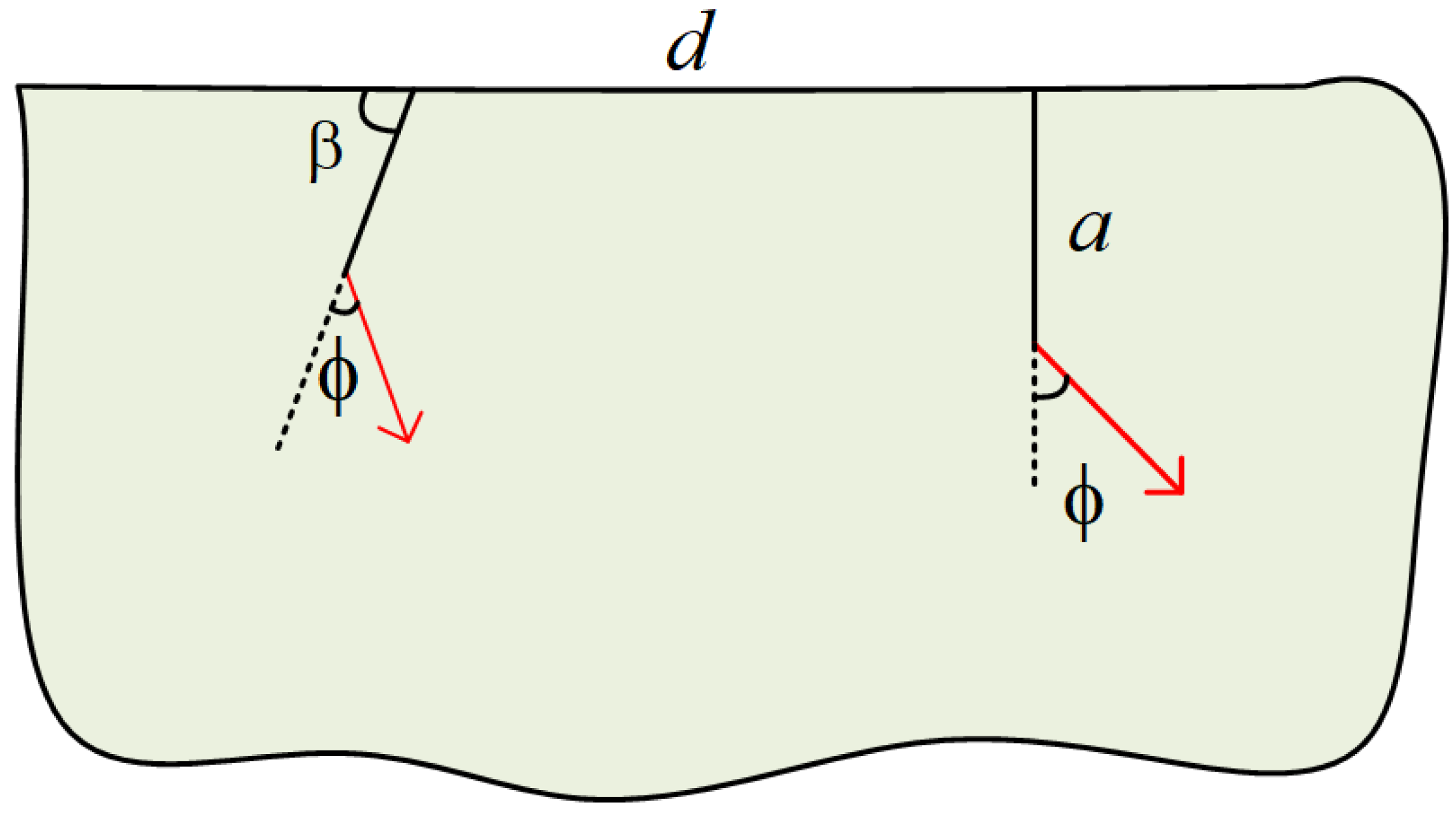
2.3.2. Fracture Simulation

As shown in Figure 3, the joint elements are inserted between the adjacent triangular elements. The two adjacent triangular elements connected by a joint element may relatively move under the action of external loads. This relative motion can be decomposed as the normal and tangential displacement perpendicular or parallel to the joint plane. According to the normal and tangential displacement of the joint element, the damaged state of the joint element can be determined. The damage variable D of the joint element is defined by:

$$D=\{\begin{array}{c}0,\hspace{1em}o<o_p\&\&s<s_p\\ \frac{o-o_p}{o_r-o_p},\hspace{1em}o\ge o_p\&\&s<s_p\\ \frac{s-s_p}{s_r-s_p},\hspace{1em}o<o_p\&\&s\ge s_p\\ \sqrt{{\left(\frac{o-o_p}{o_r-o_p}\right)}^2+{\left(\frac{s-s_p}{s_r-s_p}\right)}^2},\hspace{1em}o\ge o_p\&\&s\ge s_p\end{array}$$

(9)

where $o_p$ is the critical normal opening displacement of the joint element when the normal stress reaches the tensile strength in the case of the pure tensile state. In the case of the pure shear state, $s_p$ is the critical tangential displacement of the joint element. $o_t$ and $s_t$ is the maximum normal opening displacement and the maximum tangential displacement when the pure tensile or shear failure occurs. If the damage variable is D > 1, according to Equation (1), then we set D = 1.

Based on the damage variable $D$ of the joint element, we can obtain the reduction factors of the tangential and the normal stress of the joint element $f(D)$ in the following equation [54,55]:

$$f(D)=\left(1-\frac{a+b-1}{a+b}{e}^{\left(\frac{D(a+cb)}{(a+b)(1-a-b)}\right)}\right)\left(a(1-D)+b{(1-D)}^c\right)$$

(10)

where $a,b,c$ are the parameters obtained by fitting the experiment curve when the material is under tension and where $a=0.63,b=1.8,c=6.0$. Figure 4 shows the curve of the reduction coefficient $f(D)$.

In this way, the normal stress and tangential stress of the joint element can be expressed as follows:

$$\sigma =\{\begin{array}{ll}\frac{2o}{o_p}{f}_t& \mathrm{if}o<0\\ \left(\left[\frac{2o}{o_p}-{\left(\frac{o}{o_p}\right)}^2\right]f_t\right)f(D)& \mathrm{if}0\le o\le o_p\\ \\ f(D)f_t& \mathrm{if}o>o_p\end{array}$$

(11)

$${\tau }^{coh}=\{\begin{array}{ll}\left[\frac{2\left|s\right|}{s_p}-{\left(\frac{\left|s\right|}{s_p}\right)}^2\right]\left(-\sigma \tan \left(\varphi \right)+c\right)f\left(D\right)& \mathrm{if}0\le \left|s\right|\le s_p\\ \left(-\sigma \tan \left(\varphi \right)+c\right)f\left(D\right)& \mathrm{if}\left|s\right|\text{>}{s}_p\end{array}$$

(12)

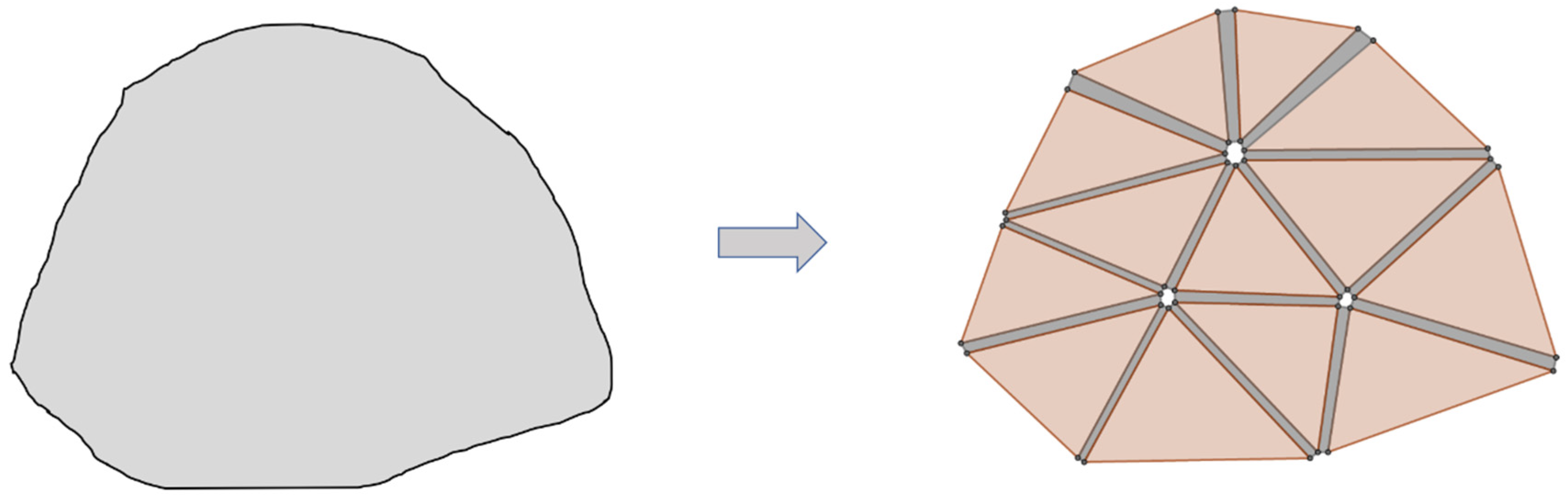
3. Model Setup of FGMs in FDEM

The variation of material properties in spatial position is referred to as the parameter gradient change of FGMs, and it can be expressed as a function related to the spatial position coordinates, such as exponential, linear, quadratic, trigonometric, and hyperbolic functions. The continuous function enables the material properties and physical parameters to change the gradient along the thickness direction. The key parameters in FGMs are usually elastic modulus, thermal expansion coefficient, thermal conductivity, and Poisson’s ratio.

The parameters of FGMs gradually change in a specific direction. This continual material change is reflected in the material parameters as a function of spatial position coordinates, which is different from the conventional method of assigning homogenous material parameters. Figure 5 shows the distribution diagram of FGM parameters changing with spatial position coordinates.

The parameter is continuously changing within the material. There are various distribution functions for a single variable with a specific direction. As shown in Figure 6, the most common distributions are quadratic, exponential, trigonometric function, hyperbolic tangent, etc. The distribution functions are as follows:

$${f\left(y\right)=f}_0{{(a}_1+\beta y)}^2$$

(13)

$$f(y)=f_0{a}_1{e}^{\beta y}$$

(14)

$$f(y)=f_0(a_1\cos \beta y+a_2\sin \beta y)$$

(15)

$$f(y)=\frac{f^{-}+f^{+}}{2}+\frac{f^{-}-f^{+}}{2}\tanh [\mathsf{\delta }(y+d)]$$

(16)

where f is a parameter of FGMs, f₀ is the reference value of this parameter, f⁻ and f⁺ are the parameter values at both ends of the material, $a_1$, $\mathsf{\delta }$, and $d$ are constants, and β is the gradient coefficient.

Different distribution functions and coefficients can lead to the different dynamic responses of materials under thermal stress. Then, the correctness of the conduction model for simulating the thermal conduction in FGMs is verified before considering the dynamic response of FGMs under thermal shock.

4. Model Validation

4.1. Verification of Steady-State Heat Conduction for the FGM Model

As shown in Figure 7, a 1 m × 1 m model is established and discretized into 914 triangular meshes. The initial temperature of the model is 0 °C, the top boundary is T₁ = 100 °C, the bottom boundary is T₁ = 0 °C, and the left and right boundaries are adiabatic boundaries. The thermal conductivity is assumed to obey the square distribution in the y direction, expressed as follows:

$$k(y)=k_0{(1+ay)}^2$$

(17)

where k₀ is the heat conduction coefficient at y = 0 and a is the gradient coefficient [56].

The analytical solution to this problem is [56]:

$$T=\frac{(1+aL)T_{1}y}{(1+ay)L}$$

(18)

To verify the correctness of the model for solving the steady-state heat conduction problem of FGMs, the temperature distribution obtained by the FDEM model is compared with the analytical solution under different gradient coefficients, as shown in Figure 8. The numerical solution is in good agreement with the analytical solution. In addition, it can be seen that a larger gradient coefficient leads to a larger temperature gradient from bottom to top along the y direction. The reason is that the larger the gradient coefficient, the greater the thermal conductivity from the top, and the smaller the temperature gradient. When $a$ = 0, the thermal conductivity is constant, so the steady-state temperature gradient in the plate is the same. Figure 9 shows the steady-state heat conduction temperature distribution of the FGM plate under the square distribution with different a. As the gradient coefficient increases, the temperature gradient near the bottom becomes larger.

Next, we consider the temperature distribution inside the plate when the thermal conductivity is an exponential function. The model size is 0.4 m × 0.4 m and the initial temperature and boundary conditions are the same as in the square distribution example. The thermal conductivity is exponentially distributed in the y direction, and its gradient function is as follows:

$$k(y)=k_0{e}^{2by}$$

(19)

where b is the gradient coefficient.

The analytical solution ($y>0$) to this problem is [56]:

$$T=T_1\frac{e^{-2by}-1}{e^{-2bL}-1}$$

(20)

Figure 10 illustrates the numerical and analytical solutions of the temperature distribution in the plate under the exponential distribution. As the gradient coefficient increases, the slope of the curve also increases. Since the thermal conductivity is exponentially distributed from top to bottom and positively correlated with the gradient coefficient, the temperature gradient at the bottom is greater than that at the top. Figure 11 presents the steady-state conduction temperature distribution of the plate under exponential distribution.

The above analysis compares the numerical solution to the analytical solution while considering the effects of two function distribution methods and gradient coefficients on the steady-state heat conduction of the plate. It can be concluded that the model has a high accuracy for simulating heterogeneous steady-state heat conduction.

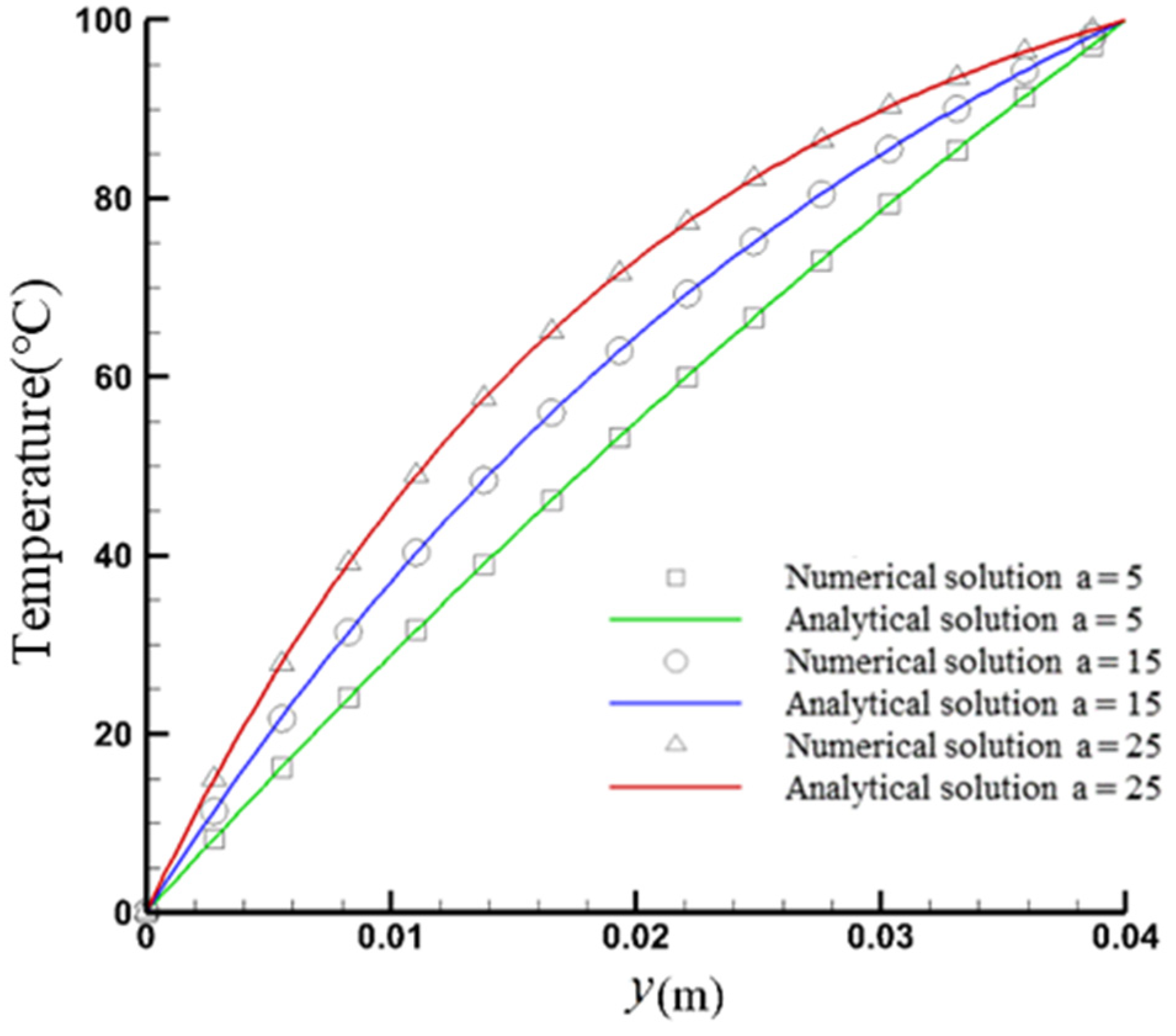
4.2. Verification of Transient Heat Conduction in FGMs

In this section, we will verify the correctness of FDEM-TM in handling the FGM transient heat transfer problem. The size of the model is shown in Figure 7. The top temperature is T₁ = 100 °C, the bottom temperature is T₂ = 0 °C, and the left and right sides are adiabatic boundaries. The parameters distribution functions of the model are as follows:

$$k(y)=k_0{e}^{\beta z}$$

(21)

$$c(y)=c_0{e}^{\beta z}$$

(22)

where c₀ is the specific heat capacity and β is the gradient parameter.

The analytical solution of the temperature distribution inside the model over time is as follows [57]:

$$T(y,t)=T\frac{1-e^{-2\mathsf{\beta }y}}{1-e^{-2\mathsf{\beta }L}}+{\displaystyle \sum _{n=1}^{\infty }{B}_n}{e}^{-\mathsf{\beta }y}{e}^{-(n^2{\mathsf{\pi }}^2/L^2+{\mathsf{\beta }}^2)\mathsf{\alpha }t}\sin \frac{n\mathsf{\pi }y}{L}$$

(23)

$$B_n=-\frac{2T_1{e}^{\mathsf{\beta }L}}{{\mathsf{\beta }}^2{L}^2+n^2{\mathsf{\pi }}^2}\times \left[\mathsf{\beta }L\frac{1+e^{-2\mathsf{\beta }y}}{1-e^{-2\mathsf{\beta }L}}\sin n\mathsf{\pi }-n\mathsf{\pi }\cos n\mathsf{\pi }\right]$$

(24)

where $\mathsf{\alpha }=k_0/c_0$L is the size of the model along the y direction.

This section takes $k_0$ = 5 W/(m·K), $c_0$ = 1 J/(kg·K), and the gradient parameter β = 1.5. Figure 12 shows the simulation results, and we compare the temperature distribution along the y direction inside the model in the time interval 0.003–0.1 s. The numerical solution agrees well with the analytical solution. Initially, the temperature gradient at the bottom of the model is small at first but large at the top. As time increases, the temperature gradient at the bottom of the model becomes larger while it becomes smaller at the top. Figure 13 presents the temperature distribution inside the model when t = 0.01 s and t = 0.1 s. From the above, it can be verified that the model is correct for solving the thermal conduction model of transient FGMs.

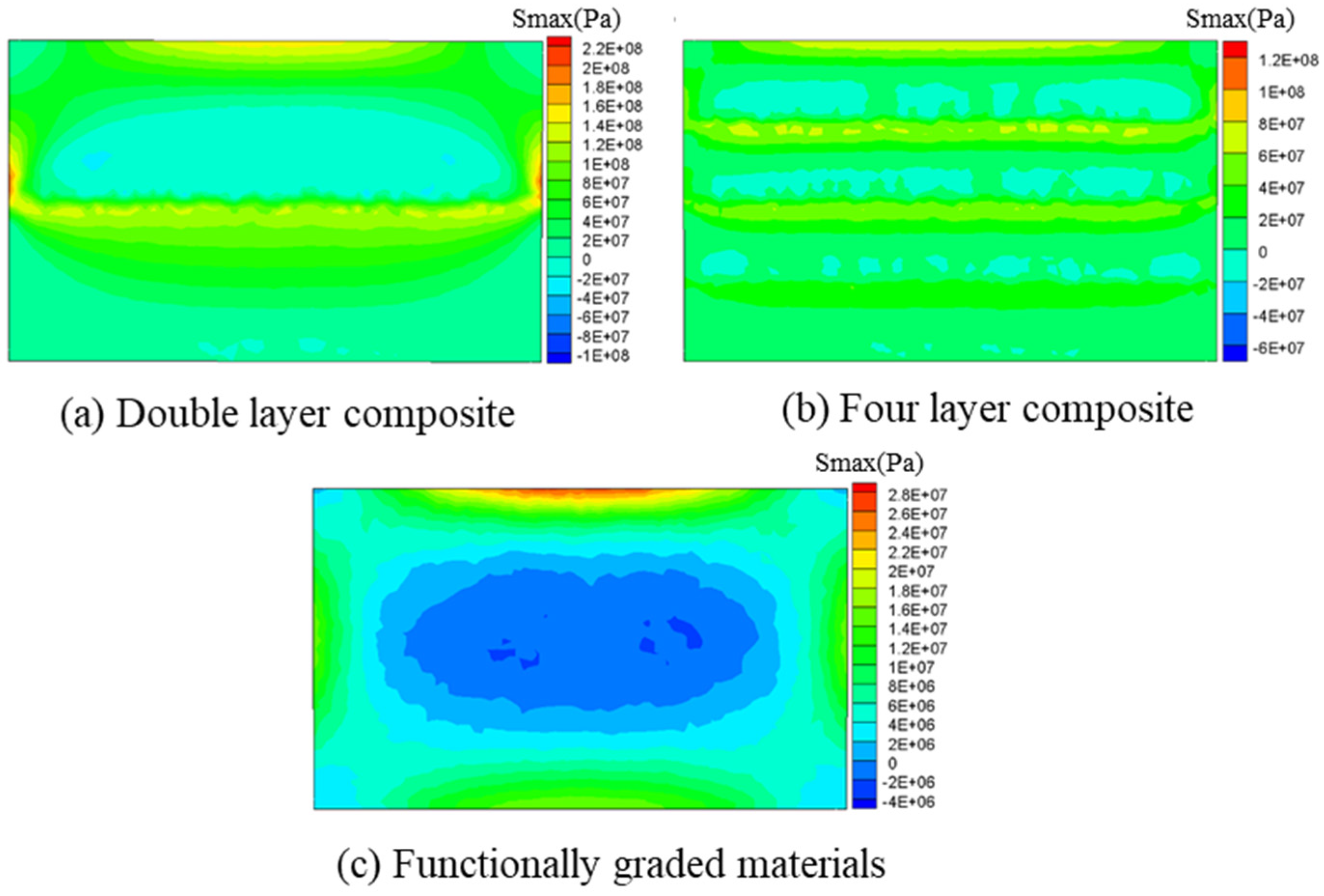
5. Thermal Stress Analysis of FGMs and Composite Materials

The composition and properties of FGMs exhibit spatial gradients without obvious interfaces by controlling the distribution of trace elements during production. Since the elastic modulus, Poisson’s ratio, thermal conductivity, and other parameters show continuous changes in space, the thermal stress inside the material can be alleviated to meet specific needs. In addition, the composite is divided into multiple layers from a macro perspective and the internal parameters of each layer are the same, which can also alleviate thermal stress by decreasing or increasing the parameters layer by layer. This reflects the advantages of FGMs in relieving thermal stress and preventing thermal damage; the thermal stresses of FGMs and composite materials are compared under the same boundary conditions in this section.

As shown in Figure 14, the initial temperature of the model is 500 °C, the environment temperature T_c = 25 °C, and the left and right boundaries are adiabatic. The heat conduction coefficient between the model and the environment is 2000 W/(m²·K). The model is divided into 4054 triangular elements. The composites are divided into two and four layers to study the effect of the different layers’ parameter distribution on the model’s residual thermal stress. The parameters distribution of the models (E-elastic modulus, k-thermal conductivity coefficient, α-thermal expansion coefficient, and v-Poisson’s ratio) are shown in Figure 15.

The exponential function distribution is used here as an example in FGMs, which is as follows:

$$E=100\times {10}^9\ast e^{(In(4)\ast y/0.03)}$$

(25)

$$k=20\ast {\mathrm{e}}^{(In(8.5)\ast y/0.03)}$$

(26)

$$\mathsf{\alpha }=9\times {10}^{-6}\ast e^{(In(4.2/9)\ast y/0.03)}$$

(27)

$$v=0.03\ast e^{(In(28/31)\ast y/0.03)}$$

(28)

The residual maximum principal stress distributions for the three different parameter distribution models are shown in Figure 16. For composite materials, there are still obvious stress concentrations and stress sudden-change phenomena at the interface of the composite material. The more layers of the composite material, the better the stress at the interface can be relieved. For FGMs, only smaller tensile stress concentrations are generated on the upper surface of the model. Next, we set a monitoring line at the model coordinates (0.025 m, 0) and (0.025 m, 0.03 m) to compare the maximum principal stress distribution of the three models. The maximum principal stress distributed along the y-direction for three different parameter distribution models is shown in Figure 17. Under the same thickness condition, the maximum principal stress of the four-layer composite material is smaller than that of the double-layer material, indicating that increasing the number of material layers can improve the thermal stress distribution inside the material. On the monitoring line, the maximum principal stress of the double-layer and four-layer composite materials can reach 1.2 × 10⁸ Pa and 5 × 10⁷ Pa, respectively, while only 1.5 × 10⁷ Pa for FGMs. The thermal stress inside the FGMs is significantly reduced. The maximum principal stress peak of the composite material is at the interface, and the maximum principal stress peaks decrease with the increase in layer numbers. The maximum principal stress distribution curve of FGM shows that stress in the FGM material is continuously distributed inside. It should be pointed out that FGMs can be regarded as special cases of composite materials when the number of layers tends to be infinite.

In summary, it can be concluded that the internal physical and mechanical properties in FGMs are continuous and there is no interfacial stress. Compared with composite materials, FGMs are better for overcoming temperature changes in an extreme environment.

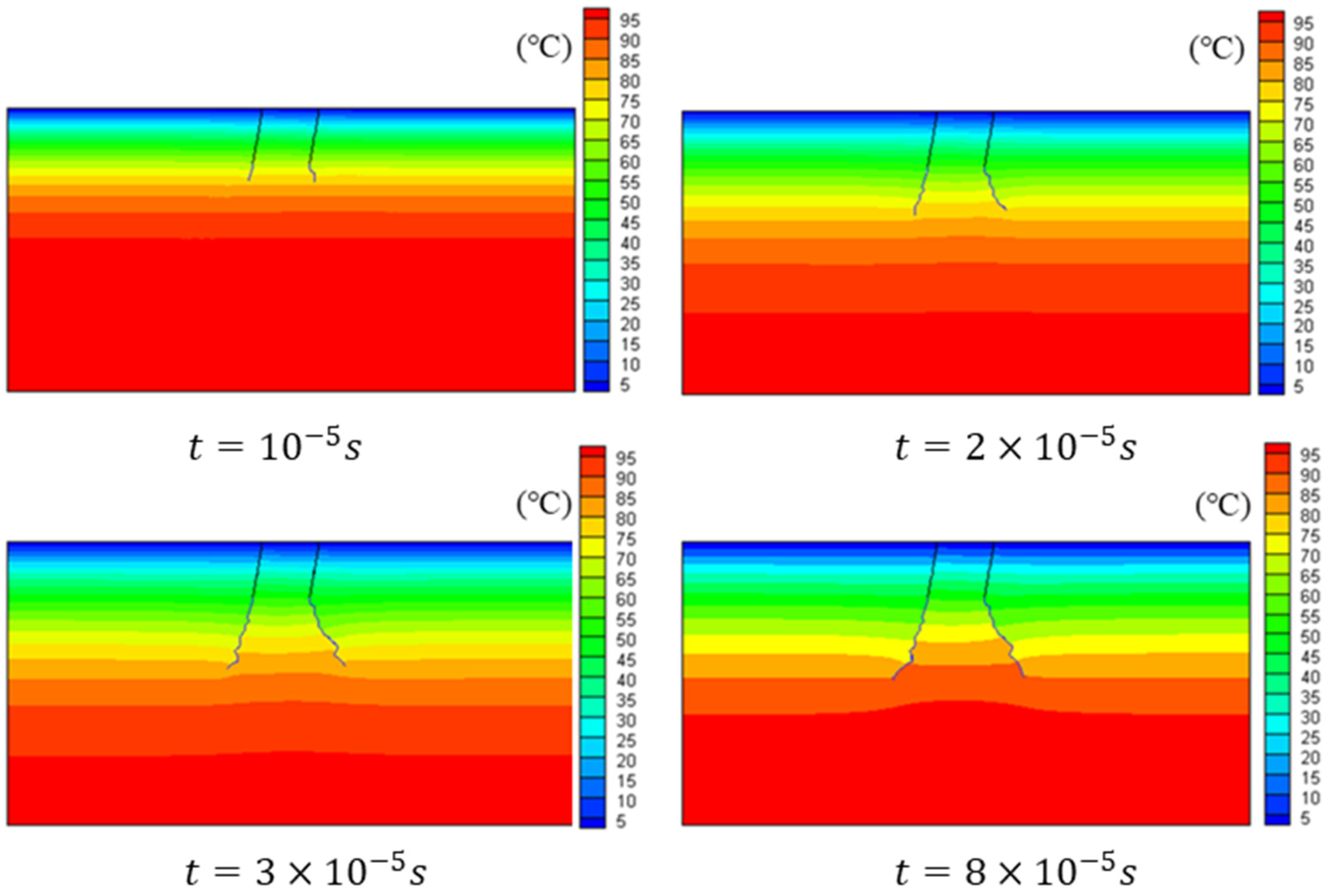
6. Thermal Cracking Simulation in FGMs

Microcracks are generated during the thermal cracking of FGMs under temperature load, affecting the stress distribution and crack propagation inside the material. Cracks in FGMs are easily affected by temperature, leading to the re-extending of cracks and damage to the material structure. In addition, the spatial distribution characteristics of these cracks, such as the inclination angle and spacing of the cracks, could not be ignored (Figure 18). The thermal cracking of FGMs under temperature load and the influence of crack spacing and the inclination on crack propagation is investigated in this section.

For this purpose, we establish an FGM model with double-edge cracks to study its crack propagation under temperature load, as shown in Figure 18. Assuming that the initial temperature of FGMs is high, the surface suddenly cools. Then, the existing cracks will further propagate and affect each other under thermal stress due to a large temperature difference. This section mainly uses the thermo-mechanical coupling model to study the influence of the inclination and spacing of the double-edge cracks on the crack propagation angle. The numerical model has a length of 0.4 m and a width of 0.2 m. The double-edge cracks are symmetrically distributed on both sides of the model. The geometric boundary conditions of the model are shown in Figure 19. The initial crack length of the model $a$ = 0.04 m, and the crack spacing is assumed to be a multiple of the crack length ($d$ = $a$, 2$a$ and 4$a$). The crack inclination angles are 60°, 70°, 80°, and 90°, respectively. The initial temperature of the model is 100 °C, the top surface temperature is 0 °C, and the left and right boundaries are adiabatic.

Here, a combination of ceramic and metal are used in FGMs. The top layer of the material has the corrosion resistance and high-temperature resistance of ceramics, and the bottom material has the high strength characteristics of the metal. The input parameters in FDEM are shown in

Table 1. Thermophysical parameters of FGMs.

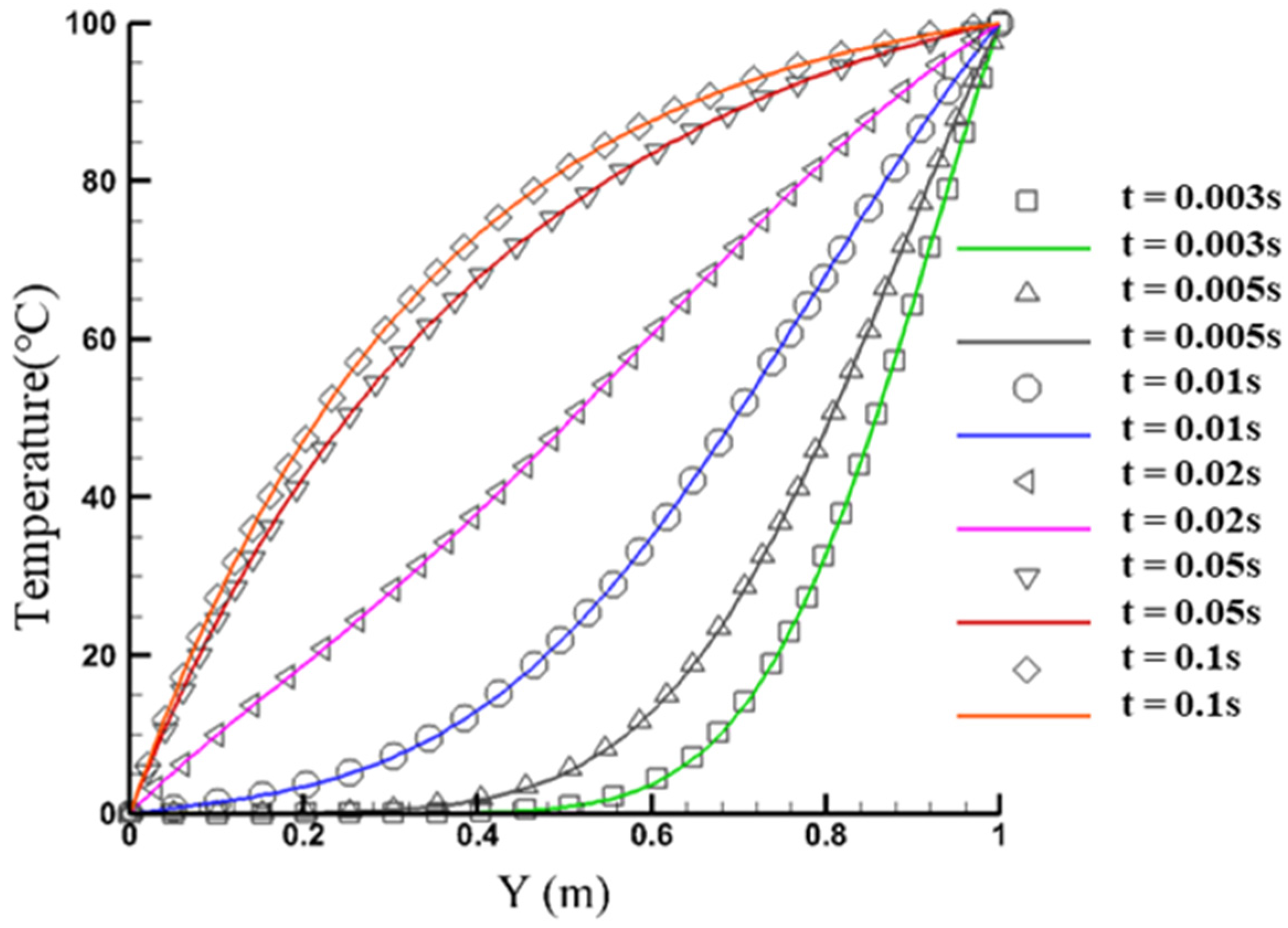
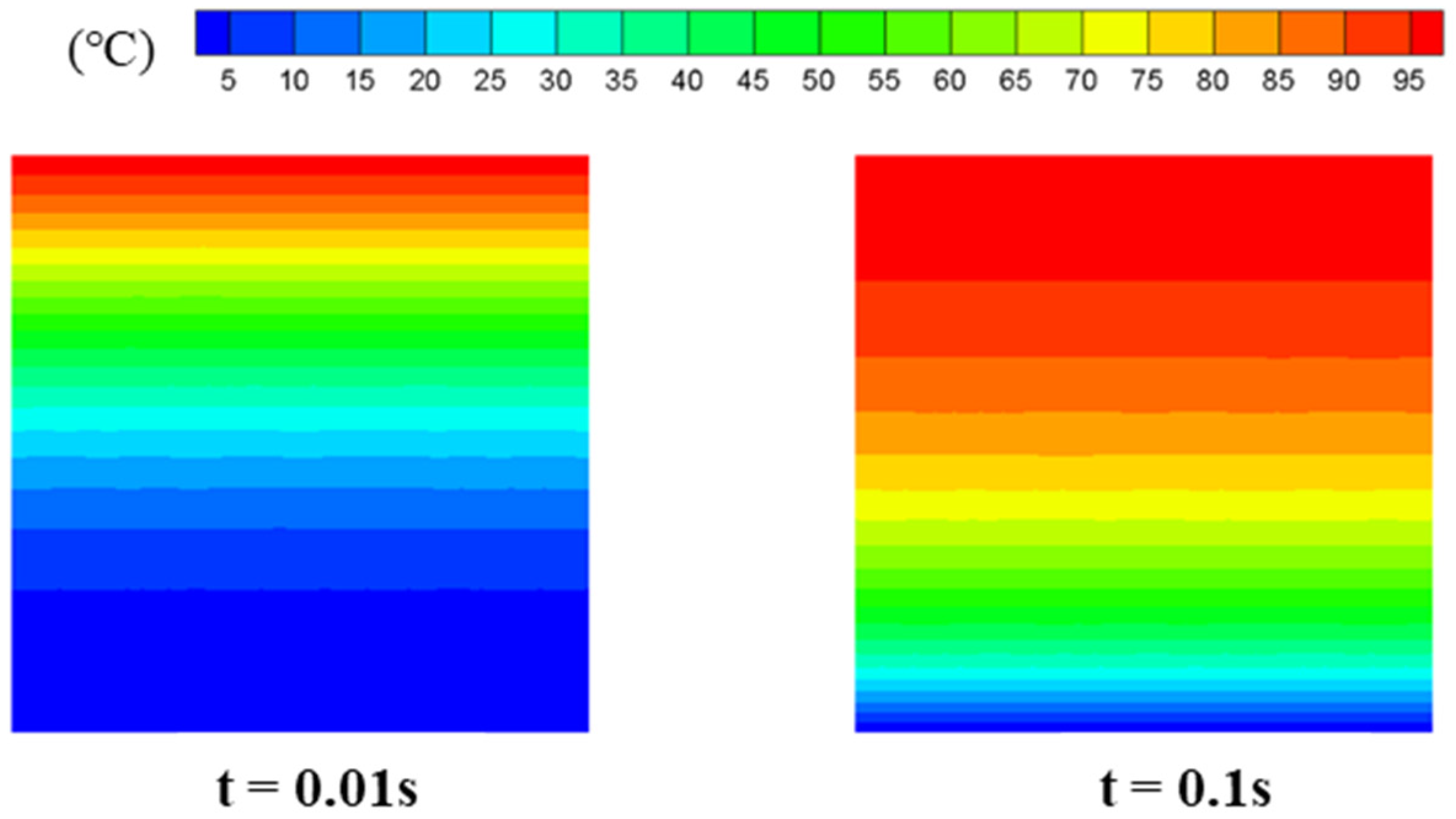
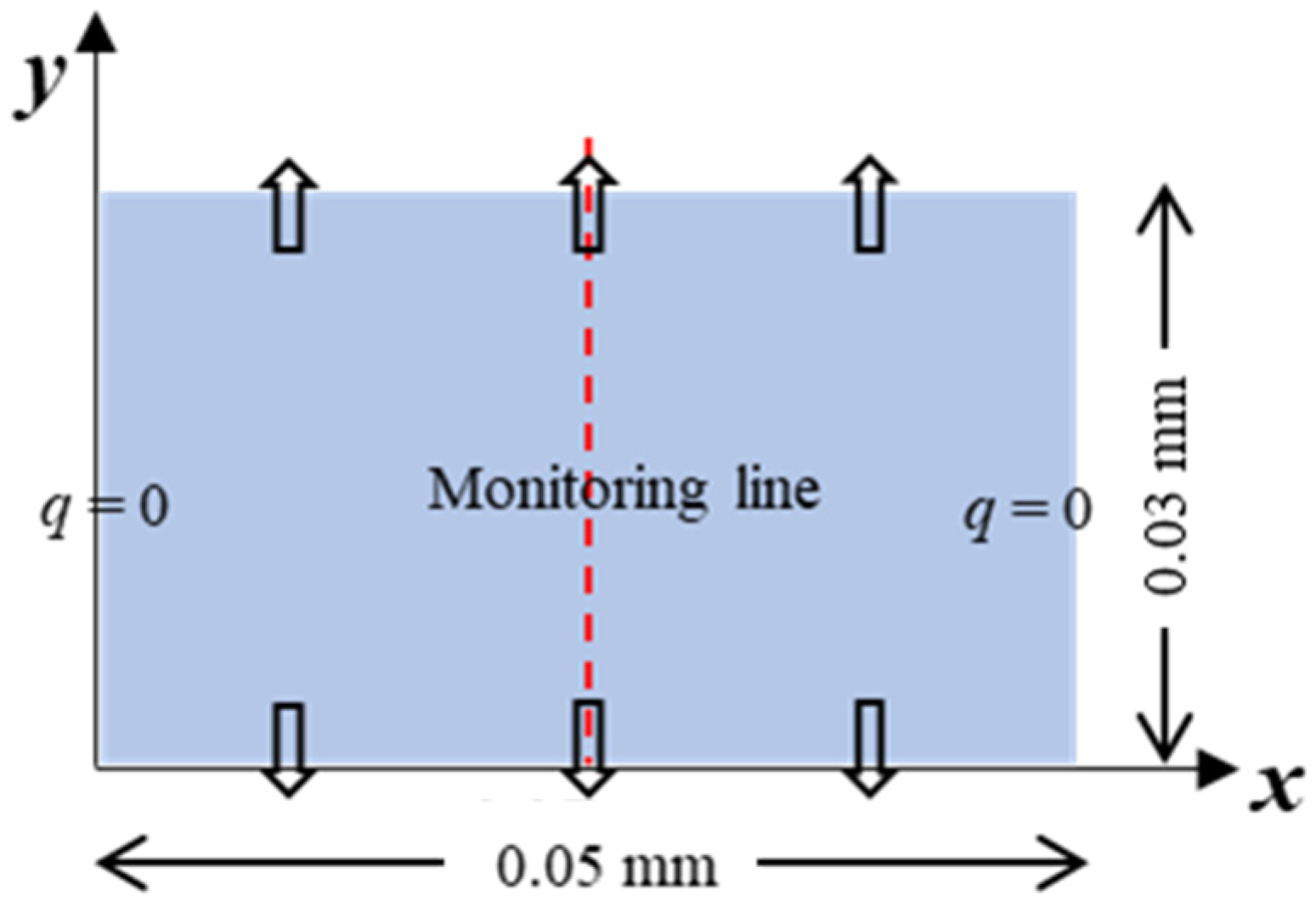
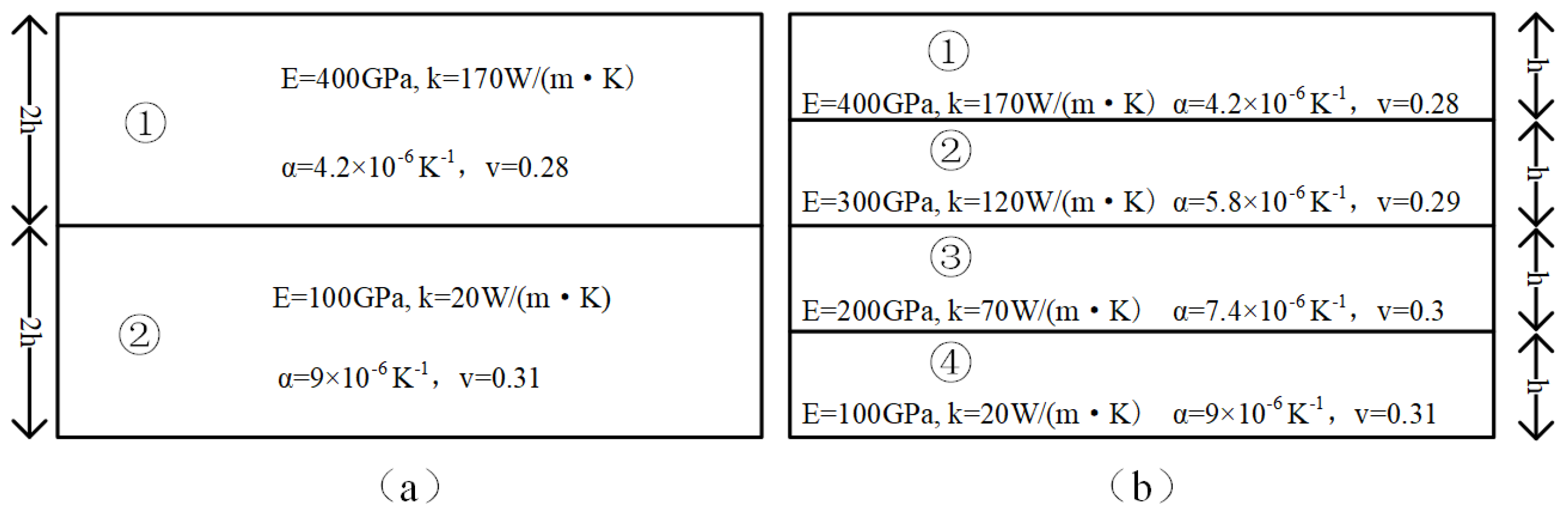
Thermal Physical Parameters	Ceramic	Metal
Elastic modulus E (GPa)	117	66
Poisson’s ratio v	0.333	0.321
Thermal expansion coefficient α (K−1)	7.11 × 10−6	10.3 × 10−6
Heat conduction coefficient k (W/(m·K))	2.036	18.1
Heat capacity Cp (J/(kg·K))	615.6	808.3

. The model considers the effects of elastic modulus, Poisson’s ratio, thermal conductivity, thermal expansion coefficient, and specific heat capacity, which obey an exponential function distribution, and the distribution functions are as follows:

$$E=66.2\times {10}^9\ast e^{(y\ast In(117/66.2)/0.2)}$$

(29)

$$k=18.1\ast e^{(y\ast In(2.036/18.1)/0.2)}$$

(30)

$$\mathsf{\alpha }=10.3\times {10}^{-6}\ast e^{(y\ast In(7.11/10.3)/0.2)}$$

(31)

$$v=0.321\ast e^{(y\ast In(0.333/0.321)\ast y/0.2)}$$

(32)

$$C_p=808.3\ast e^{(y\ast In(616.5/808.3)\ast y/0.2)}$$

(33)

The model is divided into 24,162 triangular elements. The mechanical time step used in the simulation is 1 × 10⁻¹⁰ s. Figure 20 shows the relationship between the crack inclination angle and the crack propagation angle with different crack spacing. Firstly, the effect of the crack inclination angle on the crack propagation angle with different spacings is analyzed. It can be seen that the crack inclination and crack spacing have a significant effect on crack propagation. When the crack spacing is small, the cracks propagate in the opposite direction. As the crack spacing increases, the tendency of the crack propagation in the opposite direction decreases.

Moreover, the direction of crack propagation is closer to the direction perpendicular to the initial crack with a smaller crack inclination angle. Next, the relationship between the crack inclination and propagation angle will be quantitatively studied. For the crack propagation angle on the right, the relationship between the crack inclination angle and the crack propagation angle is shown in Figure 21. It can be seen that the crack propagation angle gradually decreases with the increase in the crack inclination angle.

When the crack inclination angle β is 60°, the interaction between the cracks becomes greater. When the inclination angle β is 70° and 80°, the crack propagation angle $\mathsf{\varphi }$ decreases slowly from 49.7° to 41.6° (d = $a$). When the inclination angle β increases from 60 degrees to 90 degrees, the crack propagation angle $\mathsf{\varphi }$ decreases by about 60%. This phenomenon may be because when the crack inclination angle is larger, the crack is perpendicular to the edge of the model. Since the thermal stress direction caused by the temperature gradient is from top to bottom, the crack will preferentially propagate in the vertical direction. Figure 22 shows the relationship between crack spacing and crack propagation angle. Taking β = 60° as an example, when d increases from 0.04 to 0.16, the crack propagation angle $\mathsf{\varphi }$ decreases by about 27%. As can be seen, a larger crack spacing leads to a smaller crack propagation angle when the crack inclination angle remains constant. In addition, adjacent cracks have little effect on the crack propagation angle when the crack spacing is large.

Next, take d = a and β = 80° as an example to study the crack growth and the evolution process of temperature with time. Figure 19 shows the crack propagation over time under thermal load. It can be seen that the cracks extend to the bottom of the model under temperature load. When t = 10⁻⁵ s, the temperature gradient at the crack tip is the largest, and the right crack is affected by the left crack and starts to deflect to the right. At this time, the left crack has not yet begun to deflect along the initial crack direction. When t = 2 × 10⁻⁵ s, the right crack starts to deflect to the right due to the influence of the stress field distribution of the left crack. Until t = 3 × 10⁻⁵ s, the left crack begins to extend to the lower left. At t = 8 × 10⁻⁵ s, the propagation direction of the two cracks has deviated significantly, and the deflection angle of the right crack is φ = 43.9°.

In summary, the propagation paths of these two cracks are affected by each other under thermal load. In this example, the hindering effect of cracks on heat conduction is considered to match the actual situation. In Figure 23, the temperature distribution on both sides of the cracks is continuous and drops faster on both outsides because cracks hinder heat conduction. The simulation results of crack propagation are consistent with the theoretical research [58].

7. Conclusions

Based on the continuous–discontinuous thermo-mechanical coupling model, heat conduction, the thermoelastic problem, and double-edge crack propagation under the thermal load of FGMs are studied in this paper. The main conclusions are as follows:

(1) The simulated steady-state and the transient heat conduction processes under different parameter arrangements and gradient coefficients are in good agreement with the analytical solutions, indicating that model can well simulate the heat conduction problem of FGMs.

(2) Compared to composite materials, the internal stress distribution of the FGMs is relatively uniform, which can overcome complex environments subjected to thermal shock.

(3) The interaction between cracks affects the crack propagation path under thermal load. The inclination angle and spacing of double-edge cracks greatly influence crack propagation. When the inclination angle β increases from 60 degrees to 90 degrees, the crack propagation angle $\mathsf{\varphi }$ decreases by about 60% (d = $a$). Furthermore, when d increases from 0.04 to 0.16, the crack propagation angle $\mathsf{\varphi }$ decreases by about 27% (β = 60°). Larger crack inclination and spacing can lead to a smaller crack propagation angle. The simulation results are consistent with the theoretical research.