Abstract
In practice, the drilling path of horizontal directional drilling (HDD) projects is usually constructed by trial and error based on a preliminary designing trajectory. This study aimed to propose and test a method to predesign and optimize the drilling paths automatically, with the view of improving the efficiency of HDD design preparations. Alternating straight and curvilinear segments is a commonly used method for designing drilling paths, especially the “straight—curvilinear—horizontal straight—curvilinear—straight” five-segment arrangement. The catenary method was proposed to design the drilling path with the advantage of lower friction for the mechanical constraints. However, it is difficult to be implemented with technology limitations due to its continuously changing curvature. In this study, five-segment trajectories were combined with the catenary trajectory to utilize their advantages using the improved radial movement optimization (IRMO) algorithm. Drilling mud pressure was considered in the processes of the mechanical design to avoid collapse or possible instability. Two different examples were tested in different scenarios, theoretical and practical. The results show that the IRMO algorithm has a great potential for automatically designing and optimizing preliminary drilling paths with low time-consumption and high feasibility.
1. Introduction
Horizontal directional drilling (HDD) is a trenchless technology applied to install underground pipelines with minimal impacts on the environment or damage to existing infrastructure such as roadways and other surface structures [1]. According to the predesigned drilling trajectory, a small pilot hole is drilled first, and then the pilot hole is enlarged by a reamer that replaces the drilling head. The pipes or installations of the well are pulled back into the reamed hole from the exit toward the entry. Due to its lower cost, higher flexibility, and weaker surrounding influence, HDD has gradually become more popular than the conventional excavation methods adopted to install and replace or repair pipelines in a city [2]. The development of HDD in China has continued in the past two decades due to the broad market and stable economic growth of China. Up till November 2020, the longest known HDD in China had reached 5.2 km [3,4]. The geological conditions of the crossing area are much more complex in longer-distance crossing HDD practices, which results in more engineering problems and costs. In practice, most of the HDD drilling paths are determined by seeking or tracking the moving or static drill head to adjust it from the entry point to the exit simultaneously and iteratively [5]. Scholars have carried out various studies on improving the accuracy or efficiency of the seeking or tracking systems [6,7,8,9]. However, this method of iterative trial and correction is difficult to apply in complex practices, such as crossing rivers or buildings which may hinder the sensors. On the other hand, many scholars have focused on the predesign and optimization of HDD trajectories to ensure suitability and efficiency. For conventional trajectory design, the theoretical geometric model of trajectory was mainly developed to ascertain the accurate position of the wells, such as the “Improved Tangential Method” [10]. Moreover, some scholars added more factors in the model to realize more complex designs closed to actual projects [11,12,13]. In China, Zhou [14] took the drilling rate in meters per hour as the optimization object to establish a dynamic trajectory design optimization model, which could find the optimal drilling path with the minimum drilling time. Lu [15] focused on complex underground pipelines and obstacles and presented an optimization method for avoiding pipelines and obstacles in trajectory design. Niu [16] conducted research on the theory of the guide strength of the drilling path, which analyzed the contribution of the curved segment to the drilling path design. When it comes to artificial intelligence applications, an optimization algorithm is more intuitive and reliable than repetition tests and traditional human-computer interaction techniques [17]. The drilling path design and optimization were also developed further by several optimization algorithms. The catenary trajectory design method was introduced by Wiśniowski [18,19,20], who tried to fit the five-segment trajectory with the catenary trajectory to design the drilling path geometrically. The genetic algorithm (GA) was used to realize the fitting of the two trajectories efficiently. In another study, the ant colony optimization (ACO) algorithm was used to optimize HDD alignment by Patino-Ramirez, et al. [21], which ensured the minimal drill path length and the reduced cost associated with it. Notably, the ACO optimization method added consideration of mechanical constraints (drilling mud pressure and pipe integrity) and geometric constraints (remaining in the construction domain) simultaneously in the design.
The artificial intelligence algorithm is an excellent way to figure out a single or multidimensional nonlinear objective optimization problem which the design or optimization of trajectory can be transferred to. On the basis of previous studies, this paper tested a new numerical method, using improved radial movement optimization (IRMO) to preliminarily design and optimize the HDD trajectories and its parameters. According to the theory of catenary trajectory in previous literature, its shape is closed to the natural stress distribution of pipelines along the length so as to enable a lower drilling or pullback force during the process [18,19,20]. So, a five-segment trajectory was attempted to be realized by fitting with the catenary trajectory to get the largest similarity in shape. What is more, the drilling mud pressure is calculated in each iteration step simultaneously for consideration of the well-bore stability evaluation. The use of the IRMO algorithm can make the whole construction processing automatic with the intention to reduce the time-consuming manual adjustment. Section 2 introduces the concepts of the catenary trajectory design and five-segment trajectory design for HDD projects. Then we present the design method based on the geometrical constraints for the whole construction and each parameter. The objective functions for this method used in the IRMO algorithm are also summarized. Besides, the mechanical design is also introduced for the borehole stability consideration based on drilling mud pressure. Section 3 summarizes the framework and implementation of the IRMO algorithm applied to the trajectory design. Section 4 presents two design examples to compare and analyze the results determined by IRMO. The conclusion of this study is presented in Section 5.
2. HDD Trajectory Designs
2.1. Geometric Designs
The catenary trajectory is a chain curve with natural deflection, such as seen with ropes, cables or chains with uniform weight suspended between two points (Figure 1a). In petroleum engineering, the well path in the catenary profile has been proved to reduce the wellbore friction and torque compared to conventional trajectories [22,23]. The method for planning the catenary well path was proposed in later studies, which avoided a trial-and-error procedure and provided excellent maneuverability of planning requirements [24]. In 1985, McClendon [25] proposed an HDD trajectory design method based on a catenary trajectory. However, its gradient curvature made it difficult to be implemented in practice. Therefore, Wiśniowski et al. [20] proposed a new method that combined the catenary trajectory with a five-segment trajectory (Figure 1b) to design a drill path that was easier to be implemented using the available technology.
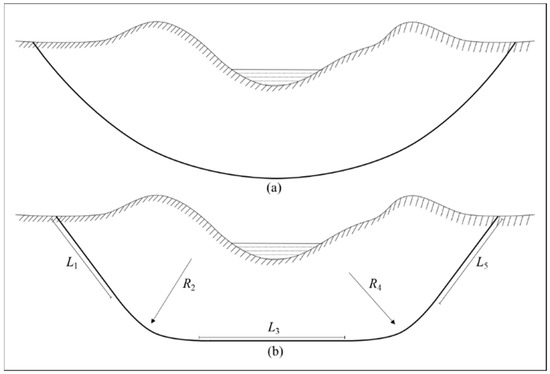
Figure 1.
Catenary trajectory (a) and five-segment trajectory (b).
The catenary trajectory is actually a hyperbolic cosine, whose standard mathematical formula is written as the following:
where, a is a parameter determined by the unit weight of pipeline q (N/m) and pullback force Np (kgf) [20]. So, the shape of the catenary trajectory is mainly associated with the crossing pipelines and the capacity of the pulling back equipment. By Equation (3), the catenary trajectory can be described in a specific coordinate, where the left point of the catenary trajectory is set as the origin point. Therefore, the depth of each point on the catenary trajectory (zci) can be fully calculated with increments. As shown in Figure 2, A and H are the horizontal and vertical distances of the exit and the entry points, respectively. (x0, z0) is the catenary vertex coordinate.
z = a × cosh(x/a)
a = Np/q
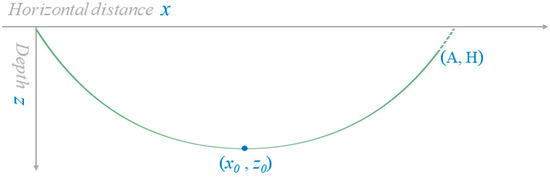
Figure 2.
Graphic representation of catenary trajectory by Equation (3).
Another concept for HDD trajectory design is the segment trajectory method, combining the most conventional methods of straight and curvilinear segments. Mostly, the geometric profile of segment trajectory (shown in Figure 1b) commonly consists of an entry straight segment (L1), an entry curved segment (L2) with bending radius (R2), a central horizontal straight segment (L3), an exit curved segment (L4) with bending radius (R4), and an exit straight segment (L5) respectively. Based on this combination form, the point coordinates of each segment can be calculated clearly by geometric constraints. As shown in Figure 3, once the angle γ and radius R of the curved segments are set, the increments of the trajectory depth and horizontal distance can be determined according to Equation (4). Furthermore, combining the inclination angle θ and length L of the adjacent straight segments, the depth of another adjacent segment can be fully determined with increasing horizontal distance (Equations (5) and (6)).
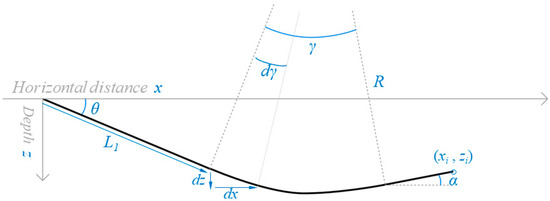
Figure 3.
The geometric profile of alternating straight and curvilinear segments.
According to Equations (4)–(6) above, the designed alternating straight and curvilinear segments can be detailed with tiny segments with coordinates. The whole geometry can be constrained only by four kinds of geometric parameters within the assigned domain, including the inclined angle of the straight segment θ (clockwise is positive and counterclockwise is negative), the length of segment Li, the angle of curved segment γ, and the curved segment radius R. If the central segment of the trajectory is considered to be horizontal and straight in design, the geometric parameters curve angle γ and deviation angle θ will be united (θ1 = γ1, θ2 = γ2), so that the geometrical design parameters of the five-segment trajectory can be simplified and containing the following:
- Length of entry straight segment, L1
- Inclined angle of entry inclined straight segment, θ1
- Radius of entry curved segment, R2
- Central straight segment length, L3
- Inclined angle of exit inclined straight segment, R4
- Radius of exit curved segment, θ2
In practice, the straight segments of drill path, L1, L3, and L5, are generally determined by the gyratory drilling processes of the drill head, while the curved segments are determined by the direct jacking [16]. The entry angle θ1 (for the entry straight segment L1) and exit angle θ2 (and the exit straight segment L5) of the trajectory are commonly restricted in valid ranges. Patino-Ramirez et al. [21] suggested the ranges could be defined between 5 and 18 degrees for trajectory design, while Wiśniowski et al. [19] recommended it could be set between 6 and 16 degrees. Another study gave higher acceptable values of deviation angles between 8 and 30 degrees [26]. Its determination is usually constrained by constructability limitations which impart conditions of geometric design. The central straight segment L3 is commonly the core part of the trajectory, which must satisfy the requirements of specific burial depths and crossing distance for the engineering. To avoid surface disturbance and damage to installed products or pipelines, the minimum depth of cover along the trajectory should not be less than the minimum allowable H in the standards.
The bending radius (R2 and R4) of curved segments mostly depends on the pipeline strength which is limited by the material properties or diameter. To prevent excessive bending stress in the pipelines, the radius of the curved segments should be limited to the minimum bending radius. More details of the minimum bending radius can be found in the published literatures [16,19,21]. In this study, the bending radius adopted was between 2000 and 3000 m for pipelines with diameter over 1000 mm.
After preliminary investigation, the assigned domains of the locations of entry and exit points are decided upon for the predesigns. Project risks are evaluated as well, which might result in more stringent limitations in the predesigns. Based on these limitations, possible trajectories are designed (fitted) to ensure the maximum similarity with the catenary trajectory in unifying the plane coordinate system by the least squares method. The sum of squares SOS is determined as the similarity measurement function to find the best fit (Equation (7)). zi and zci are the depths of the five-segment trajectory and catenary trajectory determined by Equations (3)–(6) above. The lower the difference between the depths, the higher is the similarity of the two trajectories.
Fitness_S = SOS = Σ(Δzi)2 = Σ(zi − zci)2
According to the six parameters obtained above, the length of the preliminary design trajectory can be given in Equation (8) with specific geometric constraints.
Fitness_L = ΣLi = L1 + R2 × θ1 + L3 + R4 × θ2 + (A −L1 × sin θ2 −L3 −R4 × cos θ2)/sin θ2
2.2. Mechanical Design Considering Drilling Mud Pressure
Taking into account the collapse and instability of the drill paths, we tested, step by step, the feasibility and rationality of each geometrically possible trajectory based on drilling mud pressure theory. The engineering geological conditions of the crossing area for calculation are simplified in this study. The drilling fluid is a non-Newtonian fluid mixed HDD process. It is necessary to exceed the minimum required mud pressure (MRP) to maintain the recirculation of the drilling mud. The minimum mud pressure consists of the static drilling mud pressure Ps and the drilling mud pressure loss Pl [27,28], as shown in Equation (9) [27,28].
MRP = Ps + Pl
Simultaneously, the injected pressure of the drilling fluid must be controlled below the maximum allowable drilling mud pressure (MAP) to avoid cavity shear failure (blowout) of the drill path [21]. The MAP is calculated by the Delft equation [27,29], which assumes that the soil surrounding the borehole experiences perfectly elastic deformation and that the far-field stress around the borehole is isotropic. Once the deformation reaches the plastic threshold defined by the Mohr–Coulomb criterion (the internal pressure reaches the limited pressure), shear failure of the borehole will occur as a blowout. Although the Delft equation has been continuously revised to obtain more accurate analytical solutions [30], Delft equation-based formulations are still the most commonly accepted formulations and are therefore adopted in this study, Equation (10) [29].
MAP = Plim
Once the geometrically possible trajectory is determined, the MRP and MAP of the whole construction can be calculated predictably for the mechanical considerations. For all of the steps, the maximum allowable pressure (MAP) of the fluid is predicted to avoid the triggered blowout.
3. Improved Radial Movement Optimization
3.1. Concepts of IRMO
The IRMO algorithm [31,32,33,34], which can quickly solve multidimensional objective functions of nonlinear constraint problems, is a global optimization algorithm that further improves the data structure of the traditional radial movement optimization (RMO) algorithm [34]. The IRMO algorithm simulates a group of particles [Xi,j] moving in a gradually shrinking solution space. In IRMO, one particle position, which contains the information of variables, represents a solution vector referring to a complete HDD trajectory in this study. All of the solution vectors form a solution matrix [Xi,j]. After the expression of the objective function and the range of the variables are determined, a group of initial particles are generated randomly in the IRMO algorithm. The position of each particle is evaluated by the value of the fitness function (the value of the sum of squares SOS or total length L); therefore, the local optimal solution Rbest (radial best) and global optimal solution Gbest (global best) can be obtained by one-by-one comparisons. The particle corresponding to the best value of the function is chosen as the initial center. To avoid the algorithm overreliance on the central particle and the loss of potential good particles of the previous generation, which contribute to deviation from the optimization direction of the global optimal solution, IRMO proposed generating prepositioned particles [Yi,j]. The fitness values of [Yi,j] are compared with those of [Xi,j], pre-Rbest and pre-Gbest to evaluate the optimal information that will be updated or persist. As the iteration progresses, the solution space (ranges of variables) will be narrowed so that the central particle, determined by Rbest and Gbest, will move toward the optimum. When the positions of the particles are narrowed to the smallest solution space, the optimum solution is output. The principle of updating the central particle is shown in Figure 4.
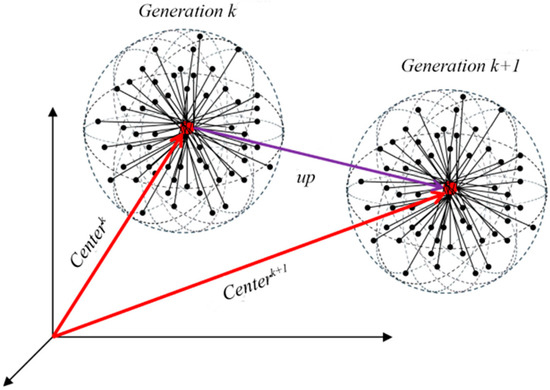
Figure 4.
Principle of updating the central particle [34].
3.2. Implementation of IRMO
According to the studies above, one solution of the five-segment trajectory can be determined by an M dimensional vector containing six variables: L1, θ1, R2, L3, R4, and θ2. The N trajectories form a standard matrix [XN,M] with N rows and M columns (M = 6). The standard matrix [XN,M] realizes the connection between the IRMO algorithm and the HDD trajectory optimization (shown in Equation (11)).
After setting the ranges of each variable and the constraint conditions, optimization begins with the initial matrix [XN,M] initiated by Equation (12).
where Xmax j is the upper limit of the j-th variable in [Xi,j], and Xmin j is the lower limit.
Xi,j = Xmin j + (Xmax j − Xmin j) × rand(0, 1)
The initial central particle cp1 is chosen from the initial [XN,M] which has the best fitness value. The central particles cpk will be updated by Rbest and Gbest, as shown in Equation (13). c1 and c2 are proportional coefficients that affect the convergence speed and accuracy of the calculation. The values of c1 and c2 are set as 0.5 and 0.4, respectively, in this study.
cpk = cpk−1 + c1 × (Gbeatk−1 − cpk−1) + c2 × (Rbeatk−1 − cpk−1)
Following Equation (14), prepositioned particles [Yi,j] are generated by the previous central particles.
Yi,jk = cpk + (Xmax j − Xmin j) × rand(−0.5,0.5) × wk
wk = 1.009 × exp(−(1/generation + 0.03307)2/0.2454)
To calculate the fitness values of [Yi,j]: If the fitness values of [Yi,jk] are better than those of [Xi,jk], the [Xi,jk+1] will be updated to [Yi,jk], otherwise [Xi,jk] will persist to the next generation. The determination of inertia weight wk uses a Gaussian function (Equation (15)).
Based on the objective functions given above (Equations (7) and (8)), the design and optimization of the HDD trajectories in this study were implemented by IRMO on MATLAB 2021b. The implementation of the IRMO algorithm for HDD trajectory optimization is shown in detail in Figure 5.
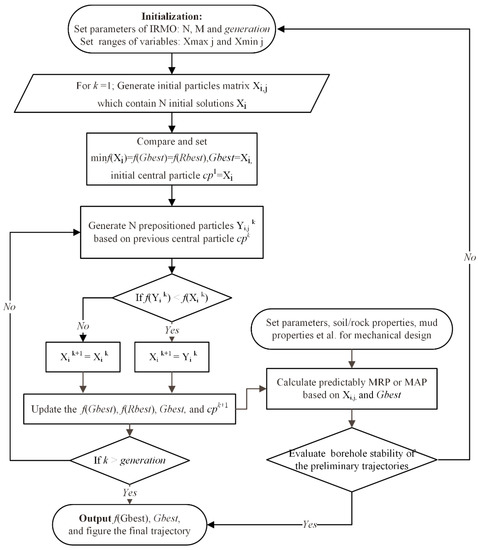
Figure 5.
The implementation of the IRMO algorithm.
4. Comparison and Analysis
This study aimed to assess the performance of IRMO in trajectory design by two examples originating from other literature. The first one gives the details of geometric design processes which are compared with the genetic algorithm (GA) to highlight the advantages of IRMO. To ensure the stability of this IRMO method for practicable consideration, the parameters are discussed based on twenty times calculation. Therefore, a further optimization, shortening the total length of trajectories, is proposed and tested to overcome the limitation of unstable parameter design. Another example tests the IRMO designs with the actual design using published data from constructed projects. To test the mechanical design part, predictions of the maximum allowable drilling mud pressure of the geometric design trajectories are compared with other studies.
4.1. Comparison and Analysis of Numerical
The first example [19] is used to test the fitting process of this method using the IRMO algorithm. The catenary trajectory parameters and five-segment trajectory parameters are shown in Table 1.

Table 1.
Parameters and range setting.
To determine the influence of different algorithm parameters on the fitting results, the value of R2 is used to manifest the similarity of fit. As shown in Table 2, the difference in the value of R2 is quite minor and is greater than 0.998 in each case. The overlap of the fitted trajectory images for series 1, 3, and 5 is relatively high (Figure 6). Moreover, the time resource of each case increases as the calculation becomes more complex.

Table 2.
Comparison of goodness of fit for different algorithm parameters.
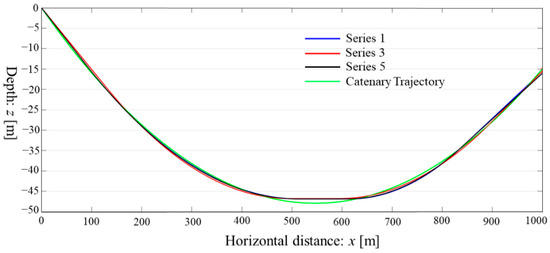
Figure 6.
Solutions of fittings: Series 1, 3, and 5.
The optimal fitting result shows a lower SOS value searched by the IRMO algorithm (in Table 3), but more time costing. Compared with the results of the genetic algorithm (GA), the IRMO algorithm can give more accurate calculations with an acceptable extra time costing.

Table 3.
Comparison of optimal fitting results.
During the 100 iterations, the global optimal SOS tends to a stable convergence when approaching the approximate 50th generation (shown in Figure 7). The optimal result can be improved when the total number of iterations is increased.
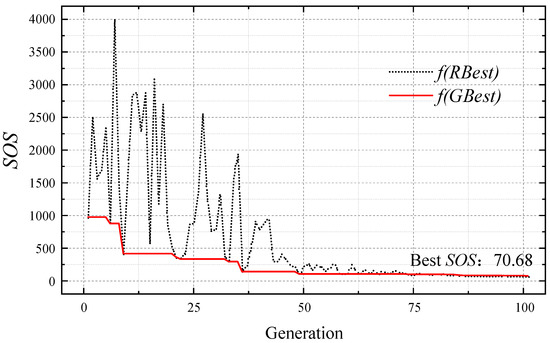
Figure 7.
The convergence process of searching for the optimal SOS: Series 3 in Table 2.
As shown in Table 4, the optimization result of L3 in this study is largely similar to that of the GA [19]. The other parameter optimization results have θ1, θ2, and R2 that are all smaller than those of the GA, while R2 is larger. The difference between the optimization results is attributed to the mutual influence and restriction of each parameter.

Table 4.
Comparison of parameter optimization results.
Taking Series 4 in Table 3. as an example, the SOS is calculated 20 times consecutively (Figure 8), and the 20 trajectories are shown in Figure 9.
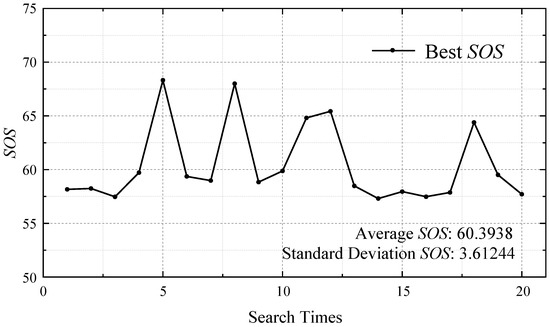
Figure 8.
The best SOS calculated 20 times by IRMO: Series 4 in Table 2.
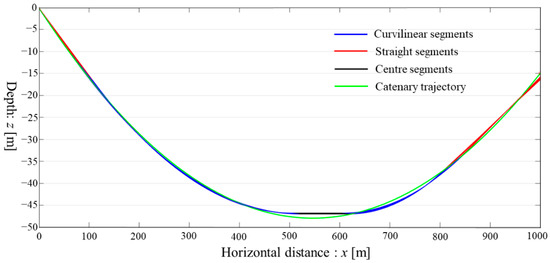
Figure 9.
Trajectories after searching 20 times by IRMO: Series 4 in Table 2.
The calculations completed by the IRMO showed great stability and accuracy, with the standard deviation of the SOS being 3.61244, consistent with the trajectory images. In Figure 9, different colors are used to distinguish each segment of the five-segment trajectory. The fitting results of each segment are highly similar as well.
The parameter collocation of the optimal fitting trajectory cannot be identical here. As the fitting similarity is higher, the mutual influences and restrictions of each parameter on the others will be enlarged causing different results. To achieve a high similarity of fitting, the results of the parameters, especially L1, R2, and R4, fluctuate in a small range after 20 calculations (Figure 10, Figure 11 and Figure 12), while the fitting results are not much different (Figure 9). The results of L3, θ1, and θ2 fluctuate relatively consistently, especially the length of the central segment L3. The optimization of L3 tends to the lower limit of its initial range (as shown in Table 1) with no difference in the 20 searches, which indicates that a shorter L3 is beneficial to the trajectory fitting. The results of θ1 and θ2 fluctuate only in the range of 0.5° (Figure 10), with standard deviations of 0.29313 and 0.212049, respectively. However, the optimization results of L1, R2, and R4 contrast obviously with the former findings. This shows that the fluctuations in the fitting are less correlated with L1, R2, and R4.
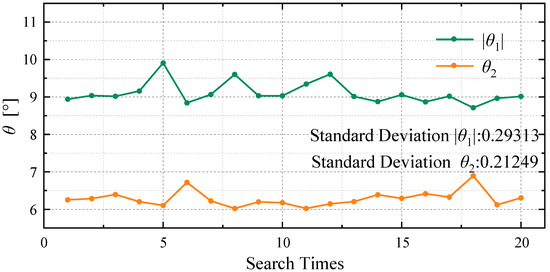
Figure 10.
The fluctuations of θ1 and θ2 for 20 calculations.
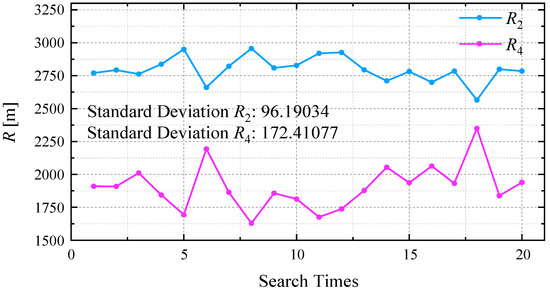
Figure 11.
The fluctuations of R2 and R4 for 20 calculations.
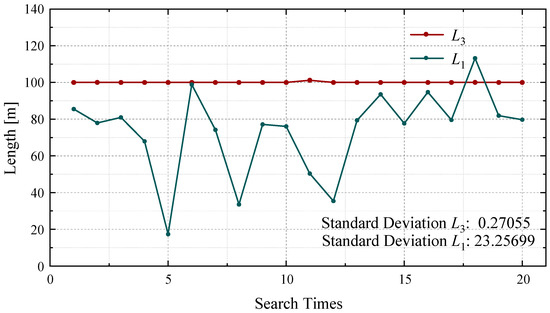
Figure 12.
The fluctuations of L1 and L3 for 20 calculations.
Wiśniowski et al. [19] suggested fixing the length of the central segment L3 and narrowing the ranges of the other parameters to further optimize the five-segment trajectory in a smaller solution space. The final optimization is clearly to be applied in practice. However, the optimization result that he obtained is one among numerous possible results. In this study, to achieve more precise and stable results of parameters, we narrowed the parameter limitations according to the volatility ranges and set the Fitness_L(Equation (8)) as the purpose to search the shortest trajectory to reduce the costs associated with the length of trajectory. The narrowed ranges are concluded in Table 5, and the parameters of the IRMO algorithm are: N = 50, M = 6, and generation = 250.

Table 5.
The narrowed optimization ranges of trajectory parameters.
After searching 20 times by IRMO in the narrowed optimization ranges above, the total length of the trajectory is obviously shortened (Figure 13) compared with Figure 6 and Figure 9, although the fitting degree is lower.
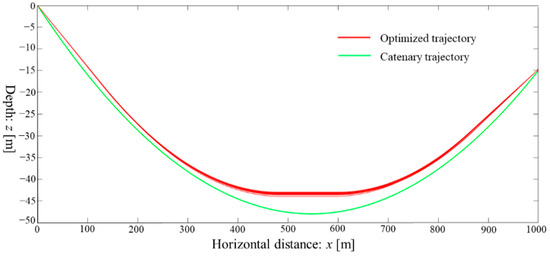
Figure 13.
The shortest total length trajectories after searching 20 times by IRMO.
The values of the shortest length searched 20 times are shown in Figure 14. The standard deviation is only 0.05813, in which the maximum decrease is 16.92 m, the minimum decrease is 10.62 m, and the average decrease is 14.53 m. The Figure 15 shows the convergence of the total length when the iteration of the IRMO is set as 250. The global optimum tends to be stable as well.
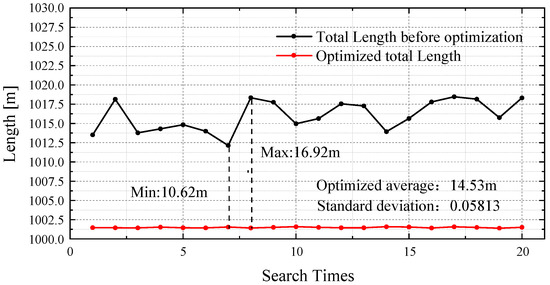
Figure 14.
Optimal length of trajectories by searching 20 times.
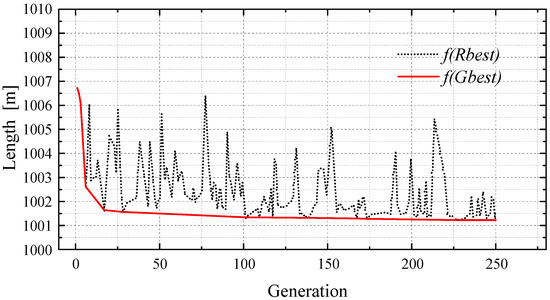
Figure 15.
The convergence progress of searching optimal length after 250 iterations.
A set of trajectory parameters before and after optimization is compared in Table 6. The results after optimization of θ1 and θ2 are smaller than before, while the results after optimization of R2, R4, L1, and L3 are larger. Moreover, the length of the exit straight segment L5 is exhibited, which demonstrates that the optimization effect of the total length is mainly contributed by the exit straight segment L5.

Table 6.
The trajectory design parameters before and after optimization.
Figure 16, Figure 17, Figure 18, Figure 19, Figure 20 and Figure 21 show the convergence of six parameters over 250 iterations in searching. The iterative convergence of the parameters carried by the central particle and the average of each generation of particles are given in the figures simultaneously. We note that the convergence of the central particle and average is relatively more stable (the fluctuation is smaller). This means that for the IRMO algorithm, if the searches for the global optimal value have unstable fluctuations (possibly falling into the local optimum), the central particle could maintain the optimal position to avoid the result becoming stuck in a local optimum (the optimum eventually coincides with the convergence of the central particle).
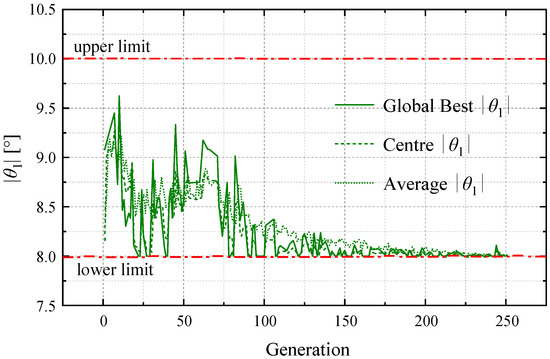
Figure 16.
The convergence progress of inclination of entry straight segment: θ1.
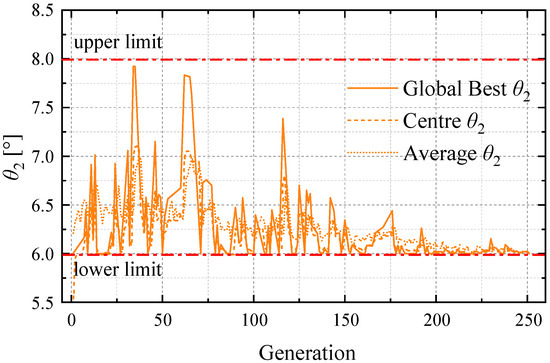
Figure 17.
The convergence progress of inclination of exit straight segment: θ2.
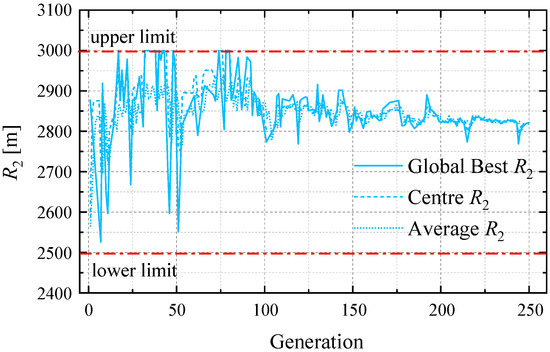
Figure 18.
The convergence progress of radius of entry curved segment: R2.
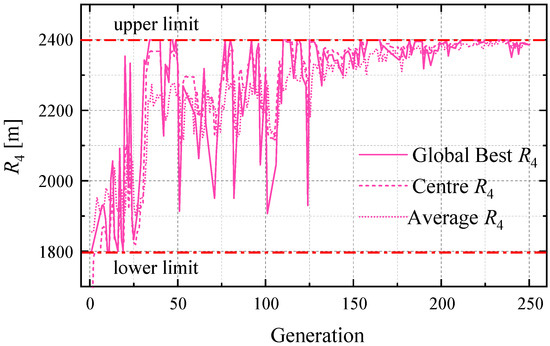
Figure 19.
The convergence progress of radius of exit curved segment: R4.
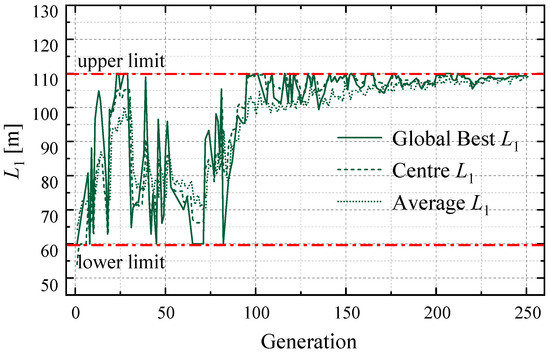
Figure 20.
The convergence progress of length of entry straight segment: L1.
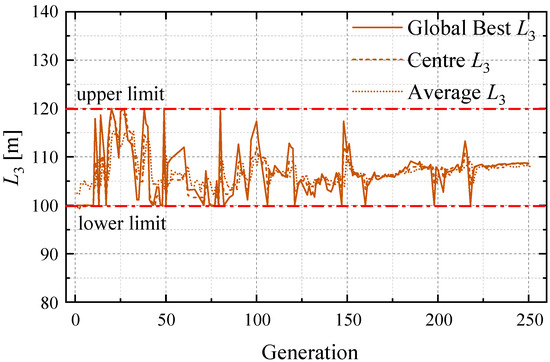
Figure 21.
The convergence progress of length of central straight segment: L3.
To highlight the optimization trends of parameters, we tagged the upper limit and lower limit (Table 5) in the following figures for each parameter. In Figure 16 and Figure 17, both θ1 and θ2 are trending to a lower value of their ranges, which means that the lower inclination of entry or exit straight segments is more conducive to optimizing the total length of the five-segment trajectory.
For the curved segments, R2 and R4, perform the different convergence trends in iteration. As shown in Figure 18, the final R2 is neither close to the upper limit of its searching range nor the lower limit. Meanwhile, the values of R4 converge to the upper limit to obtain the optimum total length (Figure 19). It could be considered that R2 plays a more influential role in the length optimization.
For the length of entry straight segment L1, an obvious convergence can be observed to its upper limit, especially after 100 generations. However, the length of the central straight segment L3 finally trends to nearly 110 m.
It is hard to say what are the relations between the lower limit or upper limit with the optimization of R2 and L3 (Figure 18 and Figure 21), but it could be concluded that the determinations of R2 and L3 are not of as much importance as the others. To some extent, their influence on the optimal results is weaker. Therefore, it is advisable to pay more attention to optimizing other parameters, including L1 R4, θ1, and θ2, in actual projects. On the other hand, the optimization result of L3 (104.96 m) is larger than the fitting result (100.00 m) (Table 6), which is conducive to the trajectory in practice if there needs to be a longer horizontal crossing.
This process of length optimization could certainly reduce the total length of the whole construction, especially when considering the cost associated with the length. As another possibility, it also proves that the trajectory can be designed and optimized with the purpose of minimal total length as in the ACO method [21]. However, for the IRMO method, the outputs of the design parameters are more specific with six parameters available which may help the engineers’ judgement. However, in this example, the maximum optimized length is only a fraction of the total length. Its practical value may need to have more practices to be proved in further study. However, it may provide valuable advice for determining certain parameters when those parameters are volatile during fitting.
4.2. Comparison of an Actual Drill Path Design
Another example containing mechanical design, the drill path of the Maxi-HDD Qin River crossing project in China [4], was tested to support this method of predesigning trajectory. The crossing project, including two parallel HDD crossing with 1016 mm diameter and 1750 m driven length, was located at an alluvial plain where the Yellow River and the Qin River intersect. Consisting of a 7° entry angle, 8° exit angle, 2290 m entry and exit radius of curved segments, 1015 m horizontal segment, 33.50 m maximum burial depth and 29.78 m minimum burial depth below the riverbed, the drill path was carefully designed manually for preventing blowout, as shown in Figure 22.
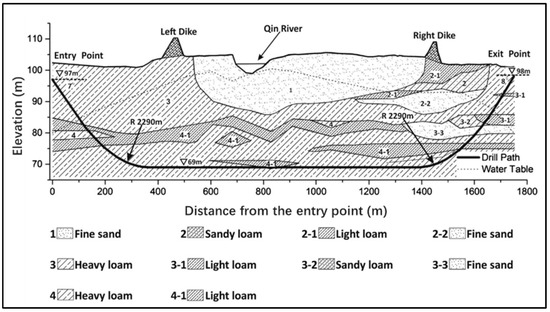
Figure 22.
The drill path profile of Maxi-HDD Qin River crossing project [4].
According to the engineering data provided in the literature [4], the geometrical design parameters are limited in the ranges given in Table 7. The minimum bending radius limitation was given differently for two cases, 2000 m and 2300 m, to illustrate its effects on trajectory design.

Table 7.
Parameters and range setting.
In terms of mechanical design, heavy loam is used to evaluate the maximum allowable mud pressure, including 1.57 g/cm3 dry density, 20.0 kPa cohesion, 15.0° friction angle, and 0.74 coefficient of lateral earth pressure. The MAP predicted at the location of minimum burial depth is 1.63 MPa, which is very close to the real pressure of about 1.7 MPa [4]. All segments of the trajectory were tested for the pressure predictions through the whole process of geometric design.
As shown in Figure 23 and Table 8, although the fitting similarity is largely reduced from the last example (mostly due to the difference of parameters ranges), both cases of trajectory design by IRMO show a great similarity with the actual design. The parameter design results arrive at similar trends as the previous conclusions. With the different minimum bending radius, the entry straight segment (L1) is designed with nearly 50 m difference while the other parameters are not much different in design. It proves that the fitting similarity has less influence on the design results than we thought. The design parameters could be designed suitably by fitting with the catenary trajectory. What is more, there is no need for extra length optimization due to the tiny differences in the total length of the designs caused by strict limitations, especially for the central segment length L3.
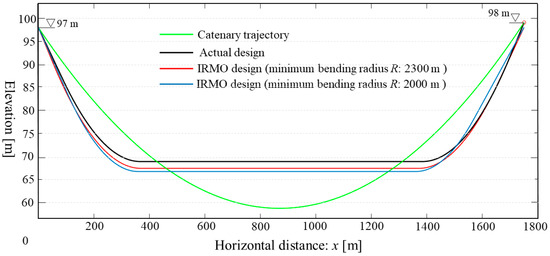
Figure 23.
Comparison of IRMO design and actual design.

Table 8.
Comparison of parameter design results.
5. Conclusions
- With the application of intelligence algorithms, specifically the IRMO algorithm, the design and optimization of HDD trajectories could obviously improve the efficiency and accuracy in this study. All the calculations and optimizations were tested on a 2.30 GHz computer (CPU: Intel i5-6300 HQ), and the total time of fitting and length optimization was stabilized within 60 s, which shows great potential for shortening the manual adjustment time required in actual projects.
- This study proposed and tested a new method to design the HDD trajectory combining five-segment trajectory with catenary trajectory. With two processes, the five-segment trajectory could be designed with a great similarity to the catenary trajectory, and simultaneously with the shortest length, thereby reducing the associated costs. Both processes were verified through data from the literature or from actual projects. It was proved that the catenary trajectory has great potential to design a traditional drilling path with precise and achievable parameters.
- Six concise parameters (L1, L3, R2, R4, θ1, and θ2) were concluded herein to design trajectories and be optimized by the IRMO algorithm. According to the analysis of the parameters, it was found that the limits of L3 and R2 have fewer impacts on the optimization results. Therefore, the optimization ranges of the other four parameters should be set carefully during the trajectory design.
- By improving the structure data of the radial movement optimization, the obtained IRMO algorithm had a great ability to solve the extremum value of the multidimensional nonlinear objective function. Benefitting from the refined parameter matrix and efficient data structure, the authors believe IRMO has further potential in more complex trajectory design such as 3D construction or in avoiding obstacles.
- It should be emphasized that the importance of the accuracy and viability of the results by algorithm are mostly based on the set of the constraints and validated ranges of input parameters which largely rely on the experience of trained engineers. This method hopes to provide more advice in terms of geometrical parameters and drilling mud pressure for current practice preparations with a large consideration of site and soil property factors. There are more factors, such as geology, rock properties, and drilling rigs that should be discussed in further study to ensure the mechanical design. What is more, the mechanical advantages of the five-segments trajectory similar to the catenary trajectory also need more experimental studies to be verified.
Author Contributions
Conceptualization, L.J. and J.W.; methodology, J.W.; software, J.W.; validation, J.W.; formal analysis, J.W.; investigation, J.W.; resources, J.W.; data curation, J.W.; writing—original draft preparation, J.W.; writing—review and editing, L.J.; visualization, J.W.; supervision, L.J.; project administration, L.J.; funding acquisition, L.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are openly available in published literature, reference number [3,12].
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yan, X.; Ariaratnam, S.T.; Dong, S.; Zeng, C. Horizontal directional drilling: State-of-the-art review of theory and applications. Tunn. Undergr. Space Technol. 2018, 72, 162–173. [Google Scholar] [CrossRef]
- Allouche, E.N.; Ariaratnam, S.T.; Lueke, J.S. Horizontal directional drilling: Profile of an emerging industry. J. Constr. Eng. Manag. 2000, 126, 68–76. [Google Scholar] [CrossRef]
- Lu, H.; Behbahani, S.; Azimi, M.; Matthews, J.C.; Han, S.; Iseley, T. Trenchless Construction Technologies for Oil and Gas Pipelines: State-of-the-Art Review. J. Constr. Eng. Manag. 2020, 146, 03120001. [Google Scholar] [CrossRef]
- Yan, X.; Ma, B.; Zeng, C.; Liu, Y. Analysis of formation fracturing for the Maxi-HDD Qin River crossing project in China. Tunn. Undergr. Space Technol. 2016, 53, 1–12. [Google Scholar] [CrossRef]
- Bennett, D.; Ariaratnam, S.T. Horizontal Directional Drilling: Good Practices Guidelines; North American Society for Trenchless Technology: Bothel, DC, USA, 2008. [Google Scholar]
- Jaganathan, A.P.; Shah, J.N.; Allouche, E.N.; Kieba, M.; Ziolkowski, C.J. Modeling of an obstacle detection sensor for horizontal directional drilling (HDD) operations. Autom. Constr. 2011, 20, 1079–1086. [Google Scholar] [CrossRef]
- Liu, T.; Wang, B.; Cui, Y.; Luo, X. Trajectory error analysis and optimization in horizontal directional drilling. J. Tsinghua Univ. Sci. Technol. 2011, 51, 592–596. (In Chinese) [Google Scholar] [CrossRef]
- Shi, T.; Wu, J.; Hu, Y.D.L. The Attitude Measurement of Horizontal Directional Drilling Equipment Based on Quaternion and Extended Kalman Filtering Method. J. Phys. Conf. Ser. 2020, 1654, 012099. [Google Scholar] [CrossRef]
- Wang, R.; Wang, B.; Kang, J.; Liu, T. Attitude measurement and error compensation for horizontal directional drilling. J. Tsinghua Univ. Sci. Technol. 2010, 50, 215–218. (In Chinese) [Google Scholar] [CrossRef]
- Eren, T.; Suicmez, V.S. Directional drilling positioning calculations. J. Nat. Gas Sci. Eng. 2020, 73, 103081. [Google Scholar] [CrossRef]
- Daniel, J.; Penn, C.; Antonangelo, J.; Zhang, H. Land Application of Urban Horizontal Directional Drilling Residuals to Established Grass and Bare Soils. Sustainability 2020, 12, 10264. [Google Scholar] [CrossRef]
- Krechowicz, M. Comprehensive risk management in horizontal directional drilling projects. J. Constr. Eng. Manag. 2020, 146, 04020034. [Google Scholar] [CrossRef]
- Saruev, L.; Shadrina, A.; Saruev, A.; Vasenin, S.; Pakharev, A. Prospects for development of technology and facilities of pilot bores horizontal directional drilling for trenchless laying of pipelines. Bull. Tomsk. Polytech. Univ. Geo Assets Eng. 2019, 330, 89–97. [Google Scholar]
- Zhou, C. Research of Horizontal Directional Drilling Trace Optimization abd Software Design in No-Dig Engineering. 2004. Available online: https://kns.cnki.net/KCMS/detail/detail.aspx?dbname=CMFD9904&filename=2004086050.nh (accessed on 8 October 2022). (In Chinese).
- Lu, Q. Research on Trajectory Design and Control Technology of Horizontal Directional Drilling. 2004. Available online: https://kns.cnki.net/KCMS/detail/detail.aspx?dbname=CMFD0506&filename=2005143742.nh (accessed on 8 October 2022). (In Chinese).
- Niu, H. Research on the Optimum Design of 3D Pilot-Hole Trace in HDD. 2008. Available online: https://kns.cnki.net/KCMS/detail/detail.aspx?dbname=CMFD2008&filename=2008095745.nh (accessed on 13 April 2022). (In Chinese).
- Liu, S.-J.; Zhou, X.-M.; Zhang, J.-W.; Xie, Z.-D. The optimization algorithm for application in directional drilling trajectories of energy field. Energy Rep. 2022, 8, 1212–1217. [Google Scholar] [CrossRef]
- Wiśniowski, R. Selected Aspects of Directional Wells Construction Design with the Use of Numeric Methods; AGH: Kraków, Poland, 2002. [Google Scholar]
- Wiśniowski, R.; Łopata, P.; Orłowicz, G. Numerical Methods for Optimization of the Horizontal Directional Drilling (HDD) Well Path Trajectory. Energies 2020, 13, 3806. [Google Scholar] [CrossRef]
- Wiśniowski, R.; Skrzypaszek, K.; Łopata, P.; Orłowicz, G. The Catenary Method as an Alternative to the Horizontal Directional Drilling Trajectory Design in 2D Space. Energies 2020, 13, 1112. [Google Scholar] [CrossRef]
- Patino-Ramirez, F.; Layhee, C.; Arson, C. Horizontal directional drilling (HDD) alignment optimization using ant colony optimization. Tunn. Undergr. Space Technol. 2020, 103, 103450. [Google Scholar] [CrossRef]
- Aadnoy, B.; Toff, V.; Djurhuus, J. Construction of Ultralong Wells Using a Catenary Well Profile. In Proceedings of the IADC/SPE Drilling Conference, Miami, FL, USA, 21–23 February 2006. [Google Scholar] [CrossRef]
- Teodoriu, C.; Asgharzadeh, A. A Novel Model for Catenary Drilling and Drill String Induced Stresses. Polar Arct. Sci. Technol. Pet. Technol. 2017, 8. [Google Scholar] [CrossRef]
- Liu, X.; Samuel, R. Catenary Well Profiles for Ultra Extended-Reach Wells. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 4–7 October 2009. [Google Scholar] [CrossRef]
- McClendon, R. Directional drilling using the catenary method. In Proceedings of the SPE/IADC Drilling Conference, New Orleans, LA, USA, 5–8 March 1985; OnePetro: Richardson, TX, USA, 1985. [Google Scholar]
- Wen, J. A Novel and High-Efficiency Reaming Assembly for Underground Pipelines Pulling Back Laying in Horizontal Directional Drilling. In Proceedings of the 2019 International Conference on Energy, Environmental and Civil Engineering(EECE 2019), Wuhan, China, 23 June 2019. [Google Scholar]
- Bourgoyne, A.T.; Millheim, K.K.; Chenevert, M.E.; Young, F.S. Applied Drilling Engineering; Society of Petroleum Engineers: Richardson, TX, USA, 1986; Volume 2. [Google Scholar]
- Shu, B.; Zhang, S.; Liang, M. Estimation of the maximum allowable drilling mud pressure for a horizontal directional drilling borehole in fractured rock mass. Tunn. Undergr. Space Technol. 2018, 72, 64–72. [Google Scholar] [CrossRef]
- Keulen, B.; Arends, G.; Mastbergen, D.R. Maximum Allowable Pressures during Horizontal Directional Drillings Focused on Sand. Geomechinics 2001. Available online: https://repository.tudelft.nl/islandora/object/uuid:ad91dad8-b958-481b-82d8-c7395d1a3874?collection=education (accessed on 20 November 2022).
- Xia, H.W. Investigation of Maximum Mud Pressure within Sand and Clay during Horizontal Directional Drilling. Ph.D. Thesis, Queen’s University, Kingston, ON, Canada, 2009. [Google Scholar]
- Jin, L.; Feng, Q. Improved radial movement optimization to determine the critical failure surface for slope stability analysis. Environ. Earth Sci. 2018, 77, 564. [Google Scholar] [CrossRef]
- Jin, L.; Feng, Q.; Pan, Z. Slope Stability Analysis Based on Morgenstern-Price Method and Improved Radial Movement Optimization Algorithm. China J. Highw. Transp. 2018, 31, 39–47. [Google Scholar] [CrossRef]
- Pan, Z.F.; Jin, L.X.; Chen, W.S. Improved radial movement optimization algorithm for slope stability analysis. Rock Soil Mech. 2016, 37, 2079–2084. [Google Scholar] [CrossRef]
- Rahmani, R.; Yusof, R. A new simple, fast and efficient algorithm for global optimization over continuous search-space problems: Radial Movement Optimization. Appl. Mech. Mater. 2014, 248, 287–300. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).