Damage Detection in a Rotor Dynamic System by Monitoring Nonlinear Vibrations and Antiresonances of Higher Orders
Abstract
1. Introduction
2. Description of the Cracked Rotor System
3. Dynamic Responses of the Cracked Rotor System
4. Analysis of the Crack Effect on the Vibrational Response of the Rotor System
4.1. Nonlinear Vibration and Appearance of Harmonic Components
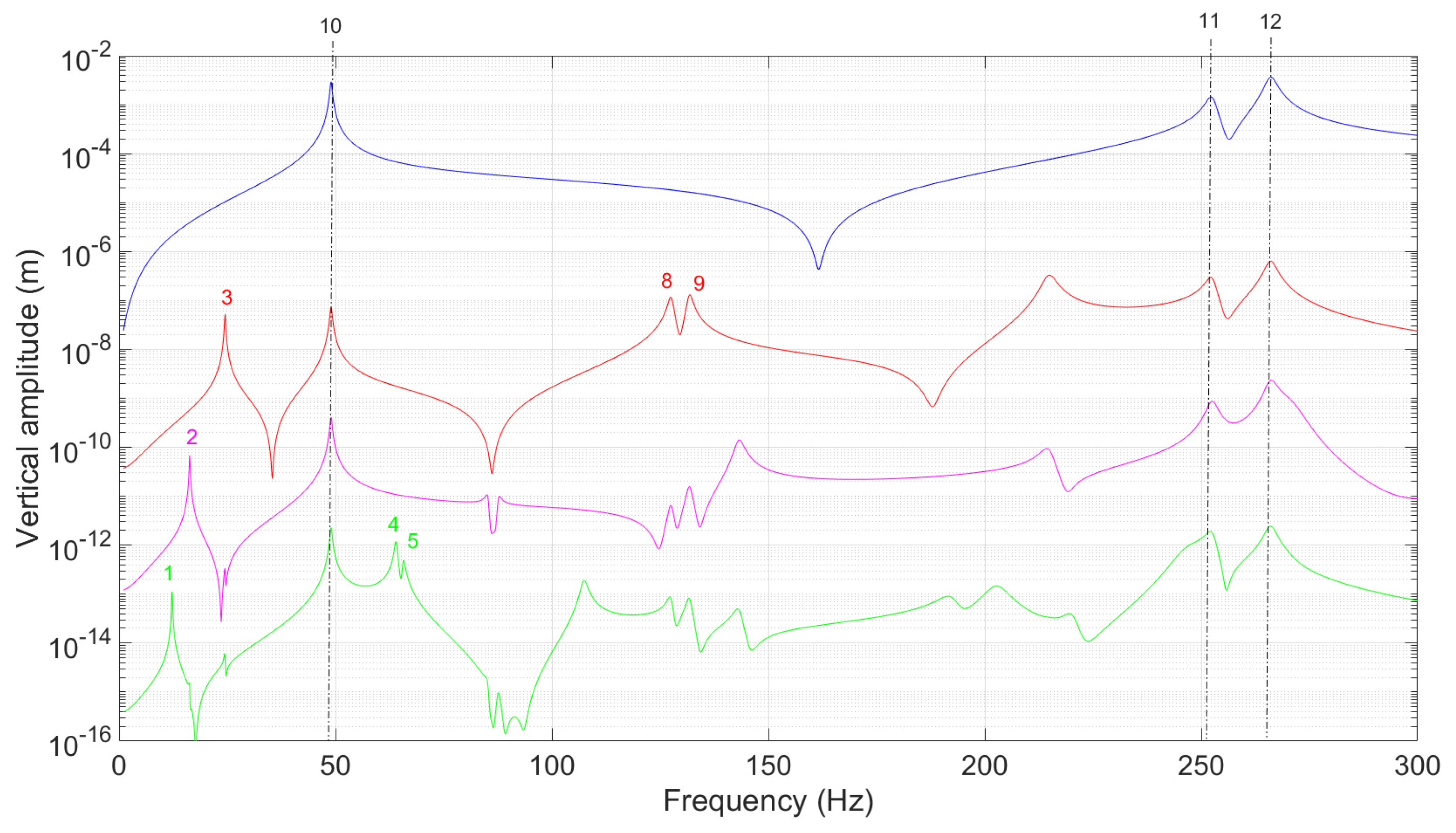
- If the size of the crack is large, the harmonic responses contribute significantly to the overall dynamic response of the rotor system, resulting in the presence of peaks when passing through critical speeds with amplitudes greater than the first-order response (see, for example, the marks in Figure 2). However, in the practical context of a rotor system with a small crack, the presence of the crack is not apparent when inspecting the overall non-linear response alone, and it is necessary to specifically examine the responses of the harmonic contributions (see Figure 3 and Figure 4). Thus, the evolution of the harmonic components offers a positive and useful way to diagnose the presence and potential propagation of cracks in a practical way in both preventive and predictive maintenance.
- Although—due to the presence of one crack—variations in the frequencies and critical speeds of a rotor system exist from a theoretical point of view, these changes are often too small to be considered as reliable indicators for the early detection of defects. This is highlighted in Table 3 and Table 4, which give the evolution of the critical speeds and the natural frequencies at rest in the case of a healthy rotor and the three cracked rotor configurations proposed in the present study. It should be noted that the calculations of the natural frequencies at rest are given for an open transverse crack, as illustrated in Figure 1. It has also been shown in previous studies [3,40,47] that the detection and identification of small defects in the presence of uncertainties (uncertainties in the vibration measurements or uncertainties in the physical model used) are often not possible if the analysis criteria are based exclusively on these evolutions of natural frequencies or critical speeds.
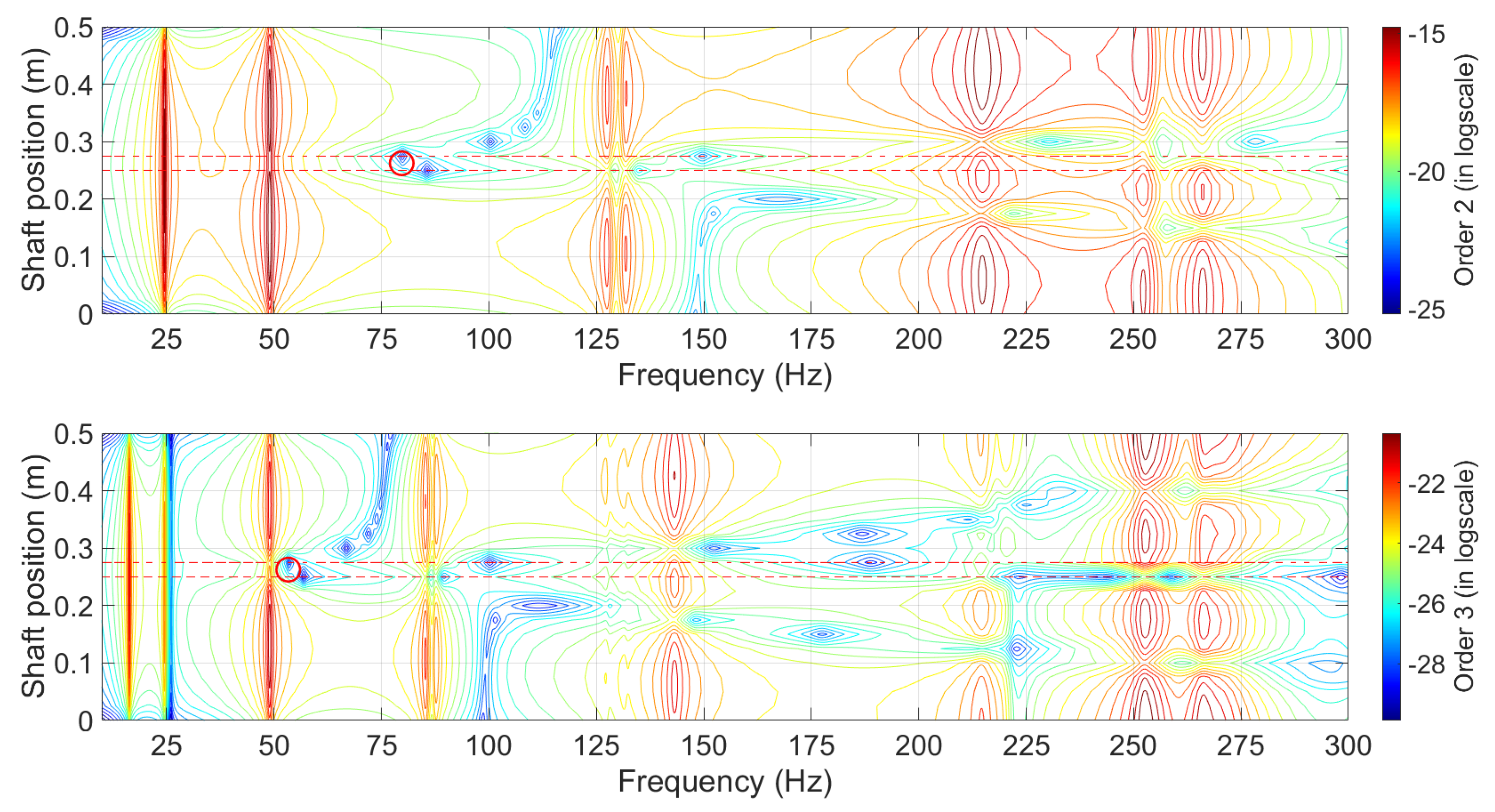
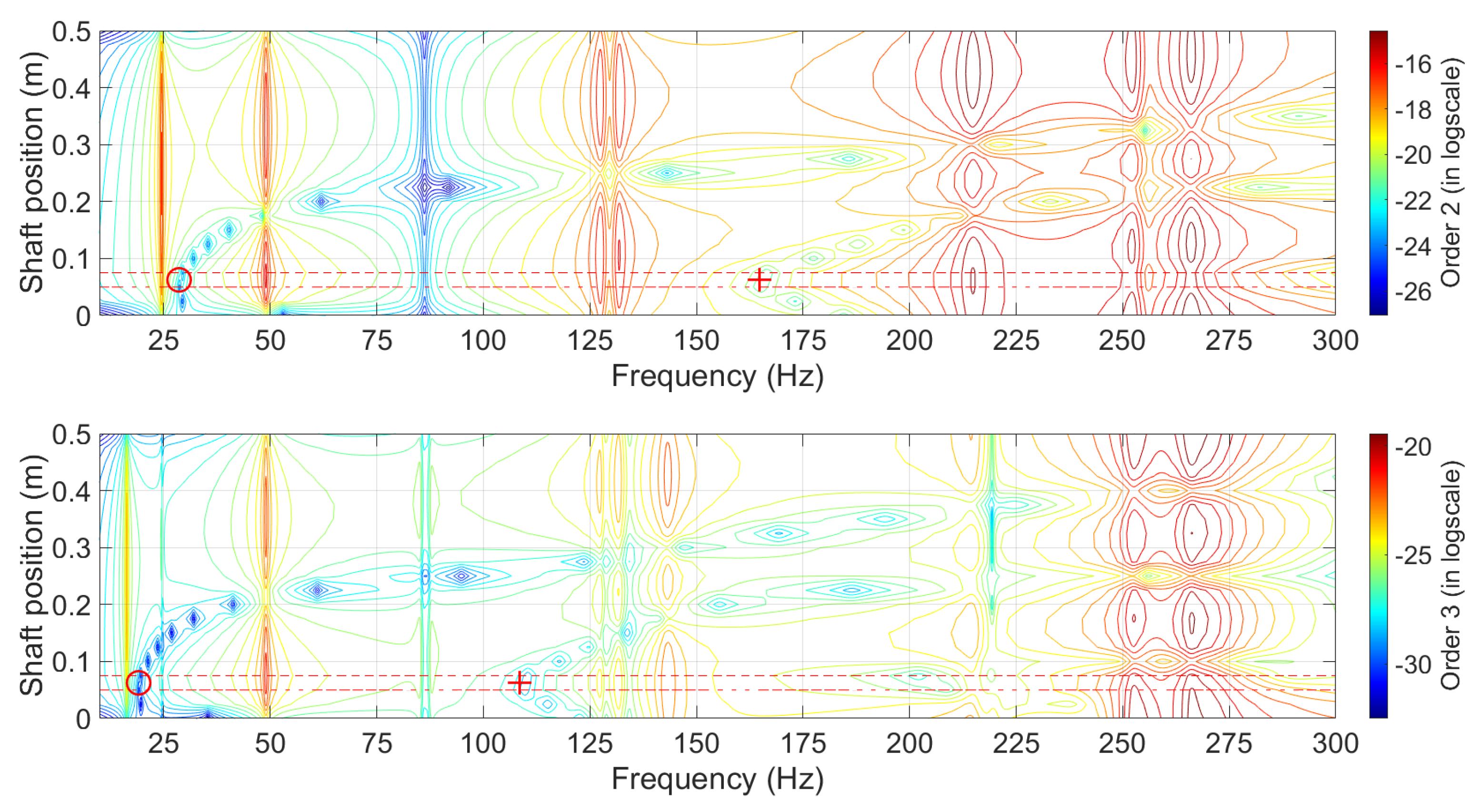
- By comparing the vibration responses of several case studies for rotor systems with small cracks positioned at different locations (i.e., cases 2 and 3 for the present study), it appears that the evolutions of the first-order response (for a chosen vertical or horizontal location on the rotor) over the frequency range are very close. More precisely, the positions of the antiresonances are identical, and the evolution of the vibratory amplitudes between the resonance and antiresonance peaks are similar (see, for example, Figure 3 and Figure 4). It was also verified that this statement is valid for all vertical and horizontal amplitudes over the rotor system. Indeed, the only modification between these various cases comes from the position of the crack, which does not greatly modify the vibrational response of the rotor system because the latter is mainly governed by the imbalance in the case of a rotor system with a small crack. On the contrary, the evolutions of the higher-order responses and the value of the antiresonance frequencies are dependent on the position of the crack (see Figure 3 and Figure 4 for the , and harmonic responses). Consequently, a nondestructive detection technique based on the tracking of antiresonances should be a reliable and effective way for monitoring and identifying the locations of cracks in rotor systems when ensuring their structural health.
4.2. Crack Location Based on the Antiresonances of Higher Order Vibrational Responses
- The antiresonance frequencies of higher orders can be defined as local characteristics of the system that depend on both the driving point and the measurement point. This observation is of primary importance because the driving point is only non-null at the crack position for higher orders, since the excitation undergone by the rotor for the harmonic components (with ) is due to the breathing behavior of the crack (for memory, see the expressions of Equations (10) and (11)).
- On the contrary, not surprisingly, the resonance frequencies and super-harmonic resonances (i.e., the fundamental critical speeds and of the critical speeds with , and ) are global quantities whose values do not depend on the measurement point.
- The minimum value of the antiresonance frequencies of orders 2 and 3 is located at the crack location on the rotor system. It should be noted that this result is also valid for the nth orders with , which are not shown in this study for the sake of conciseness.
- Focusing on the vicinity of the antiresonance frequencies of orders 2 and 3, and increasing the distance between the crack location (i.e., excitation points for the 2nd and 3rd orders, and the shaft element with reduced stiffness) and the measurement point, will lead to higher antiresonance frequency values.
- The resonance–antiresonance pattern is quite similar in both the vertical and horizontal directions. This can be explained by the fact that the only difference between the vertical and horizontal responses corresponds to the small dissymmetry in stiffness due to the breathing crack mechanism and the structural properties of the rotor supports of the rotor system under study. It should be noted that this commentary is based on the complete results of the different cases treated, which have been analyzed by the author but are not illustrated by figures in the study for the sake of brevity.
- The resonance–antiresonance pattern is quite similar for cases where the crack size is different but the crack position is the same. It should be noted that this commentary is based on additional studies conducted by the author but not illustrated in this study. More precisely, the size of the crack only leads to a local stiffness reduction on the cracked element of the rotor system: increasing the crack size decreases the local stiffness, inducing a small decrease in the resonance and antiresonance frequencies of orders 2 and 3 and an overall increase in the amplitudes. In other words, there is a very slight shift on the left for the resonance–antiresonance patterns shown in Figure 6 and Figure 7, when the crack size increases. This result is very interesting because it allows us to conclude that the resonance–antiresonance pattern of higher orders is more sensitive to the crack position than the crack size.
- Whatever the size of the crack, monitoring the antiresonance frequencies of higher orders appears to be a robust indicator of the damage location.
- Contrary to the classical analysis on linear systems [44], the resonance–antiresonance behavior for the and harmonic responses where the excitation point and the measurement point coincide is not trivial. Indeed, there is no evidence of alternating resonances and antiresonances associated with the fundamental critical speeds or (with , ) of the critical speeds.
5. Conclusions
- It was observed through this numerical study that the location of the crack corresponds to the minimum values of the antiresonance frequencies of the nth order (with ). However, no formal proof was obtained on the subject in the present paper. To the author’s knowledge, there is no theoretical study in the field of rotordynamics on the sensitivity of antiresonance frequencies of the nth order to structural changes. Additionally, no theoretical study has yet demonstrated that damage location can be effectively found by tracking the antiresonances of the nth order. It would therefore be interesting to conduct theoretical work in this direction in order to generalize the idea. It can also be pointed out that there is very little research aimed at extending the general higher-order nonlinear analysis of FRF to the detection and damage assessment of general structural systems with breathing cracks [48,49]. Solid theoretical works on the influences of breathing cracks on the higher-order responses of nonlinear structural systems are of interest due to the strong potential for applications of HOFRF (higher-order vibrational responses) to damage identification and assessment in real structural systems (rotating machines).
- It would be interesting to conduct experiments to validate the relevance of the approach proposed to detect crack locations by identifying the positioning of the antiresonance frequencies of higher orders. In a more practical context, where there are only a limited number of sensors and therefore only a limited number of measurement points on the rotor, the question arises as to how to optimally position these sensors to locate the damage. If increasing the distance between the location of the crack and the measurement point leads to an increase in the value of higher orders, then antiresonance frequencies seem to be factors favoring the possibility of robust defect detection in a practical case (by successive adaptation of the placement of the sensors for example). This deserves to be validated by extensive experimental studies.
- Many faults that reduce the lifetime of rotating machinery exist, and they significantly affect the dynamics of rotor systems. It would be interesting to better understand the possibility of damage detection for rotor systems with features such as misalignment, bows, and asymmetric shafts. These faults can also generate nonlinear responses, so the resonance–antiresonance pattern of higher orders should therefore be used with caution to avoid irrelevant damage detection on complex industrial rotating machinery.
- Even if multi-crack detection in the case of beam-like structures using the antiresonances locus of HOFRFs has been previously investigated by Chomette [43], this problem remains completely open and deserves further study for robust and reliable detection of multiple small cracks in rotating systems.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| FRF | Frequency Response Function |
| HOFRF | High-Order Frequency Response Function |
| dof | degrees of freedom |
| HBM | Harmonic Balance Method |
References
- Salawu, O. Detection of structural damage through changes in frequency: A review. Eng. Struct. 1997, 19, 718–723. [Google Scholar] [CrossRef]
- Sekhar, A.S. Vibration characteristics of a cracked rotor with two open cracks. J. Sound Vib. 1999, 223, 497–512. [Google Scholar] [CrossRef]
- Sinou, J.-J. A robust identification of single crack location and size only based on pulsations of the cracked system. Struct. Eng. Mech. 2007, 25, 691–716. [Google Scholar] [CrossRef][Green Version]
- Bamnios, Y.; Douka, E.; Trochidisi, A. Crack identification in beam structures using mechanical impedance. J. Sound Vib. 2002, 256, 287–297. [Google Scholar] [CrossRef]
- Dilena, M.; Morassi, A. The use of antiresonances for crack detection in beams. J. Sound Vib. 2004, 276, 195–214. [Google Scholar] [CrossRef]
- Dharmaraju, N.; Sinha, J.K. Some comments on use of antiresonance for crack identification in beams. J. Sound Vib. 2005, 286, 669–671. [Google Scholar] [CrossRef]
- Dansheng, W.; Hongping, Z.; Chuanyao, C.; Yong, X. An impedance analysis for crack detection in the Timoshenko beam based on the antiresonance technique. Acta Mech. Solida Sin. 2007, 20, 228–235. [Google Scholar]
- Papadopoulos, C.; Dimarogonas, A. Coupled longitudinal and bending vibrations f a rotating shaft with an open crack. J. Sound Vib. 1987, 117, 81–93. [Google Scholar] [CrossRef]
- Collins, K.; Plaut, R.; Wauer, J. Detection of cracks in rotating Timoshenko shafts using axial impulses. J. Vib. Acoust. 1991, 113, 74–78. [Google Scholar] [CrossRef]
- Liu, D.; Gurgenci, H.; Veidt, M. Crack detection in hollow section structures through coupled response measurements. J. Sound Vib. 2003, 261, 17–29. [Google Scholar] [CrossRef]
- Ostachowicz, W.; Krawczuk, M. Coupled torsional and bending vibrations of a rotor with an open crack. Arch. Appl. Mech. 1992, 62, 191–201. [Google Scholar] [CrossRef]
- Gudmundson, P. The dynamic behaviour of slender structures with cross sectional cracks. J. Mech. Phys. Solids 1983, 31, 329–345. [Google Scholar] [CrossRef]
- Davies, W.G.R.; Mayes, I.W. The vibrational behaviour of a multi-shaft multi-bearing system in the presence of a propagating transverse crack. Trans. ASME J. Vib. Acoust. Stress. Reliab. Des. 1984, 106, 146–153. [Google Scholar] [CrossRef]
- Davies, W.G.R.; Mayes, I.W. Analysis of the response of a multi-rotor-bearing system containing a transverse crack in a rotor. Trans. ASME J. Vib. Acoust. Stress. Reliab. Des. 1984, 106, 139–145. [Google Scholar]
- Pugno, N.; Surace, C.; Ruotolo, R. Evaluation of the non-linear dynamic response to harmonic excitation of a beam with several breathing cracks. J. Sound Vib. 2000, 235, 749–762. [Google Scholar] [CrossRef]
- Sinou, J.-J.; Lees, A. Influence of cracks in rotating shafts. J. Sound Vib. 2005, 285, 139–145. [Google Scholar] [CrossRef]
- Al-Shudeifat, M.-A.; Butcher, E.-A. New breathing functions for the transverse breathing crack of the cracked rotor system: Approach for critical and subcritical harmonic analysis. J. Sound Vib. 2011, 330, 526–544. [Google Scholar] [CrossRef]
- Gasch, R. A survey of the dynamic behaviour of a simple rotating shaft with a transverse crack. J. Sound Vib. 1993, 160, 313–332. [Google Scholar] [CrossRef]
- Sekhar, A.; Prabhu, B. Condition monitoring of cracked rotors through transient response. Mech. Mach. Theory 1998, 33, 1167–1175. [Google Scholar] [CrossRef]
- Sekhar, A. Crack detection through wavelet transform for a run-up rotor. J. Sound Vib. 2003, 259, 461–472. [Google Scholar] [CrossRef]
- Darpe, A.; Gupta, K.; Chawla, A. Transient response and breathing behaviour of a cracked jeffcott rotor. J. Sound Vib. 2004, 272, 207–243. [Google Scholar] [CrossRef]
- Sinou, J.-J.; Lees, A. A non-linear study of a cracked rotor. J. Eur. Mech. A/Solids 2007, 26, 152–170. [Google Scholar] [CrossRef]
- Sinou, J.-J. Detection of cracks in rotor based on the 2× and 3× super-harmonic frequency components and the crack–unbalance interactions. Commun. Nonlinear Sci. Numer. Simul. 2008, 13, 2024–2040. [Google Scholar] [CrossRef]
- Sinou, J.-J. An experimental investigation of condition monitoring for notched rotors through transient signals and wavelet transform. Exp. Mech. 2008, 49, 683–695. [Google Scholar] [CrossRef]
- Sinou, J.-J. Experimental response and vibrational characteristics of a slotted rotor. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 3179–3194. [Google Scholar] [CrossRef][Green Version]
- Kushwaha, N.; Patel, V.N. Nonlinear dynamic analysis of two-disk rotor system containing an unbalance influenced transverse crack. Nonlinear Dyn. 2022, 1–29. [Google Scholar] [CrossRef]
- Wauer, J. Dynamics of cracked rotors: Literature survey. Appl. Mech. Rev. 1990, 43, 13–17. [Google Scholar] [CrossRef]
- Dimarogonas, A. Vibration of cracked structures: A state of the art review. Eng. Fract. Mech. 1996, 55, 831–857. [Google Scholar] [CrossRef]
- Doebling, S.; Farrar, C.; Prime, M. A summary review of vibration-based damage methods. Shock Vib. Dig. 1998, 30, 91–105. [Google Scholar] [CrossRef]
- Sinou, J.-J. A review of damage detection and health monitoring of mechanical systems from changes in the measurement of linear and non-linear vibrations. In Mechanical Vibrations: Measurement, Effects and Control; Sapri, R.R., Ed.; Nova Science Publishers: Hauppauge, NY, USA, 2009; pp. 643–702. ISBN 978-1-60692-037-4. [Google Scholar]
- Kumar, C.; Rastogi, V. A brief review on dynamics of a cracked rotor. Int. J. Rotating Mach. 2009, 2009, 758108. [Google Scholar] [CrossRef]
- Bachschmid, N.; Pennacchi, P.; Tanzi, E. Cracked Rotors: A Survey on Static and Dynamic Behaviour Including Modelling and Diagnosis; Springer Science and Business Media: Berlin, Germany, 2010; pp. 129–148. [Google Scholar]
- Fan, W.; Qiao, P. Vibration-based damage identification methods: A review and comparative study. Struct. Health Monit. 2011, 10, 83–111. [Google Scholar] [CrossRef]
- Bovsunovsky, A.; Surace, C. Non-linearities in the vibrations of elastic structures with a closing crack: A state of the art review. Mech. Signal Process. 2015, 62–63, 129–148. [Google Scholar] [CrossRef]
- Sinou, J.-J.; Faverjon, B. The vibration signature of chordal cracks in a rotor system including uncertainties. J. Sound Vib. 2012, 331, 138–154. [Google Scholar] [CrossRef]
- Fu, C.; Ren, X.; Yang, Y.; Lu, K.; Wang, Y. Nonlinear response analysis of a rotor system with a transverse breathing crack under interval uncertainties. Int. J. Non-Linear Mech. 2018, 105, 77–87. [Google Scholar] [CrossRef]
- Fu, C.; Ren, X.; Yang, Y.; Lu, K.; Qin, W. Steady-state response analysis of cracked rotors with uncertain-but-bounded parameters using a polynomial surrogate method. Commun. Nonlinear Sci. Numer. Simul. 2019, 68, 240–256. [Google Scholar] [CrossRef]
- Yongfeng, Y.; Qinyu, W.; Yanlin, W.; Weiyang, Q.; Kuan, L. Dynamic characteristics of cracked uncertain hollow-shaft. Mech. Syst. Signal Process. 2019, 124, 36–48. [Google Scholar] [CrossRef]
- Fu, C.; Xu, Y.; Yang, Y.; Lu, K.; Gu, F.; Ball, A. Dynamics analysis of a hollow-shaft rotor system with an open crack under model uncertainties. Commun. Nonlinear Sci. Numer. Simul. 2020, 83, 105102. [Google Scholar] [CrossRef]
- Sinou, J.-J. Denimal, E. Reliable crack detection in a rotor system with uncertainties via advanced simulation models based on kriging and Polynomial Chaos Expansion. Eur. J. Mech. Solids 2022, 92, 104451. [Google Scholar] [CrossRef]
- Fu, C.; Sinou, J.-J.; Zhu, W.; Lu, K.; Yang, Y. A state-of-the-art review on uncertainty analysis of rotor system. Mech. Syst. Signal Process. 2023, 183, 109619. [Google Scholar] [CrossRef]
- Sinou, J.-J. On the use of non-linear vibrations and the antiresonances of Higher-Order Frequency Response Functions for crack detection in pipeline beam. Mech. Res. Commun. 2012, 43, 87–95. [Google Scholar] [CrossRef]
- Chomette, B. Nonlinear multiple breathing cracks detection using direct zeros estimation of higher-order frequency response function. Commun. Nonlinear Sci. Numer. Simul. 2020, 89, 105330. [Google Scholar] [CrossRef]
- Wahl, F.; Schmidt, G.; Forrai, L. On the significance of antiresonance frequencies in experimental structural analysis. J. Sound Vib. 1999, 219, 379–394. [Google Scholar] [CrossRef]
- D’Ambrogio, W.; Fregolent, A. The use of antiresonances for robust model updating. J. Sound Vib. 2000, 236, 227–243. [Google Scholar] [CrossRef]
- Hanson, D.; Waters, T.P.; Thompson, D.J.; Randall, R.B.; Ford, R.A.J. The role of antiresonance frequencies from operational modalanalysis in finite element model updating. J. Sound Vib. 2007, 21, 74–97. [Google Scholar]
- Sinou, J.-J. Damage assessment based on the Frequencies’ Ratio Surfaces Intersection method for the identification of the crack depth. Struct. Durab. Health Monit. 2007, 3, 133–164. [Google Scholar]
- Lin, R.M.; Ng, T.Y. Applications of higher-order frequency response functions to the detection and damage assessment of general structural systems with breathing cracks. Int. J. Mech. Sci. 2018, 148, 652–666. [Google Scholar] [CrossRef]
- Lin, R.M.; Ng, T.Y. Higher-order FRFs and their applications to the identifications of continuous structural systems with discrete localized nonlinearities. Mech. Syst. Signal Process. 2018, 108, 326–346. [Google Scholar] [CrossRef]
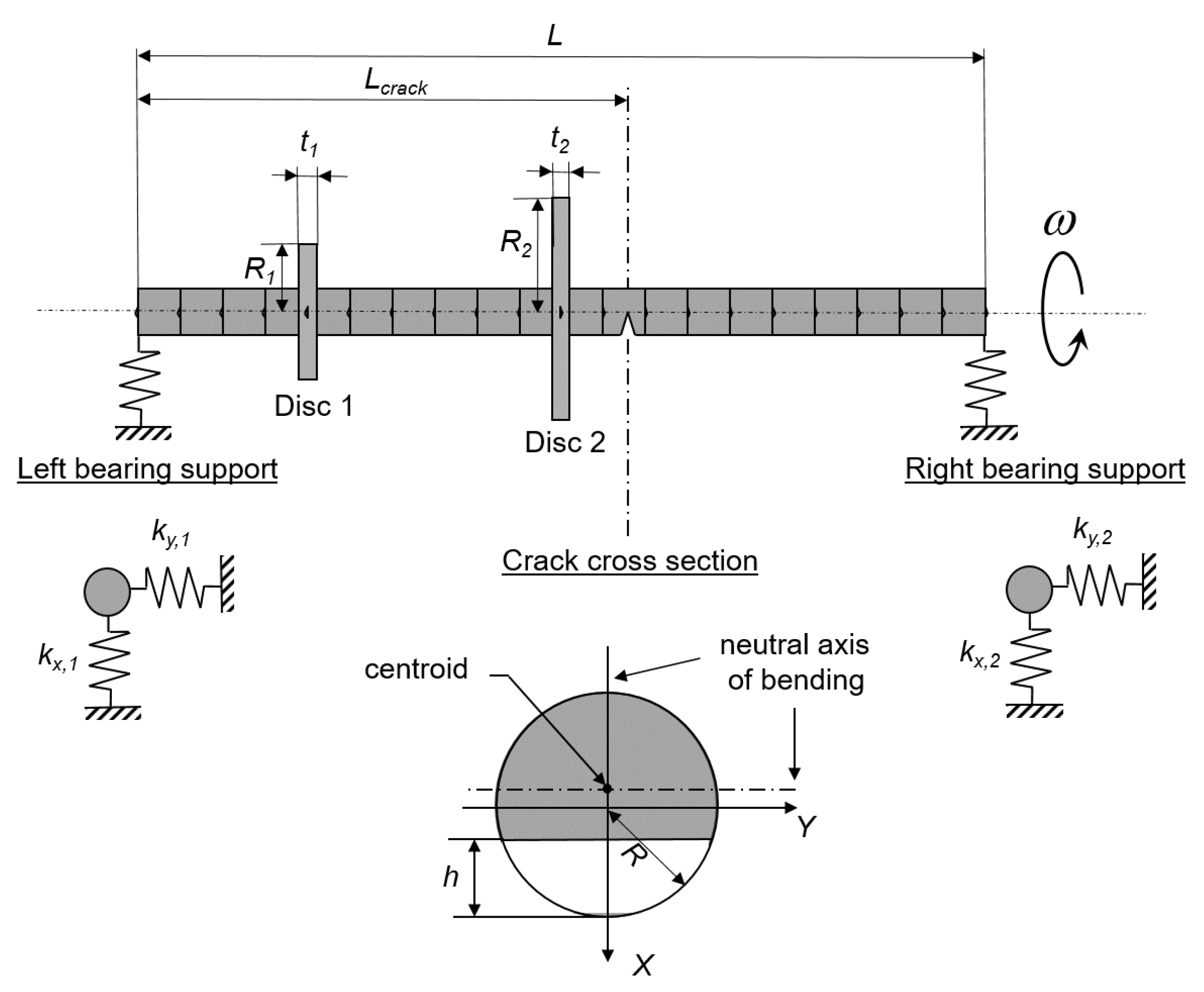



| Description | Notation | Value |
|---|---|---|
| Radius of the shaft | R | 0.005 m |
| Length of the shaft | L | 0.5 m |
| Outer radius of discs 1 and 2 | and | 0.025 m and 0.01 m |
| Thickness of discs 1 and 2 | and | 0.015 m |
| Mass unbalance | 0.001 kg | |
| Eccentricity of the mass unbalance | 0.01 m | |
| Left vertical support stiffness | 5 × 10 N/m | |
| Left horizontal support stiffness | 7.5 × 10 N/m | |
| Right vertical support stiffness | 5 × 10 N/m | |
| Right horizontal support stiffness | 5 × 10 N/m | |
| Density of the shaft rotor | 7800 kg/m | |
| Young’s modulus of elasticity for the shaft rotor | E | 2 × 10 N/m |
| Poisson ratio | 0.3 | |
| Density of discs 1 and 2 | and | 7800 kg/m |
| First Rayleigh damping coefficient | 2.6 | |
| Second Rayleigh damping coefficient | 5 × 10 |
| Case | Crack Depth | Crack Location |
|---|---|---|
| 1 | 1 | 0.3625 m |
| 2 | 0.1 | 0.2625 m |
| 3 | 0.1 | 0.0625 m |
| (Hz) | (Hz) | (Hz) | (Hz) | |
|---|---|---|---|---|
| Healthy rotor | 49.0 | 49.2 | 252.3 | 266.1 |
| Case 1 | 48.4 | 49.1 | 249.4 | 264.6 |
| Case 2 | 49.0 | 49.2 | 252.3 | 266.1 |
| Case 3 | 49.0 | 49.2 | 252.2 | 266.1 |
| (Hz) | (Hz) | (Hz) | (Hz) | |
|---|---|---|---|---|
| Healthy rotor | 49.0 | 49.2 | 256.3 | 262.3 |
| Case 1 | 47.7 | 49.0 | 248.0 | 260.8 |
| Case 2 | 48.9 | 49.1 | 256.3 | 262.3 |
| Case 3 | 49.0 | 49.2 | 256.2 | 262.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sinou, J.-J. Damage Detection in a Rotor Dynamic System by Monitoring Nonlinear Vibrations and Antiresonances of Higher Orders. Appl. Sci. 2022, 12, 11904. https://doi.org/10.3390/app122311904
Sinou J-J. Damage Detection in a Rotor Dynamic System by Monitoring Nonlinear Vibrations and Antiresonances of Higher Orders. Applied Sciences. 2022; 12(23):11904. https://doi.org/10.3390/app122311904
Chicago/Turabian StyleSinou, Jean-Jacques. 2022. "Damage Detection in a Rotor Dynamic System by Monitoring Nonlinear Vibrations and Antiresonances of Higher Orders" Applied Sciences 12, no. 23: 11904. https://doi.org/10.3390/app122311904
APA StyleSinou, J.-J. (2022). Damage Detection in a Rotor Dynamic System by Monitoring Nonlinear Vibrations and Antiresonances of Higher Orders. Applied Sciences, 12(23), 11904. https://doi.org/10.3390/app122311904






