Extraction of the Electromagnetic Parameters of a Metamaterial Using the Nicolson–Ross–Weir Method: An Analysis Based on Global Analytic Functions and Riemann Surfaces
Abstract
1. Introduction
2. Theory
2.1. The Cause of Branch Ambiguity
2.1.1. Surmounting the Branch Ambiguity Issue: Kramers–Kronig Relations
2.1.2. Surmounting the Branch Ambiguity Issue: Phase Unwrapping as Analytic Continuation
2.2. Analytic Continuation, Global Analytic Functions, and Riemann Surfaces
2.2.1. Analytic Continuation and Global Analytic Functions
2.2.2. Global Analytic Functions and Riemann Surfaces
2.3. Kramers–Kronig Relations and Phase Unwrapping Approach: A Unique Point of View within the Framework of the Global Analytic Functions on Riemann Surfaces
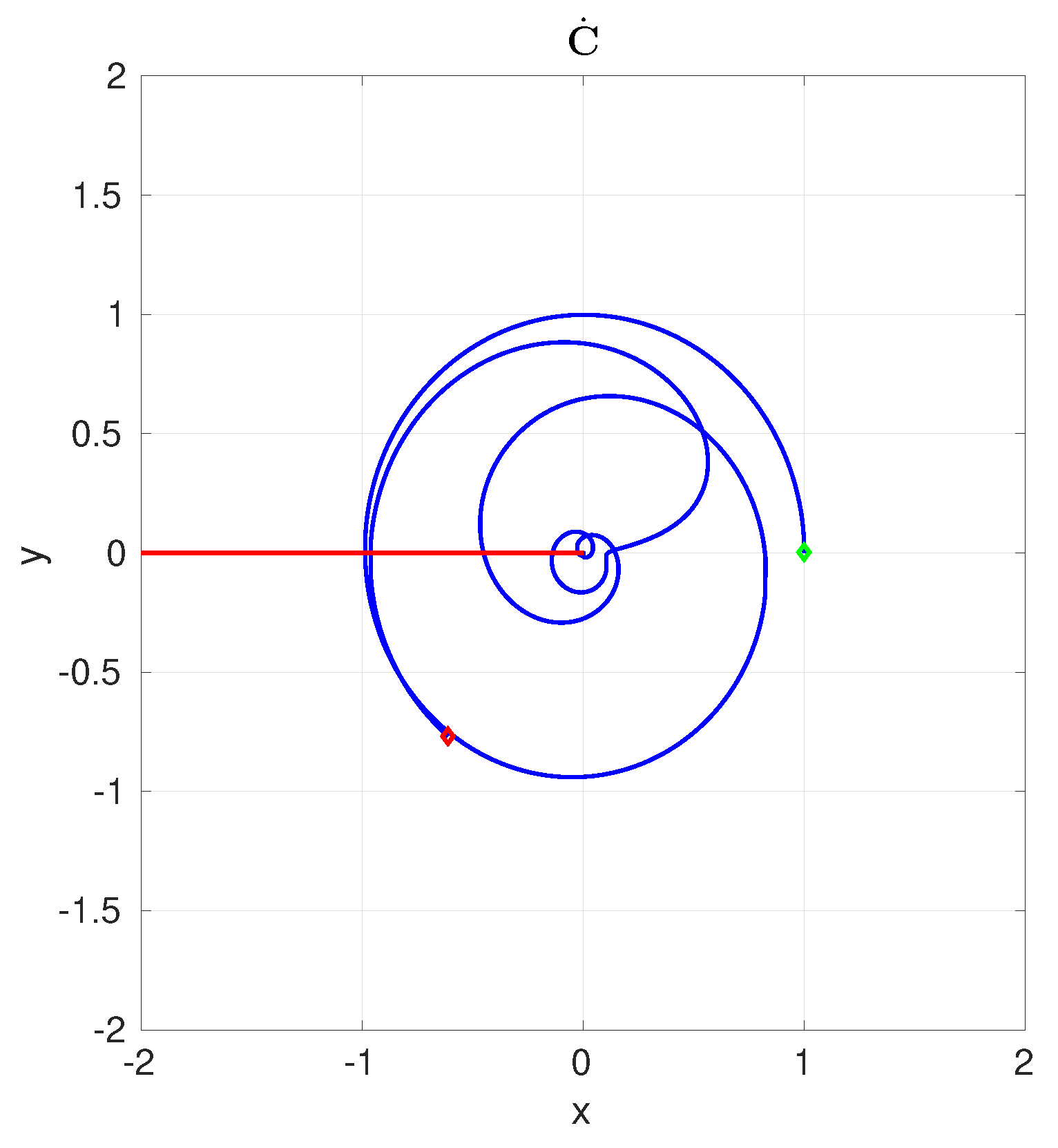
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Complex logarithm; | |
| Principal logarithm; | |
| Natural logarithm function; | |
| Absolute value function; | |
| Principal argument function; | |
| p | Branch index; |
| Complex exponential; | |
| Right inverse function; | |
| Hilbert transform; | |
| Cauchy principal value; | |
| Complex plane; | |
| Complex punctured plane; | |
| Positive real axis; | |
| Upper complex plane; | |
| A global analytic function; | |
| Germ centered at z; | |
| Value of the germ at z; | |
| Set of all the germs of ; | |
| Set of all the germs centered at z; | |
| Domain of existence of a global analytic functionv | |
| Global analytic logarithm; | |
| Lift of the global analytic logarithm; | |
| Riemann surface of ; | |
| Lift of on ; | |
| Projection from the Riemann surface to . |
References
- Xiaojian, F.; Cui, T.-J. Recent progress on metamaterials: From effective medium model to real-time information processing system. Prog. Quantum Electron. 2019, 67, 100223. [Google Scholar]
- Padilla, W.J.; Averitt, R.D. Imaging with metamaterials. Nat. Rev. Phys. 2022, 4, 85–100. [Google Scholar] [CrossRef]
- Cui, T.J.; Smith, D.R.; Liu, R. Metamaterials; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Cui, T.J.; Tang, W.X.; Yang, X.M.; Mei, Z.L.; Jiang, W.X. Metamaterials: Beyond Crystals, Noncrystals, and Quasicrystals; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Smith, D.R.; Pendry, J.B. Homogenization of metamaterials by field averaging. JOSA B 2006, 23, 391–403. [Google Scholar] [CrossRef]
- Alú, A. First-principles homogenization theory for periodic metamaterials. Phys. Rev. B 2011, 84, 075153. [Google Scholar] [CrossRef]
- Chen, L.F.; Ong, C.K.; Neo, C.P.; Varadan, V.V.; Varadan, V.K. Microwave Electronics: Measurement and Materials Characterization; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Ujan, R.; Bahadur, A.; Shabir, G.; Iqbal, S.; Saeed, A.; Channar, P.A.; Mahmood, Q.; Shoaib, M.; Arshad, I.; Saifullah, M.; et al. Facile synthesis of novel fluorescent thiazole coumarinyl compounds: Electrochemical, time resolve fluorescence, and solvatochromic study. J. Mol. Struct. 2021, 1227, 129422. [Google Scholar] [CrossRef]
- Bahadur, A.; Iqbal, S.; Ujan, R.; Channar, P.A.; AL-Anazy, M.M.; Saeed, A.; Mahmood, Q.; Shoaib, M.; Shah, M.; Arshad, I.; et al. Effect of organic solvents on solvatochromic, fluorescence, and electrochemical properties of synthesized thiazolylcoumarin derivatives. Luminescence 2021, 36, 1189–1197. [Google Scholar] [CrossRef]
- Hakim, M.L.; Alam, T.; Islam, M.T.; Baharuddin, M.H.; Alzamil, A.; Islam, M.S. Quad-Band Polarization-Insensitive Square Split-Ring Resonator (SSRR) with an Inner Jerusalem Cross Metamaterial Absorber for Ku-and K-Band Sensing Applications. Sensors 2022, 22, 4489. [Google Scholar] [CrossRef]
- Idrus, I.N.; Faruque, M.R.I.; Abdullah, S.; Khandaker, M.U.; Tamam, N.; Sulieman, A.A. An Oval-Square Shaped Split Ring Resonator Based Left-Handed Metamaterial for Satellite Communications and Radar Applications. Micromachines 2022, 13, 578. [Google Scholar] [CrossRef]
- Sgró, A.; De Carlo, D.; Angiulli, G.; Morabito, F.C.; Versaci, M. Accurate computation of Drude-Lorentz model coefficients of single negative magnetic metamaterials using a micro-genetic algorithm approach. In Multidisciplinary Approaches to Neural Computing; Springer: Cham, Switzerland, 2018; pp. 47–55. [Google Scholar]
- Hannan, S.; Islam, M.T.; Almutairi, A.F.; Faruque, M.R.I. Wide bandwidth angle-and polarization-insensitive symmetric metamaterial absorber for X and Ku band applications. Sci. Rep. 2020, 10, 10338. [Google Scholar] [CrossRef]
- Ajewole, B.; Kumar, P.; Afullo, T. I-Shaped Metamaterial Using SRR for Multi-Band Wireless Communication. Crystals 2022, 12, 559. [Google Scholar] [CrossRef]
- Islam, M.R.; Islam, M.T.; Moniruzzaman, M.; Samsuzzaman, M.; Bais, B.; Arshad, H.; Muhammad, G. Square enclosed circle split ring resonator enabled epsilon negative (ENG) near zero index (NZI) metamaterial for gain enhancement of multiband satellite and radar antenna applications. Results Phys. 2020, 19, 103556. [Google Scholar] [CrossRef]
- Simovski, C.R. On electromagnetic characterization and homogenization of nanostructured metamaterials. J. Opt. 2010, 13, 013001. [Google Scholar] [CrossRef]
- Simovski, C.R. Material parameters of metamaterials (a review). Opt. Spectrosc. 2009, 107, 726–753. [Google Scholar] [CrossRef]
- Arslanagić, S.; Hansen, T.V.; Mortensen, N.A.; Gregersen, A.H.; Sigmund, O.; Ziolkowski, R.W.; Breinbjerg, O. A review of the scattering-parameter extraction method with clarification of ambiguity issues in relation to metamaterial homogenization. IEEE Antennas Propag. Mag. 2013, 55, 91–106. [Google Scholar] [CrossRef]
- Chen, X.; Grzegorczyk, T.M.; Wu, B.I.; Pacheco, J.; Kong, J.A. Robust method to retrieve the constitutive effective parameters of metamaterials. Phys. Rev. E 2004, 70, 016608. [Google Scholar] [CrossRef]
- Szabó, Z.; Park, G.; Hedge, R.; Li, S.L. A unique extraction of metamaterial parameters based on Kramers–Kronig relationship. IEEE Trans. Microw. Theory Tech. 2010, 58, 2646–2653. [Google Scholar] [CrossRef]
- Varadan, V.V.; Ro, R. Unique retrieval of complex permittivity and permeability of dispersive materials from reflection and transmitted fields by enforcing causality. IEEE Trans. Microw. Theory Tech. 2007, 55, 2224–2230. [Google Scholar] [CrossRef]
- Angiulli, G.; Versaci, M.; Calcagno, S.; Di Barba, P. Metamaterial unit cell characterization by using a multi-fidelity surrogate modelling approach. In Proceedings of the 19th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering (ISEF), Nancy, France, 29–31 August 2019; pp. 1–2. [Google Scholar]
- Angiulli, G.; Versaci, M.; Calcagno, S.; Di Barba, P. Quick retrieval of effective electromagnetic metamaterial parameters by using a Multi-fidelity Surrogate Modelling approach. Eur. Phys. J. Appl. Phys. 2020, 90, 20901. [Google Scholar] [CrossRef]
- Yoo, S.; Lee, S.; Choe, J.H.; Park, Q.H. Causal homogenization of metamaterials. Nanophotonics 2019, 8, 1063–1069. [Google Scholar] [CrossRef]
- Cao, Z.X.; Yuan, F.G.; Li, L.H. An automated phase correction algorithm for retrieving permittivity and permeability of electromagnetic metamaterials. AIP Adv. 2014, 4, 067115. [Google Scholar] [CrossRef]
- Shi, Y.; Li, Z.Y.; Li, L.; Liang, C.H. An electromagnetic parameters extraction method for metamaterials based on phase unwrapping technique. Waves Random Complex Media 2016, 4, 417–433. [Google Scholar] [CrossRef]
- Angiulli, G.; Versaci, M. An Analytic Continuation Algorithm for Recovering the Electromagnetic Parameters of Metamaterials. In Proceedings of the 2021 Photonics & Electromagnetics Research Symposium (PIERS), Hangzhou, China, 21–25 November 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 2648–2652. [Google Scholar]
- Hasar, U.C.; Muratoglu, A.; Bute, M.; Barroso, J.J.; Ertugrul, M. Effective constitutive parameters retrieval method for bianisotropic metamaterials using waveguide measurements. IEEE Trans. Microw. Theory Tech. 2017, 65, 1488–1497. [Google Scholar] [CrossRef]
- Peiponen, K.E.; Vartiainen, E.M.; Asakura, T. Dispersion, Complex Analysis and Optical Spectroscopy: Classical Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1998; Volume 147. [Google Scholar]
- Angiulli, G.; Versaci, M. Retrieving the Effective Parameters of an Electromagnetic Metamaterial Using the Nicolson-Ross-Weir Method: An Analytic Continuation Problem along the Path Determined by Scattering Parameters. IEEE Access 2021, 9, 77511–77525. [Google Scholar] [CrossRef]
- Smith, D.R.; Vier, D.C.; Koschny, T.C.; Soukoulis, M. Electromagnetic parameter retrieval from inhomogeneous metamaterials. Phys. Rev. E 2005, 71, 036617. [Google Scholar] [CrossRef] [PubMed]
- Markushevich, A.I. Theory of Functions of a Complex Variable, 2nd ed.; Chelsea Publishing Company: New York, NY, USA, 1985. [Google Scholar]
- Peiponen, K.E.; Lucarini, V.; Vartiainen, E.M.; Saarinen, J.J. Kramers-Kronig relations and sum rules of negative refractive index media. Eur. Phys. J. Condens. Matter Complex Syst. 2004, 41, 61–65. [Google Scholar] [CrossRef]
- Francisco, C.; Nabet, B. Numerical computation of the complex dielectric permittivity using Hilbert transform and FFT techniques. J. Frankl. Inst. 1999, 336, 53–64. [Google Scholar]
- Palka, B.P. An Introduction to Complex Function Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Oppenheim, A.; Schafer, R.W. Discrete Time Signal Processing; Prentice Hall: Hoboken, NJ, USA, 2009. [Google Scholar]
- Wegert, E. Visual Complex Functions: An Introduction with Phase Portraits; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Lucarini, V.; Saarinen, J.J.; Peiponen, K.E.; Vartiainen, E.M. Kramers-Kronig relations in Optical Materials Research; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Dirdal, C.A.; Skaar, J. Superpositions of Lorentzians as the class of causal functions. Phys. Rev. A 2013, 88, 033834. [Google Scholar] [CrossRef]
- Groetsch, C.W. Element of Applicable Functional Analysis; Marcel Dekker: New York, NY, USA, 1980. [Google Scholar]
- Chellappa, S.; Franchetti, F.; Puschel, M. How to write fast numerical code: A small introduction. In International Summer School on Generative and Transformational Techniques in Software Engineering; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]






| First slab: , nm | |||
|---|---|---|---|
| 1.8 | 1.0 | ||
| 2.0 | 1.3 | ||
| PHz | PHz | ||
| PHz | PHz | ||
| Second slab: , nm | |||
| 1.8 | 1.0 | ||
| 2.5 | 1.8 | ||
| 2.0 | 1.3 | ||
| PHz | PHz | ||
| PHz | PHz | ||
| PHz | PHz | ||
| PHz | PHz |
| PE | ||||
|---|---|---|---|---|
| PUNWOS | K-K | PUNW | PUNW | |
| 512 | ||||
| 1024 | ||||
| 2048 | ||||
| 4096 | ||||
| t (s) | ||||
| PUNWOS | K-K | PUNW | PUNW | |
| 512 | ||||
| 1024 | ||||
| 2048 | ||||
| 4096 |
| PE | ||||
|---|---|---|---|---|
| PUNWOS | K-K | PUNW | PUNW | |
| 1024 | ||||
| 2048 | ||||
| 4096 | ||||
| 8192 | ||||
| 16,384 | ||||
| t (s) | ||||
| PUNWOS | K-K | PUNW | PUNW | |
| 1024 | ||||
| 2048 | ||||
| 4096 | ||||
| 8192 | ||||
| 16,384 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Angiulli, G.; Versaci, M. Extraction of the Electromagnetic Parameters of a Metamaterial Using the Nicolson–Ross–Weir Method: An Analysis Based on Global Analytic Functions and Riemann Surfaces. Appl. Sci. 2022, 12, 11121. https://doi.org/10.3390/app122111121
Angiulli G, Versaci M. Extraction of the Electromagnetic Parameters of a Metamaterial Using the Nicolson–Ross–Weir Method: An Analysis Based on Global Analytic Functions and Riemann Surfaces. Applied Sciences. 2022; 12(21):11121. https://doi.org/10.3390/app122111121
Chicago/Turabian StyleAngiulli, Giovanni, and Mario Versaci. 2022. "Extraction of the Electromagnetic Parameters of a Metamaterial Using the Nicolson–Ross–Weir Method: An Analysis Based on Global Analytic Functions and Riemann Surfaces" Applied Sciences 12, no. 21: 11121. https://doi.org/10.3390/app122111121
APA StyleAngiulli, G., & Versaci, M. (2022). Extraction of the Electromagnetic Parameters of a Metamaterial Using the Nicolson–Ross–Weir Method: An Analysis Based on Global Analytic Functions and Riemann Surfaces. Applied Sciences, 12(21), 11121. https://doi.org/10.3390/app122111121







