A Novel Approach for Selecting Effective Threshold Values in Ternary State Estimation Using Particle Swarm Optimization
Abstract
1. Introduction
- An automated and efficient thresholding event triggering swarm optimization (TETSO) technique is proposed.
- Multi-objective PSO is utilized to improve boundary selection of the TET mechanism.
- The efficiency of the proposed TETSO method is confirmed with simulation results.
2. Problem Formulation
Ternary Event-Triggering (TET)
- 1.
- Set-Valued Data: When , the circumstances of the ternary mechanism are not satisfied; hence the sensor does not transfer any measurement to the estimator. In this scenario, fusion center does not have the specific value of the existing sensor’s observations. However, based on secondary information (i.e., the observation associated with the following set ), the FC knows which observations belong to which set.
- 2.
- Set and Quantized-Valued Data: When , the estimator lacks the exact value of the current measurement (), though it has access to the quantized version of the current measurement, which is transferred to the FC. Meanwhile, the FC has access to the set-valued data (i.e., the observation belongs to either of the following two sets or ). This additional secondary information contributes to the enhancement of the approximation efficiency through quantized measurements [14,19].
- 3.
- Point-Valued Data: When , the TET mechanism conveys the specific measurement of the sensor to the FC.
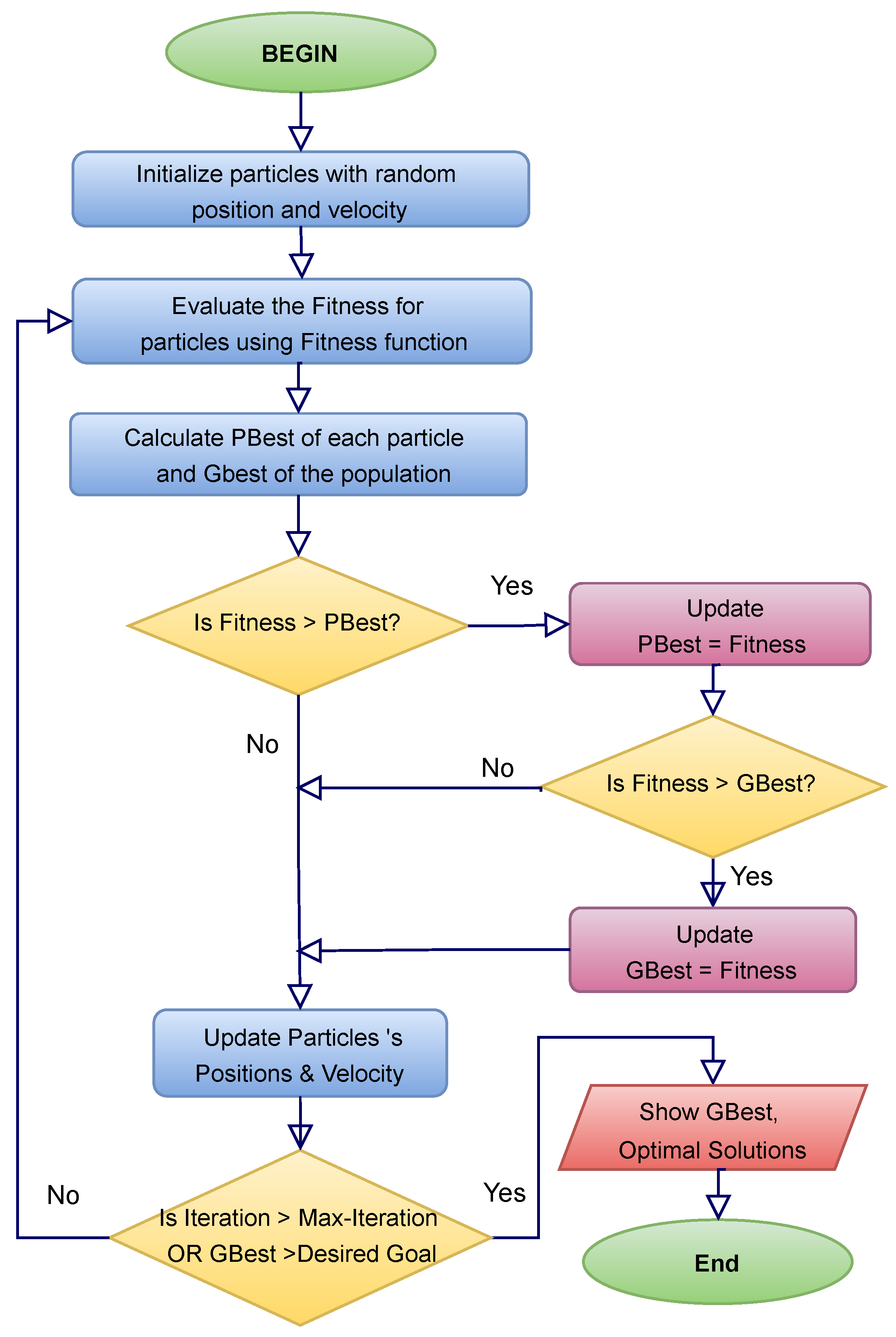
3. The Proposed TETSO Framework
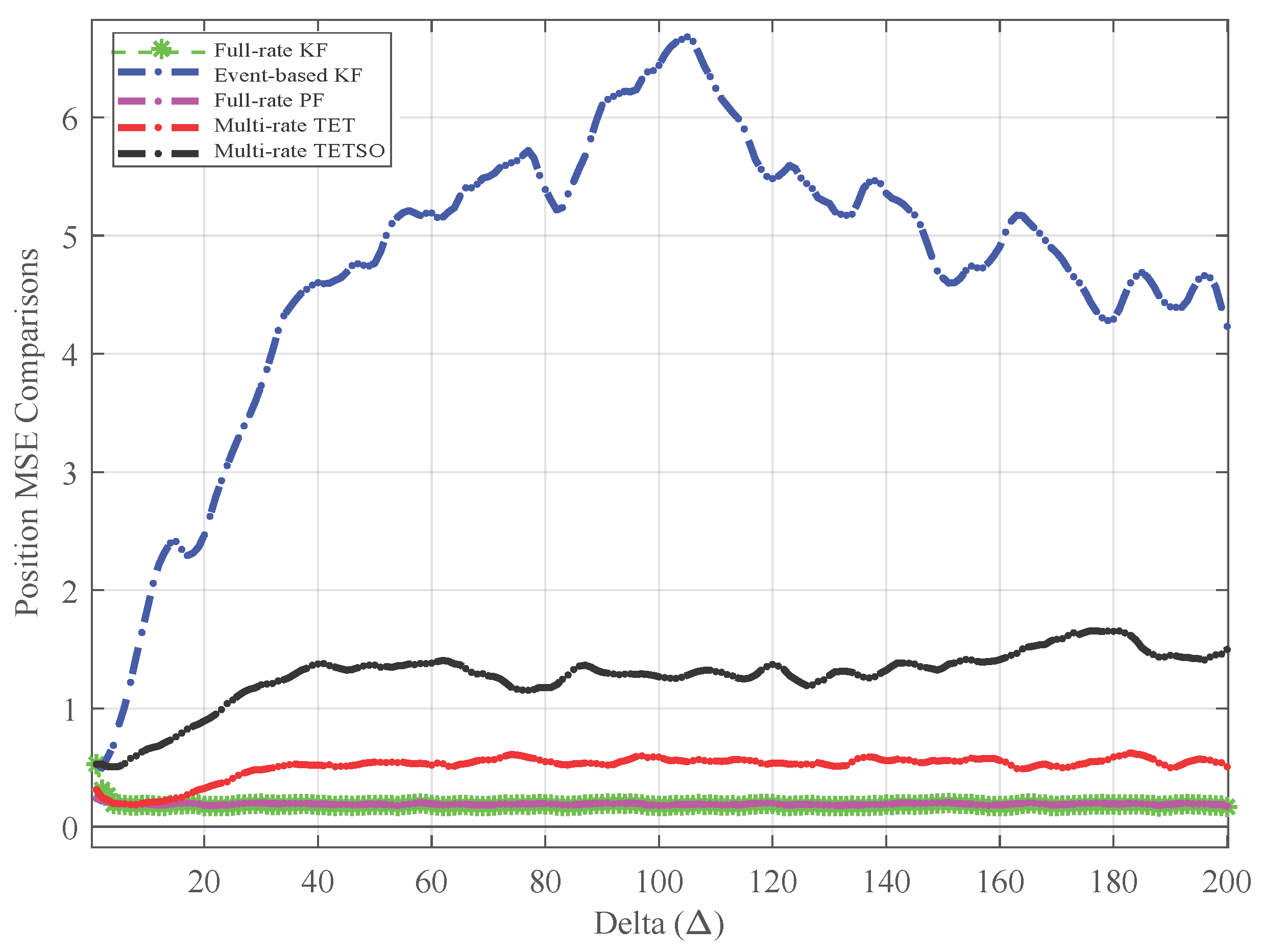
4. Simulation Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviation | Definition |
| ADAI | Adaptive distributed artificial intelligence |
| APSP | Adaptive Particle Swarm Optimization |
| CPS | Cyber-physical system |
| EBE | Event-based estimation |
| IE | Idle epoch |
| KF | Kalman filter |
| MSE | Mean square error |
| PF | Particle filter |
| PSO | Particle swarm optimization |
| QM | Quantize measurements |
| RM | Row measurements |
| SOD | Send on delta |
| TET | Ternary event triggering |
| TETSO | Ternary event triggering swarm optimization |
References
- Mohammadi, A.; Plataniotis, K.N. Event-Based Estimation With Information-Based Triggering and Adaptive Update. IEEE Trans. Signal Process. 2017, 65, 4924–4939. [Google Scholar] [CrossRef]
- Han, D.; Mo, Y.; Wu, J.; Weerakkody, S.; Sinopoli, B.; Shi, L. Stochastic event-triggered sensor scheduling for remote state estimation. In Proceedings of the 52nd IEEE Conference on Decision and Control, Firenze, Italy, 10–13 December 2013; pp. 6079–6084. [Google Scholar] [CrossRef]
- Thirukrishna, J.T.; Aishwarya, M.V.; Singh, M.; Mounisha, B.; Kaveri, N. A survey on instantaneous data transmission in Wireless Sensor Networks for Healthcare Monitoring. Res. Sq. 2021. [Google Scholar] [CrossRef]
- Poudel, S.; Moh, S.; Shen, J. Residual energy-based clustering in UAV-aided wireless sensor networks for surveillance and monitoring applications. J. Surveill. Secur. Saf. 2021, 2, 103–116. [Google Scholar] [CrossRef]
- Dogra, R.; Rani, S.; Sharma, B. A review to forest fires and its detection techniques using wireless sensor network. In Advances in Communication and Computational Technology; Springer: Singapore, 2021; pp. 1339–1350. [Google Scholar]
- Khalil, N.; Abid, M.R.; Benhaddou, D.; Gerndt, M. Wireless sensors networks for Internet of Things. In Proceedings of the 2014 IEEE Ninth International Conference on Intelligent Sensors, Sensor Networks and Information Processing (ISSNIP), Singapore, 21–24 April 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Ullah, A.; Ishaq, N.; Azeem, M.; Ashraf, H.; Jhanjhi, N.; Humayun, M.; Tabbakh, T.A.; Almusaylim, Z.A. A survey on continuous object tracking and boundary detection schemes in IoT assisted wireless sensor networks. IEEE Access 2021, 9, 126324–126336. [Google Scholar] [CrossRef]
- Yan, Z.; Goswami, P.; Mukherjee, A.; Yang, L.; Routray, S.; Palai, G. Low-energy PSO-based node positioning in optical wireless sensor networks. Optik 2019, 181, 378–382. [Google Scholar] [CrossRef]
- Mukherjee, A.; Goswami, P.; Yan, Z.; Yang, L.; Rodrigues, J.J.P.C. ADAI and Adaptive PSO-Based Resource Allocation for Wireless Sensor Networks. IEEE Access 2019, 7, 131163–131171. [Google Scholar] [CrossRef]
- Gungor, V.C.; Hancke, G.P. Industrial Wireless Sensor Networks: Challenges, Design Principles, and Technical Approaches. IEEE Trans. Ind. Electron. 2009, 56, 4258–4265. [Google Scholar] [CrossRef]
- Gungor, V.C.; Lu, B.; Hancke, G.P. Opportunities and Challenges of Wireless Sensor Networks in Smart Grid. IEEE Trans. Ind. Electron. 2010, 57, 3557–3564. [Google Scholar] [CrossRef]
- Canzian, L.; van der Schaar, M. Timely Event Detection by Networked Learners. IEEE Trans. Signal Process. 2015, 63, 1282–1296. [Google Scholar] [CrossRef]
- Davar, S.; Mohammadi, A. Event-based particle filtering with point and set-valued measurements. In Proceedings of the 25th European Signal Processing Conference (EUSIPCO), Kos Island, Greece, 28 August–2 September 2017; pp. 211–215. [Google Scholar] [CrossRef]
- Mohammadi, A.; Davar, S.; Plataniotis, K.N. Ternary-Event-Based State Estimation With Joint Point, Quantized, and Set-Valued Measurements. IEEE Signal Process. Lett. 2018, 25, 665–669. [Google Scholar] [CrossRef]
- You, K.; Xie, L. Kalman Filtering With Scheduled Measurements. IEEE Trans. Signal Process. 2013, 61, 1520–1530. [Google Scholar] [CrossRef]
- Joris, S.; Mircea, L. Event Based State Estimation With Time Synchronous Updates. IEEE Trans. Autom. Control 2012, 57, 2650–2655. [Google Scholar] [CrossRef]
- Han, D.; Mo, Y.; Wu, J.; Weerakkody, S.; Sinopoli, B.; Shi, L. Stochastic Event-Triggered Sensor Schedule for Remote State Estimation. IEEE Trans. Autom. Control 2015, 60, 2661–2675. [Google Scholar] [CrossRef]
- Shi, D.; Chen, T.; Shi, L. On Set-Valued Kalman Filtering and Its Application to Event-Based State Estimation. IEEE Trans. Autom. Control 2015, 60, 1275–1290. [Google Scholar] [CrossRef]
- Davar, S.; Mohammadi, A. Designing Optimal Thresholds for Ternary Event-based State Estimation via Multi Objective Particle Swarm Optimizer. In Proceedings of the IEEE 61st International Midwest Symposium on Circuits and Systems (MWSCAS), Windsor, ON, Canada, 5–8 August 2018; pp. 1146–1149. [Google Scholar] [CrossRef]
- Nguyen, V.H.; Suh, Y.S. Improving Estimation Performance in Networked Control Systems Applying the Send-on-delta Transmission Method. Sensors 2007, 7, 2128–2138. [Google Scholar] [CrossRef] [PubMed]
- Miskowicz, M. Send-On-Delta Concept: An Event-Based Data Reporting Strategy. Sensors 2006, 6, 49–63. [Google Scholar] [CrossRef]
- Mohammadi, A.; Asif, A. Distributed Consensus + Innovation Particle Filtering for Bearing/Range Tracking With Communication Constraints. IEEE Trans. Signal Process. 2015, 63, 620–635. [Google Scholar] [CrossRef]
- Joris, S.; Mircea, L. On Event Based State Estimation. In Proceedings of the Hybrid Systems: Computation and Control, San Francisco, CA, USA, 13–15 April 2009; pp. 336–350. [Google Scholar] [CrossRef]
- Balasubramanian, D.; Govindasamy, V. Study on Evolutionary Approaches for Improving the Energy Efficiency of Wireless Sensor Networks Applications. EAI Endorsed Trans. Internet Things 2020, 5, e2. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the International Conference on Neural Networks (ICNN’95), Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Du, W.B.; Ying, W.; Yan, G.; Zhu, Y.B.; Cao, X.B. Heterogeneous Strategy Particle Swarm Optimization. IEEE Trans. Circuits Syst. II Express Briefs 2017, 64, 467–471. [Google Scholar] [CrossRef]
- Kaur, T.; Kumar, D. Particle Swarm Optimization-Based Unequal and Fault Tolerant Clustering Protocol for Wireless Sensor Networks. IEEE Sens. J. 2018, 18, 4614–4622. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science (MHS’95), Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar] [CrossRef]
- Han, D.; You, K.; Xie, L.; Wu, J.; Shi, L. Optimal Parameter Estimation Under Controlled Communication Over Sensor Networks. IEEE Trans. Signal Process. 2015, 63, 6473–6485. [Google Scholar] [CrossRef]
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Kalman, R.E.; Bucy, R.S. New Results in Linear Filtering and Prediction Theory. J. Basic Eng. 1961, 83, 95–108. [Google Scholar] [CrossRef]
- Doucet, A.; Gordon, N.J.; Krishnamurthy, V. Particle filters for state estimation of jump Markov linear systems. IEEE Trans. Signal Process. 2001, 49, 613–624. [Google Scholar] [CrossRef]

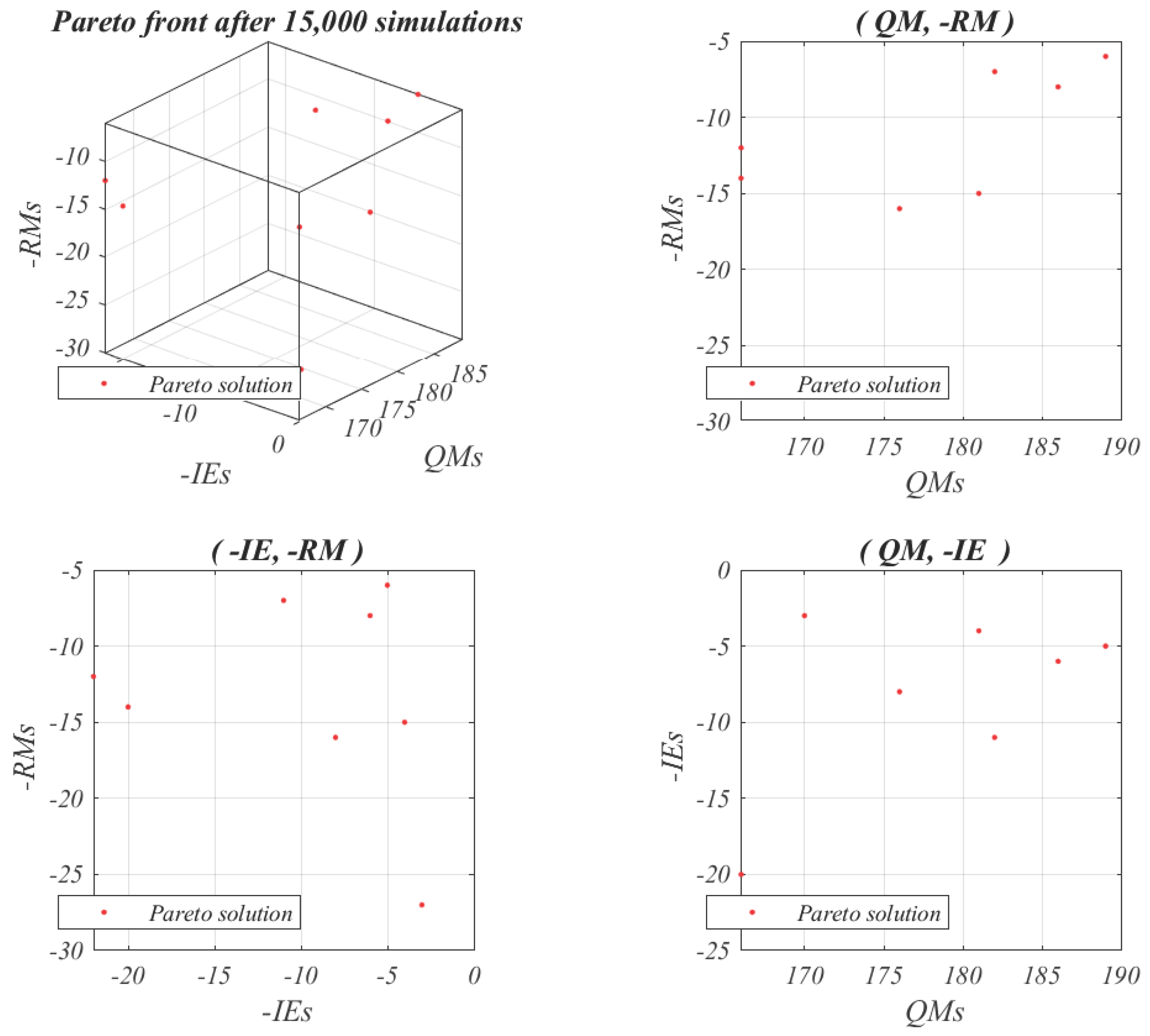

| = 30 | |
| MC simulation = 100 | Max iteration = 200 |
| = | = |
| = 0 | = 0 |
| Group | I | II | III | IV | V | VI | VII | VIII |
|---|---|---|---|---|---|---|---|---|
| IE | 6 | 3 | 20 | 4 | 5 | 22 | 8 | 11 |
| QM | 186 | 170 | 166 | 181 | 189 | 166 | 176 | 182 |
| RM | 8 | 27 | 14 | 15 | 6 | 12 | 16 | 7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Davar, S.; Fevens, T. A Novel Approach for Selecting Effective Threshold Values in Ternary State Estimation Using Particle Swarm Optimization. Appl. Sci. 2022, 12, 10693. https://doi.org/10.3390/app122110693
Davar S, Fevens T. A Novel Approach for Selecting Effective Threshold Values in Ternary State Estimation Using Particle Swarm Optimization. Applied Sciences. 2022; 12(21):10693. https://doi.org/10.3390/app122110693
Chicago/Turabian StyleDavar, Somayeh, and Thomas Fevens. 2022. "A Novel Approach for Selecting Effective Threshold Values in Ternary State Estimation Using Particle Swarm Optimization" Applied Sciences 12, no. 21: 10693. https://doi.org/10.3390/app122110693
APA StyleDavar, S., & Fevens, T. (2022). A Novel Approach for Selecting Effective Threshold Values in Ternary State Estimation Using Particle Swarm Optimization. Applied Sciences, 12(21), 10693. https://doi.org/10.3390/app122110693







