The Using of the Multilayer Plate Concept in the Calculus of Functionally Graded Plates
Abstract
1. Introduction
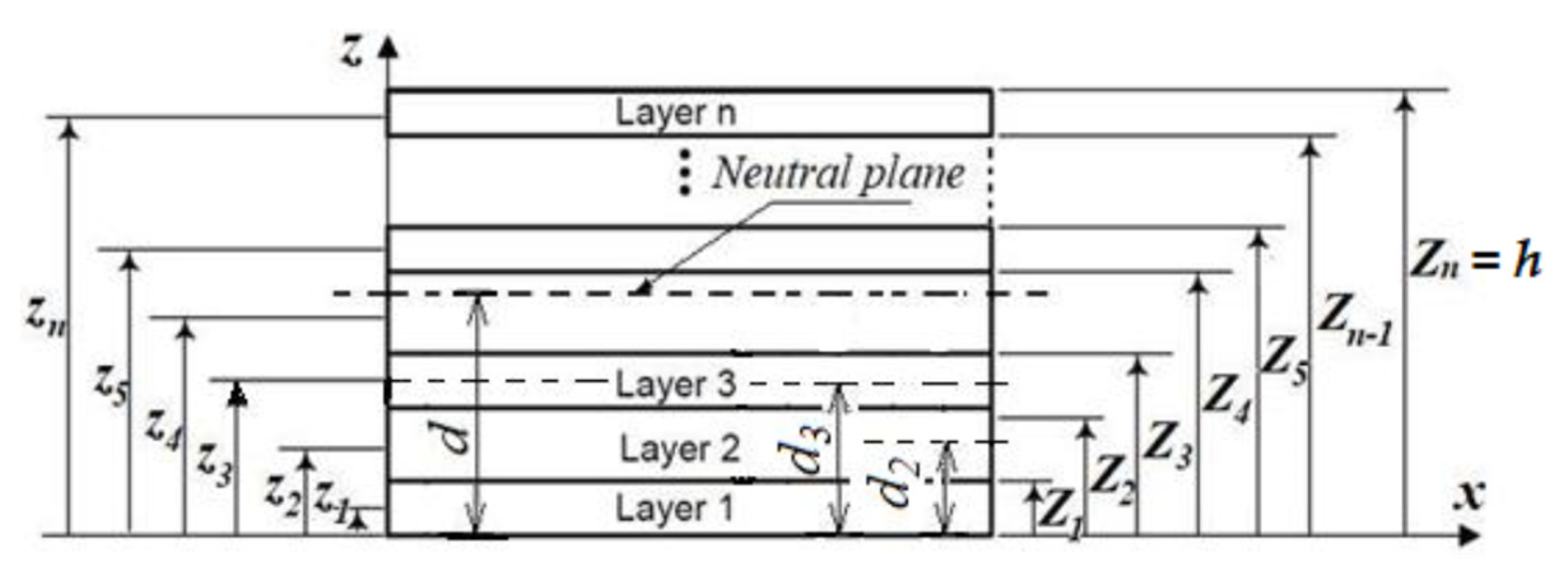
2. Multilayer Plate Concept
3. Calculus of the FGPs Bending Rigidity
3.1. The Multilayer Plate Method
3.2. Direct Integration Method
4. Calcuus of the Material Density of FGPs
4.1. Analytical Calculus by Direct Integration
4.2. Analytical Calculus by Multilayer Plate Concept
5. Case Study
5.1. Calculus of the Layer Material Properties
5.2. Calculus of the Bending Rigidity of the Plate
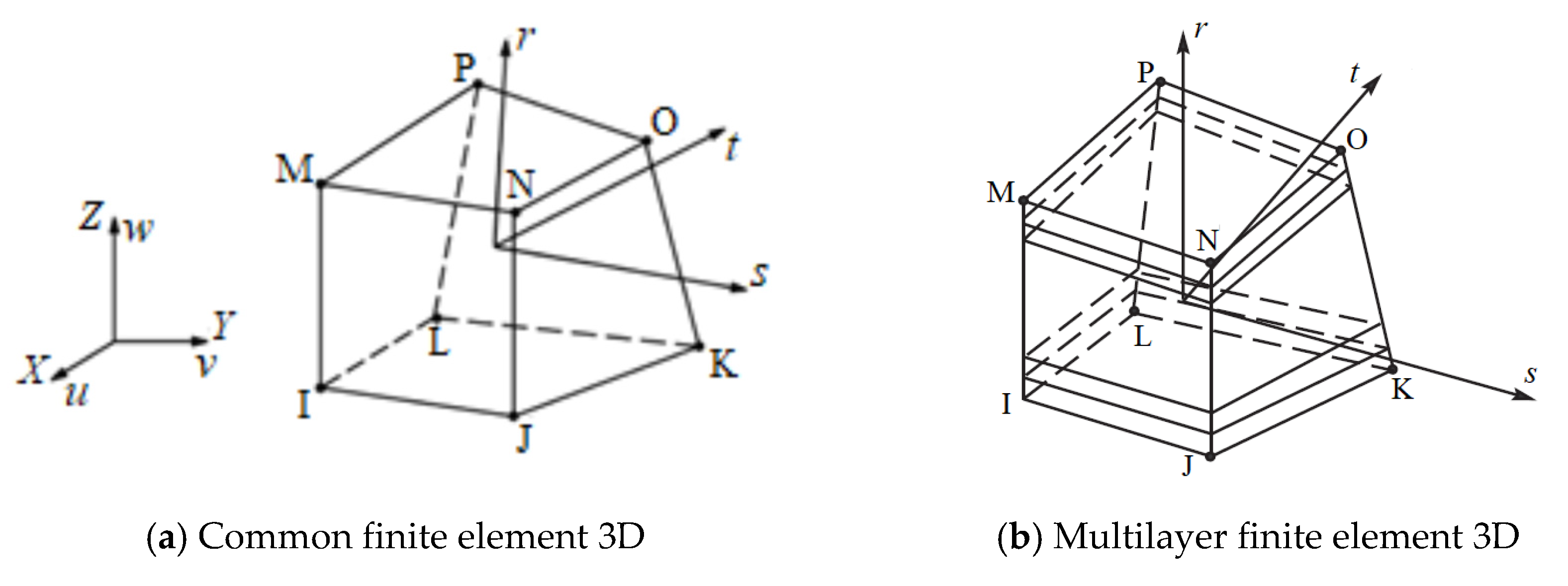
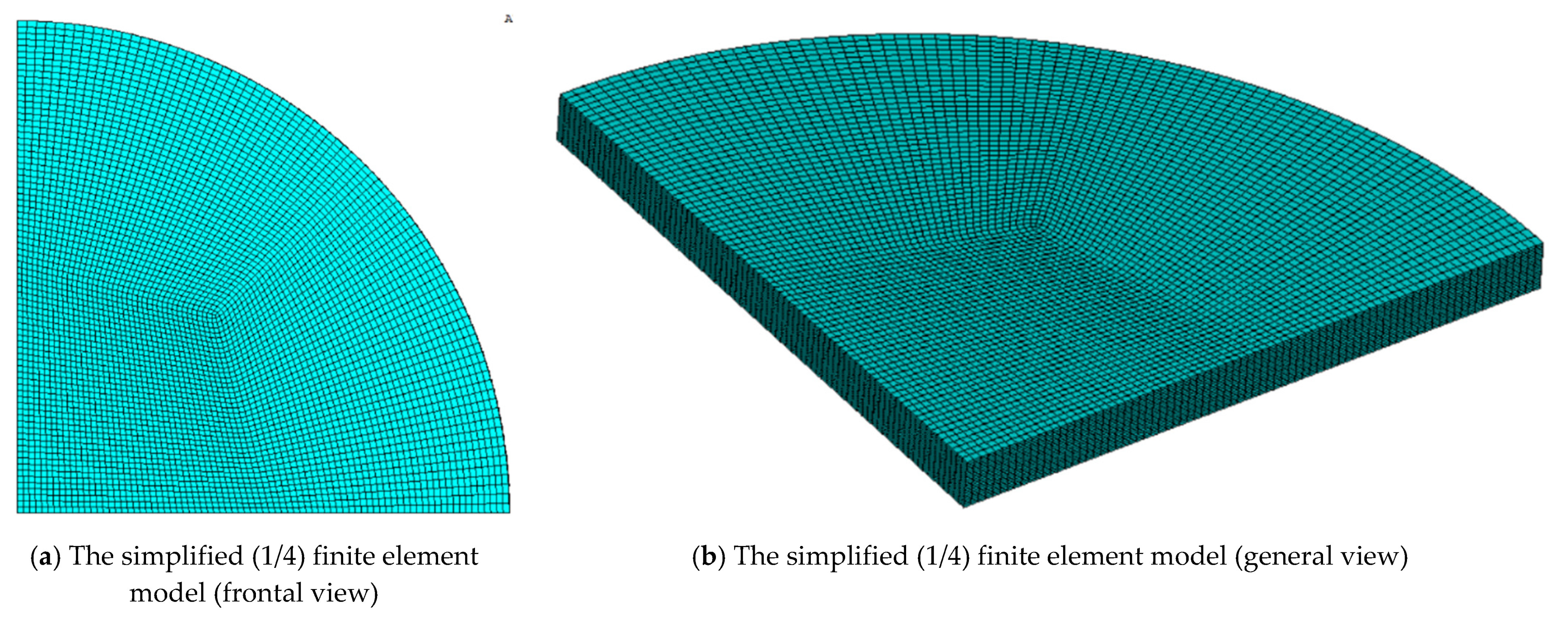
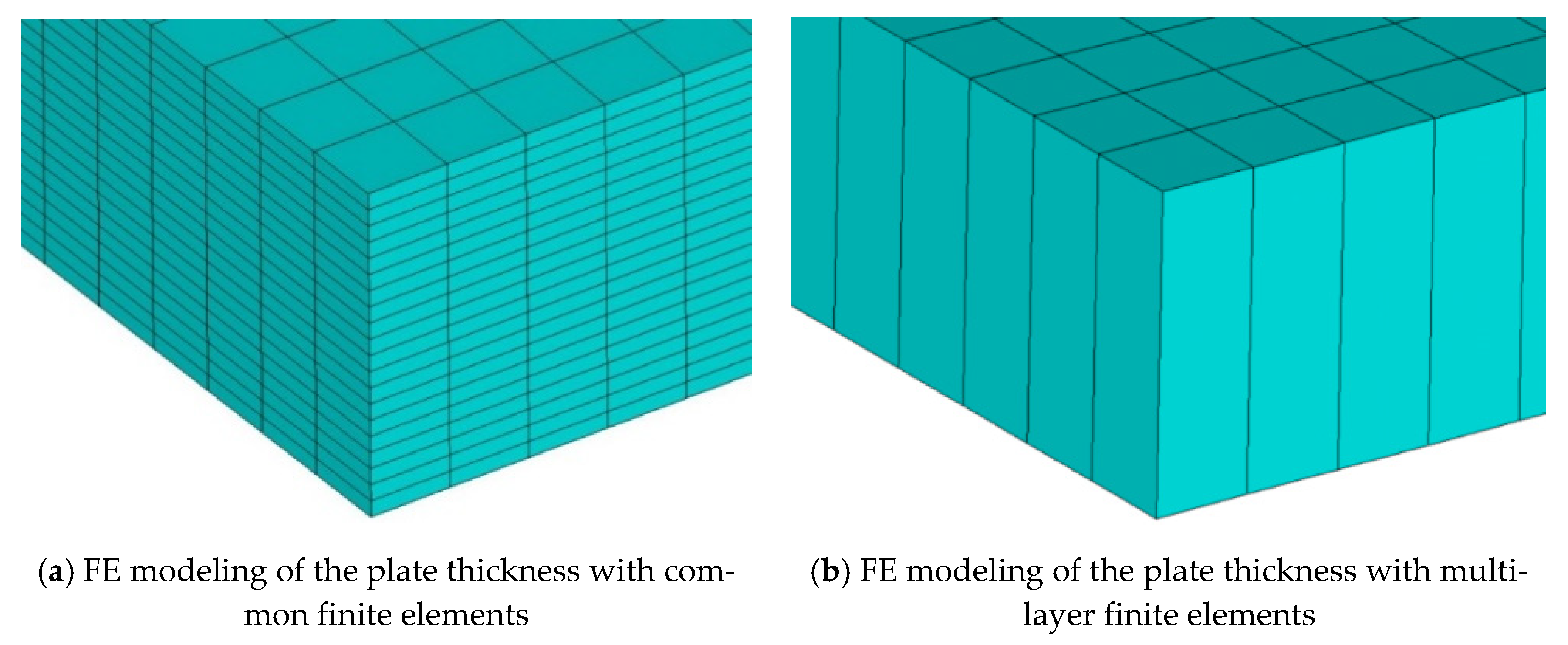
6. The Multilayer Plate Concept in the Numerical Calculus by FEM of FGPs
6.1. Finite Element Models
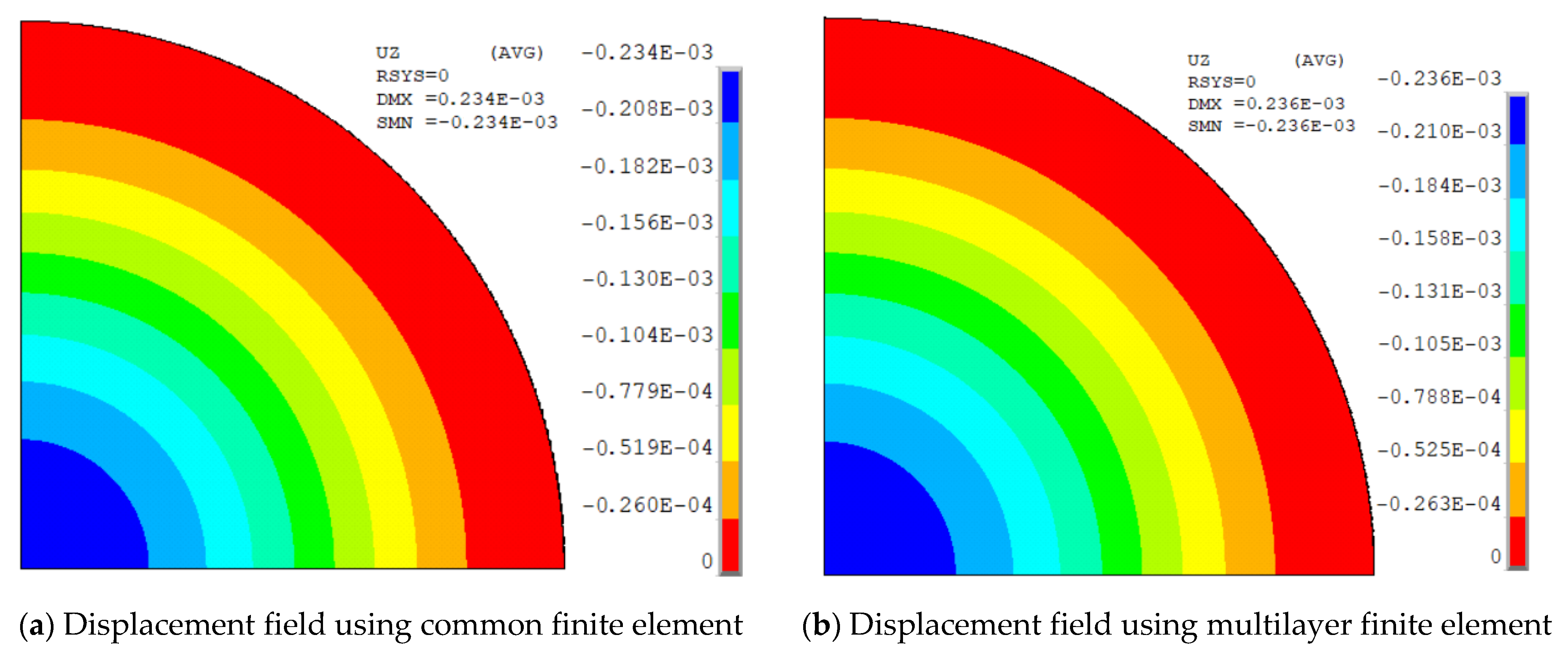
6.2. Calculus of the Maximum Transverse Displacement
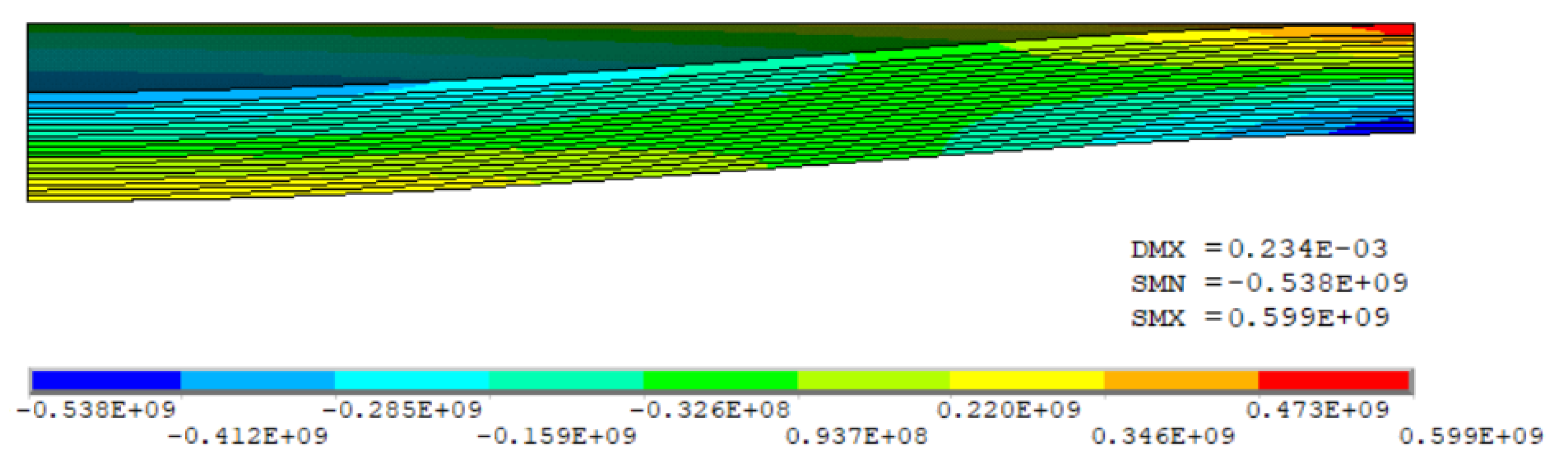
6.3. Calculus of the Stresses
6.4. Calculus of the Free Vibration Frequencies
7. Conclusions
Funding
Conflicts of Interest
References
- Anju, M.; Subha, K. A Review on Functionally Graded Plates. Int. Res. J. Eng. Technol. 2018, 5. [Google Scholar]
- Toudehdehghan, A.; Lim, J.W.; Foo, K.E.; Ma’Arof, M.; Mathews, J. A Brief Review of Functionally Graded Materials. MATEC Web Conf. 2017, 131, 03010. [Google Scholar] [CrossRef]
- Pradhan, K.K.; Chakraverty, S. Overview of functionally graded materials. In Computational Structural Mechanics; Elsevier: Amsterdam, The Netherlands, 2019; pp. 1–10. [Google Scholar]
- Mahamood, R.M.; Akinlabi, E.T.; Shukla, M.; Pityana, S.L. Functionally graded material: An overview. In Proceedings of the World Congress on Engineering, London, UK, 4–6 July 2012; Volume 3. [Google Scholar]
- Marzavan, S. EFG Method in Numerical Analysis of Foam Materials. Mech. Time Depend. Mater. 2021, 26, 409–429. [Google Scholar] [CrossRef]
- Nastasescu, V.; Marzavan, S. An overview of functionally graded material models. In Proceedings of the Romanian Academy—Series A, Bucharest, Romania, 20 September 2022; Volume 23, pp. 257–265. [Google Scholar]
- Gilewski, W.; Pełczyński, J. Material-Oriented Shape Functions for FGM Plate Finite Element Formulation. Materials 2020, 13, 803. [Google Scholar] [CrossRef]
- Alshorbagy, A.E.; Eltaher, M.; Mahmoud, F. Free Vibration Characteristics of a Functionally Graded Beam by Finite Element Method. Appl. Math. Model. 2010, 35, 412–425. [Google Scholar] [CrossRef]
- Ramu, I.; Mohanty, S. Modal Analysis of Functionally Graded Material Plates Using Finite Element Method. Procedia Mater. Sci. 2014, 6, 460–467. [Google Scholar] [CrossRef]
- Kadoli, R.; Akhtar, K.; Ganesan, N. Static Analysis of Functionally Graded Beams Using Higher Order Shear Deformation Theory. Appl. Math. Model. 2008, 32, 2509–2525. [Google Scholar] [CrossRef]
- Yang, X.; Li, W.; Li, J.; Ma, T.; Guo, J. FEM Analysis of Temperature Distribution and Experimental Study of Microstructure Evolution in Friction Interface of GH4169 Superalloy. Mater. Des. 2015, 84, 133–143. [Google Scholar] [CrossRef]
- Chung, Y.-L.; Chen, W.-T. Bending Behavior of FGM-Coated and FGM-Undercoated Plates with Two Simply Supported Opposite Edges and Two Free Edges. Compos. Struct. 2007, 81, 157–167. [Google Scholar] [CrossRef]
- Huang, C.-S.; Lee, H.-T.; Li, P.-Y.; Chang, M.-J. Three-Dimensional Free Vibration Analyses of Preloaded Cracked Plates of Functionally Graded Materials via the MLS-Ritz Method. Materials 2021, 14, 7712. [Google Scholar] [CrossRef]
- Nguyen, D.K.; Bui, V.T. Dynamic Analysis of Functionally Graded Timoshenko Beams in Thermal Environment Using a Higher-Order Hierarchical Beam Element. Math. Probl. Eng. 2017, 2017, 1–12. [Google Scholar] [CrossRef]
- Hadji, L.; Bernard, F. Bending and Free Vibration Analysis of Functionally Graded Beams on Elastic Foundations with Analitical Validation. Adv. Mater. Res. 2020, 9, 63–98. [Google Scholar] [CrossRef]
- Tarlochan, F. Functionally Graded Material: A New Breed of Engineered Material. J. Appl. Mech. Eng. 2013, 2. [Google Scholar] [CrossRef]
- El-Galy, I.M.; Saleh, B.I.; Ahmed, M.H. Functionally Graded Materials Classifications and Development Trends from Industrial Point of View. SN Appl. Sci. 2019, 1, 1378. [Google Scholar] [CrossRef]
- Gupta, A.; Talha, M. Recent Development in Modeling and Analysis of Functionally Graded Materials and Structures. Prog. Aerosp. Sci. 2015, 79, 1–14. [Google Scholar] [CrossRef]
- Sebacher, B.; Hanea, R.G.; Marzavan, S. Conditioning the Probability Field of Facies to Facies Observations Using a Regularized Element-free Galerkin (EFG) Method. Pet. Geostat. Florence 2019, 2019, 1–5. [Google Scholar]
- Kapania, R.K.; Raciti, S. Recent Advances in Analysis of Laminated Beams and Plates, Part II: Vibrations and Wave Propagation. AIAA J. 1989, 27, 935–946. [Google Scholar] [CrossRef]
- Zenkour, A.M. Generalized Shear Deformation Theory for Bending Analysis of Functionally Graded Plates. Appl. Math. Model. 2006, 30, 67–84. [Google Scholar] [CrossRef]
- Singha, M.; Prakash, T.; Ganapathi, M. Finite Element Analysis of Functionally Graded Plates under Transverse Load. Finite Elem. Anal. Des. 2011, 47, 453–460. [Google Scholar] [CrossRef]
- Marzavan, S.; Sebacher, B. A new methodology based on finite element method (FEM) for generation of the probability field of rock types from subsurface. Arab. J. Geosci. 2021, 14, 843. [Google Scholar] [CrossRef]
- Szilard, R. Theories and Applications of Plate Analysis: Classical, Numerical and Engineering Methods. Appl. Mech. Rev. 2004, 57, B32–B33. [Google Scholar] [CrossRef]
- Timoshenko, S.; Woinowsky-Krieger, S. Theory of Plates and Shells; International Edition McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Chakraverty, S.; Pradhan, K.K. Vibration of Functionally Graded Beams and Plates; Academic Press: Cambridge, MA, USA; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Marzavan, S.; Nastasescu, V. Displacement Calculus of the Functionally Graded Plates by Finite Element Method. Alex. Eng. J. 2022, 61, 12075–12090. [Google Scholar] [CrossRef]
- Bathe, K.J. Finite Element Procedures; Prentice-Hall, Inc.: Hoboken, NJ, USA, 1996. [Google Scholar]
- Huebner, K.H.; Dewhirst, D.L.; Smith, D.E.; Byrom, T.G. The Finite Element Method for Engineers, 3rd ed.; John Willey and Sons, Inc.: Hoboken, NJ, USA, 1995. [Google Scholar]
- Hughes, J.R.T. The Finite Element Method Linear Static and Dynamic Finite Element Analysis; Prentice Hall International Editions: Hoboken, NJ, USA, 1987. [Google Scholar]
- Zienkiewicz, O.C.; Taylor, R.L.; Zhu, J.Z. The Finite Element Method, 4th ed.; McGraw-Hill Book Company: New York, NY, USA, 2005. [Google Scholar]
- Kohnke, P. Theory Reference for the Mechanical APDL and Mechanical Applications; Release 12.0; ANSYS, Inc.: Canonsburg, PA, USA, 2009. [Google Scholar]
- Leissa, W.A. Vibration of Plates; National Aeronautics and Space Administration: Washington, DC, USA, 1969. [Google Scholar]
- Timoshenko, S. Vibration Problems in Engineering, 2nd ed.; D. Van Nostrand Company, Inc.: New York, NY, USA, 1937. [Google Scholar]
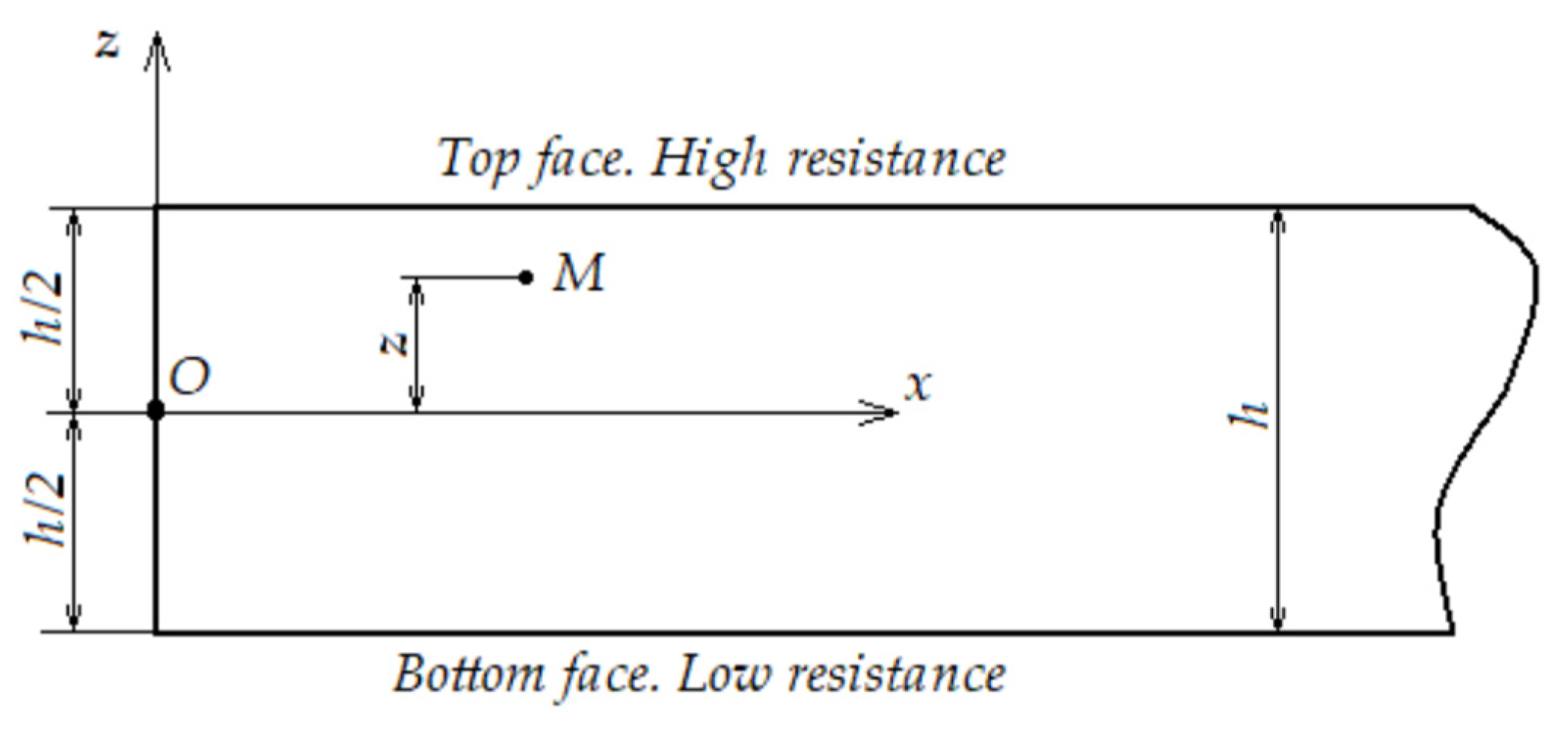

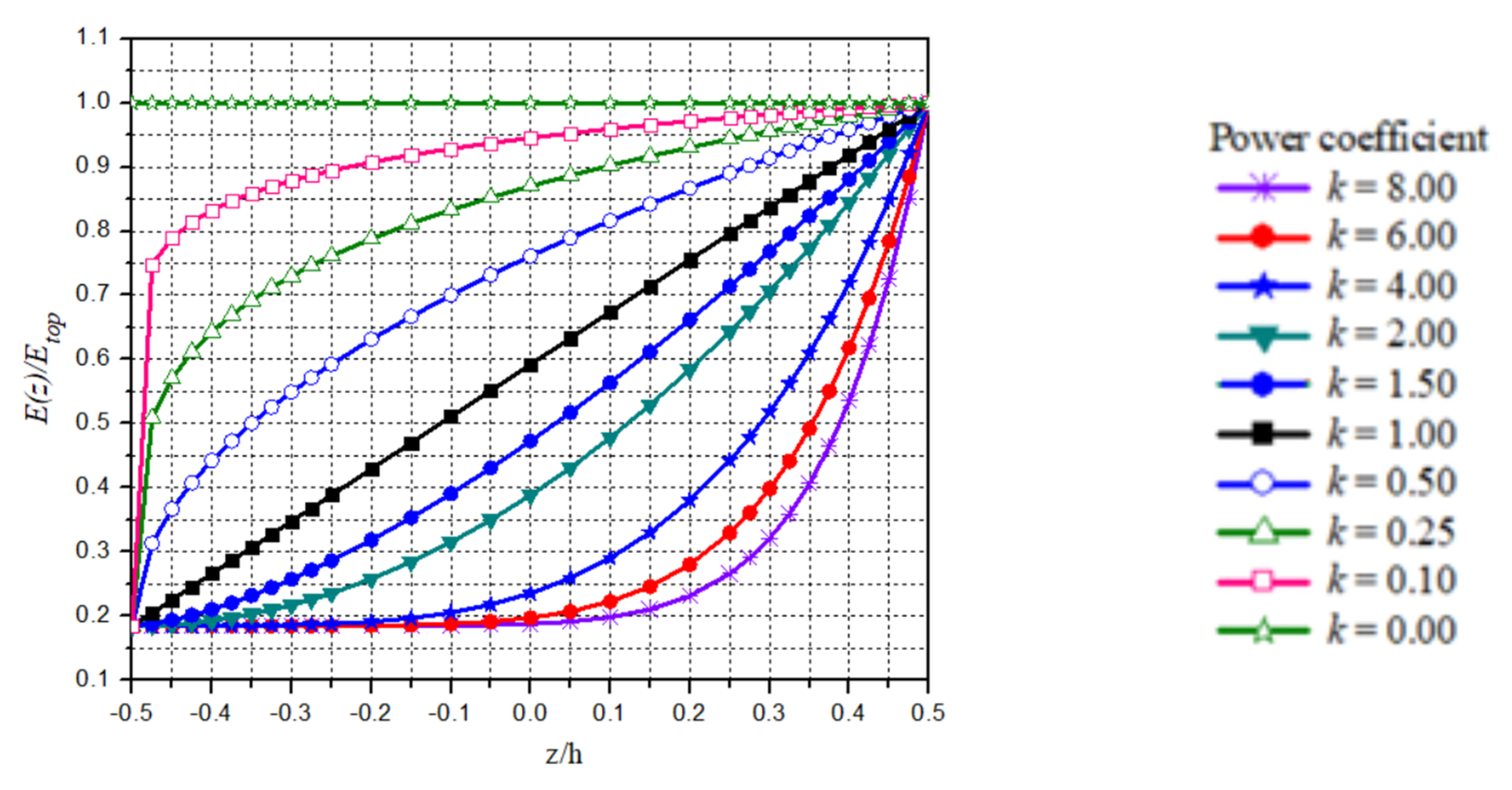
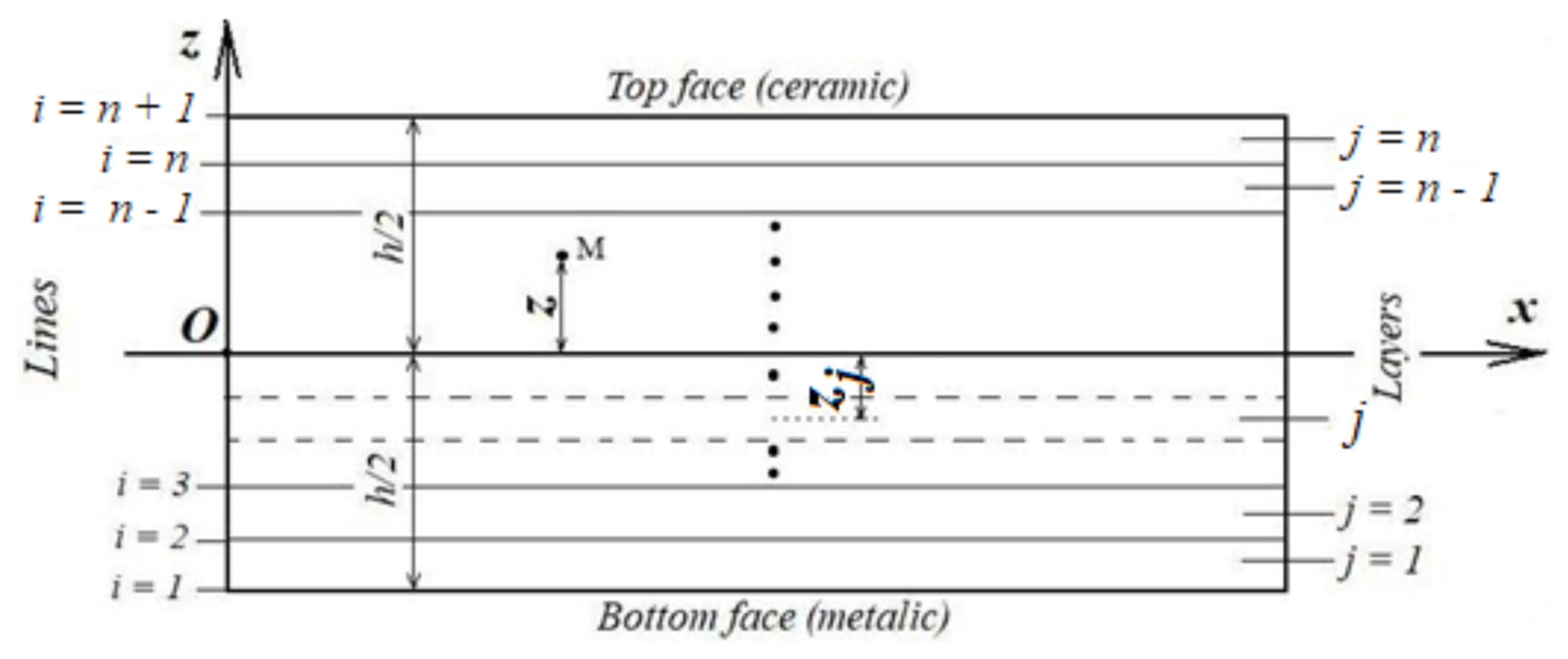


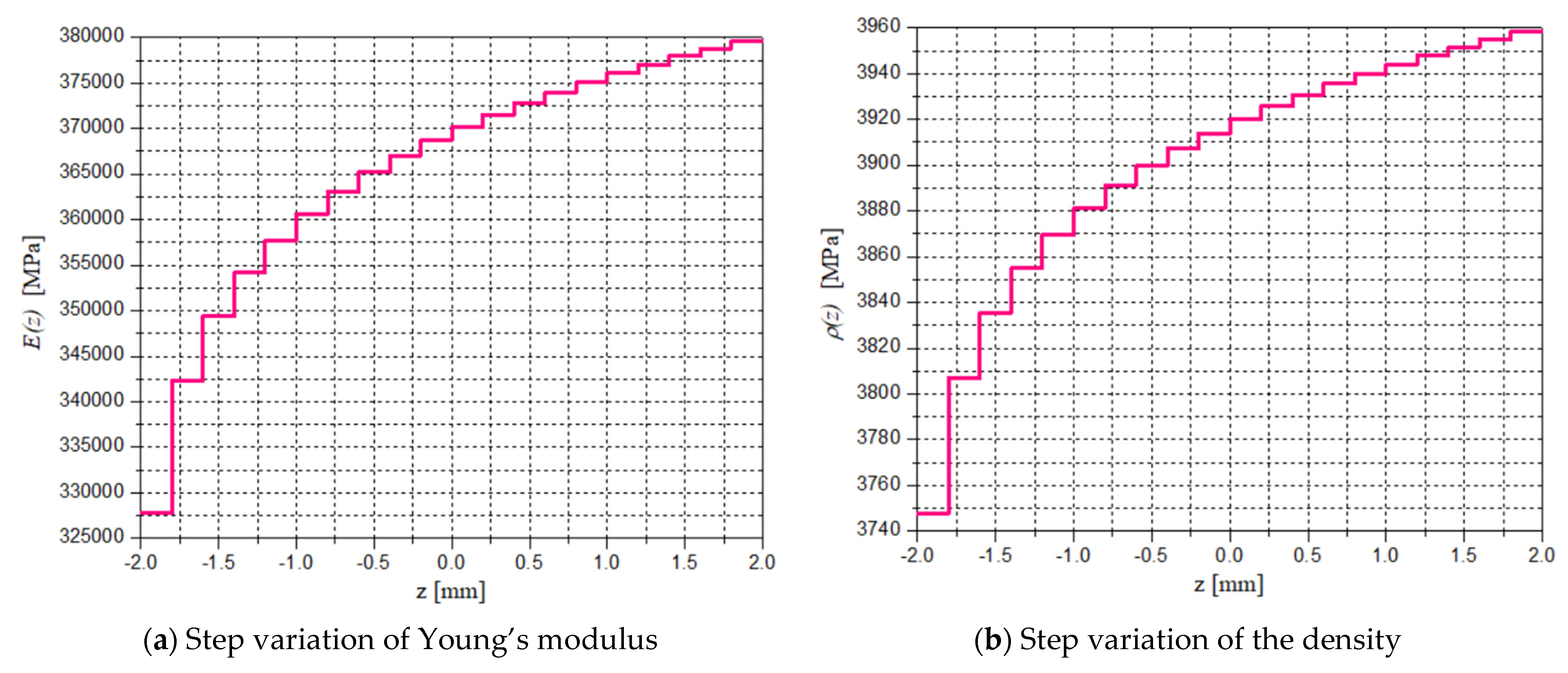









| Materials: | Ceramic Al2O3 | Aluminum |
|---|---|---|
| Positions: | Top | Bottom |
| E [MPa] | 380,000 | 70,000 |
| ρ [kg/m3] | 3960 | 2700 |
| ν [-] | 0.22 | 0.33 |
| Lines of the Plate Thickness | Layers of the Plate Thickness | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Line No. | . [m] | [MPa] | [-] | [kg/m3] | Layer No. | [m] | [MPa] | [-] | [kg/m3] |
| 1 | −0.0020 | 70,000.00 | 0.33000 | 2700.000 | - | - | - | - | - |
| 2 | −0.0018 | 336,876.41 | 0.23500 | 3784.723 | 1 | −0.0019 | 327,785.62 | 0.23853 | 3747.774 |
| 3 | −0.0016 | 346,287.79 | 0.23200 | 3822.976 | 2 | −0.0017 | 342,342.08 | 0.23336 | 3806.939 |
| 4 | −0.0014 | 351,946.21 | 0.23000 | 3845.975 | 3 | −0.0015 | 349,387.64 | 0.23086 | 3835.576 |
| 5 | −0.0012 | 356,031.06 | 0.22900 | 3862.578 | 4 | −0.0013 | 354,127.71 | 0.22918 | 3854.842 |
| 6 | −0.0010 | 359,240.23 | 0.22700 | 3875.622 | 5 | −0.0011 | 357,720.51 | 0.22791 | 3869.445 |
| 7 | −0.0008 | 361,889.02 | 0.22600 | 3886.388 | 6 | −0.0009 | 360,621.89 | 0.22688 | 3881.237 |
| 8 | −0.0006 | 364,147.46 | 0.22600 | 3895.567 | 7 | −0.0007 | 363,059.54 | 0.22601 | 3891.145 |
| 9 | −0.0004 | 366,117.92 | 0.22500 | 3903.576 | 8 | −0.0005 | 365,163.91 | 0.22526 | 3899.698 |
| 10 | −0.0002 | 367,866.95 | 0.22400 | 3910.685 | 9 | −0.0003 | 367,016.89 | 0.22461 | 3907.230 |
| 11 | 0.0000 | 369,440.26 | 0.22400 | 3917.080 | 10 | −0.0001 | 368,673.28 | 0.22402 | 3913.962 |
| 12 | 0.0002 | 370,870.65 | 0.22300 | 3922.894 | 11 | 0.0001 | 370,171.64 | 0.22349 | 3920.052 |
| 13 | 0.0004 | 372,182.46 | 0.22300 | 3928.225 | 12 | 0.0003 | 371,540.11 | 0.22300 | 3925.615 |
| 14 | 0.0006 | 373,394.26 | 0.22200 | 3933.151 | 13 | 0.0005 | 372,799.88 | 0.22256 | 3930.735 |
| 15 | 0.0008 | 374,520.54 | 0.22200 | 3937.729 | 14 | 0.0007 | 373,967.31 | 0.22214 | 3935.480 |
| 16 | 0.0010 | 375,572.84 | 0.22200 | 3942.006 | 15 | 0.0009 | 375,055.31 | 0.22176 | 3939.902 |
| 17 | 0.0012 | 376,560.50 | 0.22100 | 3946.020 | 16 | 0.0011 | 376,074.24 | 0.22139 | 3944.044 |
| 18 | 0.0014 | 377,491.16 | 0.22100 | 3949.803 | 17 | 0.0013 | 377,032.53 | 0.22105 | 3947.939 |
| 19 | 0.0016 | 378,371.21 | 0.22100 | 3953.380 | 18 | 0.0015 | 377,937.16 | 0.22073 | 3951.616 |
| 20 | 0.0018 | 379,205.97 | 0.22000 | 3956.773 | 19 | 0.0017 | 378,793.95 | 0.22043 | 3955.098 |
| 21 | 0.0020 | 380,000.00 | 0.22000 | 3960.000 | 20 | 0.0019 | 379,607.82 | 0.22014 | 3958.406 |
| Average values | 366,900.65 | 0.22967 | 3849.293 | - | - | 365,443.95 | 0.22517 | 3900.837 | |
| Layer No. | k Values | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.05 | 0.10 | 0.25 | 0.50 | 1.00 | 2.00 | 4.00 | 6.00 | 8.00 | |
| E(zj) [MPa] | |||||||||
| 1 | 327,785.62 | 284,365.90 | 193,266.96 | 119,015.30 | 77,750.00 | 70,193.75 | 70,000.12 | 70,000.00 | 70,000.00 |
| 2 | 342,342.08 | 309,258.74 | 232,228.45 | 154,897.00 | 93,250.00 | 71,743.75 | 70,009.81 | 70,000.06 | 70,000.00 |
| 3 | 349,387.64 | 321,798.24 | 254,327.10 | 179,601.55 | 108,750.00 | 74,843.75 | 70,075.68 | 70,001.18 | 70,000.02 |
| 4 | 354,127.71 | 330,414.70 | 270,503.15 | 199,682.30 | 124,250.00 | 79,493.75 | 70,290.75 | 70,008.90 | 70,000.27 |
| 5 | 357,720.51 | 337,042.23 | 283,504.64 | 217,045.91 | 139,750.00 | 85,693.75 | 70,794.50 | 70,040.22 | 70,002.04 |
| 6 | 360,621.89 | 342,455.11 | 294,488.90 | 232,565.37 | 155,250.00 | 93,443.75 | 71,772.93 | 70,134.08 | 70,010.14 |
| 7 | 363,059.54 | 347,044.82 | 304,062.87 | 246,727.19 | 170,750.00 | 102,743.75 | 73,458.56 | 70,365.31 | 70,038.59 |
| 8 | 365,163.91 | 351,037.85 | 312,588.11 | 259,835.46 | 186,250.00 | 113,593.75 | 76,130.37 | 70,862.08 | 70,121.23 |
| 9 | 367,016.89 | 354,577.52 | 320,298.89 | 272,095.27 | 201,750.00 | 125,993.75 | 80,113.87 | 71,826.82 | 70,329.97 |
| 10 | 368,673.28 | 357,760.42 | 327,356.47 | 283,652.76 | 217,250.00 | 139,943.75 | 85,781.06 | 73,560.60 | 70,803.36 |
| 11 | 370,171.64 | 360,654.88 | 333,876.99 | 294,616.34 | 232,750.00 | 155,443.75 | 93,550.43 | 76,491.09 | 71,789.11 |
| 12 | 371,540.11 | 363,311.09 | 339,947.09 | 305,069.14 | 248,250.00 | 172,493.75 | 103,887.00 | 81,203.89 | 73,704.29 |
| 13 | 372,799.88 | 365,766.99 | 345,633.31 | 315,076.52 | 263,750.00 | 191,093.75 | 117,302.25 | 88,477.44 | 77,217.75 |
| 14 | 373,967.31 | 368,052.02 | 350,987.91 | 324,690.99 | 279,250.00 | 211,243.75 | 134,354.18 | 99,321.37 | 83,359.55 |
| 15 | 375,055.31 | 370,189.50 | 356,052.79 | 333,955.49 | 294,750.00 | 232,943.75 | 155,647.31 | 115,018.37 | 93,662.78 |
| 16 | 376,074.24 | 372,198.19 | 360,862.09 | 342,905.66 | 310,250.00 | 256,193.75 | 181,832.62 | 137,169.47 | 110,343.66 |
| 17 | 377,032.53 | 374,093.47 | 365,444.00 | 351,571.48 | 325,750.00 | 280,993.75 | 213,607.62 | 167,742.94 | 136,526.29 |
| 18 | 377,937.16 | 375,888.04 | 369,822.15 | 359,978.45 | 341,250.00 | 307,343.75 | 251,716.31 | 209,126.55 | 176,518.76 |
| 19 | 378,793.95 | 377,592.59 | 374,016.48 | 368,148.45 | 356,750.00 | 335,243.75 | 296,949.18 | 264,183.40 | 236,148.17 |
| 20 | 379,607.82 | 379,216.14 | 378,044.07 | 376,100.47 | 372,250.00 | 364,693.75 | 350,143.25 | 336,311.17 | 323,162.06 |
| k | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.05 | 0.10 | 0.25 | 0.50 | 1.00 | 2.00 | 4.00 | 6.00 | 8.00 | |
| νceram [-] | 0.220 | 0.220 | 0.220 | 0.220 | 0.220 | 0.220 | 0.220 | 0.220 | 0.220 |
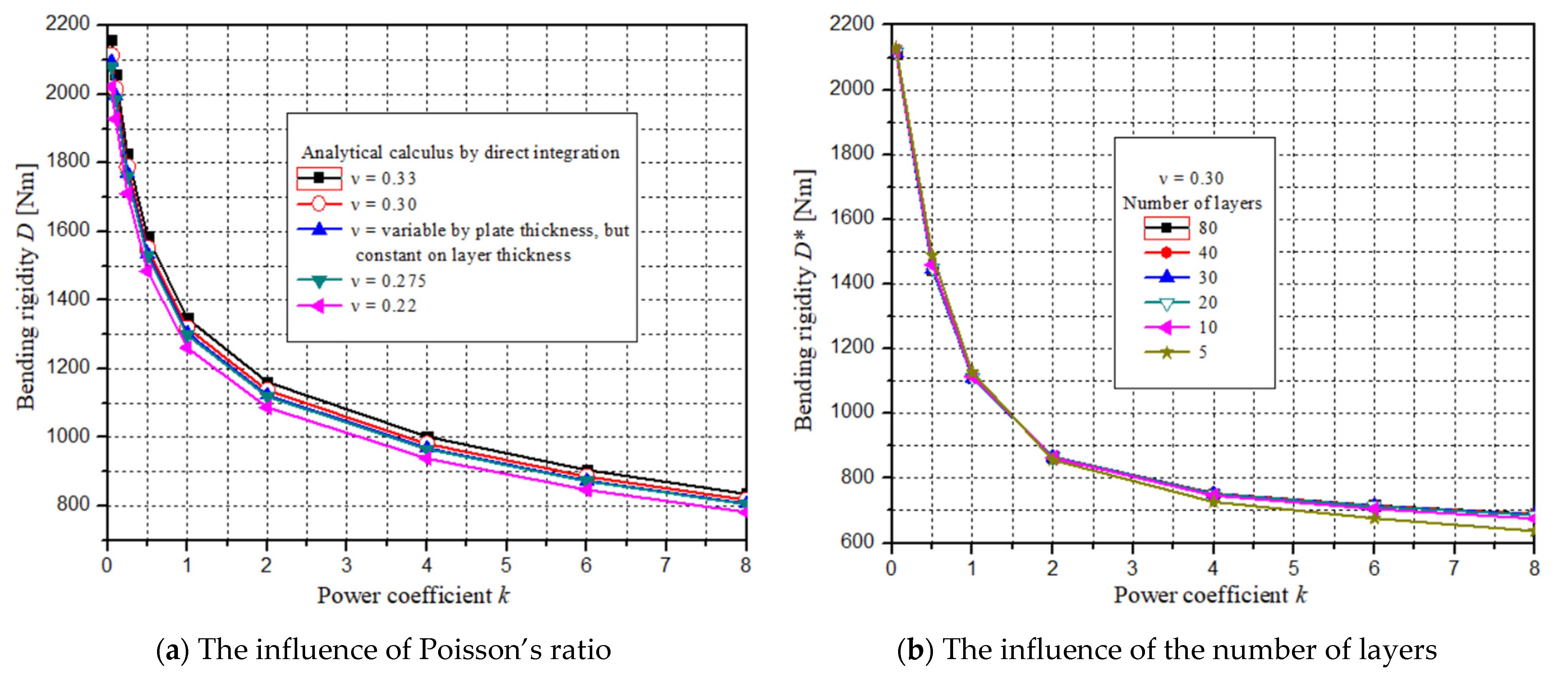
| D [Nm] | 2021.87 | 1928.13 | 1710.98 | 1484.42 | 1261.03 | 1087.29 | 938.37 | 847.36 | 781.93 |
| νmed [-] | 0.275 | 0.275 | 0.275 | 0.275 | 0.275 | 0.275 | 0.275 | 0.275 | 0.275 |
| D [Nm] | 2081.42 | 1984.91 | 1761.37 | 1528.14 | 1298.17 | 1119.31 | 966.01 | 872.32 | 804.96 |
| ν [-] | 0.286 | 0.285 | 0.284 | 0.283 | 0.282 | 0.281 | 0.280 | 0.279 | 0.279 |
| D [Nm] | 2095.33 | 1997.09 | 1771.15 | 1535.68 | 1303.74 | 1123.34 | 968.78 | 874.15 | 806.65 |
| νconst [-] | 0.300 | 0.300 | 0.300 | 0.300 | 0.300 | 0.300 | 0.300 | 0.300 | 0.300 |
| D [Nm] | 2114.30 | 2016.27 | 1789.20 | 1552.28 | 1318.68 | 1137.00 | 981.27 | 886.10 | 817.67 |
| νalum [-] | 0.330 | 0.330 | 0.330 | 0.330 | 0.330 | 0.330 | 0.330 | 0.330 | 0.330 |
| D [Nm] | 2159.14 | 2059.03 | 1827.15 | 1585.2 | 1346.65 | 1161.11 | 1002.1 | 904.89 | 835.01 |
| Power Coeff. | Multilayer Concept, D* [Nm] | |||||
|---|---|---|---|---|---|---|
| Number of Layers | ||||||
| 5 | 10 | 20 | 30 | 40 | 80 | |
| k = 0.05 | 2129.23 | 2120.22 | 2115.80 | 2114.21 | 2113.70 | 2112.71 |
| k = 0.50 | 1489.11 | 1459.76 | 1449.26 | 1446.45 | 1445.62 | 1444.36 |
| k = 1.00 | 1126.43 | 1114.23 | 1111.12 | 1110.30 | 1110.34 | 1110.15 |
| k = 2.00 | 856.44 | 863.69 | 865.58 | 865.69 | 866.06 | 866.18 |
| k = 4.00 | 727.03 | 746.87 | 751.98 | 752.66 | 753.27 | 753.59 |
| k = 6.00 | 676.06 | 705.83 | 713.71 | 714.83 | 715.71 | 716.21 |
| k = 8.00 | 637.03 | 675.67 | 686.24 | 687.80 | 688.94 | 689.62 |
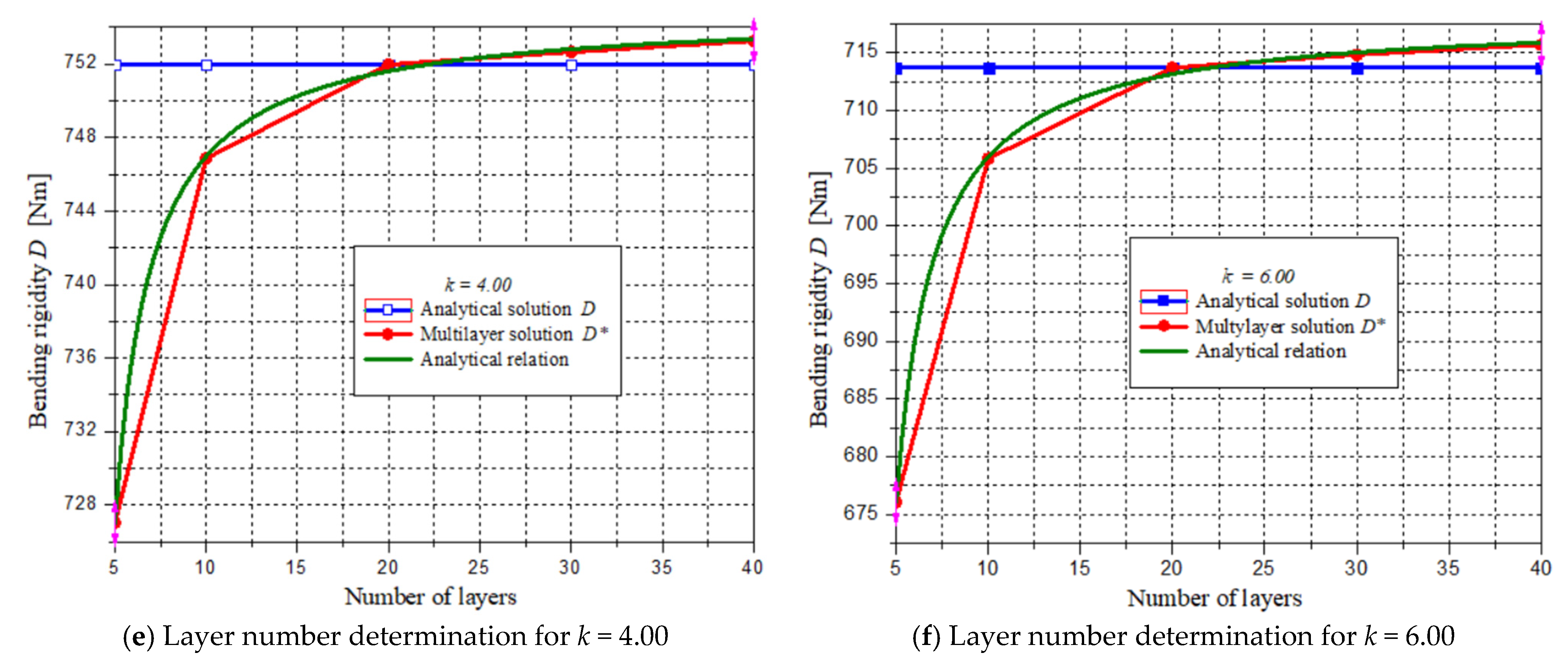
| k | Analytical Relations | Layer Number | D* (LN) [Nm] | D [Nm] | Err. [%] |
|---|---|---|---|---|---|
| 0.05 | 5 | 2129.13 | 2114.30 | 0.70 | |
| 10 | 2120.52 | 0.29 | |||
| 20 | 2115.21 | 0.04 | |||
| 30 | 2114.22 | 0.00 | |||
| 40 | 2113.04 | −0.01 | |||
| 0.50 | 5 | 1489.11 | 1449.26 | 2.75 | |
| 10 | 1459.77 | 0.73 | |||
| 20 | 1449.19 | 0.00 | |||
| 30 | 1446.60 | −0.18 | |||
| 40 | 1445.53 | −0.26 | |||
| 1.00 | 5 | 1126.43 | 1111.12 | 1.38 | |
| 10 | 1114.24 | 0.28 | |||
| 20 | 1111.05 | −0.01 | |||
| 30 | 1110.46 | −0.06 | |||
| 40 | 1110.25 | −0.08 | |||
| 2.00 | 5 | 856.44 | 865.58 | −1.06 | |
| 10 | 863.73 | −0.21 | |||
| 20 | 865.41 | −0.02 | |||
| 30 | 865.84 | 0.03 | |||
| 40 | 866.04 | 0.05 | |||
| 4.00 | 5 | 727.03 | 751.98 | −3.32 | |
| 10 | 746.97 | −0.67 | |||
| 20 | 751.62 | −0.05 | |||
| 30 | 752.82 | 0.11 | |||
| 40 | 753.37 | 0.19 | |||
| 6.00 | 5 | 676.05 | 713.71 | −5.28 | |
| 10 | 705.99 | −1.08 | |||
| 20 | 713.16 | −0.08 | |||
| 30 | 715.03 | 0.19 | |||
| 40 | 715.89 | 0.13 | |||
| 8.00 | 5 | 637.02 | 686.24 | −7.17 | |
| 10 | 675.89 | −1.51 | |||
| 20 | 685.52 | −0.11 | |||
| 30 | 688.05 | 0.26 | |||
| 40 | 689.21 | 0.43 |
| ANALYTICAL RESULT | FINITE ELEMENT RESULTS | ||||
|---|---|---|---|---|---|
| wmax [m] | Finite element size | Multilayered plate (Each layer is isotropic and homogeneous, common finite element) Model I | Multilayered plate (Each layer is isotropic and homogeneous, multilayered finite element) Model II | ||
| wmax [m] | Er. [%] | wmax [m] | Er. [%] | ||
| 0.000231 | 1.0 mm | 0.000234 | 1.30 | 0.000236 | 2.16 |
| 2.0 mm | 0.000228 | −1.30 | 0.000236 | 2.16 | |
| 3.0 mm | 0.000220 | −4.76 | 0.000236 | 2.16 | |
| Maximum Stress Values on the Clamped Edges [MPa] | ||
|---|---|---|
| Analytical calculus | 595.922 | |
| F. E. M. | Multilayered plate with common FE (Model I) | 599.000 |
| Err. [%] | 0.52 | |
| Multilayered plate with multilayered FE (Model II) | 594.000 | |
| Err. [%] | −0.32 | |
| k | d [m] | d* [m] |
|---|---|---|
| 0.05 | 0.00204 | 0.00004 |
| 0.50 | 0.00230 | 0.00030 |
| 1.00 | 0.00246 | 0.00046 |
| 2.00 | 0.00260 | 0.00060 |
| 4.00 | 0.00263 | 0.00063 |
| 6.00 | 0.00260 | 0.00060 |
| 8.00 | 0.00253 | 0.00053 |
| 10.00 | 0.00248 | 0.00048 |
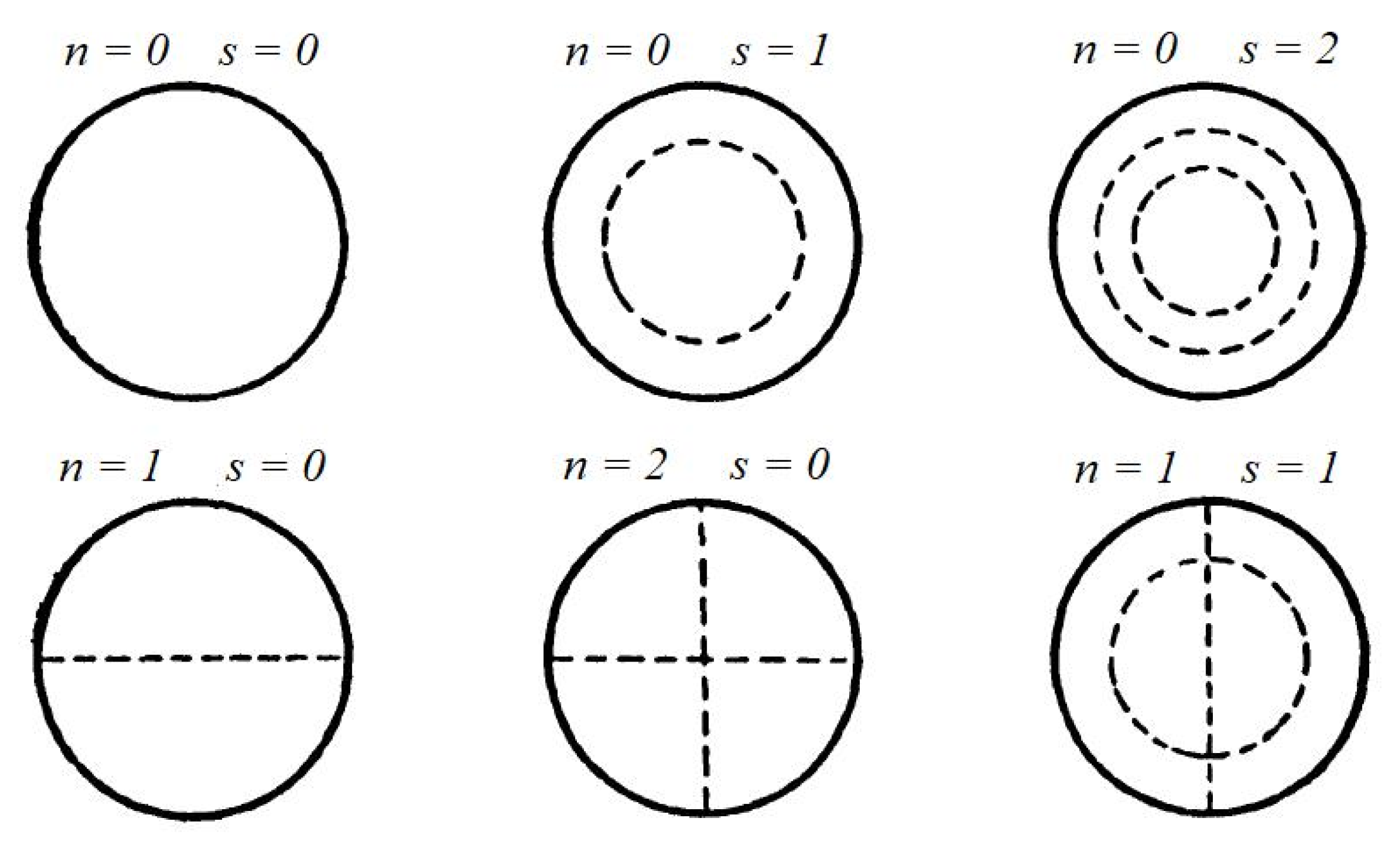
| s | n = 0 | n = 1 | n = 2 |
|---|---|---|---|
| 0 | 10.217 | 21.22 | 34.84 |
| 1 | 39.78 | ……… | ……… |
| 2 | 88.90 | ……… | ……… |
| Power coef. | Freq. No. | αi | D* | ρ* | ω* | f* |
|---|---|---|---|---|---|---|
| - | [Nm] | [kg/m3] | [rad/s] | [Hz] | ||
| k = 0.05 | 1 | 10.217 | 2115.80 | 3900.84 | 47,589.57 | 7574.12 |
| 2 | 21.22 | 98,840.24 | 15,730.93 | |||
| 3 | 34.84 | 162,280.58 | 25,827.78 | |||
| k = 0.50 | 1 | 10.217 | 1449.26 | 3539.99 | 41,345.24 | 6580.30 |
| 2 | 21.22 | 85,871.20 | 13,666.84 | |||
| 3 | 34.84 | 140,987.39 | 22,438.86 | |||
| k = 1.00 | 1 | 10.217 | 1111.12 | 3330.00 | 37,326.03 | 5940.63 |
| 2 | 21.22 | 77,523.57 | 12,338.27 | |||
| 3 | 34.84 | 127,281.86 | 20,257.55 | |||
| k = 2.00 | 1 | 10.217 | 865.58 | 3120.00 | 34,035.31 | 5416.89 |
| 2 | 21.22 | 70,688.98 | 11,250.51 | |||
| 3 | 34.84 | 116,060.50 | 18,471.62 | |||
| k = 4.00 | 1 | 10.217 | 751.98 | 2952.00 | 32,613.57 | 51,90.62 |
| 2 | 21.22 | 67,736.12 | 10,780.55 | |||
| 3 | 34.84 | 111,212.37 | 17,700.01 | |||
| k = 6.00 | 1 | 10.217 | 713.71 | 2880.00 | 32,167.55 | 5119.63 |
| 2 | 21.22 | 66,809.78 | 10,633.12 | |||
| 3 | 34.84 | 109,691.45 | 17,457.95 | |||
| k = 8.00 | 1 | 10.217 | 686.24 | 2839.99 | 31,763.84 | 5055.38 |
| 2 | 21.22 | 65,971.29 | 10,499.67 | |||
| 3 | 34.84 | 108,314.79 | 17,238.85 |
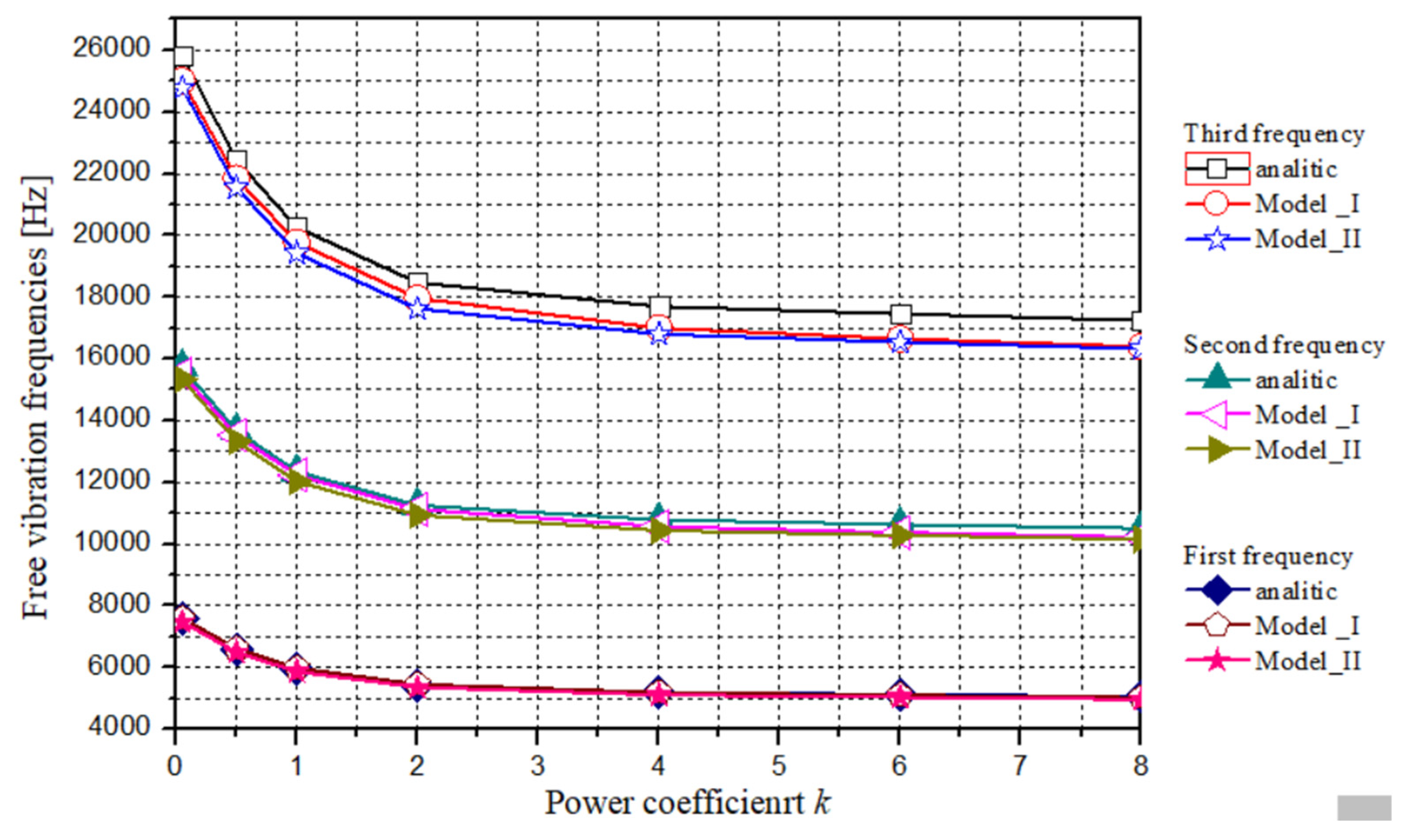
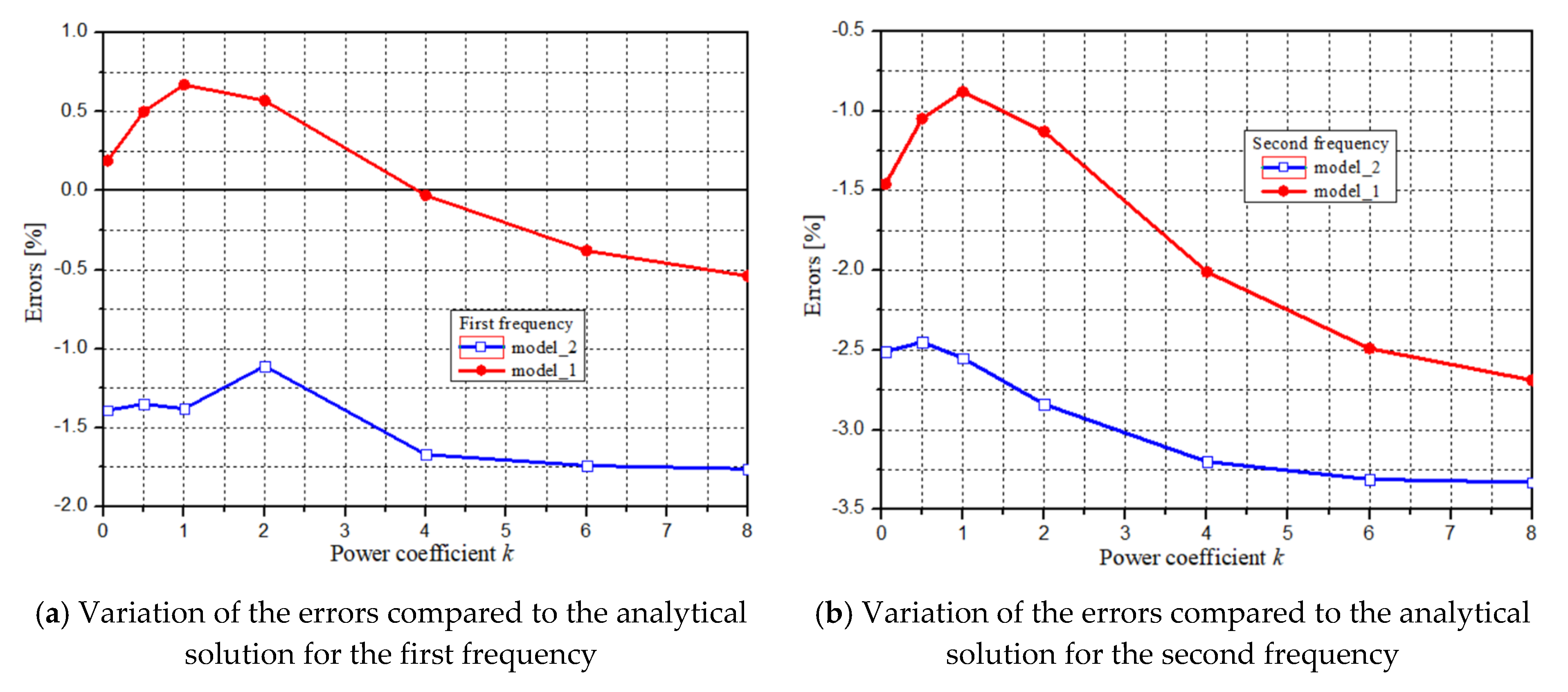
| k | Freq. No. | Multilayer Plate Concept | ||||
|---|---|---|---|---|---|---|
| Analytical Solution | FGP Model I | Er. [%] | FGP Model II | Er. [%] | ||
| 0.05 | 1 | 7574.12 | 7588.80 | 0.19 | 7468.72 | −1.39 |
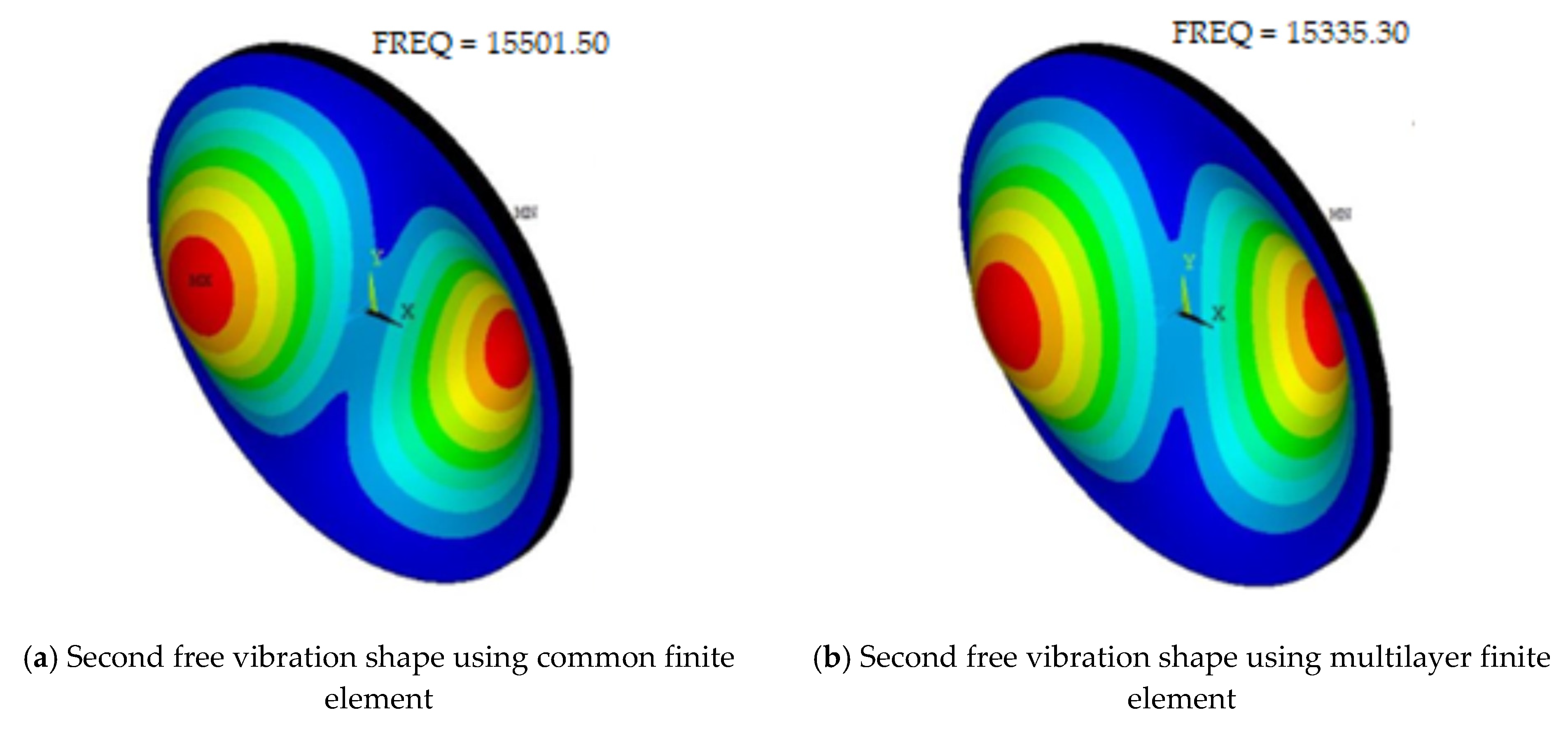
| 2 | 15,730.93 | 15,501.50 | −1.46 | 15,335.30 | −2.51 | |
| 3 | 25,827.78 | 25,014.80 | −3.15 | 24,780.60 | −4.05 | |
| 0.50 | 1 | 6580.30 | 6613.50 | 0.50 | 6491.30 | −1.35 |
| 2 | 13,666.84 | 13,523.00 | −1.05 | 13,332.00 | −2.45 | |
| 3 | 22,438.86 | 21,854.00 | −2.61 | 21,549.00 | −3.97 | |
| 1.00 | 1 | 5940.63 | 5980.30 | 0.67 | 5858.50 | −1.38 |
| 2 | 12,338.27 | 12,230.00 | −0.88 | 12,024.00 | −2.55 | |
| 3 | 20,257.55 | 19,772.00 | −2.40 | 19,422.00 | −4.12 | |
| 2.00 | 1 | 5414.63 | 5445.40 | 0.57 | 5354.50 | −1.11 |
| 2 | 11,250.51 | 11,123.00 | −1.13 | 10,931.00 | −2.84 | |
| 3 | 18,471.62 | 17,960.00 | −2.77 | 17,626.00 | −4.58 | |
| 4.00 | 1 | 5188.45 | 5186.70 | −0.03 | 5101.60 | −1.67 |
| 2 | 10,780.55 | 10,564.00 | −2.01 | 10,436.00 | −3.20 | |
| 3 | 17,700.01 | 16,998.00 | −3.97 | 16,796.00 | −5.11 | |
| 6.00 | 1 | 5117.49 | 5098.00 | −0.38 | 5028.20 | −1.74 |
| 2 | 10,633.12 | 10,368.00 | −2.49 | 10,281.00 | −3.31 | |
| 3 | 17,457.95 | 16,651.00 | −4.62 | 16,537.00 | −5.28 | |
| 8.00 | 1 | 5053.26 | 5026.10 | −0.54 | 4964.40 | −1.76 |
| 2 | 10,499.65 | 10,217.00 | −2.69 | 10,150.00 | −3.33 | |
| 3 | 17,238.82 | 16,395.00 | −4.89 | 16,327.00 | −5.29 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nastasescu, V. The Using of the Multilayer Plate Concept in the Calculus of Functionally Graded Plates. Appl. Sci. 2022, 12, 10695. https://doi.org/10.3390/app122110695
Nastasescu V. The Using of the Multilayer Plate Concept in the Calculus of Functionally Graded Plates. Applied Sciences. 2022; 12(21):10695. https://doi.org/10.3390/app122110695
Chicago/Turabian StyleNastasescu, Vasile. 2022. "The Using of the Multilayer Plate Concept in the Calculus of Functionally Graded Plates" Applied Sciences 12, no. 21: 10695. https://doi.org/10.3390/app122110695
APA StyleNastasescu, V. (2022). The Using of the Multilayer Plate Concept in the Calculus of Functionally Graded Plates. Applied Sciences, 12(21), 10695. https://doi.org/10.3390/app122110695





