On a Framework for Federated Cluster Analysis
Abstract
1. Introduction
- Client selection: Select clients participating in the training.
- Broadcast: A central server initializes a global model and shares it with the clients.
- Client computation: Each client updates the global model by applying a training protocol and shares the updates with the central server.
- Aggregation: The central server applies an aggregation function to update the global model.
- Model update: The updated global model is shared with the clients.
1.1. Motivational Example
2. Materials and Methods
2.1. Background: Related Work
2.1.1. Nonfederated k-Means Clustering
- Initialize cluster centers .
- Assign clusters for all according to (Equation (2)).
- Recalculate cluster centers by solving the following problem, i.e., calculating the mean of points assigned to the same cluster:
- Check if the convergence criterion is met, i.e., whether the assignment did not change (much) compared to the previous iteration. Let be the assignment vector of the previous iteration for data point , i.e., the k-th entry is 1 if , and zero otherwise. Let be the assignment of the current iteration. Further, let and be the assignment matrices, where the i-th row equals and , respectively. Then, the algorithm converges if the difference between the two assignment matrices is smaller than some predefined :
2.1.2. Nonfederated Fuzzy c-Means Clustering
- Initialize matrix U:= .
- In iteration t, (re)calculate cluster centers according to:
- Update membership matrix according to Equation (5).
- Check if the convergence criterion is met: for some predefined , i.e., did the memberships change by at most ? If it was not met, return to step 2 after setting . Terminate if it was met.
2.1.3. Davies–Bouldin Index
2.1.4. Federated Clustering
2.2. The Federated Fuzzy Clustering Framework
2.2.1. Federated Fuzzy c-Means with k-Means Averaging
- The central server initializes K global cluster centers .
- The central server shares with the clients.
- Client l shares for and .
- The central server updates by applying an averaging function .
- The central server checks a convergence criterion. If not converged, go back to step 2.
2.2.2. Federated Fuzzy Davies–Bouldin Index
2.2.3. The Complete Framework
- Decide on a range for number of clusters K to test: .
- For each :
- (a)
- Obtain a clustering with FedFCM as described in Section 2.2.1.
- (b)
- Calculate the FedFuzzDB index of that clustering as described in Section 2.2.2 and store the result.
- Choose with the minimum FedFuzzDB index as the number of clusters or apply the elbow method (see, e.g., [39]).
3. Results
3.1. Evaluation Method
- How reliably can the framework detect the correct number of clusters in federated datasets?
- How good is the federated clustering result, and how does it compare to an assumed central clustering result?
3.2. Experiments
3.2.1. Framework Demonstration on Artificial Data
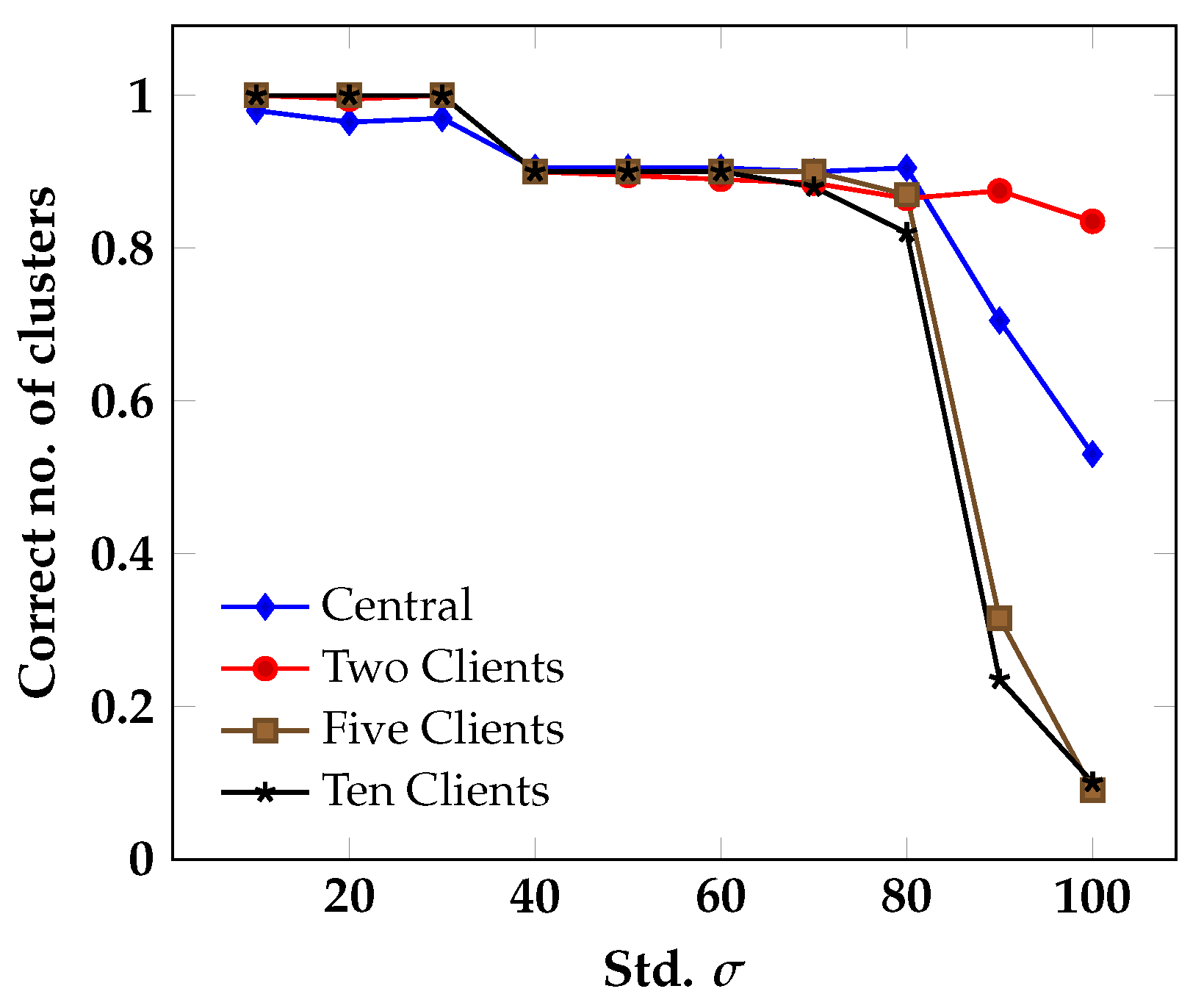
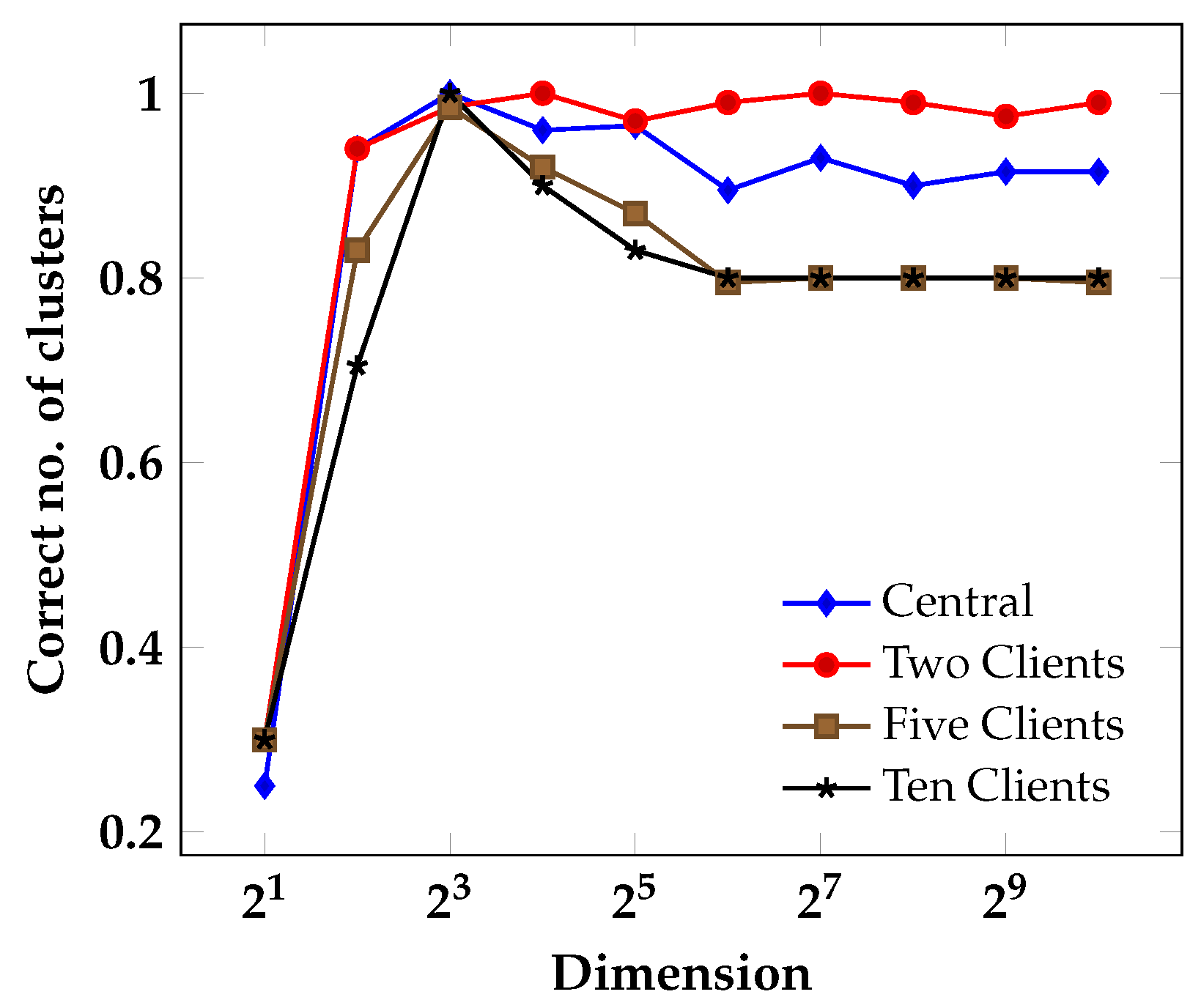
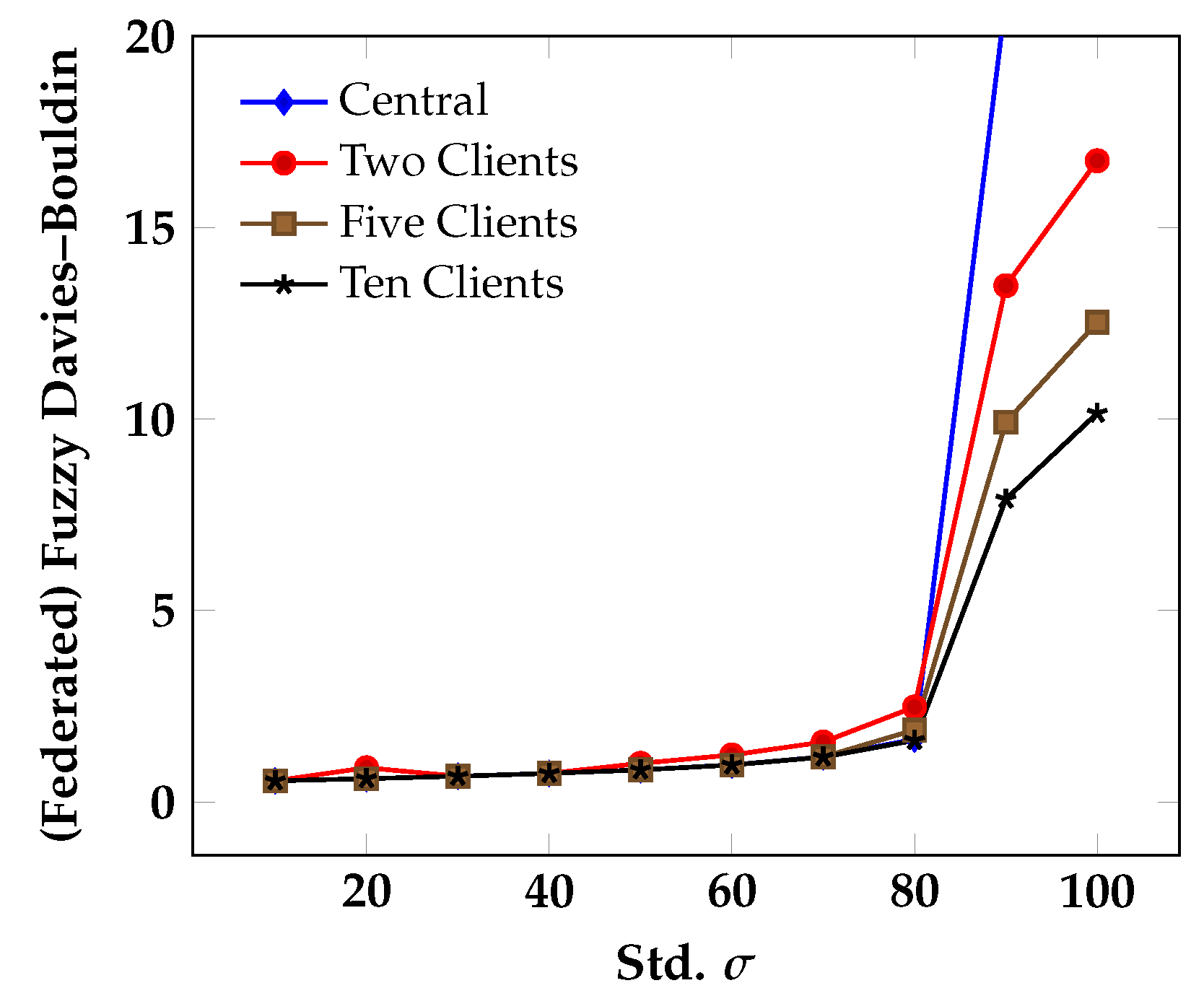
3.2.2. Evaluation on Benchmark Data
3.2.3. Evaluation on Real-World Data
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- EU. Regulation (EU) 2016/679 of the European Parliament and of the Council of 27 April 2016 on the protection of natural persons with regard to the processing of personal data (...) (General Data Protection Regulation). Off. J. Eur. Union 2016, 119, 1–88. [Google Scholar]
- Kairouz, P.; McMahan, H.B. Advances and Open Problems in Federated Learning. Found. Trends® Mach. Learn. 2021, 14, 1–210. [Google Scholar] [CrossRef]
- Hard, A.; Rao, K.; Mathews, R.; Ramaswamy, S.; Beaufays, F.; Augenstein, S.; Eichner, H.; Kiddon, C.; Ramage, D. Federated learning for mobile keyboard prediction. arXiv 2018, arXiv:1811.03604. [Google Scholar]
- Ye, D.; Yu, R.; Pan, M.; Han, Z. Federated Learning in Vehicular Edge Computing: A Selective Model Aggregation Approach. IEEE Access 2020, 8, 23920–23935. [Google Scholar] [CrossRef]
- Deist, T.M.; Jochems, A.; van Soest, J.; Nalbantov, G.; Oberije, C.; Walsh, S.; Eble, M.; Bulens, P.; Coucke, P.; Dries, W.; et al. Infrastructure and distributed learning methodology for privacy-preserving multi-centric rapid learning health care: EuroCAT. Clin. Transl. Radiat. Oncol. 2017, 4, 24–31. [Google Scholar] [CrossRef]
- Brisimi, T.S.; Chen, R.; Mela, T.; Olshevsky, A.; Paschalidis, I.C.; Shi, W. Federated learning of predictive models from federated Electronic Health Records. Int. J. Med. Inform. 2018, 112, 59–67. [Google Scholar] [CrossRef]
- Grefen, P.; Ludwig, H.; Tata, S.; Dijkman, R.; Baracaldo, N.; Wilbik, A.; D’hondt, T. Complex collaborative physical process management: A position on the trinity of BPM, IoT and DA. In IFIP Advances in Information and Communication Technology, Proceedings of the Working Conference on Virtual Enterprises, Cardiff, UK, 17–19 September 2018; Springer: Cham, Switzerland, 2018; pp. 244–253. [Google Scholar]
- Duan, M.; Liu, D.; Chen, X.; Tan, Y.; Ren, J.; Qiao, L.; Liang, L. Astraea: Self-Balancing Federated Learning for Improving Classification Accuracy of Mobile Deep Learning Applications. In Proceedings of the 2019 IEEE 37th International Conference on Computer Design (ICCD), Abu Dhabi, United Arab Emirates, 17–20 November 2019; pp. 246–254. [Google Scholar] [CrossRef]
- Wang, X.; Han, Y.; Wang, C.; Zhao, Q.; Chen, X.; Chen, M. In-Edge AI: Intelligentizing Mobile Edge Computing, Caching and Communication by Federated Learning. IEEE Netw. 2019, 33, 156–165. [Google Scholar] [CrossRef]
- Yin, X.; Zhu, Y.; Hu, J. A Comprehensive Survey of Privacy-Preserving Federated Learning: A Taxonomy, Review, and Future Directions. ACM Comput. Surv. 2021, 54, 1–36. [Google Scholar] [CrossRef]
- Khan, L.U.; Saad, W.; Han, Z.; Hossain, E.; Hong, C.S. Federated Learning for Internet of Things: Recent Advances, Taxonomy, and Open Challenges. IEEE Commun. Surv. Tutor. 2021, 23, 1759–1799. [Google Scholar] [CrossRef]
- McLachlan, G. Cluster analysis and related techniques in medical research. Stat. Methods Med. Res. 1992, 1, 27–48. [Google Scholar] [CrossRef]
- Maione, C.; Nelson, D.R.; Barbosa, R.M. Research on social data by means of cluster analysis. Appl. Comput. Inform. 2019, 15, 153–162. [Google Scholar] [CrossRef]
- Bolin, J.H.; Edwards, J.M.; Finch, W.H.; Cassady, J.C. Applications of cluster analysis to the creation of perfectionism profiles: A comparison of two clustering approaches. Front. Psychol. 2014, 5, 343. [Google Scholar] [CrossRef] [PubMed]
- Ketchen, D.J.; Shook, C.L. The application of cluster analysis in strategic management research: An analysis and critique. Strateg. Manag. J. 1996, 17, 441–458. [Google Scholar] [CrossRef]
- Punj, G.; Stewart, D.W. Cluster analysis in marketing research: Review and suggestions for application. J. Mark. Res. 1983, 20, 134–148. [Google Scholar] [CrossRef]
- Hudson, S.; Ritchie, B. Understanding the domestic market using cluster analysis: A case study of the marketing efforts of Travel Alberta. J. Vacat. Mark. 2002, 8, 263–276. [Google Scholar] [CrossRef]
- Milligan, G.W.; Cooper, M.C. Methodology review: Clustering methods. Appl. Psychol. Meas. 1987, 11, 329–354. [Google Scholar] [CrossRef]
- Kumar, H.H.; Karthik, V.R.; Nair, M.K. Federated K-Means Clustering: A Novel Edge AI Based Approach for Privacy Preservation. In Proceedings of the 2020 IEEE International Conference on Cloud Computing in Emerging Markets (CCEM), Bengaluru, India, 6–7 November 2020; pp. 52–56. [Google Scholar] [CrossRef]
- Pedrycz, W. Federated FCM: Clustering Under Privacy Requirements. IEEE Trans. Fuzzy Syst. 2022, 30, 3384–3388. [Google Scholar] [CrossRef]
- Bárcena, J.L.C.; Marcelloni, F.; Renda, A.; Bechini, A.; Ducange, P. A Federated Fuzzy c-means Clustering Algorithm. In Proceedings of the International Workshop on Fuzzy Logic and Applications (WILF 2021), Vietri sul Mare, Italy, 20–22 December 2021. [Google Scholar]
- Dennis, D.K.; Li, T.; Smith, V. Heterogeneity for the Win: One-Shot Federated Clustering. In Proceedings of the 38th International Conference on Machine Learning, PMLR 2021, Virtual, 18–24 July 2021; Meila, M., Zhang, T., Eds.; 2021; Volume 139, pp. 2611–2620. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning—Data Mining, Inference and Prediction; Springer: New York, NY, USA, 2017. [Google Scholar]
- Arthur, D.; Vassilvitskii, S. K-Means++: The Advantages of Careful Seeding. In Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms; Society for Industrial and Applied Mathematics, SODA ’07, New Orleans, LA, USA, 7–9 January 2007; pp. 1027–1035. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Bezdek, J.C.; Ehrlich, R.; Full, W. FCM: The fuzzy c-means clustering algorithm. Comput. Geosci. 1984, 10, 191–203. [Google Scholar] [CrossRef]
- Kolen, J.; Hutcheson, T. Reducing the time complexity of the fuzzy c-means algorithm. IEEE Trans. Fuzzy Syst. 2002, 10, 263–267. [Google Scholar] [CrossRef]
- Suganya, R.; Shanthi, R. Fuzzy C- Means Algorithm—A Review. Int. J. Sci. Res. Publ. 2012, 2, 1–3. [Google Scholar]
- Steinbach, M.; Ertöz, L.; Kumar, V. The challenges of clustering high dimensional data. In New Directions in Statistical Physics; Springer: Berlin/Heidelberg, Germany, 2004; pp. 273–309. [Google Scholar]
- Winkler, R.; Klawonn, F.; Kruse, R. Fuzzy C-Means in High Dimensional Spaces. Int. J. Fuzzy Syst. Appl. 2011, 1, 1–16. [Google Scholar] [CrossRef]
- Davies, D.; Bouldin, D. A Cluster Separation Measure. IEEE Trans. Pattern Anal. Mach. Intell. 1979, PAMI-1, 224–227. [Google Scholar] [CrossRef]
- Vergani, A.A.; Binaghi, E. A Soft Davies–Bouldin Separation Measure. In Proceedings of the 2018 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar] [CrossRef]
- Ghosh, A.; Chung, J.; Yin, D.; Ramchandran, K. An Efficient Framework for Clustered Federated Learning. In Advances in Neural Information Processing Systems; Larochelle, H., Ranzato, M., Hadsell, R., Balcan, M.F., Lin, H., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2020; Volume 33, pp. 19586–19597. [Google Scholar]
- Sattler, F.; Muller, K.R.; Samek, W. Clustered Federated Learning: Model-Agnostic Distributed Multitask Optimization Under Privacy Constraints. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 3710–3722. [Google Scholar] [CrossRef]
- Kim, Y.; Hakim, E.A.; Haraldson, J.; Eriksson, H.; da Silva, J.M.B.; Fischione, C. Dynamic Clustering in Federated Learning. In Proceedings of the ICC 2021—IEEE International Conference on Communications, Montreal, QC, Canada, 14–23 June 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Xie, M.; Long, G.; Shen, T.; Zhou, T.; Wang, X.; Jiang, J.; Zhang, C. Multi-center federated learning. arXiv 2021, arXiv:2108.08647. [Google Scholar]
- Stallmann, M.; Wilbik, A. Towards Federated Clustering: A Federated Fuzzy c-Means Algorithm (FFCM). In Proceedings of the International Workshop on Trustable, Verifiable and Auditable Federated Learning in Conjunction with AAAI 2022 (FL-AAAI-22), Vancouver, BC, Canada, 1 March 2022. [Google Scholar]
- McMahan, B.; Moore, E.; Ramage, D.; Hampson, S.; y Arcas, B.A. Communication-efficient learning of deep networks from decentralized data. In Proceedings of the Artificial Intelligence and Statistics, PMLR, Fort Lauderdale, FL, USA, 20–22 April 2017; pp. 1273–1282. [Google Scholar]
- Bholowalia, P.; Kumar, A. EBK-means: A clustering technique based on elbow method and k-means in WSN. Int. J. Comput. Appl. 2014, 105, 17–24. [Google Scholar]
- Milligan, G.W.; Cooper, M.C. An examination of procedures for determining the number of clusters in a data set. Psychometrika 1985, 50, 159–179. [Google Scholar] [CrossRef]
- Fränti, P.; Sieranoja, S. Clustering Basic Benchmark. 2018. Available online: http://cs.uef.fi/sipu/datasets/ (accessed on 27 March 2022).
- Mariescu-Istodor, P.F.R.; Zhong, C. XNN graph. LNCS 2016, 10029, 207–217. [Google Scholar]
- Moro, S.; Cortez, P.; Rita, P. A data-driven approach to predict the success of bank telemarketing. Decis. Support Syst. 2014, 62, 22–31. [Google Scholar] [CrossRef]
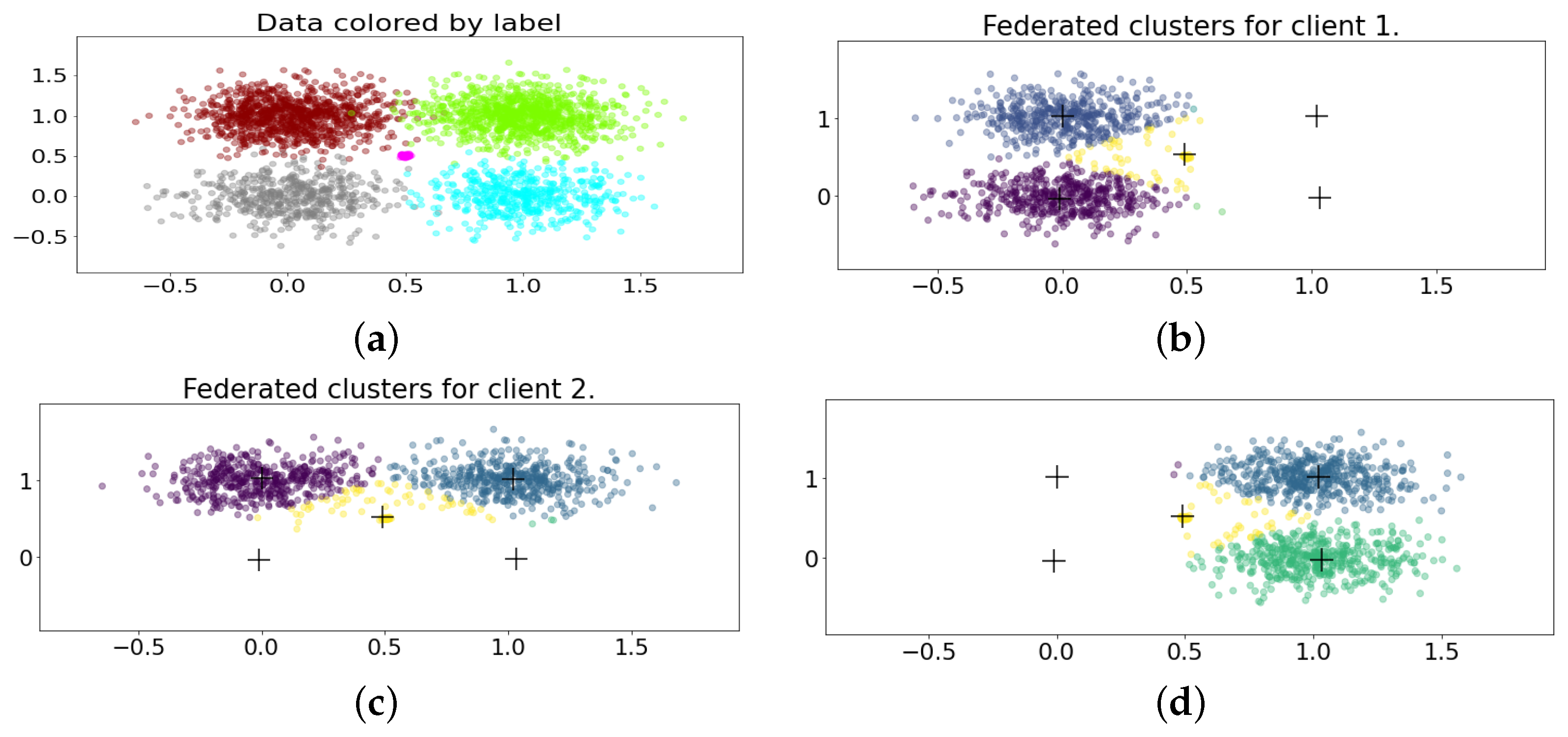
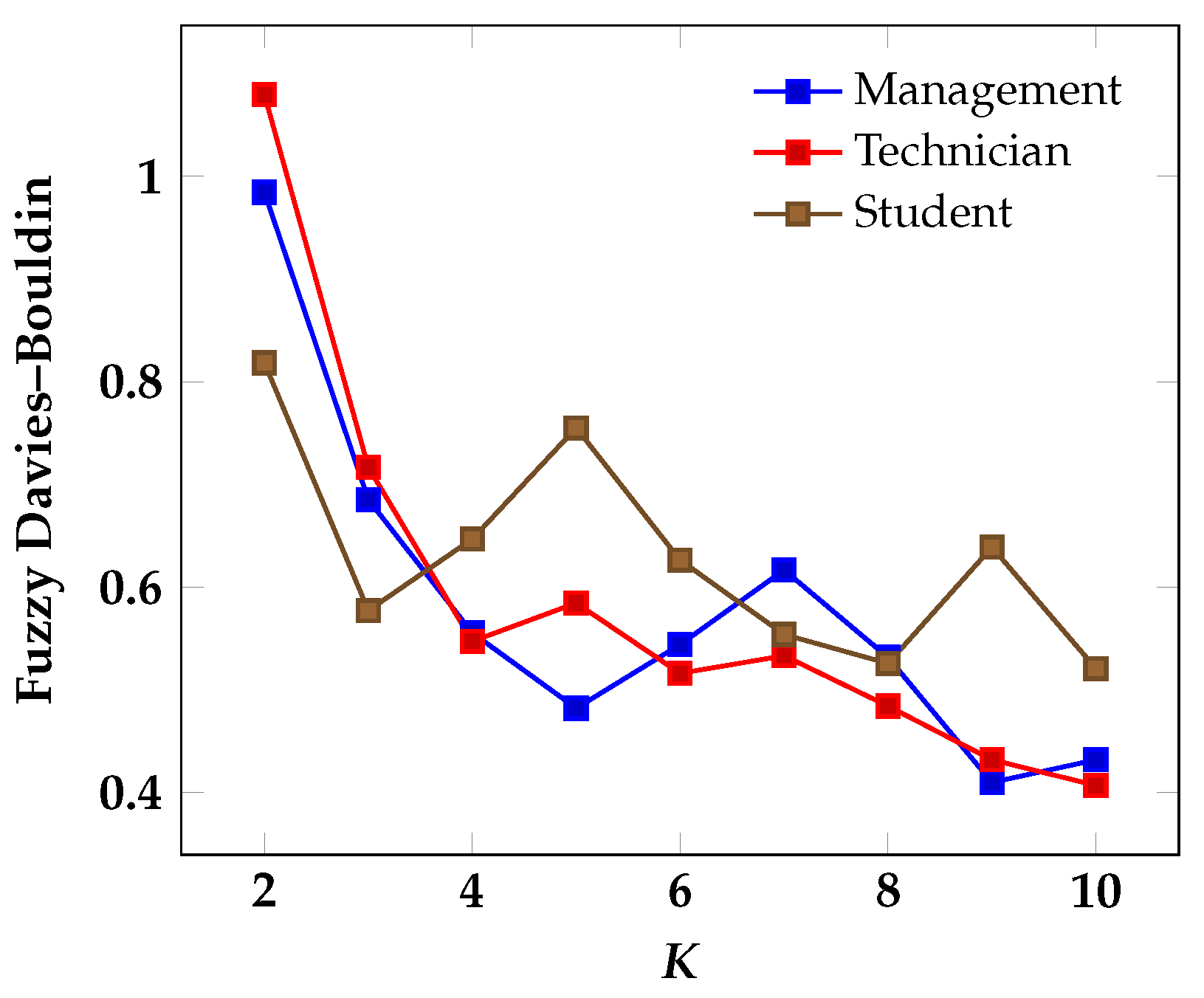
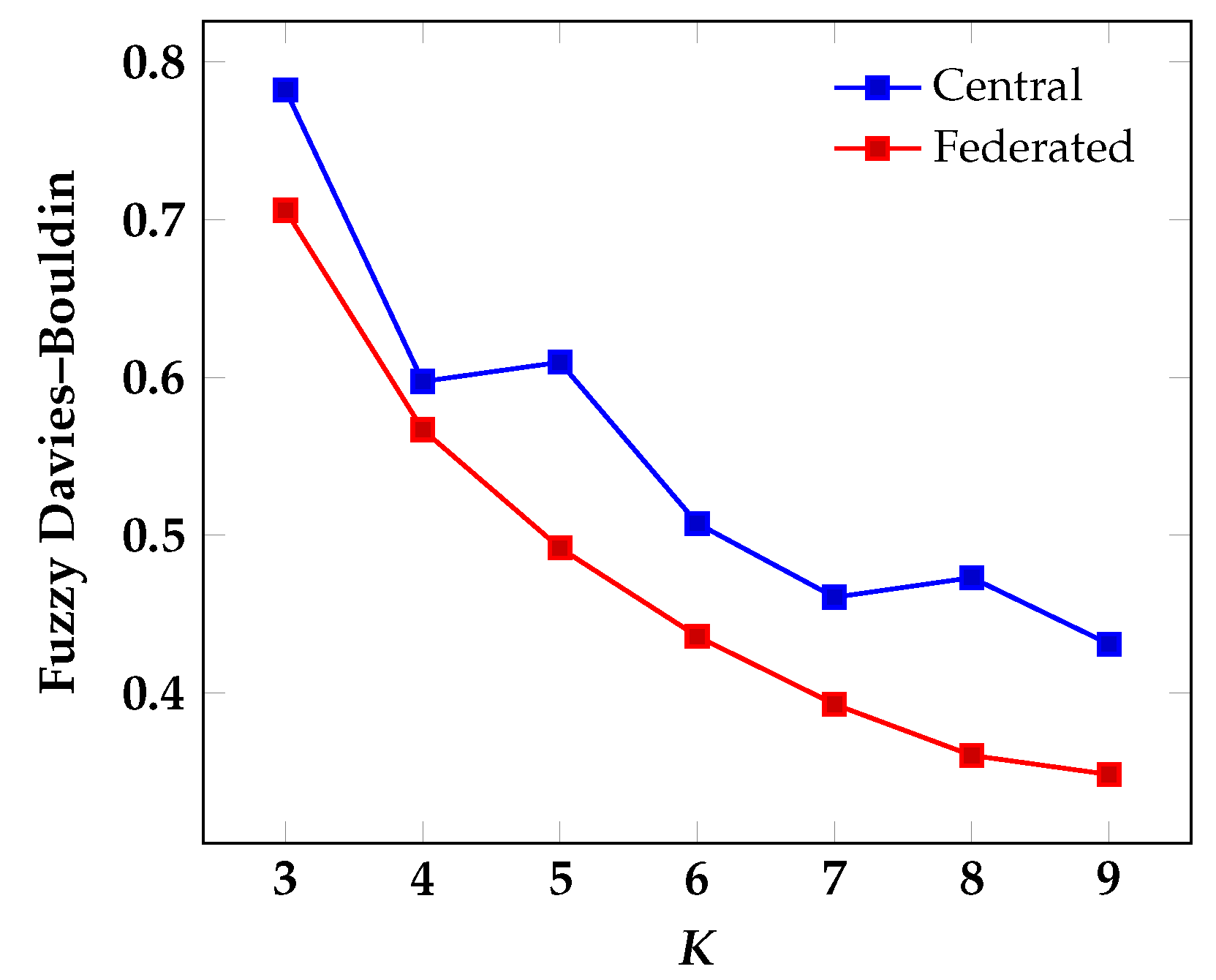
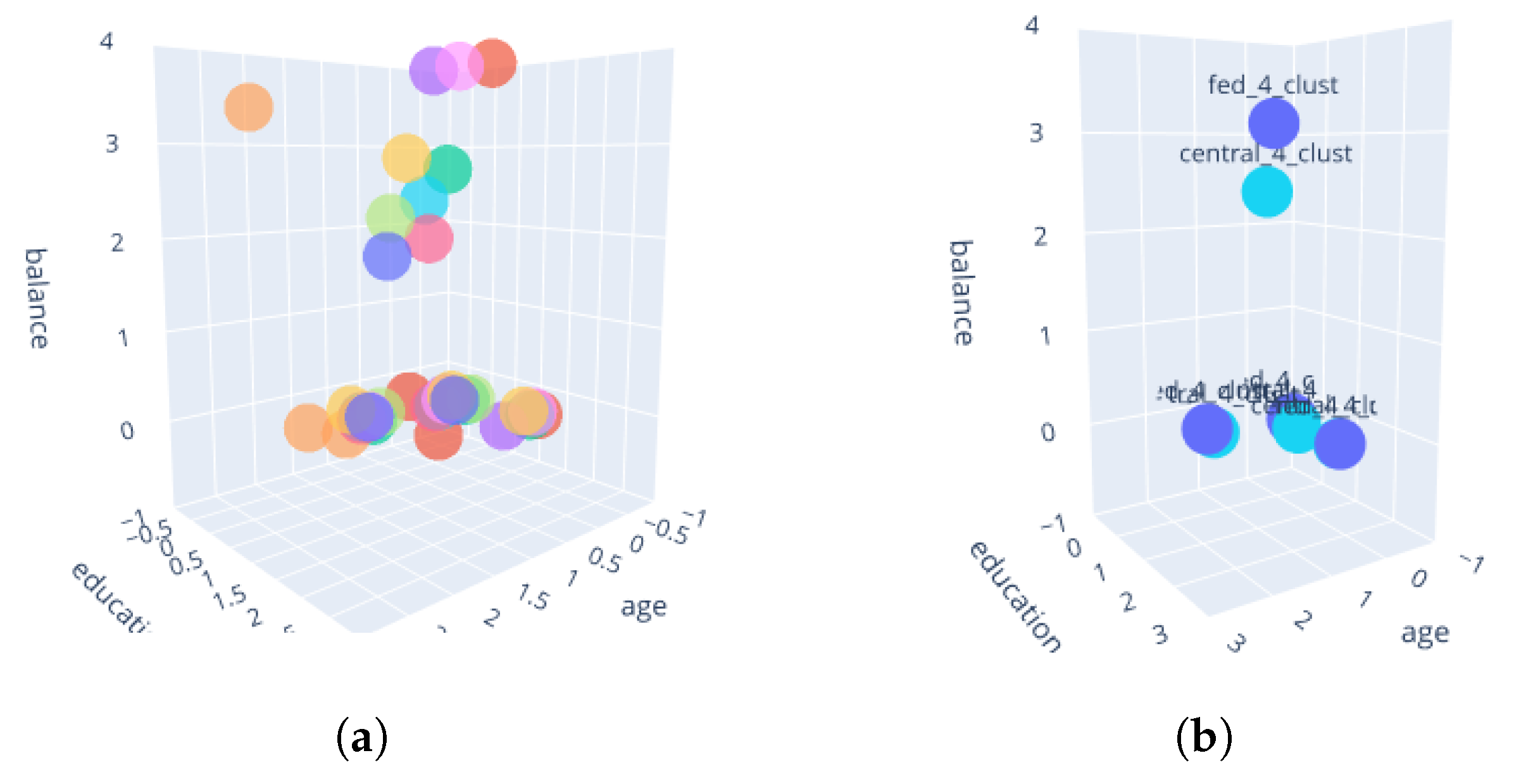
| Fuzzy Davies– Bouldin | Central (Nonfederated) | Federated | Local Client 1 | Local Client 2 | Local Client 3 |
|---|---|---|---|---|---|
| 0.8707 | 0.8179 | 0.6426 | 0.6437 | 0.6381 | |
| 0.5687 | 0.6055 | 0.7289 | 0.6991 | 0.7704 | |
| 0.4869 | 0.4951 | 1.0637 | 1.0706 | 1.1248 | |
| 0.4348 | 0.4289 | 0.9260 | 0.8927 | 0.9496 | |
| 0.5440 | 0.6202 | — | — | — | |
| 0.6707 | 0.5072 | — | — | — | |
| 0.5680 | 0.6221 | — | — | — |
| Fuzzy Davies– Bouldin | Central (Nonfederated) | Federated | Local Client 1 | Local Client 2 | Local Client 3 |
|---|---|---|---|---|---|
| 0.8707 | 1.0047 | 1.0356 | 0.8620 | 0.9685 | |
| 0.5687 | 0.9143 | 0.8880 | 0.8370 | 0.8647 | |
| 0.4869 | 1.1683 | 1.1924 | 0.9221 | 1.1662 | |
| 0.4348 | 2.9158 | 2.8867 | 2.4132 | 2.9538 | |
| 0.5440 | 1.5063 | — | — | — | |
| 0.6707 | 0.9248 | — | — | — | |
| 0.5680 | 1.2115 | — | — | — |
| Correct | Central | Two Clients | Five Clients | Ten Clients |
|---|---|---|---|---|
| k-means avg. | 92.9% | 91.4% | 88.0% | 87.2% |
| Federated avg. | 90.4% | 89.5% | 88.9% |
| Fuzzy Davies– Bouldin () | Central | Two Clients | Five Clients | Ten Clients |
|---|---|---|---|---|
| 25% Quantile | 0.6762 | 0.6771 | 0.6766 | 0.6766 |
| 50% Quantile | 0.8640 | 0.8638 | 0.8627 | 0.8627 |
| 75% Quantile | 1.3092 | 1.3073 | 1.2961 | 1.2944 |
| Minimum | 0.5460 | 0.5459 | 0.5459 | 0.5458 |
| Maximum | 56,784.5518 | 57.6910 | 23.6987 | 20.0192 |
| Fuzzy Davies– Bouldin () | Central | Two Clients | Five Clients | Ten Clients |
|---|---|---|---|---|
| 25% Quantile | 0.6762 | 0.6767 | 0.6766 | 0.6766 |
| 50% Quantile | 0.8640 | 0.8627 | 0.8623 | 0.8620 |
| 75% Quantile | 1.3092 | 1.2997 | 1.2990 | 1.2934 |
| Minimum | 0.5460 | 0.5460 | 0.5459 | 0.5459 |
| Maximum | 56,784.55 | 31,307.76 | 54,809.42 | 9021.3485 |
| Knowledge Gap () | Central | Two Clients | Five Clients | Ten Clients |
|---|---|---|---|---|
| 25% Quantile | 0.2850 | 0.2724 | 0.2700 | 0.2587 |
| 50% Quantile | 0.8904 | 0.8897 | 0.8900 | 0.8898 |
| 75% Quantile | 5.9544 | 5.9272 | 5.8335 | 5.4764 |
| Minimum | 0.0286 | 0.0278 | 0.0265 | 0.0253 |
| Maximum | 77.6472 | 77.540 | 77.7092 | 76.0134 |
| Knowledge Gap () | Central | Two Clients | Five Clients | Ten Clients |
|---|---|---|---|---|
| 25% Quantile | 0.2850 | 0.2729 | 0.2693 | 0.2679 |
| 50% Quantile | 0.8904 | 0.8888 | 0.8902 | 0.8899 |
| 75% Quantile | 5.9544 | 5.5436 | 5.4888 | 5.4320 |
| Minimum | 0.0286 | 0.0285 | 0.0283 | 0.0281 |
| Maximum | 77.6472 | 77.6472 | 77.6472 | 77.6472 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stallmann, M.; Wilbik, A. On a Framework for Federated Cluster Analysis. Appl. Sci. 2022, 12, 10455. https://doi.org/10.3390/app122010455
Stallmann M, Wilbik A. On a Framework for Federated Cluster Analysis. Applied Sciences. 2022; 12(20):10455. https://doi.org/10.3390/app122010455
Chicago/Turabian StyleStallmann, Morris, and Anna Wilbik. 2022. "On a Framework for Federated Cluster Analysis" Applied Sciences 12, no. 20: 10455. https://doi.org/10.3390/app122010455
APA StyleStallmann, M., & Wilbik, A. (2022). On a Framework for Federated Cluster Analysis. Applied Sciences, 12(20), 10455. https://doi.org/10.3390/app122010455







