Design of Mode-Locked Fibre Laser with Non-Linear Power and Spectrum Width Transfer Functions with a Power Threshold
Abstract
1. Introduction
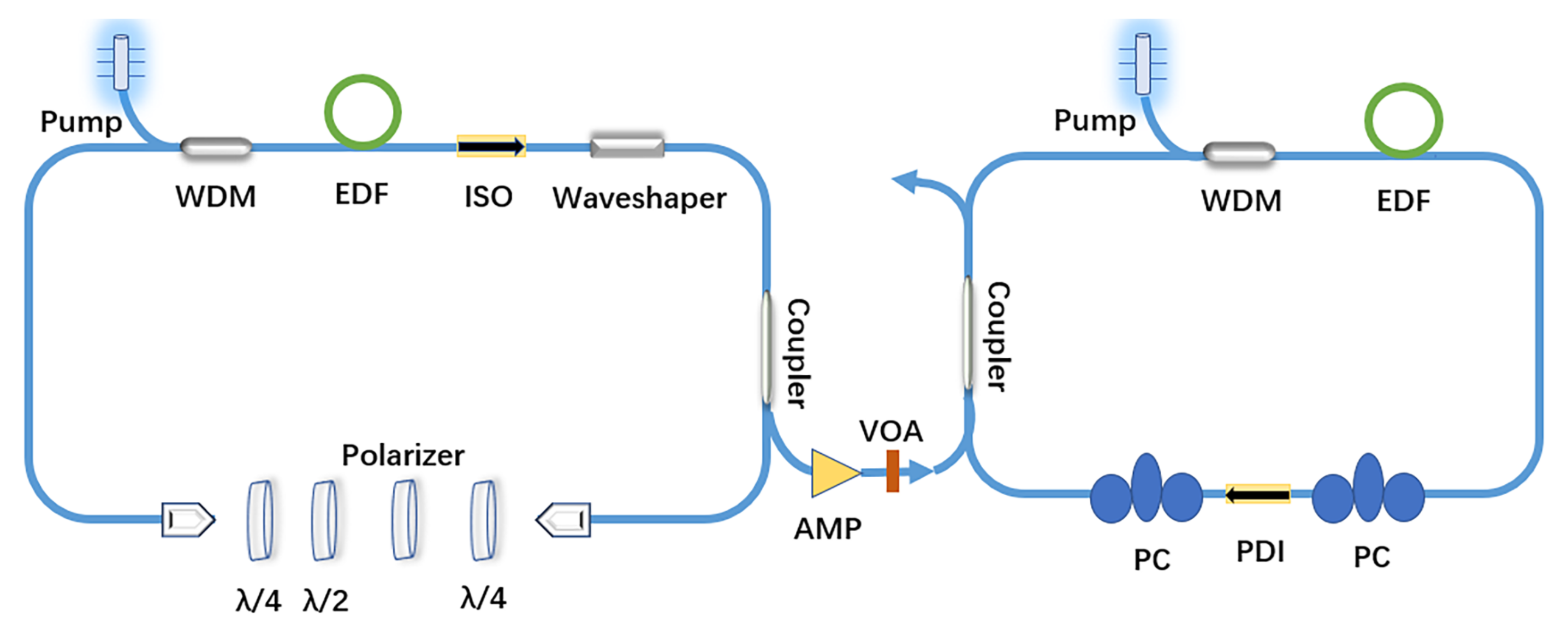
2. Design
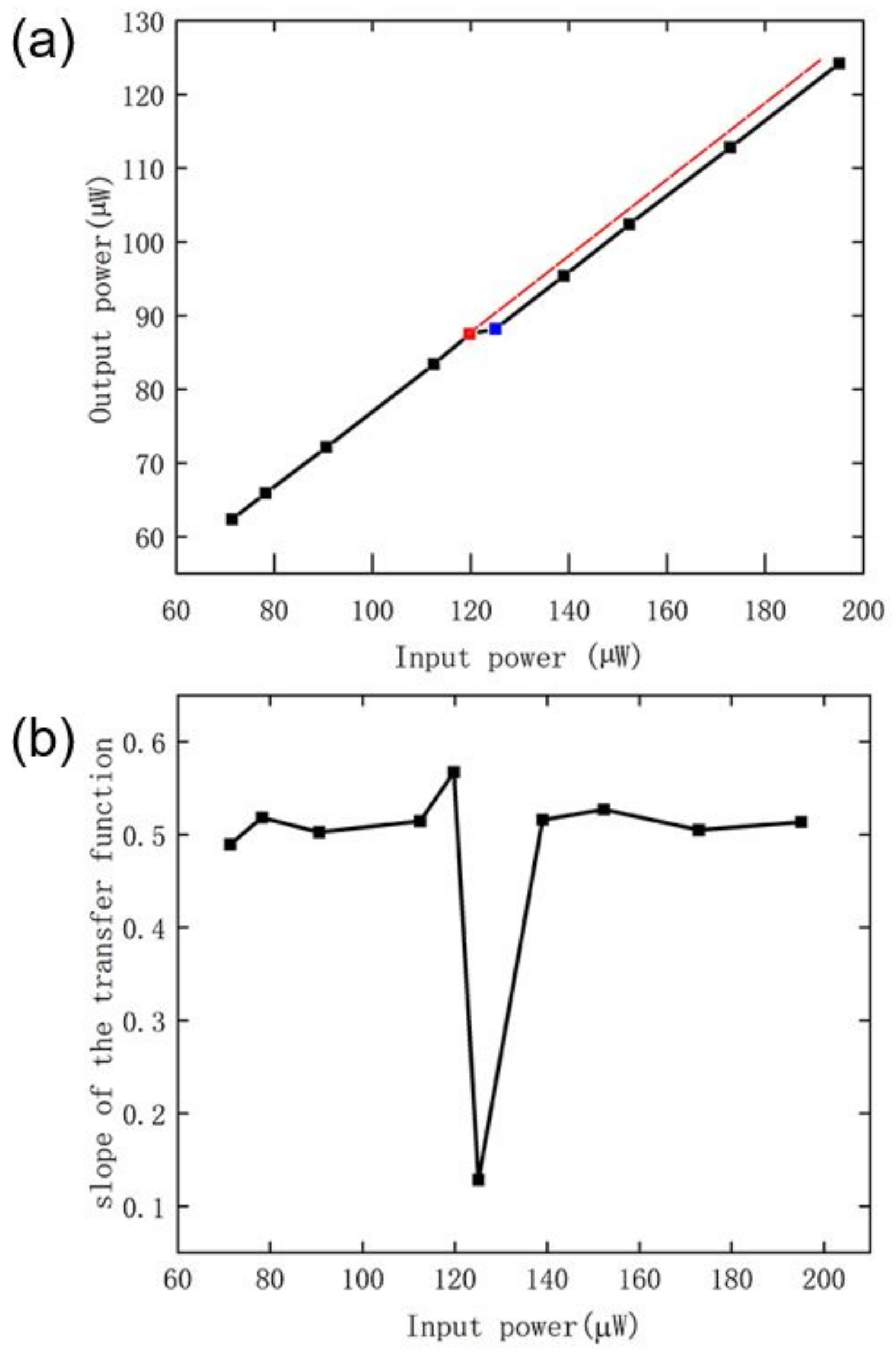
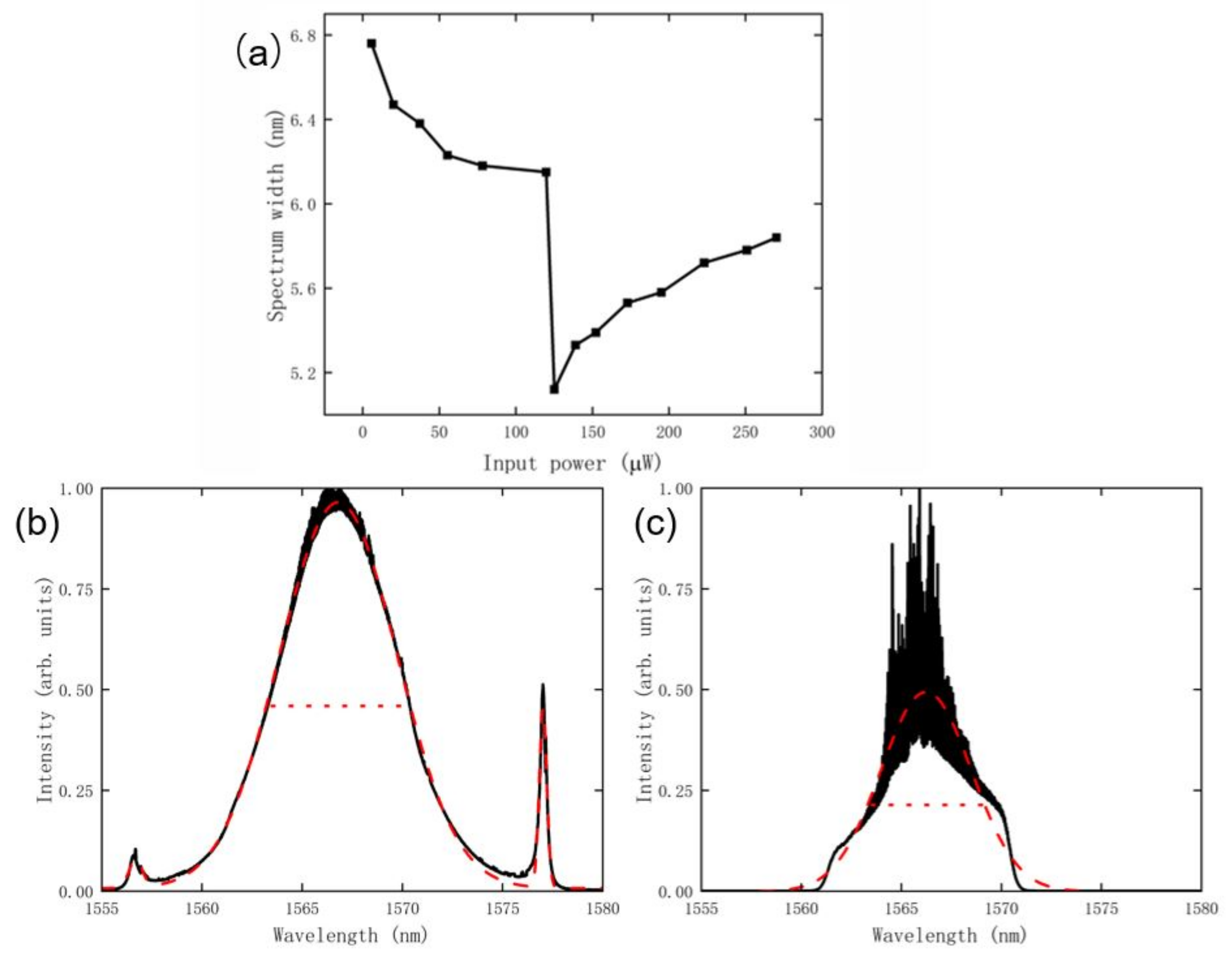
3. Results and Discussion
- (i)
- below the threshold—the output signal follows the eigen-mode excitation characteristic of the processing laser inherent properties;
- (ii)
- above the threshold—the output signal follows the input signal excitation.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Prucnal, P.R.; Shastri, B.J. Neuromorphic Photonics; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Lugnan, A.; Katumba, A.; Laporte, F.; Freiberger, M.; Sackesyn, S.; Ma, C.; Gooskens, E.; Dambre, J.; Bienstman, P. Photonic neuromorphic information processing and reservoir computing. APL Photonics 2020, 5, 020901. [Google Scholar] [CrossRef]
- Shastri, B.J.; Tait, A.N.; Ferreira de Lima, T.; Pernice, W.H.P.; Bhaskaran, H.; Wright, C.D.; Prucnal, P.R. Photonics for artificial intelligence and neuromorphic computing. Nat. Photonics 2021, 15, 102–114. [Google Scholar] [CrossRef]
- Jarajreh, M.A.; Giacoumidis, E.; Aldaya, I.; Le, S.T.; Tsokanos, A.; Ghassemlooy, Z.; Doran, N.J. Artificial neural network nonlinear equalizer for coherent optical OFDM. IEEE Photon. Technol. Lett. 2015, 27, 387–390. [Google Scholar] [CrossRef]
- Giacoumidis, E.; Le, S.T.; Ghanbarisabagh, M.; McCarthy, M.; Aldaya, I.; Mhatli, S.; Jarajreh, M.A.; Haigh, P.A.; Doran, N.J.; Ellis, A.D.; et al. Fiber nonlinearity-induced penalty reduction in CO-OFDM by ANN-based nonlinear equalization. Opt. Lett. 2015, P40, 5113–5116. [Google Scholar] [CrossRef]
- Sorokina, M.; Sygletos, S.; Turitsyn, S. Sparse identification for nonlinear optical communication systems: SINO method. Opt. Express 2016, 24, 30433–30443. [Google Scholar] [CrossRef]
- Hager, C.; Pfister, H.D. Nonlinear Interference Mitigation via Deep Neural Networks. In Proceedings of the Optical Fiber Communication Conference, San Diego, CA, USA, 11–15 March 2018; p. W3A.4. [Google Scholar]
- Shen, T.S.R.; Lau, A.P.T. Fiber nonlinearity compensation using extreme learning machine for DSP-based coherent communication systems. In Proceedings of the 16th Opto-Electronics and Communications Conference, Kaohsiung, Taiwan, 4–8 July 2011; pp. 816–817. [Google Scholar]
- Owaki, S.; Nakamura, M. Equalization of optical nonlinear waveform distortion using neural-network based digital signal processing. In Proceedings of the 2016 21st OptoElectronics and Communications Conference (OECC) Held Jointly with 2016 International Conference on Photonics in Switching (PS), Niigata, Japan, 3–7 July 2016; p. WA2-40. [Google Scholar]
- FitzHugh, R. Impulses and physiological states in theoretical models of nerve membrane. Biophys. J. 1961, 1, 445–466. [Google Scholar] [CrossRef]
- Nagumo, J.; Arimoto, S.; Yoshizawa, S. An active pulse transmission line simulating nerve axon. Proc. IRE 1962, 50, 2061–2070. [Google Scholar] [CrossRef]
- Mahowald, M.; Douglas, R. A silicon neuron. Nature 1991, 354, 515–518. [Google Scholar] [CrossRef]
- Eliasmith, C.; Stewart, T.C.; Choo, X.; Bekolay, T.; DeWolf, T.; Tang, Y.; Rasmussen, D. A Large-Scale Model of the Functioning Brain. Science 2012, 338, 1202–1205. [Google Scholar] [CrossRef]
- Engel, T.A.; Steinmetz, N.A.; Gieselmann, M.A.; Thiele, A.; Moore, T.; Boahen, K. Selective modulation of cortical state during spatial attention. Science 2016, 354, 1140–1144. [Google Scholar] [CrossRef]
- Calimera, A.; Macii, E.; Poncino, M. The Human Brain Project and neuromorphic computing. Funct. Neurol. 2013, 28, 191–196. [Google Scholar]
- Tait, A.N.; Lima, T.F.; Zhou, E.; Wu, A.X.; Nahmias, M.A.; Shastri, B.J.; Prucnal, P.R. Neuromorphic photonic networks using silicon photonic weight banks. Sci. Rep. 2017, 7, 7430. [Google Scholar] [CrossRef]
- Bueno, J.; Brunner, D.; Soriano, M.C.; Fischer, I. Conditions for reservoir computing performance using semiconductor lasers with delayed optical feedback. Opt. Express 2017, 25, 2401–2412. [Google Scholar] [CrossRef]
- Cohen, E.; Malka, D.; Shemer, A.; Shahmoon, A.; Zalevsky, Z.; London, M. Neural networks within multi-core optic fibers. Sci. Rep. 2016, 6, 29080. [Google Scholar] [CrossRef]
- Lukosevicius, M.; Jaeger, H. Reservoir Computing Approaches to Recurrent Neural Network Training. Comput. Sci. Rev. 2009, 3, 127–149. [Google Scholar] [CrossRef]
- Schrauwen, B.; Verstraeten, D.; Campenhout, J. An overview of reservoir computing: Theory, applications, and implementations. In Proceedings of the European Symposium on Artificial Neural Networks ESANN, Bruges, Belgium, 25–27 April 2007; pp. 471–482. [Google Scholar]
- Appeltant, L.; Soriano, M.C.; Van der Sande, G.; Danckaert, J.; Massar, S.; Dambre, J.; Schrauwen, B.; Mirasso, C.R.; Fischer, I. Information processing using a single dynamical node as complex system. Nat. Commun. 2011, 2, 468. [Google Scholar] [CrossRef]
- Sorokina, M. Multi-channel optical neuromorphic processor for frequency-multiplexed signals. J. Phys. Photonics 2021, 3, 014002. [Google Scholar] [CrossRef]
- Bauduin, M.; Massar, S.; Horlin, F. Non-linear satellite channel equalization based on a low complexity echo state network. In Proceedings of the 2016 Annual Conference on Information Science and Systems, Princeton, NJ, USA, 16–18 March 2016; pp. 99–104. [Google Scholar]
- Argyris, A.; Bueno, J.; Fischer, I. Photonic machine learning implementation for signal recovery in optical communications. Sci. Rep. 2018, 8, 8487. [Google Scholar] [CrossRef]
- Sorokina, M.; Sergeyev, S.; Turitsyn, S. Fiber echo state network analogue for high-bandwidth dual-quadrature signal processing. Opt. Express 2019, 27, 2387–2395. [Google Scholar] [CrossRef]
- Sorokina, M. Dispersion-managed fiber echo state network analogue with high (including THz) bandwidth. J. Lightwave Technol. 2020, 38, 3209–3213. [Google Scholar] [CrossRef]
- Sackesyn, S.; Ma, C.; Dambre, J.; Bienstman, P. Experimental realization of integrated photonic reservoir computing for nonlinear fiber distortion compensation. Opt. Express 2021, 29, 30991–30997. [Google Scholar] [CrossRef] [PubMed]
- Vandoorne, K.; Dambre, J.; Verstraeten, D.; Schrauwent, B.; Bienstman, P. Parallel reservoir computing using optical amplifiers. IEEE Trans. Neural Netw. 2011, 22, 1469–1481. [Google Scholar] [CrossRef] [PubMed]
- Hejda, M.; Robertson, J.; Bueno, J.; Hurtado, A. Spike-based information encoding in vertical cavity surface emitting lasers for neuromorphic photonic systems. J. Phys. Photonics 2020, 2, 044001. [Google Scholar] [CrossRef]
- Heuser, T.; Pflüger, M.; Fischer, I.; Lott, J.A.; Brunner, D.; Reitzenstein, S. Developing a photonic hardware platform for brain-inspired computing based on 5 × 5 VCSEL arrays. J. Phys. Photonics 2020, 2, 044002. [Google Scholar] [CrossRef]
- Shastri, B.J.; Nahmias, M.A.; Tait, A.N.; Rodriguez, A.W.; Wu, B.; Prucnal, P.R. Spike processing with a graphene excitable laser. Sci. Rep. 2016, 6, 19126. [Google Scholar] [CrossRef] [PubMed]
- Ferrari, A.; Napoli, A.; Costa, N.; Fischer, J.K.; Pedro, J.; Forysiak, W.; Richter, A.; Pincemin, E.; Curri, V. Multi-Band Optical Systems to Enable Ultra-High Speed Transmissions. In Proceedings of the European Conference on Lasers and Electro-Optics, Munich, Germany, 23–27 June 2019; p. ci23. [Google Scholar]
- Sorokina, M. Multidimensional fiber echo state network analogue. J. Phys. Photonics 2020, 2, 044006. [Google Scholar] [CrossRef]
- Schaich, F.; Wild, T. Waveform contenders for 5G—OFDM vs. FBMC vs. UFMC. In Proceedings of the 6th International Symposium on Communications, Control and Signal Processing (ISCCSP), Athens, Greece, 21–23 May 2014. [Google Scholar]
- Christodoulopoulos, K.; Tomkos, I.; Varvarigos, E.A. Elastic bandwidth allocation in flexible OFDM-based optical networks. J. Light. Technol. 2011, 29, 1354–1366. [Google Scholar] [CrossRef]
- The Mobile Broadband Standard Partnership Project. Available online: https://www.3gpp.org/ (accessed on 5 October 2022).
- Tomkos, I.; Klonidis, D.; Pikasis, E.; Theodoridis, S. Toward the 6G Network Era: Opportunities and Challenges. IEEE IT Prof. 2020, 22, 32–38. [Google Scholar]
- Lecaplain, C.; Grelu, P.; Soto-Crespo, J.; Akhmediev, N. Dissipative rogue waves generated by chaotic pulse bunching in a mode-locked laser. Phys. Rev. Lett. 2012, 108, 233901. [Google Scholar] [CrossRef]
- Peng, J.; Zeng, H. Soliton collision induced explosions in a mode-locked fibre laser. Commun. Phys. 2019, 2, 34. [Google Scholar] [CrossRef]
- Li, B.; Yu, Y.; Wei, X.; Xu, Y.; Tsia, K.K.; Wong, K.K. Real-time observation of round-trip resolved spectral dynamics in a stabilized fs fiber laser. Opt. Exp. 2017, 25, 8751–8759. [Google Scholar] [CrossRef]
- Peng, J.; Sorokina, M.; Sugavanam, S.; Tarasov, N.; Churkin, D.V.; Turitsyn, S.K.; Zeng, H. Real-time observation of dissipative soliton formation in nonlinear polarization rotation modelocked fibre lasers. Commun. Phys. 2018, 1, 20. [Google Scholar] [CrossRef]
- Benda, J.; Herz, A.V.M. A Universal Model for Spike-Frequency Adaptation. Neural Comput. 2003, 15, 2523–2564. [Google Scholar] [CrossRef]
- Izhikevich, E.M. Dynamical Systems in Neuroscience: The Geometry of Excitability and Bursting; MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Kutz, J.N.; Fu, X.; Brunton, S. Self-tuning fiber lasers: Machine learning applied to optical systems. In Proceedings of the Advanced Photonics Conference, Barcelona, Spain, 27–31 July 2014; p. NTu4A.7. [Google Scholar]
- Baumeister, T.; Brunton, S.L.; Kutz, N.J. Deep learning and model predictive control for self-tuning mode-locked lasers. J. Opt. Soc. Am. B 2018, 35, 617–626. [Google Scholar] [CrossRef]
- Ling, Q.; Gu, Z.; Gao, K. Smart design of a long-period fiber grating refractive index sensor based on dual-peak resonance near the phase-matching turning point. Appl. Opt. 2018, 57, 2693–2697. [Google Scholar] [CrossRef]
- Ellis, A.D.; McCarthy, M.E.; Al Khateeb, M.A.Z.; Sorokina, M.; Doran, N.J. Performance limits in optical communications due to fiber nonlinearity. Adv. Opt. Photon. 2017, 9, 429–503. [Google Scholar] [CrossRef]
- Da Ros, F.; Ranzini, S.M.; Dischler, R.; Cem, A.; Aref, V.; Bülow, H.; Zibar, D. Machine-learning-based equalization for short-reach transmission: Neural networks and reservoir computing. In Proceedings of the Metro and Data Center Optical Networks and Short-Reach Links IV, Online, 6–12 March 2021; p. 1171205. [Google Scholar]
- Luo, F.L.; Zhang, C. Signal Processing for 5G: Algorithms and Implementations; Wiley-IEEE Press: Chichester, UK, 2016. [Google Scholar]
- Hofer, M.; Ober, M.H.; Haberl, F.; Fermann, M.E. Characterization of ultrashort pulse formation in passively mode-locked fiber lasers. IEEE J. Quantum Electron. 1992, 28, 720. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, Z.; Peng, J.; Sorokina, M.; Zeng, H. Design of Mode-Locked Fibre Laser with Non-Linear Power and Spectrum Width Transfer Functions with a Power Threshold. Appl. Sci. 2022, 12, 10318. https://doi.org/10.3390/app122010318
Xie Z, Peng J, Sorokina M, Zeng H. Design of Mode-Locked Fibre Laser with Non-Linear Power and Spectrum Width Transfer Functions with a Power Threshold. Applied Sciences. 2022; 12(20):10318. https://doi.org/10.3390/app122010318
Chicago/Turabian StyleXie, Ziyi, Junsong Peng, Mariia Sorokina, and Heping Zeng. 2022. "Design of Mode-Locked Fibre Laser with Non-Linear Power and Spectrum Width Transfer Functions with a Power Threshold" Applied Sciences 12, no. 20: 10318. https://doi.org/10.3390/app122010318
APA StyleXie, Z., Peng, J., Sorokina, M., & Zeng, H. (2022). Design of Mode-Locked Fibre Laser with Non-Linear Power and Spectrum Width Transfer Functions with a Power Threshold. Applied Sciences, 12(20), 10318. https://doi.org/10.3390/app122010318







