Episodic Memory and Information Recognition Using Solitonic Neural Networks Based on Photorefractive Plasticity
Abstract
1. Introduction
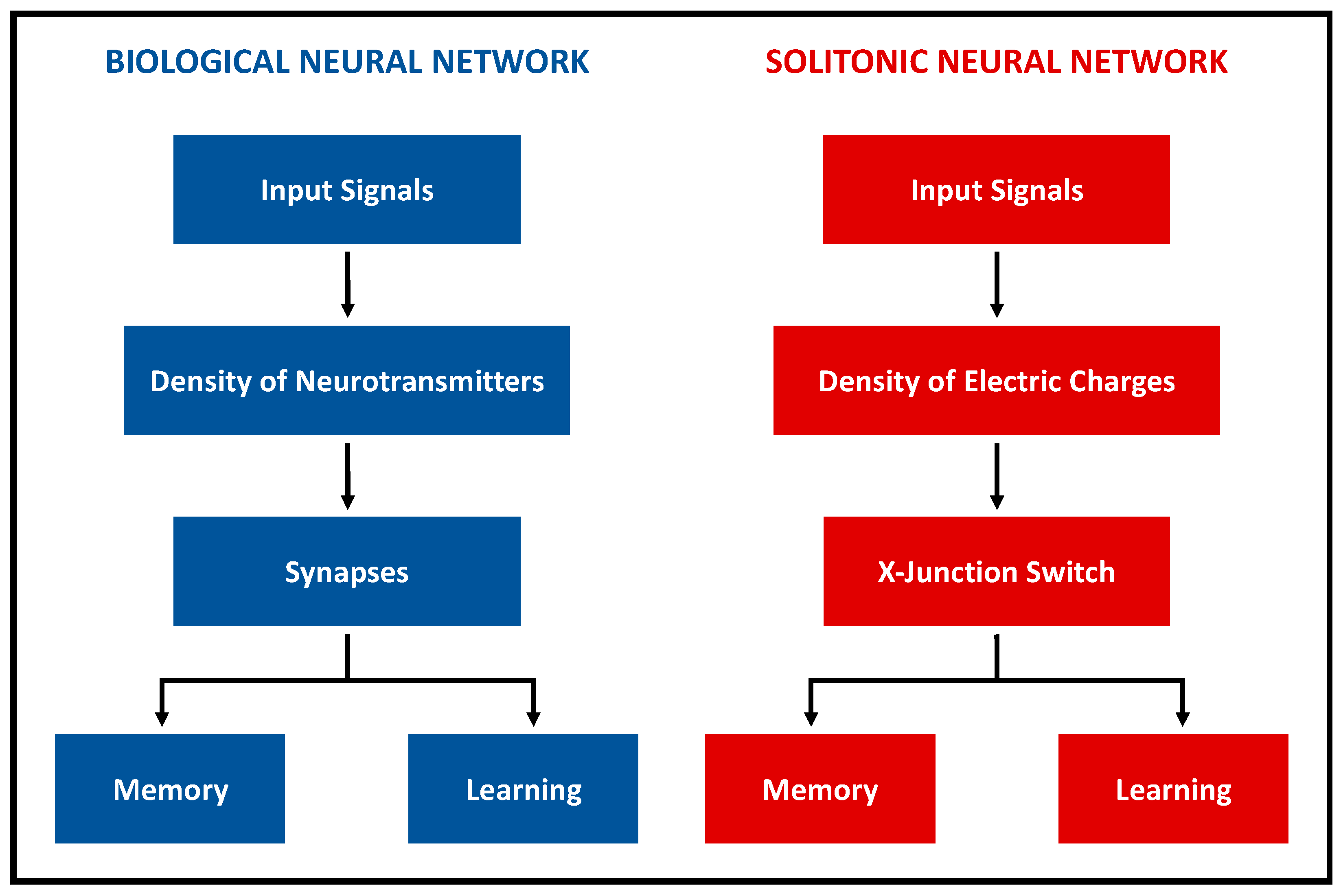
2. Biological vs. Solitonic Neural Networks
- Intensity of input signals;
- Persistence of signals along a specific path.
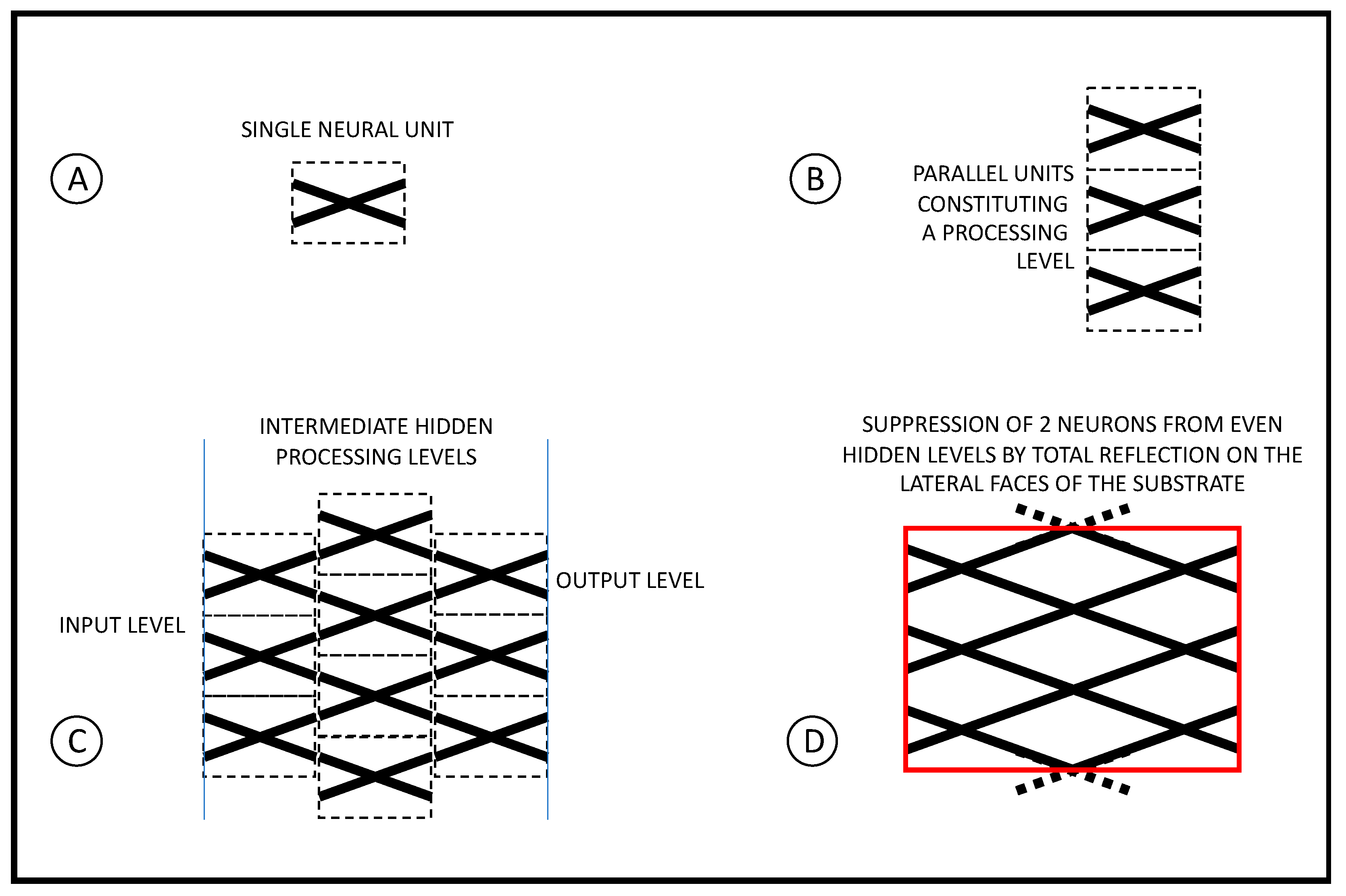
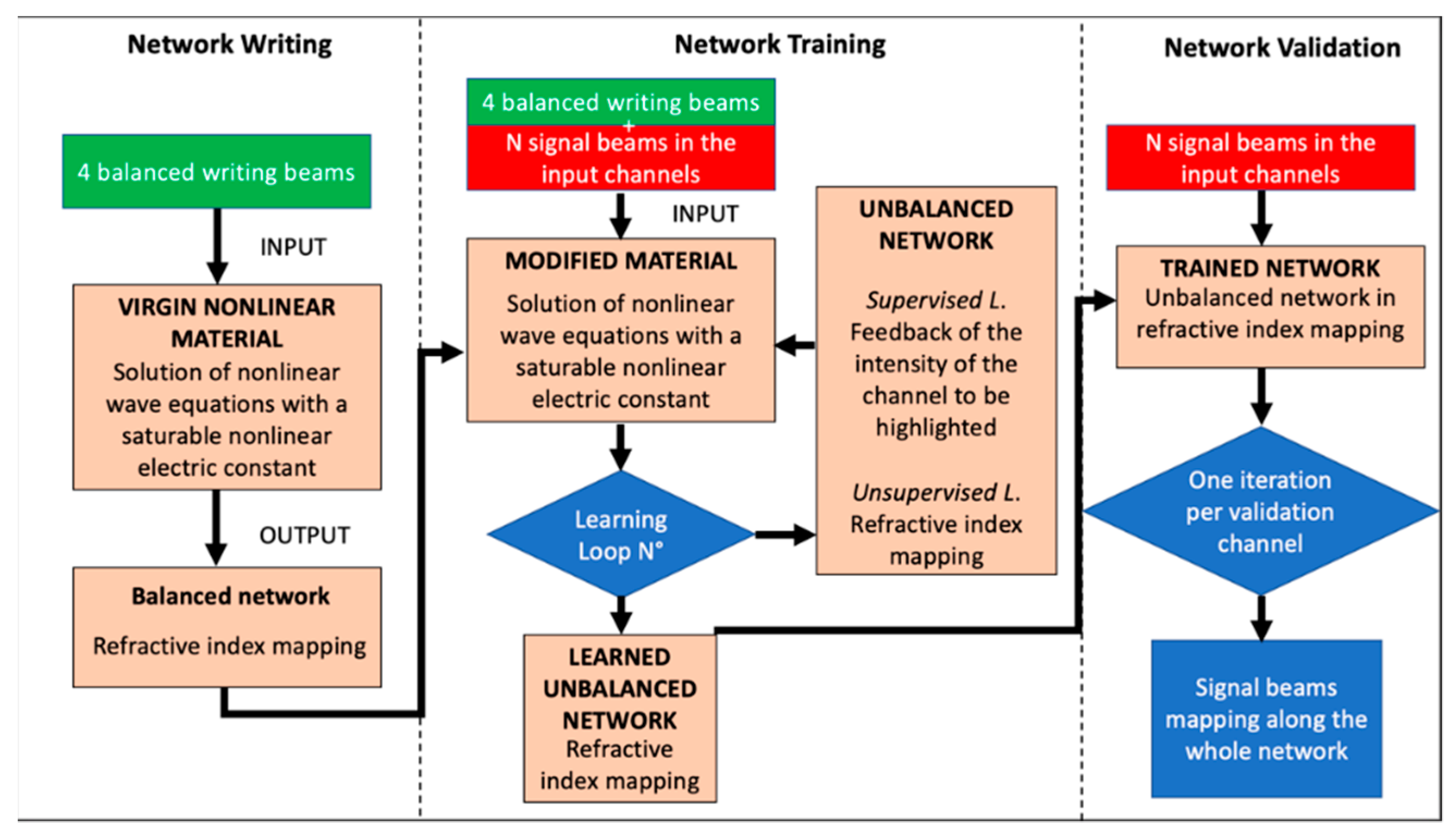
3. Architecture of a Learning SNN
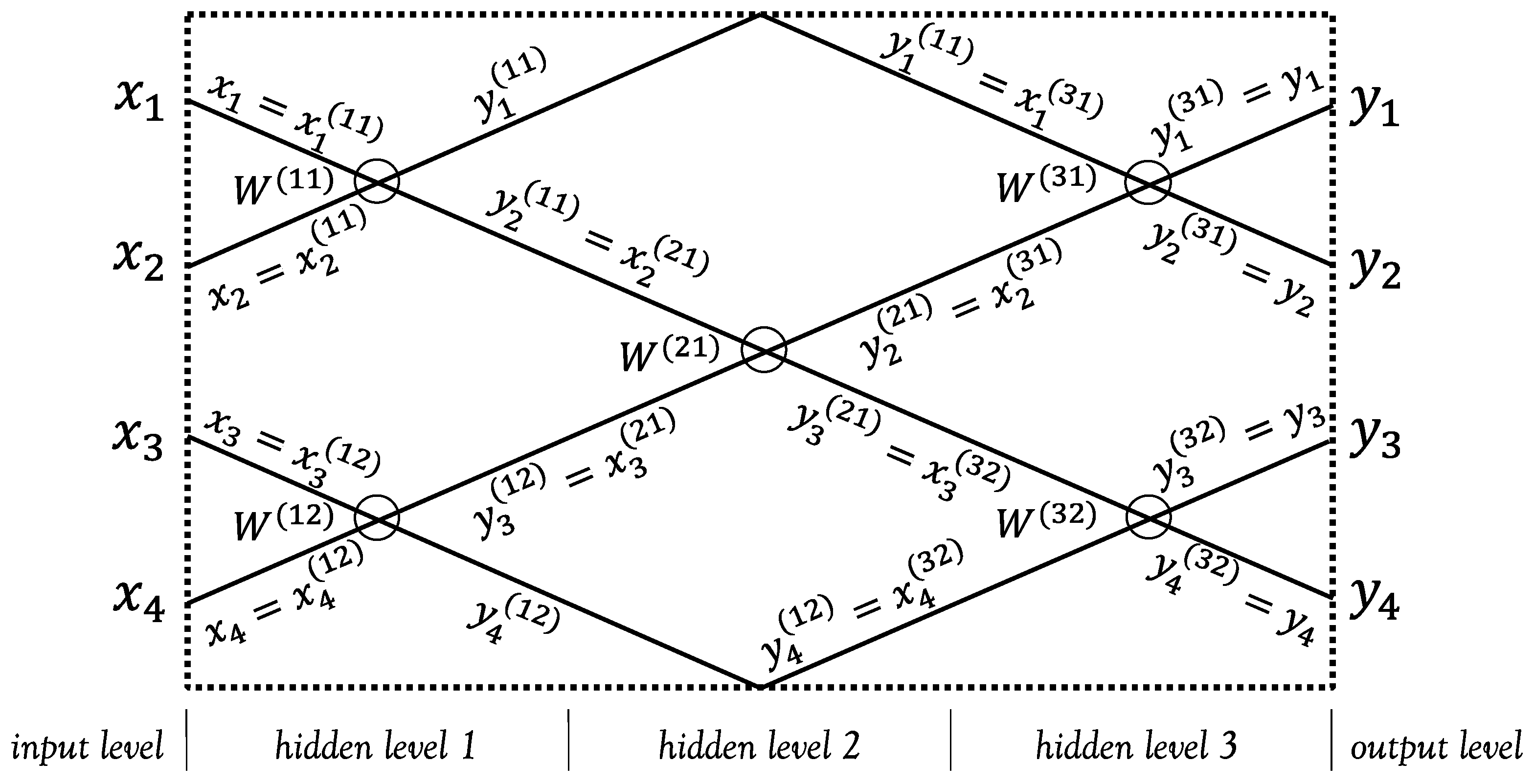
4. Mathematical Model of the SNN
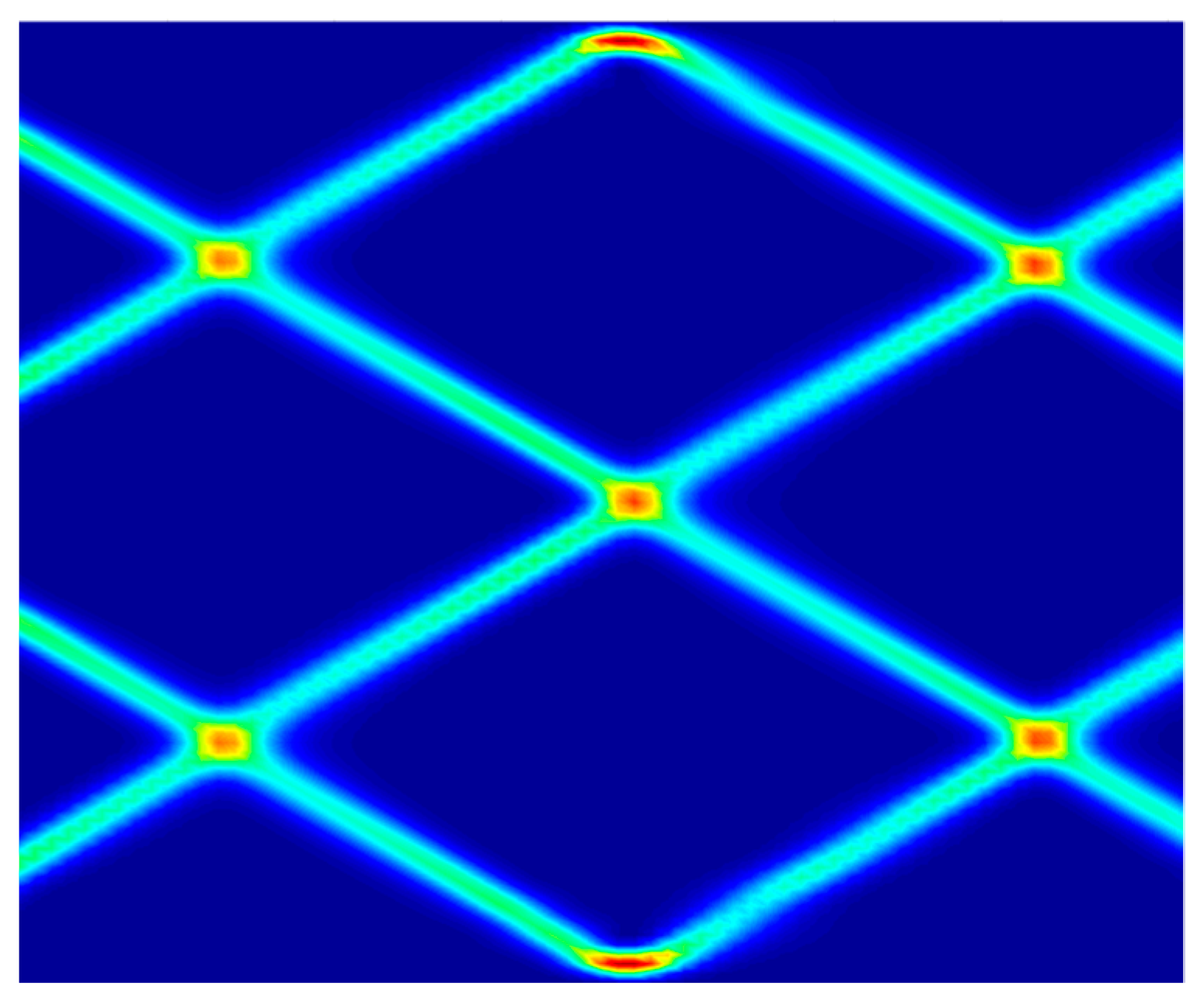
5. A 4-Bit SNN Working as an Episodic Memory
6. Comparison with the SNN Dynamics
6.1. Learning and Memorization Processes
- ▪
- Single input beam, which corresponds to a single illuminated pixel in a 4 × 4 pixel matrix (1-digit, 4-bit numbers);
- ▪
- Two input beams, which correspond to two illuminated pixels (2-digit, 4-bit numbers);
- ▪
- Three input beams, which correspond to three illuminated pixels (3-digit, 4-bit numbers).
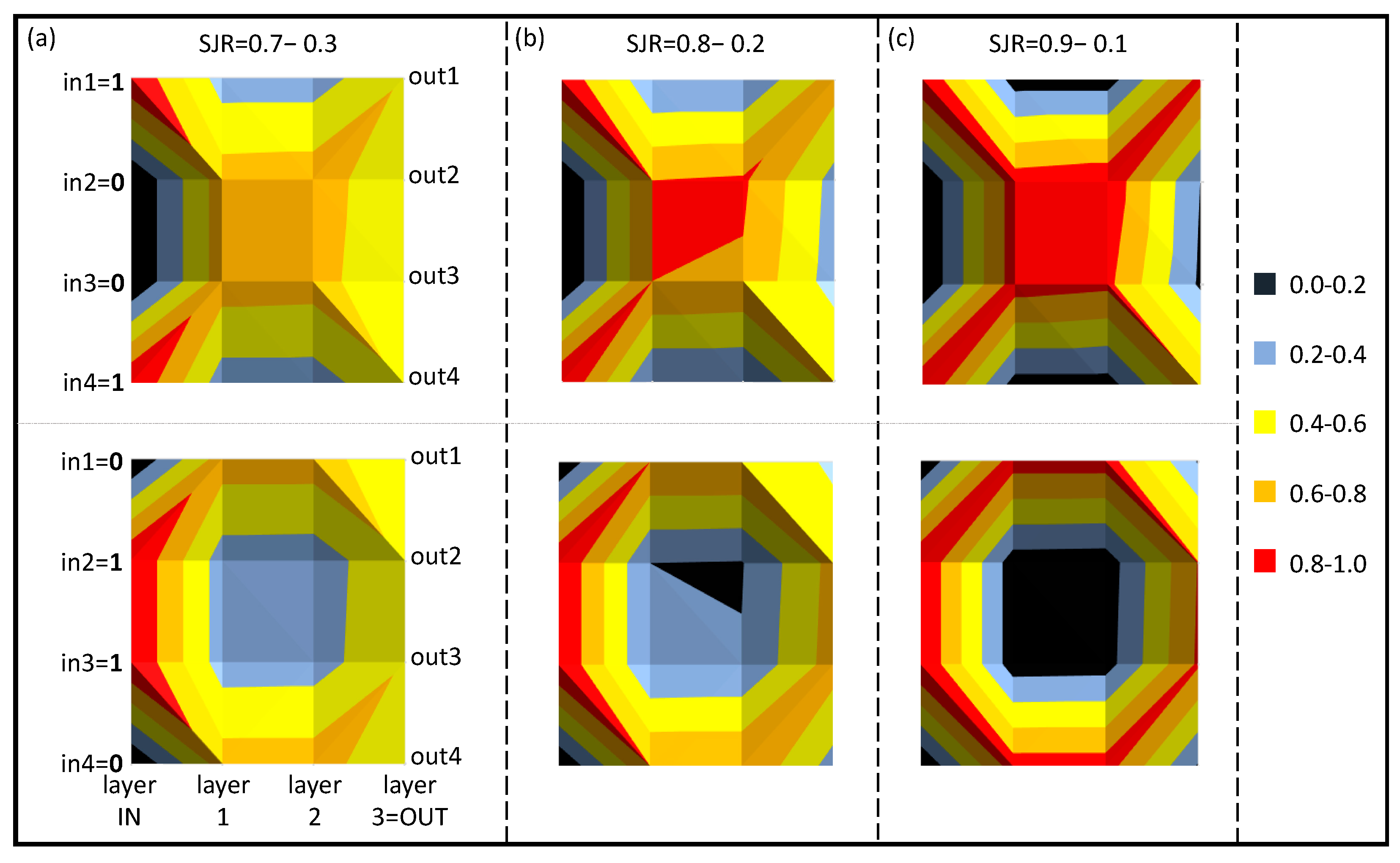
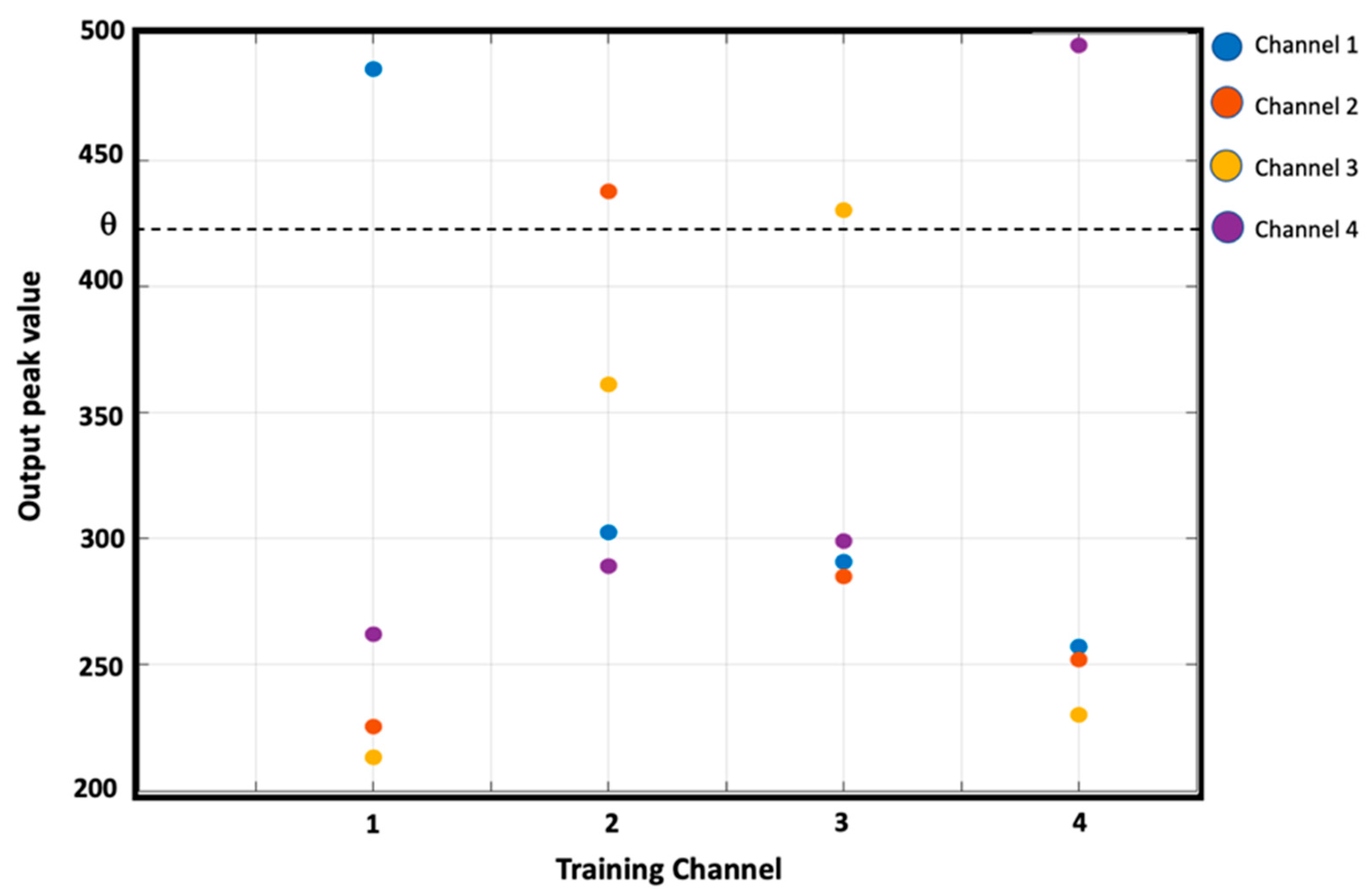
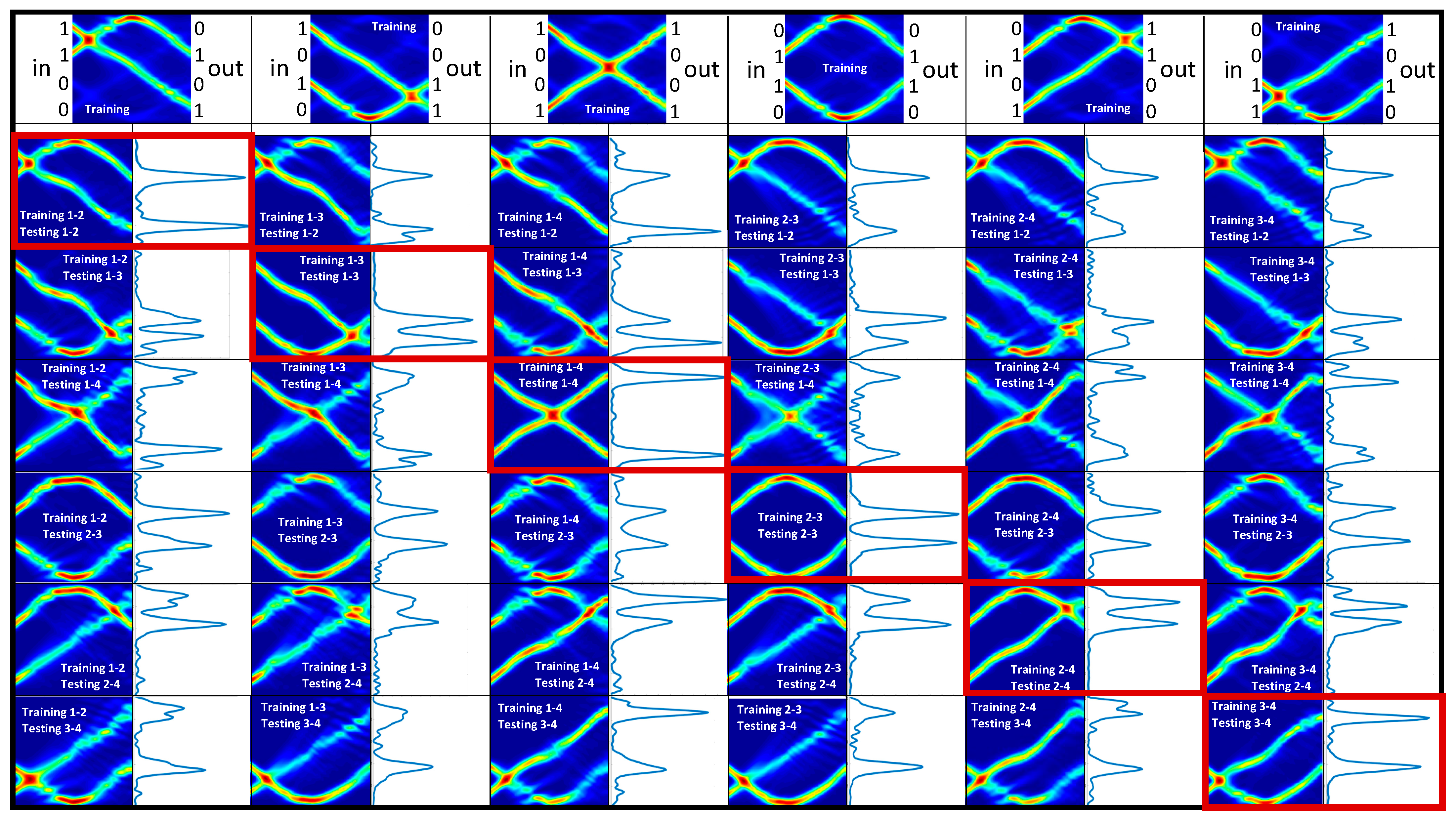
6.1.1. 1-Digit, 4-Bit Numbers
6.1.2. 2-Digit, 4-Bit Numbers
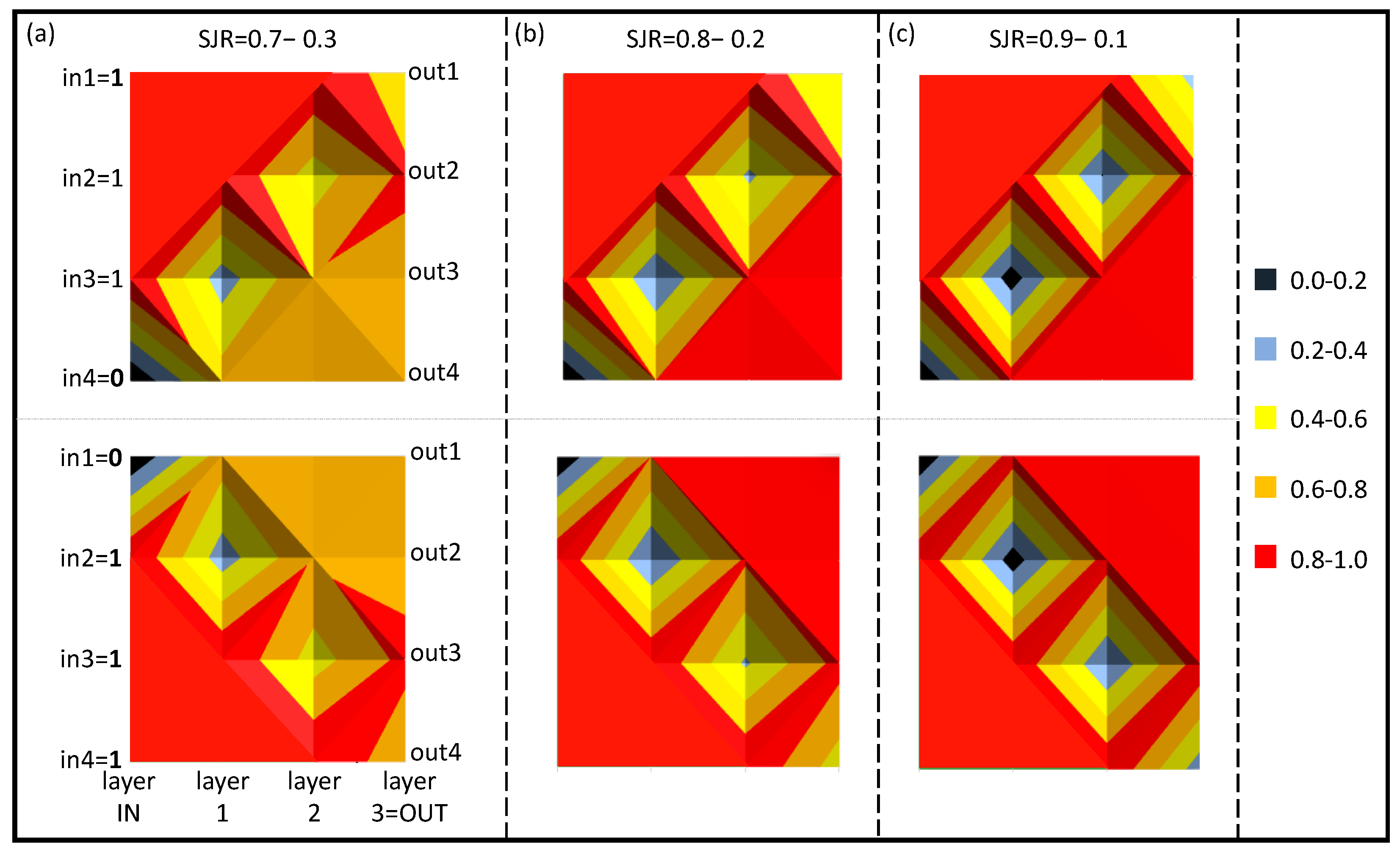
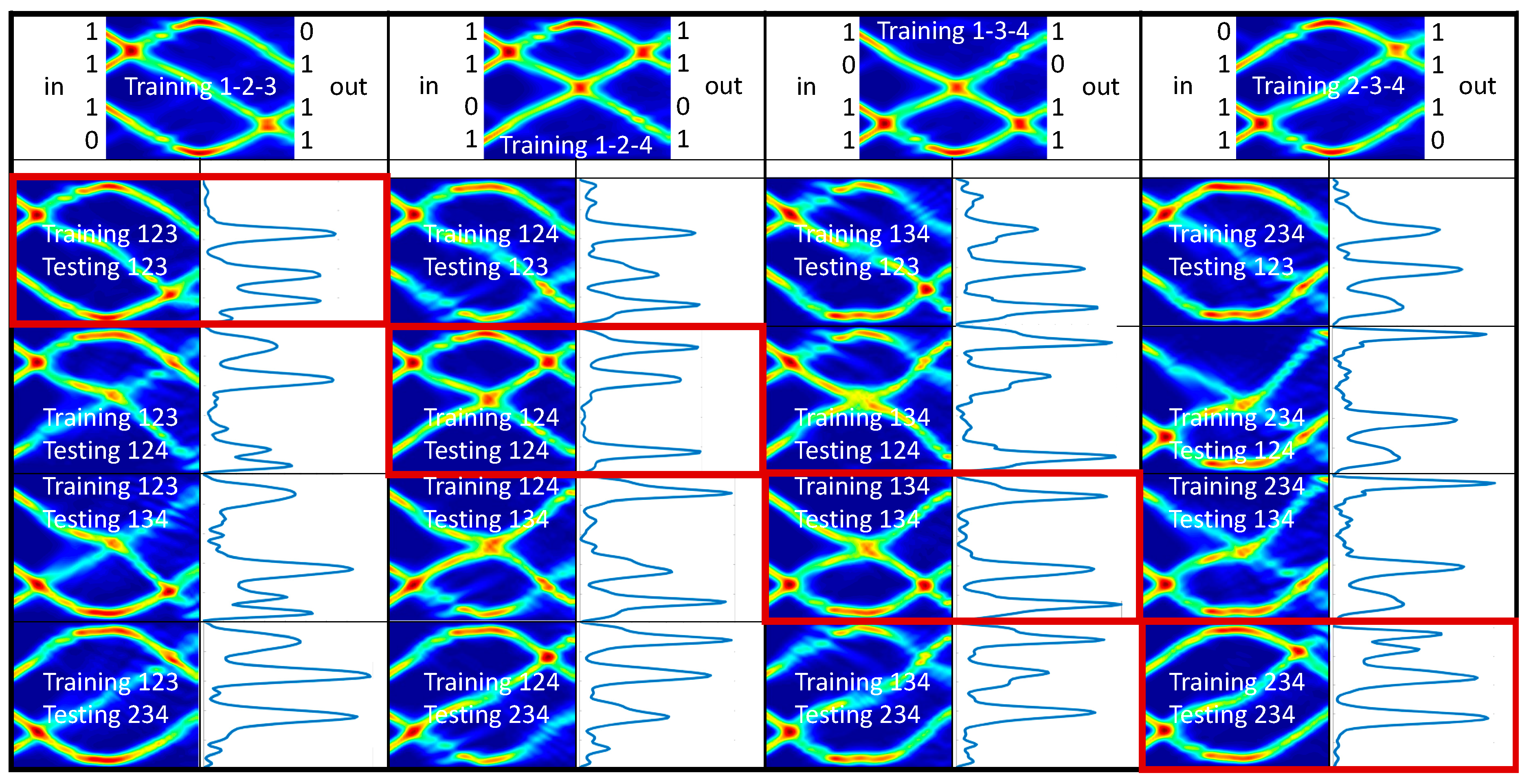
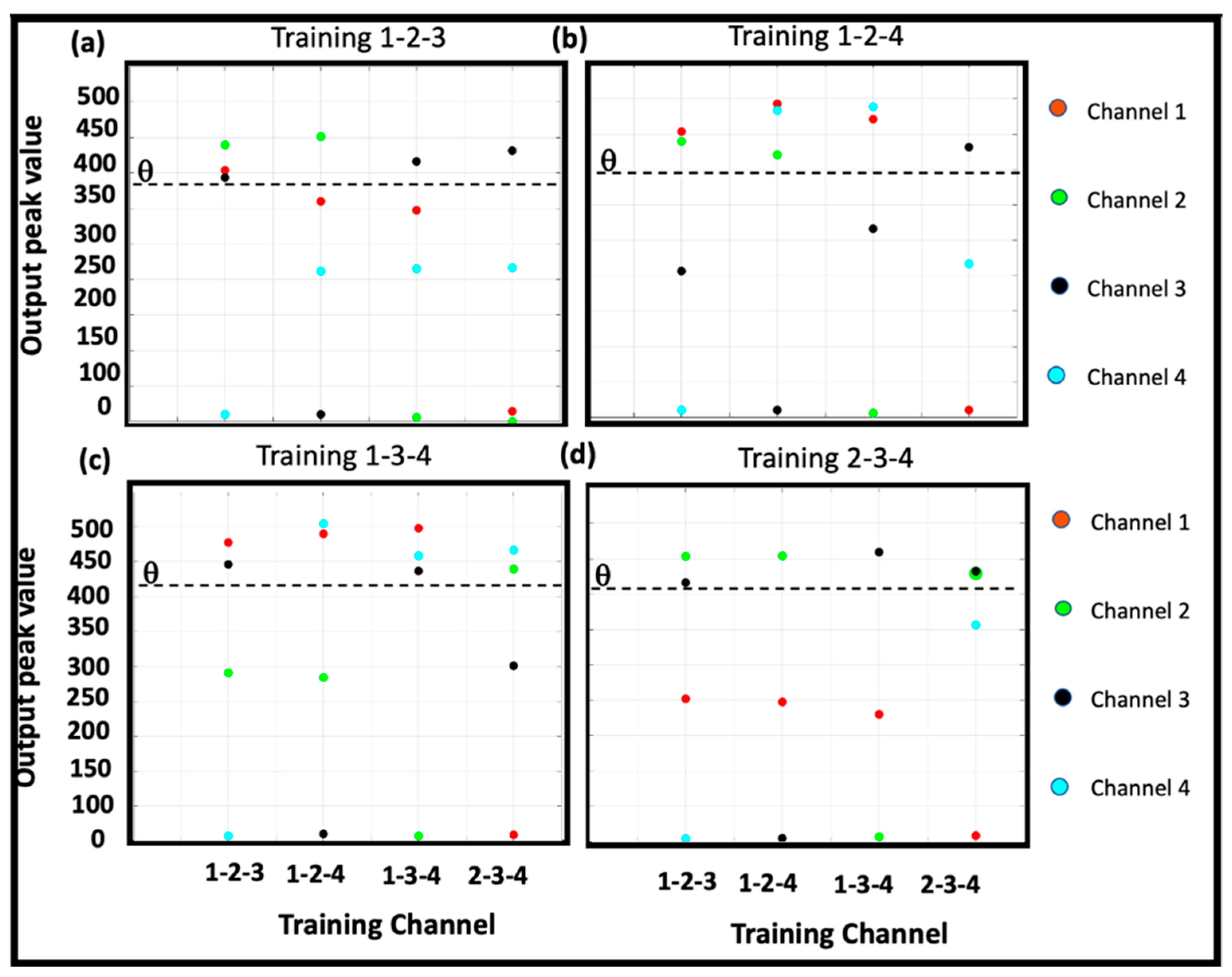
6.1.3. 3-Digit, 4-Bit Numbers
6.2. Materials and Memorization
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kandel, E.R. Search of Memory; Editions Code; 2017; ISBN 978-88-7578-675-5. [Google Scholar]
- Gerstner, W.; Kistler, W.M.; Naud, R.; Paninski, L. Neuronal Dynamics: From Single Neurons to Networks and Models of Cognition; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Denz, C. Optical Neural Networks; Tschudi, T., Ed.; Springer International Publisher: Wiesbaden, Germany, 1998. [Google Scholar] [CrossRef]
- Goodfellow, I.J.; Bengio, Y.; Courville, A. Deep learning. Genet. Program. Evolvable Mach. 2018, 19, 305–307. [Google Scholar] [CrossRef]
- Bile, A.; Tari, H.; Grinde, A.; Frasca, F.; Siani, A.M.; Fazio, E. Novel Model Based on Artificial Neural Networks to Predict Short-Term Temperature Evolution in Museum Environment. Sensors 2022, 22, 615. [Google Scholar] [CrossRef]
- Schuman, C.D.; Potok, T.E.; Patton, R.M.; Birdwell, J.D.; Dean, M.E.; Rose, G.S.; Plank, J.S. A Survey of Neuromorphic Computing and Neural Networks in Hardware. arXiv 2017, arXiv:1705.06963. [Google Scholar]
- Bile, A.; Pepino, R.; Fazio, E. Study of magnetic switch for surface plasmon-polariton circuits. AIP Adv. 2021, 11, 045222. [Google Scholar] [CrossRef]
- Tari, H.; Bile, A.; Moratti, F.; Fazio, E. Sigmoid Type Neuromorphic Activation Function Based on Saturable Absorption Behavior of Graphene/PMMA Composite for Intensity Modulation of Surface Plasmon Polariton Signals. Plasmonics 2022, 1–8. [Google Scholar] [CrossRef]
- Hesamian, M.H.; Jia, W.; He, X.; Kennedy, P. Deep Learning Techniques for Medical Image Segmentation: Achievements and Challenges. J. Digit. Imaging 2019, 32, 582–596. [Google Scholar] [CrossRef]
- Lugnan, A.; Katumba, A.; Laporte, F.; Freiberger, M.; Sackesyn, S.; Ma, C.; Gooskens, E.; Dambre, J.; Bienstman, P. Photonic neuromorphic information processing and reservoir computing. APL Photon. 2020, 5, 020901. [Google Scholar] [CrossRef]
- Scimemi, A.; Beato, M. Determining the Neurotransmitter Concentration Profile at Active Synapses. Mol. Neurobiol. 2009, 40, 289–306. [Google Scholar] [CrossRef]
- Yoshimura, T.; Roman, J.; Takahashi, Y.; Wang, W.C.V.; Inao, M.; Ishitsuka, T.; Tsukamoto, K.; Aoki, S.; Motoyoshi, K.; Sotoyam, W. Self-Organizing Lightwave Network (SOLNET) and Its Application to Film Optical Circuit Substrates. IEEE Trans. Com. Pack. Tech. 2001, 24, 500–510. [Google Scholar] [CrossRef]
- Yoshimura, T.; Inoguchi, T.; Yamamoto, T.; Moriya, S.; Teramoto, Y.; Arai, Y.; Namiki, T.; Asama, K. Self-Organized Lightwave Network Based on Waveguide Films for Three-Dimensional Optical Wiring Within Boxes. J. Lightwave Tech. 2004, 22, 2091–2101. [Google Scholar] [CrossRef]
- Xu, Z.; Kartashov, Y.V.; Torner, L. Reconfigurable soliton networks optically-induced by arrays of nondiffracting Bessel beams. Opt. Express 2005, 13, 1774–1779. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.; Kartashov, Y.V.; Torner, L.; Vysloukh, V.A. Reconfigurable directional couplers and junctions optically induced by nondiffracting Bessel beams. Opt. Lett. 2005, 30, 1180–1182. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Yoshimura, T.; Nawata, H. Micro/nanoscale self-aligned optical couplings of the self-organized lightwave network (SOLNET) formed by excitation lights from outside. Opt. Comm. 2017, 383, 119–131. [Google Scholar] [CrossRef]
- Biagio, I.; Bile, A.; Alonzo, M.; Fazio, E. Stigmergic Electronic Gates and Networks. J. Comput. Electron. 2021, 20, 2614–2621. [Google Scholar]
- Alonzo, M.; Moscatelli, D.; Bastiani, L.; Belardini, A.; Soci, C.; Fazio, E. All-Optical Reinforcement Learning In Solitonic X-Junctions. Scie. Rep. 2018, 8, 5716. [Google Scholar] [CrossRef] [PubMed]
- Bile, A.; Moratti, F.; Tari, H.; Fazio, E. Supervised and Unsupervised learning using a fully-plastic all-optical unit of artificial intelligence based on solitonic waveguides. Neural Comput. Appl. 2021, 33, 17071–17079. [Google Scholar] [CrossRef]
- Wise, F.W. Solitons divide and conquer. Nature 2018, 554, 179–180. [Google Scholar] [CrossRef]
- Hendrickson, S.M.; Foster, A.C.; Camacho, R.M.; Clader, B.D. Integrated nonlinear photonics: Emerging applications and ongoing challenges—A mini review. J. Opt. Soc. Am. B Opt. Phys. 2021, 31, 3193–3203. [Google Scholar] [CrossRef]
- Fazio, E.; Renzi, F.; Rinaldi, R.; Bertolotti, M.; Chauvet, M.; Ramadan, W.; Petris, A.; Vlad, V.I. Screening-photovoltaic bright solitons in lithium niobate and associated single-mode waveguides. Appl. Phys. Lett. 2004, 85, 2193–2195. [Google Scholar] [CrossRef]
- Jäger, R.; Gorza, S.P.; Cambournac, C.; Haelterman, M.; Chauvet, M. Sharp waveguide bends induced by spatial solitons. Appl. Phys. Lett. 2006, 88, 061117. [Google Scholar] [CrossRef]
- Fazio, E.; Alonzo, M.; Belardini, A. Addressable Refraction and Curved Soliton Waveguides Using Electric Interfaces. Appl. Sci. 2019, 9, 347. [Google Scholar] [CrossRef]
- Alonzo, M.; Soci, C.; Chauvet, M.; Fazio, E. Solitonic waveguide reflection at an electric interface. Opt. Expr. 2019, 27, 20273–20281. [Google Scholar] [CrossRef] [PubMed]
- Pettazzi, F.; Coda, V.; Fanjoux, G.; Chauvet, M.; Fazio, E. Dynamic of second harmonic generation in photovoltaic photorefractive quadratic medium. J. Opt. Soc. Am. B 2010, 27, 1–9. [Google Scholar] [CrossRef]
- Chauvet, M.; Bassignot, F.; Henrot, F.; Devaux, F.; Gauthier-Manuel, L.; Maillotte, H.; Ulliac, G.; Sylvain, B. Fast-beam self-trapping in LiNbO3 films by pyroelectric effect. Opt. Lett. 2015, 40, 1258–1261. [Google Scholar] [CrossRef] [PubMed]
- Bile, A.; Chauvet, M.; Tari, H.; Fazio, E. Addressable photonic neuron using solitonic X-junctions in Lithium Niobate thin films. Opt. Lett. submitted.
- Bile, A.; Chauvet, M.; Tari, H.; Fazio, E. All-optical erasing of photorefractive solitonic channels in Lithium Niobate thin films. Opt. Lett. submitted.
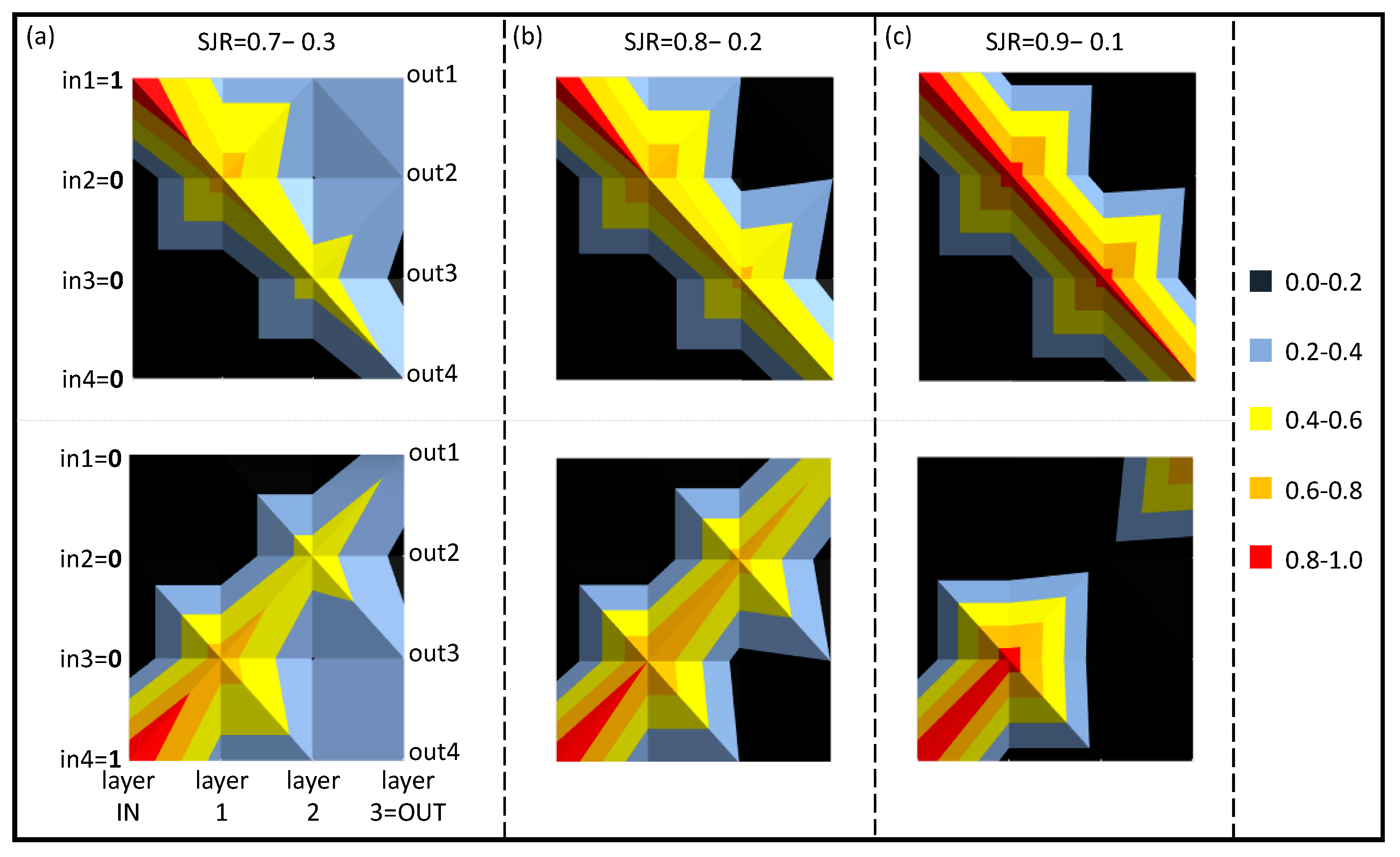


| SAT | SJR: Single Junction Ratio |
|---|---|
| 1 | 0.7−0.3 |
| 2 | 0.8−0.2 |
| 3 | 0.9−0.1 |
| (a) | Single Junction Ratio: 0.7−0.3 | (b) | Single Junction Ratio: 0.8−0.2 | (c) | Single Junction Ratio: 0.9−0.1 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| channel | 1 | 2 | 3 | 4 | channel | 1 | 2 | 3 | 4 | channel | 1 | 2 | 3 | 4 | ||
| INPUT | 1 | 0 | 0 | 0 | INPUT | 1 | 0 | 0 | 0 | INPUT | 1 | 0 | 0 | 0 | ||
| OUTPUT | 0.224 | 0.274 | 0.134 | 0.368 | OUTPUT | 0.132 | 0.198 | 0.089 | 0.581 | OUTPUT | 0.054 | 0.109 | 0.040 | 0.797 | ||
| INPUT | 0 | 1 | 0 | 0 | INPUT | 0 | 1 | 0 | 0 | INPUT | 0 | 1 | 0 | 0 | ||
| OUTPUT | 0.251 | 0.524 | 0.056 | 0.169 | OUTPUT | 0.133 | 0.670 | 0.003 | 0.193 | OUTPUT | 0.063 | 0.837 | 0.000 | 0.100 | ||
| INPUT | 0 | 0 | 1 | 0 | INPUT | 0 | 0 | 1 | 0 | INPUT | 0 | 0 | 1 | 0 | ||
| OUTPUT | 0.169 | 0.056 | 0.505 | 0.271 | OUTPUT | 0.193 | 0.003 | 0.670 | 0.133 | OUTPUT | 0.100 | 0.000 | 0.837 | 0.063 | ||
| INPUT | 0 | 0 | 0 | 1 | INPUT | 0 | 0 | 0 | 1 | INPUT | 0 | 0 | 0 | 1 | ||
| OUTPUT | 0.368 | 0.134 | 0.271 | 0.227 | OUTPUT | 0.581 | 0.089 | 0.195 | 0.135 | OUTPUT | 0.796 | 0.041 | 0.108 | 0.055 | ||
| (a) | Single Junction Ratio: 0.7−0.3 | (b) | Single Junction Ratio: 0.8−0.2 | (c) | Single Junction Ratio: 0.9−0.1 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| channel | 1 | 2 | 3 | 4 | channel | 1 | 2 | 3 | 4 | channel | 1 | 2 | 3 | 4 | ||
| INPUT | 1 | 0 | 0 | 1 | INPUT | 1 | 0 | 0 | 1 | INPUT | 1 | 0 | 0 | 1 | ||
| OUTPUT | 0.5747 | 0.4122 | 0.4285 | 0.5846 | OUTPUT | 0.6641 | 0.3066 | 0.3345 | 0.6948 | OUTPUT | 0.7849 | 0.1639 | 0.1977 | 0.8536 | ||
| INPUT | 0 | 1 | 1 | 0 | INPUT | 0 | 1 | 1 | 0 | INPUT | 0 | 1 | 1 | 0 | ||
| OUTPUT | 0.4212 | 0.586 | 0.5717 | 0.4211 | OUTPUT | 0.3236 | 0.6887 | 0.666 | 0.3218 | OUTPUT | 0.1851 | 0.827 | 0.8063 | 0.1816 | ||
| INPUT | 1 | 0 | 1 | 0 | INPUT | 1 | 0 | 1 | 0 | INPUT | 1 | 0 | 1 | 0 | ||
| OUTPUT | 0.3902 | 0.336 | 0.6588 | 0.615 | OUTPUT | 0.3314 | 0.2209 | 0.7648 | 0.7029 | OUTPUT | 0.1933 | 0.1017 | 0.8785 | 0.8266 | ||
| INPUT | 0 | 1 | 0 | 1 | INPUT | 0 | 1 | 0 | 1 | INPUT | 0 | 1 | 0 | 1 | ||
| OUTPUT | 0.6121 | 0.6637 | 0.3377 | 0.3865 | OUTPUT | 0.6999 | 0.7731 | 0.2227 | 0.3043 | OUTPUT | 0.8264 | 0.8869 | 0.1029 | 0.1839 | ||
| INPUT | 1 | 1 | 0 | 0 | INPUT | 1 | 1 | 0 | 0 | INPUT | 1 | 1 | 0 | 0 | ||
| OUTPUT | 0.508 | 0.792 | 0.2054 | 0.4946 | OUTPUT | 0.3635 | 0.8366 | 0.1482 | 0.6518 | OUTPUT | 0.1944 | 0.9057 | 0.0787 | 0.8212 | ||
| INPUT | 0 | 0 | 1 | 1 | INPUT | 0 | 0 | 1 | 1 | INPUT | 0 | 0 | 1 | 1 | ||
| OUTPUT | 0.4946 | 0.2054 | 0.7704 | 0.5296 | OUTPUT | 0.6518 | 0.1482 | 0.8086 | 0.3915 | OUTPUT | 0.8213 | 0.0787 | 0.8804 | 0.2196 | ||
| (a) | Single Junction Ratio: 0.7−0.3 | (b) | Single Junction Ratio: 0.8−0.2 | (c) | Single Junction Ratio: 0.9−0.1 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| channel | 1 | 2 | 3 | 4 | channel | 1 | 2 | 3 | 4 | channel | 1 | 2 | 3 | 4 | ||
| INPUT | 1 | 1 | 1 | 0 | INPUT | 1 | 1 | 1 | 0 | INPUT | 1 | 1 | 1 | 0 | ||
| OUTPUT | 0.6581 | 0.8561 | 0.7274 | 0.7583 | OUTPUT | 0.4993 | 0.8724 | 0.807 | 0.8213 | OUTPUT | 0.2856 | 0.9174 | 0.8994 | 0.8975 | ||
| INPUT | 0 | 1 | 1 | 1 | INPUT | 0 | 1 | 1 | 1 | INPUT | 0 | 1 | 1 | 1 | ||
| OUTPUT | 0.7653 | 0.7273 | 0.8416 | 0.6658 | OUTPUT | 0.8315 | 0.8083 | 0.8508 | 0.5094 | OUTPUT | 0.9078 | 0.9012 | 0.8952 | 0.2958 | ||
| INPUT | 1 | 0 | 1 | 1 | INPUT | 1 | 0 | 1 | 1 | INPUT | 1 | 0 | 1 | 1 | ||
| OUTPUT | 0.7305 | 0.4804 | 0.9308 | 0.8583 | OUTPUT | 0.8067 | 0.3503 | 0.959 | 0.884 | OUTPUT | 0.8973 | 0.1888 | 0.983 | 0.9309 | ||
| INPUT | 1 | 1 | 0 | 1 | INPUT | 1 | 1 | 0 | 1 | INPUT | 1 | 1 | 0 | 1 | ||
| OUTPUT | 0.8445 | 0.9342 | 0.4924 | 0.7288 | OUTPUT | 0.8591 | 0.9612 | 0.3675 | 0.8122 | OUTPUT | 0.8913 | 0.9827 | 0.2056 | 0.9205 | ||
| Material | LiNbO3 |
|---|---|
| linear ordinary refractive index | noo = 2.3247 |
| linear extraordinary refractive index | noe = 2.2355 |
| electro-optic coefficient | r33 = 3.1 × 10−11 m/V |
| electric bias | Ebias = 36 kV/cm |
| writing beam wavelength | 532 nm |
| writing beam power | 10 μW |
| signal beam | 632 nm |
| signal beam power | 0.5 μW |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bile, A.; Tari, H.; Fazio, E. Episodic Memory and Information Recognition Using Solitonic Neural Networks Based on Photorefractive Plasticity. Appl. Sci. 2022, 12, 5585. https://doi.org/10.3390/app12115585
Bile A, Tari H, Fazio E. Episodic Memory and Information Recognition Using Solitonic Neural Networks Based on Photorefractive Plasticity. Applied Sciences. 2022; 12(11):5585. https://doi.org/10.3390/app12115585
Chicago/Turabian StyleBile, Alessandro, Hamed Tari, and Eugenio Fazio. 2022. "Episodic Memory and Information Recognition Using Solitonic Neural Networks Based on Photorefractive Plasticity" Applied Sciences 12, no. 11: 5585. https://doi.org/10.3390/app12115585
APA StyleBile, A., Tari, H., & Fazio, E. (2022). Episodic Memory and Information Recognition Using Solitonic Neural Networks Based on Photorefractive Plasticity. Applied Sciences, 12(11), 5585. https://doi.org/10.3390/app12115585








