Semianalytical Lower-Bound Limit Analysis of Domes and Vaults
Abstract
:Featured Application
Abstract
1. Introduction
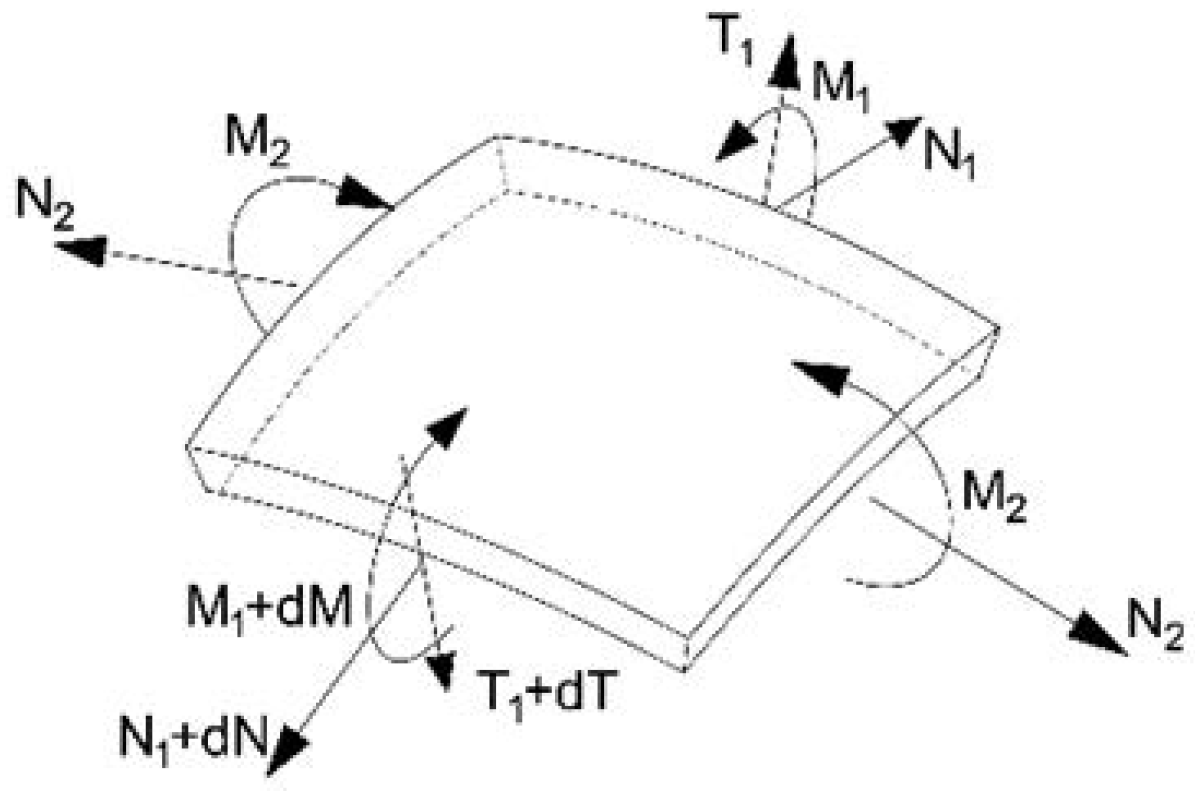
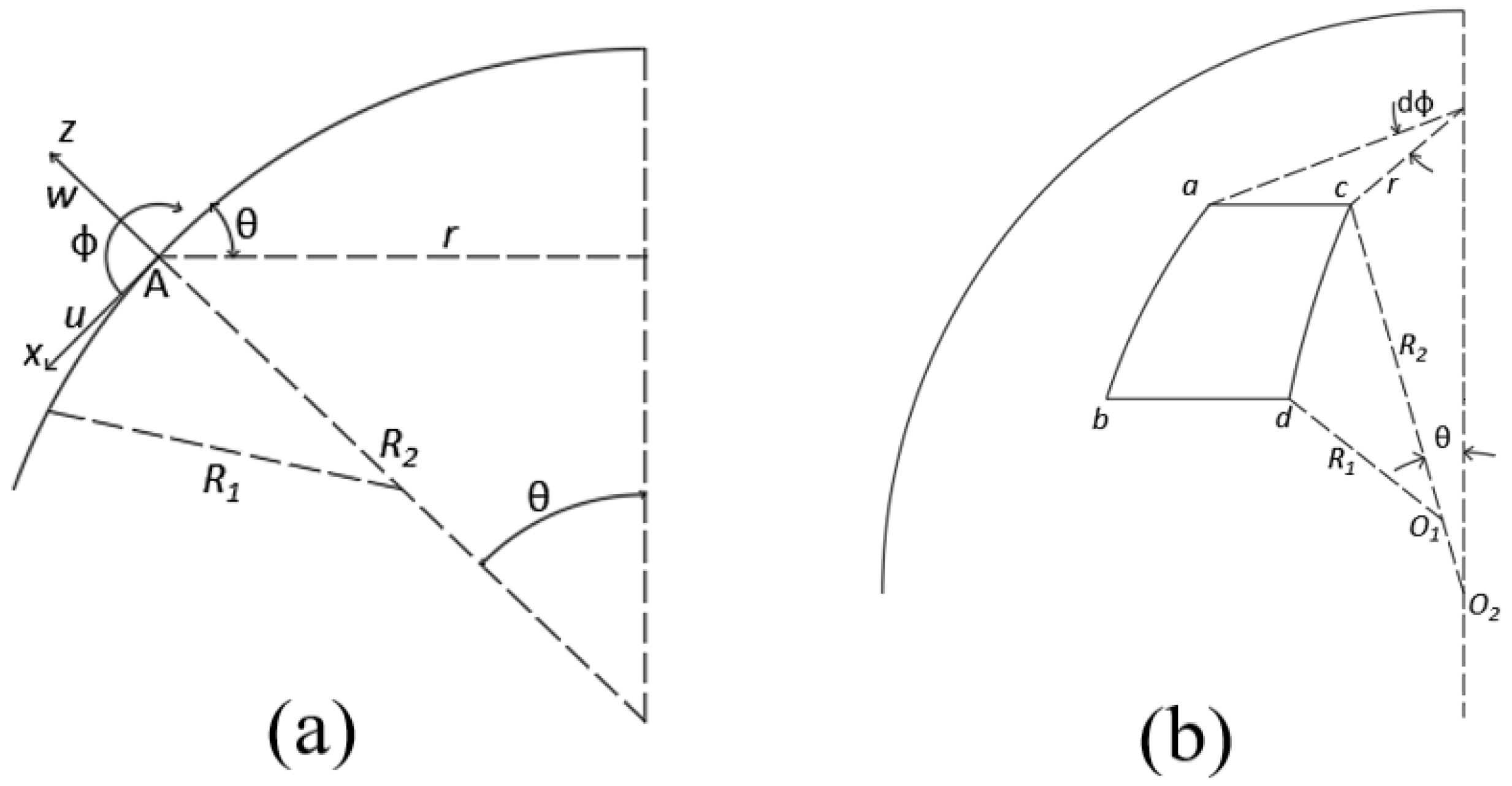
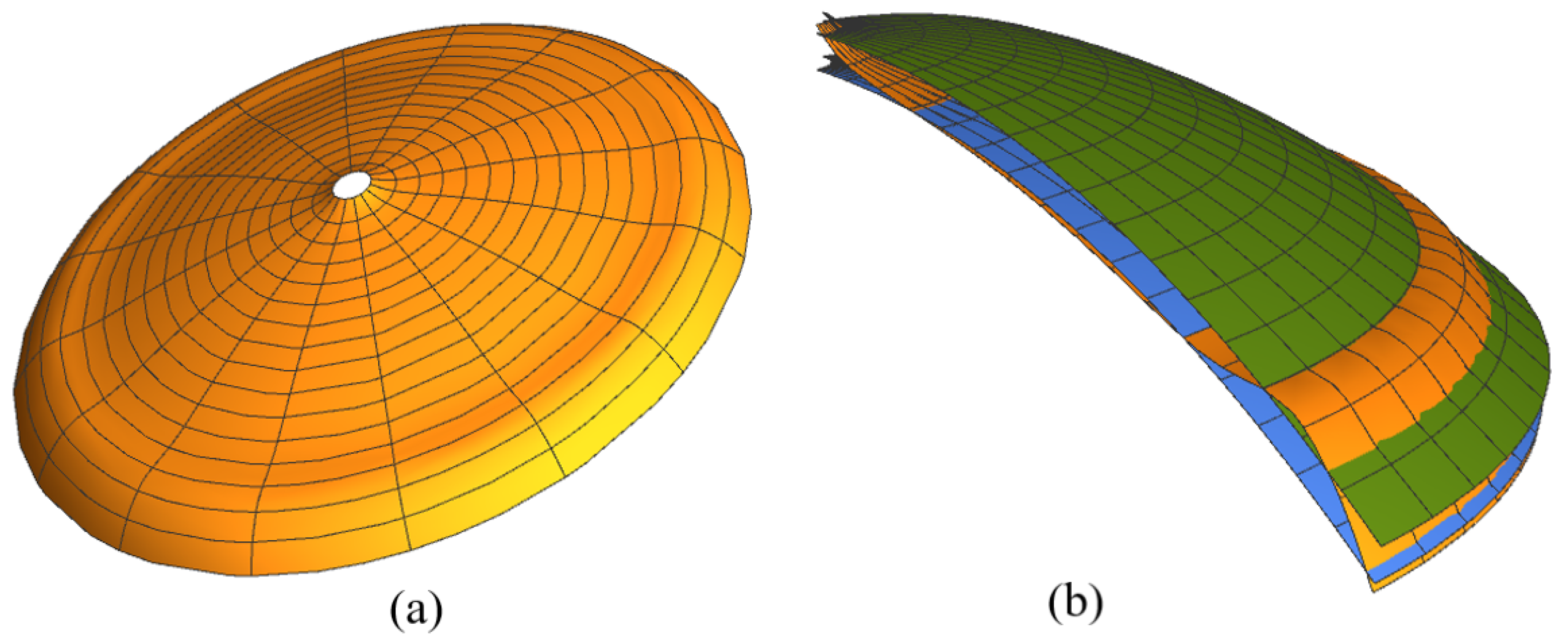
2. Equilibrium and Self-Equilibrium of Domes
3. Constitutive Equations
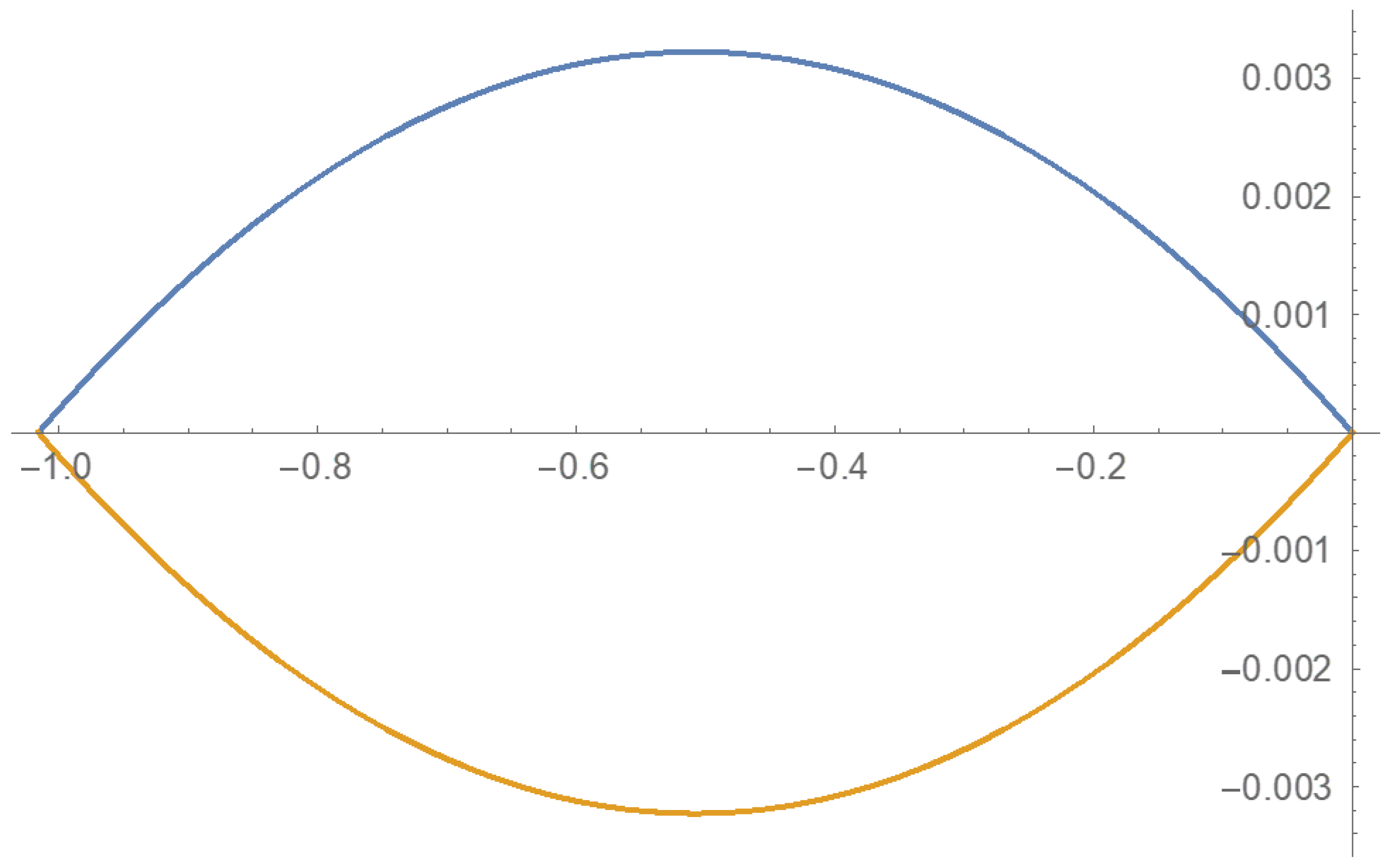
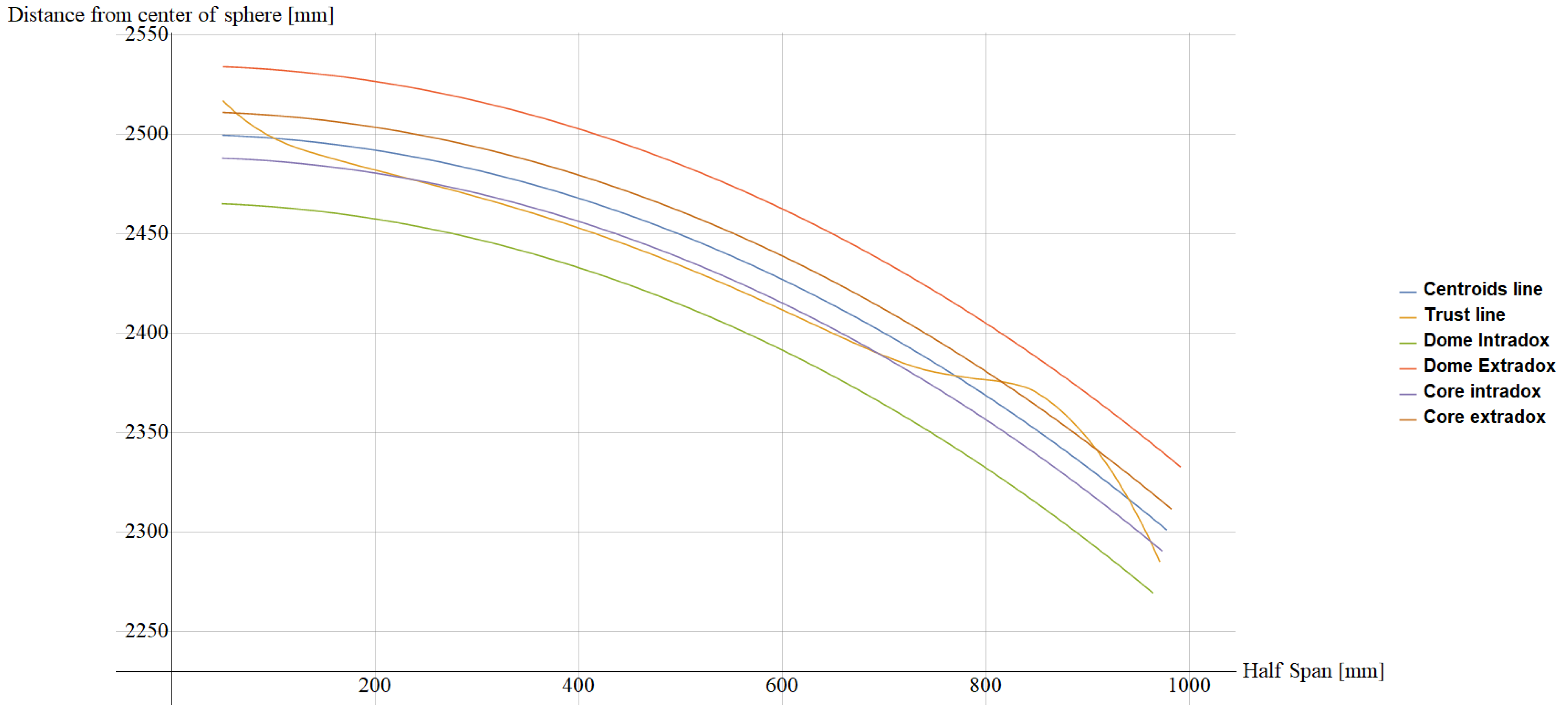
4. Case Study: Concrete Caps Collapse Load
FEM Elastic Solution
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Milani, E.; Milani, G.; Tralli, A. Limit analysis of masonry vaults by means of curved shell finite elements and homogenization. Int. J. Solids Struct. 2008, 45, 5258–5288. [Google Scholar] [CrossRef]
- Block, P.; Ciblac, T.; Ochsendorf, J. Real-time limit analysis of vaulted masonry buildings. Comput. Struct. 2006, 84, 1841–1852. [Google Scholar] [CrossRef]
- Block, P.; Ochsendorf, J. Thrust network analysis: A new methodology for three-dimensional equilibrium. J. Int. Assoc. Shell Spat. Struct. 2007, 48, 167–173. [Google Scholar]
- Block, P.; Lachauer, L. Three-dimensional (3D) equilibrium analysis of gothic masonry vaults. Int. J. Archit. Herit. 2014, 8, 826301. [Google Scholar] [CrossRef]
- Avelino, R.M.; Iannuzzo, A.; Mele, T.V.; Block, P. Assessing the safety of vaulted masonry structures using thrust network analysis. Comput. Struct. 2021, 257, 106647. [Google Scholar] [CrossRef]
- Save, M. Limit analysis and design of containment vessels. Nucl. Eng. Des. 1984, 79, 343–361. [Google Scholar] [CrossRef]
- Moncarz, P.D.; Griffith, M.; Noakowski, P. Collapse of a Reinforced Concrete Dome in a Wastewater Treatment Plant Digester Tank. J. Perform. Constr. Facil. 2007, 21, 4–12. [Google Scholar] [CrossRef]
- Teng, J.G.; Rotter, J.M. Geometrically and materially nonlinear analysis of reinforced concrete shells of revolution. Comput. Struct. 1992, 42, 327–340. [Google Scholar] [CrossRef]
- Zingoni, A.; Enoma, N. Strength and stability of spherical-conical shell assemblies under external hydrostatic pressure. Thin-Walled Struct. 2020, 146, 106472. [Google Scholar] [CrossRef]
- Zingoni, A. Stress and buckling resistance of dual-purpose concrete shells. Thin-Walled Struct. 2022, 170, 108596. [Google Scholar] [CrossRef]
- Stockdale, G.; Milani, G. Diagram based assessment strategy for first-order analysis of masonry arches. J. Build. Eng. 2019, 22, 122–129. [Google Scholar] [CrossRef]
- Mercuri, M.; Pathirage, M.; Gregori, A.; Cusatis, G. Masonry vaulted structures under spreading supports: Analyses of fracturing behavior and size effect. J. Build. Eng. 2022, 45, 103396. [Google Scholar] [CrossRef]
- Chang, Z.T.; Bradford, M.A.; Gilbert, R.I. Short-term behaviour of shallow thin-walled concrete dome under uniform external pressure. Thin-Walled Struct. 2011, 49, 112–120. [Google Scholar] [CrossRef]
- Vandepitte, D.; Lagae, G. Buckling of Spherical Domes Made of Microconcrete and Creep Buckling of Such Domes Under Long-term Loading. In Proceedings of the Inelastic Behaviour of Plates and Shells, Rio de Janeiro, Brazil, 5–9 August 1985; Bevilacqua, L., Feijóo, R., Valid, R., Eds.; Springer: Berlin/Heidelberg, Germany, 1986; pp. 291–311. [Google Scholar]
- Zoelly, R. Uber ein Knickungs Problem an der Kugelschale. Ph.D. Thesis, ETH Druck von Zurker & Furrer, Zürich, Switzerland, 1915. [Google Scholar]
- Palladino, S.; Esposito, L.; Ferla, P.; Totaro, E.; Zona, R.; Minutolo, V. Experimental and numerical evaluation of residual displacement and ductility in ratcheting and shakedown of an aluminum beam. Appl. Sci. 2020, 10, 3610. [Google Scholar] [CrossRef]
- Zona, R.; Esposito, L.; Ferla, P.; Palladino, S.; Totaro, E.; Minutolo, V. Lower bound limit analysis of parabolic domes based on spherical analytical solution. Int. J. Adv. Res. Eng. Technol. 2020, 11, 59–79. [Google Scholar] [CrossRef]
- Zona, R.; Ferla, P.; Minutolo, V. Limit analysis of conical and parabolic domes based on semi-analytical solution. J. Build. Eng. 2021, 44, 103271. [Google Scholar] [CrossRef]
- Lubliner, J. Plasticity Theory; Macmillan Pub Co.: New York, NY, USA, 1990. [Google Scholar]
- Chang, Z.T.; Bradford, M.A.; Gilbert, R.I. Limit analysis of local failure in shallow spherical concrete caps subjected to uniform radial pressure. Thin-Walled Struct. 2010, 48, 373–378. [Google Scholar] [CrossRef]
- Timoshenko, S.P. Theory of Plates and Shells, 1st ed.; McGraw-Hill: New York, NY, USA, 1964; Volume 1. [Google Scholar]
- Heyman, J. The stone skeleton. Int. J. Solids Struct. 1966, 2, 249–279. [Google Scholar] [CrossRef]
- O’Dwyer, D. Funicular analysis of masonry vaults. Comput. Struct. 1999, 73, 187–197. [Google Scholar] [CrossRef]
- Clementi, F.; Gazzani, V.; Poiani, M.; Lenci, S. Assessment of seismic behaviour of heritage masonry buildings using numerical modelling. J. Build. Eng. 2016, 8, 29–47. [Google Scholar] [CrossRef]





| Specimen | Thickness | Radius | Strength | Young’s Modulus | (Ex) | BL | (CL) | SAM | (Ex)/SAM |
|---|---|---|---|---|---|---|---|---|---|
| K4 | 7.12 | 2431 | 60 | 30,356 | 142 | 305 | 128 | 147 | 1.035 |
| K6 | 7.07 | 2438 | 46 | 25,667 | 118 | 254 | 97 | 113 | 0.958 |
| K7 | 6.91 | 2428 | 59 | 22,799 | 113 | 217 | 122 | 111 | 0.982 |
| K9 | 6.98 | 2450 | 66 | 29,013 | 137 | 276 | 137 | 127 | 0.927 |
| K33 | 6.91 | 2469 | 51 | 33,652 | 119 | 310 | 104 | 120 | 1.008 |
| K36 | 6.9 | 2479 | 76 | 31,527 | 132 | 286 | 154 | 145 | 1.098 |
| K38 | 6.86 | 2524 | 65 | 29,269 | 113 | 255 | 129 | 121 | 1.071 |
| KN12 | 7.07 | 2538 | 64 | 26,126 | 116 | 240 | 130 | 125 | 1.078 |
| KN15 | 6.94 | 2554 | 66 | 26,537 | 118 | 230 | 131 | 125 | 1.059 |
| KN19 | 6.99 | 2537 | 71 | 34,230 | 129 | 304 | 143 | 136 | 1.054 |
| KN24 | 7.1 | 2560 | 65 | 32,176 | 126 | 296 | 132 | 128 | 1.016 |
| KN26 | 7.06 | 2546 | 59 | 26,766 | 102 | 242 | 119 | 105 | 1.029 |
| KN27 | 7.09 | 2557 | 62 | 30,523 | 119 | 276 | 125 | 122 | 1.025 |
| KN28 | 7.01 | 2540 | 61 | 30,033 | 118 | 269 | 123 | 118 | 1 |
| KN29 | 6.76 | 2535 | 58 | 31,449 | 118 | 263 | 113 | 105 | 0.89 |
| KN30 | 6.98 | 2515 | 58 | 32,958 | 126 | 298 | 132 | 111 | 0.881 |
| KN31 | 7.04 | 2500 | 65 | 33,825 | 135 | 306 | 119 | 126 | 0.933 |
| KN32 | 6.93 | 2500 | 58 | 26,904 | 104 | 236 | 111 | 110 | 1.058 |
| KN33 | 7.02 | 2500 | 55 | 26,888 | 121 | 243 | 127 | 106 | 0.876 |
| KN34 | 6.94 | 2500 | 62 | 28,962 | 131 | 254 | 128 | 118 | 0.901 |
| KN35 | 6.83 | 2500 | 63 | 34,208 | 149 | 292 | 122 | 146 | 0.98 |
| KN36 | 6.98 | 2500 | 61 | 34,760 | 155 | 310 | 124 | 147 | 0.948 |
| KN37 | 6.89 | 2500 | 61 | 33,326 | 118 | 290 | 119 | 114 | 0.966 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zona, R.; Esposito, L.; Palladino, S.; Totaro, E.; Minutolo, V. Semianalytical Lower-Bound Limit Analysis of Domes and Vaults. Appl. Sci. 2022, 12, 9155. https://doi.org/10.3390/app12189155
Zona R, Esposito L, Palladino S, Totaro E, Minutolo V. Semianalytical Lower-Bound Limit Analysis of Domes and Vaults. Applied Sciences. 2022; 12(18):9155. https://doi.org/10.3390/app12189155
Chicago/Turabian StyleZona, Renato, Luca Esposito, Simone Palladino, Elena Totaro, and Vincenzo Minutolo. 2022. "Semianalytical Lower-Bound Limit Analysis of Domes and Vaults" Applied Sciences 12, no. 18: 9155. https://doi.org/10.3390/app12189155
APA StyleZona, R., Esposito, L., Palladino, S., Totaro, E., & Minutolo, V. (2022). Semianalytical Lower-Bound Limit Analysis of Domes and Vaults. Applied Sciences, 12(18), 9155. https://doi.org/10.3390/app12189155







