Abstract
An accurate model for the prediction of the rheological behavior of surrounding rocks is essential to the designing of rock bolts for tunnels under squeezing conditions. Our understanding of the state of the art suggests that the rheology of rock consists of the transient, the steady-state, and the accelerated regimes. Thus, a visco-elastic-plastic rheological model, namely the Komamura-Huang-Bingham model, was developed. The model used the Drucker-Prager yield criterion in order to consider the effects of the intermediate principal stress on the strength of the rock mass. The developed model was implemented in the framework of finite element simulations. It was validated by comparing the simulation results with the on-site monitoring data. The focus of the simulations was on the mechanical behavior of the rock bolts and the surrounding rock mechanics during the construction of the tunnel. A sensitivity analysis was performed with respect to the length of the bolts and the stress-to-strength ratio of the rock was performed. It was shown that increasing the length of the bolts up to 9 m results in a reduction in rock deformation. This critical value of the bolts’ length is approximately equal to the diameter of the investigated tunnel. A further increase in the length results in an insignificant reduction in the deformation of the surrounding rock. In the case of the Class A and B squeezing conditions suggested by Hoek, the deformation of the surrounding rock is insensitive to the length of the bolts. The elongation of the bolts does not change considerably with time, which is in contrast to the Class C and D squeezing conditions. The extent of the plastic zone is related to time and in situ stress but is independent of the length of the bolts. This is consistent with the characteristics of the nonlinear rheology of rock mass.
1. Introduction
As the construction of mountain tunnels continues to increase, the safety of construction in weak surrounding rock has caused significant concerns in the tunnel engineering community [1,2,3,4]. Among these concerns are large deformation problems resulting from the large amounts of ground stress in soft rock tunnels. This problem has become prominent because the increase in deformation caused by the nonlinear rheological behavior of the surrounding squeezing rock results in a reduced amount of space for running trains, delayed construction, and increased construction materials’ consumption and cost. In some cases, it also seriously affects the long-term safe operation and maintenance of the tunnel [5,6,7,8,9]. These safety issues have been observed in various tunnel projects, e.g., the Muzhailing Tunnel of the Gannan Weiwu Expressway and the Dali West Water Conveyance Tunnel of the Central Yunnan Water Diversion Project. Site monitoring results have suggested that deformation can be as large as 1500 mm when it was converged [10]. Therefore, it is necessary to investigate possible engineering remediation measures to control squeezing rock deformation. To this end, the rheological behavior of the squeezing rock must be considered in the design activities to create tunnel supports.
Rheological models are integral for describing rock deformation during tunnel excavation. Most of the models combine the basic elements of other models to describe the viscoelastic properties of squeezing rock [11,12,13]. They consider both the transient and the steady-state regimes of rock rheology. However, many engineering practices and laboratory test studies have shown that soft rocks exhibit nonlinear rheology under certain stress levels [14,15,16,17,18,19,20]. In other words, there is a third regime, i.e., accelerated rock rheology regimes. Therefore, a complete nonlinear rheological model should consider the transient, the steady-state, and the accelerated regimes of rock rheology [21,22]. The constitutive model [23] for viscoplastic elements in the acceleration stage of nonlinear rheology considers the two-fold criteria (such as the Mohr–Coulomb criterion) as the threshold of the acceleration regime. However, experimental and theoretical studies have shown that the intermediate principal stress significantly influences the strength of rock mass [24,25,26,27,28]. This provides the motivation for the present study, in which a non-linear rheological model is combined with the Drucker-Prager yield criterion. The latter allows for the consideration of the effect of the intermediate principal stress on the strength of rock mass.
The aim of the present paper is to determine the length of the rock bolts for tunnels by considering the nonlinear rheological behavior of squeezing rock. It is well known that rock bolts represent a popular permanent support measure to increase the strength of surrounding soft rock. Thus, they are helpful to control the large deformation of the surrounding rock and to improve the stability of the excavated surface during the excavation of tunnels [29,30]. However, the effects of the rock bolts on the long-term stability of the surrounding rock is a new topic. A few scholars have attempted to investigate the mechanical behavior of rock mass containing bolts [31,32]. However, it was still challenging to determine the length of the rock bolts because the constitutive models that were developed excluded accelerated rock rheology regimes. Safety accidents often occur due to the wrong choice of bolt length. In this context, a nonlinear visco-elastic-plastic constitutive model for rock, referred to as the Komamura-Huang-Bingham model, combined with the Drucker-Prager (DP) yield criterion is proposed in the present paper. Numerical simulations adopting the proposed rheological model are performed and there is a focus on sensitivity analysis with respect to the length of the bolts and the ground stress.
The numerical simulations in this study take place in the Central Yunnan Water Delivery Project in China. This project starts at Shigu and ends at Mengzi. A schematic diagram of the project layout is shown in Figure 1. Its total length is equal to 664 km. The DLⅡ34+481~34+768 section of the Shizishan Tunnel is considered in this paper, as shown in the enlarged view at the bottom left of Figure 1. The length of the tunnel is equal to 287 m. The burial depth ranges from 460 to 490 m, as shown in Figure 2. According to the geological data, the DLⅡ34+481~34+768 section of the Shizishan Tunnel passes through the Chenghai–Binchuan fault zone (F16), also known as the Q3 active fault zone, which affects the seismic and shear resistance of the transacting tunnel. This tunnel’s red bed mudstone has low strength and relatively poor stability. The strength-to-stress ratio of the rock amounts to 0.26. Hence, this tunnel has high in situ stress and may experience potentially significant deformation problems during excavation. The rock mass properties of the red bed stone of this tunnel are summarized in Table 1.
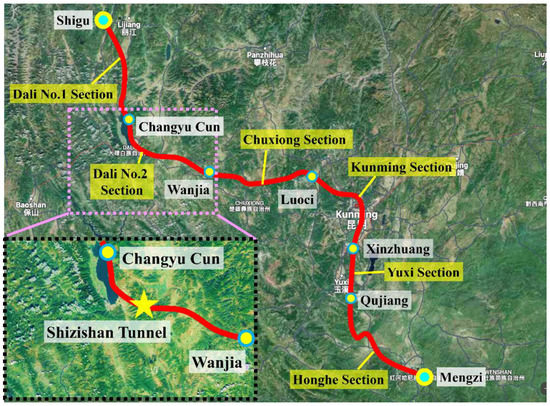
Figure 1.
Schematic layout diagram of the Central Yunnan Water Diversion Project (Dali Section II).
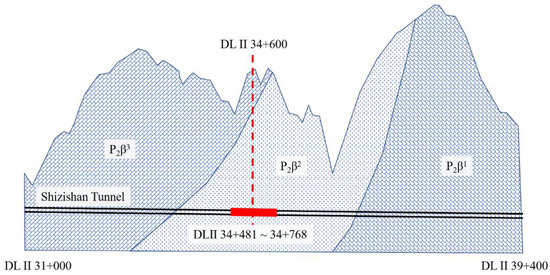
Figure 2.
The profile of physical and mechanical indicators of the rock mass in section DLII34+481~34+768.

Table 1.
Mechanical properties of the rock mass of the Shizishan Tunnel.
The rest of the paper is organized as follows: In Section 2, the visco-elastic-plastic model is presented. Section 3 is devoted to the setup of the numerical model. The focus of Section 4 is on the sensitivity analysis concerning the mechanical responses of the rock bolts and the rock mass after the tunnel’s excavation. Finally, the conclusions are presented in Section 5.
2. Visco-Elastic-Plastic Constitutive Model for Squeezing Rock
2.1. Derivation of the Komamura-Huang-Bingham Model
The Komamura-Huang model is a visco-elastic-plastic model [33]. It consists of one Hooke body and two viscoelastic bodies (generalized Kelvin body) in series. It has been proven that it is useful for the simulation of the transient and the constant stages of the rheology of soft rock [34,35]. The mathematical expression for the Komamura-Huang model is given as in [33]:
where denotes the strain, denotes the time, is the initial stress, is the Hookean elasticity modulus, and denote the elastic moduli of the two generalized Kelvin body spring elements, respectively, and are the viscosity coefficients of the two generalized viscous elements of the Kelvin body, respectively.
The Komamura-Huang model excludes the accelerated regimes of rock rheology. Herein, the Bingham body, a nonlinear viscoplastic body, is combined with the Komamura-Huang model, resulting in a Komamura-Huang-Bingham model. At the level of the materials that determine rock mass, it has been demonstrated that the Komamura-Huang-Bingham model allows for all three regimes of the rock rheology to be described as in [33], and as shown in Figure 3. It is expressed as follows:
where is the viscosity coefficient of the Bingham body for the viscous element, and and represent the long-term and instantaneous strength of the Bingham body, respectively. is a function of time and the stress
where is a dimensionless constant and is the yielding time. At the condition of , the nonlinear rheology degenerates into a linear rheology, , and the strain increases at a constant rate of . At the condition of , the value of gradually decreases with time, reflecting the accelerated rheological process of the soft rock mass in a high-stress state. At the condition of , the rheological relationship for the nonlinear rheological model transforms into a linear expression. In more detail, the Komamura-Huang-Bingham model is simplified to the Komamura-Huang model.
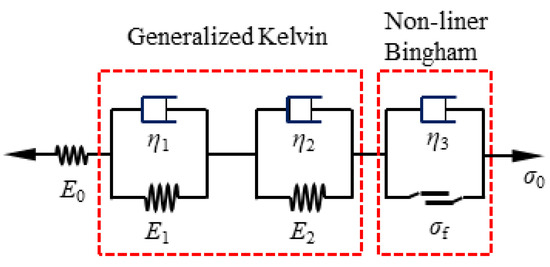
Figure 3.
One-dimensional Komamura-Huang-Bingham model.
2.2. Strain Integration Scheme of the Rheological Model
The finite element method (FEM) is a powerful numerical tool for simulating the behavior of subsurface structures under different geological and environmental conditions [11,36]. This study uses the ABAQUS software for numerical simulation, and the proposed constitutive model is implemented within the UMAT subroutine. As a result, the visco-elastic-plastic rheological model can simulate the large deformations in the soft rock mass that take place during tunnel excavation. An explicit strain integration scheme was applied to compute the strain increment. For the proposed visco-elastic-plastic constitutive model, the total strain increment () can be decomposed into the instantaneous elastic strain increment (), the viscoelastic strain increment ( and the viscoplastic strain increment ():
The elastic strain increment can be derived from Hooke’s elasticity theory:
where represents the elastic stiffness matrix of the rock mass, and is the stress increment. For the viscoelastic rheology, two Kelvin bodies are adopted in the proposed nonlinear rheological model, as shown in Figure 3. The superposition of the respective strains of the two Kelvin bodies provides the total viscoelastic strain. According to the constitutive law of the Kelvin model, the viscoelastic strain, , at a specific time-step can be obtained as
where and are the viscoelastic strains of the i-th Kelvin model at two consecutive time steps and , respectively. is the time step increment, and is the stress state exerted on the rock mass. As a result, the increment of the viscoelastic strain at a specific time step is
After the stress state () of the soft rock mass reaches the plastic yield stress state, the rock mass will experience plastic deformation. The plastic strain develops according to the yield surface of the adopted Drucker-Prager yielding criterion and the flow rule of the nonlinear Bingham body. The yield surface of the DP yielding criterion is defined as
where is the first stress invariant, is the second deviatory stress invariant, and is the cohesion of the rock mass. and are material variables related to the internal frictional angle of the rock mass:
The flow rule specifies the relationship between the plastic strain increment and the stress increment. The flow rule of the nonlinear Bingham body is adopted to compute the rate of the viscoplastic strain increment rate:
where is related to the current stress level and time, is the plastic potential function, and . is a switching function to judge whether the rock mass is in an elastic or a plastic state. If , then is equal to 0 and represents the elastic state. If , then is equal to and represents the plastic state. The associated plastic flow law is adopted in this study so that the plastic potential, , is the same as the yield function (). Hence, Equation (11) can be expressed as follows:
If the cohesion is considered constant, then the yield function, , can be expressed as a function of , , and :
Therefore, the flow vector, , in Equation (12) can be expressed as follows:
where
Substituting Equation (17) into Equation (15):
where
For the proposed rheological model, the plastic deformation will follow the laws of viscoplastic flow. The viscoplastic strain increment generated in the increment time is calculated by the difference method:
In this study, viscoelasticity is solved numerically using an explicit method. A complete implicit method with the characteristics of unconditional stability is used to solve this model. Using Taylor series expansion on in Equation (30), we achieve:
The Hermitian matrix derived from the Drucker-Prager yield criterion:
where
According to the visco-elastic-plastic incremental constitutive relationship of the rock materials, the stress and strain correlation can be expressed as
where the visco-elastic-plastic tangent modulus is . When the stress level is low (), is 0 and results in being equal to . According to the principle of virtual work, the incremental balance equation of the system can be derived as
where and are the geometric and the external load increment matrix at .
3. Numerical Model for the Tunnel with Rock Bolts
The transverse section of the tunnel at DL34+600 was selected for the numerical simulation. The width of the tunnel, D, is equal to 10.2 m. Thirty rock bolts with a length of 9 m were arranged in the circumferential direction every 12°. An axisymmetric numerical model with a height of 100 m and a width of 50 m was constructed in ABAQUS software (Figure 4a). The Y-axis was set to be the axis of the symmetrical domain, and the tunnel section was set at the mid-height of the model. Hence, the boundaries of the numerical model are far from those of the tunnel and will not impose a boundary effect to ensure that simulation is efficient enough. The four-node plane strain element (CPE4) was used to simulate the surrounding rock mass, and the grid division is as shown in Figure 4b. In this paper, the key analysis portions are densified to improve the calculation accuracy. Away from the tunnel wall, the grid size was set as 2 m, and at the tunnel wall, it was set to 0.5 m. The parameters for the rheological constitutive model of the surrounding rock mass are listed in Table 2. They were taken from [37], in which the studied rock type was the same as that of the present case. During the numerical simulation, an asymmetric boundary constraint was imposed along the X-axis of the model. A symmetric boundary constraint was set along the Y-axis. A uniformly distributed load was applied at the top boundary of the model to represent the in situ ground stress according to different burial depths. The lateral pressure coefficient was set as 0.7 to compute the in situ ground stress. During the numerical simulations, the beam elements in ABAQUS were used to simulate the rock bolts.
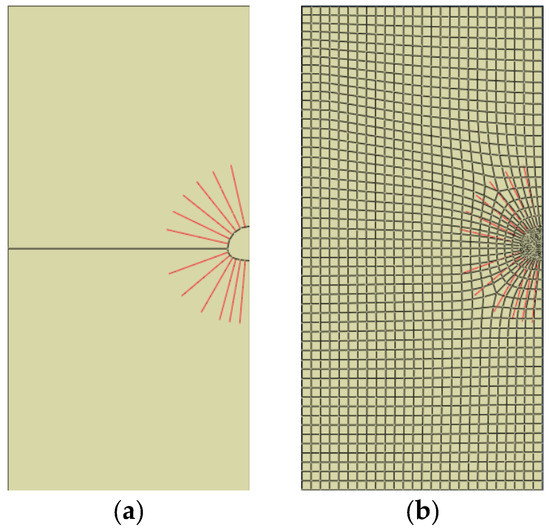
Figure 4.
Numerical model: (a) cross–section calculation; (b) meshing diagram.

Table 2.
Model parameters of the surrounding rock mass in section DL34+600 [37].
To validate of the model, the analysis results were compared to the displacement obtained from the monitoring on site. See Figure 5 for the layout of the monitoring sensors. A comparison of both arrangements can be seen in Figure 6. Their agreement is non-trivial, because parameters of the model were taken from an independent study reported in [37]. This underlines the usefulness of the model.
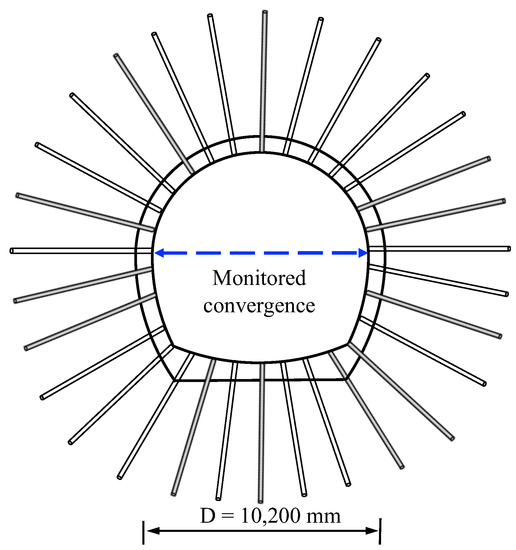
Figure 5.
Illustration of the location of the sensors for measuring the horizontal convergence.
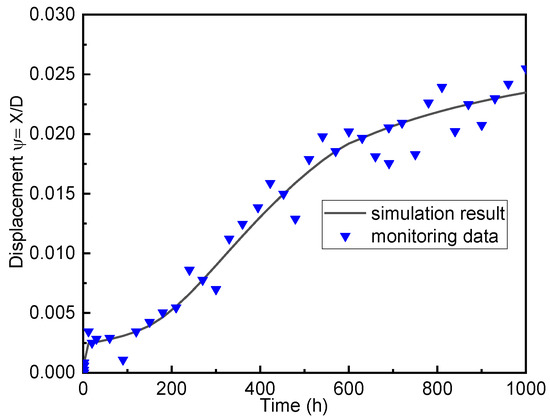
Figure 6.
Validation of the model by comparing the displacement results obtained from the simulation and the on-site monitoring.
4. Sensitivity Analyses
We aimed to investigate the effects of the in situ ground stress and the length of the rock bolts on the mechanical behavior of the tunnels by considering the nonlinear rheological behavior of squeezing rock. To this end, sensitivity analyses were performed with respect to these two variables. The in situ ground stress values that were considered were 5, 10, 15, and 25 MPa, which are associated with the strength-to-stress ratios β amounting to 0.8, 0.4, 0.26, and 0.16, respectively. They correspond to the four classes of difficulty associated with tunneling through squeezing rock, as suggested by Hoek [38] (see Table 3). They refer to the difficulty levels of few (Class A), minor severe (Class B), severe (Class C), and very severe (Class D), respectively. It should be pointed out that when the extrusion class reaches Class B and above, various supporting measures such as steel arch, shotcrete, and grilles are often used. To explore the effects of rock bolts in this study, the contribution of other support measures to stabilize the surrounding rock of the tunnel is not considered. For each value of the strength-to-stress ratio β, eight different rock bolt lengths were considered, i.e., 1, 3, 5, 7, 9, 11, 13, and 15 m. The corresponding ratios of the rock bolt length to tunnel diameter, ξ, were 0.1, 0.3, 0.5, 0.7, 0.9, 1.1, 1.3, and 1.5, respectively.

Table 3.
Classes of difficulty associated with tunneling through squeezing rock based on Hoek [38].
4.1. Mechanical Responses of the Rock Bolts
The choice of the rock bolt length is an important tunnel support parameter and is a critical design aspect in the primary tunnel support design of squeezing rock surroundings. In this study, the elongation of the rock bolt and the ratio of the displacement between the two ends of the bolt were selected as the main indicators for analyzing the design selection of the rock bolt length. In addition, the stress of the rock bolt was also analyzed to determine the optimized rock bolt length for the primary support.
4.1.1. Elongation
As shown in Figure 7, numerical models with different in situ stresses and rock bolt lengths were analyzed and calculated. Rock bolt elongation, δ, was used to investigate the behavior of the bolts themselves. Rock bolt elongation is defined as the ratio between the stretched length (ΔL)of the rock bolt and the original length of the rock bolt (L) as follows:
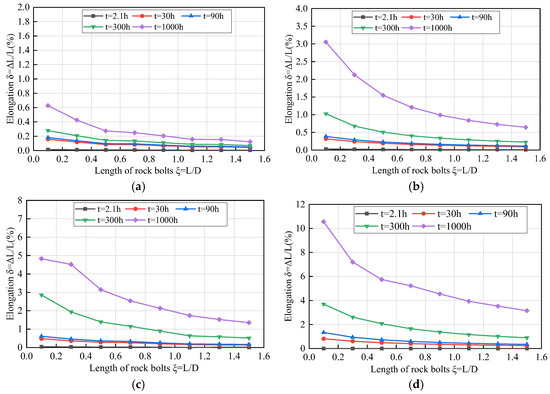
Figure 7.
Elongation at different times after the tunnel excavation: (a) β = 0.8 (Class A); (b) β = 0.4 (Class B); (c) β = 0.26 (Class C); (d) β = 0.16 (Class D).
Rock bolt elongation curves with varying bolt lengths and collected under different in situ stress conditions are shown in Figure 7. With the increase of in situ stress, the elongation gradually increased. However, under different in situ stress conditions, the elongation δ of the bolts with different lengths varied with time.
When there is Class A large extrusion deformation, the rock bolt elongates quickly during the early stage and presents a small time effect. The rock bolt length does not significantly affect the elongation strain at a low in situ stress level. Therefore, when the stress is low, the design length of the rock bolt is not critical.
When there is Class B large extrusion deformation, as time increases, the final increase value of δ is larger for shorter rock bolts. When there is Class C or D large extrusion deformation, a 1 m rock bolt can elongate by 11% after 1000 h at Class D, whereas a 9 m rock bolt only elongates by 0.45%. For the short rock bolts, the extension first reaches the peak value and then decreases to be stable. The nonlinear curve indicates that the short bolts can experience stress relaxation under high ground stress conditions.
It can be seen from Figure 7 that under the same in situ stress conditions, the longer the rock bolt length, the smaller the elongation. Hence, elongation is more sensitive to short rock bolts. In terms of the construction economy, there is an optimal value for the rock bolt length. Namely, when the length of the bolt exceeds the threshold, its elongation is no longer significantly reduced, and the influence of the length of the bolt is gradually reduced.
4.1.2. Displacement Ratio
To further discuss the influence of bolt displacement changes on the surrounding rock support, the ratio of rock bolt end displacement Δ1 to tail displacement Δ2 under different stresses is analyzed. The ratio
is defined as the rock bolt that constrains the front end of the rock bolt hole to penetrate the bedrock as seen in Figure 8. This ratio is used to characterize the anchoring capacity of the bolt. The smaller the ratio, the better the bolt anchoring capacity.
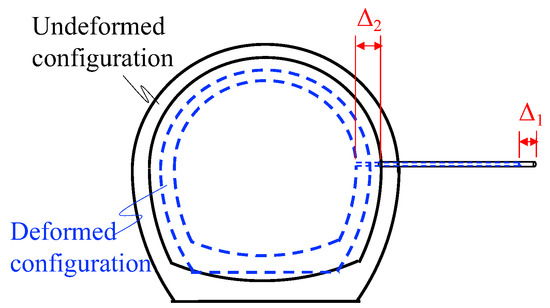
Figure 8.
Schematic diagram of the anchor ratio (Δ1/Δ2).
It can be seen from Figure 9 that when there is Class A large extrusion deformation, the displacement ratio of the rock bolt monotonously decreases as time increases and before finally becoming stable. The capacity gradually increases with time, and finally, the surrounding rock and the bolt support form a bearing circle. When there is Class B large extrusion deformation, with the continuous increase in time and after the bolt is excavated and supported in the tunnel for a specific time, the ratio first reaches its peak value and then gradually decreases to become stable. The curve in Figure 9c,d shows the non-monotonous development of the displacement ratio α, under high in situ stress conditions. This indicates that as time increases, the anchoring end (Δ1) becomes loose. As a consequence, the anchoring capacity of the bolt gradually decreases.
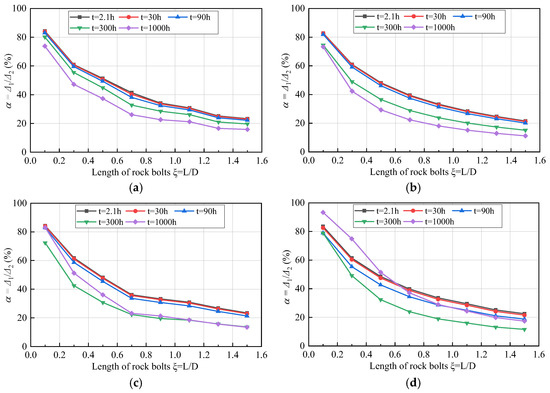
Figure 9.
vs. under different ground stress conditions: (a) β = 0.8 (Class A); (b) β = 0.4 (Class B); (c) β = 0.26 (Class C); (d) β = 0.16 (Class D).
The bolt can effectively restrain the deformation and displacement of the surrounding rock of the tunnel after excavation and can improve the stability of the surrounding rock. However, the selection of the length of the bolt is also critical. The relationship between the displacement ratio of the end and the bolt length was analyzed, as shown in Figure 9. It can be seen from the figure that under the same in situ stress conditions, as the length of the bolt increases, the value of also tends to be stable when it reaches a specific value, and in different periods, the of the bolt first decreases to a specific value and stabilizes afterward. With the increase in the in situ stress, the of the same bolt gradually decreases at the same excavation time. When there is Class C or Class D large extrusion deformation (Pi = 10 MPa and T = 1000 h), does not change much when the bolt length is longer than 9 m. This shows that the length of the bolt affects its ability to support the surrounding rock of the tunnel. Generally speaking, the longer the length of the bolt L is, the more favorable it will be for the stability of large deformation development in the surrounding rock after the tunnel is excavated. However, the longer the bolt length L, the greater the corresponding engineering investment costs and the inconvenience of the drilling and anchoring work. The construction difficulty will increase sharply, as will the construction complexity. Considering the economy as well as safety, the length of the bolt represents a critical expense. In addition, when the in situ stress is different, the change of the of the bolt of the same length will also be different, indicating that the difference in in situ stress will affect the deformation of the end of the bolt. Then, the yield of tunnel excavation will also change. It is worth noting that no matter how the ground stress changes, after the bolt length reaches 9 m, the value is ≤30%. The restriction on the deformation of the surrounding rock is no longer significant, indicating that it is feasible to constrain the deformation of the surrounding rock of the tunnel wall.
4.1.3. Axial Forces
To further study the bolt’s support, the bolt’s relative axial force was analyzed at the hole wall and at the depth of the surrounding rock, as shown in Figure 10. It can be seen that when there is Class A large extrusion deformation, as the length of the bolt increases, the axial force of the bolt at the hole wall increases linearly. However, the axial pressure at the end of the deep part of the surrounding rock decreases, which indicates that the bolt acts on the tunnel wall. When there is Class B large extrusion deformation, the axial force of the cave wall increases as time increases, indicating a nonlinear rheological behavior of the surrounding rock mass. When there is Class C and Class D large extrusion deformation, after the excavation and after the bolt has been supported in the tunnel for a certain period of time, the axial force at the wall of the bolt hole first increases to a specific value and then gradually decreases before finally becoming stable, indicating that under high ground stress conditions, as time increases, the strength of the surrounding rock decreases, stress relaxation occurs at the end of the bolt at the cave wall, and finally, the surrounding rock tends to be in a stable state. It is worth noting that under the same in situ stress conditions, the bolt’s axial force at the hole wall will become larger as the bolt increases in length, while the axial force of the anchor at the depth of the surrounding rock will become smaller. It can be seen that the bolt can effectively adjust the stress state of the surrounding rock, which is of great significance for reducing the scope of the plastic zone and for reducing displacement.
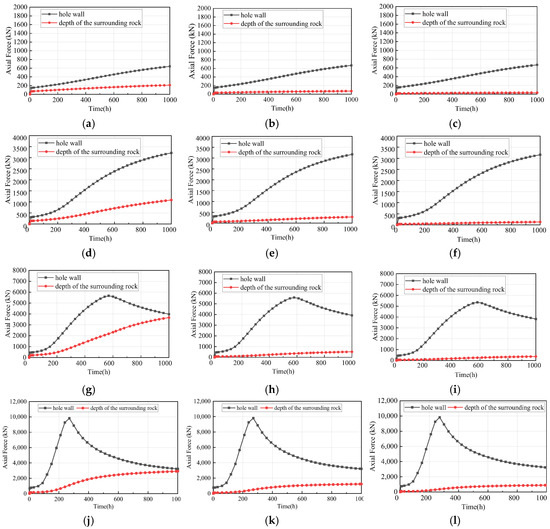
Figure 10.
Axial force vs. time under different in situ ground stress conditions: (a) β = 0.8 and ξ = 0.3; (b) β = 0.8 and ξ = 0.7; (c) β = 0.8 and ξ = 0.9; (d) β = 0.4 and ξ = 0.3; (e) β = 0.4 and ξ = 0.7; (f) β = 0.4 and ξ = 0.9; (g) β = 0.26 and ξ = 0.3; (h) β = 0.26 and ξ = 0.7; (i) β = 0.26 and ξ = 0.9; (j) β = 0.16 and ξ = 0.3; (k) β = 0.16 and ξ = 0.7; (l) β = 0.16 and ξ = 0.9.
4.2. Deformation of Surrounding Rock Mass
4.2.1. Plastic Zones
It is of great significance to study the changes in the plastic zone range of the surrounding rock to analyze the stability of the bolt support to the surrounding rock. The evolution of the plastic extent with time under different in situ stress conditions was examined, as shown in Figure 11. The range of the plastic zone is denoted by R. It is expressed by a dimensionless symbol , as
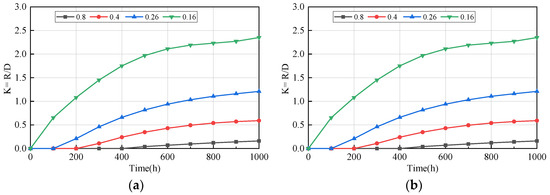
Figure 11.
Variation in the extent of plasticity with time under different in situ stresses conditions: (a) ξ = 0.3; (b) ξ = 0.9.
It is interesting to find that the increase in the plastic zone is not correlated with the rock bolt length, as Figure 11a,b refers to ξ = 0.3 and ξ = 0.9, respectively, and are they virtually identical. It can be seen from the figure that, as a whole, as the in situ stress increases, the plastic zone gradually increases. Due to the rheological effect of the development of the rock mass, the maximum value can reach 18 m and grows nonlinearly. In addition, as tunnel excavation time increases, the extent of the plastic zone gradually increases. The numerical simulation results show that the increase in the plastic zone is related to the magnitude of the in situ stress and the excavation time. This finding is consistent with the change in the nonlinear rheological properties of rock mass. It is worth noting that plastic softening in the rock mass is lower than its peak strength until it reaches the residual strength, but it still has a sufficient bearing capacity. Combining Figure 5 and Figure 7, it can be seen that the threshold of the bolt is 9 m, the maximum value of the plastic zone is 24 m, and the bolt does not need to pass through the plastic zone.
4.2.2. Displacements
Figure 12 shows the relationship between the displacement of the surrounding rock at the cave wall and the length of the bolt under different in situ stress conditions. The displacement of the surrounding rock X is expressed in a dimensionless form by means of subdividing the diameter of the tunnel, D:
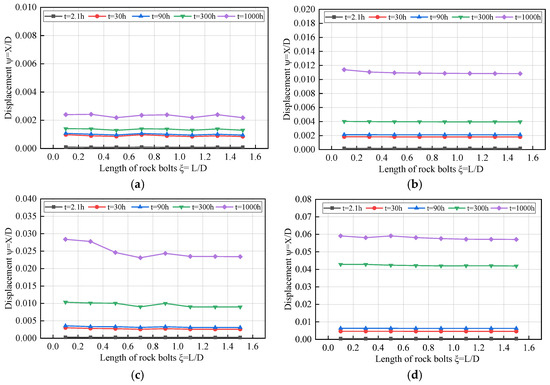
Figure 12.
Surrounding rock displacement and rock bolt length with different in situ stresses: (a) β = 0.8 (Class A); (b) β = 0.4 (Class B); (c) β = 0.26 (Class C); (d) β = 0.16 (Class D).
It can be seen from the figure that as the in situ stress increases, the displacement of the surrounding rock of the tunnel wall gradually increases, and the maximum deformation of the tunnel wall and the high in situ stress show a strong nonlinearity. The large deformation mechanism of high in situ stress in soft rock tunnels results from the coupling effect of high in situ stress and the weak surrounding rock. When there is Class A large extrusion deformation, the displacement of the surrounding rock of the tunnel wall does not change significantly. The application of bolts at this time has no significant impact on the tunnel excavation. Other forms of support should be considered if the amount of deformation in the actual project is large. When there is Class B large extrusion deformation, the change in the surrounding rock of the tunnel wall is almost linear. In these conditions, bolt support can effectively restrain the deformation and displacement of the surrounding rock of the tunnel after excavation. When there is Class C or Class D large extrusion deformation, the change in the surrounding rock becomes nonlinear, and the increase in the surrounding rock displacement is larger when the short bolt is applied. The increase in the displacement of the surrounding rock is not significant when a long bolt is used.
In addition, when the change in the surrounding rock of the cave wall reaches a specific value, it tends to be stable, indicating that after bolt support is applied, it can effectively control displacement in the applied area. It can also be seen from the deformation diagram that the rock mass anchored by the bolt forms a pressure zone, thereby improving the strength of the surrounding rock and significantly reducing the deformation and development of the plastic zone. As the rock bolt length increases, the plastic zone and the displacement of the surrounding rocks decrease. However, when the rock bolt length reaches a specific value, the plastic zone of the surrounding rock does not change much as the rock bolt length further increases, and the displacement also tends to stabilize. In summary, this optimized rock bolt length for this tunnel site is 9 m.
In order to quantify the influence of the length of the bolts on the convergence of the tunnel, the relative difference of the dimensionless displacement of the surrounding rock at t = 1000 h was calculated for short bolts (ξ = 0.1) and long bolts (ξ = 0.9). For Classes A, B, C, and D, i.e., few, minor, severe, and very severe squeezing problems, differences were equal to 2%, 8%, 18%, and 4%. Therefore, we can conclude that the influence of bolt length on tunnel convergence is significant for minor and severe squeezing problems. In cases with few squeezing problems, the rock mass is strong enough to control the deformation. As for very severe squeezing problems, the primary support for the tunnel rests on a combination of shotcrete, steel arches, and bolts. Shotcrete and the steel arches were excluded from the model. Therefore, the influence of the bolts, if bolts alone are being used as the primary support, becomes insignificant in cases with few and severe squeezing problems.
5. Discussion
It is worth mentioning that the lateral pressure coefficient λ was set as equal to 0.7 and was kept constant with respect to the strength-to-stress ratio β and the ratios of rock bolt length to tunnel diameter, ξ, when the sensitivity analyses were carried out in Section 4. In fact, λ was very important for the mechanical response of the model. This provides the motivation for the sensitivity analysis of this coefficient. Three values of λ, i.e., λ = 0.5, λ = 0.7, and λ = 1.0, were considered. The strength-to-stress ratio β was set as equal to 0.4 and the ratio of the rock bolt length to the tunnel diameter, ξ, was set equal to 0.9. The analysis results shows that the development trend for elongation is similar for the three values of the lateral pressure coefficient, as seen in Figure 13. However, the mechanical response of the bolts, herein represented by their elongation, increased significantly as the lateral pressure coefficient λ increased. Thus, in the case of a different lateral pressure coefficient λ, the optimal length of the bolts must be scrutinized for each one.
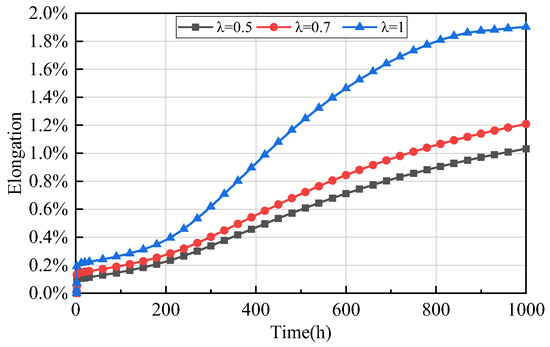
Figure 13.
Sensitivity analysis of the elongation of the bolts with respect to the lateral pressure coefficient λ when β = 0.4 and ξ = 0.9.
6. Conclusions
A nonlinear rheological model of rock materials was proposed in this study. This model combined the Komamura-Huang-Bingham with the Drucker-Prager (DP) yield criterion to improve existing rheological models. A UMAT subroutine was implemented using ABAQUS software for numerical simulation of the nonlinear rheological behavior of bolt support and surrounding rock. The model was validated by comparing the model predictions with the displacements monitored on site. The influences of the length of the bolts and the degree of the squeezing problems on mechanical responses of the soft-rock tunnels were investigated. The following conclusions were drawn:
- (1)
- When the bolt length exceeds 9 m, the elongation sensitivity to increasing the bolt length is very low. Therefore, keeping the bolt length as long as possible is not advised. Economically, there is an optimal value for the length of the bolt. When the bolt exceeds the threshold, the reinforcement effect of the bolt on the rock mass is insignificant. Such a threshold is approximately equal to the diameter of the investigated tunnel, as in the case of the lateral pressure coefficient being equal to 0.7. As for cases of different lateral pressure coefficients, the optimal length of the bolts must be scrutinized.
- (2)
- In case of few and very severe squeezing problems, corresponding to the Classes A and D, the mechanical response of the tunnels, if only bolts were used for primary support, is insensitive to the selection of rock bolt length. The disturbance effect of the bolt on the rock mass is insignificant. Even with the increase of time, the elongation of the same rock bolt length hardly changes. Even as time increases, the surrounding rock softens, and the strength decreases. As a consequence, a shorter bolt will gradually lose its function, and the anchoring end to the tunnel wall will loosen. Therefore, the anchoring capacity of the bolt will gradually decrease.
- (3)
- The size of the plastic zone is dependent on the in situ stress conditions and the time duration after the tunnel excavation, and, however, independent of the length of the bolts.
The problem of the large deformation of a soft rock tunnel is challenging. The subsequent research will be on the following two aspects:
- (1)
- Notably, the development of constitutive models of rock has been a hot topic for several decades. Each model has advantages and disadvantages. The associated flow rule used in this paper may lead to excessive dilation. In order to improve this situation, carrying out true triaxial experiments of rocks may provide a way to obtain the yield and the potential surface, resulting in a non-associated flow rule.
- (2)
- It is emphasized that a small strain continuum model was used to model large deformations in this paper. The comparison of the displacement obtained from the simulation and the monitoring on site indicates that the error remains acceptable. However, using a finite strain continuum is a more logical choice for the future work.
Author Contributions
Conceptualization, J.-L.Z.; Data curation, Y.J.; Funding acquisition, J.-L.Z.; Investigation, Y.J., N.L. and H.-H.J.; Methodology, N.L.; Software, N.L. and H.-H.J.; Supervision, J.-L.Z.; Validation, Y.J.; Writing—original draft, Y.J.; Writing—review & editing, M.-L.Z. and J.-L.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Yunnan Hydropower Survey, Design and Research Institute (Grant No. 02302530844) and the Shanghai Rising-Star Program (Grant No. 22QB1405000). The APC was funded by Yunnan Hydropower Survey, Design and Research Institute.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
The authors gratefully acknowledge the support of the team lead by Jun Sun who is a member of Chinese Academy of Science. The authors express their special gratitude to Chen Xu, Wuqiang Cai, and Gengyun Liu for their constructive comments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sun, X.; Chen, F.; Miao, C.; Song, P.; Li, G.; Zhao, C.; Xia, X. Physical modeling of deformation failure mechanism of surrounding rocks for the deep-buried tunnel in soft rock strata during the excavation. Tunn. Undergr. Space Technol. 2018, 74, 247–261. [Google Scholar] [CrossRef]
- Lei, M.; Liu, J.; Lin, Y.; Shi, C.; Liu, C. Deformation characteristics and influence factors of a shallow tunnel excavated in soft clay with high plasticity. Adv. Civ. Eng. 2019, 2019, 7483628. [Google Scholar] [CrossRef]
- Guan, K.; Zhu, W.; Wei, J.; Liu, X.; Niu, L.; Wang, X. A finite strain numerical procedure for a circular tunnel in strain–softening rock mass with large deformation. Int. J. Rock Mech. Min. Sci. 2018, 112, 266–280. [Google Scholar] [CrossRef]
- Luo, Y.; Chen, J.; Chen, Y.; Diao, P.; Qiao, X. Longitudinal deformation profile of a tunnel in weak rock mass by using the back analysis method. Tunn. Undergr. Space Technol. 2018, 71, 478–493. [Google Scholar] [CrossRef]
- Zhou, H.; Qu, C.K.; Hu, D.W.; Zhang, C.Q.; Azhar, M.U.; Shen, Z.; Chen, J. In situ monitoring of tunnel deformation evolutions from auxiliary tunnel in deep mine. Eng. Geol. 2017, 221, 10–15. [Google Scholar] [CrossRef]
- Pan, Y.; Chen, L.; Wang, J.; Ma, H.; Cai, S.; Pu, S.; Duan, J.; Gao, L.; Li, E. Research on deformation prediction of tunnel surrounding rock using the model combining firefly algorithm and nonlinear auto-regressive dynamic neural network. Eng. Comput. 2019, 37, 1443–1453. [Google Scholar] [CrossRef]
- Liu, W.; Chen, J.; Chen, L.; Luo, Y.; Shi, Z.; Wu, Y. Nonlinear deformation behaviors and a new approach for the classification and prediction of large deformation in tunnel construction stage: A case study. Eur. J. Environ. Civ. Eng. 2020, 26, 2008–2036. [Google Scholar] [CrossRef]
- Chen, J.; Liu, W.; Chen, L.; Luo, Y.; Li, Y.; Gao, H.; Zhong, D. Failure mechanisms and modes of tunnels in monoclinic and soft–hard interbedded rocks: A case study. KSCE J. Civ. Eng. 2020, 24, 1357–1373. [Google Scholar] [CrossRef]
- Sun, X.; Zhang, B.; Gan, L.; Tao, Z.; Zhao, C. Application of constant resistance and large deformation anchor cable in soft rock highway tunnel. Adv. Civ. Eng. 2019, 2019, 4347302. [Google Scholar] [CrossRef]
- Sun, J.; Jiang, Y.; Wang, B.; Fan, Y. Nonlinear Rheological Properties and Yielding Support Technology for Large Squeezing Deformation of Soft Rock Tunnel with High Ground Stress. Tunn. Constr. 2021, 41, 1627–1633. (In Chinese) [Google Scholar]
- Desai, C.S.; Sane, S.; Jenson, J. Constitutive modeling including creep-and rate-dependent behavior and testing of glacial tills for prediction of motion of glaciers. Int. J. Geomech. 2011, 11, 465–476. [Google Scholar] [CrossRef]
- Yang, S.Q.; Xu, P.; Xu, T. Nonlinear visco–elastic and accelerating creep model for coal under conventional triaxial compression. Geomech. Geophys. Geo-Energy Geo-Resour. 2015, 1, 109–120. [Google Scholar] [CrossRef]
- Sun, J.; Pan, X. Research on large squeezing deformation and its nonlinear rheological mechanical characteristics of tunnel with weak surrounding rocks. Chin. J. Rock Mech. Eng. 2012, 31, 1957–1968. (In Chinese) [Google Scholar]
- Liu, H.Z.; Xie, H.Q.; He, J.D.; Xiao, M.L.; Zhuo, L. Nonlinear creep damage constitutive model for soft rocks. Mech. Time-Depend. Mater. 2017, 21, 73–96. [Google Scholar] [CrossRef]
- Cao, P.; Youdao, W.; Yixian, W.; Haiping, Y.; Bingxiang, Y. Study on nonlinear damage creep constitutive model for highstress soft rock. Environ. Earth Sci. 2016, 75, 900. [Google Scholar] [CrossRef]
- Al-Rub, R.K.A.; Darabi, M.K.; Kim, S.M.; Little, D.N.; Glover, C.J. Mechanistic–based constitutive modeling of oxidative aging in aging–susceptible materials and its effect on the damage potential of asphalt concrete. Constr. Build. Mater. 2013, 41, 439–454. [Google Scholar] [CrossRef]
- Chen, B.-R.; Zhao, X.-J.; Feng, X.-T.; Zhao, H.-B.; Wang, S.-Y. Time-dependent damage constitutive model for the marble in the Jinping II hydropower station in China. Bull. Eng. Geol. Environ. 2013, 73, 499–515. [Google Scholar] [CrossRef]
- Chen, L.; Wang, C.P.; Liu, J.F.; Liu, Y.M.; Liu, J.; Su, R.; Wang, J. A damage–mechanism–based creep model considering temperature effect in granite. Mech. Res. Commun. 2014, 56, 76–82. [Google Scholar] [CrossRef]
- Mazotti, C.; Savoia, M. Nonlinear creep damage model for concrete under uniaxial compression. J. Eng. Mech. 2003, 129, 1065–1075. [Google Scholar] [CrossRef]
- Zhao, Y.-L.; Cao, P.; Wang, W.-J.; Wan, W.; Liu, Y.-K. Viscoelasto-plastic rheological experiment under circular increment step load and unload and nonlinear creep model of soft rocks. J. Cent. South Univ. Technol. 2009, 16, 488–494. [Google Scholar] [CrossRef]
- Sun, J. Rock rheological mechanics and its advance in engineering applications. Chin. J. Rock Mech. Eng. 2007, 26, 1081–1106. (In Chinese) [Google Scholar]
- Zienkiewicz, O.C.; Cormeau, I.C. Visco-plasticity-plasticity and creep in elastic solids-a unified numerical solution approach. Int. J. Numer. Methods Eng. 2010, 8, 821–845. [Google Scholar] [CrossRef]
- Wang, L.G.; He, F.; Liu, X.F.; Yu, Y.J. Nonlinear creep model and stability analysis of rock. Chin. J. Rock Mech. Eng. 2004, 23, 1640–1642. (In Chinese) [Google Scholar]
- Al-Ajmi, A.M.; Zimmerman, R.W. Relation between the Mogi and the Coulomb failure criteria. Int. J. Rock Mech. Min. Sci. 2005, 42, 431–439. [Google Scholar] [CrossRef]
- Cai, W.; Zhu, H.; Liang, W.; Zhang, L.; Wu, W. A New Version of the Generalized Zhang–Zhu Strength Criterion and a Discussion on Its Smoothness and Convexity. Rock Mech. Rock Eng. 2021, 54, 4265–4281. [Google Scholar] [CrossRef]
- Cai, W.; Zhu, H.; Liang, W. Three–dimensional tunnel face extrusion and reinforcement effects of underground excavations in deep rock masses. Int. J. Rock Mech. Min. Sci. 2022, 150, 104999. [Google Scholar] [CrossRef]
- Ma, X.; Haimson, B.C. Failure characteristics of two porous sandstones subjected to true triaxial stresses. J. Geophys. Res. Solid Earth 2016, 121, 6477–6498. [Google Scholar] [CrossRef]
- Mogi, K. Effect of the intermediate principal stress on rock failure. J. Geophys. Res. 1967, 72, 5117–5131. [Google Scholar] [CrossRef]
- Li, J.J.; Zheng, B.L.; Xu, C.Y. Numerical analyses of creep behavior for prestressed anchor rods. Chin. Q. Mech. 2007, 28, 124–128. (In Chinese) [Google Scholar]
- Han, W.; Luan, H.; Liu, C. Assessment of bolt reinforcement effect based on analytic hierarchy process. Geotech. Geol. Eng. 2019, 37, 803–812. [Google Scholar] [CrossRef]
- Wang, H.; Xiao, G.; Jiang, M.; Crosta, G.B. Investigation of rock bolting for deeply buried tunnels via a new efficient hybrid DEM-Analytical model. Tunn. Undergr. Space Technol. 2018, 82, 366–379. [Google Scholar] [CrossRef]
- Wang, W.; Song, Q.; Xu, C.; Gong, H. Mechanical behaviour of fully grouted GFRP rock bolts under the joint action of pre-tension load and blast dynamic load. Tunn. Undergr. Space Technol. 2018, 73, 82–91. [Google Scholar] [CrossRef]
- Sun, J. Rheological Behavior of Geomaterials and Its Engineering Applications; Architecture and Building Press: Beijing, China, 1999; pp. 123–167. (In Chinese) [Google Scholar]
- Pan, X. Study on Squeezing Large Deformation Rheological Mechanical Characteristics of Tunnel Surrounding Rocks. Ph.D. Thesis, Tongji University, Shanghai, China, 2011. [Google Scholar]
- Das, R.; Sirdesai, N.N.; Singh, T.N. Analysis of deformational behavior of circular underground opening in soft ground using three–dimensional physical model. In 51st US Rock Mechanics/Geomechanics Symposium; OnePetro: Richardson, TX, USA, 2017. [Google Scholar]
- Das, R.; Singh, P.K.; Kainthola, A.; Panthee, S.; Singh, T.N. Numerical analysis of surface subsidence in asymmetric parallel highway tunnels. J. Rock Mech. Geotech. Eng. 2017, 9, 170–179. [Google Scholar] [CrossRef]
- Sun, J.; Qin, Y.; Li, N. Nonlinear Rheological Features and Anchoring Technology for Soft Rock Tunnel with Large Squeezing Deformation. Tunn. Constr. 2019, 39, 337–347. (In Chinese) [Google Scholar]
- Hoek, E.; Marinos, P. Predicting tunnel squeezing in weak heterogeneous rock masses. Tunn. Tunn. Int. 2000, 32, 45–51. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).