Featured Application
This improved wavelet threshold denoising method can select the optimal wavelet basis, decomposition layer and threshold in an objective way, which has potential application for the data cleaning of structural health monitoring data of critical infrastructure.
Abstract
Tunnels generally operate underground or underwater in a complex environment. As a result, the health monitoring system is inevitably affected by various environmental factors, which introduces noise to the system. However, the noise contained in the monitoring sequence may disrupt structural damage identification and health state assessment as the real structural response may be overwhelmed by the noise. To properly eliminate the noise in an objective way, this study proposed an improved wavelet threshold denoising method. Firstly, it adopts a quantitative factor, namely the Sparse Index, to assist the selection of the best wavelet basis in numerous wavelet packages. Then, the decomposition layer and threshold are optimized by a comprehensive evaluation based on a variation coefficient method. At last, the application of the concrete strain health monitoring data of the Hong Kong-Zhuhai-Macao Bridge immersed tunnel verified the effectiveness of the proposed method. It is found that the combination of sym12 and five decomposition layers can obtain the best denoising results within the selected wavelet families and decomposition levels. Moreover, the proposed method achieves good denoising results under different fluctuation levels. Thus, the proposed method is reliable, can solve the problem of optimal parameter selection such as decomposition level and wavelet basis in wavelet denoising, and can be applied in the structural health monitoring of critical infrastructures.
1. Introduction
The structural performance of immersed tunnels built on soft soil will degrade with time due to the uneven settlement of foundations and the repeated action of external loads (such as vehicle flow, tidal force, and sedimentation loads). These potential problems may affect the operation and normal use of the tunnel, and even cause safety incidents such as structural damage [1,2,3,4]. Establishing a health monitoring system for immersed tunnels is an effective way to solve this problem; thus, the dynamic changes of the tunnel structure can be monitored to assist the operation and management of the tunnel [5,6,7,8]. This is of great significance for improving the reliability of the structure, ensuring its operational safety, reducing maintenance costs, preventing disasters, and improving operating service levels.
Some immersed tunnels have been built with health monitoring systems, such as the Yongjiang Immersed Tunnel [9], the Zhoutouzui Immersed Tunnel [10], and the Nanchang Honggu Tunnel [11] in China. Additionally, the structural health monitoring systems, condition evaluation methods and data analysis methods have been presented in detail for the Nanchang Honggu Tunnel [12] and the Hong Kong-Zhuhai-Macao Bridge [13]. The establishment of a health monitoring system provides strong support for the infrastructure’s operation and maintenance. However, in the process of data collection, the health monitoring system will inevitably be affected by factors such as stochastic vibrations, weak connections between devices, aging lines, unstable wireless transmission signals, and channel failures of collection devices, etc., resulting in a decline in the quality of collected data [14]. Such noise in data is not caused by the structure itself or state changes, but by the real-time health monitoring system. The noise contained in the monitoring sequence will interfere with structural damage identification and health state assessment, as the real structural response may be overwhelmed by the noise. Therefore, it is necessary to look for suitable methods to eliminate the noise.
Experience has shown that these monitoring data inevitably contain a lot of noise [15]. For the problem of denoising health monitoring data, a lot of research points to the wavelet analysis method. These methods include the Bayesian discrete wavelet packet transform denoising approach [16], an adaptive wavelet packet denoising algorithm [17], an improved wavelet threshold denoising method [18], and discrete wavelet transform (DWT)-based denoising techniques [19]. These wavelet analysis-based methods each have their own characteristics and advantages, but they also have some limitations. For example, it is still an open issue about how to choose the best wavelet basis for the wavelet decomposition, since different wavelet bases have a great impact on the separation results [18]. On the other hand, there are various evaluation indicators of wavelet decomposition effects, such as the root mean square error (RMSE), the signal-to-noise ratio (SNR), the correlation coefficient (R), and smoothness (SMOT); thus, a comprehensive evaluation indicator needs to be developed.
To solve the problems mentioned above in the preprocessing of health monitoring data of immersed tunnels, this study proposed an improved wavelet threshold denoising method. Firstly, it adopts a quantitative factor, namely the sparse index, to assist in selecting the most suitable wavelet basis. Then, the optimal wavelet basis, decomposition layer, and threshold are evaluated by the variation coefficient method. Finally, the concrete strain health monitoring data of the Hong Kong-Zhuhai-Macao Bridge (HZMB) immersed tunnel is used to verify the effectiveness of the proposed method.
2. Improved Wavelet Threshold Denoising Method
2.1. Classical Wavelet Transform Methods
A wavelet is a small range of waves with a limited length and a zero average value. Compared with the traditional Fourier transform using the infinite trigonometric function basis, the wavelet transform takes advantage of the attenuated and limited wavelet basis. Specifically, the wavelet basis can obtain the sequence characteristics in the frequency domain and time domain simultaneously, which enables a localized signal analysis. Continues wavelet transforms and discrete wavelet transforms are two frequently used methods.
In continuous wavelet transforms, the given signal is projected on a continuous family of frequency bands. The function is the sum of the products of the target signal with the scaled and shifted wavelet basis over the entire time period, as shown in Equation (1):
where defines the scale parameter and defines the shift parameter. The former reflects the frequency features of the signal, and the latter reflects the temporal features.
For a system containing big data, such as structural health monitoring system, discrete wavelet transform (DWT) is more suitable for practical analysis. DWT is obtained by selecting a discrete subset of the scale and shifting parameters according to the power of 2. In the previous continuous wavelet transform formula, let , where is the number of discrete subset layers. The function of the discrete wavelet transform is shown in Equations (2) and (3).
There are various methods to implement DWT. The Mallet algorithm is a classic method [20]. Through the repetitive decomposition process in the Mallet algorithm, the signal can be decomposed into several series of detail coefficients and one series of approximation coefficients. A schematic diagram of the Mallet algorithm is shown in Figure 1.
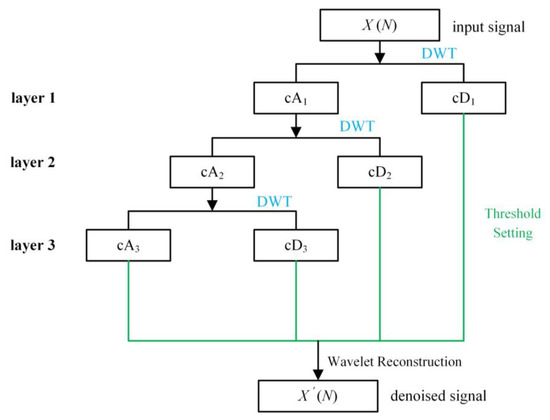
Figure 1.
Schematic diagram of the Mallet algorithm.
2.2. Basic Wavelet Threshold Denoising Method
For many structural signals, the low-frequency component is more informative as it contains the underlying character of the structure while the high-frequency component shows the details of the signal and includes lots of noise. The wavelet threshold denoising decomposes the signal into different frequency scales and removes the noise from the high-frequency component at various decomposition levels.
As shown in Figure 2, the detailed process of wavelet threshold denoising is described as follows:
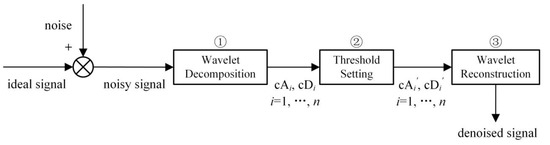
Figure 2.
Wavelet threshold denoising process.
① Wavelet decomposition: Select the appropriate wavelet basis function and the number of decomposition layers n. Conduct wavelet decomposition for n times and obtain the detail coefficients and appropriate coefficients ;
② Threshold setting: Select appropriate thresholds to process the decomposed detail coefficients (high-frequency signals) of each layer. The detail coefficients lower than the threshold are viewed as meaningless noise and set to zero, whereas the detail coefficients higher than the threshold value are retained;
③ Wavelet reconstruction: The denoising sequence is reconstructed by an inverse wavelet operation using the detail coefficients of each layer and the appropriate coefficients of the nth layer.
2.3. Commonly Used Wavelet Basis for Denoising
The disadvantage of a wavelet transform is that the wavelet basis is not unique. For the same signal, different wavelet bases will produce different results. When selecting the wavelet basis, the characteristics of the signal itself should be combined. The following characteristics of the wavelet basis should be considered:
- (1)
- Orthogonality: It can make the analysis simple and facilitate the accurate reconstruction of the signal.
- (2)
- Symmetry: The symmetrical wavelet basis makes the signal undistorted, and the running speed of the algorithm can also be improved.
- (3)
- Regularity: It determines the smoothness of the reconstructed signal, which affects the resolution in the frequency domain.
- (4)
- Vanishing moment: The higher the vanishing moment of the wavelet basis, the faster the attenuation at high frequencies. Therefore, the more concentrated the energy of the transformed signal, and the better the frequency domain locality can be maintained.
Thus, the wavelet bases considered in this method are: Daubechies wavelet families, Symlets wavelet families, Coiflets wavelet families, Biorthogonal wavelet families, and ReverseBior wavelet families. They can all apply in DWT and have high vanishing moments.
2.4. Method Improvement via Optimizing Wavelet Parameters
2.4.1. Optimal Wavelet Basis
Unlike the Fourier transform, which uses a linear combination of sine functions to fit the signal, there are different options for wavelet basis functions in wavelet transform, each of which makes different trade-offs in terms of compactness and smoothness of the wavelet. Since no wavelet basis achieves optimal effects in all cases, the selection of the wavelet basis function relies on the characteristics and the given tasks of the target signal.
This paper intends to use wavelet analysis to conduct signal denoising. Therefore, the optimal wavelet basis function is defined as the complete separation of the input signal into each frequency layer. The more zero wavelet coefficients are obtained after the wavelet transform, the lower the probability of aliasing in scale domain occurring, with the result that better separation results could be expected. In another words, the smaller the value of the detail coefficients, the lower the probability of aliasing occurring in scale domains, with the result that a better and cleaner decomposition effect can be obtained. Referring to Liu’s research results, the Sparse Index (SI) is introduced to evaluate the matching degree between the wavelet basis and the target signal [21]. The formula is shown in Equation (4):
where is an infinitesimal constant and are the detail coefficients at scale and spatial position .
If , ; else if , . SI indicates the number of non-zero detail coefficients. The smaller SI is, the better the separation results achieved.
2.4.2. Threshold Selection Rules
As mentioned above, the second step of denoising is to set an appropriate threshold to filter the detail component obtained by the wavelet decomposition. The detail includes the informative signal with large coefficients and the worthless white noise signals with small coefficients. By setting the coefficients lower than the threshold to zero, the meaningless noise can be eliminated while the effective signal can be reserved.
Threshold setting method is mainly based on an unbiased risk estimation threshold, a minimax threshold, a fixed threshold and a heuristic threshold. The fixed threshold is helpful for improving the computing efficiency of denoising. Considering that the median value of health monitoring data does not change extensively, the fixed threshold [22] is appropriate. It is calculated as in Equation (5), where is the signal length.
The threshold function reflects the tactics for dealing with the detail coefficients above and below the threshold. The hard threshold function is adopted here, considering its superiority in retaining the edge features of the signal without adding deviation. The function is shown in Equation (6):
where is the input signal, and is the threshold.
2.4.3. Optimal Decomposition Layers
The selection of optimal decomposition layers is the key to the denoising effect. If the number of layers is too low, the noise will remain in the data. If the number of layers is too high, part of the detail signal will be removed as noise. Generally, when the number of layers increases, the effect of wavelet denoising becomes first better and then worse.
There are three commonly used indexes for evaluating the denoising effect, including the root mean square error (RMSE), the signal-to-noise ratio (SNR) and smoothness (SMOT). The RMSE is the square root of the variance between the original signal and the denoised signal. The SNR is a traditional method to measure noise in signals. It refers to the ratio of the original signal energy to noise energy. The higher the SNR, the better the filtering effect. SMOT is the ratio of the variance root of the difference between the denoised signal to the original signal, reflecting the smoothness and continuity of the signal after denoising. The smaller the smoothness is, the better the denoising effect is.
The formulas of the three indexes and their changing trends according to the number of layers are shown in Table 1, where is the original signal, is the denoised signal, and is the total amount of data.

Table 1.
Formulas and characteristics of three evaluation indexes.
Since the single index is unstable and unreliable, to integrate the three indexes, a comprehensive evaluation based on the variation coefficient method is adopted [23].
The weights are derived from the coefficient of variation method with the following steps:
- (1)
- Calculate the index value of each layer
As the number of wavelet decomposition layers in a practical application generally does not exceed nine layers, the indexes are calculated according to the formulas in Table 1 for 2–9 decomposition levels.
- (2)
- Normalization of all indexes
Since the dimension of each index is different, it is necessary to carry out normalization before the integration. Assume is the calculated index in step(1), where represents the number of wavelet layers, and represents the index.
RMSE and SMOT are negatively correlated with the denoising effect, so the normalized formula is shown in Equation (7).
SNR is negatively correlated with the denoising effect, so the normalized formula is presented in Equation (8).
- (3)
- Calculate the weight of each index
The greater the variance of the index value, the more it can reflect the difference between the evaluated units, and it should account for more weights in the comprehensive score. Based on this idea, the commonly used coefficient of variation method sets the weight of the index as the quotient of the standard deviation and mean of different levels, as shown in Equation (9).
Then, the normalized weight of each index is obtained by Equation (10).
- (4)
- Calculate the score
Finally, the normalized index value is multiplied by the normalized weight. The three indexes are summed to obtain the comprehensive layer scores, as presented in Equation (11).
3. Health Monitoring Data of the HZMB Immersed Tunnel
3.1. Background of the HZMB Immersed Tunnel
The Hong Kong–Zhuhai–Macao Bridge (HZMB) spanning Lingdingyang Bay is a 55 km long mega-project, one of the largest in the world. It includes three components: the main project of bridge, island and tunnel in the sea; the ports of Hong Kong, Zhuhai and Macau; and the connecting line between the three cities. In the main project, the most challenging task was the island and tunnel project, which has a 6.7 km long undersea tunnel. The immersed tunnel section has a length of 5.67 km and consists of 33 elements [24], as shown in Figure 3. Among all the elements, E28–E33 are located on the flat curve with a radius (R) of 5500 m, and the rest are located on the straight section [25]. The closure joint is between E29 and E30, and the water depth at the bottom of the closure joint is 27.9 m.
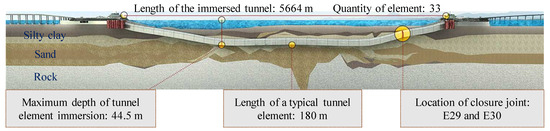
Figure 3.
Longitudinal layout of the HZMB immersed tunnel.
The standard tunnel element is 180 m long, consisting of eight segments, each of which stretches 22.5 m. The immersed tunnel provides a dual three-lane carriageway with a width of 2 × 14.55 m and a vertical clearance of 8.4 m, as shown in Figure 4.
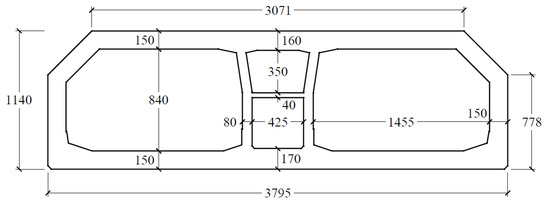
Figure 4.
Cross-sectional geometry of the HZMB immersed tunnel.
As a complex sea-crossing project, the HZMB immersed tunnel has a transition section at the head of the artificial islands where different foundation solutions are adopted, additionally the thickness of the placed backfill is uneven [26]. Meanwhile, the deposition of sediments should also be taken into consideration during the operational life of the structure, which increases the overlying load on the tunnel structure. Load changes in the tunnel longitudinal direction will also result in larger internal forces in the tunnel. All these factors make threats to the operational safety of immersed tunnel structure a great challenge.
3.2. Monitoring Items
To ensure the structural safety of the immersed tunnel, a monitoring system is installed in the representative and key areas to monitor the overall or local stress conditions of the tunnel in real time or periodically. The health monitoring system of the HZMB immersed tunnel consists of a hardware system and a software system. Among them, the hardware system includes various monitoring devices and sensors embedded in and between the elements, signal transmission cables and signal modulation and demodulation equipment. The data from the monitoring items are divided into two categories: structural response data and environmental data. The structural response data includes: ground motion, stress and strain, joint deformation and uneven settlement of element. The environmental data includes: temperature and humidity, structural temperature, and traffic loads.
3.3. Description of Sensors and Health Monitoring Data
Not all monitoring items produce real-time health monitoring data, and some, such as uneven settlement, vehicle load, etc., are obtained through regular inspection methods. Five types of monitoring data, namely ground motion, joint deformation, concrete strain, temperature, and humidity data are adopted to discuss the proposed wavelet denoising method. The details of health monitoring contents, corresponding sensors, and installation locations are listed in Table 2. The sampling frequency of the five types of data is 50 Hz.

Table 2.
Health monitoring contents and corresponding sensors.
- (1)
- Ground motion
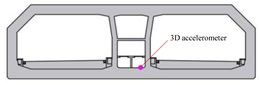
The upper part of the immersed tunnel is designed with a certain thickness of silt and fine sand covering layer, which may liquefy or move to expose the pipe joints or loosen the foundations under seismic excitation. Therefore, it is necessary to monitor the ground motion and its impact on the structure to determine the state of safety after an earthquake. Considering that the nearly 6-km tunnel is located on the seabed of different landforms, the selection of ground motion monitoring points combines factors such as soil quality, foundation scheme and weak connections. Therefore, a total of five key sections of the immersed tunnel are equipped with 3D accelerometer sensors, which can monitor the ground motion of the tunnel along the three directions of XYZ.
- (2)
- Strain of elements
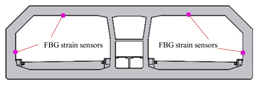
For immersed tunnels, the main body strain of the elements, the shear stress, tensile stress and compressive stress at the joints of the elements are all items that require monitoring. By embedding strain sensors in concrete, the strain and stress conditions of structural representatives or controlled components or parts during operation can be obtained at any time. In this project, ten sections were selected for monitoring, with a total of 57 strain sensors.
- (3)
- Joint deformation
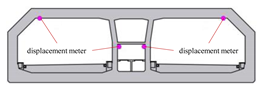
The monitored joint deformation between adjacent elements of the immersed tunnel is the relative displacement along the longitudinal direction of the tunnel. It is related to the dislocation and opening displacement of the rubber waterstop, which reflects the effect and safety reserve of the waterproofing system. Considering the existence of shear key, the pipe joint mainly produces longitudinal dislocation. Therefore, it is only necessary to monitor the longitudinal displacement of the joint.
There are a total of 34 joint sections in the whole tunnel, and each section is equipped with a pull-rope displacement gauge along the four corners of the tunnel carriageway, and the entire tunnel has a total of 136 displacement meters.
- (4)
- Temperature and humidity
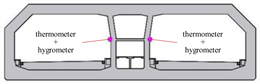
The changes of the temperature and humidity in the tunnel are directly related to the stress level of the concrete structure and the working environment of the monitoring system. Through the monitoring of air temperature, the influence of the surface temperature of the concrete structure and the ambient temperature in the tunnel on the stress of the concrete structure and the environment where the monitoring equipment is located can be eliminated, so that the identification method based on the static test can more accurately reflect the structural reference state.
The installation positions of the thermometers and the strain gauges are very close, and the quantity is the same. A total of 57 thermometers are arranged on 10 sections. Among them, 5 sections were selected for the installation of 2 hygrometers, and there are a total of 10 hygrometers in the whole tunnel.
4. Illustrative Example of Proposed Method
4.1. Noise in Health Monitoring Data of the HZMB Immersed Tunnel
The noise level of data can be preliminarily judged and identified from the fluctuation of data in a short period of time. Assuming that the structural state of the tunnel does not change significantly within one hour, and that the measured physical quantities per hour obey a normal distribution, the 3δ criterion can be used to judge the data noise. The mean value u and standard deviation δ of the day’s data are calculated. According to the 3δ criterion, points whose distance from the mean value exceeds three standard deviations are regarded as noise. Figure 5 shows part of the data of the tunnel vibration accelerometer, where the red points are abnormal points. It can be seen from Figure 5 that there is still a lot of noise in the health monitoring data of the immersed tunnel. If the noise is not eliminated, it will have an adverse impact on the structural analysis.

Figure 5.
Display of data noise level based on the 3δ criterion (signal before noise removal).
4.2. Determination of the Optimal Wavelet Basis
The main challenge in using wavelet transform is selecting the optimal wavelet basis, as different wavelet bases applied to the same signal may produce different results. Traditionally, the wavelet basis functions are usually subjectivity selected by multiple attempts and comparisons, an approach which lacks a quantitative evaluation index.
Based on the proposed method in Section 2.4, different wavelet families are applied to decompose the concrete strain data in different months at ten layers, and SI values are calculated and shown in Table 3. The results show that the order of SI value of the wavelet basis is stable among different months, indicating that the quality of the wavelet basis is determined by the characteristics of the signal. Specifically, for concrete strain data, the performance of dbN, symN and coifN wavelet families is obviously better than that of biorNr.Nd and rbioNr.Nd wavelet families.

Table 3.
SI values of wavelet basis in different months.
By summing the rankings of all wavelet bases in four months, sym12 is determined as the best wavelet basis and bior3.1 is the worst wavelet basis for concrete strain signals. Figure 6 shows their results when the decomposition layer is 10. The amplitude of the detail coefficient of each layer of the best wavelet basis is low. It can be seen from the approximate coefficient A10 that the better wavelet basis can better retain the characteristics of the original signal and separate the noise.
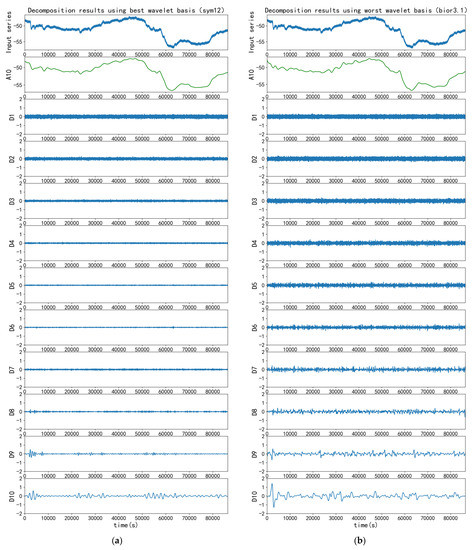
Figure 6.
Decomposition results using best and worst wavelet basis: (a) Decomposition results using sym12; (b) Decomposition results using bior3.1.
In Figure 6, it is also clearly shown that sym12 is better than bior3.1 at almost every decomposition level, so the results are that the reconstructed signal after denoising by sym12 is closer to the original signal. This shows that the proposed SI index is effective for selecting the optimal wavelet basis.
4.3. Determination of the Optimal Wavelet Decomposition Layers
The comprehensive scores of wavelet denoising with different decomposition layers are listed in Table 4. The smaller the comprehensive score is, the better the denoising effect is. Table 4 indicates that for concrete strain data, the optimal number of decomposition layers is five. In terms of subjective selection, it is appropriate to choose four to six decomposition layers.

Table 4.
Comprehensive scores of wavelet denoising with different decomposition layers.
4.4. Denoising Results
Based on the optimal wavelet basis selection, threshold setting method and optimal decomposition layers selection mentioned above, wavelet denoising is carried out with the concrete strain data on 2 June 2020.
Figure 7a shows the time series before and after denoising. It can be seen that the wavelet denoising can effectively remove the redundant information brought into the system by the external environmental noise, which helps reveal the true characteristics of the data sequence. Figure 7b zooms in to show a time section where the sequence trend changes from stable to declining. The denoised sequence manages to capture this drastic trend change and follows the original sequence closely. Figure 7c shows a relatively stable time section, where it can be seen that the denoising process significantly improved the smoothness of the sequence, and the small fluctuation of the original sequence is retained in the denoised sequence. Therefore, the proposed method achieves good denoising results under different fluctuation levels.
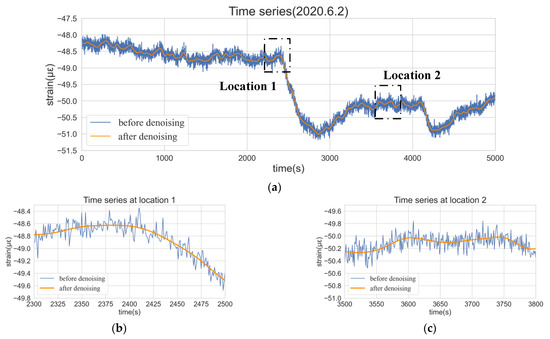
Figure 7.
Time series before and after denoising: (a) A global version; (b) A larger version at location 1; (c) A larger version at location 2.
5. Conclusions
In this study, an improved wavelet threshold denoising method was proposed based on selecting optimal wavelet bases and decomposition layers. According to the results, the following conclusions can be drawn:
- (1)
- The quantitative evaluation factor, the Sparse Index (SI), is effective for choosing the optimal wavelet basis for a given separation task, which is validated by the approximate coefficient of the original signal and reconstructed signal after denoising.
- (2)
- The variation coefficient method is suitable for comprehensive evaluation of the denoising results by integrating three indexes, namely the root mean square error (RMSE), signal-to-noise ratio (SNR) and smoothness (SMOT), which avoid the unstable and unreliable evaluation by a single index.
- (3)
- The concrete strain health monitoring data of the HZMB immersed tunnel has obvious noise phenomenon, which may cause problems if it is directly used to analyze the structural state. The application of the proposed wavelet threshold denoising method demonstrates good effect, which proves that the proposed method is reliable and can be applied in the denoising of health monitoring data of critical infrastructure.
Author Contributions
Conceptualization, X.J., Q.J. and Q.A.; methodology, Q.A.; software, Q.L.; validation, Q.L., Q.A. and X.J.; investigation, J.C.; resources, Q.J.; writing—original draft preparation, Q.A.; writing—review and editing, H.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key R&D Program of China (No. 2019YFB1600702), the Chongqing Natural Science Foundation (Distinguished Youth Fund) Project (cstc2021jcyj-jqX0012), the National Natural Science Foundation of China (No. 51978600), and the Natural Science Foundation of Chongqing Municipality (Cstc2021jcyj-bshX0131).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data available on request to the authors.
Acknowledgments
We acknowledge the full support given by the Hong Kong-Zhuhai-Macao Bridge Authority.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, H.; Binder, E.; Mang, H.; Yuan, Y.; Pichler, B. Multiscale structural analysis inspired by exceptional load cases concerning the immersed tunnel of the Hong Kong-Zhuhai-Macao Bridge. Undergr. Space 2018, 3, 252–267. [Google Scholar] [CrossRef]
- Lu, L.; Qiu, J.; Yuan, Y.; Yu, H.; Wang, H.; Mang, H. Large-scale test as the basis of investigating the fire-resistance of underground RC substructures. Eng. Struct. 2019, 178, 12–23. [Google Scholar] [CrossRef]
- Ai, Q.; Yuan, Y.; Shen, S.L.; Wang, H.; Huang, X. Investigation on inspection scheduling for the maintenance of tunnel with different degradation modes. Tunn. Undergr. Space Technol. 2020, 106, 103589. [Google Scholar] [CrossRef]
- Ai, Q.; Yuan, Y. Rapid acquisition and identification of structural defects of metro tunnel. Sensors 2019, 19, 4278. [Google Scholar] [CrossRef] [Green Version]
- Jiang, X.; Zhang, X.; Wang, S.; Bai, Y.; Huang, B. Case Study of the Largest Concrete Earth Pressure Balance Pipe-Jacking Project in the World. Transp. Res. Record 2022, 03611981221076842. [Google Scholar] [CrossRef]
- Jiang, X.; Zhang, Y.; Zhang, Z.; Bai, Y. Study on risks and countermeasures of shallow biogas during construction of metro tunnels by shield boring machine. Transp. Res. Record 2021, 2675, 105–116. [Google Scholar] [CrossRef]
- Li, C.; Yuan, Y.; He, P.; Yuan, J.; Yu, H. Improved equivalent mass-spring model for seismic response analysis of two-dimensional soil strata. Soil Dyn. Earthq. Eng. 2018, 112, 198–202. [Google Scholar] [CrossRef]
- Zhang, S.; Yuan, Y.; Li, C.; Chen, H.; Chen, Z. Seismic responses of long segmental immersed tunnel under unfavorable loads combination. Transp. Geotech. 2021, 30, 100621. [Google Scholar] [CrossRef]
- Liu, Z.G.; Huang, H.W.; Zhao, Y.H. Immersed tube tunnel real-time health monitoring system. Chin. J. Undergr. Space Eng. 2008, 4, 111–1115. (In Chinese) [Google Scholar]
- Gong, H. Health Monitoring on Immersed Tunnel. Master’s Thesis, Jinan University, Guangzhou, China, 2006. (In Chinese). [Google Scholar]
- Xu, X.; Liu, S.; Tong, L. Establishment of Nanchang Honggu Tunnel health monitoring and assessment system. J. Southeast Univ. 2019, 35, 206–212. [Google Scholar]
- Xu, X.; Tong, L.; Liu, S.; Li, H. Evaluation model for immersed tunnel health state: A case study of Honggu Tunnel, Jiangxi Province, China. Tunn. Undergr. Space Technol. 2019, 90, 239–248. [Google Scholar] [CrossRef]
- Yan, Y.; Mao, X.; Wang, X.; Yu, X.; Fang, L. Design and implementation of a structural health monitoring system for a large sea-crossing project with bridges and tunnel. Shock Vib. 2019, 2019, 2832089. [Google Scholar] [CrossRef] [Green Version]
- Peng, H.; Meng, G.; Ding, Q.; Xu, F. The influence of hydrodynamic pressure on immersed tunnel under earthquake excitation. J. Shanghai Jiao Tong Univ. 2008, 42, 1027–1031. (In Chinese) [Google Scholar]
- Li, M.; Chen, W.Z.; Yang, J.P. An analysis method for the online monitoring data of tunnel structure. Rock Soil Mech. 2016, 37, 1208–1216. (In Chinese) [Google Scholar]
- Jiang, X.; Mahadevan, S.; Adeli, H. Bayesian wavelet packet denoising for structural system identification. Struct. Control Health Monit. 2007, 14, 333–356. [Google Scholar] [CrossRef]
- Beale, C.; Niezrecki, C.; Inalpolat, M. An adaptive wavelet packet denoising algorithm for enhanced active acoustic damage detection from wind turbine blades. Mech. Syst. Signal Proc. 2020, 142, 106754. [Google Scholar] [CrossRef]
- Yu, P.; Yang, L.; Chen, P.; Wu, Y. Wavelet de-noising with improved threshold method for bridge health monitoring. In Proceedings of the 2015 International Conference on Wireless Communications & Signal Processing (WCSP), Nanjing, China, 15–17 October 2015. [Google Scholar]
- Ravizza, G.; Ferrari, R.; Rizzi, E.; Dertimanis, V. On the denoising of structural vibration response records from low-cost sensors: A critical comparison and assessment. J. Civ. Struct. Health Monit. 2021, 11, 1201–1224. [Google Scholar] [CrossRef]
- Mallat, S.G. A theory for multiresolution signal decomposition: The wavelet representation. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 674–693. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.Y.; Yao, C.L.; Xiong, J. Geophysical potential field anomaly separation method with optimal mother wavelet and spatial locating multiresolution analysis (MRA). IEEE Access 2019, 7, 62840–62851. [Google Scholar] [CrossRef]
- Donoho, D.L. De-noising by soft-thresholding. IEEE Trans. Inf. Theory 1995, 41, 613–627. [Google Scholar] [CrossRef] [Green Version]
- Chen, Q.; Wang, C.; Wen, P.; Wang, M.; Zhao, J. Comprehensive performance evaluation of low-carbon modified asphalt based on efficacy coefficient method. J. Clean. Prod. 2018, 203, 633–644. [Google Scholar] [CrossRef]
- Lin, M.; Lin, W.; Wang, Q.; Wang, X. The deployable element, a new closure joint construction method for immersed tunnel. Tunn. Undergr. Space Technol. 2018, 80, 290–300. [Google Scholar] [CrossRef]
- Li, B.; Hou, J.; Min, K.; Zhang, J. Analyzing immediate settlement of Hong Kong-Zhuhai-Macao Bridge immersed tunnel based on monitoring data. Ships Offshore Struct. 2021, 16 (Suppl. S2), 100–109. [Google Scholar] [CrossRef]
- Hu, Z.; Xie, Y.; Wang, J. Challenges and strategies involved in designing and constructing a 6 km immersed tunnel: A case study of the Hong Kong–Zhuhai–Macao Bridge. Tunn. Undergr. Space Technol. 2015, 50, 171–177. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).