Determination of Johnson–Cook Material and Failure Model Constants for High-Tensile-Strength Tendon Steel in Post-Tensioned Concrete Members
Abstract
:1. Introduction
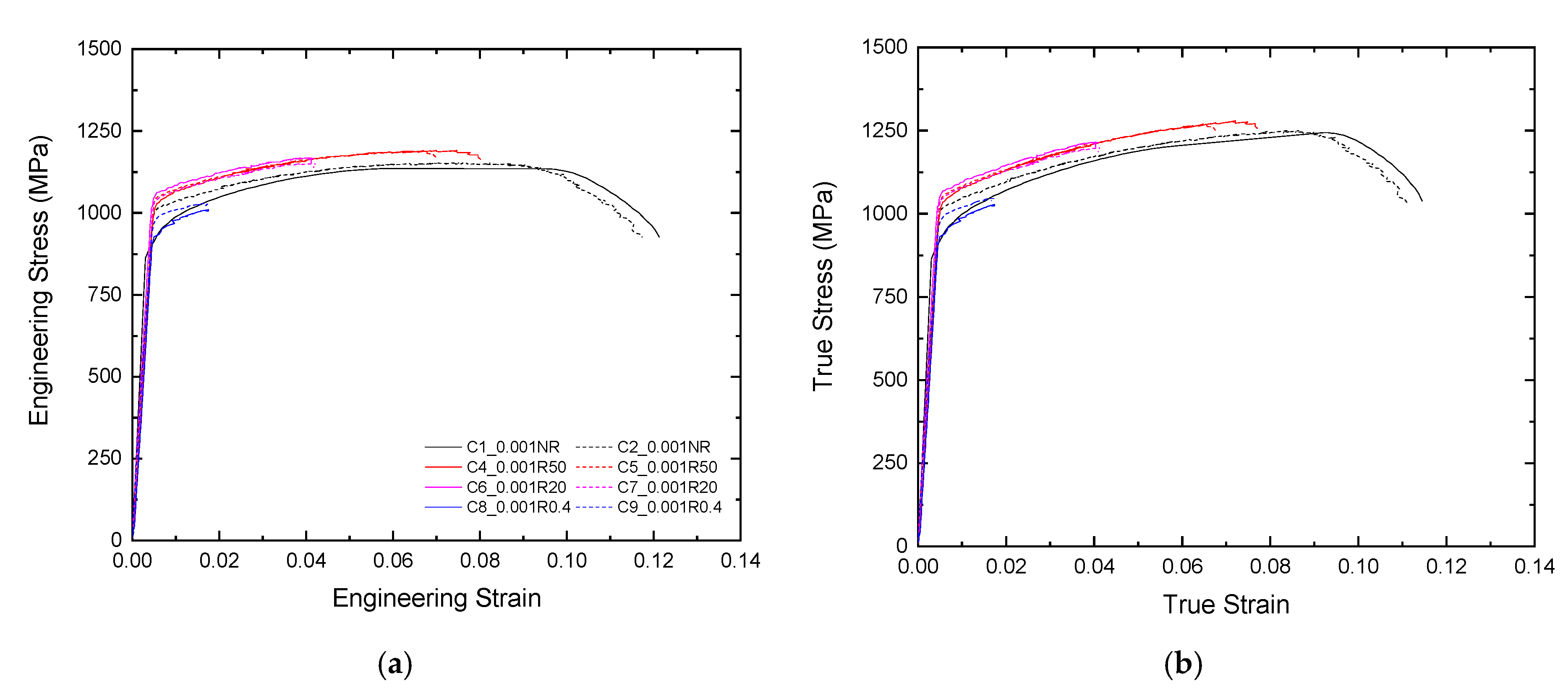
2. Materials and Experimental Procedure
3. Johnson–Cook Model
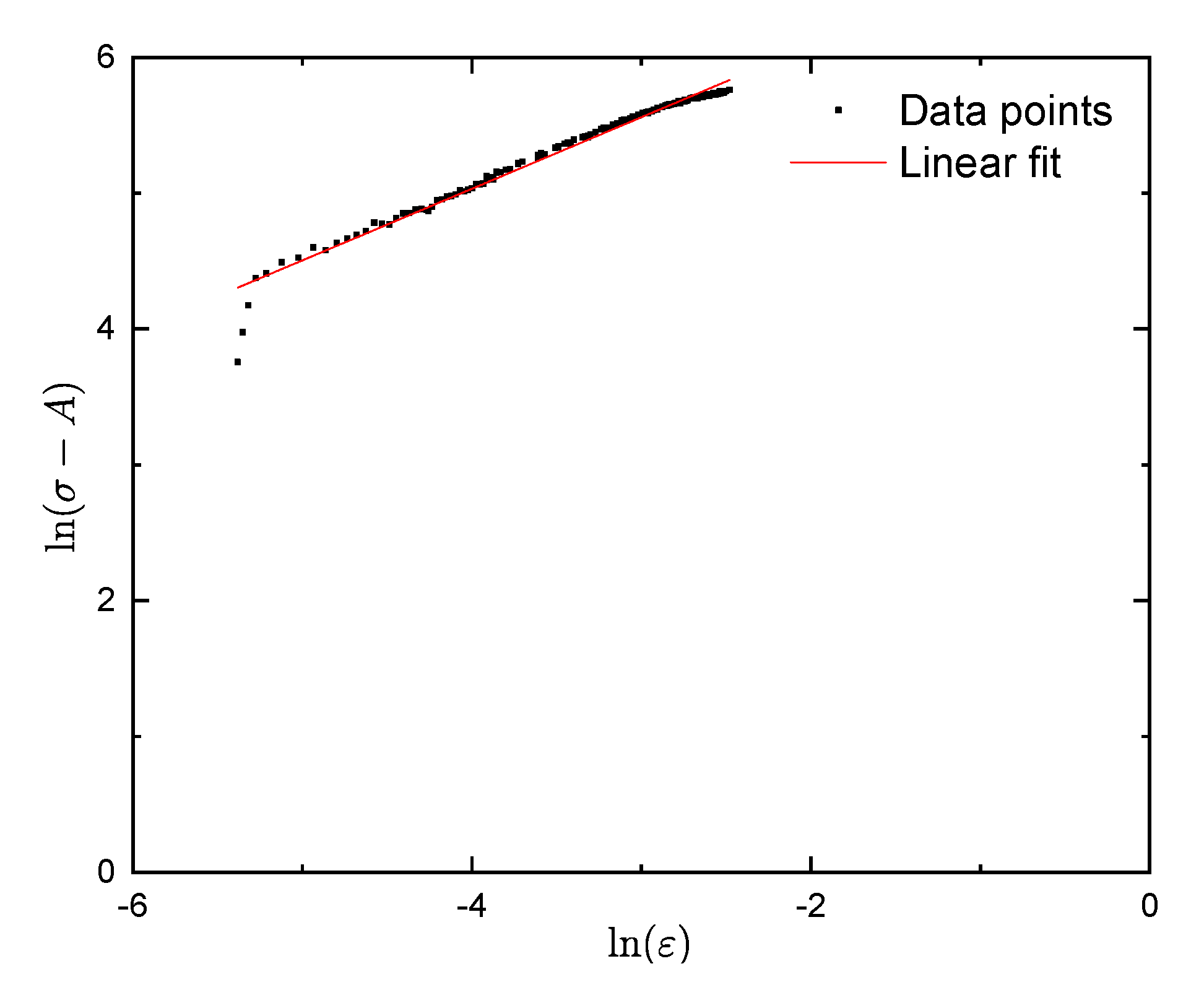
3.1. Determination of Material Constants A, B, n
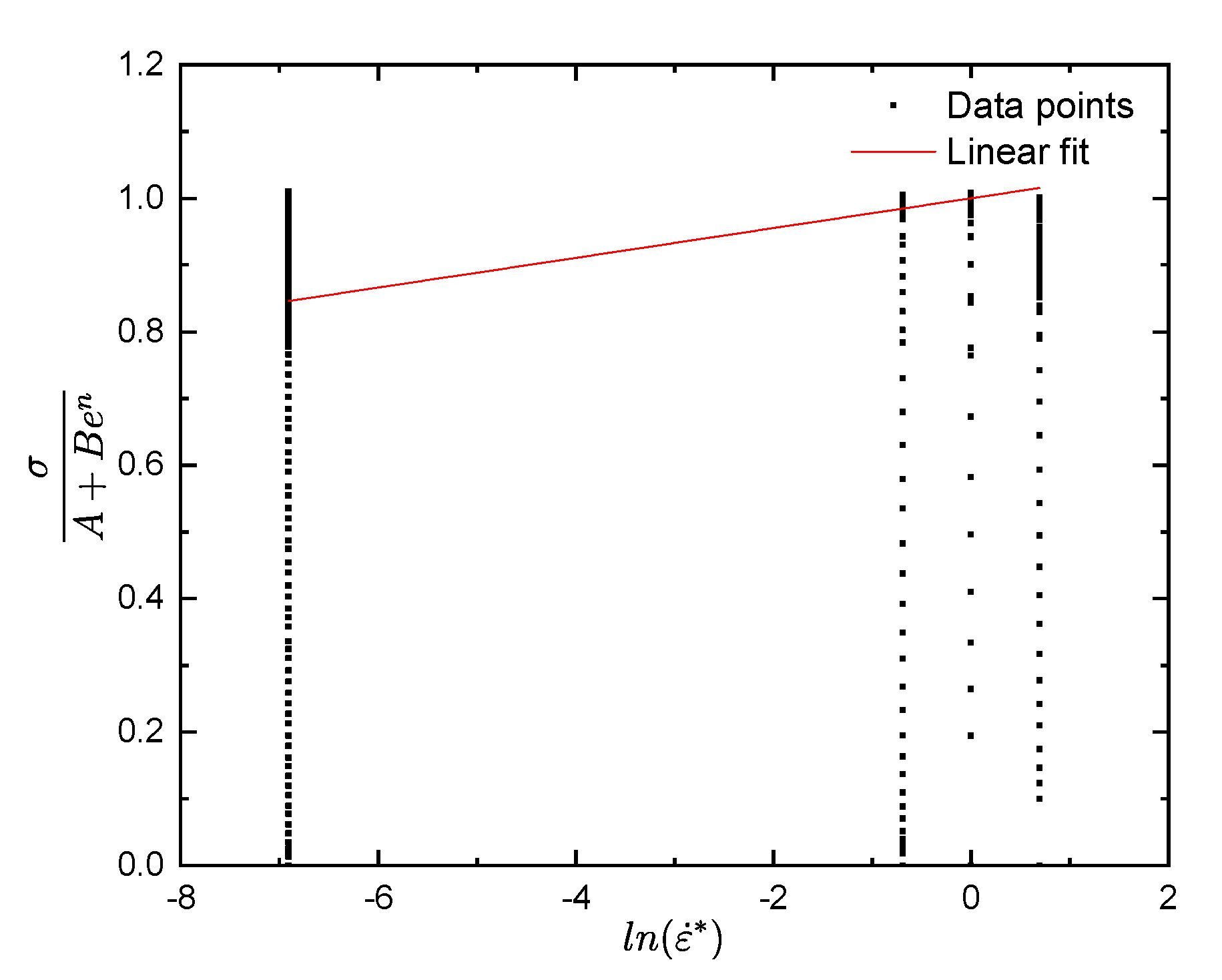
3.2. Determination of Material Constant C
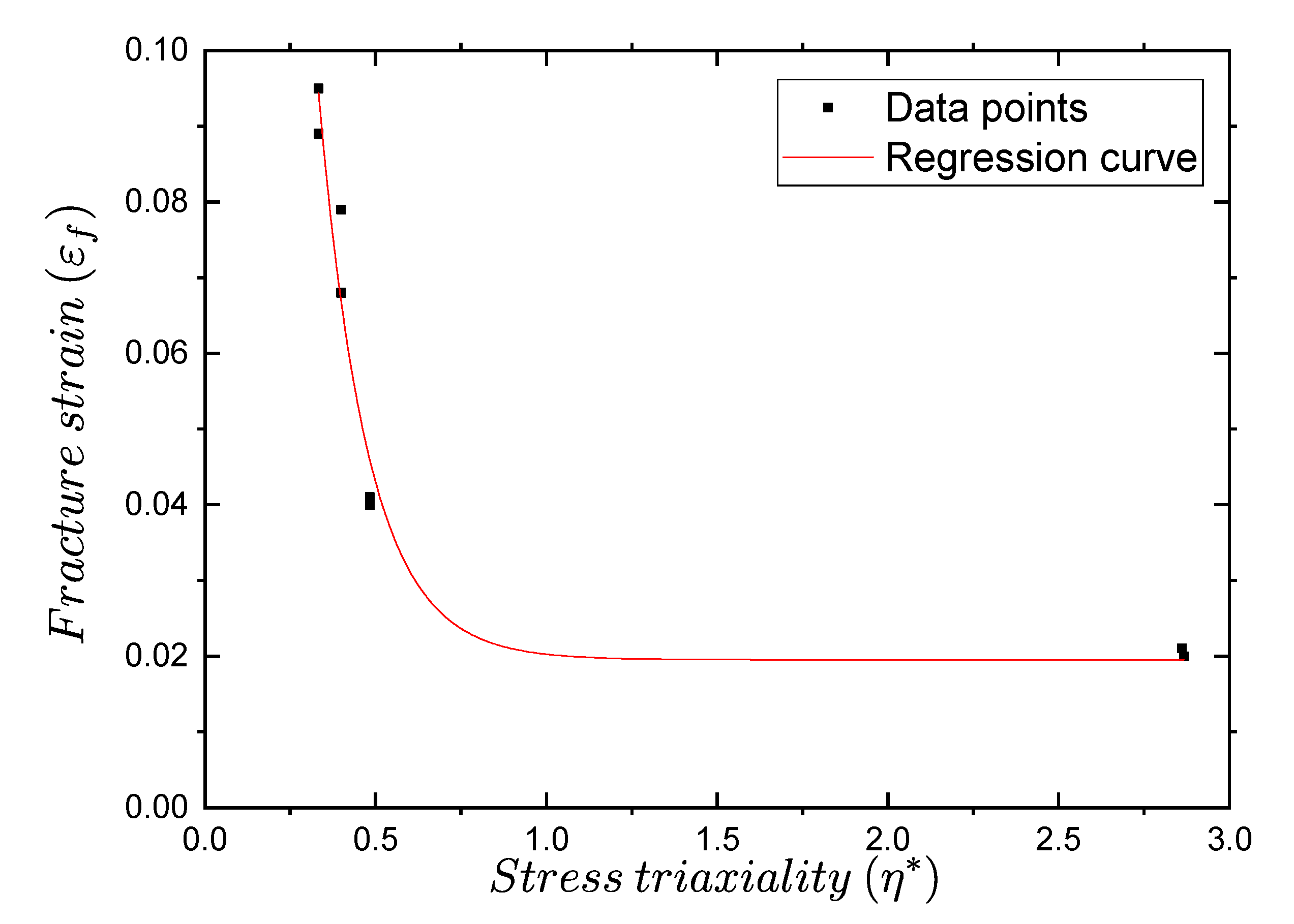
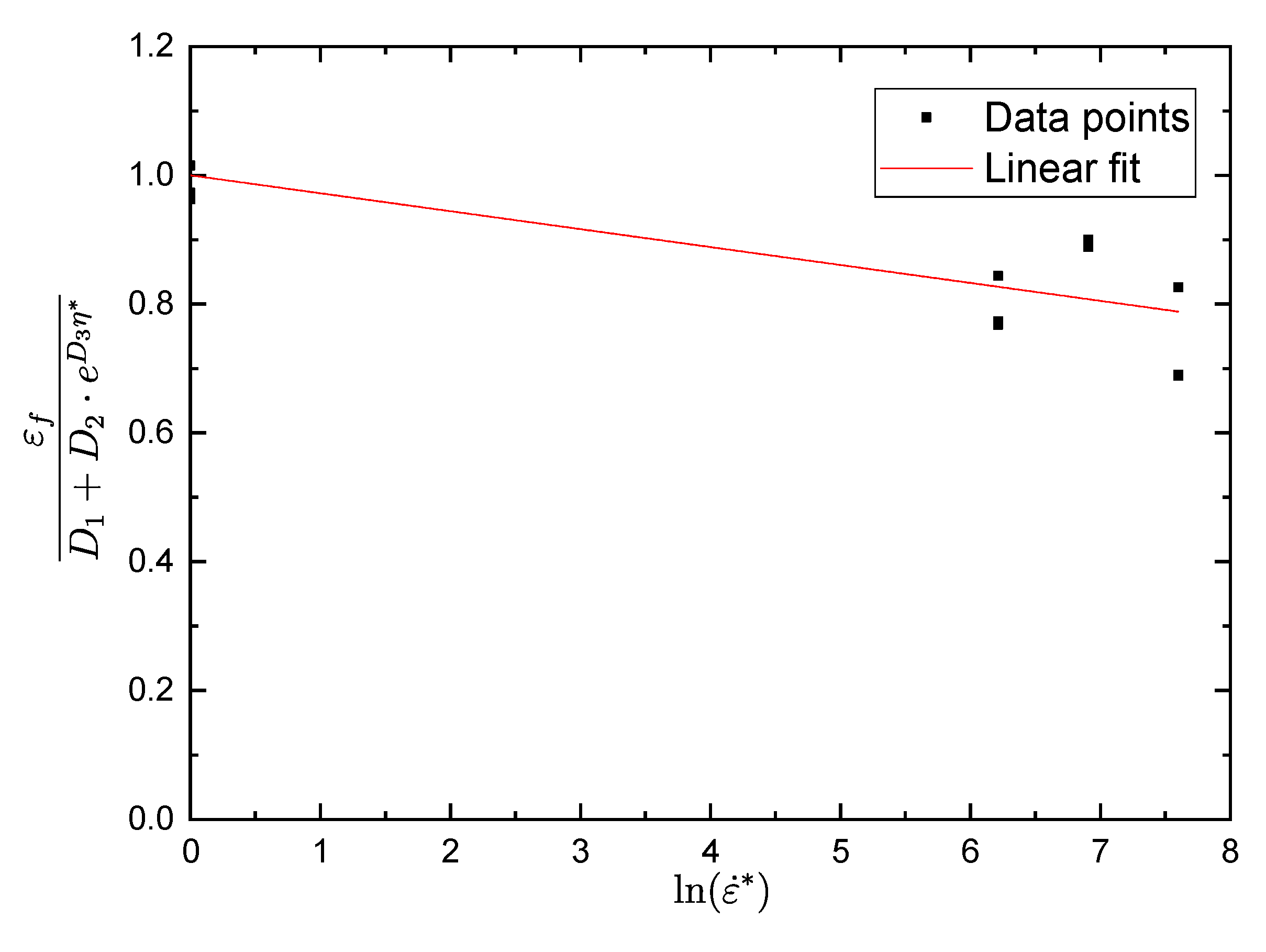
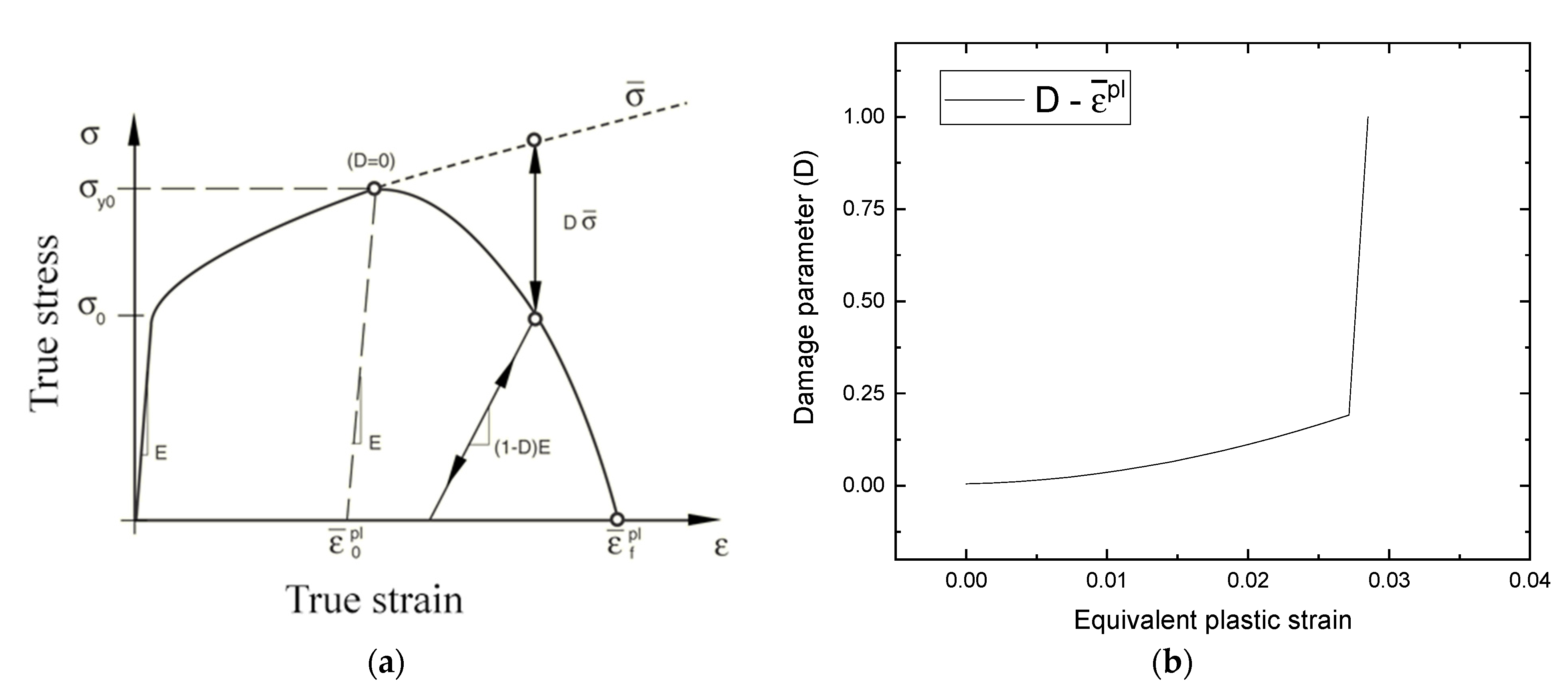
3.3. Johnson–Cook Damage Model Parameters
4. Numerical Simulation
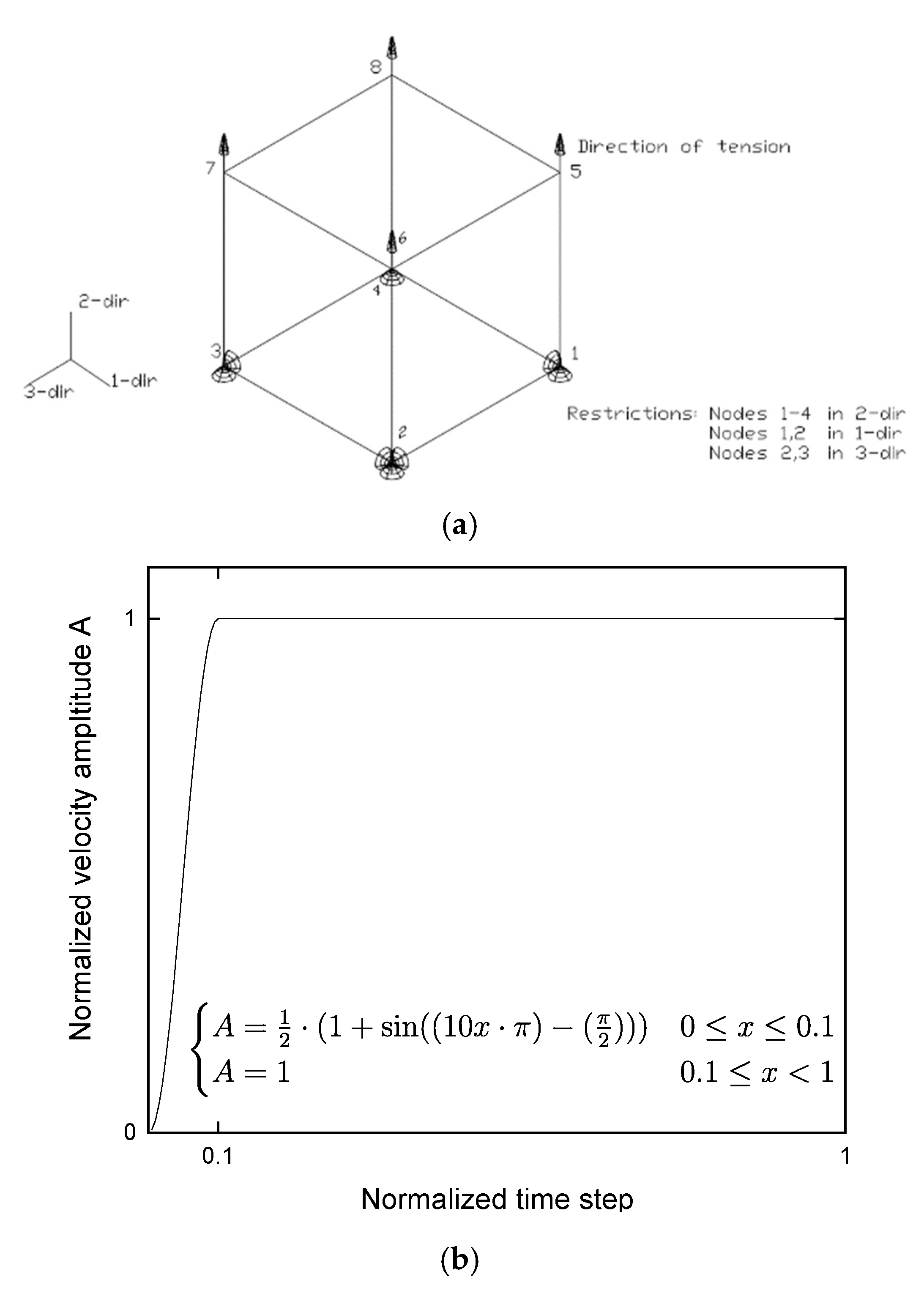
4.1. Numerical Simulation of Singular Finite Element
4.2. Numerical Simulation of Full-Scale Tensile Specimens
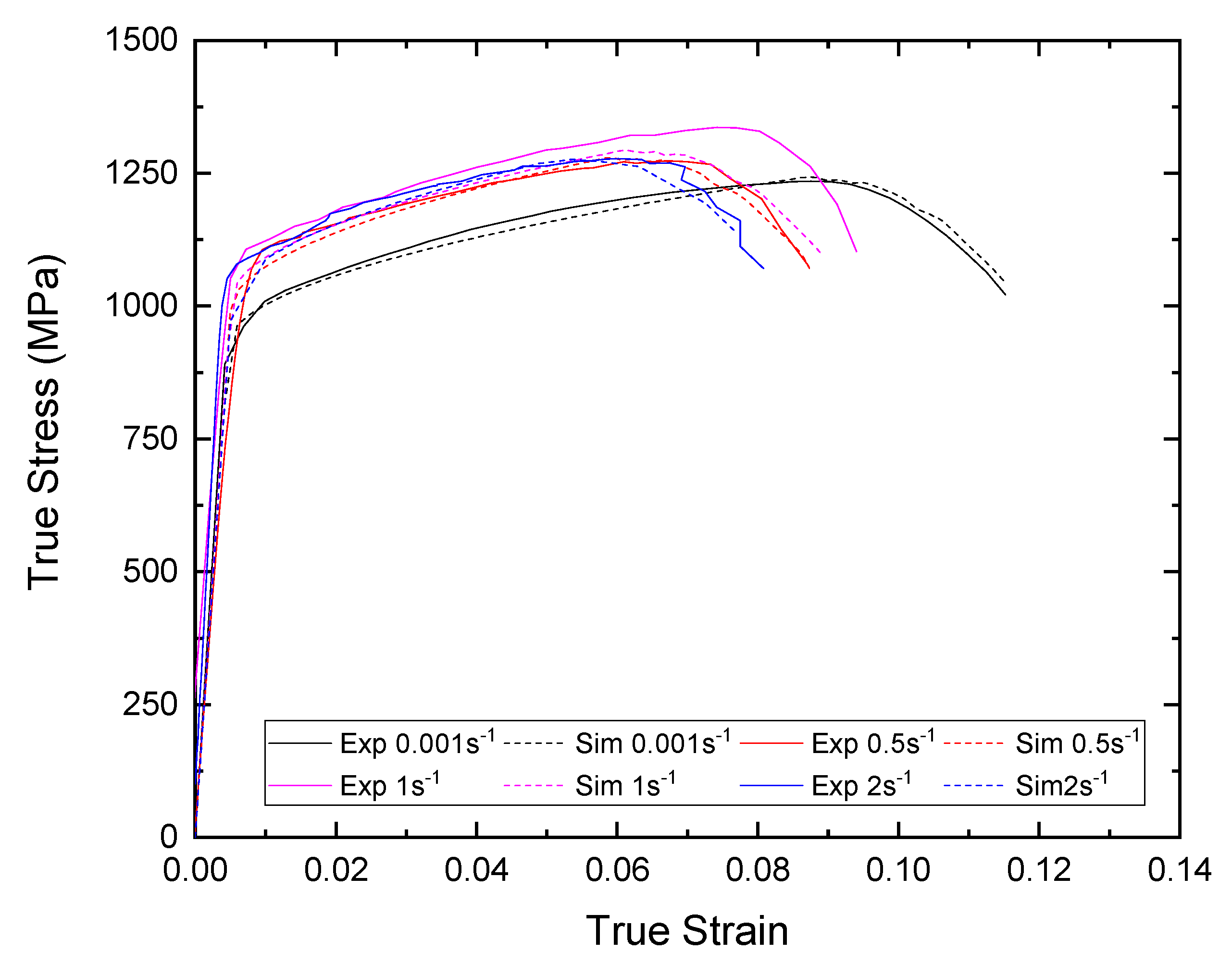
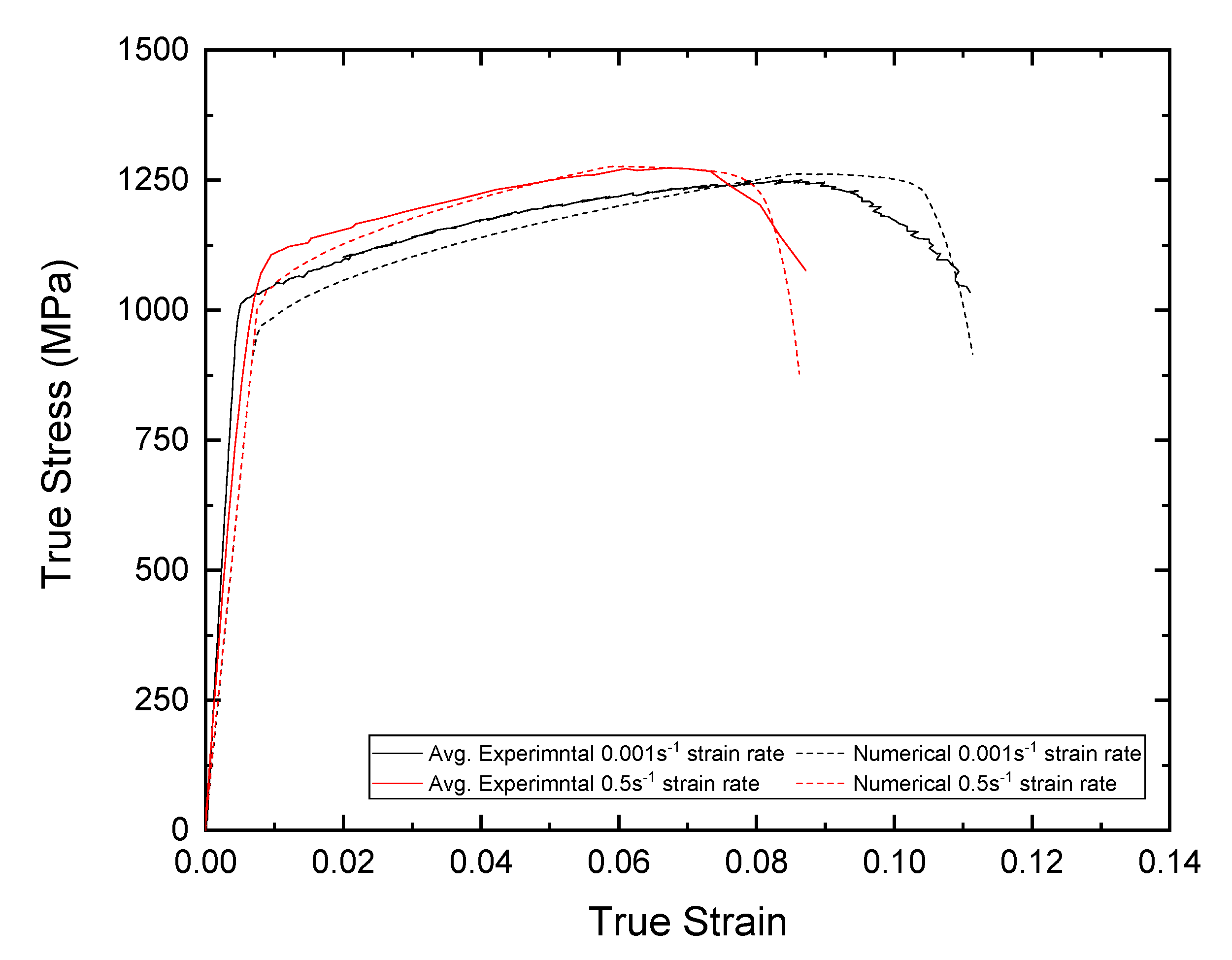
5. Numerical Model Verifications for Smooth Specimens
6. Conclusions and Recommendations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
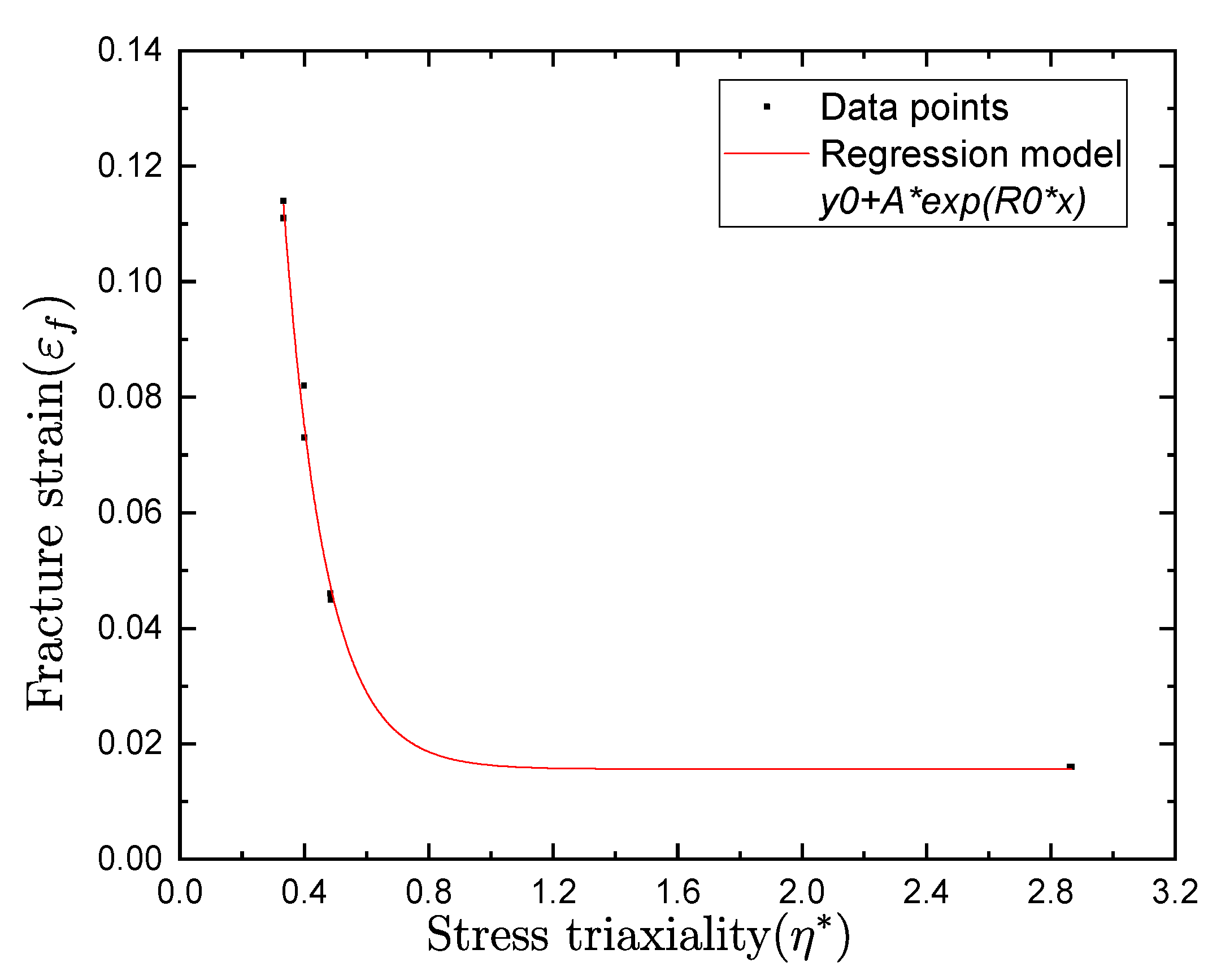
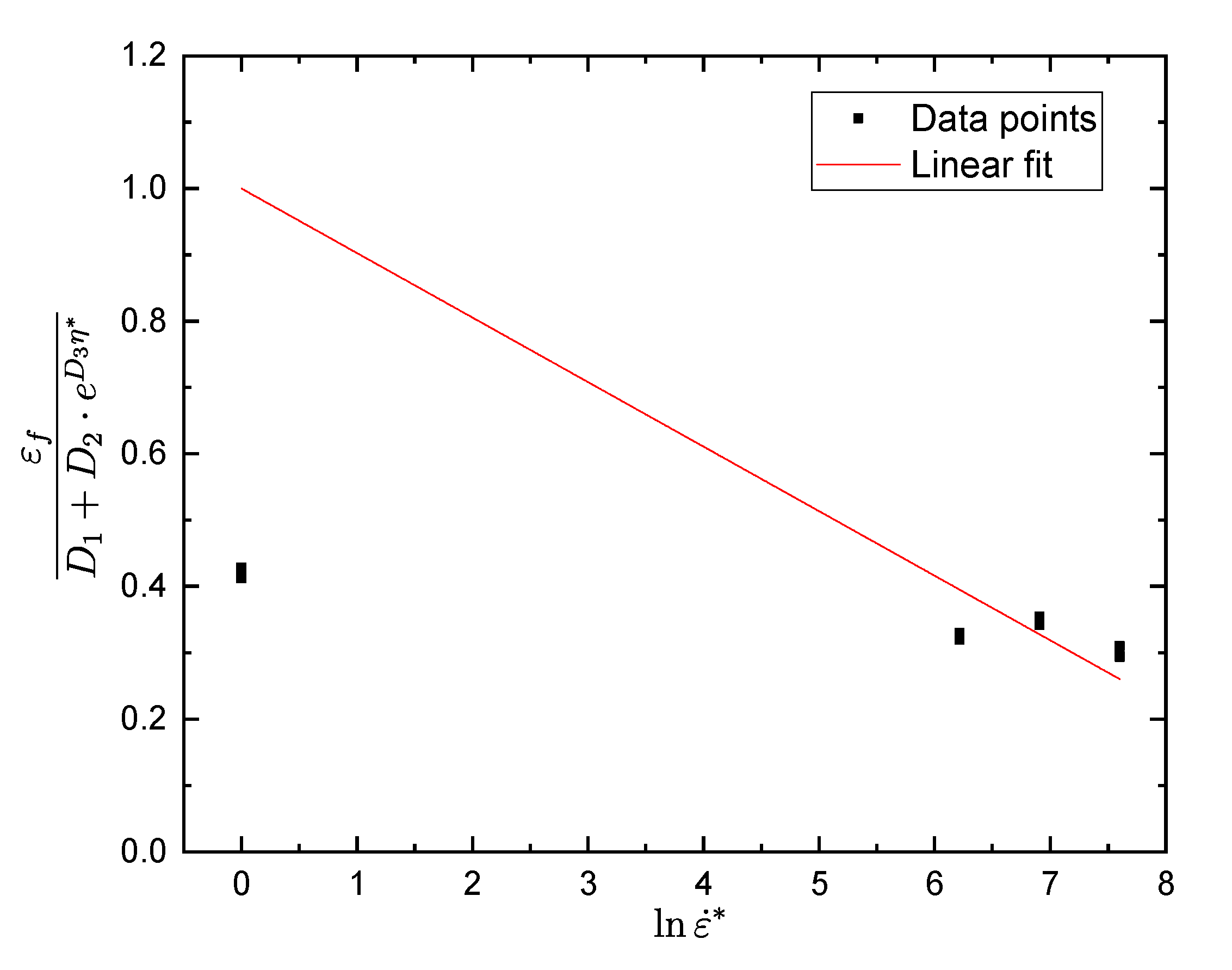
| D1 | D2 | D3 | D4 | D5 |
|---|---|---|---|---|
| 0.0156 | 1.1733 | 7.4656 | −0.0573 | 0 |
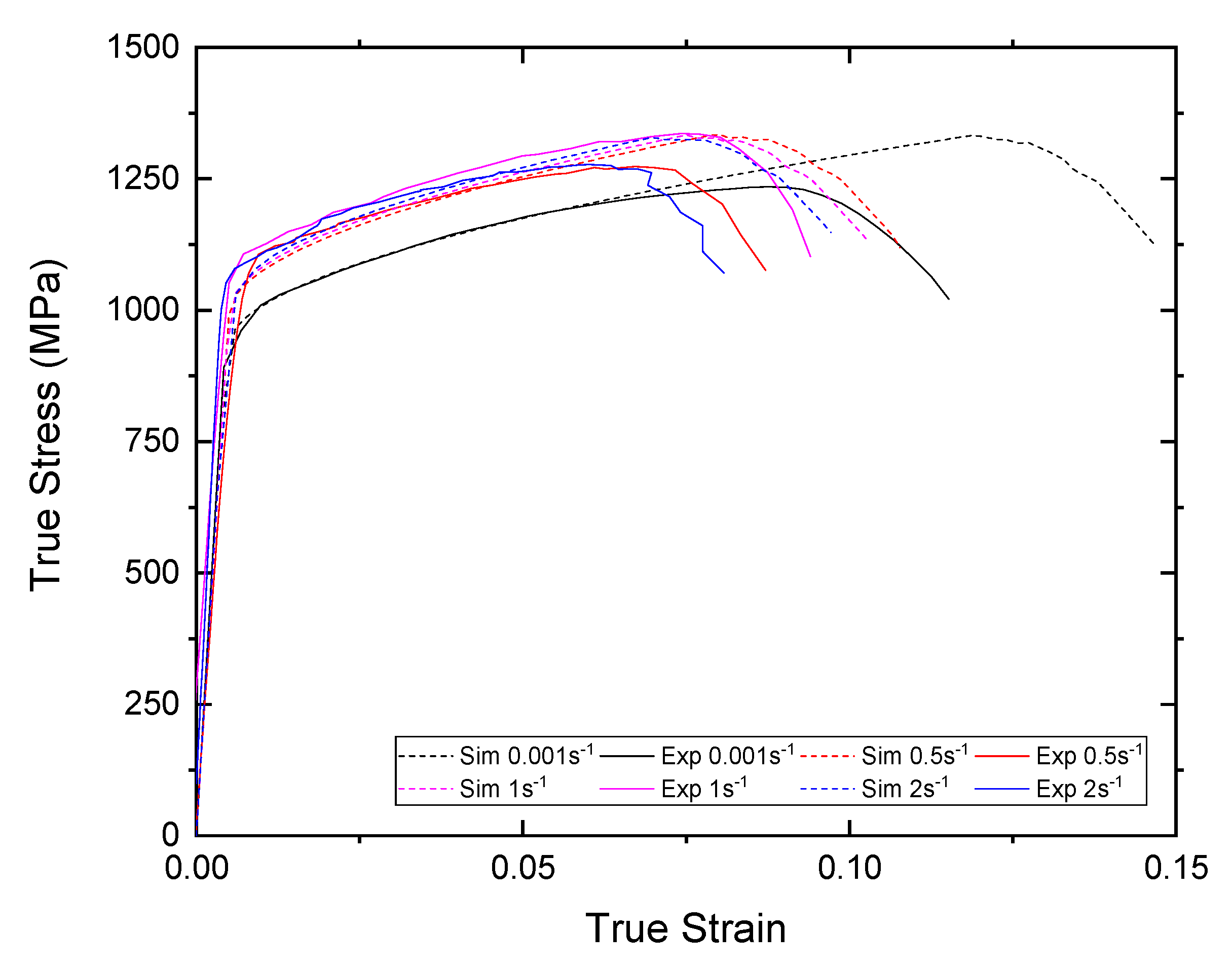
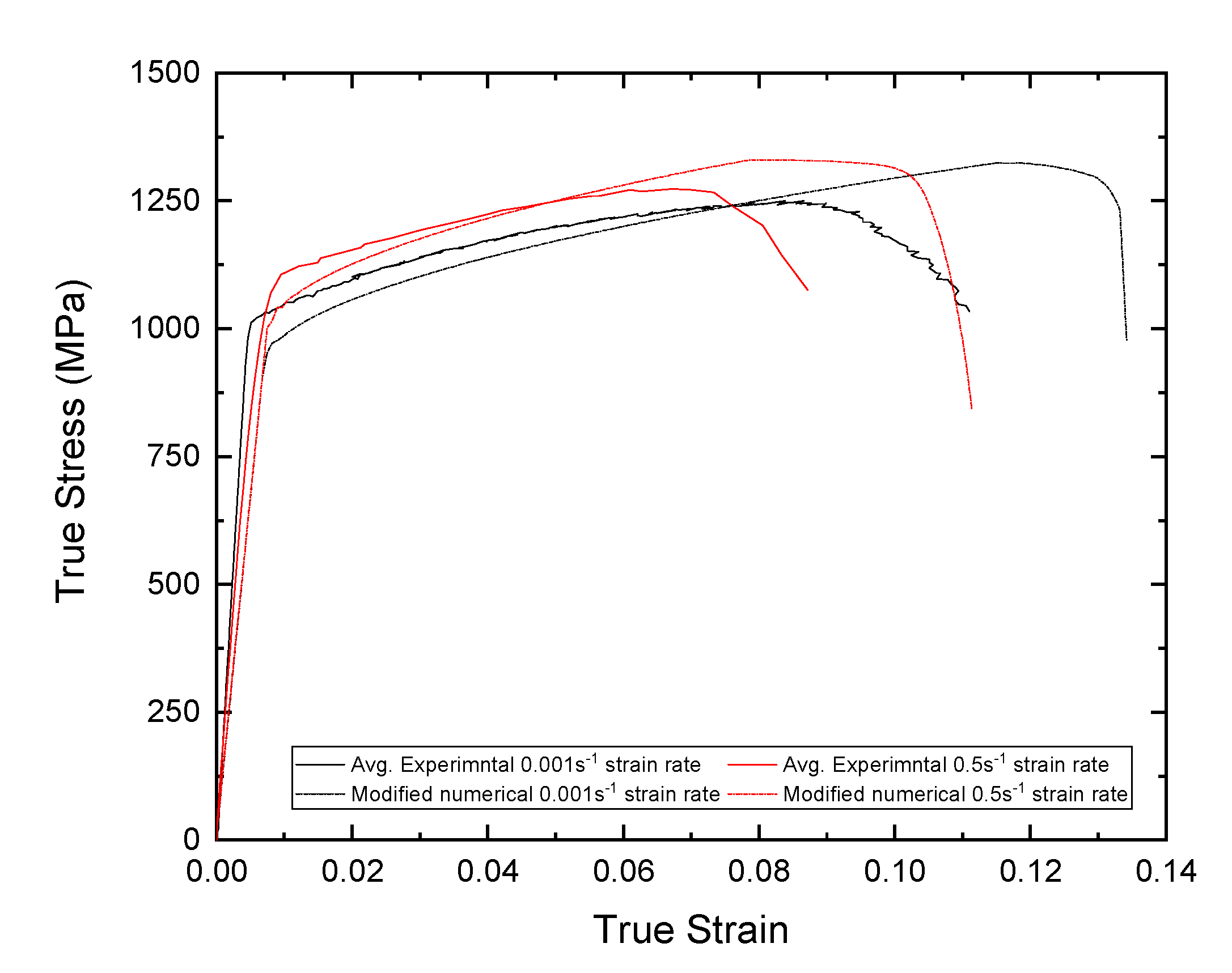
Appendix B
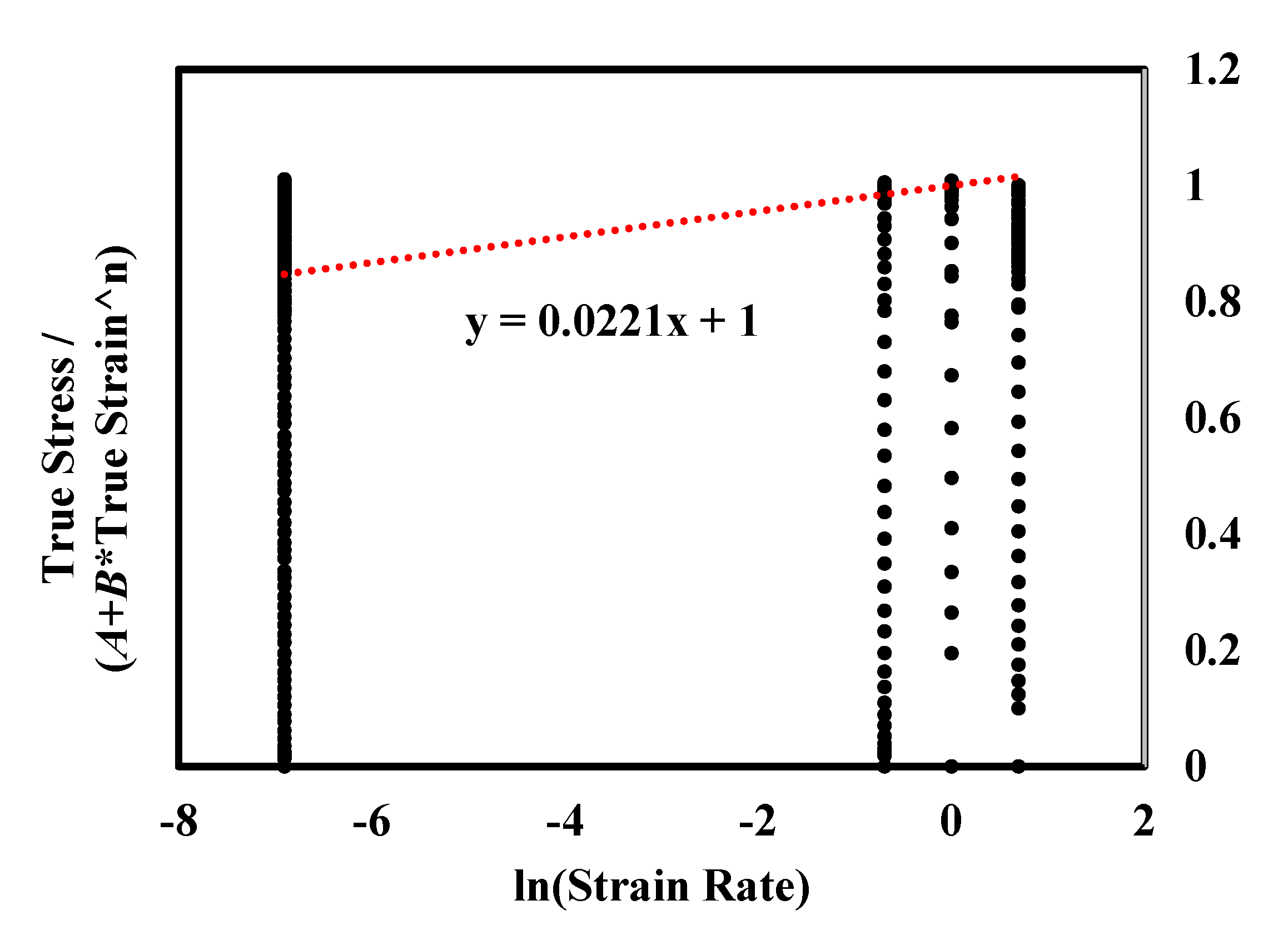
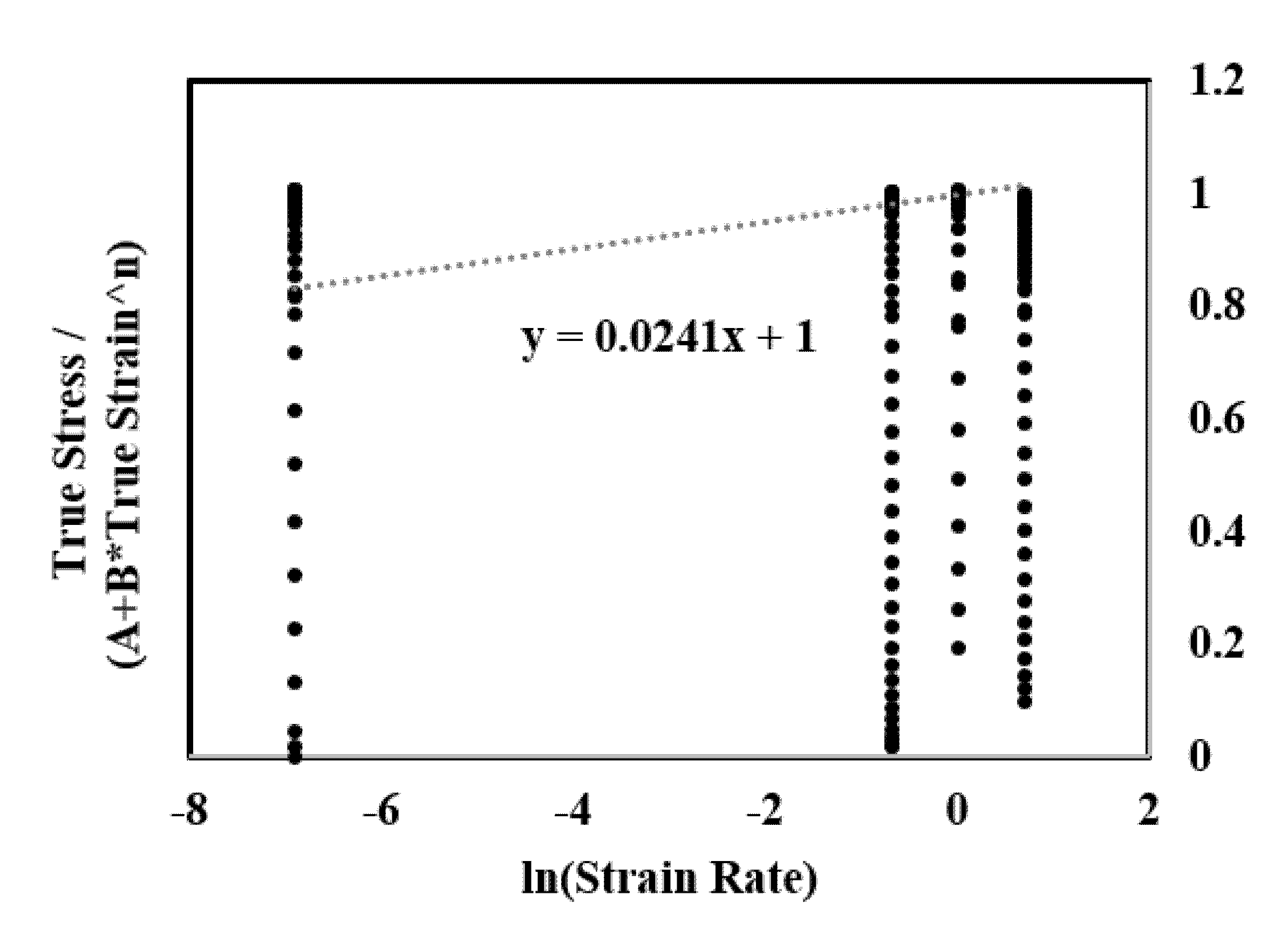
Appendix C
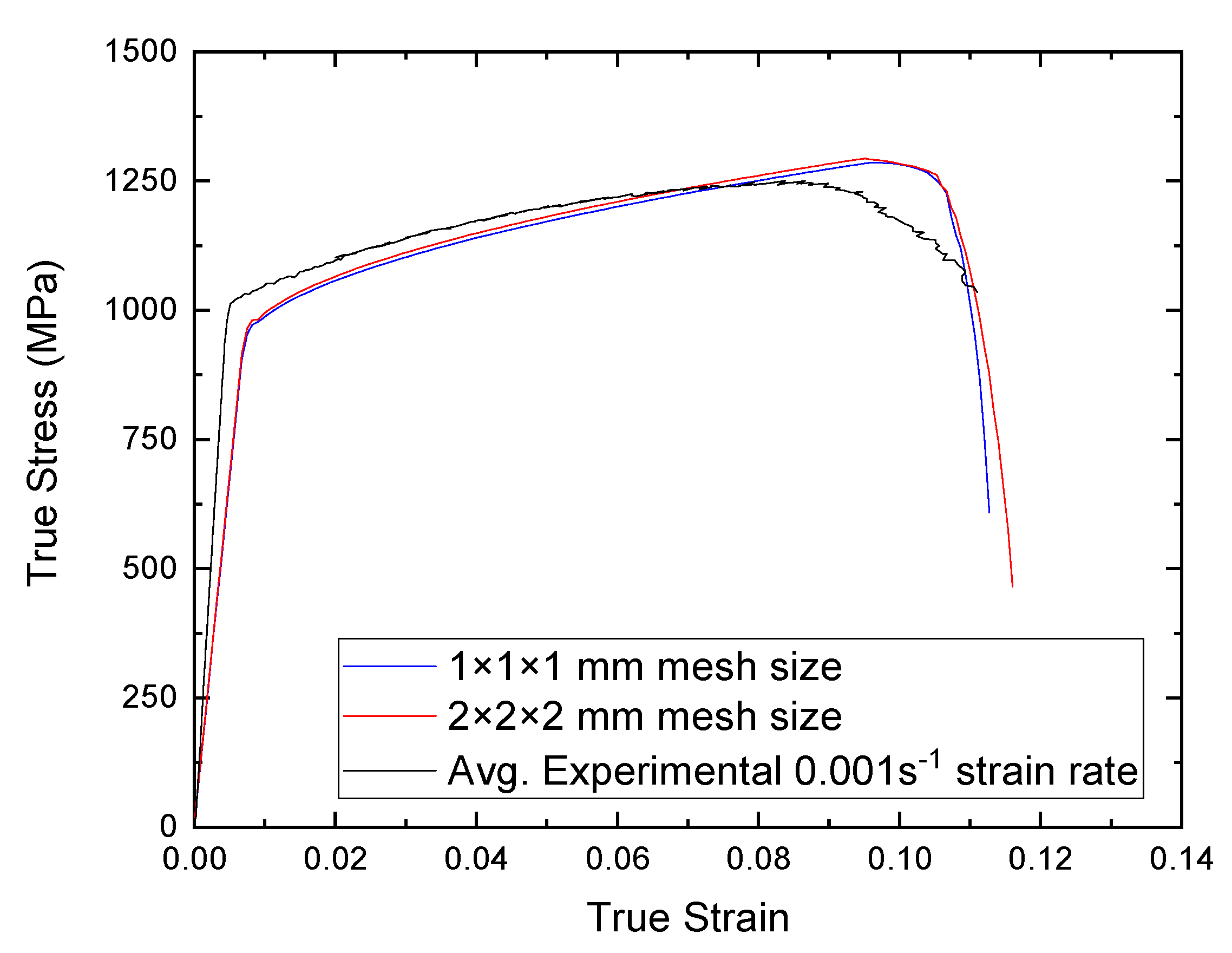
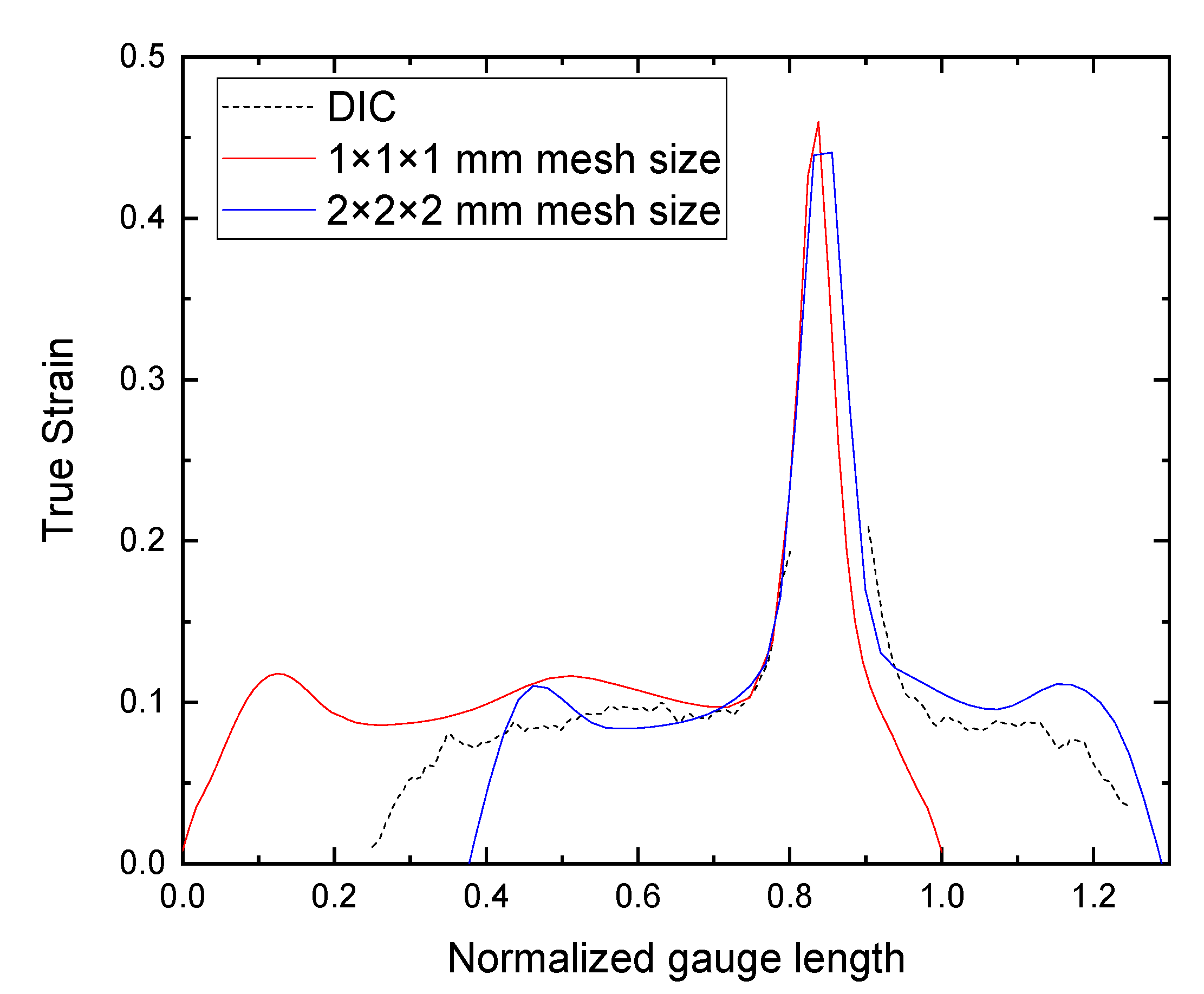
References
- Pape, T.M.; Melcher, R.E. Performance of 45-year-old corroded prestressed concrete beams. Proc. Inst. Civ. Eng. Struct. Build. 2013, 166, 547–559. [Google Scholar] [CrossRef] [Green Version]
- Abdelatif, A.O.; Owen, J.S.; Hussein, M.F.M. Re-anchorage of a ruptured tendon in bonded post-tensioned concrete beams: Model validation. Key Eng. Mater. 2013, 569–570, 302–309. [Google Scholar] [CrossRef] [Green Version]
- Jeon, C.H.; Shim, C.S. Flexural behavior of post-tensioned concrete beams with multiple internal corroded strands. Appl. Sci. 2020, 10, 7994. [Google Scholar] [CrossRef]
- Trejo, D.; Hueste, M.B.D.; Gardoni, P. Effect of Voids in Grouted, Post-Tensioned Concrete Bridge Construction: Volume 1-Electrochemical Testing and Reliability Assessment 5. Report Date 13. Type of Report and Period Covered Unclassified. 2009. Available online: https://static.tti.tamu.edu/tti.tamu.edu/documents/0-4588-1-Vol1.pdf (accessed on 19 January 2022).
- Coronelli, D.; Castel, A.; Vu, N.A.; François, R. Corroded post-tensioned beams with bonded tendons and wire failure. Eng. Struct. 2009, 31, 1687–1697. [Google Scholar] [CrossRef]
- Tamakoshi, T.; Hiraga, K.; Kimura, Y. A Case Study of Corrosion Damage of PC Steel-Investigation of Grout Unfilling and Steel Corrosion of Myoko Bridge. Civ. Eng. J. 2012, 54, 50–51. [Google Scholar]
- Jeon, C.H.; Nguyen, C.D.; Shim, C.S. Assessment of mechanical properties of corroded prestressing strands. Appl. Sci. 2020, 10, 4055. [Google Scholar] [CrossRef]
- Wuertemberger, L.; Palazotto, A.N. Evaluation of Flow and Failure Properties of Treated 4130 Steel. J. Dyn. Behav. Mater. 2016, 2, 207–222. [Google Scholar] [CrossRef] [Green Version]
- Khataei, M.; Poursina, M.; Kadkhodaei, M. A study on fracture locus of St12 steel and implementation ductile damage criteria. AIP Conf. Proc. 2010, 1252, 1303–1308. [Google Scholar] [CrossRef]
- Murugesan, M.; Jung, D.W. Johnson cook material and failure model parameters estimation of AISI-1045 medium carbon steel for metal forming applications. Materials 2019, 12, 609. [Google Scholar] [CrossRef] [Green Version]
- Banerjee, A.; Dhar, S.; Acharyya, S.; Datta, D.; Nayak, N. Determination of Johnson cook material and failure model constants and numerical modelling of Charpy impact test of armour steel. Mater. Sci. Eng. A 2015, 640, 200–209. [Google Scholar] [CrossRef]
- Johnson, G.R.; Cook, W.H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures. Eng. Fract. Mech. 1985, 21, 31–48. [Google Scholar] [CrossRef]
- Xu, K.; Wong, C.; Yan, B.; Zhu, H. A High Strain Rate Constitutive Model for High Strength Steels; SAE Technical Paper; SAE International: Warrendale, PN, USA, 2003; ISSN 0148-7191. [Google Scholar] [CrossRef]
- Vedantam, K.; Bajaj, D.; Brar, N.S.; Hill, S. Johnson-Cook strength models for mild and DP 590 steels. AIP Conf. Proc. 2006, 845, 775–778. [Google Scholar] [CrossRef]
- JIS G 3109 2010; Steel Bars for Prestressed Concrete. Japan Industrial Standard (JIS): Tokyo, Japan, 2010.
- Samantaray, D.; Mandal, S.; Bhaduri, A.K. A comparative study on Johnson Cook, modified Zerilli–Armstrong and Arrhenius-type constitutive models to predict elevated temperature flow behaviour in modified 9Cr–1Mo steel. Comput. Mater. Sci. 2009, 47, 568–576. [Google Scholar] [CrossRef]
- Akbari, Z.; Mirzadeh, H.; Cabrera, J.M. A simple constitutive model for predicting flow stress of medium carbon microalloyed steel during hot deformation. Mater. Des. 2015, 77, 126–131. [Google Scholar] [CrossRef] [Green Version]
- Maheshwari, A.K. Prediction of flow stress for hot deformation processing. Comput. Mater. Sci. 2013, 69, 350–358. [Google Scholar] [CrossRef]
- He, A.; Xie, G.; Zhang, H.; Wang, X. A comparative study on Johnson–Cook, modified Johnson–Cook and Arrhenius-type constitutive models to predict the high temperature flow stress in 20CrMo alloy steel. Mater. Des. 2013, 52, 677–685. [Google Scholar] [CrossRef]
- Wang, X.; Shi, J. Validation of Johnson-Cook plasticity and damage model using impact experiment. Int. J. Impact Eng. 2013, 60, 67–75. [Google Scholar] [CrossRef]
- Murugesan, M.; Lee, S.; Kim, D.; Kang, Y.H.; Kim, N. A Comparative Study of Ductile Damage Models Approaches for Joint Strength Prediction in Hot Shear Joining Process. Procedia Eng. 2017, 207, 1689–1694. [Google Scholar] [CrossRef]
- Bai, Y.; Wierzbicki, T. A new model of metal plasticity and fracture with pressure and Lode dependence. Int. J. Plast. 2008, 24, 1071–1096. [Google Scholar] [CrossRef]
- Bao, Y. Dependence of ductile crack formation in tensile tests on stress triaxiality, stress and strain ratios. Eng. Fract. Mech. 2005, 72, 505–522. [Google Scholar] [CrossRef]
- Bridgman, P. Studies in Large Plastic Flow and Fracture with Special Emphasis on the Effects of Hydrostatic Pressure, 1st ed.; McGraw-Hill: New York, NY, USA, 1952. [Google Scholar]
- Bao, Y.; Wierzbicki, T. On fracture locus in the equivalent strain and stress triaxiality space. Int. J. Mech. Sci. 2004, 46, 81–98. [Google Scholar] [CrossRef]
- Dassault Systemes Simulia. Abaqus; Dassault Systemes Simulia: Providence, RI, USA, 2021. [Google Scholar]
- Dassault Systemes Simulia. Abaqus Analysis User’s Manual; Dassault Systemes Simulia: Providence, RI, USA, 2021. [Google Scholar]
- GOM GmbH. GOM Correlate. GOM-Precise Industrial 3D Metrology, Braunschweig, Germany. Available online: https://www.gom.com/index.html (accessed on 22 May 2021).
- GOM GmbH. Inspection—3D Testing. In GOM Correlate Professional V8 SR1 Manual Basic; GOM mbH: Braunschweig, Germany, 2015. [Google Scholar]
- GOM GmbH. Digital Image Correlation and Strain Computation Basics. In GOM Testing-Technical Documentataion; GOM mbH: Braunschweig, Germany, 2015. [Google Scholar]
- Hillerborg, A.; Modéer, M.; Petersson, P.E. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements. Cem. Concr. Res. 1976, 6, 773–781. [Google Scholar] [CrossRef]

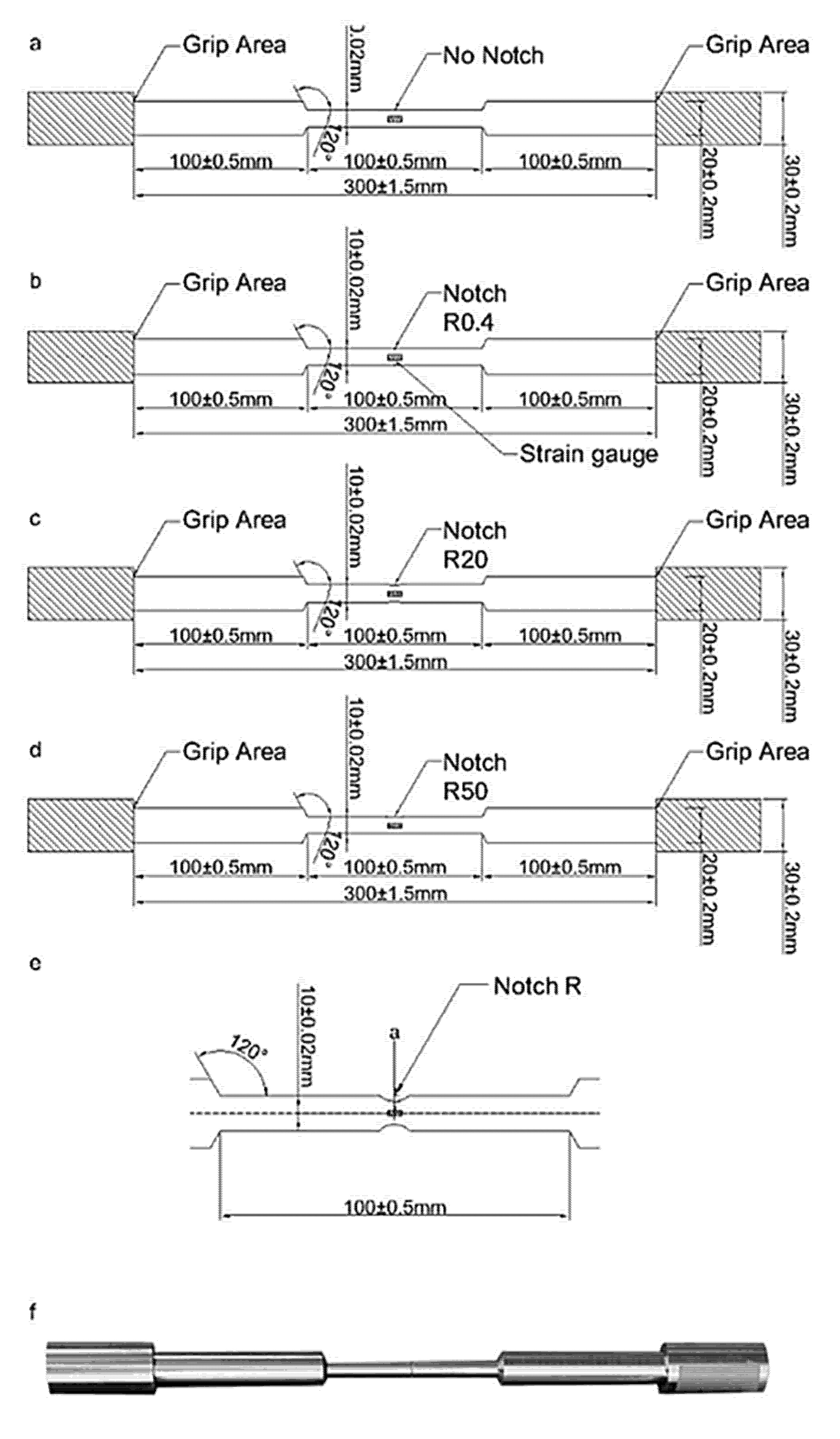
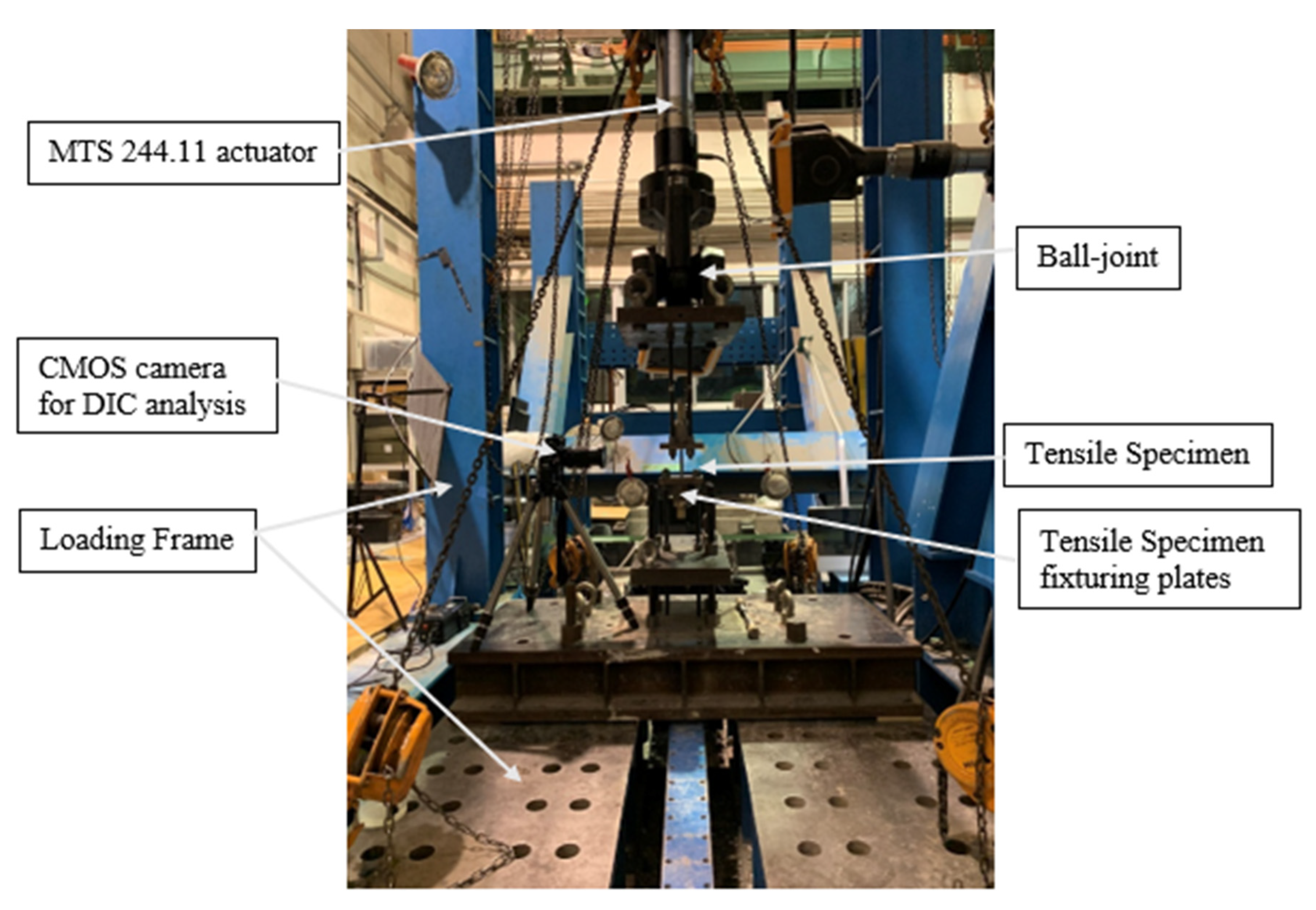
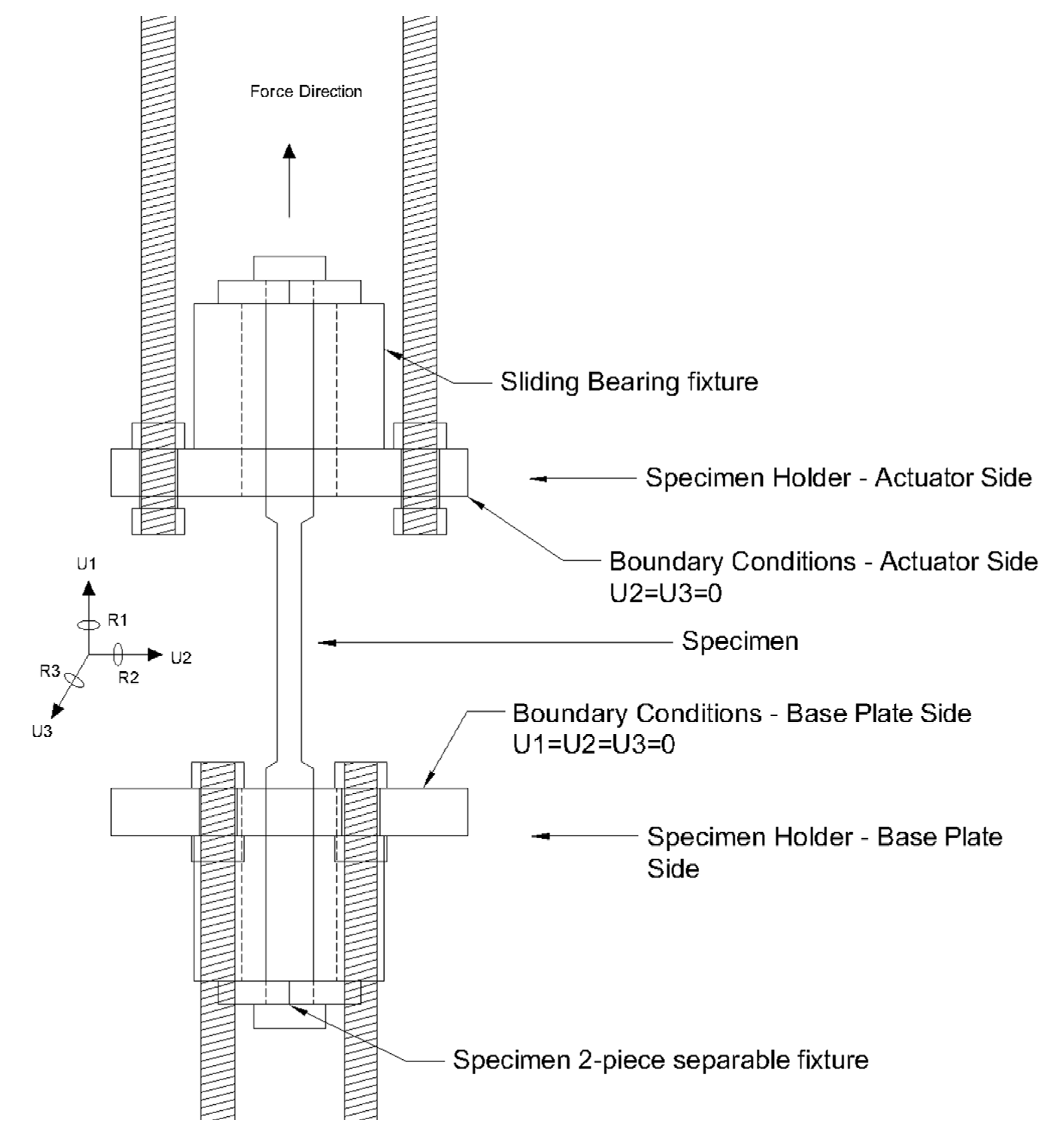






| C | Si | Mn | P | S | Cu |
|---|---|---|---|---|---|
| 0.60–0.65 | 0.12–0.32 | 0.30–0.60 | ≤0.030 | ≤0.035 | ≤0.30 |
| Specimen Nomenclature | Testing Speed (mm/s) | Strain Rate during Tensile Test (s−1) | Specimen Type | Radius R (mm) | Minimum Radius A (mm) | |
|---|---|---|---|---|---|---|
| C1_0.001_NR | 0.1 | 0.001 | Smooth | - | - | 0.333 |
| C2_0.001_NR | 0.1 | 0.001 | Smooth | - | - | 0.333 |
| C3_0.001_NR | 0.1 | 0.001 | Smooth | - | - | 0.033 |
| D1_0.5NR | 50 | 0.5 | Smooth | - | - | 0.333 |
| D2_0.5NR | 50 | 0.5 | Smooth | - | - | 0.333 |
| D3_0.5NR | 50 | 0.5 | Smooth | - | - | 0.033 |
| D1_1NR | 100 | 1 | Smooth | - | - | 0.333 |
| D2_1NR | 100 | 1 | Smooth | - | - | 0.333 |
| D3_1NR | 100 | 1 | Smooth | - | - | 0.033 |
| D1_2NR | 200 | 2 | Smooth | - | - | 0.333 |
| D2_2NR | 200 | 2 | Smooth | - | - | 0.333 |
| D3_2NR | 200 | 2 | Smooth | - | - | 0.033 |
| C4_0.001R20 | 0.1 | 0.001 | Notched | 20 | 4.5 | 0.484 |
| C5_0.001R20 | 0.1 | 0.001 | Notched | 20 | 4.48 | 0.484 |
| C6_0.001R50 | 0.1 | 0.001 | Notched | 50 | 4.5 | 0.395 |
| C7_0.001R50 | 0.1 | 0.001 | Notched | 50 | 4.48 | 0.394 |
| C8_0.001R0.4 | 0.1 | 0.001 | Notched | 0.4 | 4 | 2.867 |
| C9_0.001R0.4 | 0.1 | 0.001 | Notched | 0.4 | 3.98 | 2.961 |
| A (MPa) | B (Mpa) | C | n |
|---|---|---|---|
| 933 | 1295 | 0.0221 | 0.5376 |
| D1 | D2 | D3 | D4 | D5 |
|---|---|---|---|---|
| 0.0165 | 0.6622 | −6.4791 | −0.0279 | 0 |
| Post-Yielding Stress (MPa) | Ultimate Stress (MPa) | Fracture Strain | |
|---|---|---|---|
| Avg. Experimental 0.001 s−1 strain rate | 997 | 1231 | 0.111 |
| Numerical 0.001 s−1 strain rate | 971 | 1261 | 0.101 |
| 0.001 s−1 strain rate error (%) | 2.67 | −2.4 | 0.1 |
| Avg. Experimental 0.5 s−1 strain rate | 1069 | 1272 | 0.087 |
| Numerical 0.5 s−1 strain rate | 1041 | 1271 | 0.084 |
| 0.5 s−1 strain rate error (%) | 2.69 | 0.01 | 3.57 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gkolfinopoulos, I.; Chijiwa, N. Determination of Johnson–Cook Material and Failure Model Constants for High-Tensile-Strength Tendon Steel in Post-Tensioned Concrete Members. Appl. Sci. 2022, 12, 7774. https://doi.org/10.3390/app12157774
Gkolfinopoulos I, Chijiwa N. Determination of Johnson–Cook Material and Failure Model Constants for High-Tensile-Strength Tendon Steel in Post-Tensioned Concrete Members. Applied Sciences. 2022; 12(15):7774. https://doi.org/10.3390/app12157774
Chicago/Turabian StyleGkolfinopoulos, Ioannis, and Nobuhiro Chijiwa. 2022. "Determination of Johnson–Cook Material and Failure Model Constants for High-Tensile-Strength Tendon Steel in Post-Tensioned Concrete Members" Applied Sciences 12, no. 15: 7774. https://doi.org/10.3390/app12157774
APA StyleGkolfinopoulos, I., & Chijiwa, N. (2022). Determination of Johnson–Cook Material and Failure Model Constants for High-Tensile-Strength Tendon Steel in Post-Tensioned Concrete Members. Applied Sciences, 12(15), 7774. https://doi.org/10.3390/app12157774






