Abstract
Satellite-derived environmental parameters play important roles in environmental research on global changes and regional resources. Atmosphere effects and sensor limitations often lead to data products that vary in quality. The main goal of time series data reconstruction is to use various statistical and numerical analysis methods and to stimulate changing seasonal or annual parameters, providing more complete data sets for correlational research. This paper aims to develop a time series reconstruction algorithm for LST based on data assimilation according to the current problems of unstable precision and unsatisfactory results, and the simplistic effects of evaluation methods while using remote sensing-derived LST data as the basic parameters and the daily LST data derived from the static meteorological satellite GMS-5 as the input data. The data assimilation system used the Kalman filter as the assimilation algorithm. A complete set of global refined LST time series data sets were obtained by constantly correcting the LST values according to the regional ground-based observations. This method was implemented using MATLAB software (version R2017a), and was applied and validated through partitioning using the principal elevation in the Beijing, Tianjin, and Hebei regions. The results show that the accuracy of the reconstructed LST data series improved significantly in terms of the mean and standard deviation. Better consistency was achieved between the variables obtained over a year from the reconstructed LST data and the ground observations from the LST data set.
1. Introduction
Land surface temperature (LST) is one of the most important physical parameters in surface–atmosphere interactions, and is of great importance in many related disciplines such as global environmental change and ecological evolution [1]. As a dynamic thermal equilibrium parameter, the land surface temperature is impacted by the land surface energy balance (SEB) process. It is a dynamically changing time series parameter. In addition, land surface temperatures that are obtained by remote sensing inversion are transient samples that can have temporal or spatial gaps or can be unstable as a result of the effects of factors such as the two-way reflection of clouds and land objects [2,3]. Additionally, the distribution of an LST obtained by remote sensing inversion in land SEB studies is often inaccurate due to factors such as the indirectness and morbidity of the remote sensing inversion data. To overcome the problems of missing and low-quality data, Moderate Resolution Imaging Spectroradiometer (MODIS) products deliver level three 10-day and monthly synthetic data. However, although applying interpolation and iteration to such data solves the problem of temporal and spatial gaps in the data to some degree, missing and inaccurate data are still severe problems that affect studies of regional land surface energy parameters, directly affecting the accuracy and effects of subsequent land surface process modeling [4].
Data assimilation is a method in which new observational data are merged during the dynamic execution of a numerical model based on the data’s temporospatial distribution as well as the data’s observational and background errors [5,6,7]. The core of land surface data assimilation is to merge direct and indirect data from difference sources and different resolutions in the dynamic framework of land surface process modeling to accurately and consistently estimate each component of the hydrological and energy cycles of the land surface.
By integrating surface models and satellite data using data assimilation, Chen established a framework for the assimilation of multisource remote sensing data combined with the simultaneous estimation of states and parameters to provide accurate estimates of soil moisture on the Tibetan Plateau, providing a practical method for improving simulation accuracy when determining soil moisture [8]. Li used above-ground biomass (AGB) from Zhejiang Province to assimilate MODIS LAI (leaf area index) products, which resulted in the assimilated LAI spatio-temporal data being much more accurate compared to the observed LAI, and the changes in the assimilated LAI time series were consistent with the seasonal dynamics of bamboo forest growth [9].
As research regarding land surface data assimilation continues to become more in depth, optimization algorithms that are suitable for land surface data assimilation are being developed rapidly. Since the 1960s, the Kalman filter algorithm has been widely used in the fields of Global Positioning System (GPS) navigation, aircraft orbit correction, human–robot interaction, radar systems and missile tracking, and deformation monitoring [10,11,12,13,14]. Recently, it has been applied to practical studies, such as those on sensor data merging and microeconomics [15,16]. In addition to applications in industrial and socio-economical areas, the Kalman filter has been used in meteorology and Earth sciences. Fu et al. and Zhang introduced ground meteorological observations and meteorological satellite data and assimilated them using the Kalman filter. The reconstructed time series of solar radiation exhibited greater consistency with the in situ data set than with the time series before the optimization [17,18]. Tian et al. developed a data assimilation framework using Kalman filtering to simultaneously assimilate satellite soil moisture retrievals from the Soil Moisture Active Passive (SMAP) and Soil Moisture and Ocean Salinity (SMOS) missions using the Australian Water Resources Assessment Landscape model (AWRA-L). The results show an increased correlation between simulated surface soil moisture and in situ observations [19].
Recent studies have demonstrated that data assimilation techniques have great potential for time series reconstruction. Masiello implemented a Kalman filter approach to apply temporal constraints on the retrieval of surface emissivity and temperature from radiance measurements, and the results show that the Kalman filter strategy can retrieve temperature simultaneously with an accuracy of ±0.2 K [20]. Xu proposed a new fusion strategy for generating high-quality, all-weather LST data based on cumulative distribution function (CDF) matching and multiresolution Kalman filtering (MKF) [21]. Jia reconstructed hypothetical clear sky LST with missing or possibly cloud-contaminated pixels by assimilating high-quality satellite retrieval data into a time-evolution model built from reanalysis data through a Kalman filter data assimilation algorithm [22]. However, regarding the current reconstruction of land SEB parameters, the most prominent problem is the lack of systematic analysis and assessment methods for the reconstruction effect, including analyses of the “true value” determination and scale effects [23,24,25,26]. This study selects land surface temperature, one of the land surface energy parameters, as the object; addresses adoptability problems common to current remote-sensing inversion methods and the instability in the data accuracy; and uses the Kalman filter for data assimilation to take land surface in situ data continuously, improve the forecast accuracy, and ensure that the reconstructed land surface temperature series are more similar to the in situ data. We also extend this technique to the entire study area using the derived linear regression equation, thereby obtaining a complete time series of the land surface temperature in the study area, which can be used to obtain the refined long-term land surface temperature at larger scales.
2. Summary of Study Area and Data Sources
2.1. Summary of Study Area
The Beijing–Tianjin–Hebei (Jing–Jin–Ji) region refers to a region consisting of three districts, Hebei Province and its inner rings of Beijing and Tianjin (Figure 1), which are located in the northern part of eastern China. The region’s topographic elevation decreases gradually from northwest to southeast, and it comprises a mountainous and plain-dominated landscape. The Beijing–Tianjin–Hebei region is located on the east coast of the mid-latitude Eurasian continent, and it has a typical temperate semi-humid and semi-arid continental monsoon climate. The four seasons are able to be distinguished from one another, and precipitation is concentrated in significant wet and dry periods. The north–south temperature difference in this region is very large. Taking the Great Wall as the border, the average temperature up to the north of the Great Wall is less than 10 °C, whereas that of the northern Bashang Plateau is only −0.5 °C. The temperature to the south of the Great Wall is higher than 10 °C, and the annual mean temperature of the southern plain of Handan is 14.2 °C. The north–south temperature difference is 14.7 °C. The average temperature in the coldest month, January, ranges from −2 °C to −16 °C, and the temperature in the hottest month, July, ranges from 20–28 °C, with a north–south temperature difference of 22–44 °C [27].
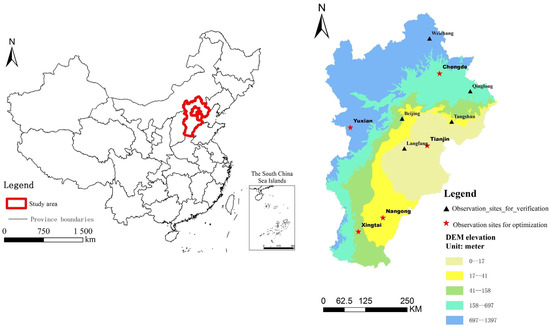
Figure 1.
Study area and distribution of observation sites.
The zoning criteria of the study area are based on the relationship between elevation and altitude. We determined the zoning of the study area using US Geological Survey (USGS) digital elevation model (DEM) data with a resolution of 30 m according to the elevation of each station and basic principles, including the average distribution of stations at a similar elevation, a combination of concurrent occurrence and the relative homogeneity of regional climate characteristics, and the continuity of the spatial distribution (Figure 1). We assumed that natural conditions, including the elevation, precipitation, dryness, and topography within a zone, were generally consistent.
2.2. Data Source
The remote sensing imagery data used in this study are from the Chinese Energy and Water Balance Monitoring System (CEWBMS), which was jointly built by the National Meteorological Administration, the Institute of Geographic Sciences and Natural Resources Research, and the Chinese Academy of Sciences. Land surface remote sensing imagery is one of the standard products obtained from this system. This system uses the Japan GMS (geostationary meteorological satellite) as its data source [28]. The land surface temperature in this study is one of the CEWBMS’ standard energy products, of which the spatial resolution is 5 km × 5 km [29].
This study uses data from 24 land surface temperature observation stations in the Beijing–Tianjin–Hebei region and their corresponding daily average surface temperatures, which were provided by the China Meteorological Science Data Sharing Centre [30]. We use the location coordinates of the 24 stations to retrieve the remote sensing-inverted daily land surface temperature data for the Beijing–Tianjin–Hebei region from 2002 for each station during that year. We introduce the daily average surface temperature of the observation stations into the Kalman filter as the “true value” to optimize the remote sensing inversion data. In addition, we obtain DEM elevation raster data with a resolution of 30 m from the USGS website, which are used to determine the elevations of the observation stations. We use the elevation data to determine a zoning strategy based on previous knowledge. Based on the characteristics of the standard products of the CEWBMS in combination with the land surface data for the study area and numerous experiments, this study selects the land surface temperature from 2002 as the study object to conduct time series reconstruction.
3. Method
3.1. Kalman Filter-Based Reconstruction Algorithm
A Kalman filter was used as the reconstruction algorithm in this study. In 1960, Kalman et al. [31] proposed the concept of a Kalman filter for the state estimation of stochastic processes. The method has been modified and widely applied in many fields of research and has been adopted as one of the most traditional data assimilation algorithms [32,33,34].
The Kalman filter is a sequential mathematical procedure for data assimilation that operates through a prediction and correction mechanism. The filter is sequential because it recalculates the solution each time a new measurement is available without using old data again. This procedure obtains a new estimate of the state from its previous estimate by adding a correction term that incorporates the information provided by new measurements, so that the prediction error is statistically minimized.
The Kalman filter addresses the general problem of trying to estimate the state of a discrete-time-controlled process that is governed by the linear stochastic difference equation [35,36].
The evolution over time of the quantity to be estimated is described, expressed by means of a state vector . The transition between states and is characterized by the transition matrix and the addition of a Gaussian white noise with covariance matrix .
The measurement vector relates to the state of the system through the measurement matrix and the addition of a Gaussian white noise with covariance matrix .
The random variables and represent the process and measurement noise, respectively. These factors are assumed to be independent (of each other), composed of white noise, and with normal probability distributions. In practice, the process noise covariance and measurement noise covariance matrices and might change with each time step or measurement; however, here, we assume that they are constant. The matrix in the measurement Equation (2) relates to the state to the measurement. In practice, might change with each time step or measurement, but, here, we assume it is constant, .
where is the nonnegative covariance matrix of and is the positive covariance matrix of .
We define N as the number of days of measurement, then define N as the number of days of measurement, then
We define to be our a state estimate at step , given knowledge of the process prior to step , and is our a state estimate at step , given measurement . We can then define the state as follows
The a estimate of the error covariance is as follows
The a estimated error covariance is as follows
In this phase, the new state vector and its covariance matrix are calculated. For this, the predicted covariance is used to calculate the Kalman gain . The new state vector is calculated adding to the predicted state vector and the measurement residual scaled with the Kalman gain.
3.2. Study Procedure
This study introduces a data assimilation technique for time series reconstruction, uses the data assimilation technique to connect remote sensing parameters and ground observations, and calibrates errors caused by the time trajectories of the remote sensing parameters and errors in the output of the simulation continuously. In combination with the Kalman filter, this study uses the daily average land surface temperature from the ground observation stations to filter and optimize the remote sensing-inverted land surface temperature time series and divides the area into zones according to DEM elevation data to build a corresponding fitting function and method to optimize the land surface temperature of the entire study area.
- At the pixel scale, we obtained the daily average surface temperature of the ground observation stations at different sites and the GMS-5-based remote sensing inversion data for the surface temperature, applied the Kalman filter to reconstruct a short-period time series of the land surface temperature from the retrieved remote sensing inversion data, and analyzed the accuracy of the reconstruction.
- For the post-reconstruction land surface temperature of each station, we built a linear fitting function using the “sub-regional and per-seasonal” method and developed a technical scheme for reconstructing the land surface temperature time series. We assumed that the conditions in each zone, including the elevation, precipitation, dryness, and topography, were generally consistent and divided the study area according to its seasonal characteristics (spring, summer, autumn, and winter). According to the land surface temperature inverted by means of remote sensing during each season in 2002 in each zone and the Kalman filter reconstruction values, we applied the least squares method to build linear fitting functions to obtain the empirical coefficient for each season and to then build a first-order linear regression function based on the fitting functions between the remote sensing inversion data and refined value of each sub-region and season in 2002.
- We optimized the original remote sensing inversion of the land surface temperature in each sub-region of the study area, analyzed and compared the accuracy and rationality of the land surface temperatures of the representative stations before and after the reconstruction, and drew conclusions. We used the established fitting function of each zone and season to calculate the remote sensing inversion data using a raster calculator, obtaining the spatial distribution of the optimized land surface temperature in the study area and the refined values for the other stations. Regarding the optimized land surface temperature, we selected the representative stations in the area for validation to analyze and compare the accuracy and rationality of the land surface temperature before and after reconstruction and conducted an error analysis.
The full procedure is explained in the flowchart of Figure 2.
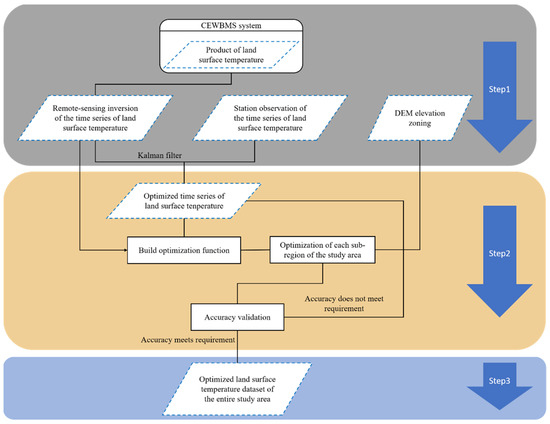
Figure 2.
Flowchart of the operation of the study.
4. Results and Discussion
4.1. Station-Based Reconstruction of Land Surface Temperature
When validating the accuracy of the remote sensing inversion of the land surface temperature and considering the effect of the elevation on the temperature, we found that the precipitation, dryness, and topography of this region were generally consistent. This study divides the existing land surface temperature observation stations in the Beijing–Tianjin–Hebei region into five sub-regions based on the DEM elevation data. We selected one meteorological station from each sub-region to conduct a correlation analysis between the in situ remote sensing inversion of the land surface temperature and the observed daily average temperature.
This study uses data from 24 ground meteorological stations in the Beijing–Tianjin–Hebei region and their corresponding daily average surface temperatures provided by the China Meteorological Data Sharing Service Network. We selected observation stations with a near-average elevation for each sub-region to retrieve the remote sensing-inversed data for the daily land surface temperature in 2002 from these five stations. In addition, we introduced the in situ data for the daily average land surface temperature from the observation station into the Kalman filter as the “true value” to optimize the remote sensing-inversed data. The statistics before and after the reconstruction are presented in Table 1.

Table 1.
The statistics of the optimized surface temperature data compared to the original data from five stations in the Beijing–Tianjin–Hebei region in 2002.
The statistical results presented in Table 2 indicate that after Kalman filter reconstruction, the average root-mean-square error (RMSE), Pearson’s coefficient, and mean absolute error (MAE) of the land surface temperature at each station improved significantly. Moreover, the change in the time series is more consistent with the change in the ground meteorological observations. Therefore, this confirms that the Kalman filter is able to optimize the time series of the short-period land surface temperature data well.

Table 2.
Correlation analysis of the remote sensing-retrieved data and the in situ values at five stations in the Beijing–Tianjin–Hebei region.
4.2. The Reconstruction of Land Surface Temperature Time Series on a Regional Scale
After applying the Kalman filter, we obtained the refined values of the inversed remote sensing data for the land surface temperature time series. However, this algorithm cannot be extended spatially. The remote sensing inversion of the land surface temperature represents the value of a land surface unit with an area of approximately 25 km2. Table 1 indicates that it is possible to build a good linear correlation between the land surface observations from the five stations in the Beijing–Tianjin–Hebei region and the image pixels with a certain area.
We used the remote sensing inversion of each observation station, including those in Tianjin, Nangong, Xingtai, Chengde, and Yuxian, and the values after Kalman filter reconstruction to build a linear fitting function for each station. The obtained function coefficients are listed in Table 3. We built a fitting equation between the remote sensing inversion value and the refined value for 2002 for each sub-region and season and applied the fitting function to the sub-region in which the station is located to obtain the refined value of the land surface temperature for each season and sub-region.

Table 3.
Fitting equation coefficients for each region and season in 2002.
We applied the linear fitting functions with the coefficients listed in Table 3 to calculate the remote sensing inversion data for the corresponding sub-regions in the study area, thereby obtaining eight optimized spatial distribution maps of land surface temperature in the study area. Next, we used 15 February, 15 May, 15 August, and 15 November as examples of each of the four seasons in 2002 to optimize the remote sensing inversion of the land surface temperature of each sub-region in the study area. The reconstruction results are shown in Figure 3.
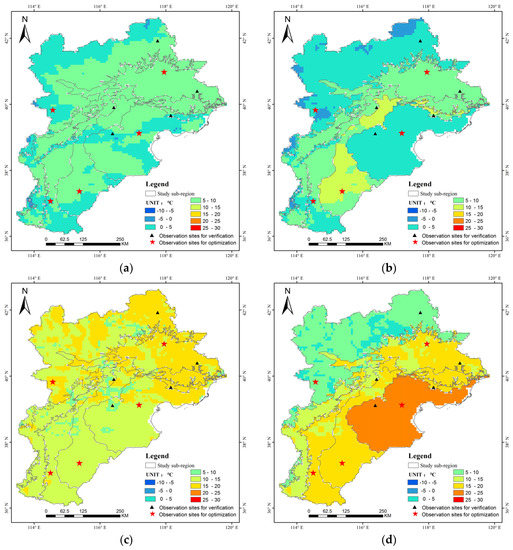
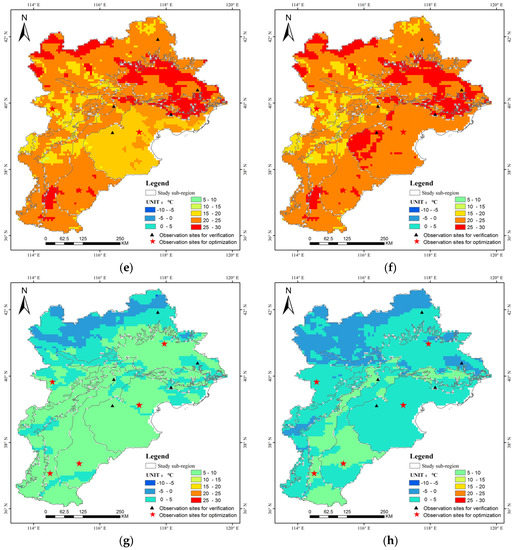
Figure 3.
The spatial distribution of the land surface temperature in the Beijing–Tianjin–Hebei region in 2002 before and after reconstruction. (a,b) 15 February; (c,d) 15 May; (e,f) 15 August; and (g,h) 15 November.
With the exception of the land surface temperature observation stations used for the fitting equations, the other ground meteorological observation stations were used to validate the optimized results of the study area. We selected Langfang, Tangshan, Beijing, Qinglong, and Weichang as validation points; conducted a statistical analysis on the 2002 remote sensing inversion of the land surface temperature in these stations (before reconstruction), on the ground meteorological observations, and on the land surface temperature values after the reconstruction of the fitting functions; and obtained the average RMSE, Pearson’s coefficient, and MAE, which are listed in Table 4.

Table 4.
The mean and RMSE of the derived, the in situ, and the reconstructed surface temperature.
Figure 3 shows that the average and Pearson’s coefficient of the land surface temperature values are all more similar after reconstruction than before reconstruction, and the MAE also decreased. In addition, regarding the RMSE, the majority of the land surface temperature observation stations exhibit RMSE values less than those obtained before reconstruction, indicating that the data dispersion decreases. Among the validation points, the RMSE value of the Langfang station after reconstruction is greater than that before reconstruction, but the change is small. This result may be caused by a systematic error.
4.3. Error Analysis and Discussion
The Kalman filter reconstruction results presented in Table 2 and the validation of the reconstruction results for the entire study area presented in Table 4 indicate that the reconstruction of the short-period land surface temperature time series and its application have good overall effects. However, the improvement in the accuracy is not significant at individual stations, which may be caused by the following errors:
First, there could have been a satellite sensor calibration error. Japan’s GMS-5 geostationary meteorological satellite was launched in 1995. It had been running beyond its intended service life, which was intended to end in 2002, or perhaps even in 2000. The functionality of the sensor declined continuously during its extended service life, resulting in its digit number (DN) values only being able to be used after complex calibration and adjustment. The land surface temperature product used in this study was calibrated against GMS-5 data prior to delivery. However, the data still exhibit errors.
Second, remote sensing inversion data are characterized by indirectness and morbidity. The signal received by the sensor is energy from a very complex land surface temperature process that includes atmospheric reflection, absorption, transmission to the land surface, and reflection back. Remote sensing inversion requires a large number of unknown parameters that are usually computed using empirical or semi-empirical formulas. Therefore, the inversion cannot achieve precise quantification. In addition, the parameters that were used in the subsequent atmospheric calibration and model selection are all uncertain, which could have affected the accuracy of the data to some degree.
Third, there could have been an error in the in situ data from the meteorological stations, including systematic errors and accidental errors. In addition, the observations from the meteorological stations are point data, whereas the GMS-5 inversion yields area data. A comparison between the two reveals a fanning out problem from points to areas that neglects the scaling effect to some degree.
Fourth, the method used in this study generates errors from two sources. During Kalman filter application, the initial value is uncertain and requires an empirical range. Thus, the accuracy of the initial value can impact the reconstruction results [37]. During the fitting of the reconstruction functions, according to previous research that found that the LST in situ data and satellite inversions exhibit a linear relationship, we built a simple first-order linear regression equation to spatially extend the reconstruction of the short-period land surface temperature time series that neglected the effects of scaling, complex topography, and environmental factors. Thus, this could have resulted in errors.
5. Conclusions
To solve problems associated with missing data in the time series of remote sensing-inversed energy parameters, this study uses a new method to reconstruct land surface temperature time series based on a data assimilation approach, designs a refined assimilation algorithm that is validated and calibrated in the study area, and develops a technique that is able to reconstruct the remote sensing inversion of the daily land surface temperature to provide more comprehensive and consistent long-term time series data sets for land surface process modeling and related research. The main conclusions are as follows:
- At the site-pixel scale, based on the data assimilation approach, it is possible to effectively improve the accuracy and consistency of the entire data set using reconstruction algorithms such as the Kalman filter. We selected representative stations from the study area, used the Kalman filter as the assimilation algorithm, and continuously introduced the daily average LST in situ into the Kalman filter as the “true value” to optimize the remote sensing inversion data. After Kalman filter reconstruction, the average RMSE, Pearson’s coefficient, and MAE of the land surface temperature were significantly improved. As indicated in Table 1, the average temperature of the Chengde area was 0.65 °C greater than it was before reconstruction, showing an increase of 24.4%. The maximum increase in the RMSE was 18.25%. In addition, the changes in the time series are very consistent with those of the land surface observations. Furthermore, when there is a large number of missing data and poor accuracy, the algorithm is able to reconstruct the missing data, improve the quality of the entire data set, and recover the trends of the original time series. These results indicate that the Kalman filter performs well when optimizing short-period land surface temperature time series.
- Based on the site-scale results, we proposed a “sub-elevation-per season segmentation fitting” scheme that is able to extend the site-based reconstruction method to the entire study area. We performed time series reconstruction and reconstruction on the daily remote sensing inversion data for the land surface temperature over the course of a whole year in the study area and achieved satisfactory application results. This method is based on the following three assumptions: the relationship between the remote sensing inversion data and ground meteorological observations is linear; conditions such as the precipitation, dryness, and topography are generally consistent within each sub-region; and the Kalman filter reconstruction results are reliable. We selected one land surface temperature ground meteorological observation station in each sub-region of the study area, divided the data into four seasons (spring, summer, autumn, and winter), and built linear regression equations based on the relationship between the remote sensing inversion data and the Kalman filter-refined value to optimize each sub-region in the study area. Our validation results reveal that with the exception of Langfang, where the RMSE of the land surface temperature observation station is greater than that before reconstruction, the average and RMSE of the land surface temperatures at the other stations are all closer to the observational averages than they were before reconstruction. The Pearson’s coefficient and MAE of the land surface temperature were significantly improved compared with before reconstruction. The changes in the optimized year-round land surface temperature time series are more consistent with those observed in the ground meteorological observations, and the land surface temperature data are more comprehensive spatially and more continuous temporally.
- This study employed the Kalman filter, which is an auto-regression data processing algorithm for reconstruction, as the data assimilation algorithm. The Kalman filter has been widely used for more than 40 years and has yielded refined solutions for most of the problems that it has been applied in. Recently, numerous scholars have proposed improved algorithms for different applications. Future work can employ new data assimilation methods such as the improved Kalman filter algorithm and Gaussian kernel density estimation to achieve better reconstruction results.
Author Contributions
Conceptualization, R.Q. and L.L.; methodology, R.Q. and L.L.; software, R.Q.; validation, R.Q. and H.Z.; formal analysis, R.Q.; investigation, R.Q.; resources, R.Q.; data curation, R.Q.; writing—original draft, R.Q.; review and editing, L.L. and S.L.; funding acquisition, G.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Resources Science and Technology Program of Hunan Province, Research and Application of Key Technologies for Intelligent Interpretation of Remote Sensing Images (2021-05) and Research on Key Technologies for Monitoring Agricultural Land for Facilities in Hunan Province in the Context of Rural Revitalization (2020-33).
Data Availability Statement
The data presented in this study are available upon request from the first author for noncommercial use.
Acknowledgments
The authors would like to thank the anonymous reviewers for their constructive and valuable comments that significantly contributed to improving this paper. All authors have read and agreed to the published version of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Li, Z.L.; Tang, B.H.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef] [Green Version]
- Rees, M.; Condit, R.; Crawley, M.; Pacala, S.; Tilman, D. Long-term studies of vegetation dynamics. Science 2001, 293, 650–655. [Google Scholar] [CrossRef] [PubMed]
- Defries, R.S.; Townshend, J.R.G. NDVI-derived land coverclassification at a global scale. Int. J. Remote Sens. 1994, 15, 3567–3586. [Google Scholar] [CrossRef]
- Zhou, L.; Tucker, C.J.; Kaufmann, R.K.; Slayback, D.; Shabanov, N.V.; Myneni, R.B. Variations in northern vegetation activity inferred from satellite data of vegetation index during 1981 to 1999. J. Geophys. Res. Atmos. 2001, 106, 20069–20083. [Google Scholar] [CrossRef]
- Abreu, M.C.; de Souza, A.; Lyra, G.B.; Pobocikova, I.; Cecílio, R.A. Analysis of monthly and annual rainfall variability using linear models in the state of Mato Grosso do Sul, Midwest of Brazil. Int. J. Climatol. 2021, 41, E2445–E2461. [Google Scholar] [CrossRef]
- Bouras, E.H.; Jarlan, L.; Er-Raki, S.; Albergel, C.; Richard, B.; Balaghi, R.; Khabba, S. Linkages between rainfed cereal production and agricultural drought through remote sensing indices and a land data assimilation system: A case study in Morocco. Remote Sens. 2020, 12, 4018. [Google Scholar] [CrossRef]
- Reichle, R.H. Data assimilation methods in the Earth sciences. Adv. Water Resour. 2008, 31, 1411–1418. [Google Scholar] [CrossRef]
- Chen, W.; Huang, C.; Yang, Z.L.; Zhang, Y. Retrieving Accurate Soil Moisture over the Tibetan Plateau Using Multisource Remote Sensing Data Assimilation with Simultaneous State and Parameter Estimations. J. Hydrometeorol. 2021, 22, 2751–2766. [Google Scholar] [CrossRef]
- Li, X.; Du, H.; Mao, F.; Zhou, G.; Chen, L.; Xing, L.; Liu, T. Estimating bamboo forest aboveground biomass using EnKF-assimilated MODIS LAI spatiotemporal data and machine learning algorithms. Agric. Forest Meteorol. 2018, 256, 445–457. [Google Scholar] [CrossRef]
- Liu, Y.; Li, S.; Fu, Q.; Liu, Z.; Zhou, Q. Analysis of Kalman filter innovation-based GNSS spoofing detection method for INS/GNSS integrated navigation system. IEEE Sens. J. 2019, 19, 5167–5178. [Google Scholar] [CrossRef]
- Ren, X.; Yang, Y.; Zhu, J.; Xu, T. Comparing satellite orbit determination by batch processing and extended Kalman filtering using inter-satellite link measurements of the next-generation BeiDou satellites. Gps Solut. 2019, 23, 25. [Google Scholar] [CrossRef]
- Li, C.; Fahmy, A.; Sienz, J. An augmented reality based human-robot interaction interface using Kalman filter sensor fusion. Sensors 2019, 19, 4586. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hou, B.; He, Z.; Li, D.; Zhou, H.; Wang, J. Maximum correntropy unscented Kalman filter for ballistic missile navigation system based on SINS/CNS deeply integrated mode. Sensors 2018, 18, 1724. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, N.; Zhang, W.; Liao, K.; Zhu, H.H.; Li, Q.; Wang, J. Deformation prediction of reservoir landslides based on a Bayesian optimized random forest-combined Kalman filter. Environ. Earth Sci. 2022, 81, 1–14. [Google Scholar] [CrossRef]
- Gao, B.; Hu, G.; Gao, S. Multi-sensor optimal data fusion based on the adaptive fading unscented Kalman filter. Sensors 2018, 18, 488. [Google Scholar] [CrossRef] [Green Version]
- Braxton, J.C.; Herkenhoff, K.F.; Rothbaum, J.L.; Schmidt, L. Changing Income Risk across the US Skill Distribution: Evidence from a Generalized Kalman Filter (No. w29567); National Bureau of Economic Research: Cambridge, MA, USA, 2021. [Google Scholar] [CrossRef]
- Fu, J.; Jiang, D.; Huang, Y. A Kalman filter-based method for reconstructing GMS-5 global solar radiation by introduction of in situ data. Energies 2013, 6, 2804–2818. [Google Scholar] [CrossRef]
- Zhang, X. A statistical approach for sub-hourly solar radiation reconstruction. Renew. Energy 2014, 71, 307–314. [Google Scholar] [CrossRef]
- Tian, S.; Renzullo, L.J.; Pipunic, R.C. Satellite soil moisture data assimilation for improved operational continental water balance prediction. Hydrol. Earth Syst. Sci. 2021, 25, 4567–4584. [Google Scholar] [CrossRef]
- Masiello, G.; Serio, C.; De Feis, I.; Amoroso, M.; Venafra, S.; Trigo, I.F.; Watts, P. Kalman filter physical retrieval of surface emissivity and temperature from geostationary infrared radiances. Atmos. Meas. Tech. 2013, 6, 3613–3634. [Google Scholar] [CrossRef] [Green Version]
- Xu, S.; Cheng, J. A new land surface temperature fusion strategy based on cumulative distribution function matching and multiresolution Kalman filtering. Remote Sens. Environ. 2021, 254, 112256. [Google Scholar] [CrossRef]
- Jia, A.; Ma, H.; Liang, S.; Wang, D. Cloudy-sky land surface temperature from VIIRS and MODIS satellite data using a surface energy balance-based method. Remote Sens. Environ. 2021, 263, 112566. [Google Scholar] [CrossRef]
- Prata, A.J.; Cechet, R.P. An assessment of the accuracy of land surface temperature determination from the GMS-5 VISSR. Remote Sens. Environ. 1999, 67, 1–14. [Google Scholar] [CrossRef]
- Wang, M.Y.; Lu, D.R. An improved algorithm to retrieve land surface temperature by GMS 5 data. Chin. J. Geophys. 2005, 48, 1108–1120. [Google Scholar] [CrossRef]
- Wang, H.Q.; Zhao, G.X.; Wang, L.Z. Effect of land surface non-uniformity on land surface temperature retrieval and retrieval tests of land surface temperature by real satellite measurements. J. Infrared Millim. Waves 2003, 22, 191–196. [Google Scholar]
- Jiang, D.; Fu, J.; Huang, Y. Reconstruction of Time Series Data of Environmental Parameters: Methods and Application. Int. J. Geogr. Inf. Sci. 2011, 13, 339–446. [Google Scholar] [CrossRef]
- Li, H.; Zhou, Y.; Jia, G. Quantifying the response of surface urban heat island to urbanization using the annual temperature cycle model. Geosci. Front. 2022, 13, 101141. [Google Scholar] [CrossRef]
- Cai, S.; Guo, L. Japan GMS-5 Meteorological Satellite. Int. Space 1995, 8, 17–20. [Google Scholar]
- Wang, N.; Jiang, D.; Rosema, A. Chinese Energy and Water Balance Monitoring System Based on Remote Sensing Technique. Remote Sens. Inf. 2002, 6, 7–10. [Google Scholar] [CrossRef]
- China Meteorological Data Service Centre. Available online: https://www.nmic.cn//metdata/page/index.html (accessed on 21 January 2022).
- Rosema, A. Using METEOSAT for operational evapotranspiration and biomass monitoring in the Sahel region. Remote Sens. Environ. 1993, 46, 27–44. [Google Scholar] [CrossRef]
- Huang, C.; Li, X.; Lu, L. Retrieving soil temperature profile by assimilating MODIS LST products with ensemble Kalman filter. Remote Sens. Environ. 2008, 112, 1320–1336. [Google Scholar] [CrossRef]
- SAKOV, P.; Bocquet, M. Asynchronous data assimilation with the EnKF in presence of additive model error. Tellus A Dyn. Meteorol. Oceanogr. 2018, 70, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Aravéquia, J.A.; Szunyogh, I.; Fertig, E.J. Evaluation of a strategy for the assimilation of satellite radiance observations with the local ensemble transform Kalman filter. Mon. Weather Rev. 2011, 139, 1932–1951. [Google Scholar] [CrossRef] [Green Version]
- Welch, G.; Bishop, G. An Introduction to the Kalman Filter; University of North Carolina at Chapel Hill: Chapel Hill, NC, USA, 1995. [Google Scholar]
- Fu, M.; Deng, Z.; Zhang, J. Kalman Filtering Theory and Its Application in Navigation System; Science Press: Beijing, China, 2003; pp. 17–22. [Google Scholar]
- Suzdaleva, E.; Utia, A.V. Initial conditions for Kalman filtering: Prior knowledge specification. In Proceedings of the 7th WSEAS International Conference on Systems Theory and Scientific Computation, Athens, Greece, 24 August 2007. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).