Abstract
Building deep shafts in water-rich granite formations with large fissures has difficulties, such as high-water pressure and high construction risks, and is prone to water inrush and shaft flooding. This paper relies on the No. 1 vertical auxiliary shaft project of Gaoligongshan tunnel and obtains the uneven distribution of water pressure on the outside of the lining in the horizontal direction through on-site monitoring data. In order to explain this phenomenon, based on the statistical parameters of actual fractures in the field and the Monte Carlo method, the DFN built in FLAC3D6.0 is used to generate a discrete fracture network, and a dual medium model, considering the distribution of large fractures, is established. The reason for the uneven distribution of water pressure is obtained through research: the large fissures in the surrounding rock make the hydraulic conductivity of each part of the stone body formed after grouting of the surrounding rock different. This results in different osmotic pressures from the hydrostatic pressure outside the grouting ring to the outside of the lining through the grouting ring. Based on the distribution characteristics of water pressure outside the lining, the safety of the lining under non-uniform pressure is studied. The lining safety factor is defined as the ratio of the lining’s normal service limit state load to the actual load. The normal service limit state load is the load when the RFPA software is used to establish a load-structure model to simulate the load when the lining has obvious cracks under the action of external load; the actual load is the monitoring load. The new method and mine design code method are used to evaluate the lining safety and make a comparative analysis. The results show that the new method can effectively calculate the lining safety factor and has a larger safety reserve.
1. Introduction
The pressure on the shaft lining is an important basis for the process of shaft design and support, especially in the water-rich rock stratum. The pressure outside the lining includes surrounding rock pressure and water pressure, in which water pressure plays a major role. At present, the research on the water pressure outside the lining mainly focuses on tunnels and mines. The research shows that the water pressure outside the lining is generally uniformly distributed in the horizontal direction, and the stratum is mostly soil or rock mass with dense joints [1,2,3]. However, there are few studies on water-rich, large, fractured rock mass.
At present, the mathematical models used to simulate fractured rock mass include the continuous medium, dual medium, and discrete fracture network models. J. C. S. Long, Todorka Samardzioska, Chen Jianghong, and other scholars have used the equivalent medium model to study the seepage–stress and seepage–thermal couplings of fractured rock masses. The results show that the equivalent continuum model is suitable for a rock mass with a uniform fracture development and small opening degree [4,5,6,7,8]. The dual medium model is the superposition of two different media, i.e., the porous and fractured media. It is considered that the two media are uniformly and continuously distributed in the entire space, and there are two water heads at each point in the space. For example, scholars Pan, G., Granet, P., Wang, and E. have shown that the model can simulate the seepage of fissure channels in granite, limestone, carbonatite, and other rock masses, and the simulation effect is good [9,10,11,12,13]. The discrete fracture network model considers the rock mass as a discontinuous medium, constructs a three-dimensional fracture network based on the field fracture data, and uses the discontinuous medium seepage theory to study the flow of fluid in the fracture network. Research by Wang, J., D. Gottron., S. Nadimi., etc., show that this model is suitable for rock masses with small fracture density and large fracture size [14,15,16,17]. The above mathematical model can effectively simulate fractured rock mass at the technical level, and the simulation of fractured rock mass depends not only on the selection of model, but also on the construction of fracture network.
Fracture network construction mainly uses the Monte Carlo method [18,19,20,21] or actual fracture acquisition data to generate fractures, as well as the related discrete software (such as DFN (FLAC), PFC, UDEC, 3DEC, etc.), to build discrete fracture network models [22,23,24,25]; fractal geometric theory partitions different fracture distribution areas [26,27]. This method can establish practical fractured rock mass, according to the different fractures (size and direction) in different rock masses, and the simulation effect is good [28,29,30]. The research on the network construction technology and mathematical model of fractured rock mass is relatively mature, but the research on how to effectively simulate the water-rich, large, fractured granite stratum is still blank.
The simulation of fractured rock mass is to better analyze the distribution characteristics of water pressure outside the shaft lining and accurately evaluate the safety of the lining. At present, there is no clear evaluation method for the safety of shaft lining, and the mine design code only gives the safety factor. In recent years, with the rapid development of computer technology, the safety evaluation of shafts mostly adopts quantitative methods. The influence degree and weight of each index are obtained through mathematical model operation, and then the weight is adjusted to determine whether the evaluation object has reached a safe state. Specific methods include the fuzzy comprehensive evaluation method [31,32], evaluation method combined with TOPSIS [33], neural network technology evaluation method [34,35], and so on.
In summary, due to the existence of steeply dipping large fissures in the stratum and their uneven distribution, the construction of deep shafts in water-rich granite strata with large fissures has the characteristics of unclear water pressure distribution, difficult construction, and high-water pressure. Shafts are prone to collapse, water inrush, and other disasters during the construction process. Based on the No. 1 vertical auxiliary shaft project in the Gaoligongshan tunnel, this paper studies the distribution characteristics of water pressure outside the shaft lining and lining safety evaluation, in order to provide guidance for the No. 2 shaft project. The main research ideas are shown in Figure 1.
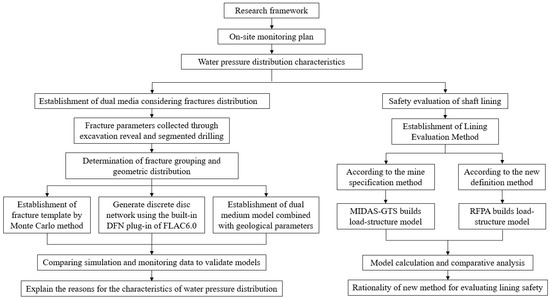
Figure 1.
Research ideas.
2. Analysis of Water Pressure Distribution Characteristics Outside the Lining of No. 1 Vertical Auxiliary Shaft
2.1. Project Overview
The Gaoligongshan tunnel is a key control project of the Dali-Ruili Railway. The terrain and geological conditions are extremely complex. Along the way, it passes through many unfavorable geological bodies, such as fault fracture and fissure water development zones.
The tunnel is set as an auxiliary tunnel plan of “1 through parallel heading + 1 inclined shaft (main and auxiliary shaft) + 2 vertical shafts (main and auxiliary shaft)”. Among them, the main shaft of the No. 1 shaft has a depth of 762.59 m and inner diameter of 6 m; the auxiliary shaft has a depth of 764.74 m and inner diameter of 5.0 m. The main function of the main shaft is to discharge the harmful gas generated and transport the waste residue during the construction process, and the main function of the auxiliary shaft is to transport fresh air, deliver construction materials, equipment, construction personnel, and serve as a safe escape. The stratum of No. 1 shaft is shown in Figure 2.
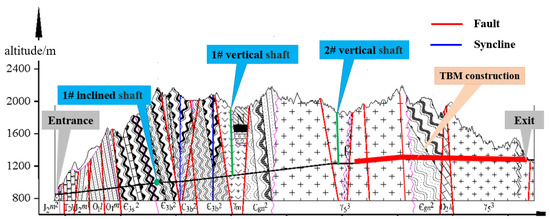
Figure 2.
Strata section of No. 1 vertical shaft.
At about 19:00 p.m. on 15 January 2018, during the mucking and leveling process at a depth of 630.3 m of the auxiliary shaft, the shaft wall on the left side of it suddenly collapsed, forming a “bowl shaped” water inrush point, with a water inflow of about 300 m3/h, resulting in flooding (as shown in Figure 3). On 19 January 2018, YunGui company organized four parties to hold an expert meeting. The analysis showed that, due to the complex hydrogeological conditions around the shaft and lack of understanding of the distribution characteristics of external water pressure of the lining, the pre reinforcement measures in the construction project were unreasonable, thus resulting in the accumulation of groundwater around the shaft wall exceeding its bearing capacity; the shaft wall collapsed and gushed water.

Figure 3.
No. 1 vertical auxiliary shaft flooded. (a) Water inrush; (b) Gushing water; (c) Flooded shaft.
According to the core sample of the drilled rock mass, the revealed depth is 764.74 m. The specific conditions are as follows: 0~9.3 m is strongly weathered stratum, mainly saturated soil, which contains sub prismatic gravel sand, filled with brown-yellow silty clay between particles; breccia is seen in some parts, followed by pebble soil, mainly strongly weathered quartz sandstone, filled with fine round gravel and sandy soil. At 30–70 m is the strongly weathered mixed granite stratum, and the surrounding rock is mainly brownish-yellow mixed granite and gneiss-like structure, containing medium-coarse sand grains; maroon-red iron infestation is occasionally seen along the joint surface. At 9.3~30 and 70~764.74 m are weakly weathered mixed granite strata, with hard lithology, block and fragment structure, general stability, general cementation, and a relatively complete/broken rock mass. The integrity of local surrounding rock of shaft wall is relatively poor, and a small amount of vertical weak interlayer is developed, which easily causes wall caving and dropped pieces (as shown in Figure 4).

Figure 4.
Pictures of weakly and strongly weathered granite. (a) Weakly; (b) Weakly; (c) Strongly; (d) Strongly.
Affected by atmospheric precipitation and surface water, the strata of vertical auxiliary well No. 1 have good water richness, no obvious water barrier, irregular water outlet direction and horizon, hydraulic connection with the outside of the wellbore, and a relatively stable supply. The water pressure increases proportionally with the wellbore, and it is predicted that the maximum water inflow volume of the wellbore is 6200 m3/d, and the maximum hydrostatic pressure is 7.6 MPa. According to the measurement data of the exploration holes, the logging contents include conventional logging (apparent resistivity, spontaneous potential, natural gamma, and gamma), inclinometer, and temperature logging. The logging curves determine four aquifers, which are 154.50–156.25, 340.00–343.70, 495.45–498.90, and 693.50–694.75 m (as shown in Figure 5).
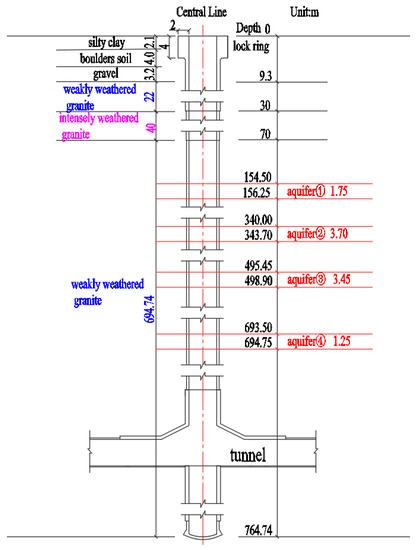
Figure 5.
Geological and hydrological conditions of No. 1 vertical auxiliary shaft.
2.2. Monitoring Plan and Monitoring Data Analysis
2.2.1. Monitoring Plan
The monitoring positions was the S1ZK0 + 660 m (the depth is 660 m) and S1ZK0+735m (the depth is 735 m) sections of the No. 1 vertical auxiliary shaft, which was a mixed granite stratum that contained bedrock fissure water. The water head height of the shaft was basically at the wellhead, which means that the hydrostatic pressure outside the grouting ring was 6.6 MPa and 7.35 MPa, respectively, and groundwater seepage pressure outside the lining was monitored. The specific location and lining type are shown in Figure 6, and the arrangement of test elements is shown in Figure 7.
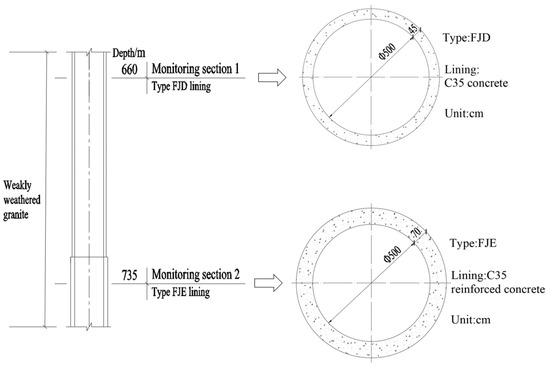
Figure 6.
Monitoring section position and lining type.
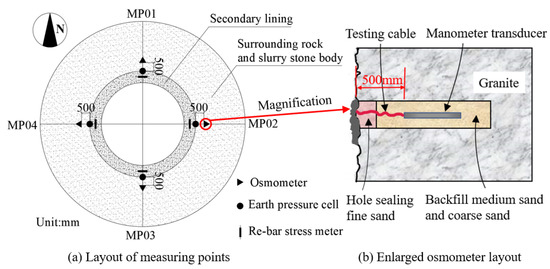
Figure 7.
Layout of measuring points and piezometers.
2.2.2. Monitoring Data Analysis
Through the above monitoring plan, the monitoring results of water pressure outside the lining of the two monitoring planes are shown in Figure 8.
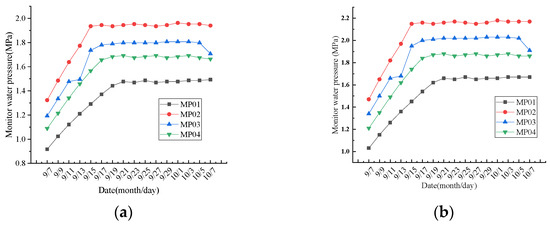
Figure 8.
Monitoring results of water pressure outside the lining at S1ZK0 + 660 m and S1ZK0 + 735 m of the No. 1 vertical auxiliary shaft [36]. (a) S1ZK0 + 660 m; (b) S1ZK0 + 660 m.
From the analysis in Figure 8, it can be seen that the water pressure outside the lining on the same level was unevenly distributed; that is to say, the water pressure values of different measuring points were not equal, and the maximum difference was close to 0.44 MPa, of which, the water pressure range at −660 m was 1.49 ~ 1.94 MPa, and the water pressure range at −735 m was 1.67 ~ 2.17 MPa.
It can be seen from the analysis of monitoring data (as shown in Figure 8) that the water pressure outside the lining on the same level was unevenly distributed, which is inconsistent with common sense. After analysis, it is believed that, due to the uneven distribution of steeply dipping large fissures in the Gaoligongshan stratum (as shown in Figure 9), the hydraulic conductivity of each part of the “slurry-rock mass” stone body formed by the surrounding rock after grouting is different, and the water pressure of the groundwater outside the grouting circle is reduced differently after passing through the grouting circle, thus resulting in different water pressures at different measuring points.

Figure 9.
On-site fissures reveal pictures. (a) On-site fracture picture 1; (b) On-site fracture picture 2.
3. Interpretation of Water Pressure Characteristics Based on Dual Medium Model
3.1. Selection of Research Sections
According to the actual construction and on-site monitoring conditions, the S1ZK0 + 660 m and S1ZK0 + 735 m were selected as the research sections. S1ZK0 + 660 m was lined with FJD type plain concrete, and S1ZK0 + 735 m was lined with FJE type reinforced concrete (as shown in Figure 6).
According to the literature, the indoor hydraulic conductivity of intact granite ranges from 2 × 10−11 to 5 × 10−13 m/s. Scholars, such as Zhongbo Yu [37], gave the hydraulic conductivity of strongly weathered granite a range of 3.3 × 10−6 to 5.2 × 10−5 m/s. In addition, it was learned that most of the engineering geology is weakly weathered granite, so the hydraulic conductivity is in the order of 1 × 10−6 ~ 1 × 10−8 m/s. Through on-site drilling exploration, it was found that the geological RQD values were mostly stable at about 50% and 80%. Therefore, it is considered that the surrounding rock grade of 0 ~ −340 m was grade III, and −340 m ~ −764 m was grade II. Combined with the surrounding rock parameters provided in the “Code for Design of Railway Tunnels”, the model parameters of S1ZK0 + 660 m and S1ZK0 + 735 m are shown in Table 1.

Table 1.
Model geological parameters.
3.2. Establishment of Dual Media Model
When a shaft is built in a rock mass with large fissures, the reduction of the water pressure outside the lining is closely related to the existence of large fissures. Generally speaking, when the fracture is larger, the hydraulic conductivity of the rock mass is larger, and the hydraulic conductivity of the stone body formed after grouting is larger. The osmotic pressure formed by the hydrostatic pressure on the outside of the grouting ring after passing through the grouting ring, that is, the osmotic pressure on the outside of the lining, is also greater. The dual medium model is a combination of porous and fractured media. This model can generate fractures of different sizes and well-simulate large, fractured rock masses. In this paper, the random discrete fracture network (DFN) embedded in FLAC3D is used to establish a dual medium model.
In the fractured rock mass, the Monte Carlo and statistical methods are generally used to generate the same fracture network as the actual fracture. Specific steps: collect on-site fracture parameters (including the number of groups and geometric parameters), perform statistical analysis on the fracture parameters, and use simulation software to generate a fracture network according to the fracture statistics. Figure 10 shows the fractures revealed during the construction of the Gaoligongshan tunnel shaft site.

Figure 10.
On-site construction cracks revealed. (a) On-site fracture picture 1; (b) On-site fracture picture 2.
Since only part of the on-site fissure parameters can be collected through the on-site excavation of the shaft, the fissure parameters inside the rock mass, where the grouting circle is located cannot be collected, use the method of on-site sub-drilling to collect. A total of 66 sub-drilling holes were drilled at the site, with a drilling depth of 771 m. According to the situation revealed by on-site drilling, the fracture parameters were counted. The on-site drilling revealed the situation, as shown in Figure 11.

Figure 11.
Rock mass samples revealed by on-site drilling. (a) 643.40 m–654.70 m; (b) 654.70 m–666.80 m; (c) 666.80 m–678.70 m; (d) 713.30 m–724.50 m; (e) 724.50 m–735.70 m; (f) 735.70 m–747.50 m.
The field revealed that there are about three groups of fractures in the field [38]. Considering the actual situation on the site, with the increase of the excavation depth and influence of geological conditions, such as faults, the changes of the deep in-situ stress field are more complicated. The occurrence of fissures is closely related to the distribution of in-situ stress, so it is necessary to supplement the original basis to investigate the distribution of deep strata fissures. Through the investigation of deep shafts, bottom wells, and strata, it is found that there are still three groups of obvious fissures in deep strata, including two groups of small fissures and one group of large fissures. Considering the computational efficiency and research focus, the research only focuses on the influence of large fractures and ignores small fractures.
According to the research results on the geometric parameters of rock mass fractures, the geometric parameters of rock mass fractures generally obey one or several probability density distributions. Generally speaking, the position of the center point of the fracture obeys a uniform distribution; the length of the trace obeys a negative exponential distribution or log-normal distribution; the occurrence (two-dimensional is described by the inclination of the fracture, and three-dimensional is described by the inclination and inclination of the fracture) is subject to a univariate or bivariate Fisher distribution, bivariate normal distribution, or lognormal distribution, etc. According to the investigation of fissures in the shaft of the Gaoligongshan tunnel, the fissures are divided into three groups, and the center point obeys the uniform distribution, trace length obeys the normal distribution, and occurrence rate obeys the normal distribution. According to the field excavation fissure investigation and subsection drilling investigation, three groups of fissure group parameters are shown in Table 2.

Table 2.
Field revealed fracture group parameters.
Using the built-in DFN plug-in of FLAC3D6.0, select an appropriate area to set random seeds, build a fracture group template according to the fracture group parameters and general law of fracture occurrence distribution, and establish a disc discrete fracture network according to the fracture group template. Then, the fracture network is corrected according to the distribution law of fractures in the field, and the fractures that are too discrete are removed. The constructed fracture network is shown in Figure 12.
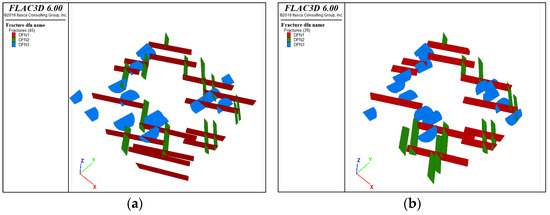
Figure 12.
Establishment of discrete fracture network of two sections. (a) S1ZK0 + 660 m; (b) S1ZK0 + 735 m.
The diameter of the No. 1 vertical auxiliary shaft of the Gaoligongshan tunnel is 5 m, and the influence range of construction excavation is generally 3 to 5 times the diameter; so, the model size plane is taken as 60 m × 60 m. Considering the deep shaft and incomplete data revealed by fractures, only typical fracture development sites were studied. Combined with the fissure group data obtained in the field, the fissure data near the S1ZK0 + 660 m and S1ZK0 + 735 m sections are relatively complete, and the fissure distribution characteristics are obvious, most of which belong to the above-mentioned three groups of fissures. In addition, the distance between the grouting bottom hole and grouting hole radius of the S1ZK0 + 660 m and S1ZK0 + 735 m sections is 5 m, and the effective diffusion radius of the slurry is 2 m; so, the grouting thickness is taken as 6 m. The S1FK0+649.1~+774.74 section adopts the modified urea-formaldehyde resin material, and the grouting parameters are shown in Table 3. Therefore, a dual medium model of S1ZK0 + 660 m and S1ZK0 + 735 m sections was established. The model boundary was set as the permeable boundary, and the displacement of the surrounding and lower boundaries were fixed. The self-weight load, corresponding to the depth, was applied to the upper boundary, and the lateral stress coefficient was taken as 0.8, according to the field test. The two-section model is shown in Figure 13.

Table 3.
Field grouting parameters.

Figure 13.
Dual-medium model diagram of two sections. (a) S1ZK0 + 660 m; (b) S1ZK0 + 735 m.
3.3. Interpretation of the Distribution Characteristics of Water Pressure Outside the Lining
According to the dual medium model established above, the actual hydrostatic pressure outside the grouting ring was used as the boundary condition. By changing the random seed, the osmotic pressure formed by the groundwater reduction through the grouting circle under different fracture conditions was simulated. By setting four water pressure monitoring points in the four directions of the model, the layout of the measuring points was the same as that of the monitoring scheme (as shown in Figure 7, water pressure on the outside of the lining). The monitoring results are shown in Figure 14.
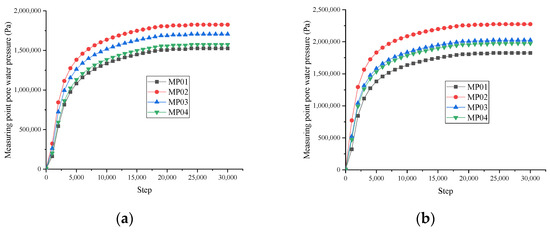
Figure 14.
Simulation of pore water pressure changes at measuring points. (a) S1ZK0 + 660 m; (b) S1ZK0 + 735 m.
It can be seen from Figure 15 that the error range between the simulation results and measured data was −5% to 10%, thus indicating that the simulation results are reasonable. It can be seen from Figure 14 that the pore water pressure on the outside of the lining was unevenly distributed in different directions, which is consistent with the monitoring data.
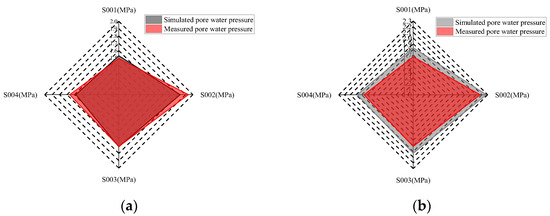
Figure 15.
Comparison of simulation results with monitoring results. (a) S1ZK0 + 660 m; (b) S1ZK0 + 735 m.
Comprehensive analysis shows that, due to the existence of large fissures in the surrounding rock, the hydraulic conductivity of the stone bodies formed after grouting of the surrounding rock in different regions are different. Therefore, when the hydrostatic pressure outside the grouting ring passes through the grouting rings with different hydraulic conductivity in all directions to the outside of the lining, the osmotic pressure in different directions on the outside of the lining is different (as shown in Figure 16).
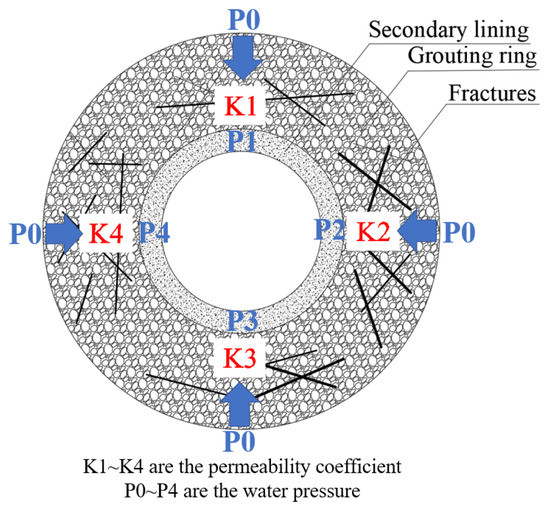
Figure 16.
Description of the principle of water pressure characteristics.
4. Safety Evaluation of Shaft Lining
It can be seen from the above research that the shaft damage was mainly caused by the asymmetric water pressure on the outside of the lining, so it is necessary to evaluate the safety of the lining under asymmetric loads. At present, there is no clear specification for the safety evaluation of tunnel shaft lining. In engineering, the safety of tunnel shaft lining is generally calculated in accordance with the “Code for design of coal mine shaft and chamber”. Therefore, this chapter defines a new method to evaluate the safety of shaft lining and calculates the safety of shaft lining by using the above two methods and conducting a comparative analysis.
4.1. Calculation Method of Safety Factor of Shaft Lining
(1) Calculate the lining safety factor according to the mine code.
The MIDAS-GTS software was used to establish a two-dimensional load-structure model and calculate the axial force and bending moment of the lining. The safety factor of the shaft lining was calculated according to the safety factor calculation formula of “Code for design of coal mine shaft and chamber“.
Shaft linings may occur in two forms of failure: compressive and tensile. The “Code for design of coal mine shaft and chamber“ (GB 50384–2016) stipulates that the bearing capacity of the circular ring section of the concrete shaft wall should be calculated separately under the actions of both uniform and uneven pressure.
Under the action of uniform pressure, the calculation of the safety factor of the bearing capacity of the ring section of the plain concrete shaft wall is shown in Equation (1).
Under the action of uneven pressure, the calculation of the safety factor of the bearing capacity of the ring section of the plain concrete shaft wall is shown in Equation (2).
When the eccentric distance is , it should be calculated according to the following equation:
When the eccentric distance , it should be calculated according to the following equation:
where represents the safety factor; represents the calculated value of axial force on the annular section of shaft wall per meter height, MN/m; represents the stability coefficient of plain concrete members; represents the shaft wall thickness, m; represents the calculated width of shaft wall section, taken as 1.0 m; represents the design value of axial compressive strength, N/mm2; represents the design value of concrete tensile strength, N/mm2; represent the calculated value of axial force of sections A and B, MN; represent the calculated value of bending moment of sections A and B, MN·m; and represents the distance from the point of application of axial force to the point of resultant force, mm.
The specification stipulates that the safety factor of wellbore lining is not less than 1.35 under uniform water and soil pressure, and the safety factor of wellbore lining is not less than 1.1 under uneven water and soil pressure.
(2) Calculate the lining safety factor based on the ratio of the normal service limit state load to the actual load.
The lining analysis model was established using RFPA software, and the field monitoring load around the lining was used as the actual and initial loads; the single-step increment was set to 0.1 MPa for simulation analysis. When the lining has obvious cracks, the load at this time is defined as the normal service limit state load.
When defining the safety factor K to equal the ratio of the normal service limit state load to the actual load, the formula is as follows:
where represents the safety factor, MPa; represents the normal service limit state load, MPa; and represents the actual load, MPa.
4.2. Establishment of Safety Evaluation Model for Shaft Lining
4.2.1. Specific Modeling Method
The MIDAS-GTS software is used to establish a two-dimensional load-structure model, and the inner diameter of the model lining is 5 m. The lining was simulated using beam elements with lining thicknesses of 45 and 70 cm. Model boundaries used surface spring constraints. The pressure applied to the lining was the monitored total pressure (surrounding rock pressure + water pressure), and the axial force and bending moment of the lining under this pressure were calculated.
Method 2: A two-dimensional load-structure model was established by using RFPA software. The size of the model was 7000 × 7000 mm, and the model was divided into 700 × 700 units. Four cavities were, respectively, set on the outside of the lining in four directions, up, down, left, and right, and the actual total pressure (confining pressure + water pressure) on the shaft lining was simulated by applying water pressure in the cavities. The initial pressure head was set in the cavity, and the cavity water pressure was continuously increased by 0.1 MPa per step, until the lining structure was damaged. In order to prevent the whole model from moving, a fixed frame was set on the outside of the cavity. The fixed frame was made of materials with a high elastic modulus and high tensile and compressive strength, and the contact point between the fixed frame and lining had been passivated. According to the actual engineering situation, the failure of the shaft lining occurs after the lining strength reaches the design strength, so the compressive strength of the lining material was selected as the design strength of the concrete material. The Method 2 model is shown in Figure 17.
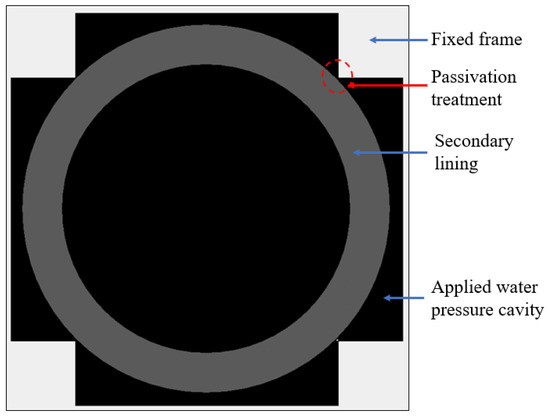
Figure 17.
Method 2 numerical model diagram.
4.2.2. Model Loading Plan
(1) Method 1 model loading plan.
The model load loading scheme is based on the stable value of the field monitoring data (as shown in Figure 8), and the MIDAS-GTS load loading scheme is shown in Figure 18 and Figure 19.

Figure 18.
S1ZK0 + 660 m section MIDAS-GTS load loading plan. (a) Uniform pressure; (b) Non-uniform pressure.

Figure 19.
S1ZK0 + 735 m section MIDAS-GTS load loading plan. (a) Uniform pressure; (b) Non-uniform pressure.
(2) Method 2 model loading plan.
The model load loading plan is based on the stable value of the field monitoring data (as shown in Figure 8). The RFPA load loading plan is shown in Figure 20 and Figure 21.
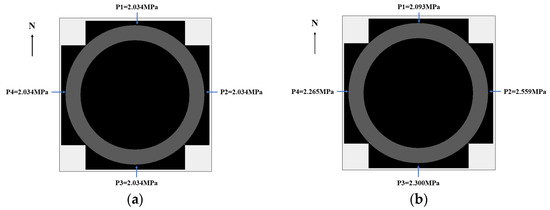
Figure 20.
S1ZK0 + 660 m section RFPA load loading plan. (a) Uniform pressure; (b) Non-uniform pressure.
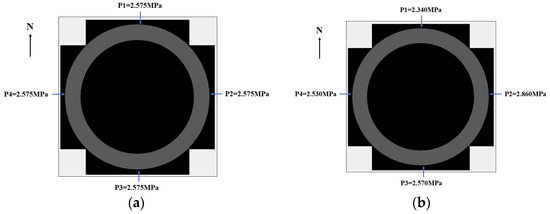
Figure 21.
S1ZK0 + 735 m section RFPA load loading plan. (a) Uniform pressure; (b) Non-uniform pressure.
4.3. Model Calculation Result Analysis
4.3.1. Calculation of Safety Factor of S1ZK0 + 660 m Section Lining
(1) Calculate the lining safety factor according to Method 1.
For the Method 1 loading plan, the simulation results of the S1ZK0 + 660 m section are shown in Figure 22.
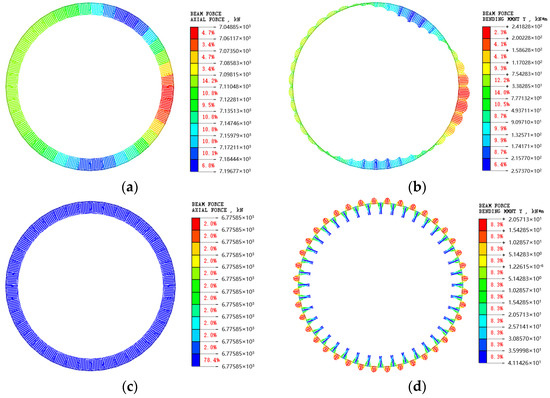
Figure 22.
Simulated internal force of S1ZK0 + 660 m section. (a) Non-uniform axial force diagram; (b) Non-uniform bending moment diagram; (c) Uniform axial force diagram; (d) Uniform bending moment diagram.
It can be seen from Figure 22, that under the action of non-uniform pressure, the maximum bending moment of the lining was 257.4 kN m, and the corresponding axial force was 7198 kN. Under the action of uniform pressure, the maximum bending moment of the lining was 41.2 kN·m, and the corresponding axial force was 6775 kN. The bending moment and axial force were substituted into the formula to obtain the safety factor of the lining structure, as shown in Table 4.

Table 4.
S1ZK0 + 660 m section lining safety factor calculation value, according to Method 1.
It can be seen from Table 4 that the safety factors of the S1ZK0 + 660 m lining section under non-uniform pressure and uniform pressure are 1.9 and 2.1, respectively, and their values were both greater than the minimum values specified in the mine design code, thus indicating that the lining design meets the safety requirements.
(2) Calculate the lining safety factor according to Method 2.
For the Method 2 loading plan, the simulation results of the S1ZK0 + 660 m section are shown in Figure 23 and Table 5.

Figure 23.
S1ZK0 + 660 m lining damage diagram. (a) Uniform pressure (step 15-2); (b) Non-uniform pressure (step 18-1).

Table 5.
S1ZK0 + 660 m section lining safety factor calculation value, according to Method 2.
It can be seen from Table 5 that the safety factors of S1ZK0 + 660 m lining section under non-uniform pressure and uniform pressure are 1.72 and 1.88, respectively, and their values are all greater than the minimum value specified in the mine design code, thus indicating that the lining design meets the safety requirements.
4.3.2. Calculation of Safety Factor of S1ZK0 + 735 m Section Lining
(1) Calculate the lining safety factor according to Method 1.
For the Method 1 loading plan, the simulation results of the S1ZK0 + 660 m section are shown in Figure 24.
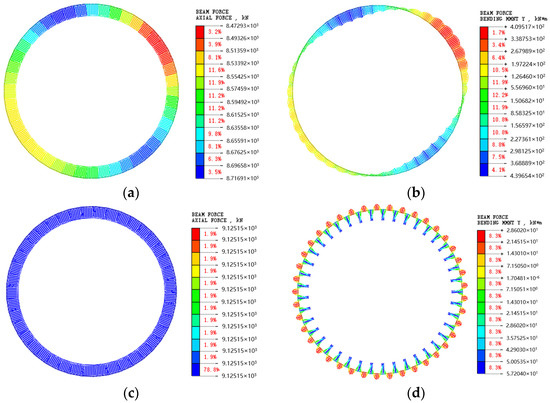
Figure 24.
Simulated internal force of S1ZK0 + 735 m section. (a) Non-uniform axial force diagram; (b) Non-uniform bending moment diagram; (c) Uniform axial force diagram; (d) Uniform bending moment diagram.
It can be seen from Figure 24 that, regarding the simulated internal force of the S1ZK0 + 735 m section, under the action of non-uniform pressure, the maximum bending moment of the lining was 439.7 kN m, and the corresponding axial force was 8187 kN. Under the action of non-uniform pressure, the maximum bending moment of the lining was 57.2 kN·m, and the corresponding axial force was 9125 kN. The bending moment and axial force were substituted into the formula to obtain the safety factor of the lining structure, as shown in Table 6 (the S1ZK0 + 735 m section lining safety factor calculation value, according to Method 1).

Table 6.
S1ZK0 + 735 m section lining safety factor calculation value, according to Method 1.
It can be seen from Table 6, regarding the S1ZK0 + 735 m section lining safety factor calculation value, according to Method 1, that the safety factors of the S1ZK0 + 735 m lining section under non-uniform pressure and uniform pressure were 1.6 and 2.0, respectively, and their values were both greater than the minimum values specified in the mine design code, thus indicating that the lining design meets the safety requirements.
(2) Calculate the lining safety factor according to Method 2.
For the Method 2 loading scheme, the simulation results of the S1ZK0 + 735 m section are shown in Figure 25 and Table 7 (S1ZK0 + 735 m section lining safety factor calculation value, according to Method 2).

Figure 25.
S1ZK0 + 660 m lining damage diagram. (a) Uniform pressure (step 11-2); (b) Non-uniform pressure (step 13-1).

Table 7.
S1ZK0 + 735 m section lining safety factor calculation value, according to Method 2.
It can be seen from Table 7, regarding S1ZK0 + 735 m section lining safety factor calculation value, according to Method 2, that the safety factors of S1ZK0 + 735 m lining section under non-uniform pressure and uniform pressure were 1.43 and 1.51, respectively, and their values were all greater than the minimum value specified in the mine design code, thus indicating that the lining design meets the safety requirements.
4.3.3. Comparative Analysis of the Calculation Results of the Two Methods
In order to illustrate the rationality of the new method and correctness of the evaluation results, according to the calculation results of the above two methods (as shown in Table 8. Comparison of the calculation results of the two methods), they are compared and analyzed.

Table 8.
Comparison of the calculation results of the two methods.
It can be seen from Table 8, regarding the comparison of the calculation results of the two methods, that the newly defined lining safety factor calculation method (Method 2) and lining safety factor calculation method (Method 1), according to the “Code for design of coal mine shaft and chamber”, were consistent in the judgment results of lining safety, thus indicating that the new method can effectively calculate the safety of the lining. In addition, the calculated values of Method 2 were all smaller than the calculated values of Method 1, thus indicating that designing the lining with Method 2 has a greater safety reserve.
5. Conclusions
Relying on the No. 1 vertical auxiliary shaft project in the Gaoligongshan tunnel, this paper adopts on-site monitoring and numerical simulation methods to study the water pressure distribution characteristics and lining safety evaluation technology of deep vertical shafts in water-rich, fractured granite stratum. The main conclusions are as follows:
- (1)
- For a deep shaft located in a water-rich, steep-dipping, large, fractured granite stratum, the water pressure on the outside of the lining on two horizontal planes of the shaft was monitored on-site, and the results showed that the water pressure distribution on the outside of the lining on the same horizontal plane was uneven.
- (2)
- For the uneven distribution of water pressure outside the shaft lining, a dual medium model, considering the existence of cracks, was established, and the reasons for the uneven distribution of water pressure were obtained by analyzing the two sections S1ZK0 + 660 m and S1ZK0 + 735 m. Due to the existence of large fissures in the surrounding rock, the hydraulic conductivity of the stone bodies formed after grouting of the surrounding rock in different regions was different. When the hydrostatic pressure outside the grouting ring reaches the outside of the lining through the grouting rings with different hydraulic conductivity in all directions, the osmotic pressure in different directions on the outside of the lining was different.
- (3)
- Based on the above water pressure distribution characteristics, in order to study the safety of the lining under the action of non-uniform pressure, the ratio of the lining’s normal service limit state load to the actual load was defined as the lining safety factor. The normal service limit state load is the load when the lining has obvious cracks under the action of external load using RFPA software; the actual load is the monitoring load. Using this new method, the safety factors of the lining sections of the shafts S1ZK0 + 660 m and S1ZK0 + 735 m, under the action of non-uniform pressure, were 1.72 and 1.43, respectively. In addition, according to the “Code for Design of Shafts and Chambers of Coal Mine Shafts”, the safety factors of lining sections of vertical shafts S1ZK0 + 660 m and S1ZK0 + 735 m, under the action of non-uniform pressure, were 1.9 and 1.6, respectively. The calculation results of the two methods were both less than the specified value of 1.1, thus indicating that the lining design meets the safety requirements.
- (4)
- Comparing the calculation results of the two methods, it can be seen that, under the same conditions, the judgment results of the two methods for the safety of the lining were consistent, thus indicating that the new method can effectively calculate the safety of the lining. In addition, the calculated values of the new method were all smaller than the calculated values of the mine code method, thus indicating that the design of the lining with the new method has a greater safety reserve.
Author Contributions
Conceptualization, M.H. and X.Y.; software, X.Y. and J.L.; validation, X.Y.; formal analysis, X.Y.; investigation, X.Y.; data curation, X.Y., J.L. and Z.T.; writing—original draft preparation, X.Y.; writing—review and editing, X.Y. and M.H.; supervision, M.H.; project administration, M.H. and Z.T.; funding acquisition, M.H. All authors have read and agreed to the published version of the manuscript.
Funding
The authors acknowledge the financial support provided by the National Key R&D Program (P2019G055) and general program of the National Nature Science Foundation of China (No. 518783).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
Firstly, we thank the authors for their contributions to the article. Secondly, in addition to the authors of the article, Zhangminqing, who works for China Railway Construction Management Co., Ltd., also made important contributions to the conceptualization, project administration, and funding acquisition of the article. Thank you very much.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ren, J. Experimental Study on Water and Soil Pressure Model of Deep Shaft Construction in Highly Permeable Stratum. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2015. [Google Scholar]
- Ru, H.; Mao, W. Water rich characteristics and water inflow calculation of a coal mine aquifer in Xinjiang. China Water Transp. 2012, 12, 176–178. [Google Scholar]
- Lu, Y. Study on Collapse Mechanism of Mixed shaft in Yixin Mine. Ph.D. Thesis, University of Science and Technology Beijing, Beijing, China, 2008. [Google Scholar]
- Long, J.C.S. Porous media equivalents for networks of discontinuous fractures. Water Resour. Res. 1982, 18, 32–37. [Google Scholar] [CrossRef]
- Todorka, S.; Popov, V. Numerical comparison of the equivalent continuum, non-homogeneous and dual porosity models for flow and transport in fractured porous media. Adv. Water Res. 2005, 28, 235–255. [Google Scholar] [CrossRef]
- Gutierrez, M.; Youn, D.-J. Effects of fracture distribution and length scale on the equivalent continuum elastic compliance of fractured rock masses. J. Rock. Mech. Geot. Eng. 2015, 7, 626–637. [Google Scholar] [CrossRef]
- Gao, Y.; Ye, X.; Xia, Q. Numerical simulation of single fracture seepage based on equivalent continuum model. Ground Water 2016, 38, 40–43. [Google Scholar]
- Bai, G.; Liang, B.; Li, S. Water rock coupling mathematical model of equivalent continuous medium under the influence of mining and its application. J. China Coal Soc. 2009, 34, 461–465. [Google Scholar]
- Pan, G.; Wu, Q. Study on seepage and seepage model of dual medium fracture network in Jiaozuo mining area. Carsol. Sin. 1998, 17, 363–369. [Google Scholar]
- Granet, S.; Fabrie, P.; Lemonnier, P.; Quintard, M. A two-phase flow simulation of a fractured reservoir using a new fissure element method. J. Petrol. Sci. Eng. 2001, 32, 35–52. [Google Scholar] [CrossRef]
- Chen, H. Stress of Fractured Rock Mass Injury-Seepage Coupling Theory Experimental and Engineering Application Research. Ph.D. Thesis, Central South University, Changsha, China, 2010. [Google Scholar]
- Zhu, B.; Gao, F.; Yang, J.; Wang, G.; Chen, Z. Simulation study on fracture-pore dual seepage in deep thin-bed coal and rock mass. J. China Univ. Min. Technol. 2014, 43, 987–994. [Google Scholar]
- Pan, X.; Song, L.; Niu, T.; Zhang, Y.; Gao, Y. Geological modeling method of granite buried hill dual-porosity medium reservoir. J. Southwest Univ. Sci. Technol. 2019, 41, 33–44. [Google Scholar]
- Wang, J.; Chen, X.; Zhang, Z. Seepage calculation of fracture water based on discrete fracture network model. Carsol. Sin. 2016, 35, 363–371. [Google Scholar]
- Gottron, D.; Henk, A. Upscaling of fractured rock mass properties—An example comparing Discrete Fracture Network (DFN) modeling and empirical relations based on engineering rock mass classifications. Eng. Geol. 2021, 294, 106382. [Google Scholar] [CrossRef]
- Nadimi, S.; Forbes, B.; Moore, J.; Podgorney, R.; McLennan, J.D. Utah FORGE: Hydrogeothermal modeling of a granitic based discrete fracture network. Geothermics 2020, 87, 101853. [Google Scholar] [CrossRef]
- Wang, P.; Liu, C.; Qi, Z.; Liu, Z.; Cai, M. A Rough Discrete Fracture Network Model for Geometrical Modeling of Jointed Rock Masses and the Anisotropic Behaviour. Appl. Sci. 2022, 12, 1720. [Google Scholar] [CrossRef]
- Zhang, Y.; Peng, L. 3D fracture network of rock mass based on Monte Carlo method model research. J. Gan. Sci. 2020, 32, 124–131. [Google Scholar]
- Cadini, F.; de Sanctis, J.; Bertoli, I.; Zio, E. Monte Carlo simulation of radionuclide migration in fractured rock for the performance assessment of radioactive waste repositories. Reliab. Eng. Syst. Saf. 2013, 111, 241–247. [Google Scholar] [CrossRef]
- Mehmet, S.; Celal, K.; Can, A. Estimating rock mass properties using Monte Carlo simulation: Ankara andesites. Comput. Geosci. 2010, 37, 959–969. [Google Scholar] [CrossRef]
- Ahmed, S.; Ahmad, K.; Shuyu, S. Multi-scale Coupling between Monte Carlo Molecular Simulation and Darcy-Scale Flow in Porous Media. Procedia Comput. Sci. 2016, 80, 1354–1363. [Google Scholar] [CrossRef][Green Version]
- Shan, D.; Yan, T.; Li, W. Random fracture network reservoir and wellbore heat flow coupled numerical simulation. Nat. Gas. Ind. 2019, 39, 143–150. [Google Scholar]
- Zhu, Y.; Wang, X.; Deng, S.; Chen, W.; Shi, Z.; Xue, L.; Lv, M. Grouting process simulation based on 3D fracture network considering fluid-structure interaction. Appl. Sci. 2019, 9, 667. [Google Scholar] [CrossRef]
- Li, D.; Liu, J.; Chen, L. Modification of 3D fracture network modeling technology and its engineering application. J. Under Space Eng. 2020, 16, 1476–1483. [Google Scholar]
- Zhang, J.; Sheng, J.; Huang, T. Study on permeability and fractal characteristics of rock fracture network. Chem. Min. Pro. 2020, 49, 29–34. [Google Scholar]
- Liu, B.; Jin, A.; Gao, Y.; Xiao, S. Research on DFN model construction method based on fractal geometry theory. Rock. Soil. Mech. 2016, 37, 625–630. [Google Scholar]
- Lili, S.; Jian, Y.; Dingbang, C.; Wenjing, M.; Heyuan, W.; Jiwei, Z.; Shuaifeng, Y.; Keliang, C. The fractal description model of rock fracture networks characterization. Chaos Solitons Fractals 2019, 129, 71–76. [Google Scholar] [CrossRef]
- Liu, B.; Yang, Y. Determination of rock mass mechanical parameters of Lijiang tunnel based on the coupling method of discrete fracture network and discrete element. Sci. Technol. Eng. 2020, 20, 9567–9573. [Google Scholar]
- Song, X.; Zhang, C.; Wang, T. Influence of geometric parameters of discrete fracture network on mechanical parameters of fractured rock mass. China Min. Mag. 2021, 30, 160–169. [Google Scholar]
- Cui, W.; Wang, X.; Jiang, Z.; Wang, C.; Wang, X. Simulation research on grouting process of rock mass rough fracture network based on modified cube law. Rock. Soil. Mech. 2021, 42, 2250–2258. [Google Scholar] [CrossRef]
- Wang, X.; Huo, D. Application of fuzzy comprehensive evaluation method in coal mine safety evaluation. China Min. Mag. 2008, 5, 75–78. [Google Scholar]
- Meng, L.; Feng, X. Application of analytic hierarchy process and fuzzy comprehensive evaluation method in coal mine safety production evaluation. Coal. Eng. 2012, 8, 114–116. [Google Scholar]
- Jia, B.; Yin, B.; Wang, H.; Wang, S. AHP coupled TOPSIS coal mine safety evaluation model and its application. China Saf. Sci. J. 2015, 25, 99–105. [Google Scholar]
- Zhou, Z.; Wang, L. Research on coal mine safety early warning evaluation mechanism based on BP neural network. J. Saf. Sci. Technol. 2011, 7, 134–138. [Google Scholar]
- Li, Y.; Cheng, W.; Nan, W. Study on comprehensive evaluation of mine safety based on BP network. China Min. Mag. 2006, 7, 80–83. [Google Scholar]
- Yao, X. Research on Stress Characteristics and Support Technology of Lining in High Water Pressure Deep Shaft. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2021. [Google Scholar]
- Yu, Z.; Huang, Y. Principles of Groundwater Hydrology, 1st ed.; Science Press: Beijing, China, 2008; p. 16. [Google Scholar]
- Li, J.; Wang, Y.; Tan, Z.; Du, W.; Liu, Z. Study on water inflow variation law of No.1 shaft auxiliary shaft in highligongshan based on dual medium model. Symmetry 2021, 13, 930. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).