Featured Application
Resource and environmental effects of the Tibetan Plateau.
Abstract
Himalayan orogenesis remains enigmatic in terms of Tibetan Plateau geodynamics originating from the Cenozoic India–Eurasian continental collision. India underthrusts below Tibet to the Yarlung–Tsangpo suture, which has been identified as the northernmost boundary for underplating. However, the way in which the historical evolution of continental subduction induces plateau uplift and the way it controls the variation in uplift between outboard and inboard areas is still unclear. To interpret the evolutionary mechanisms involved in the Himalayan growth history, we constructed different 3-D dynamic models at important stages to address these questions related to the formation of the Himalayas on the basis of paleoenthalpy evidence encoded in fossil leaves from recently documented assemblages in southern Tibet. The results show that (1) the effect of crustal thickening was the predominant factor in the early evolution from the Paleocene to the early Eocene, which resulted in a moderate growth rate. (2) The consecutive slab break-off eastward from the western syntaxis and the associated slab rebound significantly accelerated orogenesis from the late Eocene to the Oligocene. The upwelling asthenospheric flow was a key control of increasing crustal buoyancy, which resulted in the fastest growth of the Himalayas during the early Miocene. (3) Thereafter, the gradually enhanced monsoon and surface erosion during accompanying the increasing mountain height resulted in a slowdown of the orogenic rate, which counterbalanced the buoyant force produced by asthenospheric flow driving continuous Himalayan growth.
1. Introduction
Himalayan uplift is one of the most important orogenic and climate forcing events of the Cenozoic (e.g., [1]). As the largest and most active collisional orogen at present (e.g., [2]), the Himalayas are the result of the Indian plate colliding with Eurasia, which first occurred at the center portion of the Yarlung–Tsangpo suture zone (YTSZ) between ca. 65 Ma and 63 Ma (e.g., [3]), and India continues to plunge into Eurasia along the main boundary thrust (MBT) (Figure 1). The India–Eurasia collision is characterized by a significant level of uplift, particularly along the high Himalayas, and an integral rise of the Tibetan Plateau ranging across thousands of kilometers, constituting the highest landscape on Earth in northeastern India (Figure 1). However, the way in which the historical evolution of continental subduction induces plateau uplift and the way it controls the variation in uplift between outboard and inboard areas is still unclear.
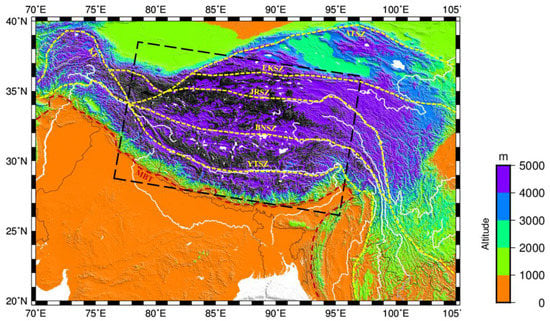
Figure 1.
Tectonic map of the Himalayan orogen, including the major topographic features and sutures: YTSZ, Yarlung–Tsangpo suture zone; BNSZ, Bangong–Nujiang suture zone; JRSZ, Jinsha River suture zone; EKSZ, East Kunlun suture zone; ATSZ, Altyn Tagh suture zone; KF, Karakorum fault; MBT, main boundary thrust. Dashed lines indicate the main orogenic region focused by this study.
The growth of Himalayan orogen was reconstructed using a paleoaltimeter based on paleoenthalpy contained in fossil leaves from two newly reported assemblages in southern Tibet (Liuqu and Qiabulin) and four previously known floras from the Himalaya foreland basin, using climate leaf analysis, multivariate program analysis, and isotopic data [4]. Zircon U–Pb dating has constrained the Liuqu flora to the latest Paleocene (ca. 56 Ma) and the Qiabulin flora to the earliest Miocene (ca. 21 Ma), the latter of which marked the starting point for a sudden change to accelerated uplift in the Himalayas. The proto-Himalayas grew slowly from ≈1000 m in the late Paleocene to Eocene (>42 Ma) to ≈2.3 km at the beginning of the Miocene (23 Ma) and reached at least 5 km by approximately 15–11 Ma (e.g., [4]). The Himalaya–Tibet edifice and the Himalayan foreland basin have been gradually drying since 56 Ma, most likely due to the Himalayan orogen’s uplift [4].
To assess the role of active tectonics and geometric variations in shaping the topography of the northwestern Himalayas, new constraints on deformation over geomorphic timescales are used, including morphometric analysis using high-resolution digital elevation models and field observations of rock type (e.g., [5]). The regional distribution of topographic growth indicates consistent active growth over million-year to millennial timescales in the Himalayas with a structural and/or tectonic control on topographic evolution. With a focus on deformation restoration, Li et al. [6] estimated that at least 1630 km of shortening (along 94° E) has occurred between India and Asia since 55 Ma, and Asia and the Himalayas have accommodated 1010 km and 620 km of the shortening, respectively. Wang et al. [7] suggested that slab break-off triggered lithosphere-asthenosphere interaction at the convergent margin. Jolivet et al. [8] showed that the closure of the former Tethys Ocean can best be explained by asthenospheric mantle flow transporting India northward, forming the Himalayas and the Tibetan Plateau, by comparing the tectonic and kinematic records from last 50 Ma with seismic tomography and anisotropy models.
The 3-D evolutionary models of Himalayan orogenesis were developed, and they revealed a substantial temporal relationship between the Indian slab’s southward drift, lateral migration of slab detachment, and subsequent dynamic rebound with major alteration in Himalayas and coeval monsoon intensification (e.g., [9]). They further claimed that from 30 to 25 Ma, anchoring off the subducting Indian plate steepened the dip of the Himalayan thrust, resulting in crustal shortening deep within the Himalayan orogenic wedge. At around 13 Ma, slab detachment spread inward from both Himalayan syntaxes, causing a rapid rise in the mountain range. However, in their modeling, slab subduction evolved into slab rollback, the surface elevation is not constrained in detail in their focused dynamic processes, and the 3-D features of the heterogeneous uplift of the Himalayas remained unclear. Therefore, we tested several construction models at different evolutionary stages to quantify the Himalayan uplift history and mechanism in accordance with geological evidence (e.g., [4]) to provide insight into the Himalayan uplift on the basis of 3-D subduction modeling.
2. Materials and Methods
To estimate the multifactor-controlled Himalayan uplift evolution, we used a dynamic slab subduction model to simulate the effects on the uplift height of the controlling factors, including plate convergence thickening, slab rebounding, lithospheric flow, and surface erosion. Modeling reproduces the 1800 km width, 1600 km length, and 300 km depth viscoelastic domain along the Indian–Eurasian plate convergent margin beneath the Himalayas (Figure 1 and Figure 2) with subduction velocity (Vs) and erosion rate (Ve) varying among different stages (Table S1). Horizontal resolution is approximately 20–22.5 km per grid. Continental collision occurs through the incoming plate slowly thrusting underneath the overriding plate along the plate boundary, extending to a depth of 100 km beneath the YTSZ and facilitating slab detachment and break-off, thus generating slab rebound forces upward and causing significant lithospheric flows beneath the tectonic complex of the lithosphere. Our simulation is inclusive of poloidal and toroidal mantle flows around the slab edge and lateral variation along the MBT during subduction-controlled orogenic processes, which are evolving self-consistently through time during the entire period of prescribed slab growth based on convergence rate [10,11].
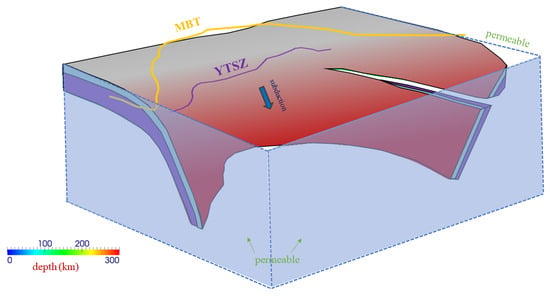
Figure 2.
Conceptual figure of model domain and the slab geometry (splitting from west to east). The bottom and perpendicular planes are prescribed as adiabatic and permeable, and the top surface is set to be permeable. Detailed model settings are available in the Supplemental Information.
The model is constructed on the basis of the finite difference method based on code Stag3D [11] and focuses on subduction regimes and geodynamics [10,12]. An anelastic liquid approximation and the equations of conservation of mass, momentum, and energy are used in this study (e.g., [12,13]):
where is the pressure deviation from hydrostatic pressure, is the reference thermal expansivity, (, = 1, 2, 3) is the stress tensor, and is the Kronecker delta. The energy equation includes an advection term, thermal diffusion term, viscous dissipation term, adiabatic heating term, and radioactive heating term.
In this model, subducted plate geometry is kinematically prescribed according to Slab2.0 on the basis of seismic tomographic data [14] for depths of <60 km. The slab topography with a depth of 60–100 km adopts the extrapolation method and is assumed to feature steep subduction (45°) before 42 Ma (Figure 2) and shallow subduction (15°) after 42 Ma. The model dimensions are 72 × 72 × 72 grids. The Indian lithosphere is estimated to be >40 km thick according to Yoshii [15]. The temperature boundary condition agrees with the plate cooling model [16]. The slab’s bottom and perpendicular planes are prescribed as adiabatic and permeable, while the top surface is set to be a constant temperature (0 °C) and permeable, allowing crustal extrusion and uplift. The composite upper mantle viscosity under a given condition is
where ηdf and ηds are the diffusion creep and dislocation creep viscosities for olivine, respectively (model setting details are available in the Supplemental Information).
The thickness of the upper and lower crusts is prescribed to be 20 km. The upper crust is a pure elastic body, and the viscosity coefficient η is infinite; the lower crust is a maxwell body, and η is approximately 1.0 × 1019 Pa·s. The elastic modulus E of the crust is assumed to be 90–120 GPa (the reference value is 98 GPa), and the elastic modulus of the upper mantle is E = 170 GPa. Density ρ uses the global CRUST2.0 data from PREM and Stanford University (the upper crust is 2.6 × 103 kg/m3, the lower crust is 2.9 × 103 kg/m3, and the upper mantle is 3.3 × 103 kg/m3) (Table S2). The kinematic plate subduction modeling method [12] is used to calculate subduction velocities inside a prescribed 3-D constrained volume of the oceanic lithosphere. The subduction velocity is set to vs. = 4.4–11.8 cm/year, as shown in Table S1. Current global MORVEL plate motion data have indicated a subduction velocity of 4–5 cm/year at the MBT [17,18], which is in accordance with our assumption.
The uplifted land surface has slowly been eroded, with erosion reducing the thickness of the continental crustal surface. The erosion rates reach the highest value in the High Himalayas at 2.7 ± 0.3 mm/a (1σ errors) and fall to <0.6 mm/a in the foothills to the south of the high mountains [19], which suggests an average erosion rate as low as <1 mm/a for the present-day Himalayas. Lenard et al. [20] further suggested that during the past six million years, the erosion rates were on average approximately 1 mm/a, which is close to the modern erosion rates in the Himalayas. During the Quaternary, there has been a marked increase in the erosion rate due to glacial erosion, especially in the High Himalaya (e.g., [21]). Considering these factors, we assumed the average erosion rate to be 0.2–0.4 mm/a (Table S1) in our modeling. The composite model setting, including model configuration, initial and boundary conditions, and physical parameters are illustrated in the Supplemental Information.
Slab thrusting, detachment, and subsequent possible delamination give a rise to the uplift of the overriding continental terrain surface. To simulate the steady subduction of the Indian plate, previously developed subduction models applied to various subduction zones have been utilized (SI). The evolution scenario is shown in Figure 3, and the surface uplift velocity is shown in Figure 4.
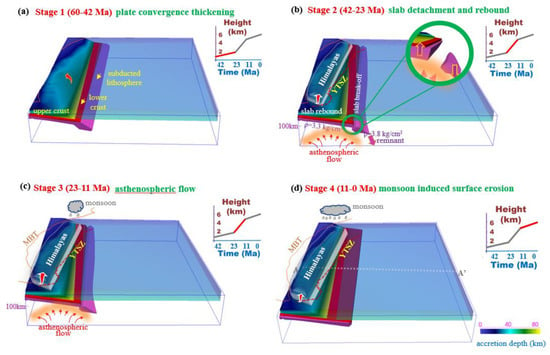
Figure 3.
The four stages of the Himalayan uplift based on 3-D subduction modeling. Red arrows denote the elevation of the Himalayas. MBT, main boundary thrust; YTSZ, Yarlung–Tsangpo suture zone. The insets are modified from Ding et al. [4]. (a) Plate-convergence-induced thickening (60−42 Ma). (b) Progressive uplift of the Himalayas caused by slab detachment and rebound (42−23 Ma). (c) Upward asthenospheric flow causing rapid uplift of the Himalayas (23−11 Ma). (d) Slowed uplift of the Himalayas affected by surface erosion (11−0 Ma).
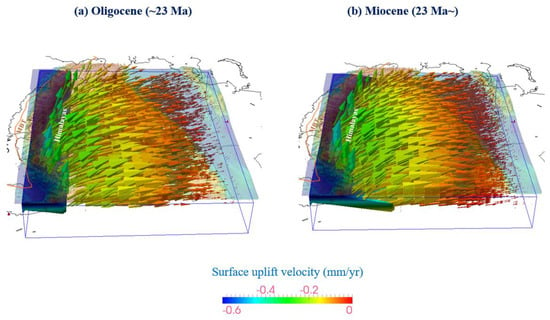
Figure 4.
The vertical surface deformation field in and around the Himalayan orogen. (a,b) indicate the variation in vertical flow velocity (mm/year) in the Oligocene (42−23 Ma) and Miocene (23−11 Ma), respectively.
The first stage of the early plate collision period (60−42 Ma) is prescribed by a subduction velocity of 11.8 cm/year. The dominant uplift force is plate-convergence-induced thickening, and the Himalayan uplift rate is moderate (insets indicating the time-height covariation) until the region reaches a height of around 2 km. From 42 to 11 Ma, the Himalayas experienced a dramatic increase in elevation from 2 km to around 4-5 km. During this stage, slab break-off occurred, resulting in slab rebound and the occurrence of upward lithospheric flows, which are the prevailing driving forces of buoyancy; this mechanical mechanism explains such rapid uplift. Since 11 Ma, the Himalayan uplift slowed, probably due to the cessation of upward buoyant forces, and the monsoon-associated surface erosion became another crucial control affecting the surface height, which led to a gradually declining growth rate for the Himalayas. The subduction velocity during this period has passively decreased to an average of 4.4 cm/year since the late Miocene. The elevation of the surface topography increased continuously, reaching the current configuration characterized by significantly high topography with low relief.
3. Results
Considering the influence of crustal deformation, developed folds, and arc magmatism, the regions adjacent to the Yarlung–Zangpo suture zone are conjectured to have undergone rapid crustal thickening accompanied by structural shortening after the initial collision, which is evidenced by the formation of adakitic rocks (e.g., [22,23]). The Himalayan orogen is inferred to have featured a north-south compressional setting according to magmatic rock exhumation. The effect of crustal thickening was predominant in determining the uplift rate in the Paleocene and Eocene during the early evolution of the Himalayas (Figure 5a and Figure 6a). The velocity field of the Himalaya orogen slows from south (>0.3 mm/year) to north (<0.1 mm/year), indicating strong shortening between India and Eurasia (Figure 4). In the second stage, the Himalayan uplift was linked to the detachment of the subducted Indian Plate. The mean compressive stress increased within the Indian plate and decreased the slab pull (e.g., [24]). Associated rebound occurred, facilitating uplift and increasing the elevation of the Himalayas by approximately 1.5 km prior to 23 Ma (Figure 5b and Figure 6b). After slab break-off, the upwelling asthenospheric mantle flow also affected the acceleration of the uplift rate after 23 Ma in stage 3 (Figure 5c and Figure 6c). Guo and Wilson [25], using Sr-Nd-Pb isotope data, indicated a change in the distribution of magmatism in Tibet, implying that asthenospheric mantle flow triggered further melting. Subducted Indian slab rollback could also have resulted in east-west-trending slab break-off ([26], shown in Figure 2). A large number of small tears within the underthrusting Indian plate are due to the upwelling of asthenospheric flow [27].
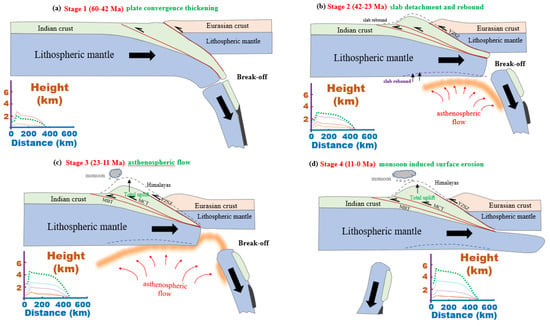
Figure 5.
Schematic illustration of the 2-D tectonic evolution of the Himalayan orogeny corresponding to the four evolutionary stages of the Himalayas. The insets indicating variation of the height along the distance are specified in Figure 6. (a) Plate-convergence-induced thickening (60−42 Ma). (b) Progressive uplift of the Himalayas caused by slab detachment and rebound (42−23 Ma). (c) Upward asthenospheric flow causes rapid uplift of the Himalayas (23−11 Ma). (d) Slowed uplift of the Himalayas affected by surface erosion (11−0 Ma).
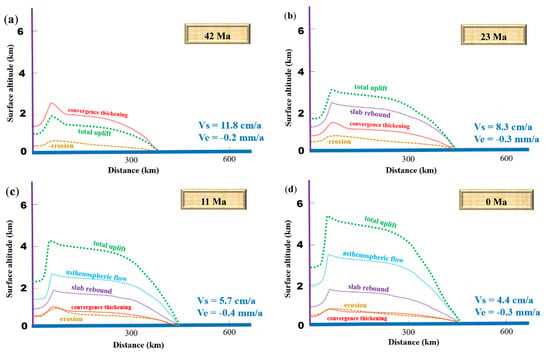
Figure 6.
Model calculation of the surface height in the four periods along the profile AA’ in Fig. 3d. The curves indicate the net uplift effect for the Himalayas due to different tectonic processes, including convergence-induced thickening, slab rebound, asthenospheric flow, and surface erosion, at the end of the four evolutionary stages of the Himalayas. (a) 60−42 Ma. (b) 42−23 Ma. (c) 23−11 Ma. (d) 11−0 Ma.
To explore the uplift rate of the Himalayas and its relationship to stress variation, we calculated the stress state in the underthrusting and overlying plates. Govin et al. [28] showed that the Himalayan uplift is caused by increased fault slip rates in response to stresses. Our results imply that the vertical flow velocity indicating the Himalayan uplift in the Miocene (23−11 Ma) was significantly higher than that in the Oligocene, which is a result of the bending of the Indian lithosphere due to lithospheric flow beneath the Himalayas (Figure 4). From the results, we found that the vertical flow velocity (uplift) was much greater than the average erosion rate (Figure 4 and Figure 6). Although the strong monsoon climate results in a high erosion rate (e.g., [29]), erosion has not kept pace with the uplift of the Himalayas. The vertical velocity field reveals a phase of rapid uplift of the Himalayas in the Miocene (Figure 4b), and the range is still rising at a maximum rate of ~2 mm/year (e.g., [30]).
The onset of slab detachment to reproduce surface morphometry results in significant surface uplift in southern Tibet (Figure 3d, Figure 5d and Figure 6d). The modeled uplift rates exhibit gradual along-subduction gradients (Figure 4 and Figure 6), with faster uplift occurring predominantly in the regions adjacent to the Himalayas, where the plate interface is shallower and descends rapidly. The fact that the along-subduction variation in uplift rates has long wavelengths and low gradients suggests potential mechanisms responsible for plate-subduction-induced lithospheric flow. Hence, fast and steady uplift during the period from the late Eocene to the early Miocene (42-11 Ma) played a critical role in constructing the Himalayas into the highest mountain system on Earth.
4. Discussion
4.1. 3-D Numerical Modeling and Subduction Evolution
Dynamic models have been used to investigate Himalayan tectonic models, which are primarily focused on pro- and retro-plate interactions with contrasts in physical properties such as rigidity, density, rheology, widths, and lengths (e.g., [31]). The slab geometry determined in previous studies, however, is based on the model calculation and varies with time; thus, it is very difficult to reach the current tomography of the downgoing plate beneath the Himalayas. For this reason, a kinematically prescribed slab based on seismic tomography is helpful for high-resolution simulation of surface evolution. Hence, we aimed to construct such a 3-D, time-evolving kinematic model using seismic tomographic data to constrain the final geometry of the subducted Indian plate. With the modeling, we can explore lithospheric crustal-scale subduction processes and forearc surface development. The growth of the Himalayas is a complex process involving the collision of Gondwanan terranes and thickening of the crust close to the MBT first, instead of the rise of the Tibetan Plateau as a single entity (e.g., [32]). This indicates that Indian plate subduction is the major control for Tibetan uplift, especially for the southern part adjacent to the MBT, i.e., the Himalayas. According to estimates of the rise of the Tibetan Plateau (e.g., [4]), the uplift of the Himalayas (which at present reach elevations of at least 5.5 km) could be divided into four stages (insets in Figure 3). The proto-Himalayas grew slowly from ~1 km in the late Paleocene to ~2.5 km at the beginning of the Miocene (42−23 Ma) and produced significant uplift (e.g., from 2.5 to >5 km) at 23−11 Ma. Finally, the Himalayas reached the present-day elevation of ~6 km in the third stage (11 Ma to present). This proposal was adopted by this study for numerical modeling with further refinement of the subduction parameters. We consider that due to the comparison between the Himalaya–Tibet edifice and the Himalaya foreland basin from precipitation patterns, a characteristic feature is that the uplift of the Himalaya orogen may have generated progressive drying across southern Tibet over the past 56 Myr and intensified the monsoon over 11−0 Ma [33]. Hence, the surface erosion involving the monsoon effect was included in our modeling with the erosion rate prescribed in different stages (Table S1 and Figure 5 and Figure 6).
4.2. Slab Detachment and Asthenospheric Flow
In this work, we calculated the Himalayan subduction and orogenic processes from the Eocene to the present day and related their covariation to an integrated subduction model that governs Himalayan elevation. In the modeling, we considered the steepened dip of the Himalayan thrust affected by the anchoring of the Indian subducted lithosphere (e.g., [9]). Slab detachment of the Indian crust subducted beneath the Himalayan orogen is the crucial factor for the rapid uplift in the Oligocene to early Miocene. In this context, slab detachment results in a buoyancy force on both the subducted and overlying crust and leads to the accelerated uplift of the Himalayas (Figure 5 and Figure 6) (e.g., [34]). To explain this significant uplift, Husson et al. [35] suggested that the rise presumably occurred by means including convergence crustal thickening, and She and Fu [36] inferred that the upwelling of the mantle material is the dominant driver of the acceleration of uplift. This interpretation is supported by our modeling showing that the upwelling of asthenospheric flow facilitates the uplift of surface topography to ~3.5 km, and the effect of crustal thickening is comparatively weaker in our model (Figure 6). With continued convergence, we estimated that the sunken remnants of the detached lower lithosphere caused slab rebound and played a crucial role in elevating the Himalayas since 23 Ma (Figure 3b).
4.3. Orogenic Uplift and Surface Erosion
Moreover, the rise of the Himalayan orogen is thought to explain the development of the South Asian monsoon (e.g., [4,37]). In the fourth stage (11–0 Ma), the enhanced erosion and monsoon intensification contributed to shaping the peculiar topographic profile of the Himalayans we observed today (e.g., [38]). The variation in mantle convection and climate-induced erosion could modulate the crustal motion velocities (e.g., [39]) and affect the rise of the orogen (Figure 5d and Figure 6d). The cold and dense lower lithosphere pushing into the hotter asthenosphere will cause convective instability in the mantle lithosphere (e.g., [40]). In this regard, the horizontal extension and thinning of the crust are a result of the thinning of the mantle lithosphere and thus slow acceleration in the Himalayas (Figure 5d). Furthermore, the enhanced climate change by uplifted mountains in turn influenced the precipitation and resultant surface erosion in the early and middle Miocene (e.g., [41]). Clift et al. [38] provide ample evidence by analyzing the chemistry and mineralogy of sediments record and suggest that Indian monsoon efficiently erodes the Himalayas. The potential counterbalancing relationship between orogenic uplift and surface erosion obtained from water, freeze-thaw, chemical weathering, and physical erosion observations from environmental measurements implies a nonlinear inverse relationship that is considered to predominantly control the current surface topography of the Himalayas and the Tibetan Plateau according to 3-D subduction modeling.
5. Conclusions
Through 3-D modeling of subduction beneath the Himalayas, we obtained the following results. During the early evolution of the Himalayas (60–42 Ma), the effect of crustal thickening was predominant in determining the surface uplift rate. The effects of slab break-off and associated slab rebound caused significant Himalayan uplift in the Oligocene (42–23 Ma). The upwelling asthenospheric mantle flow was the dominant driver of the rapid uplift of the Himalayas in the Miocene (23–11 Ma). The enhanced erosion and monsoon intensification counterbalance the further uplift of the Himalayas, and growth has slowed since 11 Ma, resulting in the present-day height of the Himalayas.
Supplementary Materials
The supplementary information is available for download: https://www.mdpi.com/article/10.3390/app12157413/s1. References [42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60] are mentioned in Supplementary Materials file. Table S1: Main model parameters; Table S2: Parameters for model domains.
Author Contributions
L.D. conceived the original idea and provided the funding. Y.J. designed the 3-D thermomechanical code, performed the numerical experiments, and interpreted the results. W.Z. and R.Q. elaborated the numerical study and wrote the manuscript. Y.Z., C.X. and D.Z. provided comments to improve the manuscript. All authors discussed the results and interpretations and participated in writing the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This study benefited from financial support from the Second Tibetan Plateau Scientific Expedition and Research Program (2019QZKK0708) and the CAS Pioneer Hundred Talents Program.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data including the model code and results are available in figures or from the authors upon reasonable request.
Acknowledgments
We are thankful to P. Tackley for sharing the Stag3D code used in this study. We are grateful for the earthquake catalog from the IRIS [61]. Figures were created with Generic Mapping Tools, which included the coasts and borders [62], and with Paraview software developed by Kitware, Inc.
Conflicts of Interest
All the authors listed certify that they have no involvement in any organization or entity with any financial interest (including honoraria; educational grants; participation in speakers’ membership, bureaus, consultancies, stock ownership, employment, or other equity interest; and patent-licensing arrangements or expert testimony) or nonfinancial interest (including professional or personal relationships, knowledge or beliefs, affiliations) in the subject materials or matter discussed.
References
- DeCelles, P.G.; Kapp, P.; Gehrels, G.E.; Ding, L. Paleocene-Eocene foreland basin evolution in the Himalaya of southern Tibet and Nepal: Implications for the age of initial India-Asia collision. Tectonics 2014, 33, 824–849. [Google Scholar] [CrossRef]
- Takada, Y.; Matsu’ura, M. A unified interpretation of vertical movement in Himalaya and horizontal deformation in Tibet on the basis of elastic and viscoelastic dislocation theory. Tectonophysics 2004, 383, 105–131. [Google Scholar] [CrossRef]
- Ding, L.; Maksatbek, S.; Cai, F.; Wang, H.; Song, P.; Ji, W.; Xu, Q.; Zhang, L.; Muhammad, Q.; Upendra, B. Processes of initial collision and suturing between India and Asia. Sci. China Earth Sci. 2017, 60, 635–651. [Google Scholar] [CrossRef]
- Ding, L.; Spicer, R.; Yang, J.; Xu, Q.; Cai, F.; Li, S.; Lai, Q.; Wang, H.; Spicer, T.; Yue, Y. Quantifying the rise of the Himalaya orogen and implications for the South Asian monsoon. Geology 2017, 45, 215–218. [Google Scholar] [CrossRef] [Green Version]
- Dey, S.; Thiede, R.C.; Biswas, A.; Chauhan, N.; Chakravarti, P.; Jain, V. Implications of the ongoing rock uplift in NW Himalayan interiors. Earth Surf. Dyn. 2021, 9, 463–485. [Google Scholar] [CrossRef]
- Li, Y.; Wang, C.; Dai, J.; Xu, G.; Hou, Y.; Li, X. Propagation of the deformation and growth of the Tibetan–Himalayan orogen: A review. Earth-Sci. Rev. 2015, 143, 36–61. [Google Scholar] [CrossRef]
- Wang, W.; Pandit, M.K.; Zhao, J.-H.; Chen, W.-T.; Zheng, J.-P. Slab break-off triggered lithosphere-asthenosphere interaction at a convergent margin: The Neoproterozoic bimodal magmatism in NW India. Lithos 2018, 296, 281–296. [Google Scholar] [CrossRef]
- Jolivet, L.; Faccenna, C.; Becker, T.; Tesauro, M.; Sternai, P.; Bouilhol, P. Mantle flow and deforming continents: From India-Asia convergence to Pacific subduction. Tectonics 2018, 37, 2887–2914. [Google Scholar] [CrossRef]
- Webb, A.A.G.; Guo, H.; Clift, P.D.; Husson, L.; Müller, T.; Costantino, D.; Yin, A.; Xu, Z.; Cao, H.; Wang, Q. The Himalaya in 3D: Slab dynamics controlled mountain building and monsoon intensification. Lithosphere 2017, 9, 637–651. [Google Scholar] [CrossRef]
- Ji, Y.; Yan, R.; Zeng, D.; Xie, C.; Zhu, W.; Qu, R.; Yoshioka, S. Slab dehydration in Sumatra: Implications for fast and slow earthquakes and arc magmatism. Geophys. Res. Lett. 2021, 48, e2020GL090576. [Google Scholar] [CrossRef]
- Tackley, P.; Xie, S. STAG3D: A code for modeling thermo-chemical multiphase convection in Earth’s mantle. In Computational Fluid and Solid Mechanics 2003; Elsevier: Amsterdam, The Netherlands, 2003; pp. 1524–1527. [Google Scholar]
- Ji, Y.; Yoshioka, S.; Matsumoto, T. Three-dimensional numerical modeling of temperature and mantle flow fields associated with subduction of the Philippine Sea plate, southwest Japan. J. Geophys. Res. Solid Earth 2016, 121, 4458–4482. [Google Scholar] [CrossRef]
- Yoshioka, S.; Murakami, K. Temperature distribution of the upper surface of the subducted Philippine Sea Plate along the Nankai Trough, southwest Japan, from a three-dimensional subduction model: Relation to large interplate and low-frequency earthquakes. Geophys. J. Int. 2007, 171, 302–315. [Google Scholar] [CrossRef] [Green Version]
- Hayes, G.P.; Moore, G.L.; Portner, D.E.; Hearne, M.; Flamme, H.; Furtney, M.; Smoczyk, G.M. Slab2, a comprehensive subduction zone geometry model. Science 2018, 362, 58–61. [Google Scholar] [CrossRef] [PubMed]
- Yoshii, T. Regionality of group velocities of Rayleigh waves in the Pacific and thickening of the plate. Earth Planet. Sci. Lett. 1975, 25, 305–312. [Google Scholar] [CrossRef]
- Grose, C.J.; Afonso, J.C. Comprehensive plate models for the thermal evolution of oceanic lithosphere. Geochem. Geophys. Geosystems 2013, 14, 3751–3778. [Google Scholar] [CrossRef]
- Argus, D.F.; Gordon, R.G.; DeMets, C. Geologically current motion of 56 plates relative to the no-net-rotation reference frame. Geochem. Geophys. Geosystems 2011, 12. [Google Scholar] [CrossRef] [Green Version]
- DeMets, C.; Gordon, R.G.; Argus, D.F. Geologically current plate motions. Geophys. J. Int. 2010, 181, 1–80. [Google Scholar] [CrossRef] [Green Version]
- Vance, D.; Bickle, M.; Ivy-Ochs, S.; Kubik, P.W. Erosion and exhumation in the Himalaya from cosmogenic isotope inventories of river sediments. Earth Planet. Sci. Lett. 2003, 206, 273–288. [Google Scholar] [CrossRef]
- Lenard, S.J.; Lave, J.; France-Lanord, C.; Aumaitre, G.; Bourles, D.L.; Keddadouche, K. Steady erosion rates in the Himalayas through late Cenozoic climatic changes. Nat. Geosci. 2020, 13, 448–452. [Google Scholar] [CrossRef]
- Pedersen, V.K.; Egholm, D.L. Glaciations in response to climate variations preconditioned by evolving topography. Nature 2013, 493, 206–210. [Google Scholar] [CrossRef]
- Guan, Q.; Zhu, D.-C.; Zhao, Z.-D.; Dong, G.-C.; Zhang, L.-L.; Li, X.-W.; Liu, M.; Mo, X.-X.; Liu, Y.-S.; Yuan, H.-L. Crustal thickening prior to 38 Ma in southern Tibet: Evidence from lower crust-derived adakitic magmatism in the Gangdese Batholith. Gondwana Res. 2012, 21, 88–99. [Google Scholar] [CrossRef]
- Shellnutt, J.G.; Lee, T.-Y.; Brookfield, M.E.; Chung, S.-L. Correlation between magmatism of the Ladakh Batholith and plate convergence rates during the India–Eurasia collision. Gondwana Res. 2014, 26, 1051–1059. [Google Scholar] [CrossRef]
- Mugnier, J.-L.; Huyghe, P. Ganges basin geometry records a pre-15 Ma isostatic rebound of Himalaya. Geology 2006, 34, 445–448. [Google Scholar] [CrossRef] [Green Version]
- Guo, Z.; Wilson, M. Late Oligocene–early Miocene transformation of postcollisional magmatism in Tibet. Geology 2019, 47, 776–780. [Google Scholar] [CrossRef]
- Replumaz, A.; Funiciello, F.; Reitano, R.; Faccenna, C.; Balon, M. Asian collisional subduction: A key process driving formation of the Tibetan Plateau. Geology 2016, 44, 943–946. [Google Scholar] [CrossRef]
- Zou, Y.; Tian, X.; Yu, Y.; Pan, F.B.; Wang, L.; He, X. Seismic evidence for the existence of an entrained mantle flow coupling the northward advancing Indian plate under Tibet. Earth Planet. Phys. 2019, 3, 62–68. [Google Scholar] [CrossRef]
- Govin, G.; Najman, Y.; Copley, A.; Millar, I.; Van der Beek, P.; Huyghe, P.; Grujic, D.; Davenport, J. Timing and mechanism of the rise of the Shillong Plateau in the Himalayan foreland. Geology 2018, 46, 279–282. [Google Scholar] [CrossRef] [Green Version]
- Clark, M.K.; Bilham, R. Miocene rise of the Shillong Plateau and the beginning of the end for the Eastern Himalaya. Earth Planet. Sci. Lett. 2008, 269, 337–351. [Google Scholar] [CrossRef]
- Liang, S.; Gan, W.; Shen, C.; Xiao, G.; Liu, J.; Chen, W.; Ding, X.; Zhou, D. Three-dimensional velocity field of present-day crustal motion of the Tibetan Plateau derived from GPS measurements. J. Geophys. Res. Solid Earth 2013, 118, 5722–5732. [Google Scholar] [CrossRef]
- Huangfu, P.; Li, Z.-H.; Gerya, T.; Fan, W.; Zhang, K.-J.; Zhang, H.; Shi, Y. Multi-terrane structure controls the contrasting lithospheric evolution beneath the western and central–eastern Tibetan plateau. Nat. Commun. 2018, 9, 3780. [Google Scholar] [CrossRef]
- Spicer, R.A.; Su, T.; Valdes, P.J.; Farnsworth, A.; Wu, F.-X.; Shi, G.; Spicer, T.E.; Zhou, Z. Why ‘the uplift of the Tibetan Plateau’ is a myth. Natl. Sci. Rev. 2021, 8, nwaa091. [Google Scholar] [CrossRef]
- Kroon, D.; Steens, T.; Troelstra, S.R. Onset of monsoonal related upwelling in the western Arabian sea. Proc. Ocean Drill. Program Sci. Results 1991, 117, 257–263. [Google Scholar]
- Chemenda, A.I.; Burg, J.-P.; Mattauer, M. Evolutionary model of the Himalaya–Tibet system: Geopoem: Based on new modelling, geological and geophysical data. Earth Planet. Sci. Lett. 2000, 174, 397–409. [Google Scholar] [CrossRef]
- Husson, L.; Bernet, M.; Guillot, S.; Huyghe, P.; Mugnier, J.-L.; Replumaz, A.; Robert, X.; Van der Beek, P. Dynamic ups and downs of the Himalaya. Geology 2014, 42, 839–842. [Google Scholar] [CrossRef] [Green Version]
- She, Y.; Fu, G. Uplift mechanism of the highest mountains at eastern himalayan syntaxis revealed by in situ dense gravimetry. Geophys. Res. Lett. 2020, 47, e2020GL091208. [Google Scholar] [CrossRef]
- Boos, W.R.; Kuang, Z. Dominant control of the South Asian monsoon by orographic insulation versus plateau heating. Nature 2010, 463, 218–222. [Google Scholar] [CrossRef] [PubMed]
- Clift, P.D.; Hodges, K.V.; Heslop, D.; Hannigan, R.; Van Long, H.; Calves, G. Correlation of Himalayan exhumation rates and Asian monsoon intensity. Nat. Geosci. 2008, 1, 875–880. [Google Scholar] [CrossRef]
- Iaffaldano, G.; Husson, L.; Bunge, H.-P. Monsoon speeds up Indian plate motion. Earth Planet. Sci. Lett. 2011, 304, 503–510. [Google Scholar] [CrossRef]
- Chen, Q.; Freymueller, J.T.; Wang, Q.; Yang, Z.; Xu, C.; Liu, J. A deforming block model for the present-day tectonics of Tibet. J. Geophys. Res. Solid Earth 2004, 109. [Google Scholar] [CrossRef]
- Beaumont, C.; Jamieson, R.A.; Nguyen, M.; Lee, B. Himalayan tectonics explained by extrusion of a low-viscosity crustal channel coupled to focused surface denudation. Nature 2001, 414, 738–742. [Google Scholar] [CrossRef]
- Burkett, E.R.; Billen, M.I. Three-dimensionality of slab detachment due to ridge-trench collision: Laterally simultaneous boudinage versus tear propagation. Geochem. Geophys. Geosyst. 2010, 11, Q11012. [Google Scholar] [CrossRef]
- Hirth, G.; Kohlstedf, D. Rheology of the upper mantle and the mantle wedge: A view from the experimentalists. Geophys. Monogr.-Am. Geophys. Union 2003, 138, 83–106. [Google Scholar]
- Ranalli, G. Rheology of the Earth; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Stein, C.A.; Stein, S. A model for the global variation in oceanic depth and heat flow with lithospheric age. Nature 1992, 359, 123–129. [Google Scholar] [CrossRef]
- Müller, R.D.; Sdrolias, M.; Gaina, C.; Roest, W.R. Age, spreading rates, and spreading asymmetry of the world’s ocean crust. Geochem. Geophys. Geosyst. 2008, 9, Q04006. [Google Scholar] [CrossRef]
- Hacker, B.R.; Abers, G.A.; Peacock, S.M. Subduction factory 1. Theoretical mineralogy, densities, seismic wave speeds, and H2O contents. J. Geophys. Res. Solid Earth 2003, 108, 2029. [Google Scholar] [CrossRef]
- Ji, Y.; Yoshioka, S.; Manea, V.C.; Manea, M.; Matsumoto, T. Three-dimensional numerical modeling of thermal regime and slab dehydration beneath Kanto and Tohoku, Japan. J. Geophys. Res. Solid Earth 2017, 122, 332–353. [Google Scholar] [CrossRef] [Green Version]
- Pollack, H.N.; Hurter, S.J.; Johnson, J.R. Heat flow from the Earth’s interior: Analysis of the global data set. Rev. Geophys. 1993, 31, 267–280. [Google Scholar] [CrossRef]
- Li, C.-F.; Lu, Y.; Wang, J. A global reference model of Curie-point depths based on EMAG2. Sci. Rep. 2017, 7, srep45129. [Google Scholar] [CrossRef]
- Li, C.F.; Wang, J.; Lin, J.; Wang, T. Thermal evolution of the North Atlantic lithosphere: New constraints from magnetic anomaly inversion with a fractal magnetization model. Geochem. Geophys. Geosyst. 2013, 14, 5078–5105. [Google Scholar] [CrossRef] [Green Version]
- Turcotte, D.L.; Schubert, G. Geodynamics; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Ji, Y.; Yoshioka, S.; Manea, V.C.; Manea, M. Seismogenesis of dual subduction beneath Kanto, central Japan controlled by fluid release. Sci. Rep. 2017, 7, 16864. [Google Scholar] [CrossRef] [Green Version]
- Suenaga, N.; Ji, Y.; Yoshioka, S.; Feng, D. Subduction thermal regime, slab dehydration, and seismicity distribution beneath Hikurangi based on 3-D simulations. J. Geophys. Res. Solid Earth 2018, 123, 3080–3097. [Google Scholar] [CrossRef]
- Ji, Y.; Yoshioka, S. Slab dehydration and earthquake distribution beneath southwestern and central Japan based on three-dimensional thermal modeling. Geophys. Res. Lett. 2017, 44, 2679–2686. [Google Scholar] [CrossRef]
- Suenaga, N.; Yoshioka, S.; Ji, Y. 3-D thermal regime and dehydration processes around the regions of slow earthquakes along the Ryukyu Trench. Sci. Rep. 2021, 11, 11251. [Google Scholar] [CrossRef] [PubMed]
- Ji, Y.; Yoshioka, S.; Banay, Y.A. Thermal state, slab metamorphism, and interface seismicity in the Cascadia subduction zone based on 3-D modeling. Geophys. Res. Lett. 2017, 44, 9242–9252. [Google Scholar] [CrossRef] [Green Version]
- Wang, K.; Hyndman, R.D.; Yamano, M. Thermal regime of the Southwest Japan subduction zone: Effects of age history of the subducting plate. Tectonophysics 1995, 248, 53–69. [Google Scholar] [CrossRef]
- Iwamori, H. Heat sources and melting in subduction zones. J. Geophys. Res. Solid Earth 1997, 102, 14803–14820. [Google Scholar] [CrossRef]
- Christensen, U.R. The influence of trench migration on slab penetration into the lower mantle. Earth Planet. Sci. Lett. 1996, 140, 27–39. [Google Scholar] [CrossRef] [Green Version]
- Trabant, C.; Hutko, A.R.; Bahavar, M.; Karstens, R.; Ahern, T.; Aster, R. Data products at the IRIS DMC: Stepping stones for research and other applications. Seismol. Res. Lett. 2012, 83, 846–854. [Google Scholar] [CrossRef]
- Wessel, P.; Smith, W.H. New, improved version of Generic Mapping Tools released. Eos Trans. Am. Geophys. Union 1998, 79, 579. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).