2. Development of Thin Film Blackbody Radiation Source
The thermal radiation of a blackbody can be a photon source at any frequency. According to the Planck equation for radiation power in a single frequency band and one spatial mode, the power is
This equation approaches the Nyquist formula, with
PN = kT at low and high frequencies, while taking into account quantum corrections using the Callen-Welton formula
where the first term describes zero fluctuations. The radiation power can be transferred to another matched load only by the second term. The blackbody radiation can be easily controlled by changing its electron temperature; in this case, a thin film resistor can be used as a source of radiation of hot photons.
It seems reasonable to create such a blackbody as a thin metal film with resistance on the order of that of free space (Z0 = 377 Ω). It is important to keep in mind that the thickness of such a film is small compared to wavelength and skin depth. In the case of different dielectrics with refractive indexes n1 and n2 adjacent to film, film conductivity per square is σ = 1/R□, the transfer matrix element is T12 = 0.5 (1 + n1/n2 + σZ0/n2), and the absorption coefficient is A = 4 Z0σ/(n1 + n2 + σZ0)2. In the case of vacuum on both sides of the film with a refractive index n = 1, the coefficient of absorbance for a normally incident wave is A = 4 σZ0/(2 + σZ0)2. The maximum value of the absorption coefficient that can be achieved is Amax = 0.5 with resistance per square 1/σ = R□ = Z0/2 = 188 Ω. For an arbitrary value of the refractive index of the second material n2, the absorption coefficient will be A = 4 σZ0/(1 + n2 + σZ0)2. It approaches the maximum value of Amax = 1/(n2 + 1) if the resistance of the film is R□ = Z0/(n2 + 1). For thick silicon substrate, the optimal value is R□ = 84 Ω and Amax = 0.2. This is one of the important conclusions of our research. At first glance, it seems that square resistance should be equal to Z0 for perfect matching. However, such a film is very thin compared to the skin depth, it is semitransparent, and increasing resistance towards Z0 will just increase transmission and reduce absorption. On the other hand, reducing resistance leads to increasing reflection that, again, reduces absorption.
To model the absorption coefficient of thin film, CST Studio Suite was used. A schematic image of the project is presented in
Figure 1a. Thin film on a substrate of the chosen material was placed inside the wave guiding structure (circular waveguide), and the two waveguide ports (377 Ω) were placed on both sides of the guiding structure to generate/receive the signal and determine S-parameters. The main feature of modelling such projects in CST is that when considering the film’s characteristics (skin depth and film thickness), the material of the metallic film must be determined as a “thin panel”, and the TLM module (in T-solver) is used for calculation. In the opposite case, the thin film will be treated as a “thick” metal surface, and regardless of the thickness (even zero), the transmittance coefficient will be zero. The absorption coefficient is calculated from S-parameters by the following formulas:
where
A1 and
A2 are the absorption coefficients in case of irradiation from the film side and the substrate side, respectively. The guiding structure is required because the waveguide port positioning should be used for calculation in this module. The results of modeling in CST with numerical calculation from [
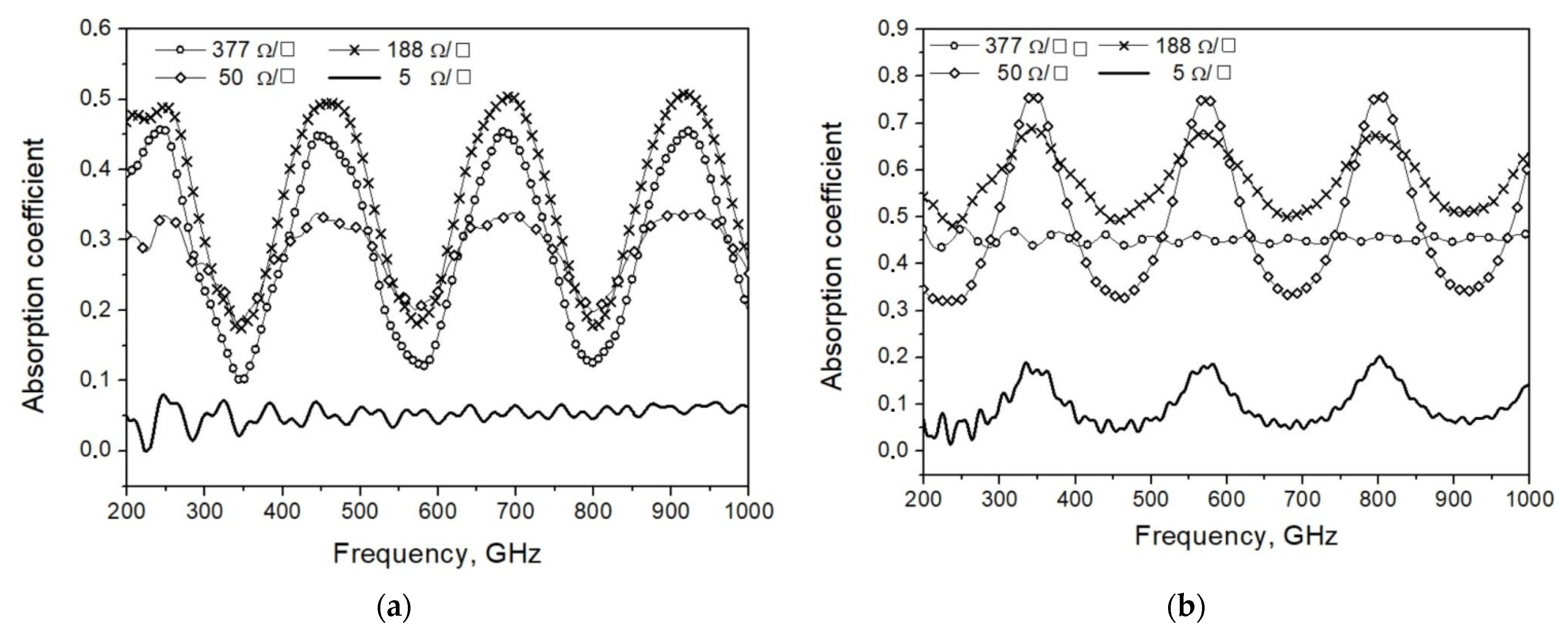
6] for film with a sheet resistance of 550 Ω/□ on sapphire substrate (340 μm thick) (
Figure 1b) was compared to check the method. The modeling of films with different resistance values (Ω/□) is presented in
Figure 2. The largest absorbance was observed for films with resistance of 188 Ω/□.
The bare dielectric substrate with refractive index
n at both sides should have a reflection coefficient
R = [(
n − 1)/(
n + 1)]
2, so for silicon with
n = 3.4,
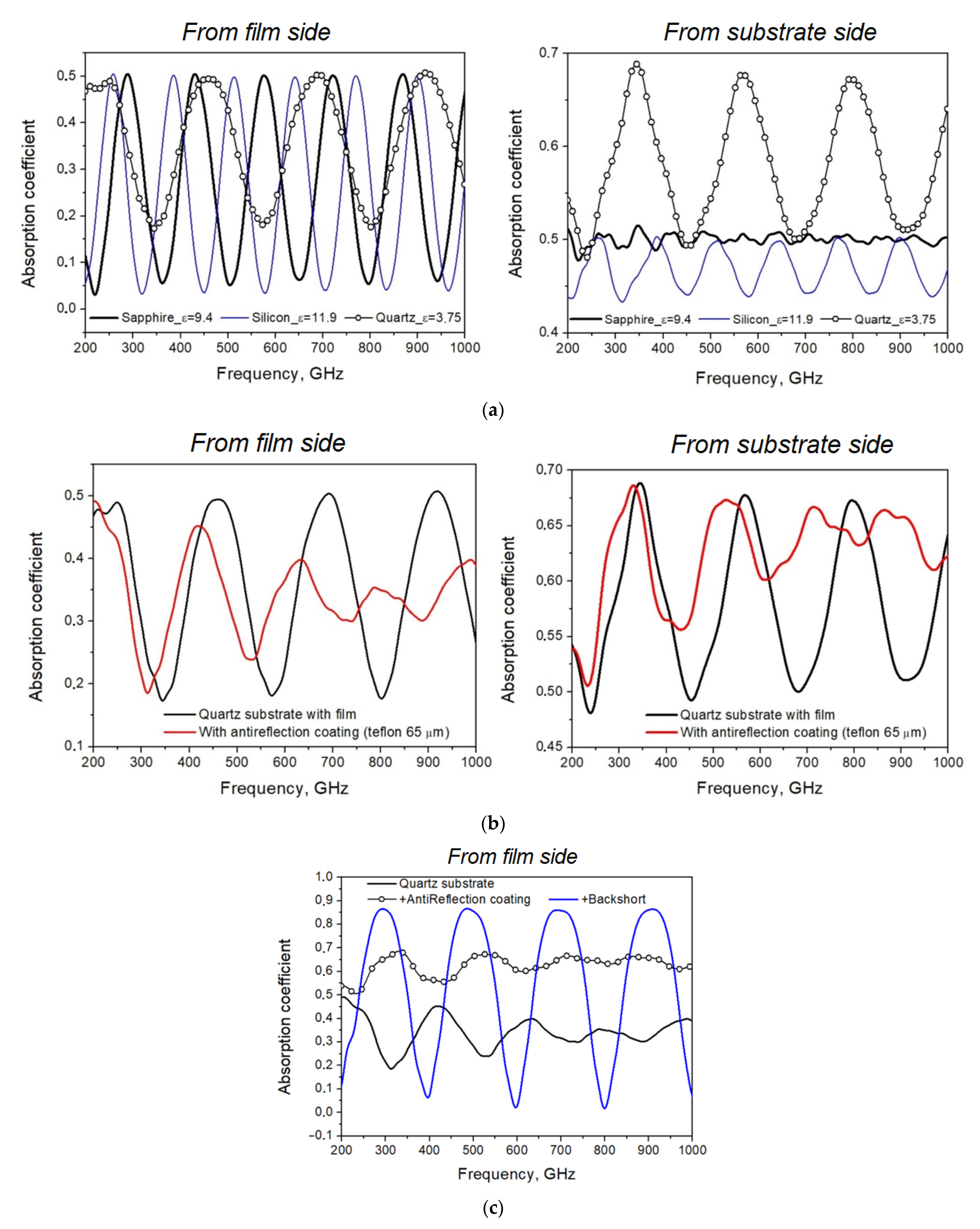
R = 0.3. Antireflection coating with electrical thickness of one-quarter wavelength and refractive index
na =
n0.5 can be used to decrease reflections in the relatively narrow band. The modeled absorption coefficients of film with resistance of 188 Ω/□ on different 340 μm substrates (sapphire, quartz, silicon) and on substrate with additional antireflective coating are presented in
Figure 3.
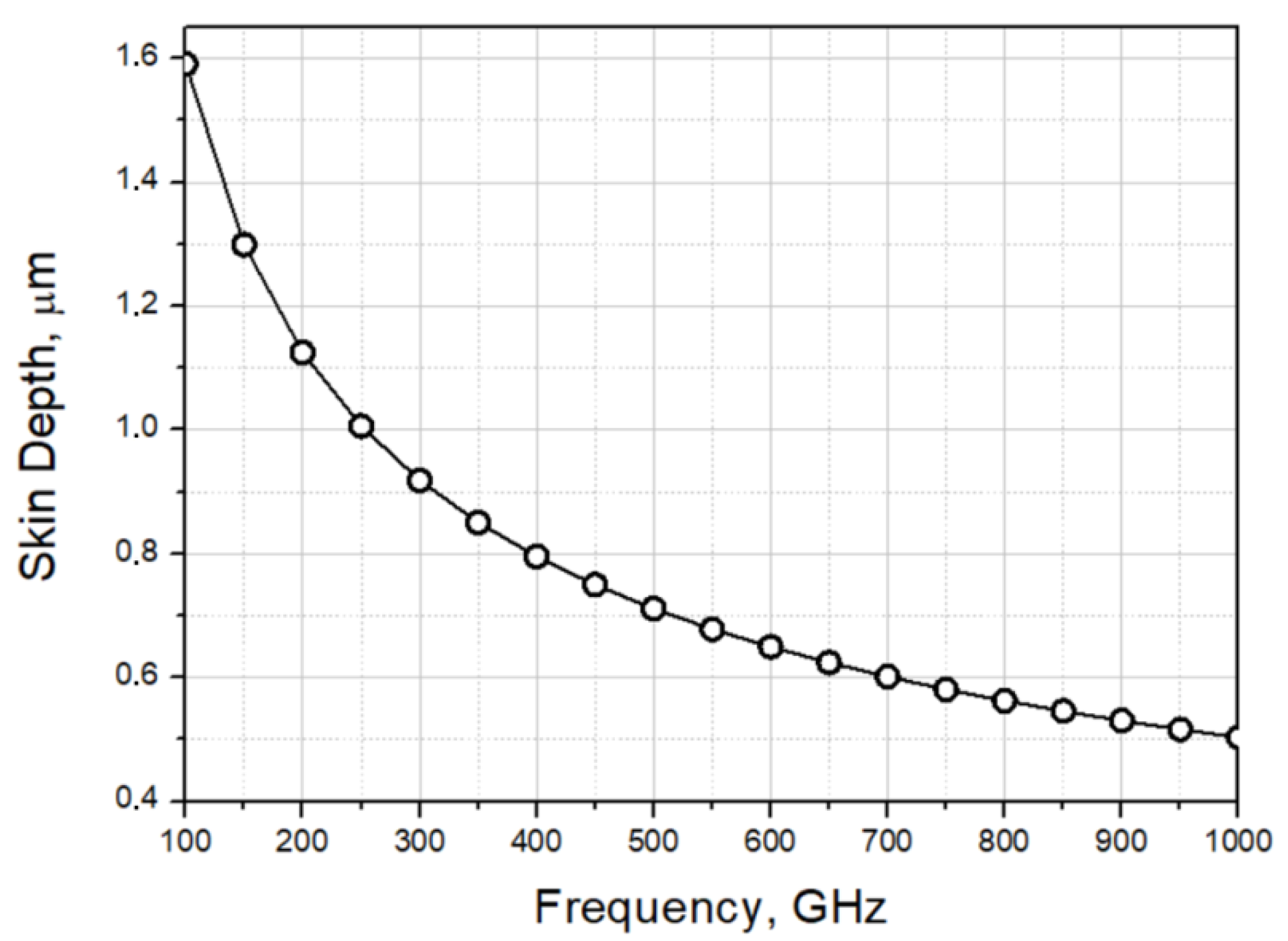
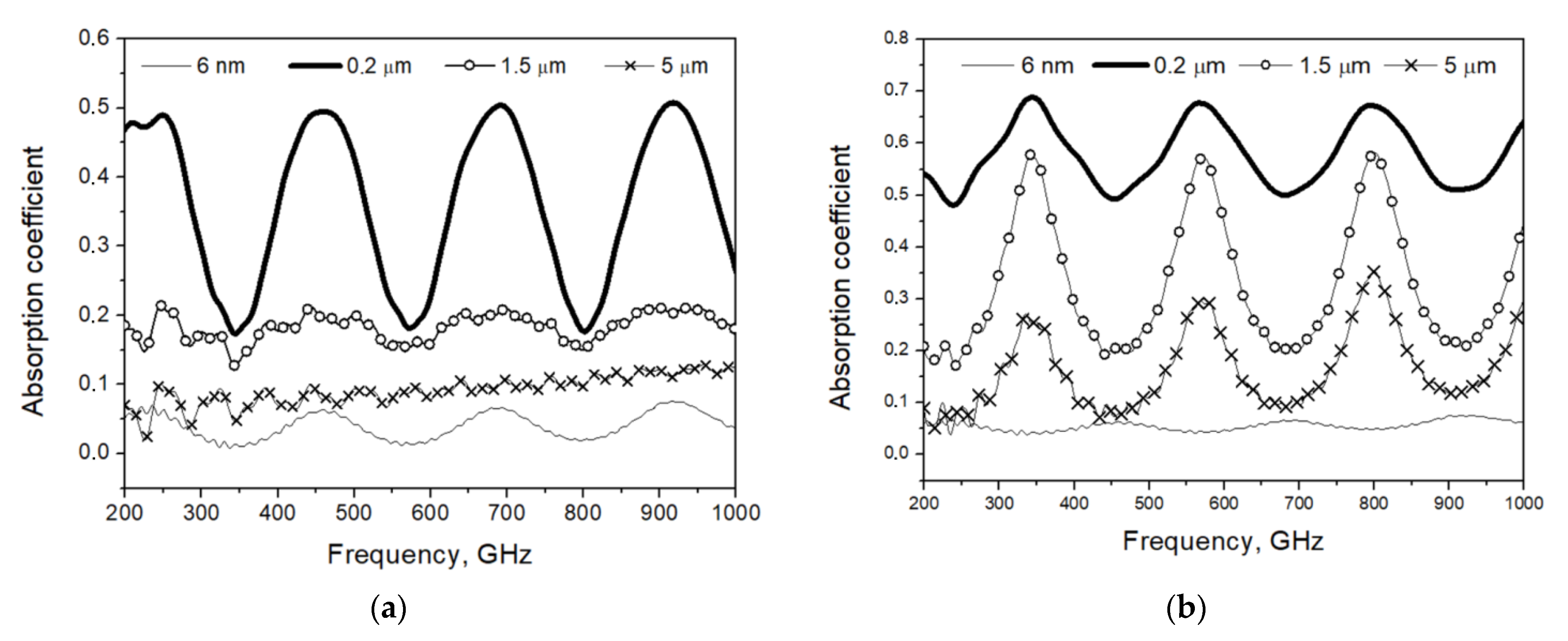
When using a substrate of finite thickness, the absorption spectrum becomes more complex because the periodic spectrum of the Fabry–Perot dielectric resonator is superimposed on the smooth dependence. This dependency is shown for the case of a resistive thin film with resistance per square of 30–300 Ω/□, which is too thin compared to the skin depth. So, for NiCr film with resistivity
ρ = 10
−6 Ωm, the resistance per square is 180 Ω/□ if the film thickness is 6 nm, but the skin depth of such film at
f = 100 GHz is Δ = 503(
ρ/
f)
0.5 = 1.5 μm. The calculated dependence of the skin depth on frequency is shown in
Figure 4. This means that more than 90% of power is transmitted through the substrate (see
Figure 5).
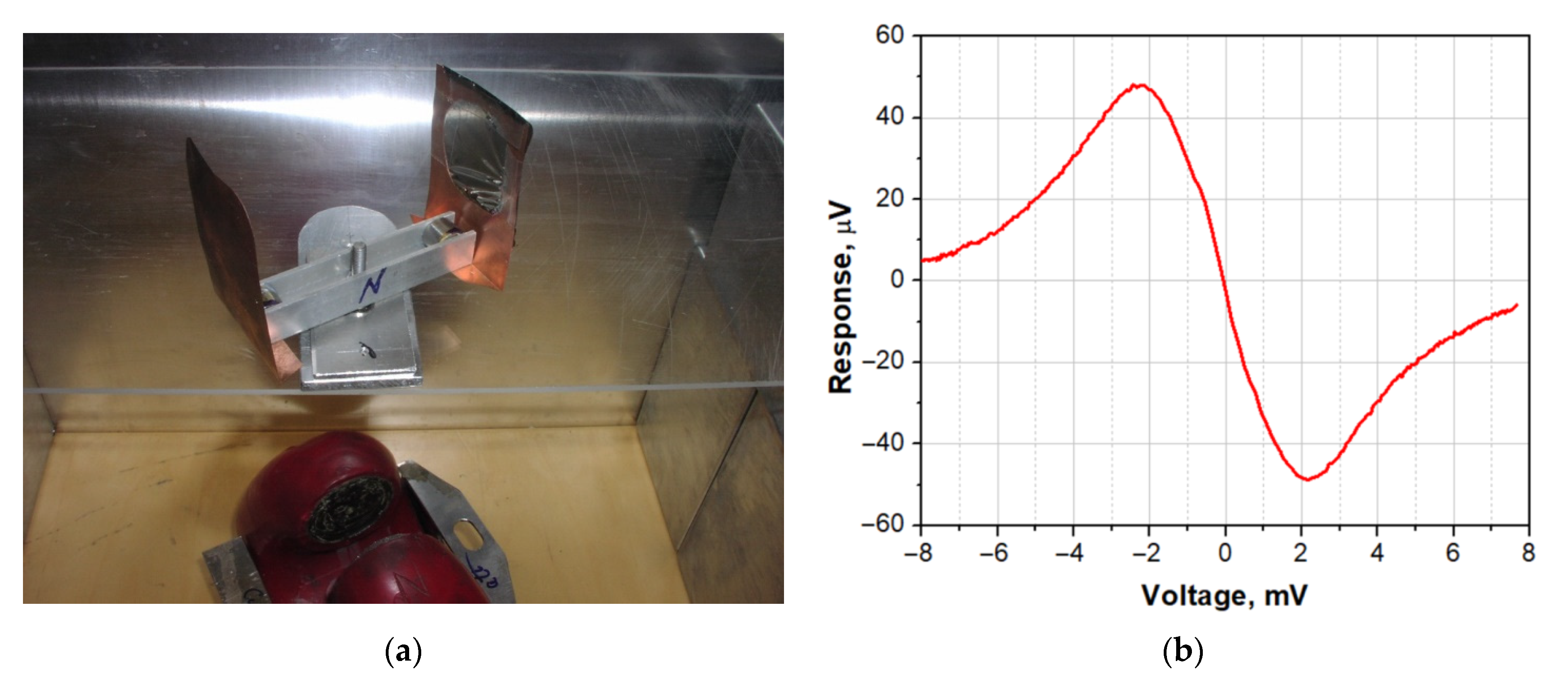
To increase the emissivity of a flat BB absorber, it is favorable to use relatively thick free-standing foil instead of an absorber comprising thin film on a dielectric substrate. For constantan with resistivity of 0.5 μΩ m at a signal frequency of 350 GHz, the skin depth is 0.6 μm, so 50 μm-thick foil is definitely opaque. In [
7], 50 μm constantan foil was mounted (glued by black thermally conductive STYCAST epoxy on copper foil to equalize the temperature) at a temperature stage of 0.4 K. On the reverse side, two resistors were glued to the copper carrier, one to measure the temperature and one for heating, and a miniature permanent magnet was mounted on this rotatable holder. The reflectance coefficient of the foil at a frequency of 350 GHz was measured by a BWO spectrometer/reflectometer; it was 0.7 ± 0.05, meaning that the blackness was
k = 0.3 ± 0.05. Since such a source has high inertia, cold aperture switching was used for remote switching from cold to hot load by the external permanent magnet [
8,
9]. The whole assembly, which is fixed on an axle, can be rotated by the external magnet, and in this way, the hot or cold emitter appears in the aperture of the immersion lens. A demonstration of the room-temperature model of rotating cryogenic absorber and reflector is presented in
Figure 6.
Using an integrating cavity in which the radiation is multiply reflected from the walls, accompanied by absorption in the semi-transparent film, can be a more effective method for increasing the absorption. Examples of devices with integrating cavities are shown in
Figure 7,
Figure 8 and
Figure 9.
A series of samples on silicon substrate (24 × 5 × 0.5 mm) with different thicknesses of NiCr thin film was made to investigate the influence of film resistance and location on the efficiency of integrating cavity. The samples were mounted inside a spherical copper integrating cavity 33 mm in diameter with a 3.6 × 1.8 mm waveguide port,
Figure 9b. The sample with thin film was glued at an angle of 10° in the middle of the sample holder. The reflectance coefficient was measured using a P2-69 reflection and transmission spectrometer in the frequency range of 52–80 GHz. At a frequency of 70 GHz for film with 100 Ω/□ resistance, the reflectance coefficient was −6.5 dB, indicating that the blackness was about 80%.
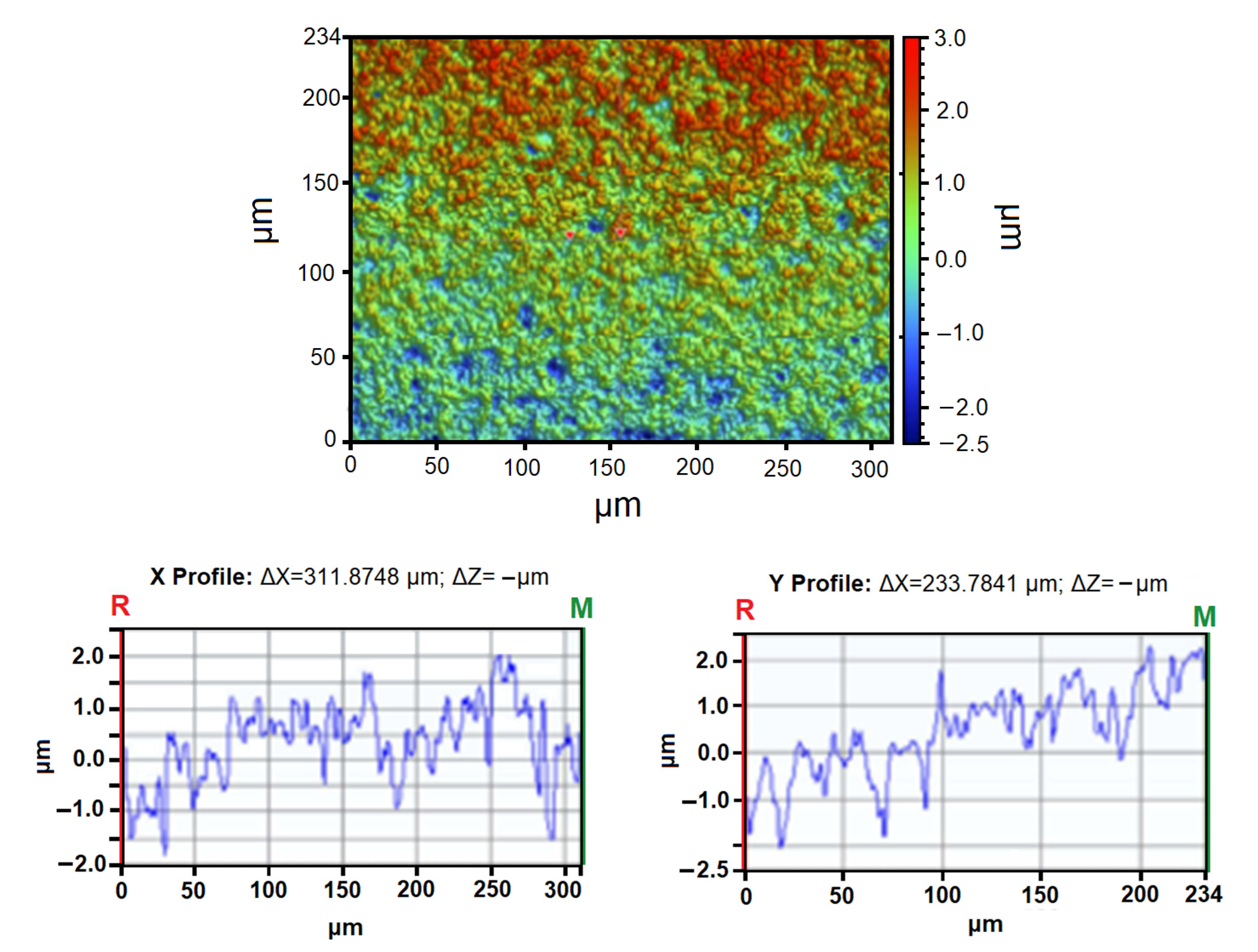
To increase scattering in the integrating cavity, the second type of sample was deposited on unpolished Si substrate 32 mm in diameter, which completely filled the middle of the cavity (a photo of the film surface and its profile are shown in
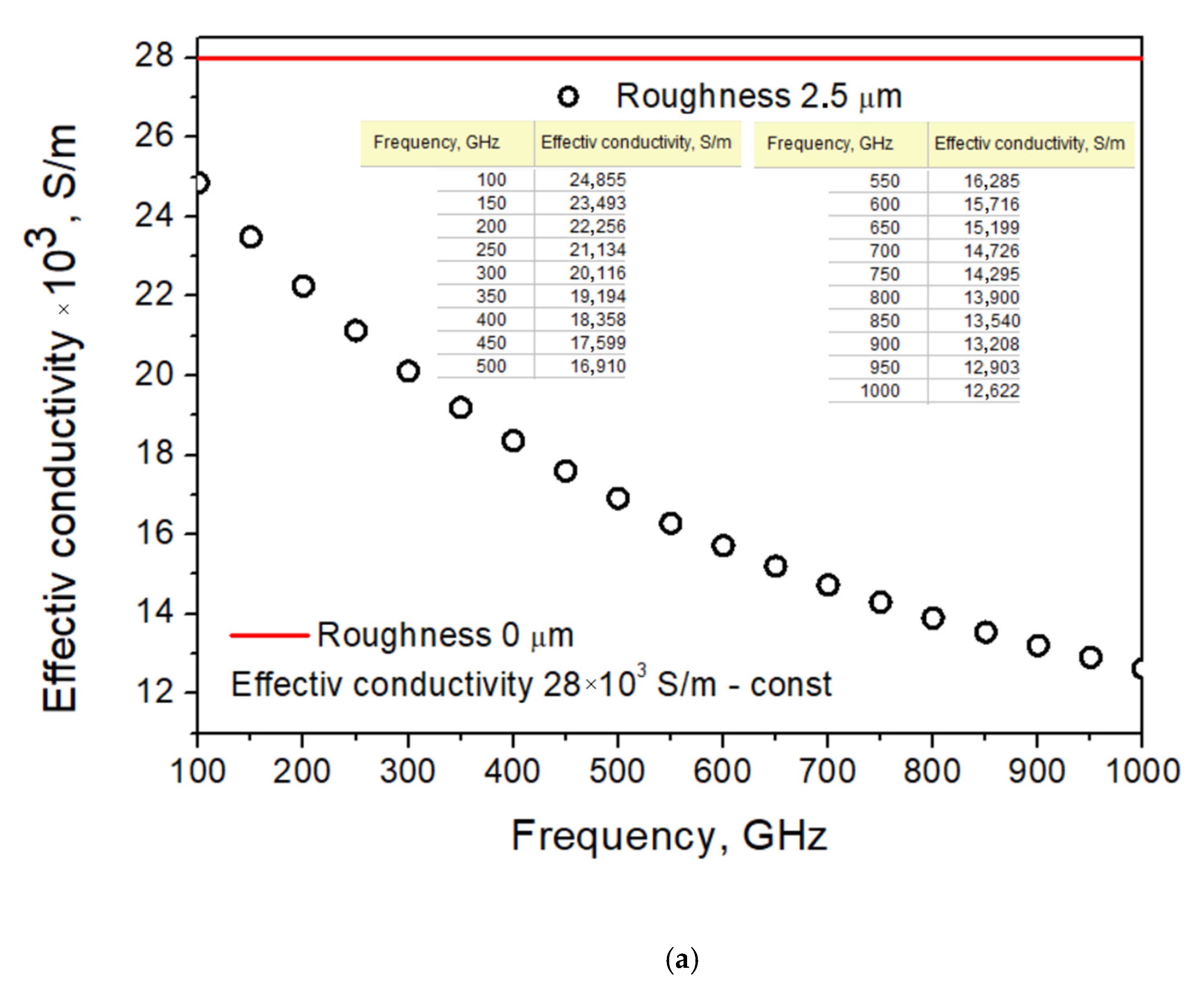
Figure 10). In this case, the blackness was more than 85%. The roughness of the surface was more than 1 μm, and resistance of NiCr thin film was 200 Ω/□, in contrast to the film on polished substrate (20 Ω/□), which was deposited by the same process as the film on unpolished substrate. The calculated dependence of effective conductivity on frequency for film roughness of 2.5 μm is presented in
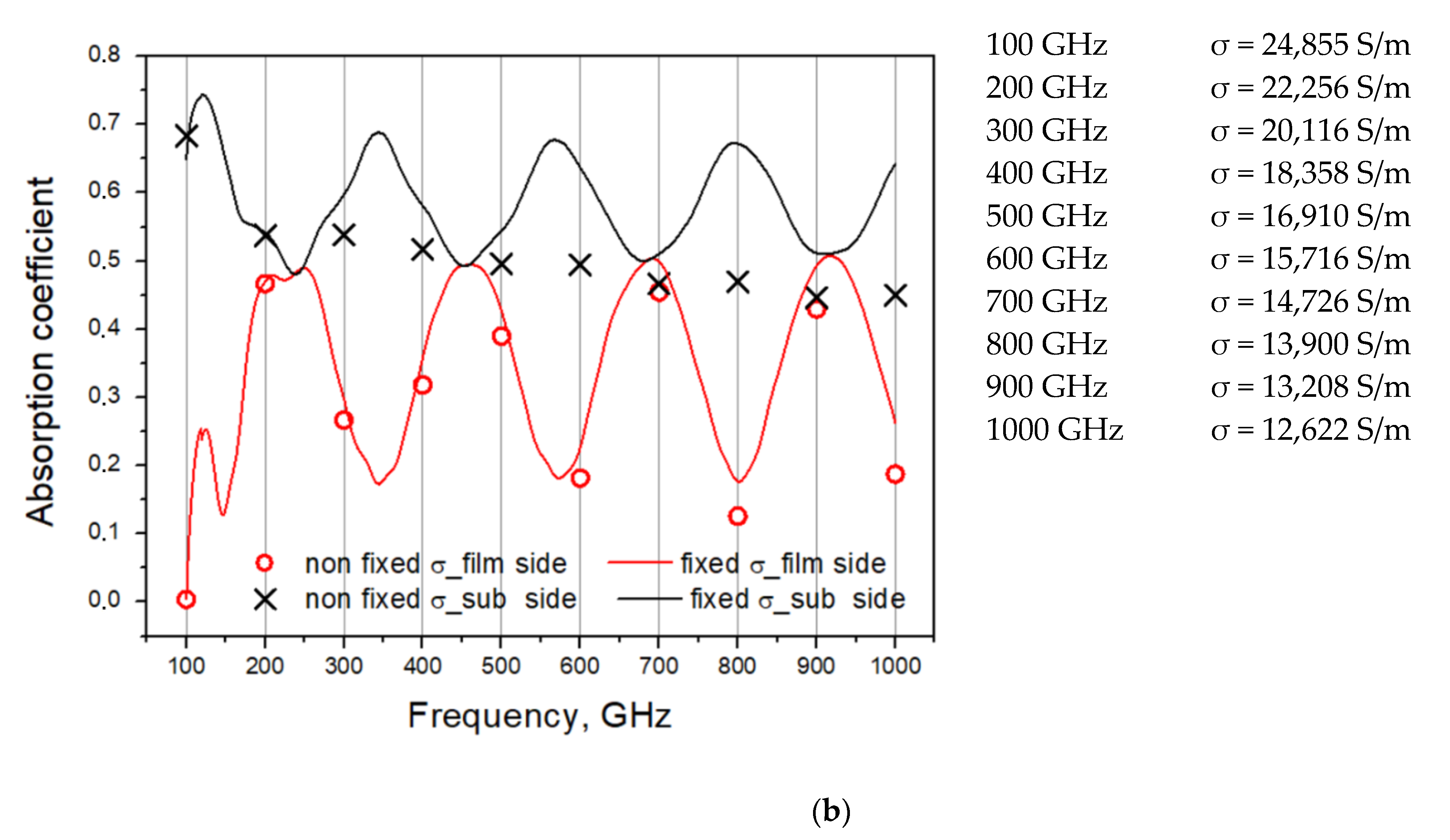
Figure 11a, and a comparison of absorption coefficients for perfect (with negligible roughness and fixed conductivity) and “real” substrate is presented in
Figure 11b.
3. Fast Electrical Modulation of Radiation Temperature of Cryogenic Source
For measurements of SINIS detector optical response, a source of thermal blackbody radiation inside the cryostat was used in [
12]. Thin nichrome film on a sapphire or silicon substrate was used as such source. At the sides of the NiCr film, gold contact pads were made to apply the heating current. The source was suspended on thin wires for thermal and electric insulation from the copper stage at a temperature of 0.5 K. The heating current was applied through the wires connected to the Au contact pads. DC current of a few mW provided heating up the BB source to 10–15 K. The temperature of the source was measured by an RuO
2 thick-film resistor thermometer glued to the back side of the substrate. The radiation from the thermal source illuminated the detector through the mesh filters with 350 GHz central frequency and 70 GHz bandwidth. A hemispherical sapphire lens was used to focus the radiation onto the detector. The radiation power was calculated using Planck’s formula, taking into account the frequency band of filters. The relative value of power at different temperatures of the source depended only on the accuracy of temperature measurements.
To investigate the dynamic characteristics of the detector, a pulse of radiation with a sharp front was used. This pulse was formed by heating the blackbody source on a sapphire substrate. The heat capacity of sapphire is Csapphire = 29 × T3 nJ/K. The heat capacity of nichrome film and gold contacts with thickness less than 1 μm is low compared to the heat capacity of sapphire substrate. Applying an electrical pulse with energy of 1 μJ heats the source to ~3.5 K, and after that, the source holds this temperature up to a hundred milliseconds. The test measurements with pulse heating of sources on silicon substrates show that the response time of the RuO2 thermometer is about 200 microseconds. For estimation of the temperature and power of the source on sapphire substrate, depending on the applied power under DC current, we compared the detector response with the measured response of the BB source on silicon substrate.
For estimation of the radiation power variation over time, we modeled the process of thermal dynamics in the source before and after heating by current pulse. A two-dimensional thermal conductivity equation was solved by the finite element method. We used the value of 0.253
T mJ/g K [
13] for a specific heat capacity of NiCr. The thermal conductivity of sapphire in such calculations was taken of 3.5 ×
T3 W/(m K).
The temperature difference between the nichrome film and the sapphire substrate at
T = 4 K was less than 0.2 K and changed with temperature as
T−3. Such estimation used the Kapitza resistance at the indium–sapphire interface [
14], which is larger compared to the nichrome–sapphire clean interface. Based on this, the Kapitsa resistance was not taken into account in the calculation. Examples of such calculations are shown in
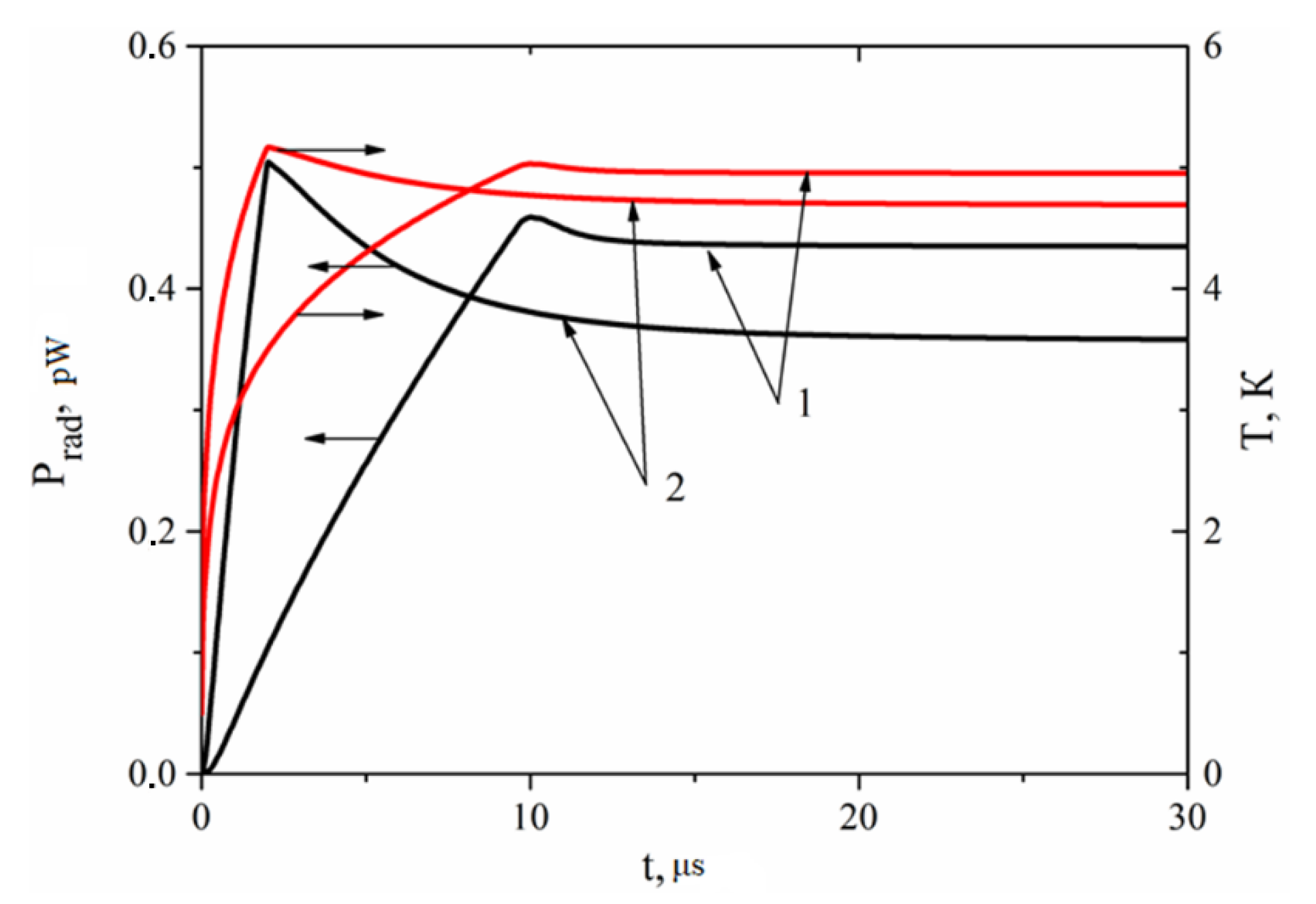
Figure 12.
At the end of the pulse, the radiation power approaches maximum and then exponentially decreases with a time constant of ~4 μs. This decay corresponds to heat redistribution from the heating area to the area under the 2–3 mm-wide gold contact pads.
The BB source was heated by current pulses of 5–90 V from the pulse generator. The output signal of the preamplifier was applied to one of the inputs of the 2-channel oscilloscope Tektronix TDS 1012B operating in waiting mode. The heating pulses were fed through 1:10 or 1:100 dividers to the second input of the oscilloscope. The amplitude of these pulses had to be reduced because a noticeable parasitic interaction was found between the oscilloscope channels, affecting the detector; the electrical signal caused additional heating of the absorber. In order to reduce the electrical pulse interference penetrating into the registration system and bypass the detector, measurements were made in the bias reversal mode of the detector. The response to radiation was obtained by subtracting the signals at positive and negative bias voltages. Adding them together brings the level of interference. The results were averaged during 1024 cycles. The period between cycles was up to 5 s depending on the level of source heat, in order to ensure cooling of the source between heating pulses.
We estimated the time constant of preamplifier τ
amp and twisted pair τ
RC. The measured capacitance in the feed line is
C = 80–100 pF, and the dynamic resistance of the detector at the working point is in the range from tens to hundreds of kΩ, so the time constant of such RC circuit is up to 10 μs. Some measurements of the time constant of the whole system were carried out at room temperature using an optocoupler pair instead of a detector. A pulse from the heater generator was applied to the LED of the pair. The photodiode of the optocoupler was connected in series with a resistor R (from 1 to 100 kΩ) to the input of the transmission line. A simulated output signal with
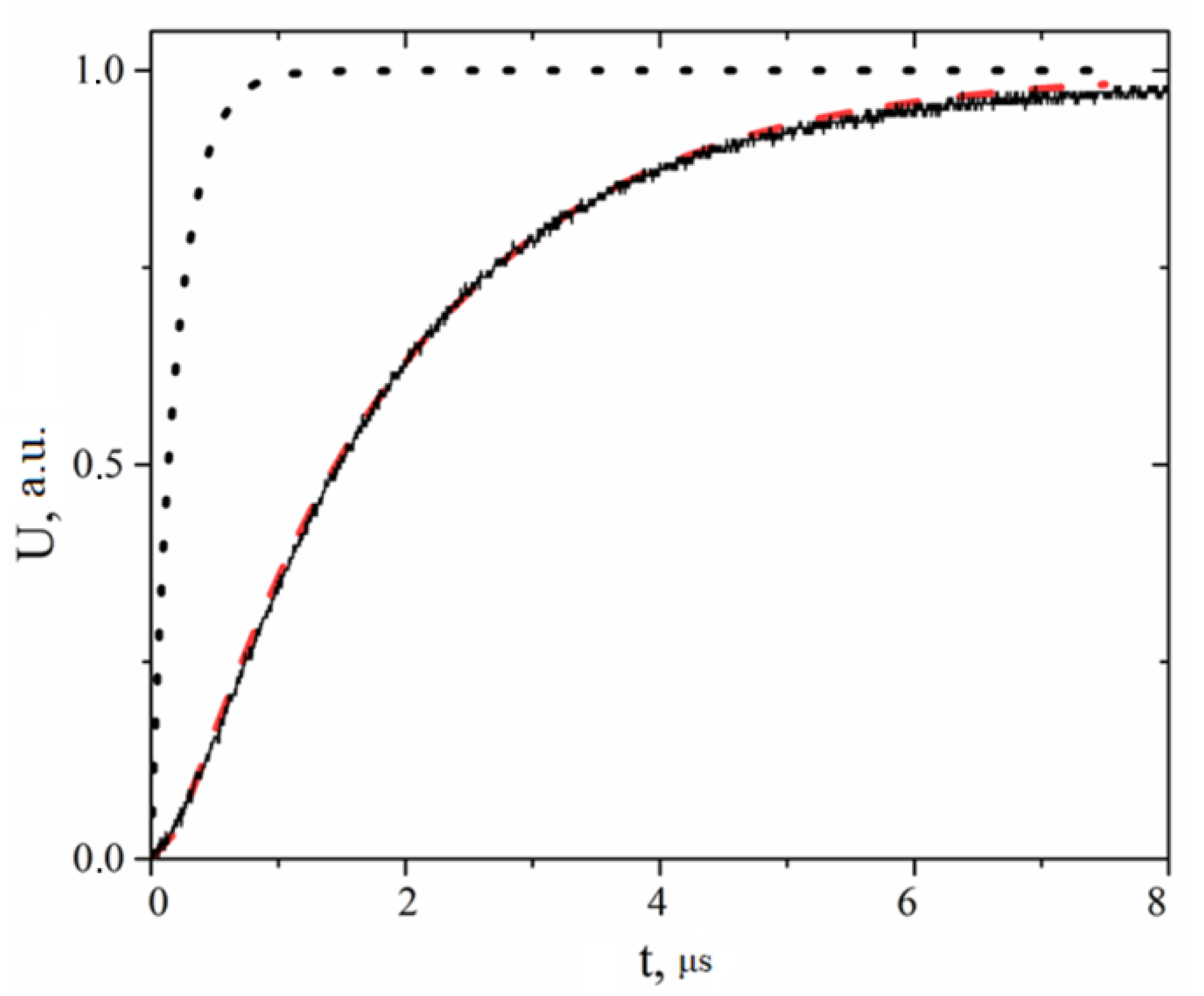
R = 14 kΩ is shown in
Figure 13. It can be described by an exponent, and for the case shown in the figure, the time constant is 1.8 μs.
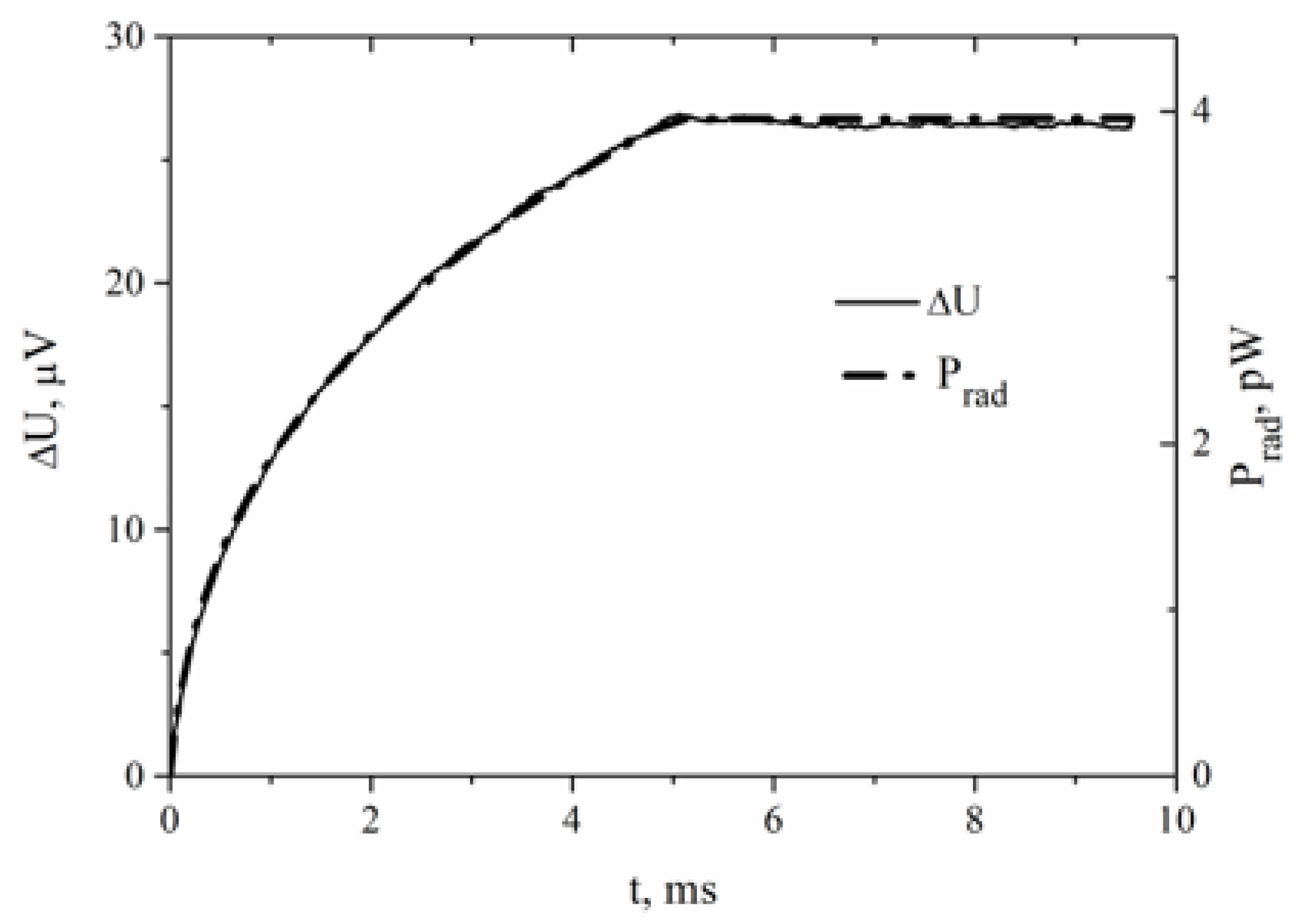
The performance of the BB source is tested by the detector response when millisecond heating pulses of moderate voltage are applied (see
Figure 14). The temperature of the source is calculated by its thermal capacity and applied pulse energy. The power of radiation is calculated from the equation for a single mode SINIS detector. The detector response is proportional to the calculated radiation power, which confirms the correctness of the described procedure for estimation of the radiation power. The radiation power after applying pulses with front duration of 1 ms was estimated in the same way.
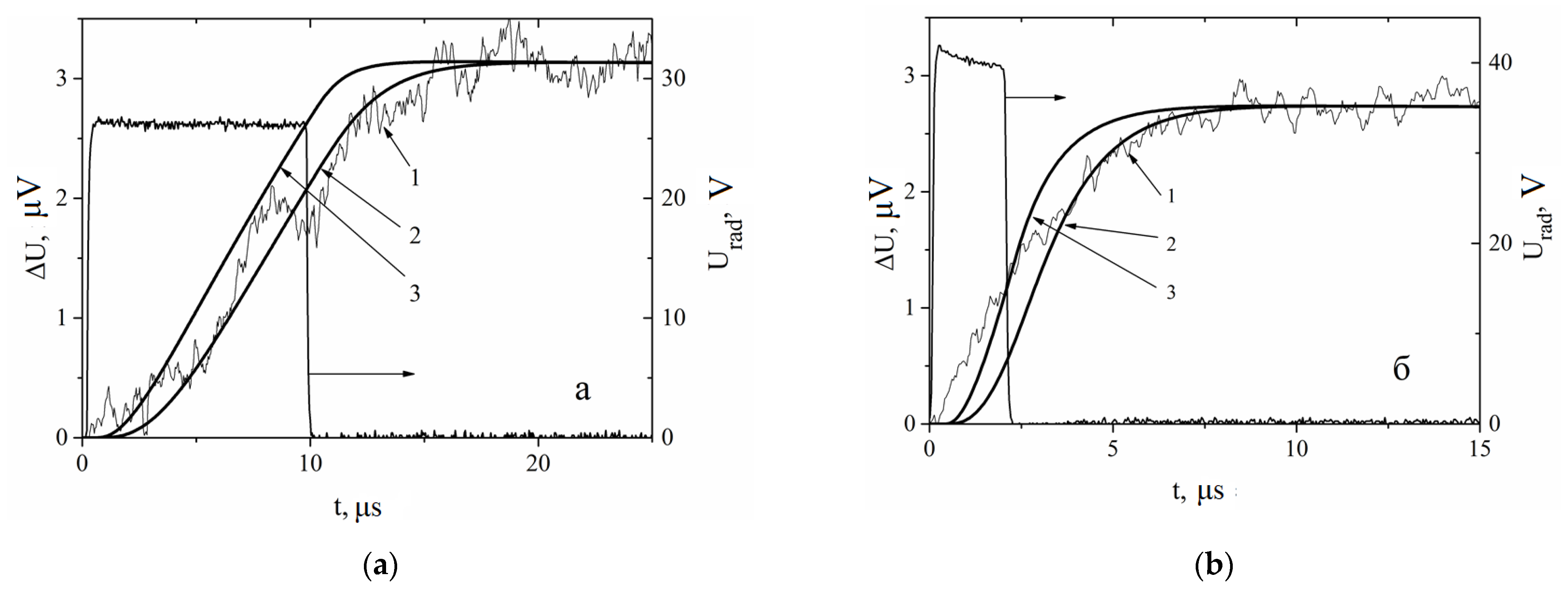
The measurement results of a SINIS detector response time presented in
Figure 15. Unlike the previous cases, for this measurement, the voltage pulses had higher amplitude but shorter duration. As shown in
Figure 15, the pulse duration and amplitude were chosen so that the total heat power of the pulses would be close in both cases. The main feature of the presented data is the noticeable difference between the detector response and the output signal rise time of 1.8 μs. Agreement with the experiment is achieved if we take into account the proper response time of the detector τ
det. For 10 μs heating pulses, t
bol = 1.8 ± 0.5 μs. At such values, the standard deviation of δU in the experiment is minimal at 0.19 μV, which practically coincides with δU in the constant signal level region and is less than the value of 0.33 μV without taking into account the detector’s own time constant.
For 2 μs pulses using the same procedure of operating the detector time, the response is t
det = 0.8 ± 0.3 μs (
Figure 15b). Apparently, this discrepancy is due to a greater overheating of the emitting nichrome film relative to the sapphire substrate than was calculated, which led to a faster increase in the response at the beginning of the process. This is clearly seen in
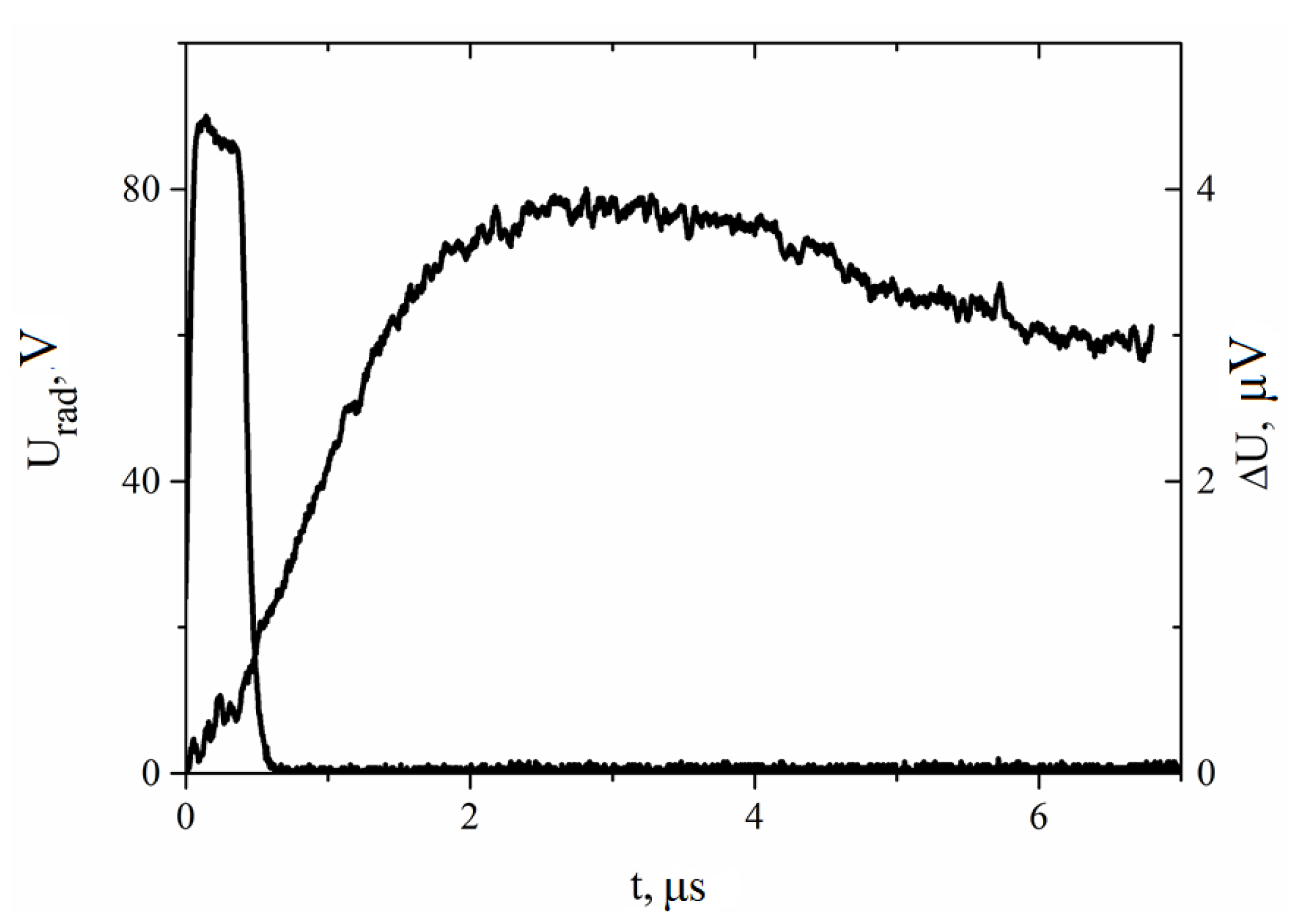
Figure 16, which shows the results for heating pulses with a duration of 0.4 μs and an amplitude of 90 V. In this case, the dependence ΔU(t) shows a maximum at t = ~3 μs, which is much later than the end of the heating pulse. Obviously, at this time, the intensity of radiation corresponds to the actual response value and is 1.3–1.4 times greater than the asymptotic value at t = ~7 μs. According to the simulation, this difference may only be 5–6%. It is not possible to achieve agreement with the experiment by changing the parameters of the model in a wide range. The overheating of the film may be due to the poor thermal conductivity of the surface layer of sapphire. According to the results shown in
Figure 15, with heating pulses of 20 V and 10 μs, the overheating of the film is too small, and the estimation t
det = 1.8 ± 0.5 μs is close to the true value of the detector’s response time.