Next Article in Journal
Screening Additives for Amending Compacted Clay Covers to Enhance Diffusion Barrier Properties and Moisture Retention Performance
Next Article in Special Issue
Three-Dimensional Modeling of Soil-Structure Interaction for a Bridge Founded on Caissons under Seismic Conditions
Previous Article in Journal
Empirical Perturbation Analysis of Two Adversarial Attacks: Black Box versus White Box
Previous Article in Special Issue
Design Proposal for Masonry Infill Walls Subject to Seismic Actions
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Applied Sciences
Volume 12
Issue 14
10.3390/app12147340
applsci-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

Seismic Analysis of Slender Monumental Structures: Current Strategies and Challenges

by
Maria Giovanna Masciotta
1,* and
Paulo B. Lourenço
2
1
Department of Engineering and Geology, University G. d’Annunzio of Chieti-Pescara, 65127 Pescara, Italy
2
Department of Civil Engineering, Institute for Sustainability and Innovation in Structural Engineering, University of Minho, 4800-058 Guimarães, Portugal
*
Author to whom correspondence should be addressed.
Appl. Sci. 2022, 12(14), 7340; https://doi.org/10.3390/app12147340
Submission received: 22 June 2022 / Revised: 18 July 2022 / Accepted: 20 July 2022 / Published: 21 July 2022
(This article belongs to the Special Issue Advanced Seismic Evaluation of Relevant Architectures)
Browse Figures
Versions Notes

Abstract

:
The preservation and seismic risk mitigation of built cultural heritage is considered today as a major priority in the international political agenda. Among the great variety of heritage structures spread worldwide, masonry towers belong to one of the most vulnerable categories against earthquake actions due to their morphological and material singularity. The proper understanding of the structural behavior of these artefacts at the micro, meso and macro scales, combined with a thorough knowledge of the best analysis practices deriving from the shared experience of the scientific community working in this field, is a fundamental prerequisite to appropriately address their seismic assessment. In this context, the present work offers an extensive discussion on the major challenges that slender monumental towers pose in terms of characterization of their actual behavior under seismic actions. A critical appraisal of the principal analysis methods applicable to the study of these structures is also presented along with a brief review of the existing modelling strategies for their numerical representation. Relevant examples are discussed in support of each argument. In spite of being a relatively young discipline, earthquake engineering has made remarkable progress in the last years and appropriate modi operandi have been consolidating to tackle the seismic assessment of unconventional systems, such as slender heritage structures. The work is conceived in a format of interest for both practitioners and researchers approaching the seismic assessment of this type of structures, and for those in need of an overall practical review of the topic.

1. Introduction

Earthquakes do not kill people, buildings do. Since 1960, 40% of natural disaster deaths occurred due to earthquake events and 60% of these deaths were caused by collapse of masonry buildings [1]. As is widely known, an earthquake is the result of a sudden release of energy in the Earth’s crust that creates seismic waves. These waves result in shaking or rapid movements of the ground, often leading to loss of life and destruction of property. Earthquakes also have the potential to generate a tsunami when the epicenter is located offshore and the seabed abruptly moves, causing displacements of a large amount of water. Past seismic events have clearly shown that structures constructed with strict adherence to seismic safety standards are less likely to be damaged during an earthquake. The Kobe earthquake of 1995, which is counted among the strongest, deadliest, and costliest earthquakes to ever strike Japan and for which the ground shaking in some regions was significantly larger than that considered in the seismic design code of the time, represents an example in this regard. In fact, buildings constructed after the 1981 revision of Japan’s building codes were far less likely to collapse than older buildings during this event; whereas all the reinforced concrete buildings which saw a story collapse were built prior to a 1971 code change regarding beam and column ductility [2]. Although some types of ancient buildings have proved remarkably resistant to earthquake forces for centuries, it must be stressed that their resistance has been achieved only by good conceptual design, with no seismic analysis [3,4]. Besides being conceived in the absence of modern building codes and regulations, more than half of existing heritage buildings are made of unreinforced masonry, thereby featuring a very high seismic vulnerability because of the fragility and inherent complexity of the constituent materials, the frequent use of round unshaped stones, the lack of adequate connections between structural elements or the poor adhesion between units and mortar, to mention a few.
Among the great variety of heritage constructions spread worldwide, slender monumental structures represent a peculiar category still embellishing the skylines and landscapes of many cities. Their main distinguishing feature is the height, which served to guarantee the visibility from the surroundings as a sign of power and to enable the various functions these structures were conceived for, whether as bell or clock towers, watchtowers, chimneys, or minarets. Unlike ordinary masonry buildings, such structures present unique morphological and typological characteristics, which may adversely affect their capability to withstand dynamic actions (e.g., complex geometries, wall thickness, significant dead loads, presence of large openings in elevation, irregularities or contiguity with adjacent buildings) [4,5,6,7,8,9,10,11,12,13,14,15]. Different geometrical and mechanical properties, as well as different boundary conditions, can result in distinct damage patterns under earthquake forces. As far as ancient masonry towers are concerned, the possible collapse mechanisms that can activate with higher probability—based on past earthquake experiences—concern the following [7,8,9,15,16,17,18,19,20]: (1) global overturning of the tower due to the formation of a flexural hinge at the base; (2) vertical splitting of the walls (very frequent in slender towers); (3) diagonal cracking of masonry and overturning of the upper part around the base (Heyman’s rocking mechanisms); (4) combination of diagonal overturing and vertical splitting; (5) failure of the belfry; (6) sliding of the structure along a horizonal crack surface located near the base. When a tower is not extremely slender and depending on the frequency content of the input forces, earthquake-induced flexural damages are commonly associated with significant shear cracks; conversely, in the case of isolated slender towers, a cantilever behavior with flexural failure is mainly expected. The adoption of fairly simple and moderate-cost strengthening measures (e.g., improving the wall integrity and the connection between orthogonal walls) can drastically reduce the high seismic vulnerability exhibited by this type of structures, turning unacceptable failures into acceptable damage scenarios in case of earthquakes.
Nowadays, the protection of historic monumental structures is of strategic importance in many countries, yet numerous uncertainties still arise about their behavior against seismic actions, making their structural evaluation a critical issue. This work reviews and examines the main challenges underlying the seismic assessment of slender monumental constructions, beginning with the difficulties associated with the description of the internal structure of the masonry material and with the influence of higher modes in the global dynamic response of these systems, and proceeding with an extensive discussion about the selection of the most adequate structural analysis procedures and modelling strategies. Finally, considerations on the methods and tools that engineering offers to scientifically tackle problems related to the seismic analysis of slender monumental structures are provided.

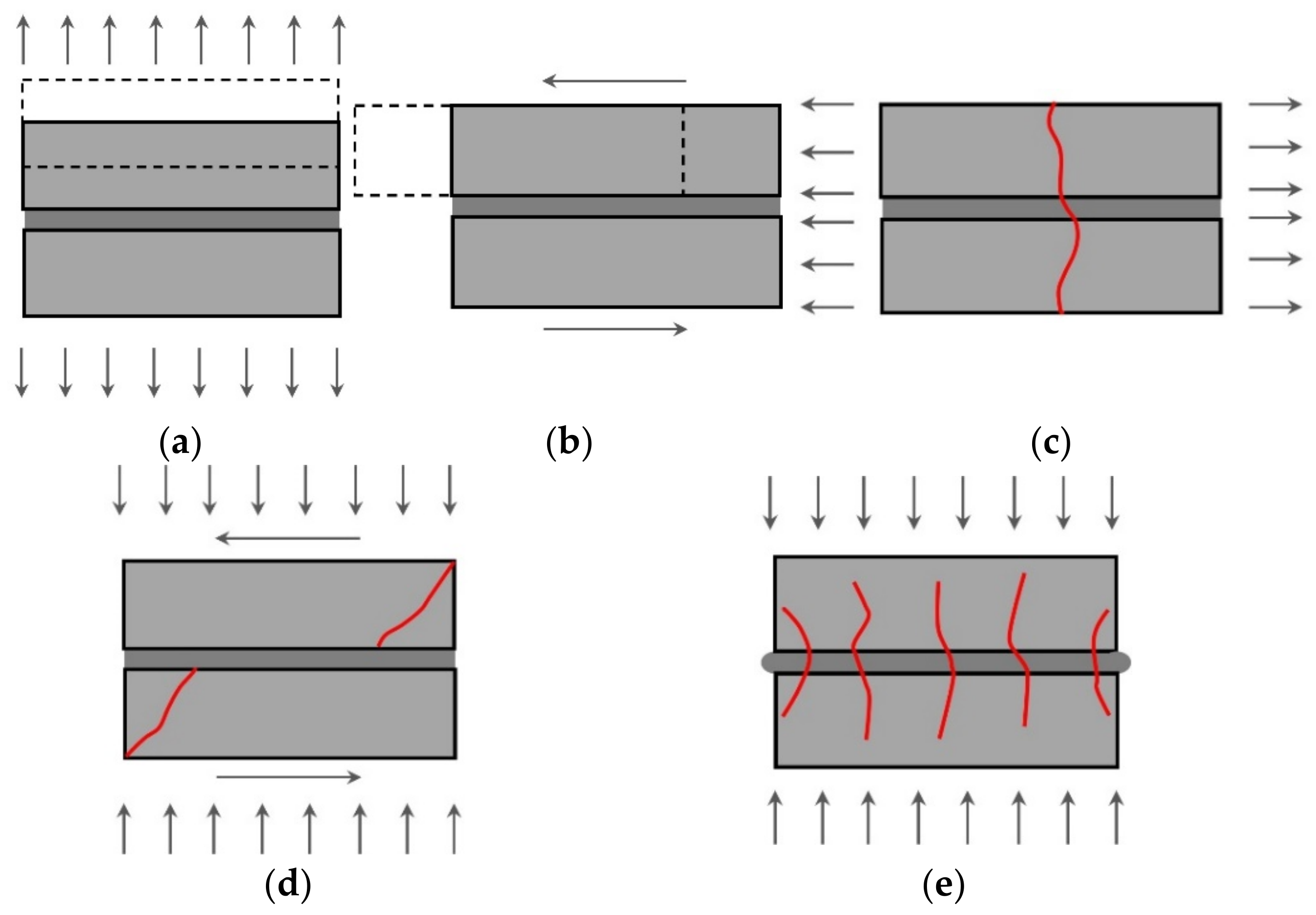
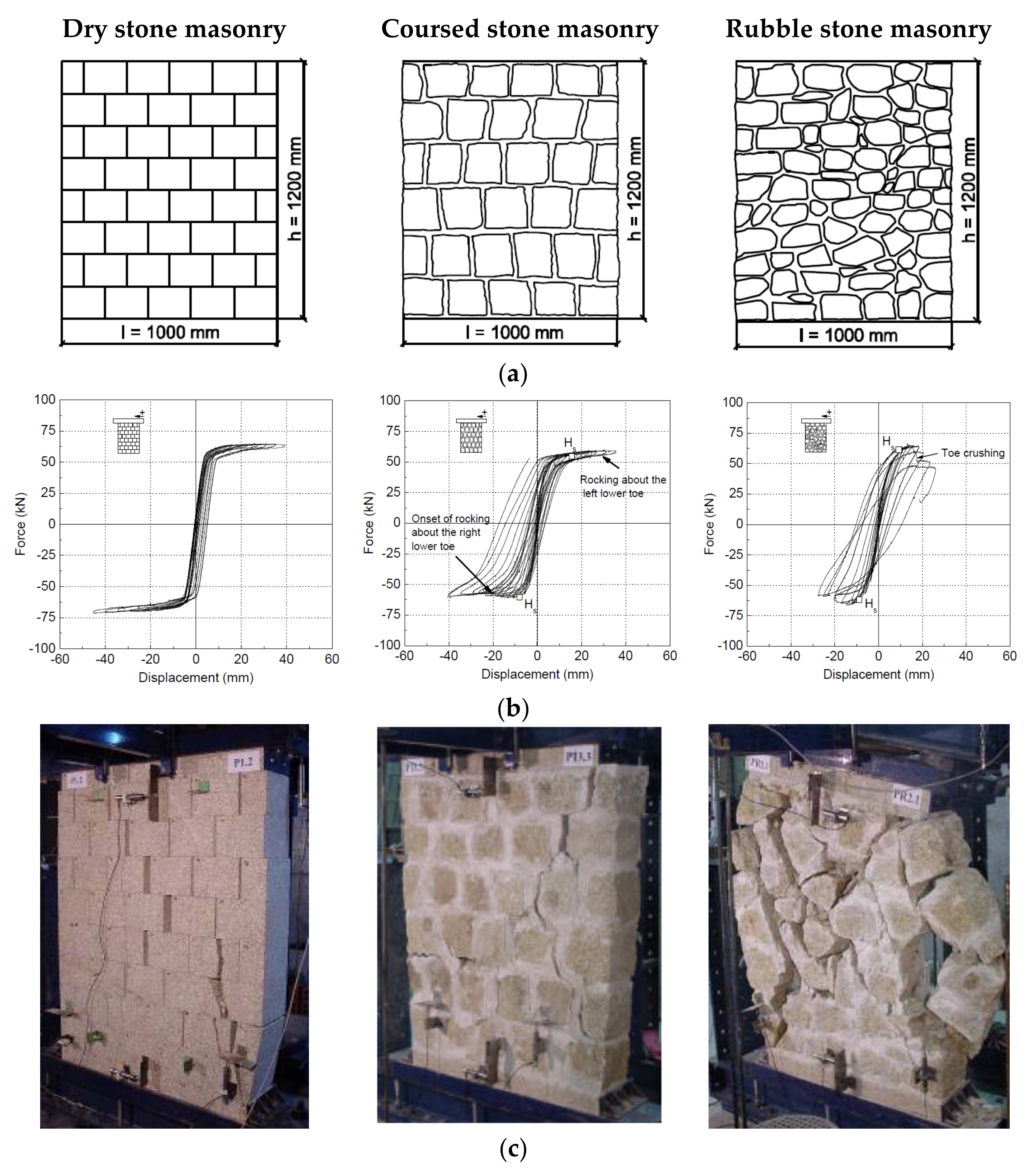
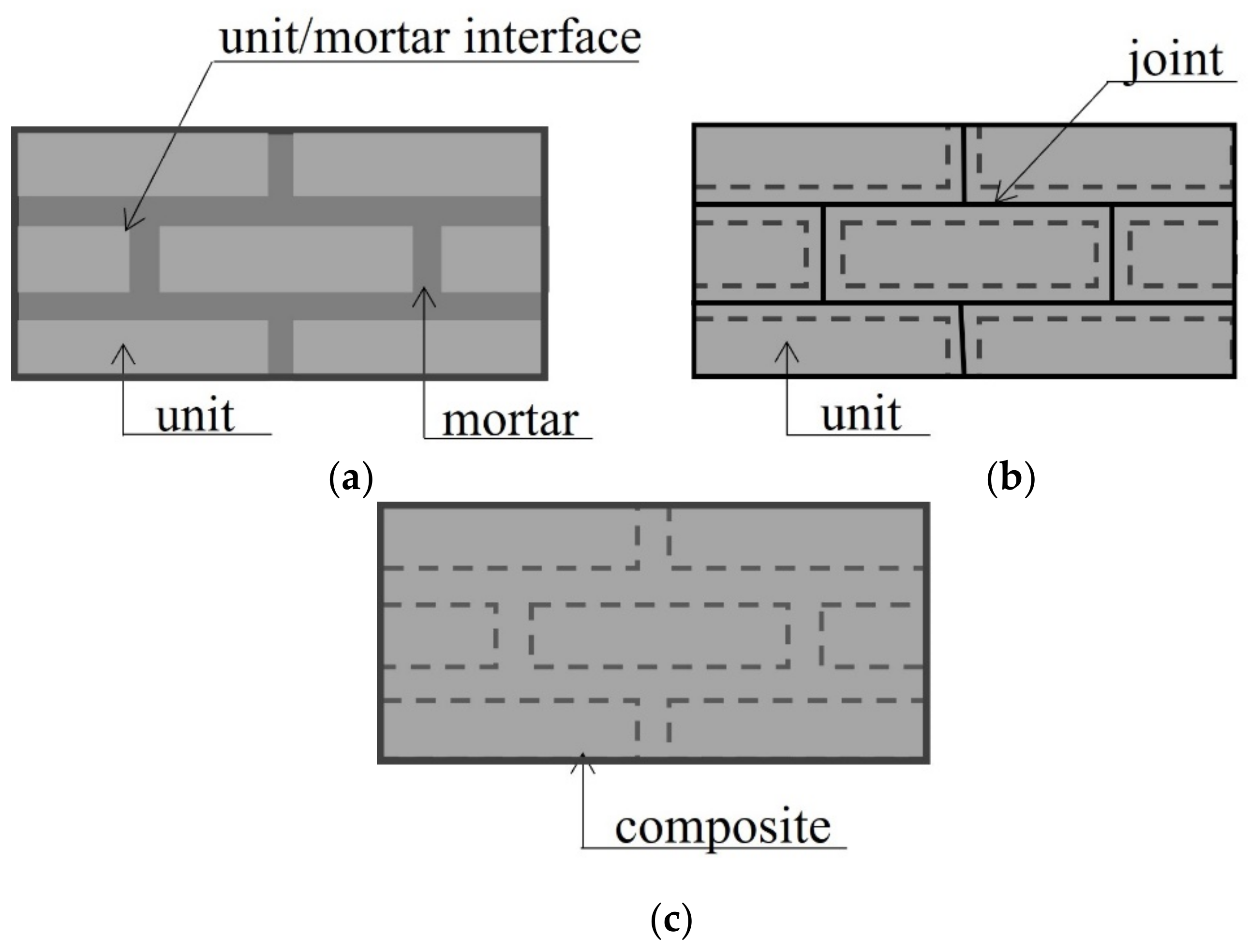
2. Masonry as a Complex Material with Internal Structure

Masonry is a non-homogeneous material formed by units and joints, with or without mortar, and different bond arrangements [21]. Unlike modern masonry, which mainly consists of regularly arranged units, with or without steel reinforcement, ancient masonry is formed by rather complex three-dimensional arrangements of stone or brick units (Figure 1), usually unreinforced. Such a visible internal structure, combined with the variability of materials, unit shape and surface treatments, makes the behavior of historical masonry structures highly indeterminate and difficult to predict and assess with accuracy [22,23,24,25,26].
Due to its composite character, masonry mechanics are strongly influenced by the individual properties of its constituents as well as by the bond between them, where the latter is often the weakest link in masonry assemblages. Five basic failure mechanisms can generally occur in masonry [27]: (a) tensile cracking of the joints, (b) shear sliding along the joints, (c) direct tensile cracking of the units, (d) diagonal tensile cracking of the units and (e) compressive crushing (Figure 2). The first two modes are essentially joint mechanisms, where failure occurs at low values of normal stress due to the poor bond strength between joints and units, which is typical for strong unit-weak mortar joint combinations, widely present in ancient stone masonry. The third failure mode is a unit mechanism, which is common in masonry with low-strength units but high-strength mortar, usually with greater tensile bond strength. Instead, the last two failure modes are combined mechanisms involving both units and mortar joints. The preponderance of one failure mode over another or the combination of various failure modes is essentially related to the internal structure of masonry, including the orientation of bed joints with respect to the principal stresses.
Figure 3 shows the results obtained from masonry walls with the same geometry but different units shape and arrangement, under combined vertical and cyclic horizontal in-plane loading [21]. Three types of walls are considered, namely dry stone (without mortar), coursed masonry and rubble stone masonry (the last two with the same low-strength mortar). While the in-plane behavior of the dry masonry wall with regular large units is characterized by a rocking response with no strength degradation (no damage in the stones) and remarkable lateral displacement capacity, the response of the coursed masonry wall is predominantly flexural, with a slight strength degradation associated with the progressive spreading of flexural cracks through the joints and a considerable lateral displacement capacity, with rocking mechanisms playing a minor role. By contrast, the response of the rubble masonry wall is essentially controlled by shear, showing a significant strength degradation and a low lateral deformation capability, with consequent brittle failure after the formation of diagonal smeared shear cracks. Despite the geometry and material be the same, distinct failure modes, ultimate lateral strengths and hysteretic behaviors are found for the three walls due to aspects such as roughness of the joints, unit dimensions and interlocking. Randomly assembled masonry typically features very low friction as compared to regularly arranged units with sawn or rough surfaces [28]. The connection between leaves, in case of multi-leaf masonry, also influences the masonry behavior. Past seismic events have shown that the systematic presence of headers between leaves plays a key role in the out-of-plane response of masonry walls; analogously, the presence of proper connection between perpendicular walls or between walls and floors is determinant to ensure a monolithic behavior and prevent out-of-plane failures.
Despite the existence of common features for masonry, i.e., relatively high resistance in compression, very low tensile strength and anisotropy for different loading directions, the complex mechanical behavior of unreinforced masonry structures cannot be univocally stereotyped since there can be as many different responses as the number of masonry types and specific combinations of geometries and materials.

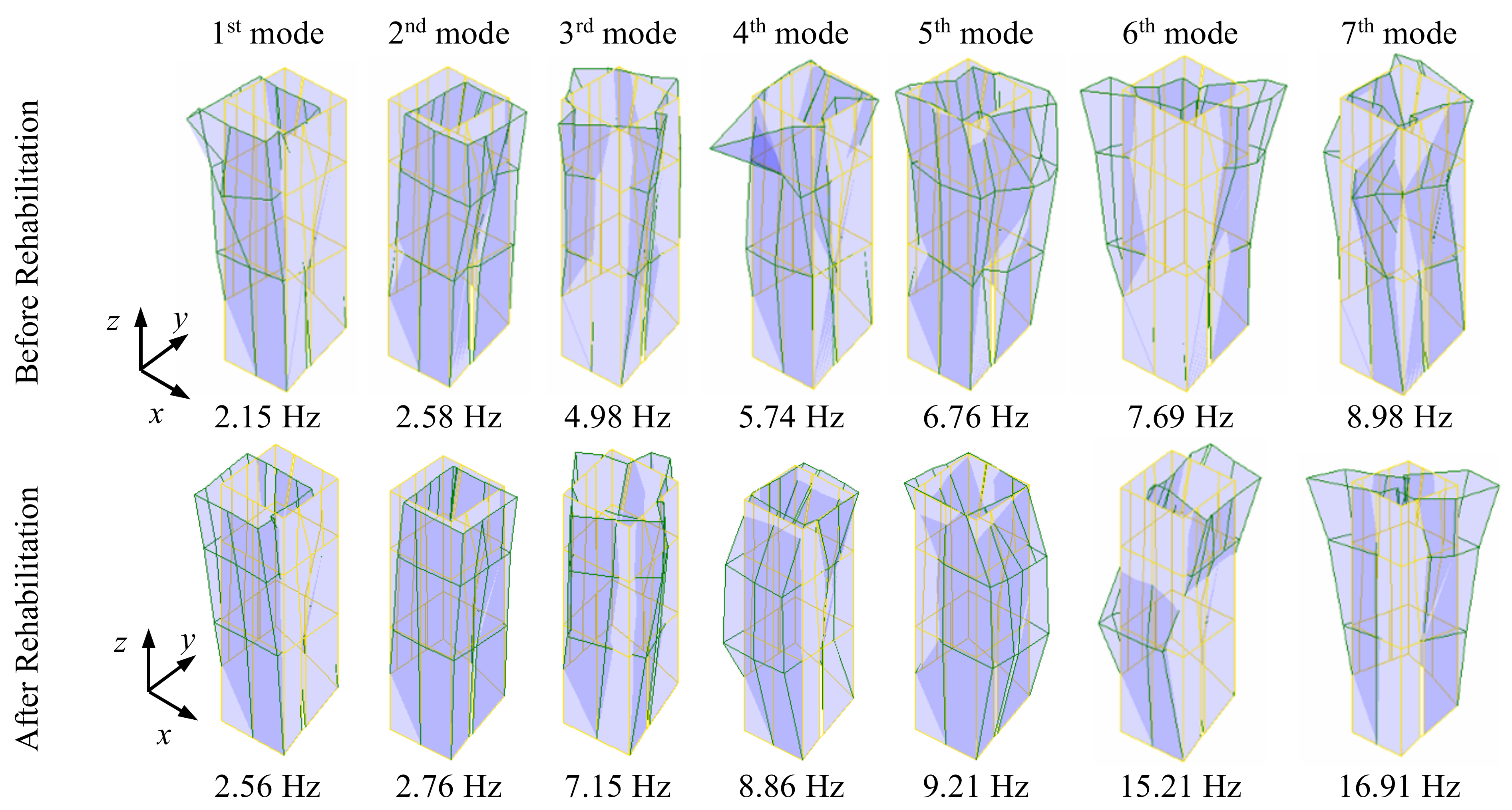
3. Dynamic Amplification and Higher Modes

In the of case of slender monumental historical structures, mostly built using masonry, the problems associated with the accurate modelling of the material internal structure add up to the uncertainties related to their dynamic behavior during earthquakes. Although apparently fixed to the naked eye, each structure does experience small oscillations that are dependent on its physical and mechanical properties, like mass, stiffness and energy dissipation, as well as on its boundary conditions. These small movements allow one to obtain vibration modes, i.e., different patterns in which the system tries to oscillate naturally, described by specific dynamic features, i.e., frequencies, mode shapes and damping ratios. Vibration modes can be tracked over time in a continuous or intermittent way for manifold objectives, including the calibration of realistic numerical models, the validation of strengthening interventions or the assessment of the structural conditions in pre- and post-seismic scenarios [29,30,31,32,33,34,35,36,37]. Characterizing ancient masonry constructions from a dynamic point of view allows a better interpretation of their structural behavior, which is complex and rather diverse, especially during earthquakes [19,38]. The most common procedure to identify the dynamic properties of historical structures is through operational modal analysis [30,39,40,41,42], a dynamic identification technique for estimation that requires only records of the structural response to freely available ambient excitations (like wind, traffic, microtremors and human walking), thereby allowing one to take into account the true operational and boundary conditions of the system. With the input load being unknown, modal parameters are identified from output-only data by applying suitable stochastic modal identification techniques, either in the frequency domain and/or in the time domain [30].
Among the main crucial aspects to consider in the seismic assessment of slender monumental structures is the considerable dynamic amplification that can occur if relevant frequencies of the structure are in the range of the predominant frequencies of the ground motion [43,44,45]. Indeed, the application of a dynamic force to a vibrating system causes oscillations that will tend to increase in amplitude whenever the frequency of the applied force coincides or approaches one of the system’s natural frequencies, leading to the so-called resonance phenomenon. As an example, Figure 4 and Table 1 show the response measured by the strong motion recorders installed in the Church of the Jerónimos Monastery in Lisbon, Portugal (one located at the base of the structure near the chancel, and the other one installed on the nave extrados) during the 6-magnitude earthquake occurred on 12 February 2007. A dynamic amplification occurred in both transversal and vertical directions; indeed, the peaks of the frequency content of the measured response spectra fell exactly within the range of natural frequencies estimated for the church. This phenomenon affected the vibration response of the structure, but the estimated frequency downshifts did not exceed the confidence limits established around each predicted value, meaning that only minor damage took place during the earthquake, see [46,47] for details. In the worst-case scenario, dynamic amplification can originate from an extreme structural response, with large vibrations triggering important nonlinear phenomena and even partial or global collapses (Figure 5).
As slender monumental towers do not belong to the category of single-mode dominated structures, the amplification of the dynamic response can interest multiple modes, especially high-frequency modes, whose effects on the seismic behavior of slender systems cannot be neglected. In fact, structures are more prone to experience local damage in case of out-of-phase vibrations due to the unsynchronized movements of the different structural nodes, which is typical for higher modes [48], and slender structures do feature a significantly higher mode response. Figure 6 displays the experimental modes identified before and after the rehabilitation works of the Mogadouro clock tower, a historic masonry structure located in northeast Portugal. The tower exhibited severe structural damage and a consolidation intervention was carried out to restore its sound state (Figure 7) [46,49].
The dynamic properties of the damaged tower reflected its structural condition, namely a lower-stiffness system with ongoing non-linear phenomena effects that turned into a higher-stiffness system with reduced non-linear phenomena, as demonstrated by the increase of frequency values along with a decrease of damping ratios after rehabilitation (Table 2). The close inspection of the mode shapes (Figure 6) revealed how the presence of local damage mechanisms was causing large modal displacements in the upper part of the tower, where higher mode effects are particularly important in the case of high-frequency content ground motions. It follows that, as far as slender monumental structures are concerned, depending on the intensity of the seismic action, amplifications may occur in elevation which may be even larger if the structure behaves inelastically. The influence of higher mode effects will depend to a considerable extent on the frequency content of the earthquake and on the magnitude of the plastic deformations of the structure, leading to changes in the dynamic properties that might strongly affect the overall dynamic response of the system to seismic forces.

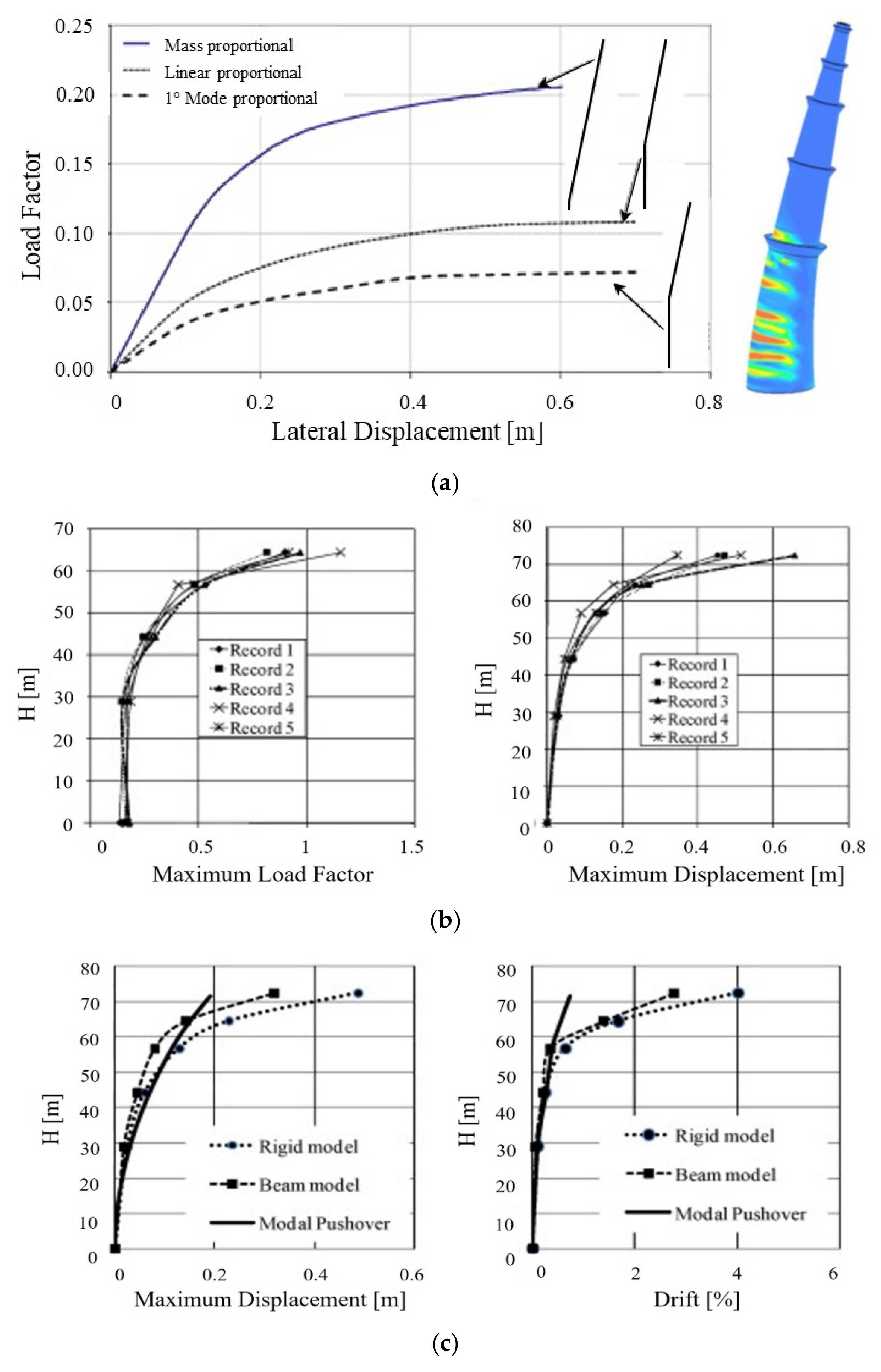
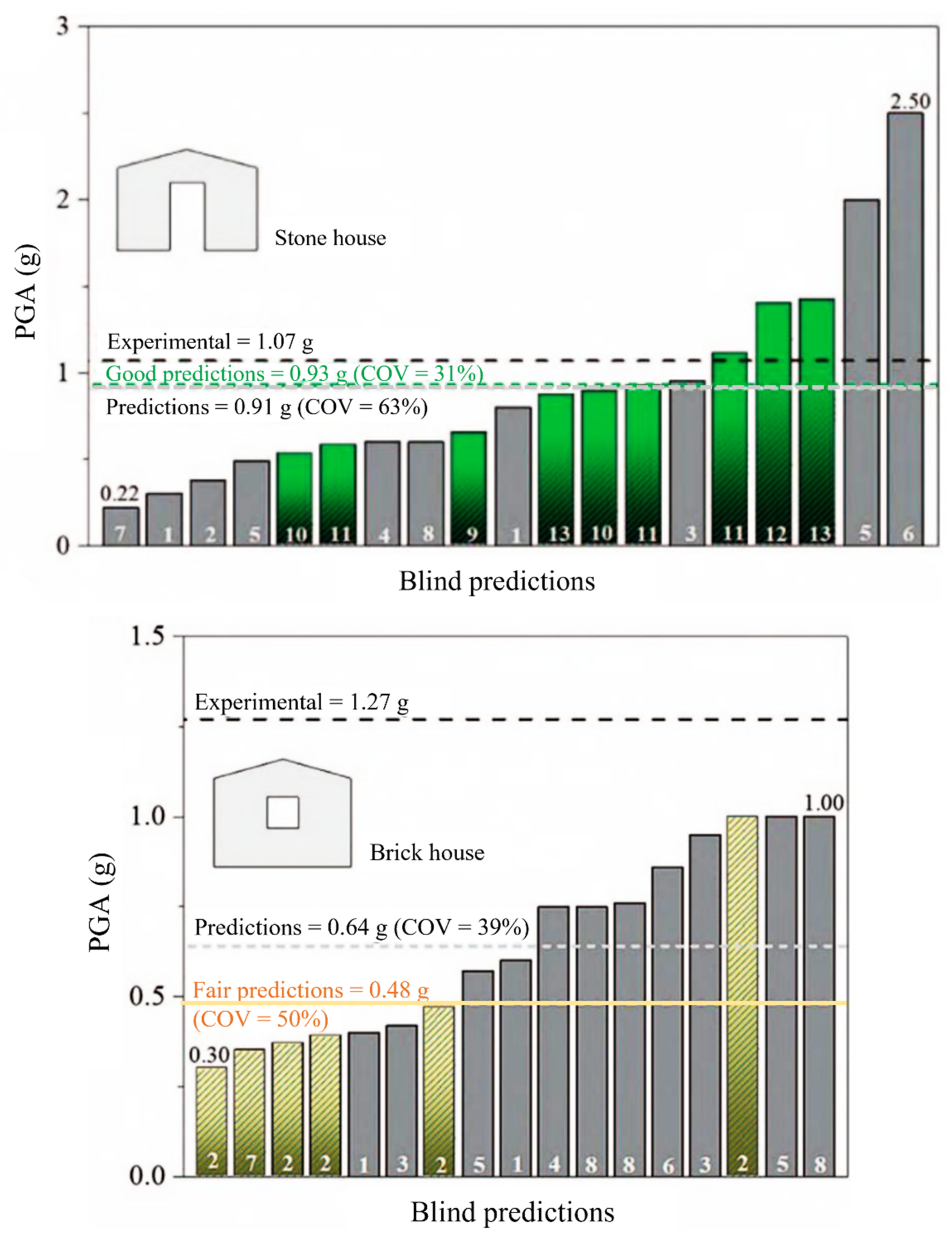
4. Structural Analysis Methods

In the light of the above considerations, it is clear that the inherent characteristics of slender monumental structures considerably affect their behavior under horizontal loads. Most of these structures were built in ancient times, in the absence of specific seismic codes, thus they were essentially conceived to withstand static vertical loads. In recent times, national and international standards [50,51,52] have imposed the evaluation of their seismic performance, encouraging the use of sophisticated nonlinear analysis methods [6]. However, in spite of the latest computational developments, structural analysis in earthquake engineering remains a complex task because the activated structural behavior is typically nonlinear and uncertain, and the input data concerning the ground motions are random and unpredictable [3,53]. The accuracy of the analysis method is of crucial importance, since a conservative approach may lead to unnecessary expensive interventions [54] (likely with a loss of cultural value), while a non-conservative approach may leave buildings exposed to excessive risk.
In the framework of the seismic analysis of slender structures belonging to the cultural heritage, linear and non-linear methods, static or dynamic, can be used for their global assessment [7,55,56,57], while limit analysis methods can be adopted to evaluate predefined mechanisms [51,58,59]. The main differences among the various global analysis procedures concern the assumptions about the behavior of the structure, the modelling of the seismic action and the computation of the structural response to that action.
Linear analysis methods assume the structural behavior is linear elastic and the seismic demand is computed through the q-factor approach (defined as seismic behavior factor, in Europe, or seismic response modification factor, in the USA), namely by introducing an elastic force reduction factor which accounts for the typology, energy dissipation capacity and regularity of the structure, where the latter aspect is rather arguable for ancient masonry constructions. In the case of linear static analysis or “lateral force method”, the seismic action may be modelled through equivalent lateral forces proportional to the inertial masses and distributed according to the main vibration mode of the structure in the examined direction, whereas, in the case of linear dynamic analysis or “response spectrum analysis”, the effects induced by the seismic action, represented by the elastic response spectrum, are computed—and then combined—for all vibration modes with effective modal mass larger or equal to 5% and activating at least 85% of the overall mass. However, time-dependent response and loading history are not available with this type of analyses.
Among the main issues concerning the seismic behavior of slender monumental structures is the influence of the vertical stresses induced by gravity loads, whose values are often of the same order of magnitude as the ultimate compressive strength of the material [7]. This aspect, combined with the very low tensile strength of masonry, means that the non-linear behavior of these structures can be triggered even by a moderate increase in the stress level in the case of earthquakes, thus the use of inelastic procedures such as non-linear static or dynamic analyses seems far more adequate for their assessment.
In what concerns non-linear static analysis, viz. the classical “pushover analysis”, the seismic force is applied to the structure as an incremental static lateral loading, usually assuming a first-modal or mass-proportional force distribution, and results are plotted in the form of a capacity curve (base shear vs. roof top horizontal displacement). Pushover analysis represents one of the most rational analysis methods for practical applications, but it was originally devised for single-mode dominated structures. To account for multiple modes contribution, several proposals have emerged in the literature in the last two decades and the recourse to such methods is explicitly allowed by the EC8 Part 3 [60]. One of these methods is the “modal pushover analysis” (MPA) introduced by [61] that combines classical pushover and response spectrum approaches. The effects induced by the seismic action are computed by combining the results of N pushover analyses, where N is the number of modes chosen based on the amount of activated mass, carried out assuming an invariant inertia force distribution for each mode. Despite the conceptual simplicity and computational attractiveness, MPA relies on the same approximations of all multi-mode methods, such as the superposition of effects and the modal combination rules, which are valid for elastically responding structures but rather questionable in the inelastic range. It follows that the non-linear dynamic analysis or “time history analysis” seems to be a more suitable option for the seismic assessment of masonry structures. Here, the seismic input is represented by spectrum-compatible accelerograms, whose appropriate selection is important to account for the variability associated with different input characteristics in terms of amplitude, energy and frequency content. According to the Italian [50,51] and European [52] codes, at least seven time-history analyses need to be carried out to embrace a wide range of responses, and mean output values are to be considered [62]. Incremental dynamic analysis methods employing multiple non-linear dynamic analyses under scaled ground motion records have also been developed in order to force the structure all the way from elasticity to final global dynamic instability and to have a comprehensive evaluation of the seismic performance of structures [63]. Yet, their application to special constructions, such as ancient monumental structures, is still in its infancy.
Considering the peculiar behavior of slender masonry structures, not all analysis methods result adequate. In this regard, Figure 8 displays the results obtained from different types of analysis carried out for the seismic assessment of the Qutb Minar tower [64], the highest monumental structure in India and one of the tallest masonry towers in the world (Figure 9). It is interesting to note that the nonlinear static and dynamic analyses provide quite a different response of the structure to earthquakes. The non-linear static analysis shows a diffuse cracking in the lowest part of the tower and a base overturning mechanism, but the maximum load factor results are very dependent on the adopted force distribution (Figure 8a): in fact, the load factors proportional to the first mode and to the linear distribution equal, respectively, 35% and 53% of the load factor proportional to the mass. The collapse section varies as well: in the case of forces proportional to the mass, the analysis shows a base collapse mechanism, whereas for the other analyses the collapses occur at the level of the first balcony. By contrast, the non-linear dynamic analysis proves that the most vulnerable parts of the minaret are the top two stories (Figure 8b), which is in agreement with the damage observed during past earthquakes. Such a difference in the results is due to the influence that higher modes have on the seismic behavior of the tower, modes whose participation is not considered in the standard pushover. To account for this aspect, the seismic assessment was repeated using a modal pushover analysis and considering seven modes for each direction. While displacements and drifts for the first three levels (Figure 8c) are similar to those estimated with the non-linear dynamic analyses, MPA is not able to reproduce satisfactory the failure mechanism of the last two levels. This inconsistency is explained by the variation of the tower’s dynamic properties during the damage process, variation that cannot be caught with a modal pushover because the influence of each mode is considered constant throughout the analysis. An alternative is to adopt adaptive pushover analysis [65,66], in which the load distribution depends on the current main mode of vibration, but poor results have been obtained for these complex and relatively brittle structures.
Given the time-dependency of the problem, the non-linearity of the material and the influence of higher modes on the seismic behavior of slender monumental structures, non-linear dynamic analyses appear to be the most appropriate numerical procedures to evaluate the performance of these special constructions against earthquakes [67,68]. It is noted that the definition of collapse and other performance levels is quite difficult, and the pros and cons of adopting such a complex tool must be carefully considered. Depending on the prominence of the monument and on the objectives of the analysis, a balance between accuracy and complexity must be achieved.

5. Modelling Strategies

One final aspect deserving attention is the numerical modelling of slender masonry structures, which introduces different challenges due to the inherent difficulties associated with the description of the complex behavior of the masonry material. According to the level of accuracy desired, three main modelling strategies can be adopted, see Figure 10: (1) detailed micro-modelling, in which units and mortar are represented by continuum elements whereas unit-mortar interfaces are represented by discontinuous elements accounting for potential crack and slip planes; (2) simplified micro-modelling, in which expanded units are represented by continuum elements while the behavior of mortar joints and unit-mortar interfaces is lumped into “average” discontinuous elements; (3) macro-modelling, where no distinction among units, mortar and unit-mortar interfaces exists but masonry is treated as a homogeneous anisotropic continuum [69]. Several efforts have also been made in the last decade to improve the so-called homogenization techniques, trying to link micro- and macro-modelling approaches by deriving the constitutive relations of masonry from the individual characteristics of the components of a selected elementary cell [22,28,70,71,72,73,74,75].
Regardless of the modelling strategy, a thorough experimental description of the material is always required. As for micro-modelling, this must be obtained from laboratory tests in the masonry constituents and small masonry samples, whereas, for macro-modelling, tests must be performed in masonry specimens of sufficient size under homogeneous states of stress and strain [27]. In either case, the task is not trivial considering that the mechanical behavior of masonry is influenced by a large number of factors (see also Section 2), such as the material properties of units and mortar, the shape and dimensions of the units, the bond arrangement, the inner core, the joint thickness, the quality of workmanship, the degree of curing, environment and age.
In addition to the different modelling approaches in terms of material, three main methods can be adopted for the numerical simulation of heterogeneous masonry constructions, including slender monumental structures: (1) the macro element approach; (2) the discrete element method; and (3) the finite element method. The difference among the various strategies is mainly related to the assumptions about the material and structural behavior, input parameters, modelling effort and computational time required.
The macro element approach relies on the assumption of a no-tension masonry material, usually with infinite compressive strength and no sliding between units. It is a very simple tool that can be applied to evaluate the failure mechanisms of historical masonry structures (kinematic limit analysis), allowing a good estimation of the collapse load factor and displacement capacity of monolithic macro-blocks in which the structure can be ideally subdivided according to the most probable collapse mechanisms. The analysis is not computationally demanding, but it requires an a priori knowledge of the possible disconnections between the rigid blocks composing the kinematic chain, which is not straightforward when a large variety of mechanisms are possible in the structure. Usually, these are selected on the basis of post-earthquake surveyed crack patterns or based on the analyst experience [4,76,77]; yet, an incorrect evaluation of the collapse mechanisms can lead to neglect the mechanism with the lowest load factor and, consequently, to overestimate the real maximum capacity of the structure [70]. Conversely, an incorrect evaluation of the collapse mechanisms may also lead to incorrect overly conservative interventions, if the mechanism with the lowest safety factor assumed by the analyst cannot occur. Moreover, loading history and crack evolution can be hardly included. Remarkable advances have been made towards the automatic assessment of partial failure mechanisms in masonry structures [78,79,80], but further efforts are needed to fully convert kinematic limit analysis into an automatized process free of arbitrary decisions, which replicates the real conditions of the building.
The distinct element method (DEM) idealizes masonry as a discontinuum material consisting of an assemblage of distinct rigid or deformable bodies whose joints are modelled as contact surfaces with suitable interface laws. Originated from the study of rock mechanics in the 1980s [81], this approach enables to simulate various sources of nonlinearities in masonry structures, including large displacements caused by sliding at the joints with consequent contact update, or the complete separation between blocks. The natural field of application of DEM is composed of structures formed by regularly shaped masonry or stone blocks, such as stone bridges, columns and pillars, arches, and vaults. DEM is also appropriate for modelling the out-of-plane behavior of multi-leaf masonry walls taking into account the real units’ arrangement. Some applications to masonry structures can be found in [82,83,84,85,86,87]. The application to complex structures of relevant size remains controversial, mainly because of the high number of block elements needed to obtain a realistic discretization of the construction and of the large number of contact points required for the accurate representation of interface stresses, which make the analysis computationally non-viable, especially for 3D problems [23,28].
The finite element method (FEM) remains the most used tool for the advanced analysis of the seismic behavior of masonry constructions, allowing to use different element types and material modelling strategies, including discrete micro-models or continuous macro-models. As mentioned previously, micro-modelling considers the behavior of units, mortar and unit-mortar interfaces separately, thus leading to more accurate results, but mesh preparation can be unwieldy. Owing to the high level of refinement required, its application is mostly limited to the analysis of small structural portions, the computational effort being extremely demanding at large scale [74,88,89,90]. By contrast, macro-modelling considers masonry as a homogeneous continuum and requires a reduced computational effort, thereby being preferred when dealing with large structures and a compromise between accuracy and efficiency is sought [91]. However, due to the impossibility to execute ad-hoc experimental tests for the characterization of the various parameters necessary to describe the anisotropic behavior of the material in the inelastic range, isotropic macro-models can be adopted for the non-linear analysis of masonry structures, which is an acceptable simplification at the structural level [92,93,94,95,96]. Some recent applications of FEM-based modelling approaches to slender masonry structures can be found in [33,38].
Figure 11 and Figure 12 report the results of the blind predictions provided by several experts on the out-of-plane behavior of two U-shaped masonry structures tested on the shaking table of the LNEC (National Laboratory of Civil Engineering), Lisbon, Portugal, the first specimen being built with granite stones and the second specimen with fired clay bricks, together with lime-based mortar [97]. Several types of analyses were adopted to evaluate the seismic capacity of the structures in terms of failure mechanisms and PGA at collapse, using the three afore-mentioned modelling approaches (Figure 11). The same input parameters, i.e., geometry, material properties, normalized acceleration response spectrum and accelerogram envelope, were provided to the experts for both specimens, see [98]. In the blind predictions of the stone house, 13 idealized collapse mechanisms were proposed, recording an error of about 28% between the average PGA of good predictions and the experimental PGA. Within the good predictions, 80% of the estimated PGAs were lower than or equal to the test PGA. As for the brick house, eight different collapse mechanisms were proposed, and all predictions presented a PGA lower than the experimental one. The high dispersion of the results demonstrates that the peculiar and case-specific character of masonry structures continues to pose significant challenges to the study of these constructions, despite the fact that predictions were generally on the safe side. The most advanced and sophisticated models and analysis methods do not necessarily lead to exact results. Predictions of the structural response greatly depend on the analyst’s experience and modelling skills.

6. Discussion and Conclusions

Historical masonry towers and slender structures may experience many problems during their service life, including soil settlements, compression damage, deterioration processes, lightning strikes, or excessive bell vibrations, but earthquakes remain one of the most challenging problems to face. This is related to the fact that the majority of these peculiar structures were conceived exclusively to withstand gravity loads, thus featuring quite a poor behavior under strong horizontal actions. In many cases, slender structures are simplistically assimilated to cantilever beams made of no-tension material with failure mechanisms occurring due to the formation of a flexural hinge at the base. Yet, past earthquakes have demonstrated that the behavior of these monumental constructions can be much more complex than expected and as mentioned in the Introduction, other mechanisms can be activated with higher probability [8]. Therefore, the accurate assessment of historical towers and slender monumental structures is of paramount importance to predict their performance during seismic events and to evaluate the real need for strengthening measures aiming at reducing their vulnerability.
To achieve a thorough understanding of cultural heritage structures, a scientific approach combining different diagnosis and analysis tools is required. It is an iterative multi-disciplinary process of knowledge accumulation demanding a variety of complementary activities and integrated analysis methods to correctly interpret the empirical evidence and relate the observed phenomena with the initial hypotheses made on the structure, till reliable and consistent conclusions about its behavior can be drawn (Figure 13). To this end, engineers need to act according to a step-by-step methodology organized in stages similar to those used in medicine [47,99]: condition survey (anamnesis), identification of the causes triggering damage and decay (diagnosis), choice of the remedial measures (therapy) and control of the efficiency of the interventions (control). Anamnesis must involve both a thorough visual inspection and a deep historical survey in order to shed light on the past life of the structure, including its conception, building techniques and alterations, thus allowing a better interpretation of the actual condition. Diagnosis should be based on both qualitative and quantitative investigation methods, where the former implies the direct observation of the structural damage and material decay (whose origins may find support in the historical findings), while the latter requires material experimental tests, structural monitoring and numerical analysis. The afore-mentioned tasks are indispensable to understand the root causes of the observed “symptoms” and eventually drive the selection of the best “therapy”, trying to keep interventions to the minimum necessary to guarantee safety and durability without compromising the authenticity of the construction. Appropriate control tools can be finally used to assess the effectiveness of the adopted remedial measures [100].
Nevertheless, engineers must be aware that restrictions in the inspection and removal of specimens in structures of historical value, as well as the high costs involved in the execution of experimental characterization tests, often result in limited information about the internal morphology of structural members or the properties of existing materials [99]. These difficulties can be successfully overcome by combining non-destructive diagnostic investigations (e.g., thermography, ground penetrating radar, sonic and ultrasonic tests, or dynamic testing procedures) and monitoring, so that valuable input data at local and global levels can be obtained for the characterization of the analyzed structures as well as for the calibration of realistic numerical models able to predict the structural response. It is important to bear in mind that, given the remarkable singularity of slender monumental constructions, the most sophisticated methods and tools developed to carry out advanced structural analyses may not always provide sufficiently adequate results. A careful and time-consuming stepped approach is needed.
This manuscript reviewed and discussed the main issues associated with the seismic analysis of slender monumental structures, pointing out—in a format of interest to both practitioners and researchers—relevant aspects that must be considered in the analysis process. The singularity of tall masonry structures, the appropriate reproduction of the constitutive aspects of the material in the dynamic field, and the high computational cost required to perform accurate analyses pose many challenges to the assessment of their actual behavior during earthquakes. Notwithstanding, the significant progresses that occurred in the last decade in the earthquake engineering field with respect to the possibilities of advanced numerical and experimental techniques for cultural heritage structures have allowed us to develop an adequate methodological framework to address the problem.

Author Contributions

Conceptualization, M.G.M. and P.B.L.; methodology, M.G.M.; validation, M.G.M. and P.B.L.; formal analysis, M.G.M.; investigation, M.G.M.; resources, P.B.L.; visualization, M.G.M.; data curation, M.G.M.; writing—original draft preparation, M.G.M.; writing—review and editing, M.G.M. project administration, P.B.L. All authors have read and agreed to the published version of the manuscript.

Funding

This work was carried out within the framework of the National Operational Programme on Research and Innovation (Attraction and International Mobility) PON-AIM 2014-2020 Line 2, co-financed by the European Social Fund and by the National Rotation Fund.

Institutional Review Board Statement

Not applicable.

Data Availability Statement

Data, models, or codes supporting the results shown in this study are available from the corresponding author upon reasonable request.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Daniell, J.; Wenzel, F.; Schaefer, A. The economic costs of natural disasters globally from 1900–2015. In Natural Disasters Since 1900—Over 8 Million Deaths and 7 Trillion US Dollars Damage, Proceedings of the EGU General Assembly Conference, Vienna, Austria, 17–22 April 2016; EGU General Assembly: Vienna, Austria, 2016; Volume 18, p. 1899. Available online: phys.org (accessed on 20 April 2022).
  2. Ghosh, S. Observations on the performance of structures in the Kobe earthquake of January 17. PCI J. 1995, 40, 14–22. [Google Scholar] [CrossRef]
  3. Fajfar, P. Analysis in seismic provisions for buildings: Past, present and future. In Recent Advances in Earthquake Engineering in Europe; Pitilakis, K., Ed.; Geotechnical, Geological and Earthquake Engineering; Springer: Cham, Switzerland, 2018; Volume 46. [Google Scholar]
  4. Sarhosis, V.; Milani, G.; Formisano, A.; Fabbrocino, F. Evaluation of different approaches for the estimation of the seismic vulnerability of masonry towers. Bull. Earthq. Eng. 2018, 16, 1511–1545. [Google Scholar] [CrossRef] [Green Version]
  5. Cabboi, A.; Gentile, C.; Saisi, A. From continuous vibration monitoring to FEM-based damage assessment: Application on a stone-masonry tower. Constr. Build. Mater. 2017, 156, 252–265. [Google Scholar] [CrossRef]
  6. Casolo, S.; Milani, G.; Uva, G.; Alessandri, C. Comparative seismic vulnerability analysis on ten masonry towers in the coastal Po Valley in Italy. Eng. Struct. 2013, 49, 465–490. [Google Scholar] [CrossRef]
  7. Valente, M.; Milani, G. Non-linear dynamic and static analyses on eight historical masonry towers in the North-East of Italy. Eng. Struct. 2016, 114, 241–270. [Google Scholar] [CrossRef]
  8. Milani, G.; Shehu, R.; Valente, M. A kinematic limit analysis approach for seismic retrofitting of masonry towers through steel tie-rods. Eng. Struct. 2018, 160, 212–228. [Google Scholar] [CrossRef]
  9. Kouris, E.-G.S.; Kouris, L.-A.S.; Konstantinidis, A.A.; Kourkoulis, S.K.; Karayannis, C.G.; Aifantis, E.C. Stochastic Dynamic Analysis of Cultural Heritage Towers up to Collapse. Buildings 2021, 11, 296. [Google Scholar] [CrossRef]
  10. Bartoli, G.; Betti, M.; Biagini, P.; Borghini, A.; Ciavattone, A.; Girardi, M.; Lancioni, G.; Marra, A.M.; Ortolani, B.; Pintucchi, B.; et al. Epistemic Uncertainties in Structural Modeling: A Blind Benchmark for Seismic Assessment of Slender Masonry Towers. J. Perform. Constr. Facil. 2017, 31, 4017067. [Google Scholar] [CrossRef]
  11. Valente, M. Seismic vulnerability assessment and earthquake response of slender historical masonry bell towers in South-East Lombardia. Eng. Fail. Anal. 2021, 129, 105656. [Google Scholar] [CrossRef]
  12. Riva, P.; Perotti, F.; Guidoboni, E.; Boschi, R. Seismic analysis of the Asinelli Tower and earthquakes in Bologna. Soil. Dyn. Earthq. Eng. 1998, 17, 525–550. [Google Scholar] [CrossRef]
  13. Milani, G.; Shehu, R.; Valente, M. Role of inclination in the seismic vulnerability of bell towers: FE models and simplified approaches. Bull. Earthq. Eng. 2017, 15, 1707–1737. [Google Scholar] [CrossRef]
  14. Acito, M.; Bocciarelli, M.; Chesi, C.; Milani, G. Collapse of the clock tower in Finale Emilia after the May 2012 Emilia Romagna earthquake sequence: Numerical insight. Eng. Struct. 2014, 72, 70–91. [Google Scholar] [CrossRef]
  15. Preciado, A.; Santos, J.C.; Silva, C.; Ramírez-Gaytán, A.; Falcon, J.M. Seismic damage and retrofitting identification in unreinforced masonry Churches and bell towers by the september 19, 2017 (Mw = 7.1) Puebla-Morelos earthquake. Eng. Fail. Anal. 2020, 118, 104924. [Google Scholar] [CrossRef]
  16. Ruggieri, S.; Tosto, C.; Rosati, G.; Uva, G.; Ferro, G.A. Seismic Vulnerability Analysis of Masonry Churches in Piemonte after 2003 Valle Scrivia Earthquake: Post-event Screening and Situation 17 Years Later. Int. J. Arch. Herit. 2020, 16, 717–745. [Google Scholar] [CrossRef]
  17. De Matteis, G.; Brando, G.; Corlito, V. Simplified Assessment of the Seismic Vulnerability of Churches after the 2009 L’Aquila Earthquake: An Interdisciplinary Approach; Springer International Publishing: New York, NY, USA, 2019; pp. 1280–1289. ISBN 9783319994406. [Google Scholar]
  18. Heyman, J. Leaning towers. Meccanica 1992, 27, 153–159. [Google Scholar] [CrossRef]
  19. Valente, M.; Milani, G. Effects of Geometrical Features on the Seismic Response of Historical Masonry Towers. J. Earthq. Eng. 2018, 22, 2–34. [Google Scholar] [CrossRef]
  20. Magrinelli, E.; Acito, M.; Bocciarelli, M. Numerical insight on the interaction effects of a confined masonry tower. Eng. Struct. 2021, 237, 112195. [Google Scholar] [CrossRef]
  21. Vasconcelos, G.; Lourenço, P.B. In-plane experimental behavior of stone masonry walls under cyclic loading. J. Struct. Eng. (ASCE) 2009, 135, 1269–1277. [Google Scholar] [CrossRef]
  22. Milani, G.; Esquivel, Y.W.; Lourenço, P.B.; Riveiro, B.; Oliveira, D.V. Characterization of the response of quasi-periodic masonry: Geometrical investigation, homogenization and application to the Guimarães castle, Portugal. Eng. Struct. 2013, 56, 621–641. [Google Scholar] [CrossRef] [Green Version]
  23. Roca, P.; Cervera, M.; Gariup, G.; Pelà, L. Structural Analysis of Masonry Historical Constructions. Classical and Advanced Approaches. Arch. Comput. Methods Eng. 2010, 17, 299–325. [Google Scholar] [CrossRef] [Green Version]
  24. Sacco, E.; Addessi, D.; Sab, K. New trends in mechanics of masonry. Meccanica 2018, 53, 1565–1569. [Google Scholar] [CrossRef] [Green Version]
  25. D’Altri, A.M.; Sarhosis, V.; Milani, G.; Rots, J.; Cattari, S.; Lagomarsino, S.; Sacco, E.; Tralli, A.; Castellazzi, G.; de Miranda, S. Modeling Strategies for the Computational Analysis of Unreinforced Masonry Structures: Review and Classification. Arc. Computat. Methods Eng. 2020, 27, 1153–1185. [Google Scholar] [CrossRef]
  26. Andreini, M.; De Falco, A.; Giresini, L.; Sassu, M. Mechanical characterization of masonry walls with chaotic texture: Procedures and results of in-situ tests. Int. J. Archit. Herit. 2014, 8, 376–407. [Google Scholar] [CrossRef]
  27. Lourenço, P.B. Computational Strategies for Masonry Structures. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1996. [Google Scholar]
  28. Lourenço, P.B.; Oliveira, D.V.; Milani, G. Computational advances in masonry structures: From mesoscale modeling to engineering application. In Developments and Applications in Computational Structures Technology; Topping, B.H.V., Adam, J.M., Pallarés, F.J., Bru, R., Romero, M.L., Eds.; Saxe-Coburg Publications: Kippen, Scotland, 2016; pp. 1–23. [Google Scholar]
  29. Limongelli, M.P.; Dolce, M.; Spina, D.; Guéguen, P.; Langlais, M.; Wolinieck, D.; Maufroy, E.; Karakostas, C.Z.; Lekidis, V.A.; Morfidis, K.; et al. S2HM in some European countries. In Seismic Structural Health Monitoring; Limongelli, M.P., Celebi, M., Eds.; Springer Tracts in Civil Engineering; Springer: Cham, Switzerland, 2019; pp. 303–343. ISBN 978-3-030-13975-9. [Google Scholar]
  30. Masciotta, M.G.; Ramos, L.F. Dynamic identification of historic masonry structures. In Long-Term Performance and Durability of Masonry Structures; Ghiassi, B., Lourenço, P.B., Eds.; Woodhead Publishing Series in Civil and Structural Engineering; Woodhead Publishing: Sawston, UK, 2019; pp. 241–264. ISBN 9780081021101. [Google Scholar]
  31. Fragonara, L.Z.; Boscato, G.; Ceravolo, R.; Russo, S.; Ientile, S.; Pecorelli, M.L.; Quattrone, A. Dynamic investigation on the Mirandola bell tower in post-earthquake scenarios. Bull. Earthq. Eng. 2017, 15, 313–337. [Google Scholar] [CrossRef] [Green Version]
  32. Gentile, C.; Saisi, A. Ambient vibration testing of historic masonry towers for structural identification and damage assessment. Constr. Build. Mater. 2007, 21, 1311–1321. [Google Scholar] [CrossRef]
  33. Ubertini, F.; Cavalagli, N.; Kita, A.; Comanducci, G. Assessment of a monumental masonry bell-tower after 2016 Central Italy seismic sequence by long-term SHM. Bull. Earthq. Eng. 2018, 16, 775–801. [Google Scholar] [CrossRef]
  34. Bayraktar, A.; Türker, T.; Sevım, B.; Altunişik, A.C.; Yildirim, F. Modal Parameter Identification of Hagia Sophia Bell-Tower via Ambient Vibration Test. J. Nondestruct. Eval. 2009, 28, 37–47. [Google Scholar] [CrossRef]
  35. Invernizzi, S.; Lacidogna, G.; Lozano-Ramírez, N.E.; Carpinteri, A. Structural monitoring and assessment of an ancient masonry tower. Eng. Fract. Mech. 2019, 210, 429–443. [Google Scholar] [CrossRef]
  36. Foti, D.; Ivorra, S.; Sabba, M.F. Dynamic investigation of an ancient masonry bell tower with operational modal analysis a non-destructive experimental technique to obtain the dynamic characteristics of a structure. Open Constr. Build. Technol. J. 2012, 6, 384–391. [Google Scholar] [CrossRef] [Green Version]
  37. Fabbrocino, F. Estimation of the natural periods of existing masonry towers through empirical procedure. Int. J. Sustain. Mater. Struct. Syst. 2016, 2, 250–261. [Google Scholar] [CrossRef]
  38. Azzara, R.M.; Girardi, M.; Padovani, C.; Pellegrini, D. Experimental and numerical investigations on the seismic behaviour of the San Frediano bell tower in Lucca. Ann. Geophys. 2018, 61, AC59. [Google Scholar] [CrossRef]
  39. Masciotta, M.G.; Ramos, L.F.; Lourenço, P.B.; Vasta, M. Structural monitoring and damage identification on a masonry chimney by a spectral-based identification technique. In Proceedings of the International Conference on Structural Dynamics (EURODYN), Porto, Portugal, 30 June–2 July2014; Cunha, A., Caetano, E., Ribeiro, P., Müller, G., Eds.; pp. 211–218, ISBN 978-972752165-4. [Google Scholar]
  40. Azzara, R.M.; Girardi, M.; Iafolla, V.; Lucchesi, D.M.; Padovani, C.; Pellegrini, D. Ambient Vibrations of Age-old Masonry Towers: Results of Long-term Dynamic Monitoring in the Historic Centre of Lucca. Int. J. Archit. Herit. 2021, 15, 5–21. [Google Scholar] [CrossRef] [Green Version]
  41. Casciati, S.; Al-Saleh, R. Dynamic behavior of a masonry civic belfry under operational conditions. Acta Mech. 2010, 215, 211–224. [Google Scholar] [CrossRef]
  42. Pallarés, F.J.; Betti, M.; Bartoli, G.; Pallarés, L. Structural health monitoring (SHM) and Nondestructive testing (NDT) of slender masonry structures: A practical review. Constr. Build. Mater. 2021, 297, 123768. [Google Scholar] [CrossRef]
  43. Lu, J.; Han, X.; Wang, Z.; Li, C. Research on Dynamic Properties of Ancient Masonry Pagoda with Solid Structure in China. Int. J. Archit. Herit. 2022, 16, 746–766. [Google Scholar] [CrossRef]
  44. Gatti, M. Relation between dynamic amplification, structural height and damage in buildings affected by the recent Italian earthquakes. Geomat. Nat. Hazards Risk 2020, 11, 1154–1174. [Google Scholar] [CrossRef]
  45. Mehrotra, A.; Liew, A.; Block, P.; DeJong, M. An Integrated Modeling Approach that Combines Elastic Amplification and Rocking Analysis for Seismic Assessment of a Masonry Tower. In Proceedings of the 12th International Conference on Structural Analysis of Historical Constructions (SAHC 2020), Barcelona, Spain, 16–18 September 2020; Available online: https://www.scipedia.com/public/A._Mehrotra_2021a (accessed on 14 July 2022).
  46. Ramos, L.F.; Marques, L.; Lourenço, P.B.; De Roeck, G.; Campos-Costa, A.; Roque, J. Monitoring historical masonry structures with operational modal analysis: Two case studies. Mech. Syst. Signal. Process. 2010, 24, 1291–1305. [Google Scholar] [CrossRef] [Green Version]
  47. Masciotta, M.G.; Roque, J.C.A.; Ramos, L.F.; Lourenço, P.B. A multidisciplinary approach to assess the health state of heritage structures: The case study of the Church of Monastery of Jerónimos in Lisbon. Constr. Build. Mater. 2016, 116, 169–187. [Google Scholar] [CrossRef] [Green Version]
  48. Masciotta, M.G.; Pellegrini, D. Tracking the variation of complex mode shapes for damage quantification and localization in structural systems. Mech. Syst. Signal. Process. 2022, 169, 108731. [Google Scholar] [CrossRef]
  49. Pellegrini, D.; Girardi, M.; Lourenço, P.B.; Masciotta, M.G.; Mendes, N.; Padovani, C.; Ramos, L.F. Modal analysis of historical masonry structures: Linear perturbation and software benchmarking. Constr. Build. Mater. 2018, 189, 1232–1250. [Google Scholar] [CrossRef]
  50. DM 14 Gennaio 2008, NTC 2008, Nuove Norme Tecniche per le Costruzioni. Ministero delle Infrastrutture (GU n.29 04/02/2008), Rome, Italy and Circolare 2 Febbraio 2009, n. 617 Istruzioni per l’applicazione delle «Nuove norme Tecniche per le Costruzioni» di cui al Decreto Ministeriale 14 Gennaio 2008 (GU n. 47 del 26–2-2009—Suppl. Ordinario n.27).
  51. DM 17 Gennaio 2018, NTC 2018, Aggiornamento delle Norme Tecniche per le Costruzioni. Ministero delle Infrastrutture (GU n.42 20/02/2018), Rome, Italy and Circolare 21 Gennaio 2019, n. 7 Istruzioni per l’applicazione dell’«Aggiornamento delle Norme Tecniche per le Costruzioni» di cui al Decreto Ministeriale 17 Gennaio 2018 (GU n. 35 del 11–2-2019).
  52. Eurocode 8, EN 1998-1; Design of Structures for Earthquake Resistance. Part 1: General Rules, Seismic Actions and Rules for Buildings. European Committee for Standardization: Brussels, Belgium, 2005.
  53. Pelà, L.; Aprile, A.; Benedetti, A. Seismic assessment of masonry arch bridges. Eng. Struct. 2009, 31, 1777–1788. [Google Scholar] [CrossRef]
  54. Torelli, G.; D’Ayala, D.; Betti, M.; Bartoli, G. Analytical and numerical seismic assessment of heritage masonry towers. Bull. Earthq. Eng. 2020, 18, 969–1008. [Google Scholar] [CrossRef] [Green Version]
  55. Preciado, A. Seismic vulnerability and failure modes simulation of ancient masonry towers by validated virtual finite element models. Eng. Fail. Anal. 2015, 57, 72–87. [Google Scholar] [CrossRef]
  56. De Silva, F.; Ceroni, F.; Sica, S.; Silvestri, F. Non-linear analysis of the Carmine bell tower under seismic actions accounting for soil–foundation–structure interaction. Bull. Earthq. Eng. 2018, 16, 2775–2808. [Google Scholar] [CrossRef]
  57. Rafael, S. Preliminary Assessment of the Seismic Vulnerability of Three Inclined Bell-towers in Ferrara, Italy. Int. J. Archit. Herit. 2022, 16, 485–517. [Google Scholar]
  58. Micelli, F.; Cascardi, A. Structural assessment and seismic analysis of a 14th century masonry tower. Eng. Fail. Anal. 2020, 107, 104198. [Google Scholar] [CrossRef]
  59. Castellazzi, G.; Gentilini, C.; Nobile, L. Seismic Vulnerability Assessment of a Historical Church: Limit Analysis and Nonlinear Finite Element Analysis. Adv. Civ. Eng. 2013, 2013, 517454. [Google Scholar] [CrossRef] [Green Version]
  60. Eurocode 8, EN 1998-3; Design of Structures for Earthquake Resistance. Part 3: Assessment and Retrofitting of Buildings. European Committee for Standardization: Brussels, Belgium, 2005.
  61. Chopra, A.K.; Goel, R.K. A modal pushover analysis procedure for estimating seismic demands for buildings. Earthq. Eng. Struct. Dyn. 2002, 31, 561–582. [Google Scholar] [CrossRef] [Green Version]
  62. Karanikoloudis, G.; Lourenço, P.B. Structural assessment and seismic vulnerability of earthen historic structures. Application of sophisticated numerical and simple analytical models. Eng. Struct. 2018, 160, 488–509. [Google Scholar] [CrossRef] [Green Version]
  63. Vamvatsikos, D. Incremental dynamic analysis. In Encyclopedia of Earthquake Engineering; Beer, M., Kougioumtzoglou, I., Patelli, E., Au, I.K., Eds.; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
  64. Peña, F.; Lourenço, P.B.; Mendes, N.; Oliveira, D.V. Numerical models for the seismic assessment of an old masonry tower. Eng. Struct. 2010, 32, 1466–1478. [Google Scholar] [CrossRef] [Green Version]
  65. Lagomarsino, S.; Cattari, S. Seismic Performance of Historical Masonry Structures Through Pushover and Nonlinear Dynamic Analyses. In Perspectives on European Earthquake Engineering and Seismology. Geotechnical, Geological and Earthquake Engineering; Ansal, A., Ed.; Springer: Cham, Switzerland, 2015; Volume 39. [Google Scholar]
  66. Galasco, A.; Lagomarsino, S.; Penna, A. On the use of pushover analysis for existing masonry buildings. In Proceedings of the 13th European Conference on Earthquake Engineering, Geneva, Switzerland, 3–8 September 2006; p. 1080. [Google Scholar]
  67. Porcu, M.C.; Montis, E.; Saba, M. Role of model identification and analysis method in the seismic assessment of historical masonry towers. J. Build. Eng. 2021, 43, 103114. [Google Scholar] [CrossRef]
  68. Kita, A.; Cavalagli, N.; Venanzi, I.; Ubertini, F. A new method for earthquake-induced damage identification in historic masonry towers combining OMA and IDA. Bull. Earthq. Eng. 2021, 19, 5307–5337. [Google Scholar] [CrossRef]
  69. Lourenço, P.B. Computations on historic masonry structures. Prog. Struct. Eng. Mater. 2002, 4, 301–319. [Google Scholar] [CrossRef]
  70. Quinteros, R.D.; Oller, S.; Nallim, L.G. Nonlinear homogenization techniques to solve masonry structures problems. Compos. Struct. 2012, 94, 724–730. [Google Scholar] [CrossRef]
  71. Petracca, M.; Pelà, L.; Rossi, R.; Oller, S.; Camata, G.; Spacone, E. Regularization of first order computational homogenization for multiscale analysis of masonry structures. Comput. Mech. 2016, 57, 257–276. [Google Scholar] [CrossRef] [Green Version]
  72. Trovalusci, P.; Masiani, R. Non-linear micropolar and classical continua for anisotropic discontinuous materials. Int. J. Solids Struct. 2003, 40, 1281–1297. [Google Scholar] [CrossRef]
  73. Adessi, D.; Di Re, P.; Gatta, C.; Sacco, E. Multiscale analysis of out-of-plane masonry elements using different structural models at macro and microscale. Comput. Struct. 2021, 247, 106477. [Google Scholar] [CrossRef]
  74. Silva, L.C.; Lourenço, P.B.; Milani, G. Derivation of the out-of-plane behaviour of masonry through homogenization strategies: Micro-scale level. Comput. Struct. 2018, 209, 30–43. [Google Scholar] [CrossRef]
  75. Geers, M.G.D.; Kouznetsova, V.G.; Brekelmans, W.A.M. Multi-scale computational homogenization: Trends and challenges. J. Comput. Appl. Math. 2010, 234, 2175–2182. [Google Scholar] [CrossRef]
  76. Sepe, V.; Speranza, E.; Viskovic, A. A method for large-scale vulnerability assessment of historic towers. Struct. Contr. Health Monitor. 2008, 15, 389–415. [Google Scholar] [CrossRef]
  77. Mendes, N. Masonry macro-block analysis. In Encyclopedia of Earthquake Engineering; Beer, M., Kougioumtzoglou, I., Patelli, E., Au, I.K., Eds.; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
  78. Chiozzi, A.; Grillanda, N.; Milani, G.; Tralli, A. UB-ALMANAC: An adaptive limit analysis NURBS-based program for the automatic assessment of partial failure mechanisms in masonry churches. Eng. Fail. Anal. 2018, 85, 201–220. [Google Scholar] [CrossRef]
  79. Milani, G. Fast Vulnerability Evaluation of Masonry Towers by Means of an Interactive and Adaptive 3D Kinematic Limit Analysis with Pre-assigned Failure Mechanisms. Int. J. Archit. Herit. 2019, 13, 941–962. [Google Scholar] [CrossRef]
  80. Funari, M.F.; Mehrotra, A.; Lourenço, P.B. A Tool for the Rapid Seismic Assessment of Historic Masonry Structures Based on Limit Analysis Optimisation and Rocking Dynamics. Appl. Sci. 2021, 11, 942. [Google Scholar] [CrossRef]
  81. Cundall, P.A.; Strack, O.D.L. Discussion: A discrete numerical model for granular assemblies. Géotechnique 1980, 30, 331–336. [Google Scholar] [CrossRef] [Green Version]
  82. Ferrante, A.; Loverdos, D.; Clementi, F.; Milani, G.; Formisano, A.; Lenci, S.; Sarhosis, V. Discontinuous approaches for nonlinear dynamic analyses of an ancient masonry tower. Eng. Struct. 2021, 230, 111626. [Google Scholar] [CrossRef]
  83. Clementi, F.; Milani, G.; Ferrante, A.; Valente, M.; Lenci, S. Crumbling of Amatrice clock tower during 2016 Central Italy seismic sequence: Advanced numerical insights. Frat. Ed Integrità Strutt. 2020, 51, 313–335. [Google Scholar] [CrossRef] [Green Version]
  84. Ferrante, A.; Clementi, F.; Milani, G. Advanced numerical analyses by the Non-Smooth Contact Dynamics method of an ancient masonry bell tower. Math. Methods Appl. Sci. 2020, 43, 7706–7725. [Google Scholar] [CrossRef]
  85. Lemos, J.V. Discrete element modeling of masonry structures. Int. J. Archit. Herit. 2007, 1, 190–213. [Google Scholar] [CrossRef]
  86. Giamundo, V.; Sarhosis, V.; Lignola, G.P.; Sheng, Y.; Manfredi, G. Evaluation of different computational modelling strategies for the analysis of low strength masonry structures. Eng. Struct. 2014, 73, 160–169. [Google Scholar] [CrossRef] [Green Version]
  87. Malomo, D.; Dejong, M.J. A Macro-Distinct Element Model (M-DEM) for out-of-plane analysis of unreinforced masonry structures. Eng. Struct. 2021, 244, 112754. [Google Scholar] [CrossRef]
  88. Chaimoon, K.; Attard, M.M. Modeling of unreinforced masonry walls under shear and compression. Eng. Struct. 2007, 29, 2056–2068. [Google Scholar] [CrossRef]
  89. Ferrero, C.; Rossi, M.; Roca, P.; Calderini, C. Experimental and numerical analysis of a scaled dry-joint arch on moving supports. Int. J. Mason. Res. Innov. 2021, 6, 405–421. [Google Scholar] [CrossRef]
  90. Drougkas, A.; Roca, P.; Molins, C. Nonlinear micro-mechanical analysis of masonry periodic unit cells. Int. J. Solids Struct. 2016, 80, 193–211. [Google Scholar] [CrossRef]
  91. Da Silva, L.C.M.; Milani, G. A FE-Based Macro-Element for the Assessment of Masonry Structures: Linear Static, Vibration, and Non-Linear Cyclic Analyses. Appl. Sci. 2022, 12, 1248. [Google Scholar] [CrossRef]
  92. Yu, L.; Dong, Z.; Li, G. Simplified mechanical models for the seismic collapse performance prediction of unreinforced masonry structures. Eng. Struct. 2022, 258, 114131. [Google Scholar] [CrossRef]
  93. Kita, A.; Cavalagli, N.; Masciotta, M.G.; Lourenço, P.B.; Ubertini, F. Rapid post-earthquake damage localization and quantification in masonry structures through multidimensional non-linear seismic IDA. Eng. Struct. 2020, 219, 110841. [Google Scholar] [CrossRef]
  94. Ghiassi, B.; Soltani, M.; Tasnimi, A.A. A simplified model for analysis of unreinforced masonry shear walls under combined axial, shear and flexural loading. Eng. Struct. 2012, 42, 396–409. [Google Scholar] [CrossRef] [Green Version]
  95. Saloustros, S.; Pelà, L.; Cervera, M.; Roca, P. An Enhanced Finite Element Macro-Model for the Realistic Simulation of Localized Cracks in Masonry Structures: A Large-Scale Application. Int. J. Archit. Herit. 2018, 12, 432–447. [Google Scholar] [CrossRef]
  96. Cannizzaro, F.; Pantò, B.; Lepidi, M.; Caddemi, S.; Caliò, I. Multi-directional seismic assessment of historical masonry buildings by means of macro-element modelling: Application to a building damaged during the L’Aquila earthquake (Italy). Buildings 2017, 7, 106. [Google Scholar] [CrossRef] [Green Version]
  97. Candeias, P.; Costa, A.C.; Mendes, N.; Costa, A.A.; Lourenço, P.B. Experimental Assessment of the Out-of-Plane Performance of Masonry Buildings Through Shaking Table Tests. Int. J. Archit. Herit. 2017, 11, 31–58. [Google Scholar] [CrossRef] [Green Version]
  98. Mendes, N.; Costa, A.A.; Lourenço, P.B.; Bento, R.; Beyer, K.; de Felice, G.; Gams, M.; Griffith, M.C.; Ingham, J.M.; Lagomarsino, S.; et al. Methods and Approaches for Blind Test Predictions of Out-of-Plane Behavior of Masonry Walls: A Numerical Comparative Study. Int. J. Archit. Herit. 2017, 11, 59–71. [Google Scholar]
  99. Lourenço, P.B. Recommendations for restoration of ancient buildings and the survival of a masonry chimney. Constr. Build. Mater. 2006, 20, 239–251. [Google Scholar] [CrossRef] [Green Version]
  100. Masciotta, M.G.; Ramos, L.F.; Lourenço, P.B. The importance of structural monitoring as a diagnosis and control tool in the restoration process of heritage structures: A case-study in Portugal. J. Cult. Herit. 2017, 27, 36–47. [Google Scholar] [CrossRef] [Green Version]
Applsci 12 07340 g001 550
Figure 1. Examples of ancient masonry section with complex arrangements of units.
Figure 1. Examples of ancient masonry section with complex arrangements of units.
Applsci 12 07340 g001
Applsci 12 07340 g002 550
Figure 2. Masonry failure mechanisms (adapted from [27]): (a) joint tensile cracking; (b) joint slipping; (c) unit direct tensile cracking; (d) unit diagonal tensile cracking; (e) masonry crushing.
Figure 2. Masonry failure mechanisms (adapted from [27]): (a) joint tensile cracking; (b) joint slipping; (c) unit direct tensile cracking; (d) unit diagonal tensile cracking; (e) masonry crushing.
Applsci 12 07340 g002
Applsci 12 07340 g003 550
Figure 3. Experimental results on stone masonry shear walls [21]: (a) specimen geometries; (b) force−displacement diagrams; (c) failure mechanisms.
Figure 3. Experimental results on stone masonry shear walls [21]: (a) specimen geometries; (b) force−displacement diagrams; (c) failure mechanisms.
Applsci 12 07340 g003
Applsci 12 07340 g004 550
Figure 4. Seismic response of the Church of Jerónimos Monastery, Portugal (adapted from [46,47]): (a) exterior view; (b) location of strong motion recorders (A1: chancel base; A2: nave vault extrados); (c,d) acceleration response at the base and at the top of the nave during the earthquake; (e) measured response spectra.
Figure 4. Seismic response of the Church of Jerónimos Monastery, Portugal (adapted from [46,47]): (a) exterior view; (b) location of strong motion recorders (A1: chancel base; A2: nave vault extrados); (c,d) acceleration response at the base and at the top of the nave during the earthquake; (e) measured response spectra.
Applsci 12 07340 g004
Applsci 12 07340 g005 550
Figure 5. Amplification effects during the 2016 Bagan earthquake in Myanmar.
Figure 5. Amplification effects during the 2016 Bagan earthquake in Myanmar.
Applsci 12 07340 g005
Applsci 12 07340 g006 550
Figure 6. Experimental mode shapes of the Mogadouro clock tower—undeformed structure in yellow wireframe (reprinted with permission from Ref. [49]. Copyright 2018, Elsevier).
Figure 6. Experimental mode shapes of the Mogadouro clock tower—undeformed structure in yellow wireframe (reprinted with permission from Ref. [49]. Copyright 2018, Elsevier).
Applsci 12 07340 g006
Applsci 12 07340 g007 550
Figure 7. Overview of the Mogadouro tower before, during and after the rehabilitation works.
Figure 7. Overview of the Mogadouro tower before, during and after the rehabilitation works.
Applsci 12 07340 g007
Applsci 12 07340 g008 550
Figure 8. Seismic assessment of the Qutb Minar tower. Comparison of the results from different analysis methods [64]: (a) capacity curves for pushover analyses, (b) maximum load factor and displacements along the minaret height for dynamic analyses, (c) displacements and drifts along the minaret height for modal pushover and non-linear dynamic analyses.
Figure 8. Seismic assessment of the Qutb Minar tower. Comparison of the results from different analysis methods [64]: (a) capacity curves for pushover analyses, (b) maximum load factor and displacements along the minaret height for dynamic analyses, (c) displacements and drifts along the minaret height for modal pushover and non-linear dynamic analyses.
Applsci 12 07340 g008
Applsci 12 07340 g009 550
Figure 9. Qutb Minar tower: (a) exterior view and (b) detail of the fluted shaft.
Figure 9. Qutb Minar tower: (a) exterior view and (b) detail of the fluted shaft.
Applsci 12 07340 g009
Applsci 12 07340 g010 550
Figure 10. Modelling strategies for masonry structures (adapted from [27]): (a) detailed micro-modelling, (b) simplified micro-modelling, (c) macro-modelling.
Figure 10. Modelling strategies for masonry structures (adapted from [27]): (a) detailed micro-modelling, (b) simplified micro-modelling, (c) macro-modelling.
Applsci 12 07340 g010
Applsci 12 07340 g011 550
Figure 11. Examples of models adopted for the blind predictions of the (a) tested masonry structures: (b) models with rigid macro-blocks; (c) FEM models and (d) DEM models.
Figure 11. Examples of models adopted for the blind predictions of the (a) tested masonry structures: (b) models with rigid macro-blocks; (c) FEM models and (d) DEM models.
Applsci 12 07340 g011
Applsci 12 07340 g012 550
Figure 12. Seismic acceleration capacity (PGA) obtained from the blind predictions [98] (green and yellow bars correspond to good and fair mechanism predictions).
Figure 12. Seismic acceleration capacity (PGA) obtained from the blind predictions [98] (green and yellow bars correspond to good and fair mechanism predictions).
Applsci 12 07340 g012
Applsci 12 07340 g013 550
Figure 13. Framework of the scientific approach to the analysis of architectural heritage.
Figure 13. Framework of the scientific approach to the analysis of architectural heritage.
Applsci 12 07340 g013
Table
Table 1. Dynamic amplification recorded in of the Church of Jerónimos Monastery, Portugal, during the earthquake of 12 February 2007 (maximum results of acceleration in mg).
Table 1. Dynamic amplification recorded in of the Church of Jerónimos Monastery, Portugal, during the earthquake of 12 February 2007 (maximum results of acceleration in mg).
EventSensor A1 (Base)Sensor A2 (Nave)A2/A1
xyzxyzxyz
Event 10.240.290.262.848.476.7511.8329.2125.96
Event 20.120.140.152.675.496.0622.2539.2140.4
Table
Table 2. Dynamic response of Mogadouro Tower before and after rehabilitation.
Table 2. Dynamic response of Mogadouro Tower before and after rehabilitation.
ModeBeforeAfterΔf
(%)		BeforeAfterΔξ
(%)
f (Hz)CVf (%)f (Hz)CVf (%)ξ (%)CVξ (%)ξ (%)CVξ (%)
1st2.151.852.560.21+19.32.68219.51.250.13−53.3
2nd 2.581.052.760.30+6.71.7194.01.350.17−21.0
3rd 4.980.697.150.27+43.72.0565.31.200.14−41.3
4th 5.741.568.860.47+54.42.4024.31.310.13−45.7
5th 6.761.139.210.21+36.12.1431.71.160.12−45.6
6th 7.692.9415.212.24+97.92.3356.02.540.24+9.1
7th 8.981.2116.911.40+88.32.3046.41.490.23−35.1
Avg–1.49–0.73+49.52.2376.81.470.17−40.3 *
* Average value of damping calculated only for negative differences.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Masciotta, M.G.; Lourenço, P.B. Seismic Analysis of Slender Monumental Structures: Current Strategies and Challenges. Appl. Sci. 2022, 12, 7340. https://doi.org/10.3390/app12147340

AMA Style

Masciotta MG, Lourenço PB. Seismic Analysis of Slender Monumental Structures: Current Strategies and Challenges. Applied Sciences. 2022; 12(14):7340. https://doi.org/10.3390/app12147340

Chicago/Turabian Style

Masciotta, Maria Giovanna, and Paulo B. Lourenço. 2022. "Seismic Analysis of Slender Monumental Structures: Current Strategies and Challenges" Applied Sciences 12, no. 14: 7340. https://doi.org/10.3390/app12147340

APA Style

Masciotta, M. G., & Lourenço, P. B. (2022). Seismic Analysis of Slender Monumental Structures: Current Strategies and Challenges. Applied Sciences, 12(14), 7340. https://doi.org/10.3390/app12147340

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop