Advanced Model of Spatiotemporal Mining-Induced Kinematic Excitation for Multiple-Support Bridges Based on the Regional Seismicity Characteristics
Abstract
:1. Introduction
2. Materials and Methods
2.1. Excitation Modelling
2.1.1. Theoretical Background for Dynamic Behaviour of Multiple-Support Structures under Spatially Varying Ground Motion
- —sub-vector of dynamic nodal displacement of a structure,
- —sub-vector of quasi-static nodal displacement of a structure,
- —sub-vector of quasi-static nodal displacement of the ground.
2.1.2. Conditional Random Field Simulation of Ground Motions for Multiple-Support Structures
- Dij—separation distance between two field points (i, j),
- ωd—predominant frequency of the shock,
- v—wave velocity,
- α—space scale parameter (α > 0), depending on local geological conditions,
- σ—standard deviation of the recorded shock.
- maximum ground acceleration of the original record,
- —uniform random variable from a range <0, 1>.
- —vector of unknown values (generated signal),
- —vector of known values (registered signal),
- —conditional covariance matrix of the random field,
- —vector of conditional mean values.
- —truncation parameter, depending on the ratio . If this ratio reaches 4.0 for a given signal, the truncation can be disregarded (. This condition is usually met in case of mining tremors, where the intensive shock phase is relatively short.
2.1.3. The Proposed Spatiotemporal Mining-Induced Kinematic Excitation (SMIKE) Model
- The loss of coherency resulting from scattering of waves in the heterogeneous ground and their superpositioning;
- The wave-passage effect resulting from the difference in the arrival times of waves at different supports;
- The site-response effect that takes into account the local soil conditions.
2.1.4. Empirical Regression Relationship of Amplitude Decay with a Distance from the Epicenter for Space Scale Parameter Estimation
- The relation between the peak epicentral acceleration and the seismic energy within the range for tremors of local magnitudewhere: and are expressed in [m/s2] and [J], respectively.
- The function describing the decrease in bedrock peak acceleration outside the epicentral zone (which is assumed to be 1 km in radius) for tremors of local magnitude with increasing epicentral distance (up to 10 km)where: , is the epicentral distance in [km], and 0.5 km is the mean depth of tremors in the USCB.
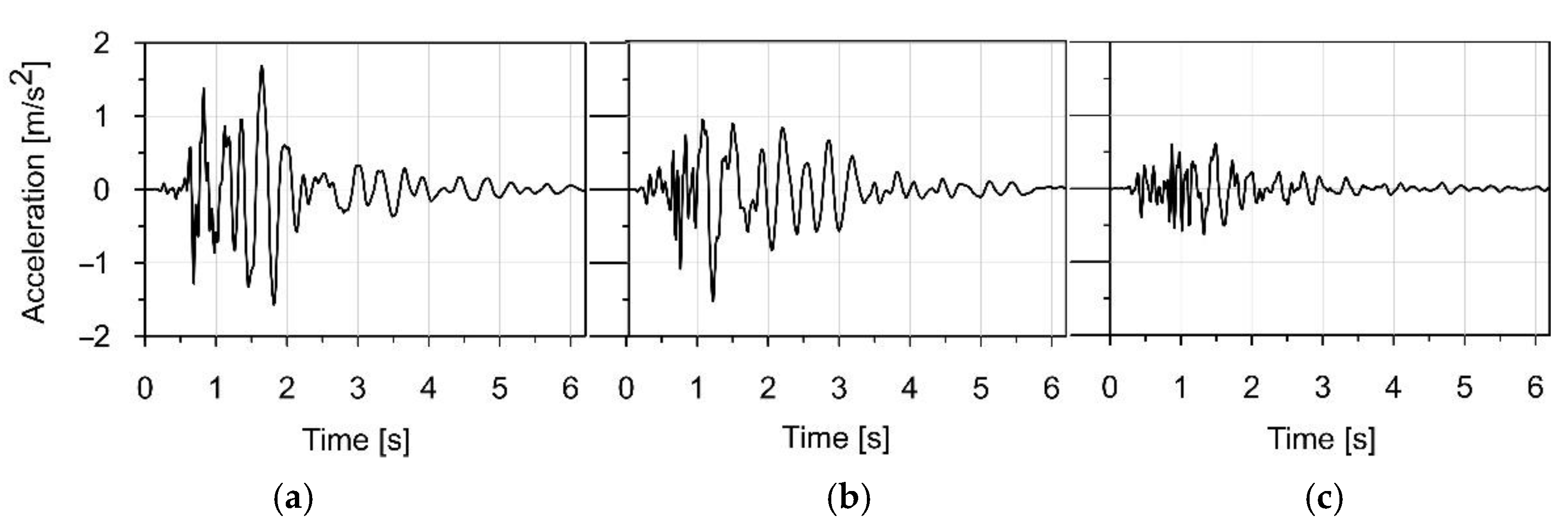
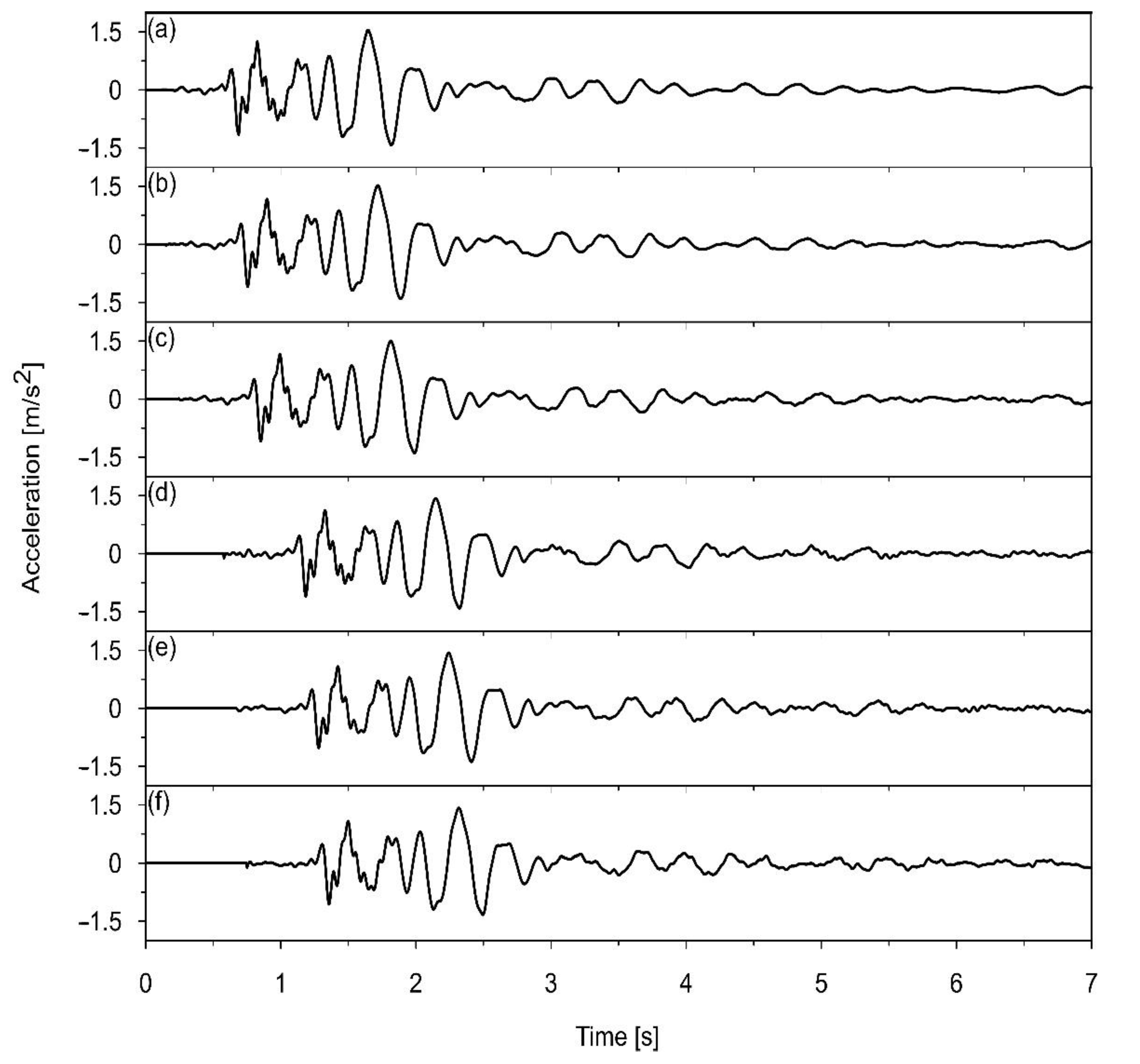
2.1.5. The Mining-Induced Shock Registered in the Upper Silesian Coal Basin
2.2. Modelling of the Structure and Experimental Set-Up
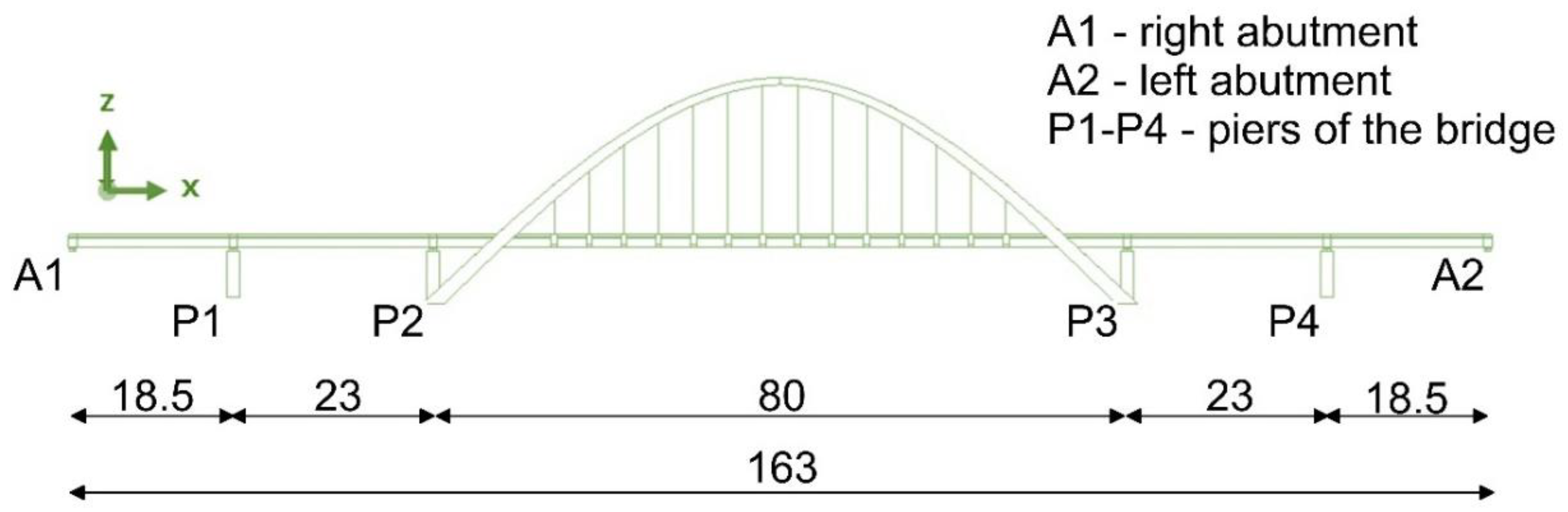
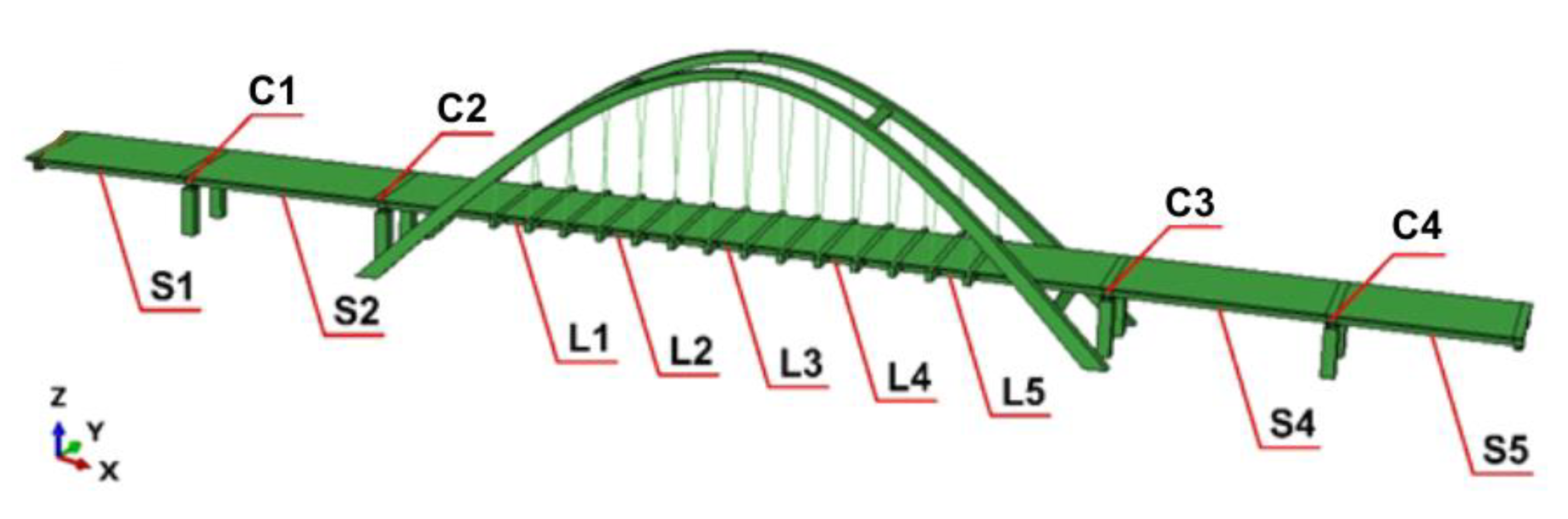
2.2.1. Structural Design and Numerical Model of Analyzed Bridge
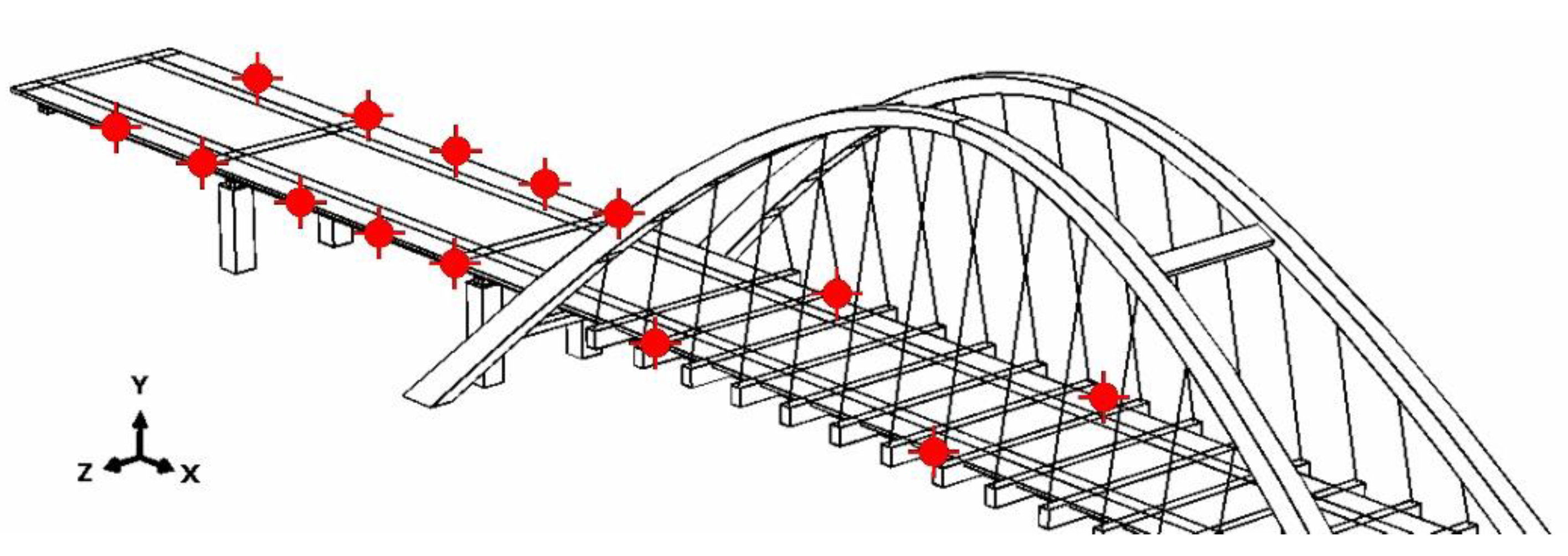
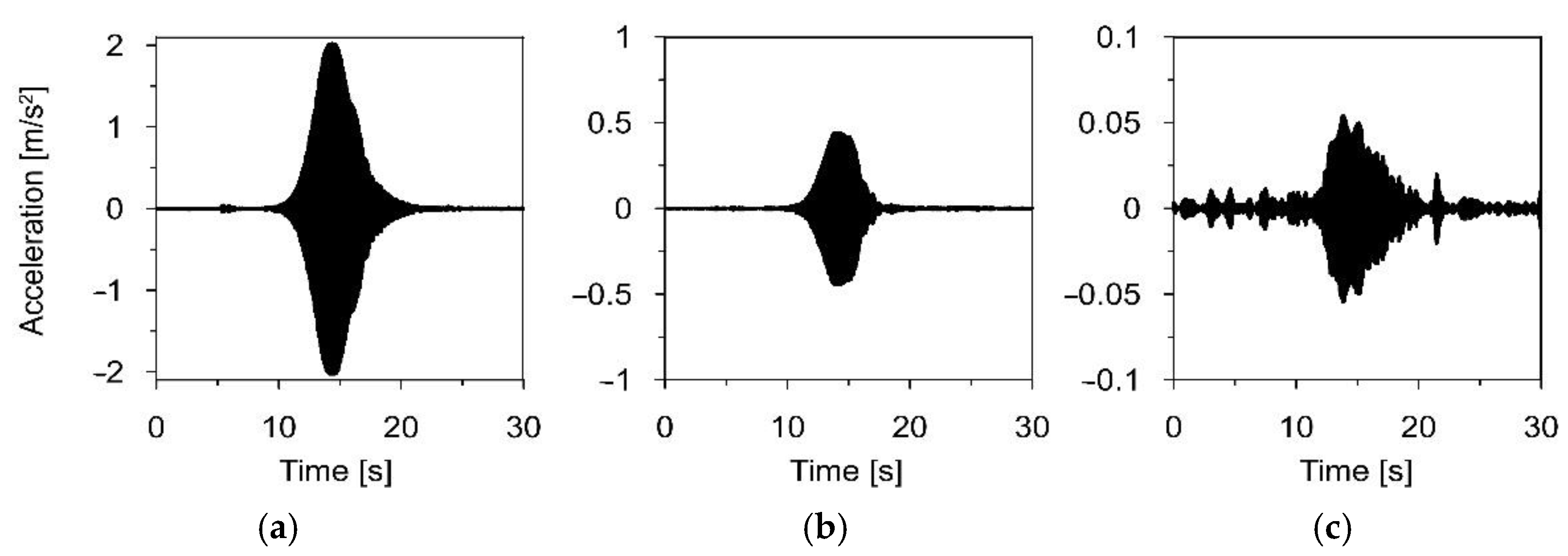
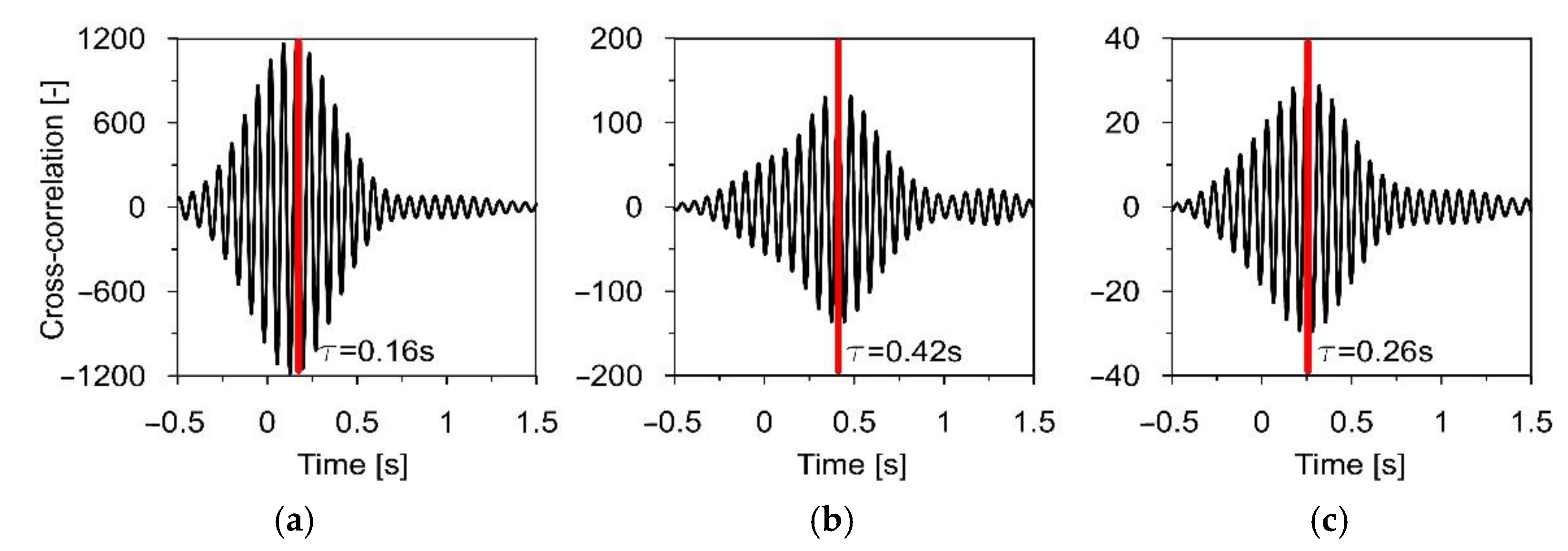
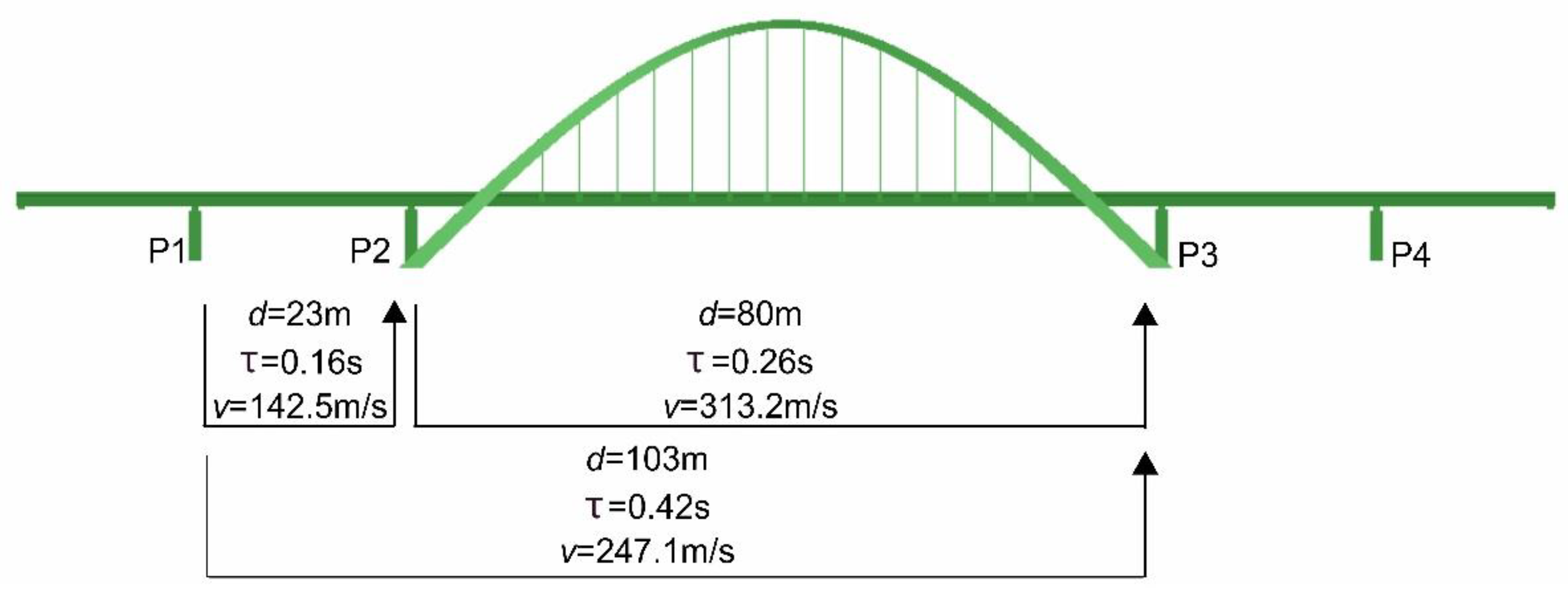
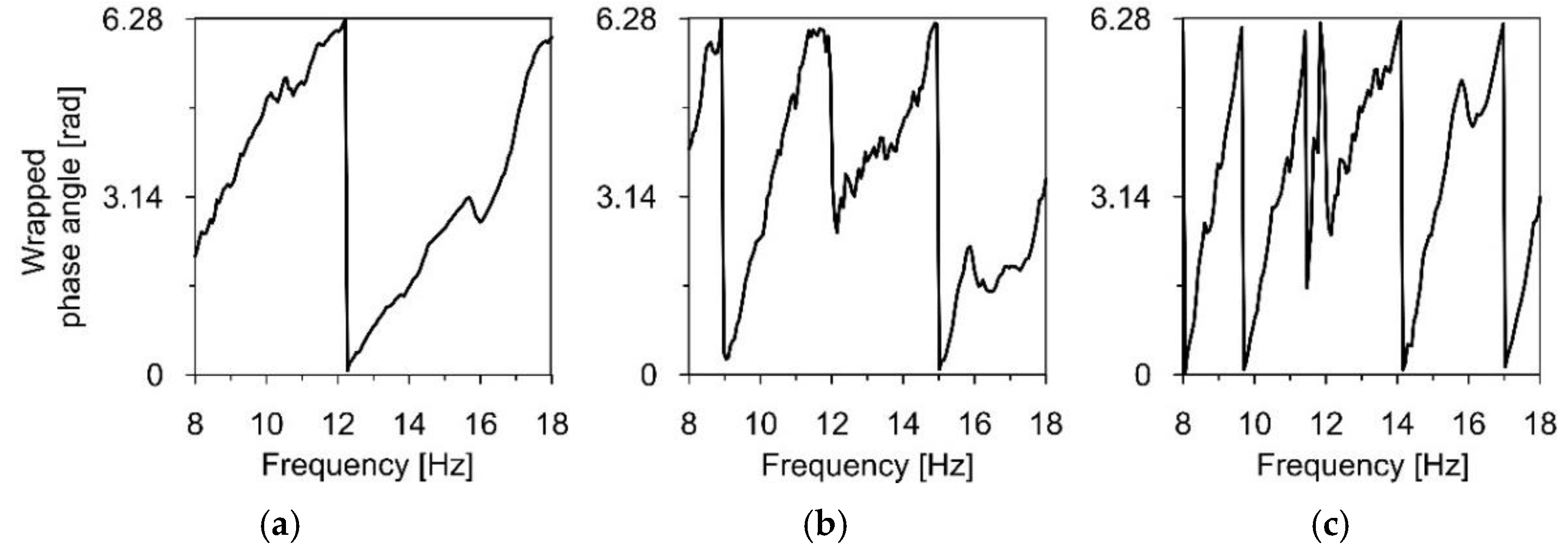
2.2.2. Theoretical Background and Experimental Set-Up for Apparent Wave Velocity Estimation
3. Results
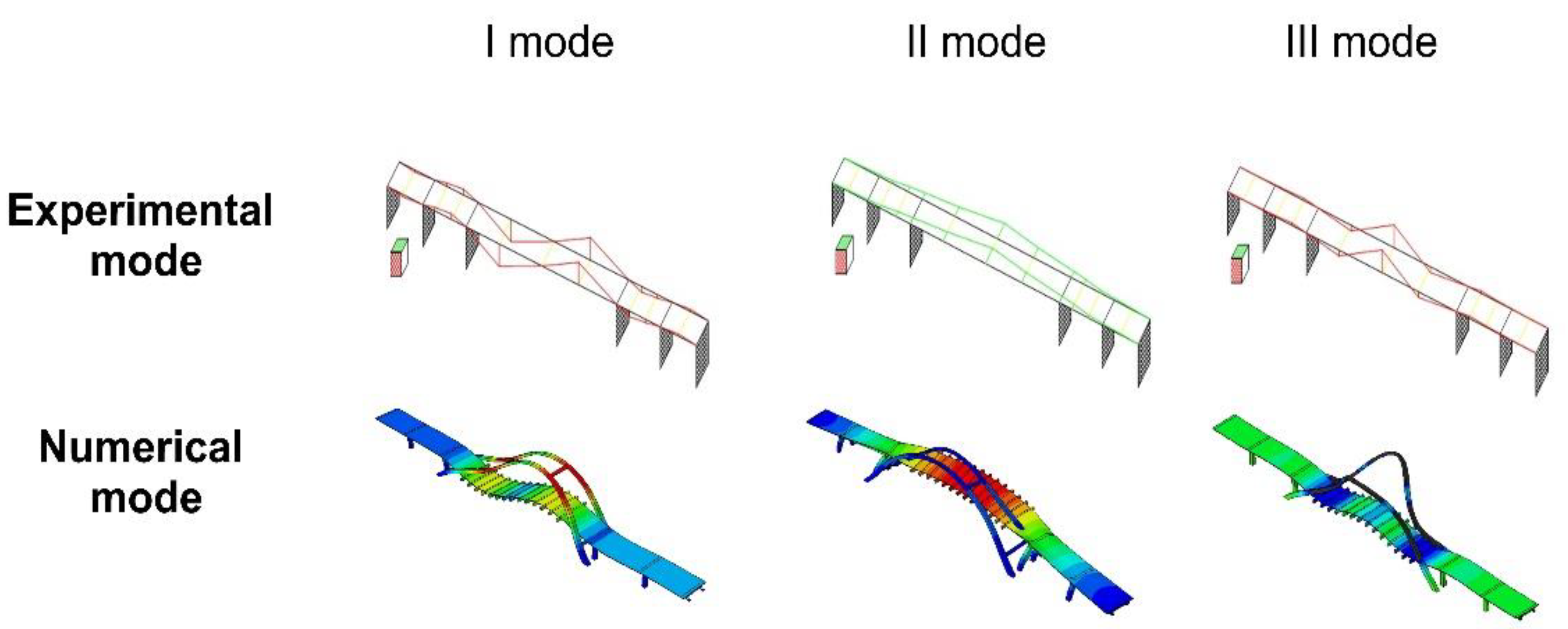
3.1. Experimental and Numerical Evaluation of Natural Frequencies and Modes of Vibration of the Bridge
3.2. Experimental Evaluation of Damping Properties of the Bridge
3.3. Determination of Parameters of the SMIKE Model Used for the Dynamic Analyses
3.3.1. Experimental Evaluation of Wave Propagation Velocity
3.3.2. Determination of the Space Scale Parameter for Conditional Random Field Simulation of Ground Motions Based on the USCB Regression Function
3.4. Resultant Data of the Spatially Varying Mining-Induced Kinematic Excitation
4. Discussion
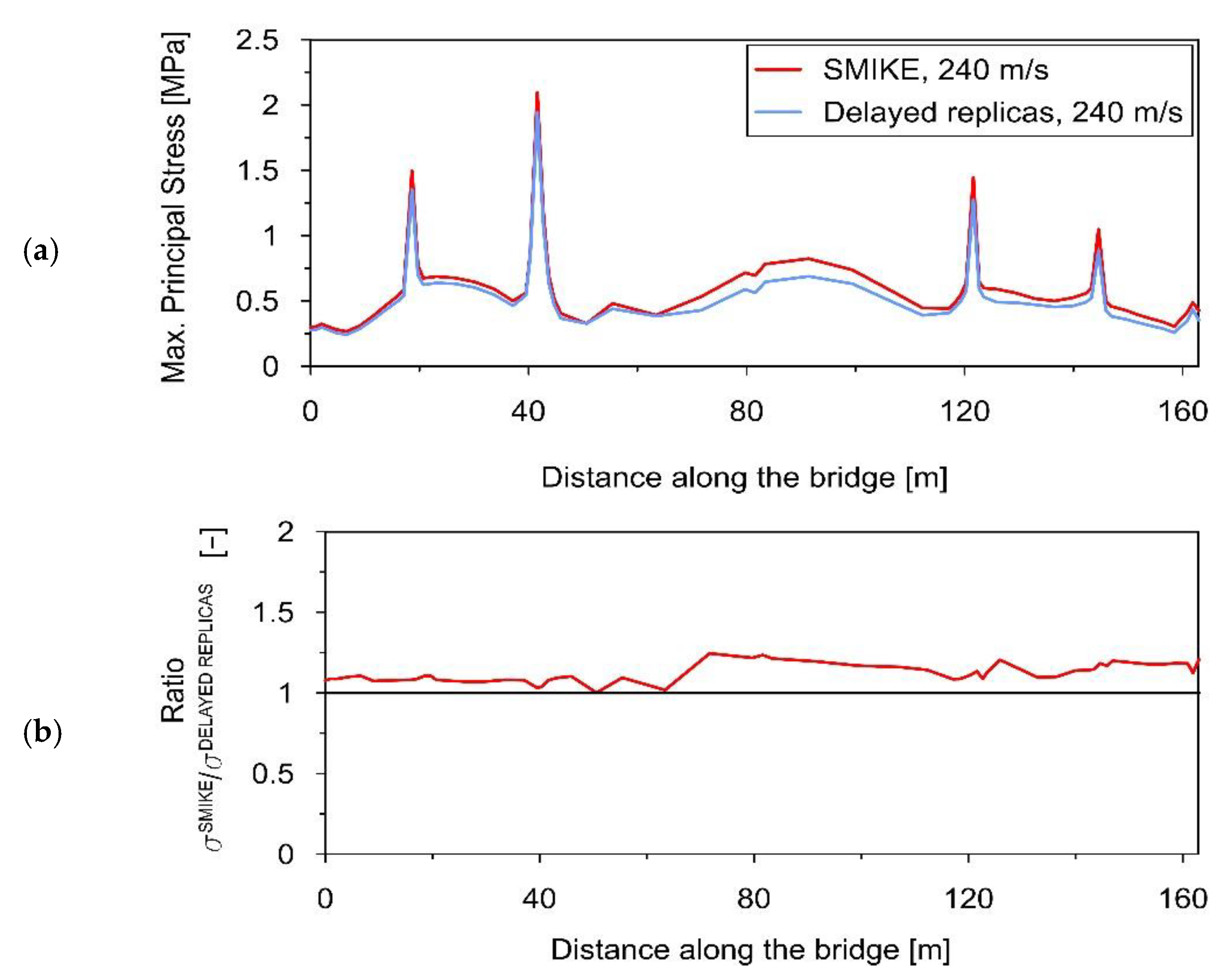
4.1. The Main Assumptions of the Presented Dynamic Analyses
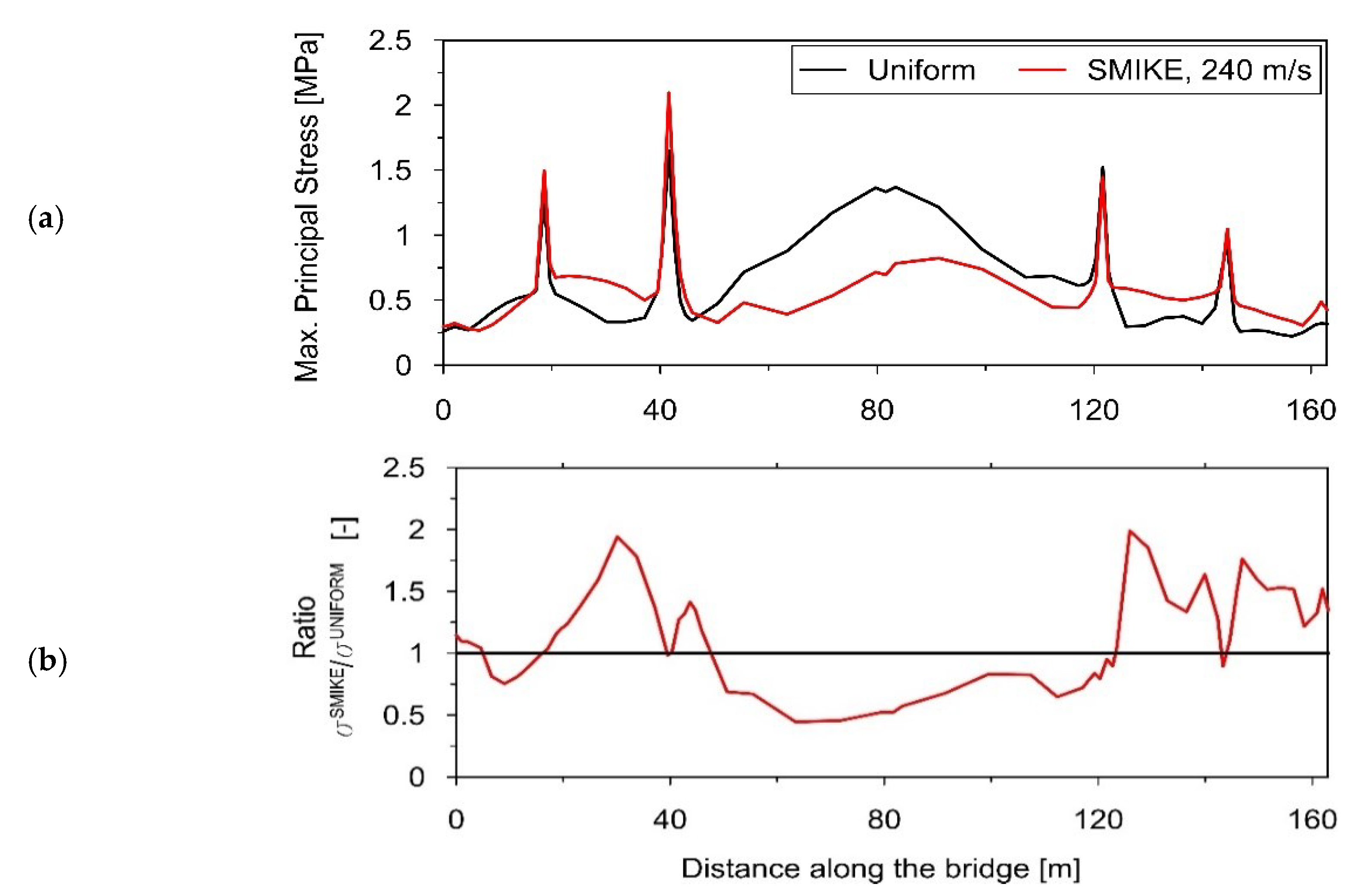
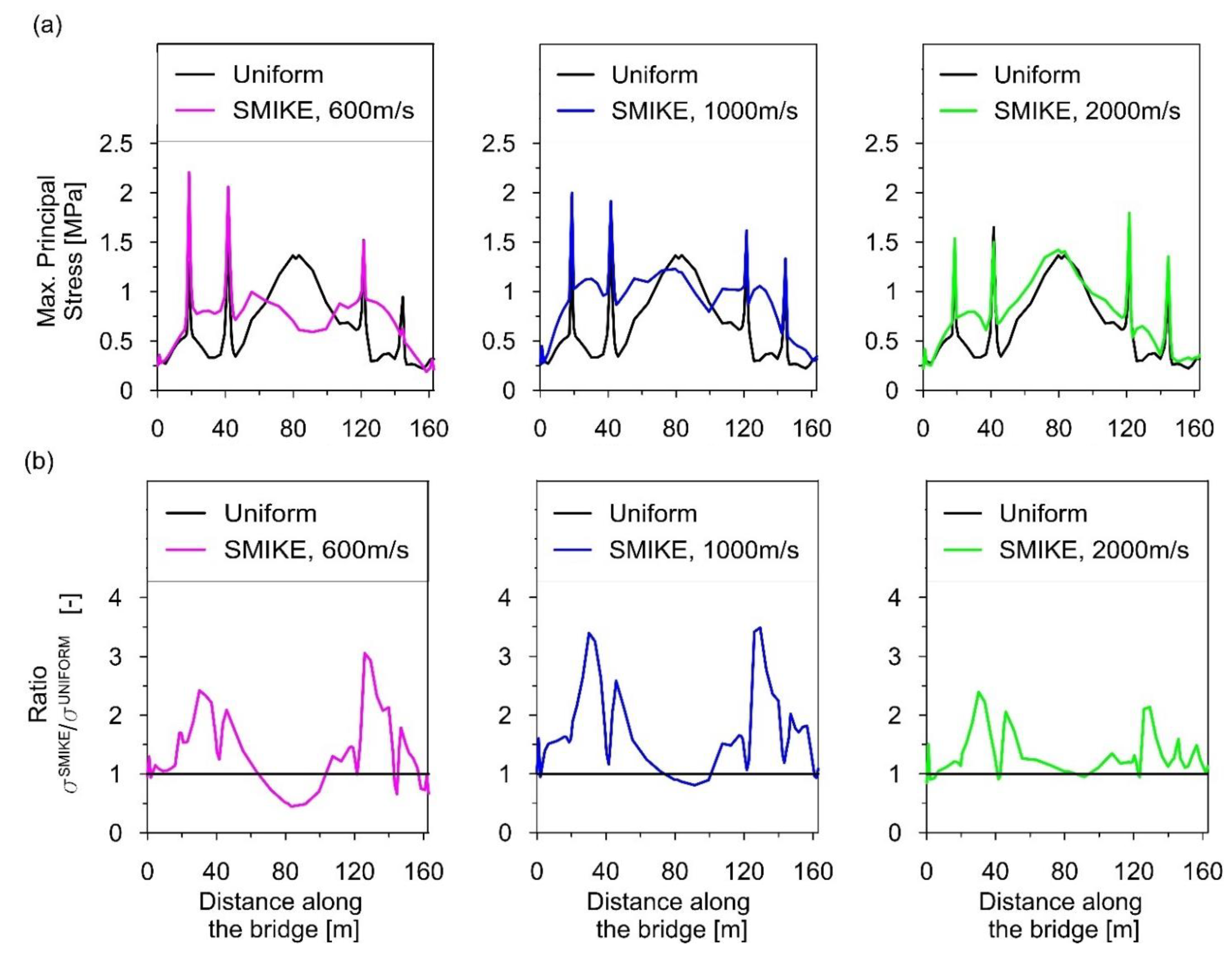
4.2. The SMIKE Model vs. the Uniform Model of Kinematic Excitation
4.3. The Impact of SMIKE Model Parameters on the Dynamic Performance of the Bridge
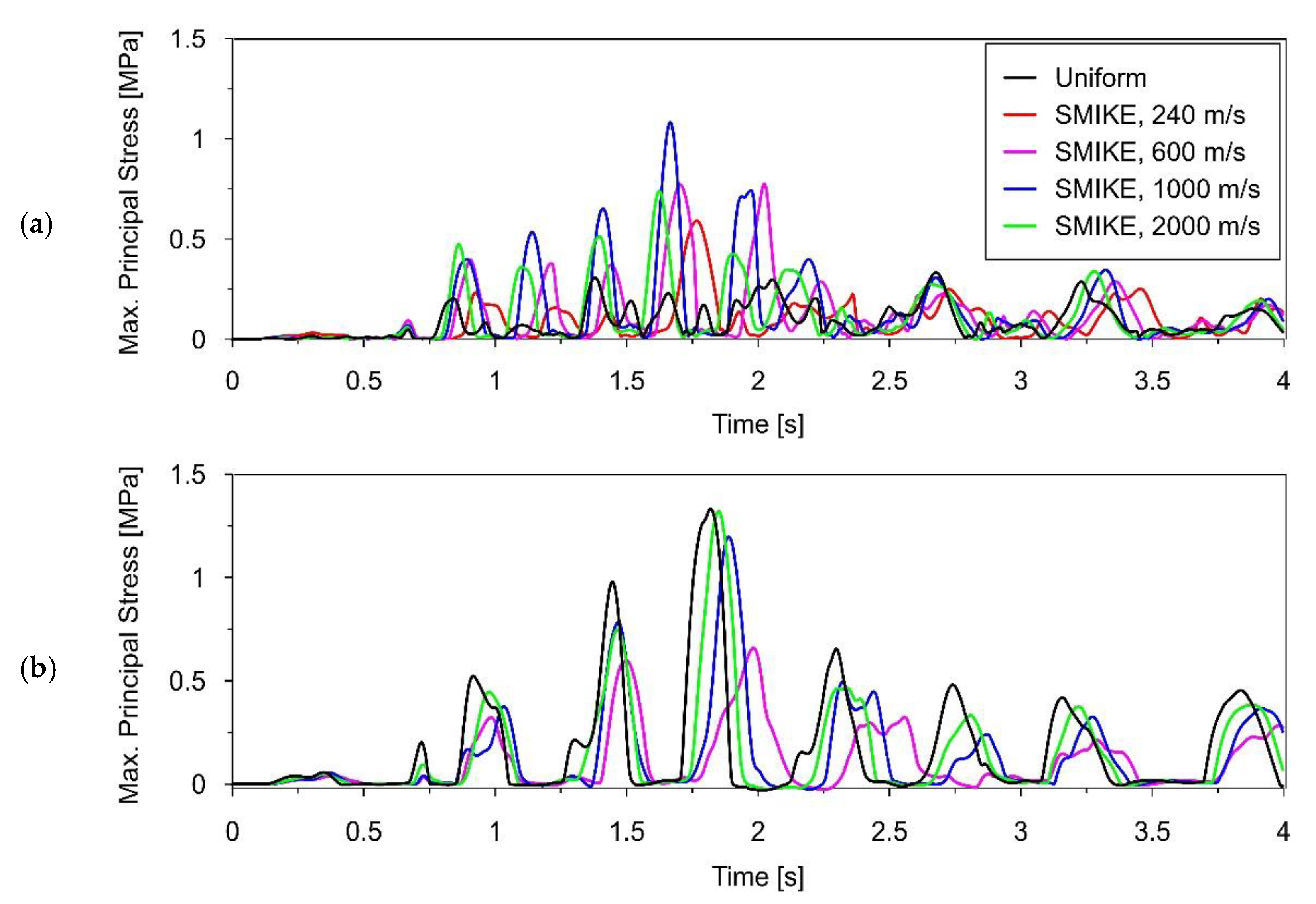
4.3.1. The Impact of the Wave Propagation Velocity
- about 2—for ,
- about 3—for ,
- about 3.5—for ,
- about 2.5—for .
4.3.2. The Impact of Regional Seismicity Characteristics
5. Conclusions
- The advanced model of spatiotemporal mining-induced kinematic excitation (SMIKE) for multiple-support structures exposed to mining-induced seismicity is proposed. The uniqueness of this model results from the possibility of its application for any region of mining activity, as it is based on empirical regression functions characterizing different such regions.
- The proposed SMIKE model takes into account the loss of coherency resulting from the scattering of waves in the heterogeneous ground, the wave-passage effect originated in the different arrival times of waves to consecutive supports, and the site-response effect resulting from the local soil conditions. Hence, it covers the key phenomena of spatial variability of mining-induced ground motion.
- The two parameters of the SMIKE model can be estimated relatively easily in practice. The space scale parameter α can be determined from the regression functions for different mining areas delivered by seismologists. The apparent wave velocity in the ground v can either be detected experimentally or assumed based on the literature for foundation geological conditions.
- The proposed model was applied to assess the dynamic performance of the five-span bridge under the mining-induced shock recorded in the Upper Silesian Coal Basin (USCB), Poland. The space scale parameter α = 7 was determined on the basis of regression curves valid for the USCB region. This value lies within the range of the space scale parameters adopted in the literature. The apparent wave passage velocity v = 240 m/s, obtained from discrete experimental data acquired via the vibroseis excitation in situ experiment, is typical for the geological conditions in the field.
- The dynamic response levels, in terms of maximal principal stresses, were evaluated and compared assuming both the classic uniform excitation model and the proposed spatiotemporal mining-induced kinematic excitation (SMIKE) model. The impact of the wave velocity appears to be crucial: the introduction of the experimentally evaluated velocity modifies (either amplifies or reduces, depending on the span slenderness) the dynamic response level even twice. The introduction of the space scale parameter, based on the regional seismicity characteristics, changed the stress levels up to 20% in comparison with results obtained for the “traveling” wave only.
- The presented analyses show how the SMIKE model application affects the level of the dynamic performance of particular spans of the bridge in the context of the spans’ slenderness. For various wave velocities, the response level is up to 3.5 times higher with the SMIKE model than with the uniform one for stocky spans due to the quasi-static effects. The opposite situation is spotted for slender spans. The decrease in the average excitation amplitudes, introduced by the SMIKE model causes a reduction in the global dynamic response level.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Gueha, S.K. Mining Induced Seismicity. In Induced Earthquakes; Springer: Dordrecht, The Netherlands, 2000. [Google Scholar] [CrossRef]
- Linzer, L.M.; Bejaichund, M.; Cichowicz, A.; Durrheim, R.J.; Goldbach, O.D.; Kataka, M.O.; Kijko, A.; Milev, A.M.; Saunders, I.; Spottiswoode, S.M.; et al. Recent research in seismology in South Africa. S. Afr. J. Sci. 2007, 103, 419–426. [Google Scholar]
- Marcak, H.; Mutke, G. Seismic activation of tectonic stresses by mining. J. Seismol. 2013, 17, 1139–1148. [Google Scholar] [CrossRef]
- Lasocki, S. Site specific prediction equations for peak acceleration of ground motion due to earthquakes induced by underground mining in Legnica-Głogów Copper District in Poland. Acta Geophys. 2013, 61, 1130–1155. [Google Scholar] [CrossRef]
- Hradil, P.; Kaláb, Z.; Knejzlík, J.; Kořínek, R.; Salajka, V.; Kanický, V. Response of a panel building to mining induced seismicity in Karvina area (Czech Republic). Acta Montan. Slovaca 2009, 14, 143–151. [Google Scholar]
- Tatara, T. An Influence of Surface Mining-Related Vibration on Low-Rise Buildings; Scientific Notebooks of Cracow University of Technology, No. 74; Cracow University of Technology: Cracow, Poland, 2002. (In Polish) [Google Scholar]
- Uzoegbo, H.C.; Li, K. Mine-Induced Seismic Events and Its Effect on Nearby Settlements in South Africa; National Research Foundation (NRF) and Hydraform Africa Ltd.: Pretoria, South Africa, 2002. [Google Scholar]
- Zerva, A. Spatial Variation of Seismic Ground Motions: Modeling and Engineering Applications; CRC Press/Balkema–Taylor & Francis Group: Boca Raton, FL, USA, 2009. [Google Scholar]
- Léger, P.; Idé, M.I.; Paultre, P. Multiple-support seismic analysis of large structures. Comput. Struct. 1990, 36, 1153–1158. [Google Scholar] [CrossRef]
- Boroń, P.; Dulińska, J.M.; Jasińska, D. Impact of High Energy Mining-Induced Seismic Shocks from Different Mining Activity Regions on a Multiple-Support Road Viaduct. Energies 2020, 13, 4045. [Google Scholar] [CrossRef]
- Fayun, L.; Yajie, J.; Limin, S.; Wen, X.; Haibing, C. Seismic response of pile groups supporting long-span cable-stayed bridge subjected to multi-support excitations. Soil Dyn. Earthq. Eng. 2017, 101, 182–203. [Google Scholar] [CrossRef]
- Sextos, A.G.; Kappos, A.J. Evaluation of seismic response of bridges under asynchronous excitation and comparisons with Eurocode 8-2 provisions. Bull. Earthq. Eng. 2009, 7, 519–545. [Google Scholar] [CrossRef]
- Hoseini, S.S.; Ghanbari, A.; Davoodi, M. A New Approach in Equivalent Spring-Dashpot Method for Seismic Soil-Structure Interaction Analysis of Long Bridges Including Non-uniform Excitations. Transp. Infrastruct. Geotechnol. 2019, 6, 165–188. [Google Scholar] [CrossRef]
- Novak, M.S.; Lazarevic, D.; Atalic, J.; Uros, M. Influence of Multiple-Support Excitation on Seismic Response of Reinforced Concrete Arch Bridges. Appl. Sci. 2020, 10, 17. [Google Scholar] [CrossRef] [Green Version]
- Shen, J.; Li, R.; Shi, J.; Zhou, G. Modified Multi-Support Response Spectrum Analysis of Structures with Multiple Supports under Incoherent Ground Excitation. Appl. Sci. 2019, 9, 1744. [Google Scholar] [CrossRef] [Green Version]
- Qin, H.; Li, L. Error Caused by Damping Formulating in Multiple Support Excitation Problems. Appl. Sci. 2020, 10, 8180. [Google Scholar] [CrossRef]
- Boron, P.; Dulinska, J. Dynamic Response of a Road Viaduct to a Mining Tremor Using Multiple Support Response Spectrum Method. IOP Conf. Ser. Mater. Sci. Eng. 2019, 471, 052065. [Google Scholar] [CrossRef]
- Drygala, I.J.; Dulinska, J.M.; Polak, M.A. Seismic Assessment of Footbridges under Spatial Variation of Earthquake Ground Motion (SVEGM): Experimental Testing and Finite Element Analyses. Sensors 2020, 20, 1227. [Google Scholar] [CrossRef] [Green Version]
- Bahbouh, L.; Yamada, H.; Katsuchi, H.; Sasaki, E.; Theeraphong, C. The behaviour of Akashi Kaikyo Bridge under multi support seismic excitation for low frequency motions. Earthq. Resist. Eng. Struct. 2009, 104, 345–355. [Google Scholar] [CrossRef] [Green Version]
- Dulińska, J. Dynamic Response of Multiple-Support Structures to Non-Uniform Mining Related Paraseismic Excitation; The Cracow University of Technology Press: Krakow, Poland, 2006. (In Polish) [Google Scholar]
- Dulinska, J.M.; Jasinska, D. Influence of seismic wave velocity on the dynamic response of a steel pipeline with a progressive damage and failure material model. In Recent Advances in Civil Engineering: Structural Mechanics; Stypula, K., Ed.; The Cracow University of Technology Press: Cracow, Poland, 2015; pp. 45–61. [Google Scholar]
- Song, Y.; Wang, Z.; Liu, Z.; Wang, R. A spatial coupling model to study dynamic performance of pantograph-catenary with vehicle-track excitation. Mech. Syst. Signal Process. 2021, 151, 107336. [Google Scholar] [CrossRef]
- Fan, W.; Zhang, S.H.; Zhu, W.D.; Zhu, H. Vibration analysis and band-gap characteristics of periodic multi-span power transmission line systems. Eng. Struct. 2021, 238, 111669. [Google Scholar] [CrossRef]
- Clough, R.W.; Penzien, J. Dynamics of Structures; McGraw Hill Kogakusha Ltd.: Tokyo, Japan, 1975. [Google Scholar]
- Capatti, M.C.; Tropeano, G.; Morici, M.; Carbonari, S.; Dezi, F.; Leoni, G.; Silvestri, F. Implications of non-synchronous excitation induced by nonlinear site amplification and of soil-structure interaction on the seismic response of multi-span bridges founded on piles. Bull. Earthq. Eng. 2017, 15, 4963–4995. [Google Scholar] [CrossRef]
- EN 1998-2; Eurocode 8: Design of Structures for Earthquake Resistance—Part 2: Bridges. CEN: Brussels, Belgium, 2005.
- Jankowski, R.; Walukiewicz, H. Modeling of two-dimensional random fields. Probab. Eng. Mech. 1997, 12, 115–121. [Google Scholar] [CrossRef]
- Jankowski, R.; Wilde, K. A simple method of conditional random field simulation of ground motions for long structures. Eng. Struct. 2000, 22, 552–561. [Google Scholar] [CrossRef]
- Jankowski, R. Numerical Simulations of Space-Time Conditional Random Fields of Ground Motions. Lect. Notes Comput. Sci. 2006, 3993, 56–59. [Google Scholar] [CrossRef]
- Jankowski, R. Non-linear FEM analysis of pounding-involved response of buildings under non-uniform earthquake excitation. Eng. Struct. 2012, 37, 99–105. [Google Scholar] [CrossRef]
- Burkacki, D.; Jankowski, R. Response of cylindrical steel tank under stochastically generated non-uniform earthquake excitation. AIP Conf. Proc. 2020, 2239, 020004. [Google Scholar] [CrossRef]
- Johnson, S.W.; Chambers, D.; Boltz, M.S.; Koper, K.D. Application of a convolutional neural network for seismic phase picking of mining-induced seismicity. Geophys. J. Int. 2021, 224, 230–240. [Google Scholar] [CrossRef]
- Boettcher, M.S.; Kane, D.L.; McGarr, A.; Johnston, M.J.S.; Reches, Z. Moment Tensors and Other Source Parameters of Mining-Induced Earthquakes in TauTona Mine, South Africa. Bull. Seism. Soc. Am. 2015, 105, 1576–1593. [Google Scholar] [CrossRef]
- Barthwal, H.; van der Baan, M. Passive seismic tomography using recorded microseismicity: Application to mining-induced seismicity. Geophysics 2018, 84, B41–B57. [Google Scholar] [CrossRef]
- Fuławka, K.; Pytel, W.; Pałac-Walko, B. Near-Field Measurement of Six Degrees of Freedom Mining-Induced Tremors in Lower Silesian Copper Basin. Sensors 2020, 20, 6801. [Google Scholar] [CrossRef]
- Rudziński, Ł.; Lasocki, S.; Orlecka-Sikora, B.; Wiszniowski, J.; Olszewska, D.; Kokowski, J.; Mirek, J. Integrating Data under the European Plate Observing System from the Regional and Selected Local Seismic Networks in Poland. Seismol. Res. Lett. 2021, 92, 1717–1725. [Google Scholar] [CrossRef]
- Hejmanowski, R.; Witkowski, W.T.; Guzy, A.; Malinowska, A. Identification of the ground movements caused by mining-induced seismicity with the satellite interferometry. Proc. Int. Assoc. Hydrol. Sci. 2020, 382, 297–301. [Google Scholar] [CrossRef]
- Sobiesiak, M.; Poiata, N.; Bernard, P.; Rudzinski, L.; Lasocki, S. Automated detection and location of mining induced seismicity from Rudna Copper Mine, SW Poland. In Proceedings of the American Geophysical Union, Fall Meeting 2019, San Francisco, CA, USA, 9–13 December 2019. [Google Scholar]
- Krawczyk, A.; Grzybek, R. An evaluation of processing InSAR Sentinel-1A/B data for correlation of mining subsidence with mining induced tremors in the Upper Silesian Coal Basin (Poland). E3S Web Conf. 2018, 26, 00003. [Google Scholar] [CrossRef] [Green Version]
- Dubiński, J.; Stec, K.; Bukowska, M. Geomechanical and tectonophysical conditions of mining-induced seismicity in the Upper Silesian Coal Basin in Poland: A case study. Arch. Min. Sci. 2019, 64, 163–180. [Google Scholar] [CrossRef]
- Tatara, T. Dynamic Resistance of Building under Mining Tremors; Cracow University of Technology Press: Krakow, Poland, 2012. (In Polish) [Google Scholar]
- Pachla, F.; Tatara, T. Resistance of residential and rural buildings due to mining exploitation in the coal mining area. Zesz. Nauk. Inst. Gospod. Surowcami Miner. Energ. PAN 2017, 101, 45–60. (In Polish) [Google Scholar]
- Abaqus/Standard User’s Manual; Dassault Systèmes Simulia Corp: Johnston, RI, USA, 2020.
- Bednarski, Ł.; Sieńko, R.; Howiacki, T. Estimation of the value and variability of elastic modulus of concrete in the existing structures on the basis of continuous in situ measurements. Cem. Wapno Beton 2014, 6, 396–404. [Google Scholar]
- Azaria, M.; Hertz, D. Time delay estimation by generalized cross correlation methods. IEEE Trans. Acoust. Speech Signal Process. 1984, 32, 280–285. [Google Scholar] [CrossRef]
- Yahia, A.H.; El-Dahshan, E.-S.; Guirges, A.K. Time delay estimation, using correlation approaches applied to seismic time picking. J. Appl. Geophys. 2011, 10, 1–10. [Google Scholar] [CrossRef]
- Piersol, A. Time delay estimation using phase data. IEEE Trans. Acoust. Speech Signal Process. 1981, 29, 471–477. [Google Scholar] [CrossRef]
- Hanus, R. Time delay estimation using phase of cross-spectral density function. Meas. Autom. Robot. 2007, 53, 206–208. [Google Scholar]
- Hanus, R. Statistical errors of time delay estimation using phase of cross-spectral density function. Meas. Autom. Robot. 2006, 12, 10–13. [Google Scholar]
- Friedlander, B.; Francos, J.M. Model based phase unwrapping of 2-D signals. IEEE Trans. Signal Process. 1996, 44, 2999–3007. [Google Scholar] [CrossRef]
- Boroń, P.; Dulińska, J.; Jasińska, D. Two-Step Finite Element Model Tuning Strategy of a Bridge Subjected to Mining-Triggered Tremors of Various Intensities Based on Experimental Modal Identification. Energies 2021, 14, 2062. [Google Scholar] [CrossRef]
- Zahid, F.B.; Ong, Z.C.; Khoo, S.Y. A review of operational modal analysis techniques for in-service modal identification. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 398. [Google Scholar] [CrossRef]
- van Overschee, P.; de Moor, B. Subspace Identification for Linear Systems: Theory-Implementation-Applications; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1996. [Google Scholar]
- Peeters, B.; de Roeck, G. Stochastic System Identification for Operational Modal Analysis: A Review. J. Dyn. Syst. Meas. Control 2001, 123, 659–666. [Google Scholar] [CrossRef]
- Allemang, R.J.; Brown, D.L. A Complete review of the Complex Mode Indicator Function (CMIF) with applications. In Proceedings of the ISMA2006: International Conference on Noise and Vibration Engineering, Leuven, Belgium, 18–20 September, 2006; pp. 3209–3246. [Google Scholar]
- Kim, B.H.; Stubbs, N.; Park, T. A new method to extract modal parameters using output-only responses. J. Sound Vib. 2005, 282, 215–230. [Google Scholar] [CrossRef]
- Cao, S.; Nian, H.; Yan, J.; Lu, Z.; Xu, C. Modal analysis and damage localization in plate-type structures via TDD and PE methods based on the data of an integrated highspeed camera system. Mech. Syst. Signal Process. 2022, 178, 109309. [Google Scholar] [CrossRef]
- Ewins, D.J. Modal Testing: Theory, Practice, and Application, 2nd ed.; Research Studies Press Ltd.: Philadelphia, PA, USA, 2000. [Google Scholar]
- Sung, Y.-C.; Lin, T.-K.; Chiu, Y.-T.; Chang, K.-C.; Chen, K.-L.; Chang, C.-C. A bridge safety monitoring system for prestressed composite box-girder bridges with corrugated steel webs based on in-situ loading experiments and a long-term monitoring database. Eng. Struct. 2016, 126, 571–585. [Google Scholar] [CrossRef]







| Subsurface Type | Amplification Factor for Tremor Energy: | ||
|---|---|---|---|
| 105 [J] | 106 [J] | 107 [J] | |
| Rock | 1.0 | 1.0 | 1.0 |
| Quaternary 22 m | 0.7 | 1.4 | 2.2 |
| Quaternary 15 m | 2.1 | 4.4 | - |
| Quaternary and tertiary 70 m | 0.6 | 1.4 | 1.4 |
| Mode | Natural Frequency [Hz] | Differences [%] | |
|---|---|---|---|
| FE Analysis Model No. 1 | OMA | ||
| 1 | 1.57 | 1.50 | 4.6 |
| 2 | 1.87 | 2.48 | 24.6 |
| 3 | 3.48 | 3.36 | 3.6 |
| 4 | 14.30 | 14.26 | 0.3 |
| Series No. | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Frequency range [Hz] | 8–50 | 8–25 | 8–15 | 8–28 | 8–50 |
| Wave Component Frequency [Hz] | Wave Velocity Determined for Support Pairs [m/s] | ||
|---|---|---|---|
| P1–P2 | P2–P3 | P1–P3 | |
| 10 | 135 | 344 | 254 |
| 12 | 142 | 298 | 239 |
| 14 | 148 | 304 | 245 |
| 16 | 148 | 307 | 250 |
| Mean apparent velocity | 142.5 | 313.2 | 247.1 |
| Wave Component Frequency [Hz] | Wave Velocity Determined for Support Pairs [m/s] | ||
|---|---|---|---|
| P1–P2 | P2–P3 | P1–P3 | |
| 10 | 130 | 335 | 247 |
| 12 | 140 | 280 | 229 |
| 14 | 144 | 297 | 240 |
| 16 | 151 | 297 | 245 |
| Mean apparent velocity | 141.0 | 302.0 | 239.9 |
| Wave Component Frequency [Hz] | Differences [%] in the Wave Velocities Obtained with Different Methods for Support Pairs | ||
|---|---|---|---|
| P1–P2 | P2–P3 | P1–P3 | |
| 10 | 3.7 | 2.6 | 2.8 |
| 12 | 1.4 | 6.0 | 4.2 |
| 14 | 2.7 | 2.3 | 2.0 |
| 16 | 2.1 | 3.3 | 2.0 |
| Mean apparent velocity | 1.1 | 3.6 | 2.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boroń, P.; Dulińska, J.M.; Jasińska, D. Advanced Model of Spatiotemporal Mining-Induced Kinematic Excitation for Multiple-Support Bridges Based on the Regional Seismicity Characteristics. Appl. Sci. 2022, 12, 7036. https://doi.org/10.3390/app12147036
Boroń P, Dulińska JM, Jasińska D. Advanced Model of Spatiotemporal Mining-Induced Kinematic Excitation for Multiple-Support Bridges Based on the Regional Seismicity Characteristics. Applied Sciences. 2022; 12(14):7036. https://doi.org/10.3390/app12147036
Chicago/Turabian StyleBoroń, Paweł, Joanna Maria Dulińska, and Dorota Jasińska. 2022. "Advanced Model of Spatiotemporal Mining-Induced Kinematic Excitation for Multiple-Support Bridges Based on the Regional Seismicity Characteristics" Applied Sciences 12, no. 14: 7036. https://doi.org/10.3390/app12147036
APA StyleBoroń, P., Dulińska, J. M., & Jasińska, D. (2022). Advanced Model of Spatiotemporal Mining-Induced Kinematic Excitation for Multiple-Support Bridges Based on the Regional Seismicity Characteristics. Applied Sciences, 12(14), 7036. https://doi.org/10.3390/app12147036






