1. Introduction
In recent years, machine learning algorithms have been used extensively for image classification tasks. Typically, these tasks are performed by deep neural networks (DNNs) and the related field of science is called deep learning (DL). DNN models generally show substantially higher efficiency than competitive deterministic algorithms. However, the outcomes of DL algorithms depend largely on the quality of the training datasets. The capacity of such a dataset, typically reaching hundreds of thousands of images, determines the ultimate success of the algorithm. Numerous entities construct training datasets, via data gathering and labeling, due to the high value of such datasets in many industries.
The majority of publicly available training datasets can only be used in non-commercial applications, with the commercial use of such datasets prohibited. Therefore, commercial entities are generally required to construct their own databases. In these cases, the developed datasets are labeled either automatically or by crowdsourcing [
1]. The verification of the label quality is commonly outsourced to a third party.
Given that such a third party is often composed of untrained volunteers, the image labeling can be erroneous. Willers et al. [
2] showed that labeling quality is one of the largest underlying causes behind the reliability degradation of DL algorithms. This can cause substantial problems in the deployment of DL algorithms in safety-critical applications. The large number of safety standards for artificial intelligence algorithms indicates the need to evaluate the quality of training dataset labeling. For example, ISO/TR 4804:2020 and ISO/DIS 21448 both indicate that labeling should be reviewed. However, no widely accepted procedures governing label review exist.
In practice, labeling noise is rarely evaluated. It is typically assumed that the data are either perfect or have a negligible error rate. However, the error rate in popular databases, including verification datasets, can be as high as 10% [
3]. This can significantly reduce the maximum accuracy of the corresponding DL algorithms. Moreover, such a high proportion of mislabeling implies that such algorithms should not be expected to reach 100% accuracy.
The problem of labeling noise has been addressed by researchers in recent years. The simplest method to evaluate the quality of a training dataset is to fully label the same set multiple times using different annotators. For each image, the labels of each annotator can then be compared to detect inaccuracies. The level of agreement between a fixed number of annotators when assigning categorical labels can be measured using inter-annotator agreement metrics [
4]. However, this substantially increases preparation cost, as the dataset must be annotated multiple times.
Fully automated approaches to noisy label detection also exist. Such works, however, do not attempt to evaluate the number of erroneous labels detected but instead seek to implement adaptive, noise-tolerant DL algorithms. Thus, these solutions are only appropriate for the training of DL algorithms on noisy datasets and cannot be used to verify the accuracy of training datasets provided by an external supplier.
Reed et al. [
5] modified the loss function to provide a reduced penalty when an image label is suspected to be incorrect. According to the authors, this solution also allows the use of databases in which not all labels are known. Goldberger and Ben-Reuven [
6] added an additional softmax layer to the DNN model, creating an S-Model architecture. The authors assume that the dataset noise has a certain distribution, which is modeled in their proposed solution. This approach uses the expectation-maximization algorithm. Han et al. [
7] presented co-teaching. This method uses two DNNs which, by exchanging data, decide if an image sample is incorrectly labeled. Both of the cooperating DNNs must make the same decision for a label to be judged as inaccurate. The MentorNet network proposed by Jiang et al. [
8] assigns different weights to input images. Images whose labels are assigned with low probability are given decreased weight in subsequent iterations of the algorithm and thus effectively cease to participate in the learning process. In more recent work, Chen et al. [
9] presented an iterative cross-validation method that determines which images within the training dataset should be removed in the next iteration. The authors show that the accuracy of a DNN trained with such iterative pruning leads to accuracy improvements. However, as for the methods outlined below, this approach does not determine whether the removed images were incorrectly labeled or whether they showed some outlying, abnormal, or atypical content, which confuses the DNN and reduces its accuracy when applied to the validation set.
Very recently, Northcutt et al. [
10] proposed confidence learning (CL). As in [
9], the authors use N-fold cross-validation but performed the procedure only once, rather than iteratively. Probability thresholds are determined for each class independently. Such thresholds determine if a given sample is classified confidently. The probabilities are obtained from the final softmax layer of a DNN. Images within the training dataset that are classified inaccurately but confidently are considered erroneously labeled and thus removed from the dataset. The newly filtered set is then used to prepare the final DNN model. The authors of the CL method tested its effectiveness using the ResNet-50 architecture with moderately high mislabel probabilities of 20–70%. Unfortunately, the number of erroneous images that were removed from the dataset was not logged. As in other work, the approach focuses on the increase in the classification performance of the final DNN model, which was shown to be higher than all the other methods reviewed here.
The CL method has been used to analyze known databases of images [
3]. The researchers selected suspicious images using this approach and then manually verified the images to detect incorrect labels. They determined that 0.15–10% of all images are mislabeled. This is an important finding, given that the analyzed reference databases should be free of such faults. This highlights the strong competition between algorithms that has led to them achieving very high classification accuracy, often exceeding 99%. In this study, the final number of incorrect labels was a relatively small fraction of the initial CL predictions. This indicates that the performance of the label noise detection can be improved by further balancing precision versus recall.
The type of noise used throughout the literature is also important to investigate. Authors typically use a confusion matrix model. Such a model assumes a label has a certain probability of being replaced by a different label, depending on the class of the object in the image. This type of noise model is known as class-dependent noise (CDN). The proposed algorithmic solutions assume the presence of such predefined noise and attempt to reconstruct the noise model. In this manner, a significant improvement in learning is achieved. This noise model was adopted, e.g., in [
7,
9,
10].
Uniform noise (UNI) is a much simpler noise model used throughout the literature. In this model, label errors occur independently from the class of object in the corresponding image. Only the fraction of altered labels changes. Such simple random permutation of labels was used, e.g., in [
5,
6,
8].
Chen et al. [
11] demonstrated that instance-dependent noise (IDN) is present in real image databases. The probability of a labeling error within a dataset depends not only on the class of object in the image but also on the image characteristics. For example, consider an image of the written number “1”. When skewed away from a vertical orientation, this could be more easily mistaken for the written number “7”. Unfortunately, previous work on the topic has not accounted for this highly realistic form of noise.
In this paper, we introduce MultiNET flexible confident learning, a novel method for the detection of noisy labels. We propose to extend the current state-of-the-art CL method by introducing a flexible detection threshold to improve the detection rate of incorrect labels while maintaining a minimal number of false positive detections. We further enhance the CL method by aggregating the decisions of several DNNs and show that this significantly improves noisy label detection. Finally, we evaluate the MultiNET algorithm using UNI, CDN, and IDN noise models. We apply these models to four popular image databases: CIFAR-10 [
12], CIFAR-100 [
13], GTSRB [
14], and MNIST [
15]. The results show a significant improvement in label error detection performance, making the proposed solution an attractive tool for the verification of the annotation quality of large image datasets. Note that we study the effectiveness of noisy label detection, not the accuracy of DNNs trained on the corresponding datasets. This is something that has not been done before in related works.
2. MultiNET Flexible Confident Learning
The proposed MultiNET is a modification of the CL algorithm which allows for a significant improvement in the detection of noisy labels over the original CL idea. We concentrated on the possibility of combining several various classifiers to improve the reliability of classification. We also add the mechanism for adjusting the sensitivity of the CL technique to allow a user to select the confidence level of detected wrong labels. Thus, there are two important differences explained in details below.
First, a flexible confidence threshold is used for error detection. This approach allows the mislabeling detection certainty to be controlled and enables, among other uses, the iterative detection of errors within image databases, starting with the most obvious mistakes and gradually progressing to more subtle errors. Secondly, the detection capabilities provided by the DNNs of different architectures are combined. This increases detection confidence and decreases the possibility of false negatives—the designation of correctly labeled images as incorrectly labeled. Both modifications increase the efficiency of automatic noisy label detection and decrease the false positive rate, thus improving the practical application of the CL algorithm.
2.1. Flexible Confidence Threshold
The original CL method performs
N-fold validation. That is, the DNN is trained on a
fraction of the database, while the remainder of the database is searched for mislabeling. The DNN classifications are designated as either confident or uncertain. The threshold for a confident detection is determined as follows:
where
is the probability threshold for the confident detection of class
j,
is the collection of images for which the DNN’s estimated class is
j, and
is the probability that the image
x belongs to class
j as indicated by the DNN (i.e., the
j-th node of the softmax layer at the output of the DNN). The proposed threshold is an average of out-of-sample classification probabilities within a set of images that are classified as a given class. An image label is assumed to be noisy if the detection is confident and the DNN classification does not match the label.
The CL algorithm does not allow the sensitivity threshold to be adjusted and is therefore highly dependent on the training set used. For images within the validation set that are similar to those within the training set, the probability of accurate classification is high. However, images which differ will have a lower chance of being classified accurately. In such cases, potentially mislabeled images may not be designated as such.
Our solution allows the user to control the level of certainty so that an appropriate balance can be achieved between the detection of obvious errors and a minimal number of false positives. To achieve this, we replace the average confidence level of the original CL-method by a
q-quantile. The threshold definition then takes the form
where
Q{
A;
q} returns the value of the
q-quantile calculated within a set of probabilities
A. The value of
q can be adjusted to modify the label noise detection threshold. For example,
indicates median probabilities, while
q < 0.5 and
q > 0.5 decrease and increase the threshold, respectively.
In addition to increased flexibility, our proposed solution improves robustness to the presence of noisy labels within the training set. This is due to the replacement of the average value with a robust quantile-based measure.
2.2. Combining Multiple DNN Architectures
The original CL algorithm used a single DNN with a ResNet-50 architecture. Although further work used different architectures, only a single architecture was used for the evaluation of a given known image database (see Table 1 in [
3]). This single architecture approach can over- or underestimate the number of detections due to the differing capabilities of DNNs of different internal designs. Each DNN architecture was designed for a different task—a given architecture achieves varying levels of classification accuracy across different datasets. Moreover, some DNNs are more or less prone to overfitting and have better or worse generalization capabilities. Hence, they exhibit different label noise detection properties.
Given that use of a single DNN can bias results, we propose the use of several (specifically, eight) different architectures to train the DNNs. We combine the individual DNN decisions using a simple AND operator. That is, the decision to indicate a label as noisy is only made if all DNNs agree.
The use of the AND operator substantially increases the requirements for detection, as all DNNs must agree on this decision. If applied to the original CL algorithm, this would lead to a significant decrease in the detection of mislabeled images. With our algorithm, using the q-quantile approach, the detection threshold can be decreased appropriately.
We found experimentally that the resulting combination of the AND operator and a relatively low confidence threshold was the most reliable technique for the detection of noisy labels and was superior to the use of CL with a single DNN.
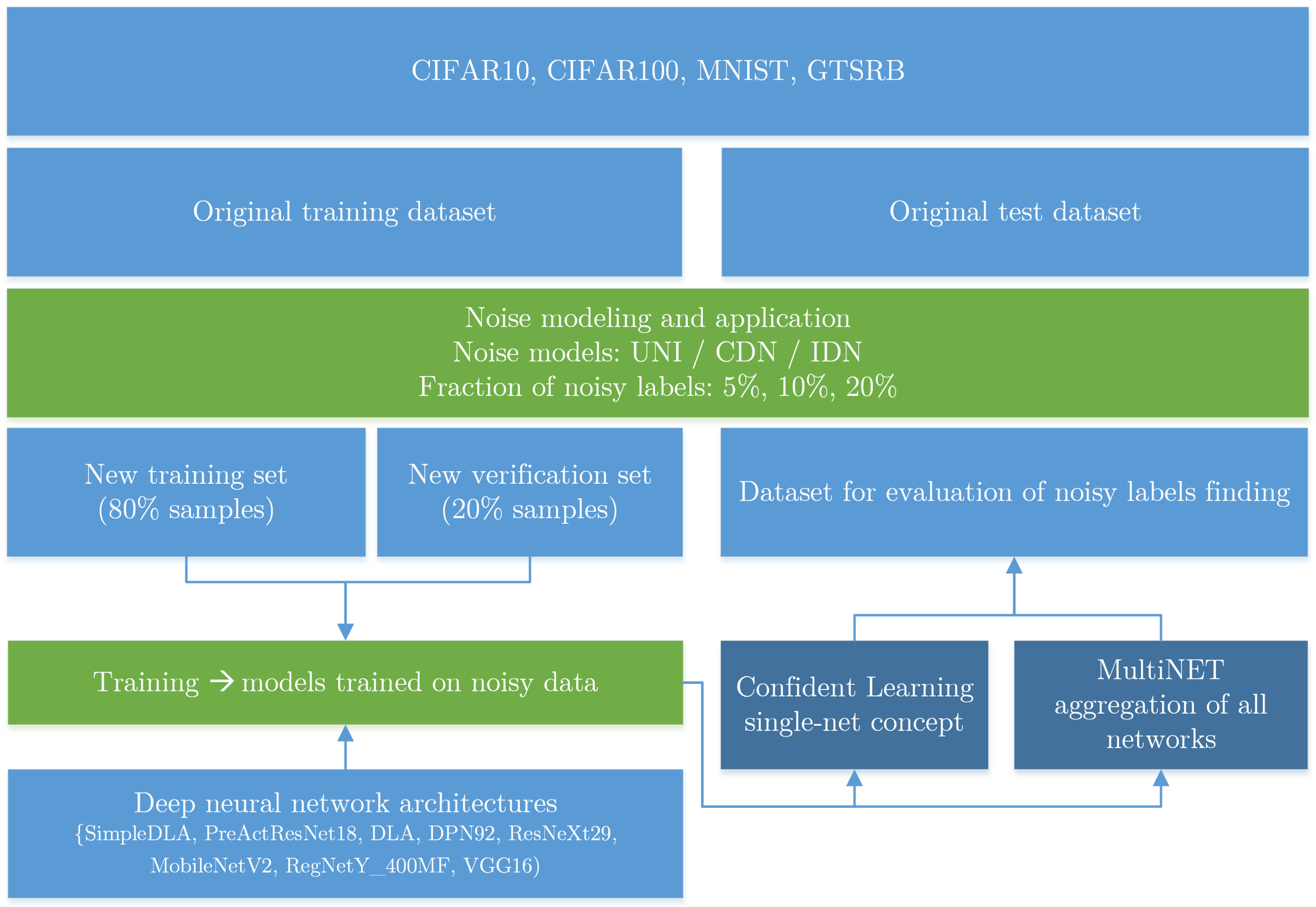
3. Experimental Verification
The primary experimental objective was to compare our novel flexible MultiNET algorithm with the original CL algorithm of Northcutt et al. [
10].
In contrast to the majority of the literature, our focus was on the number of inaccurate labels that were successfully detected by the algorithm and the number of false positives which occurred. To our knowledge, no works exist which follow a similar line of investigation. An overview of the experiment is presented in
Figure 1.
Four popular image databases were used in the experiments: CIFAR10 [
12], CIFAR100 [
13], GTSRB [
14], and MNIST [
15]. The CIFAR10 and CIFAR100 databases contain images of different types, such as dog, cat, tree, car, etc. The GTSRD database contains images of 43 types of road sign, and the MNIST database contains handwritten numerals. The number of images and the number of classes within each database are given in
Table 1.
For use during the learning process, we divided each original training dataset into a new training set containing 80% of the images and a new verification set containing 20% of the images. The original verification set was used as an evaluation set to test the effectiveness of noisy label detection. Label noise was applied to all datasets according to the three noise models: UNI, CDN, and IDN. Three noise levels, defined as the percentage of noisy labels, were analyzed: 5%, 10%, and 20%. These noise values were chosen to reflect the levels of noise present in real databases.
Consistency was maintained between the type and intensity of noise in both the learning set and the evaluation set. For example, a DNN trained on a set perturbed by UNI noise at a level of 10% was then applied to a verification set that was perturbed by the same type and level of noise. This approach was used because the type and level of noise should be constant across the entire image set, as the entirety of a given dataset is typically prepared by the same entity before being divided.
We used eight state-of-the-art DNN architectures that currently achieve the highest classification efficiency on popular image databases. Details of the architectures are presented in
Table 2. All operations were performed by the PyTorch Python library [
16], using stochastic gradient descent (SGD) optimization [
17] with cross-entropy loss.
During each 200-epoch training phase, popular methods of training dataset augmentation were used to improve DNN efficiency. The value of 200 was taken as a safe number of epochs, since most networks stabilized their accuracies around 100–150 epochs. These methods included brightness normalization, image rotation (limited to 20 degrees for the MNIST database and not used for the GTSRB database to avoid the misinterpretation of road signs) and random cropping.
The 200-epoch training phase of a single model took from 15 min (for the simplest models and MNIST or CIFAR10 databases) to 3 h (for most complex architectures and the CIFAR100 set) on a utilized NVidia A5000 24 GB graphic card. The classification of all images in any image dataset with any of the trained models took usually less then a minute on this GPU.
Noise Generation
In the experiments, we used all three noise models described in the introduction: uniform noise (UNI), class-dependent noise (CDN), and instance-dependent noise (IDN). The application of UNI noise to the tested databases was straightforward—a defined fraction of labels were randomly changed to another class. However, the application of CDN and IDN noise was more complex and is described in this section.
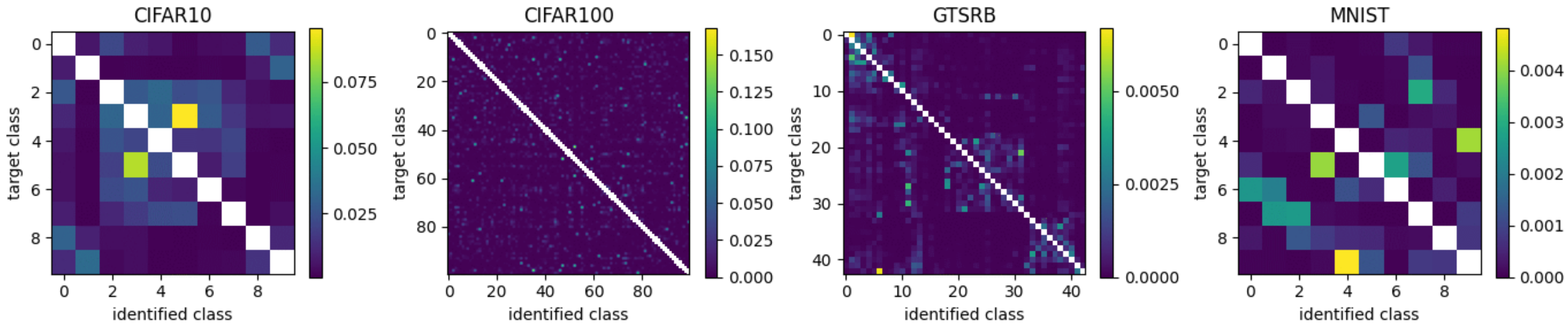
To obtain the matrices for CDN noise application, we used the classification results of DNNs trained on full sets with accurate labels. The resulting confusion matrices for all datasets are presented in
Figure 2. In contrast to some previous works, instead of using the confusion matrix corresponding to the final training epoch, we opted to use an average matrix containing the average probability of incorrect classifications across all 200 training epochs and all eight DNN architectures. A confusion matrix that represents only the final training epoch does not reflect the time required for the DNN to develop a high score. Some classes require many training epochs, while other more unique or distinctive classes will be classified within few epochs. Therefore, we argue that misclassification behavior across the entire training process better reflects the probability of inaccurate labeling than the discrete results corresponding to only the final training epoch or a single DNN architecture.
The evolution of misclassification probability for the three most common error types is shown in
Figure 3. These errors displayed the largest probability of class switching. The spread of probabilities across each DNN architecture is shown by the faded regions. It can be observed that the probability stabilizes at approximately the 100th epoch and that there is little variation in probability between the different architectures. This suggests similar types of misclassification errors result from each DNN model.
Note that the probability scale varies for each dataset. For CIFAR10 and CIFAR100, the average probability of misclassification is within the range 10–20%, while for MNIST it is approximately 1%. This is because the images within the MNIST dataset are considerably easier to classify than those within the CIFAR10 and CIFAR100 datasets. Moreover, the GTSRB dataset produces a final error rate of zero—no errors are present. This is a further argument for the use of average probability in the place of final result. Despite the obvious errors present throughout the training process, the final result would indicate no possibility of misclassification for the GTSRB dataset. Instead, the average probability gives a more intuitive interpretation of misclassification and considers, for example, that a “Speed limit 20 km/h” image can be mistaken for a “Speed limit 30 km/h” image.
We included the IDN noise model in our experiments as it has been identified as the most reliable such model [
11]. When using this model, the probability of misclassification is calculated individually for each image in the database. It is determined by averaging the DNN response (behind the softmax layer) over all epochs and all trained models. This reflects the tendency of the networks to alter the designated class of a given image during the learning process.
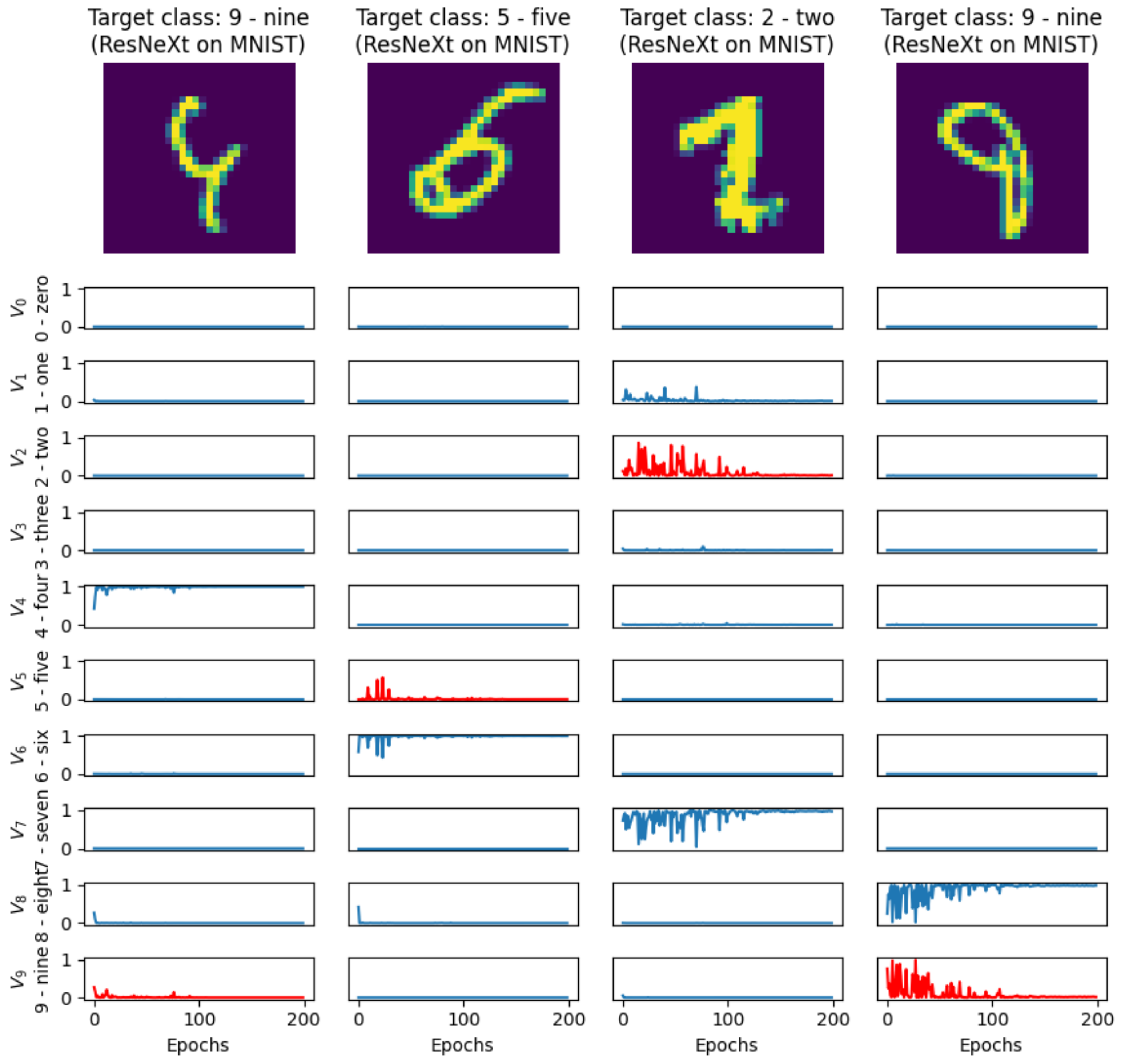
Examples of four misclassified images from the MNIST database are presented in
Figure 4. For all 10 classes, the decision outputs
,
of a sample DNN architecture (ResNeXt29 in this case) are shown below the images. The output corresponding with the target class—the class to which the image actually belongs, according to the reference data from the MNIST database—is highlighted in red. These are obvious examples for which human evaluation would produce a similar outcome to that of a DNN. Such examples confirm that misclassification chance is primarily dependent on the specific image, not on the class to which the image belongs.
We define
as the classification output, averaged over all 200 epochs and all eight utilized DNN architectures.
Figure 5 shows boxplots of
for the 30 most difficult images to classify. That is, the images with the lowest median
. The figure additionally presents the six most difficult images below each plot. The CIFAR10 and CIFAR100 datasets include images of objects positioned or viewed in a manner that is very rare in the learning database (e.g., the ostrich or the horse’s head images in CIFAR10) or images that are extremely difficult to classify for a human (e.g., the lion or the beetle images in CIFAR100). Moreover, some of the most difficult images are degraded or have very low resolutions (e.g., the majority of the examples from GTSRB).
The application of IDN noise to the datasets required the retrieval of the most difficult-to-classify images, such as those presented in
Figure 5. For each image,
was determined, where
i denotes the classification number produced by the DNN output. Following this, the sum of probabilities was normalized over all classes, such that
. With the probabilities normalized, the new corrupted class could be determined randomly. Moving through the images from most difficult, noise was applied to each image label until the proportion of affected labels reached the designated noise level.
4. Results
The classification performance of DNNs trained on data affected by different levels of label noise is shown in
Figure 6. Each image database is presented in a separate graph, and different noise models are color-coded. Faded regions indicate the range of classification accuracies across the different DNN architectures.
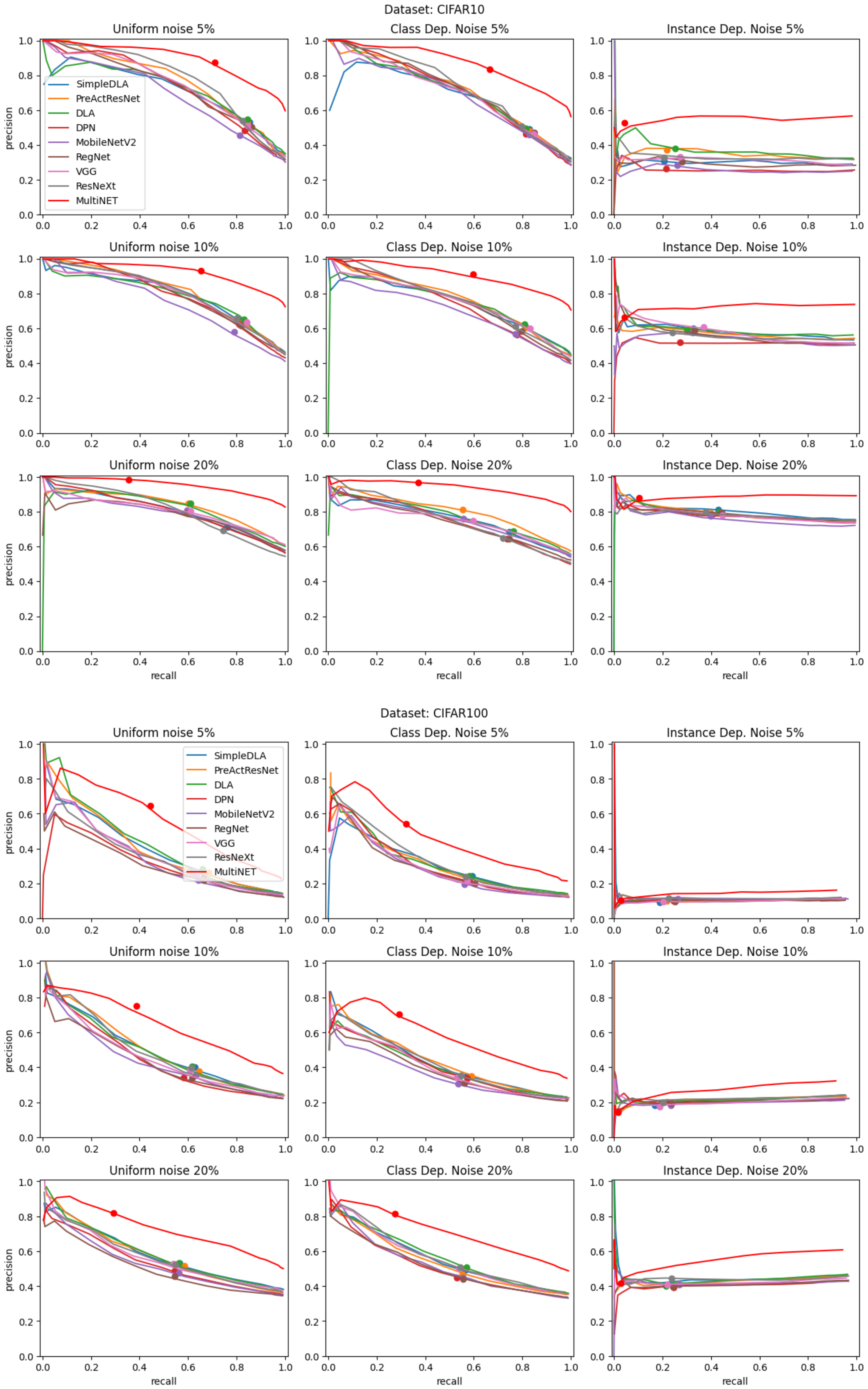
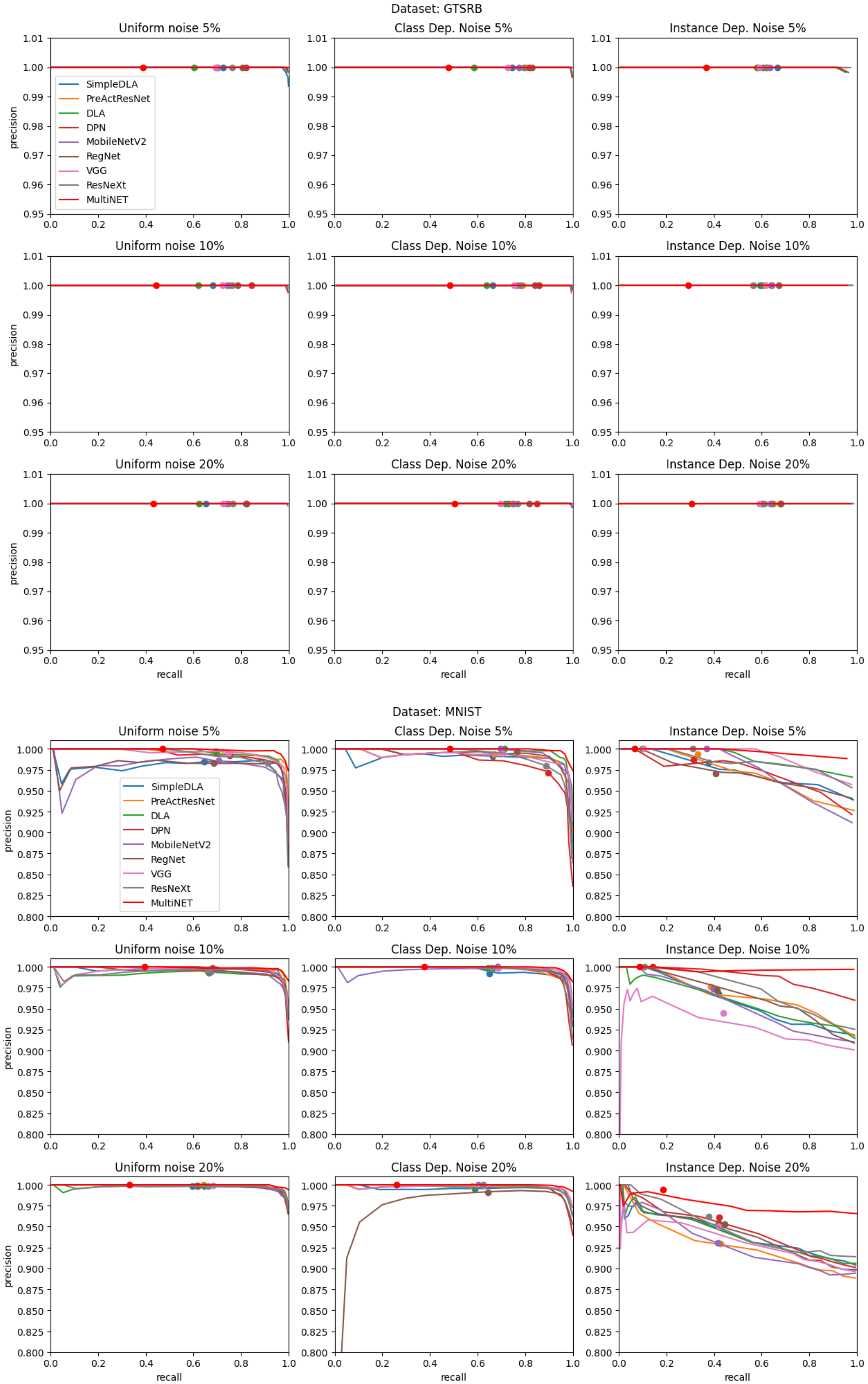
The results of noisy label detection are presented in the form of precision–recall curves in
Figure 7 and
Figure 8. Precision and recall are defined using true positive (TP), false positive (FP), and false negative (FN) detections as follows:
Each curve was created by stepping a q-quantile value from 0 to 0.99. This corresponds with moving from the right side to the left side of each plot. The red line indicates the results of the MultiNET algorithm, while the results of a variety of algorithms which combine a single DNN with a q-quantile approach are indicated by the additional lines. The results of each algorithm when using mean probability instead of a q-quantile—corresponding to the classic CL algorithm—are presented as larger dots. The red dot shows the results of the CL algorithm when using a combination of DNNs, as in our approach. The graphs are grouped according to the image database used and the type and level of label noise.
An area under the precision–recall curve (AUC) measure was used to compare the efficiency of noisy label detection. The results are summarized in
Table 3, wherein we highlight in bold the best results for each noise type and level combination.
5. Discussion
The graphs shown in
Figure 6 confirm that for three of the four databases used, the effect of label noise is evident over the range studied. For the CIFAR10 and CIFAR100 databases, IDN noise is noticeably less impactful than UNI or CDN noise. We posit that this may be related to the nature of the images to which IDN noise was applied. For the CIFAR10 and CIFAR100 databases, the images identified as being most difficult to classify (see
Figure 5) were not easily confused for images from another class. Rather, were they images of objects positioned or viewed in an unusual manner or objects of unusual color. Therefore, the introduction of IDN noise to such images would not be expected to lead to the propagation of classification errors to other images.
The opposite is true for the MNIST database, wherein IDN noise caused a substantially greater decrease in classification performance than CDN and UNI noise. In this case, the written digits that were relabeled due to noise were very similar to those of different classes. These similarities can be observed in
Figure 4 and
Figure 5. As such, the introduction of erroneous labels to these types of images confused the DNNs and caused a significant efficiency drop. Notably, this behavior was observed for each of the tested DNN architectures, as demonstrated by the faded region around the IDN curve for the MNIST dataset (see
Figure 6).
The GTSRB database produces distinctive behavior, with the performance results for all algorithms close to 100% (see
Figure 8). The application of noise of any type or level had no significant statistical effect on DNN efficiency. We hypothesize that this effect has two sources. The first is the ease with which each of the architectures can classify well-defined images, such as traffic signs. The impact of sign scaling and background variation does not pose a substantial problem for current DNN architectures. The second presumed source is highlighted by the ineffectiveness of noise on classification performance. This suggests that the database itself is highly robust and redundant. Thus, the presented analysis can be considered as a means of evaluating databases for their robustness against intrinsic label noise.
The graphs presented in
Figure 6 also show that UNI and CDN noise result in very similar misclassification rates. The majority of the literature concerning label noise uses CDN noise and suggests that UNI noise is both unrealistic and easier for DNNs to handle. Our experiments prove that both noise types have similar effects on final classification. Only IDN noise introduces a qualitatively different degree of difficulty. This effect is less apparent for the CIFAR10 and CIFAR100 databases and more apparent for the MNIST database.
The graphs shown in
Figure 7 and
Figure 8, in addition to the AUC results presented in
Table 3, confirm that the proposed MultiNET algorithm achieves significantly better mislabel detection performance than the original CL method. For the CIFAR10 and CIFAR100 databases, a clear improvement can be observed in the precision–recall relationship for all noise types when a combination of DNNs was utilized. The use of the MNIST database produces the smallest increase in detection efficiency. This is due to the inherent high classification performance of DNNs when applied to simple written digits. Nevertheless, the improvement is still noticeable. The improvement in detection performance when using the GTSRB database could not be measured due to the 100% detection precision in all noise scenarios.
In addition to improved performance when using multiple DNN architectures, the introduction of the q-quantile value allows for smooth movement along the precision–recall curve. This presents a variety of mislabeling detection strategies. It is possible to optimize either precision, recall, or a combination of both, according to the needs of the user.
6. Conclusions
Combating label noise in image databases is currently a topic of high interest for many researchers. The majority of solutions within the literature modify either the DNN architecture itself or the learning method. No solutions investigate the efficiency of noisy label detection.
Our paper focused on the detection of mislabeled images. We proposed MultiNET, a novel algorithm based on the current state-of-the-art confidence learning algorithm. Two mechanisms of the algorithm are adapted: the use of a set of DNNs, each trained using a different architecture, and the introduction of a q-quantile value, allowing the algorithm sensitivity to be tuned. Our main idea was as follows:
Four image databases (CIFAR10, CIFAR100, MNIST, and GTSRB) were used to experimentally validate the effectiveness of MultiNET in detecting label noise. Each dataset contained different types of images and different classification targets. Three different noise types (uniform, class-dependent, and instance-dependent) were introduced to imitate real-world scenarios.
The experimental results demonstrate the superiority of the MultiNET algorithm when compared to the original confident learning algorithm. First, the MultiNET algorithm achieves a significantly higher ratio of correct detections to false detections. This is particularly noticeable in databases for which classification is somewhat challenging (e.g., CIFAR100). Secondly, MultiNET allows the detection sensitivity to be varied, thus enabling an iterative approach to progressively detecting errors, from the most obvious to the most subtle.
The proposed algorithm could be a useful tool for the verification of image databases. Specifically, it allows for the automatic verification of large databases in which the labeling may be erroneous due to, for example, crowdsourcing.
Summarizing, the main research contribution of the work consists of:
A new idea to assemble several classifiers in an algorithm providing a reliable estimation of noisy labels in image datasets;
A mechanism for the modification of detection sensitivity;
A comprehensive evaluation of the efficiency of finding noisy labels (the previous works concentrated only the final accuracy on the improved network);
The utilization of instance-dependent noise—a recently introduced most realistic model of label noise in image databases.
A natural extension of the algorithm is the use of a voting method in place of the AND operator. For example, a decision about detection certainty could be made if N of M networks (N < M) agreed. This approach could be applied to difficult classification tasks for which the used architectures display highly variable levels of accuracy. Moreover, all the architectures used show very similar levels of accuracy for all tested image databases. The use of a voting method will be considered in future research using more unusual image datasets.