Multirotor Unmanned Aerial Vehicle Configuration Optimization Approach for Development of Actuator Fault-Tolerant Structure
Abstract
:Featured Application
Abstract
1. Introduction
2. Overview of Multirotor UAVs
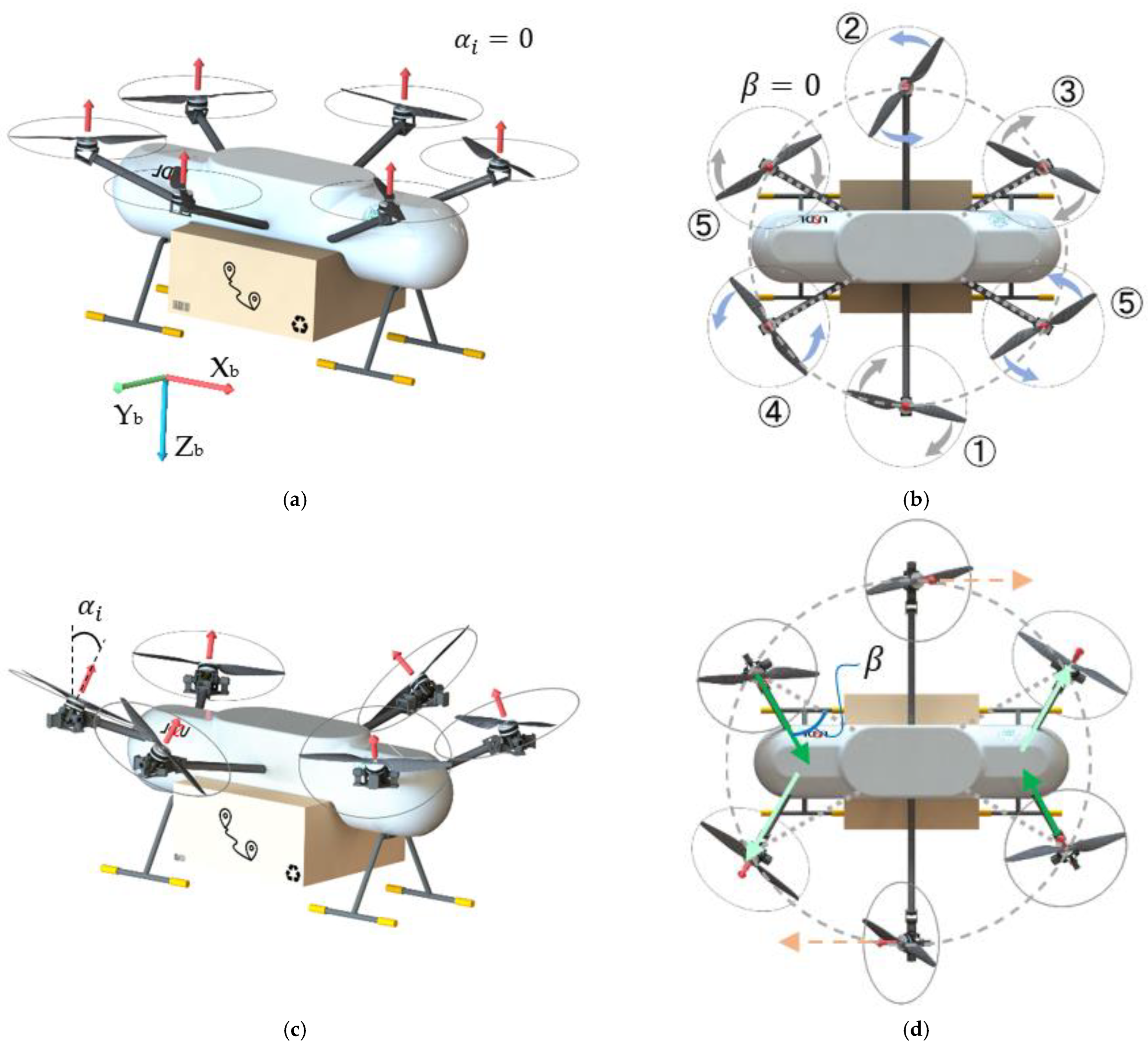
2.1. Multirotor UAV Configuration
2.2. AMS Based Multirotor Configuration Assessment
2.3. Multirotor UAV Configuration with Failed Actuator
3. Controllability Criteria
3.1. Null Controllability
3.2. Maneuverability Requirement
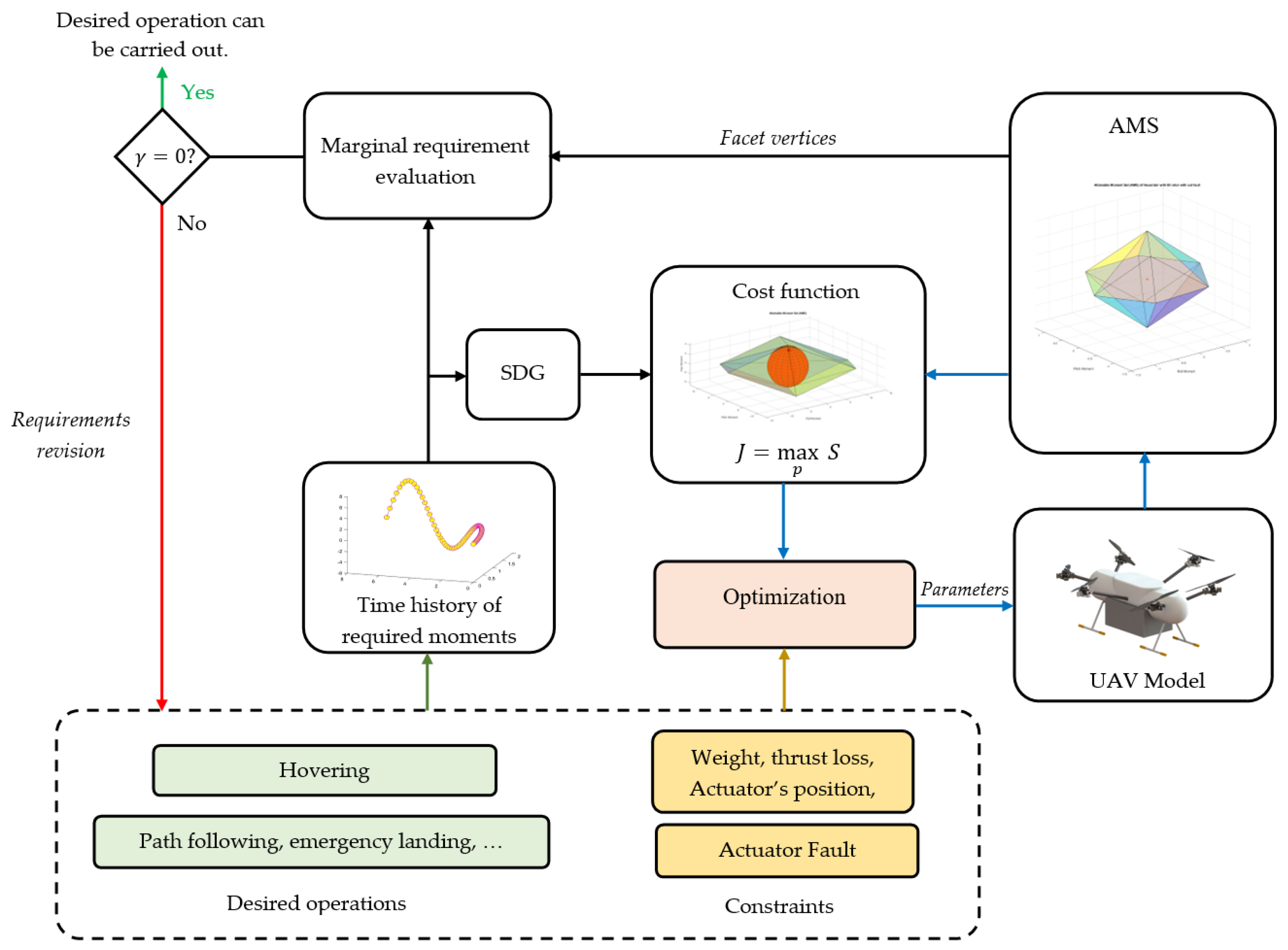
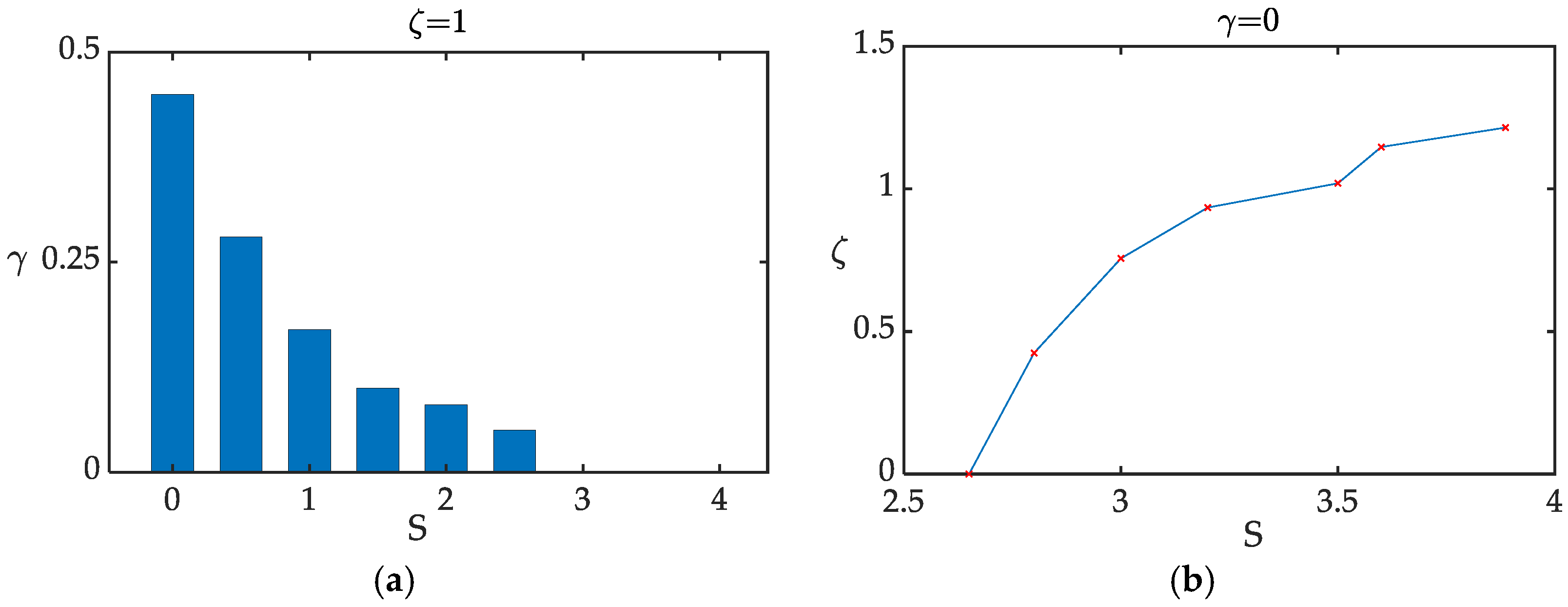
4. Optimization
4.1. Optimization Framework
4.2. Optimization Formulation
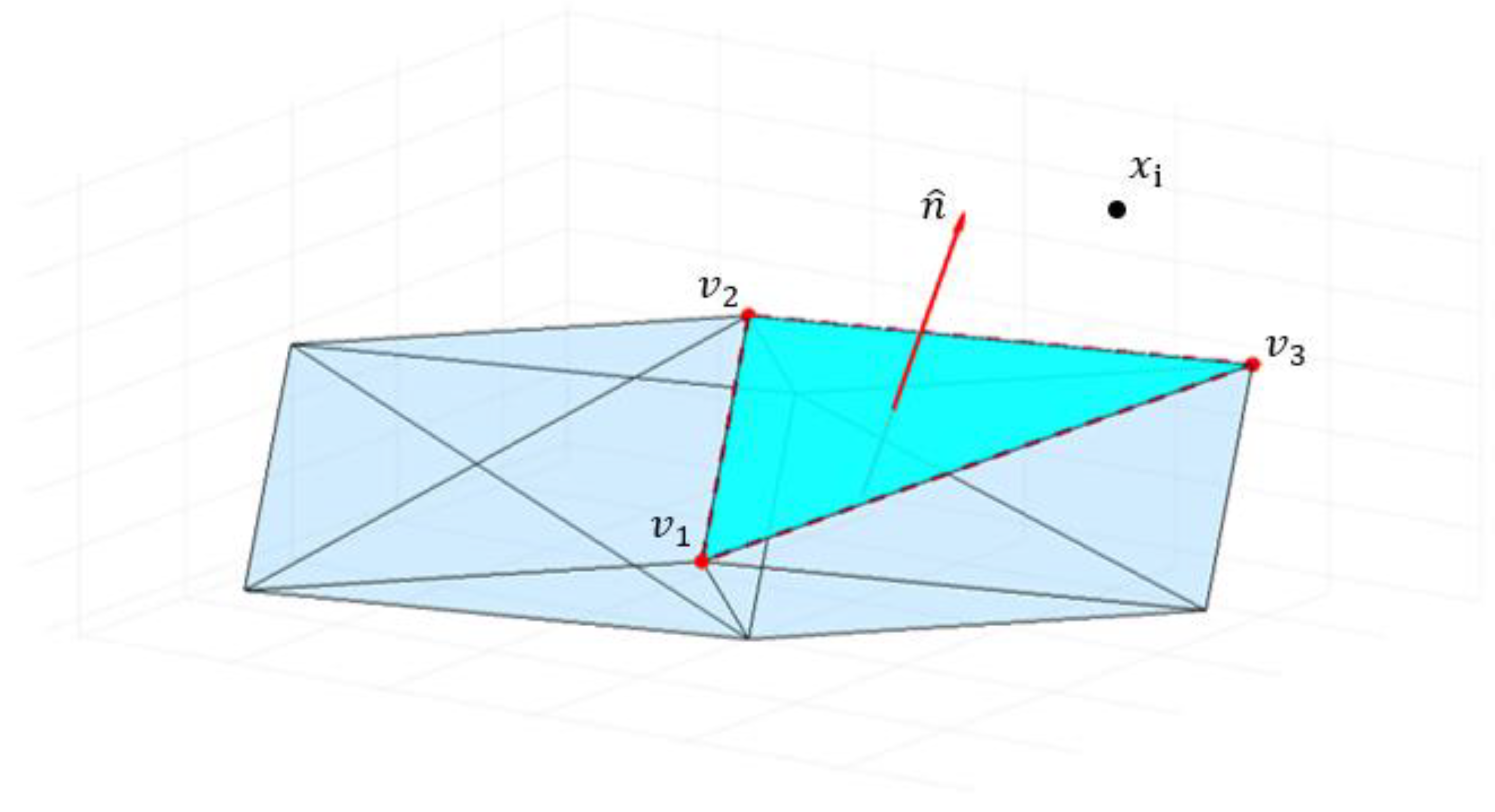
4.3. Inside-AMS-Point Check
| Algorithm 1 Inside-AMS-point check | |
| 1 | for i = 1, 2,…,n required moment with n number of points |
| 2 | is a facet from AMS for |
| 3 | for k = 1, 2, 3 vertices of AMS facet |
| 4 | marginal requirement |
| 5 | for all i |
| 6 | for all j |
| 7 | for all k |
| 8 | n = norm () //norm vector for each facet |
| 9 | = dot (n, ( − ) //signed distance between each facet and points in a moment’s history |
| 10 | If > |
| 11 | outside point= // is outside of the AMS |
| 12 | Else if < |
| 13 | inside point= // is inside the AMS |
| 14 | If z* = size(outside point)! = 0 |
| 15 | performance requirement not fulfilled |
| 16 | If z* = size(outside point) = 0 |
| 17 | performance requirement fulfilled |
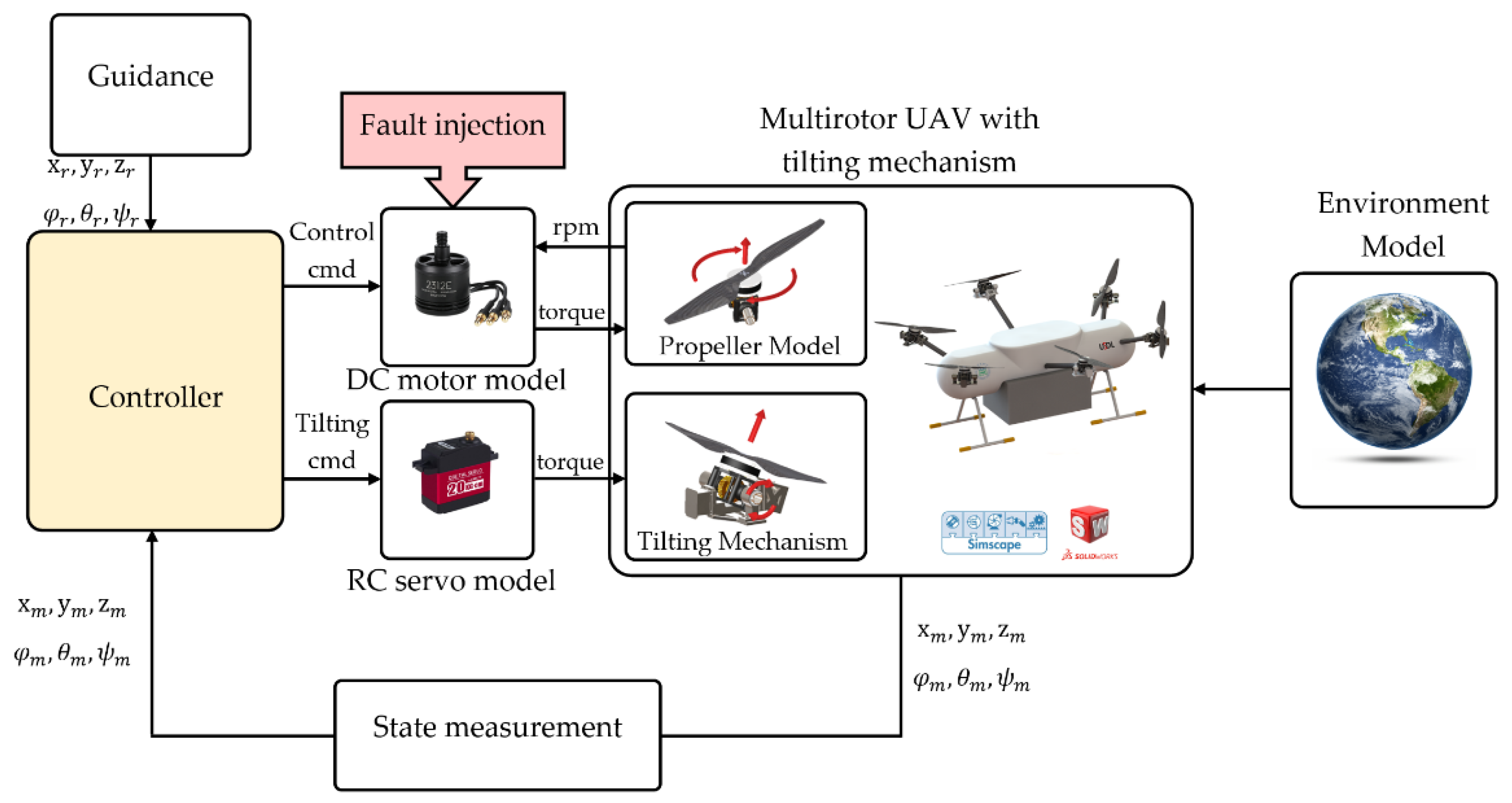
5. Implementation
5.1. Plant Modeling and Simulation
5.2. Parameter Selection
6. Result and Discussion
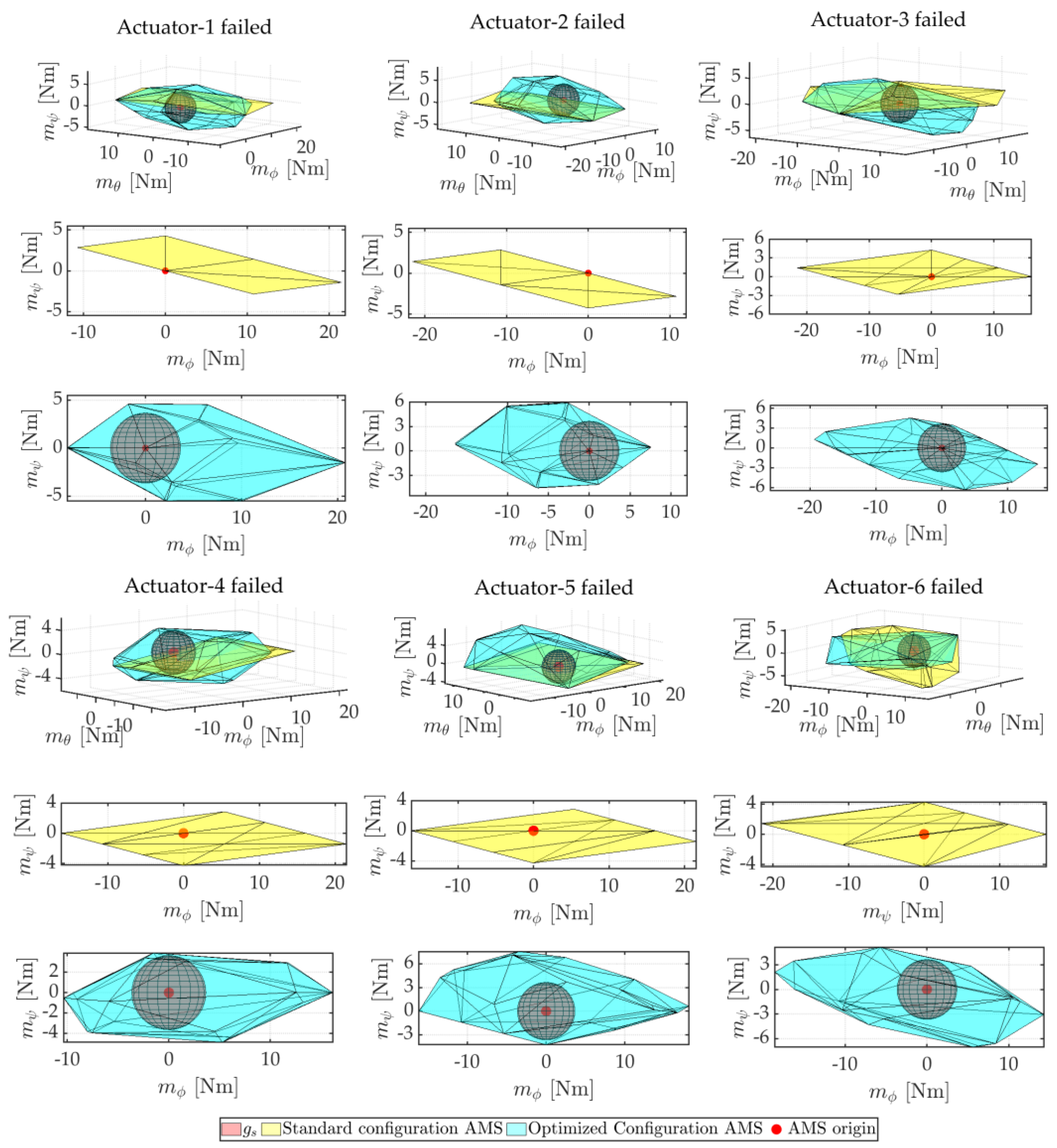
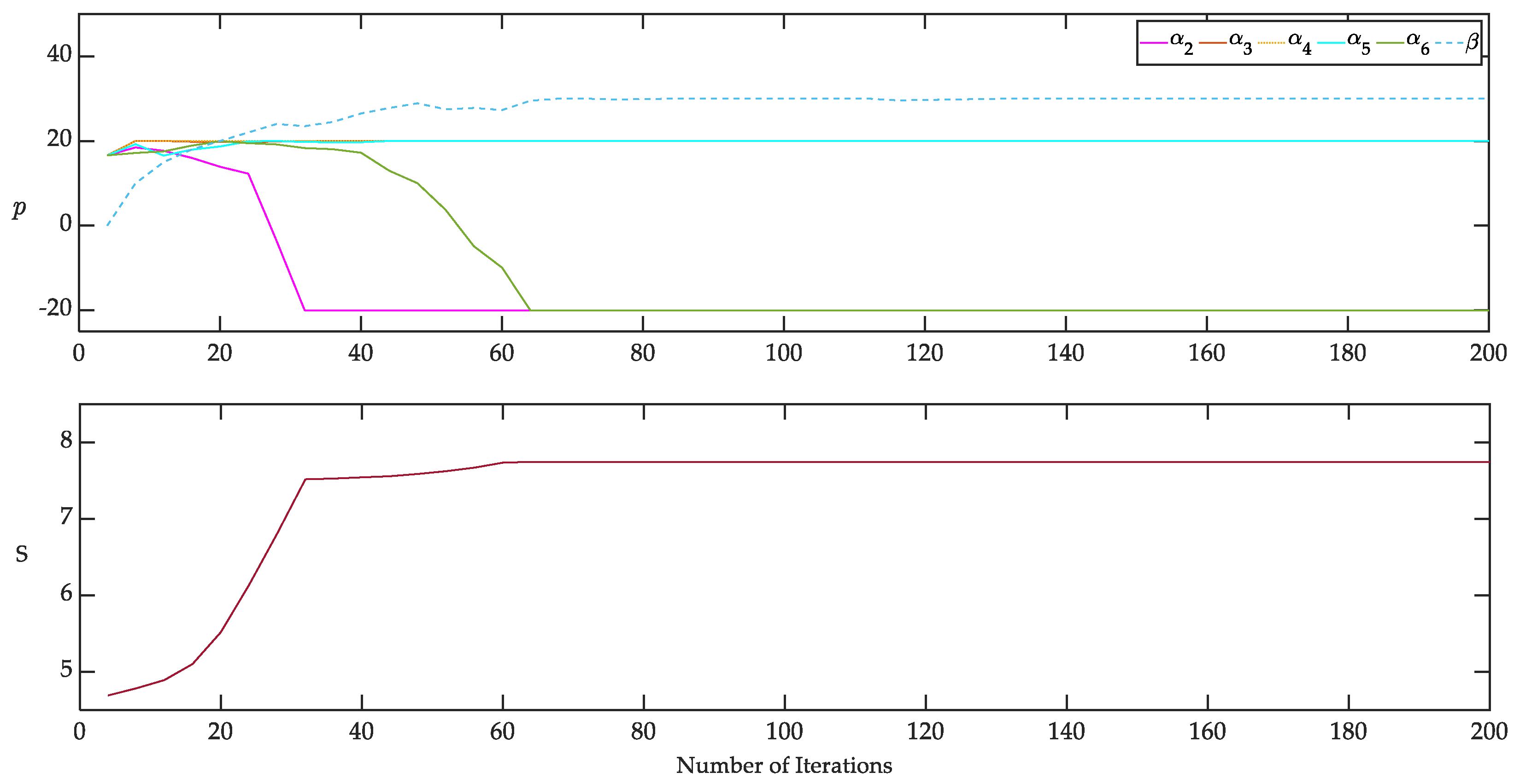
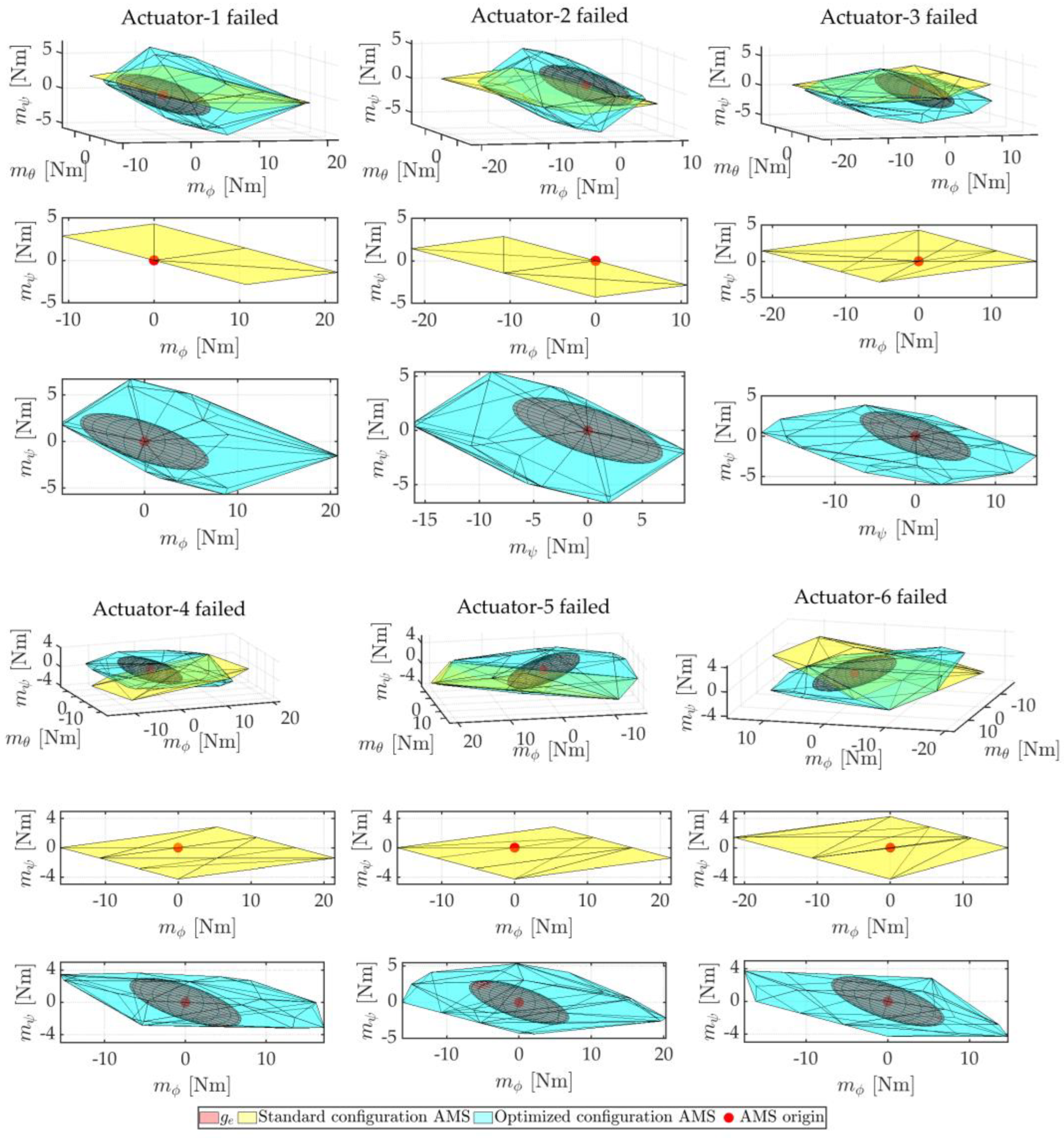
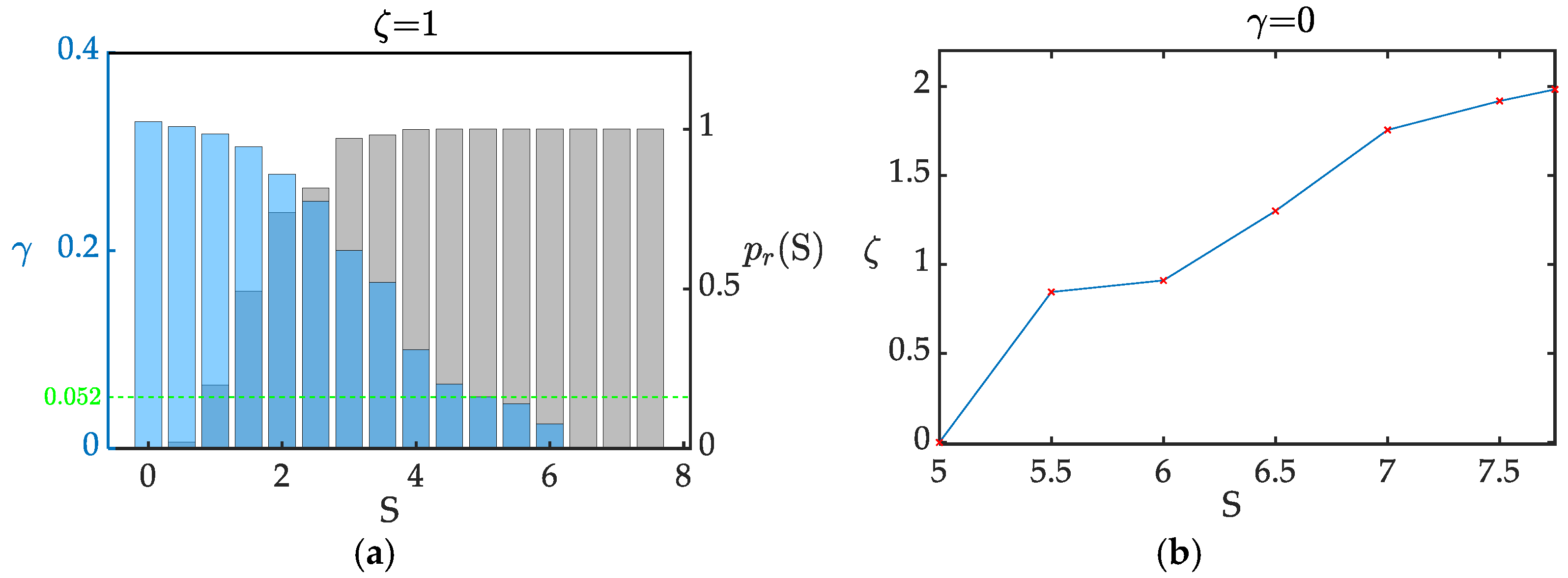
6.1. Optimization Result
6.1.1. Null Controllability
6.1.2. Maneuver Requirement
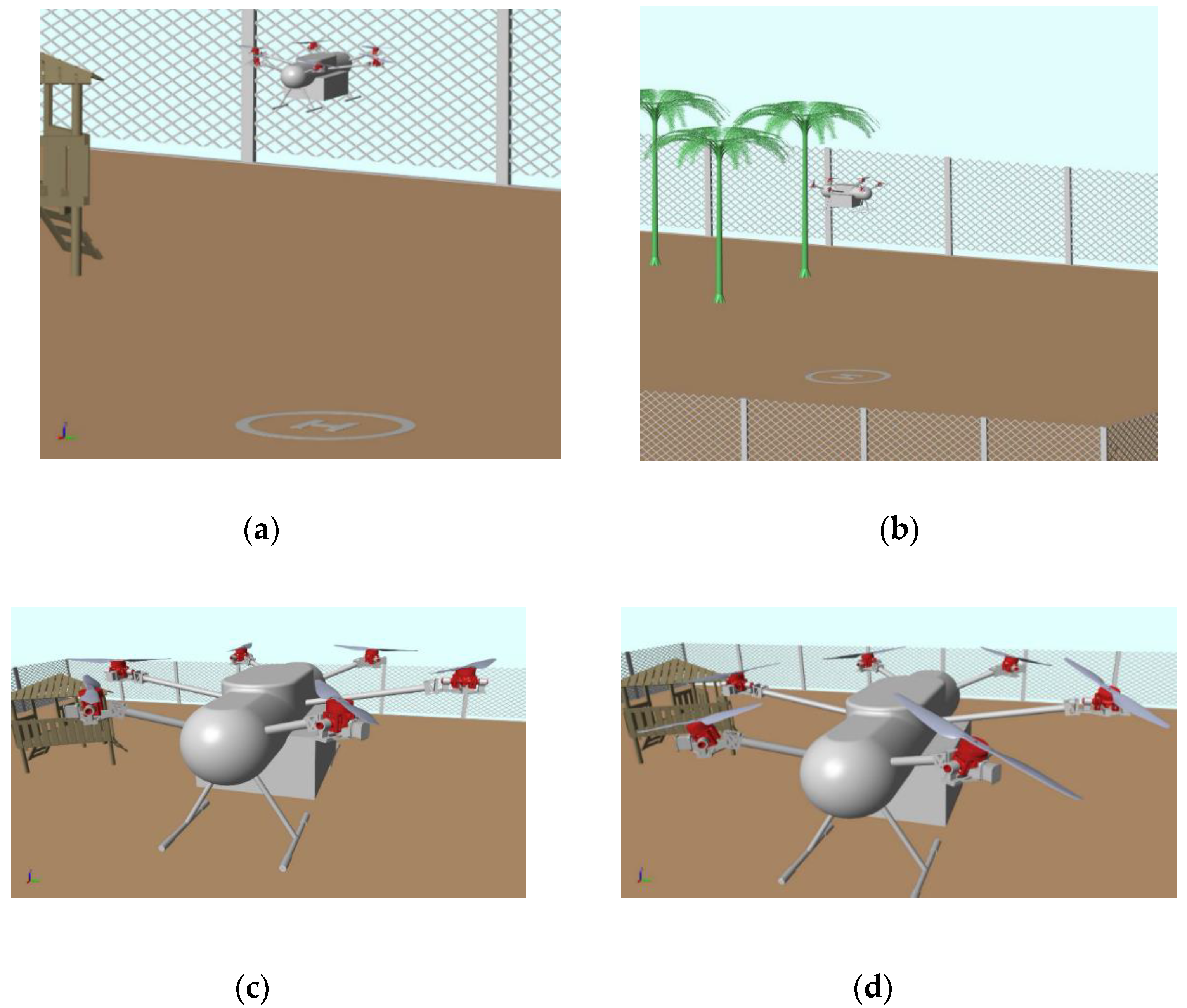
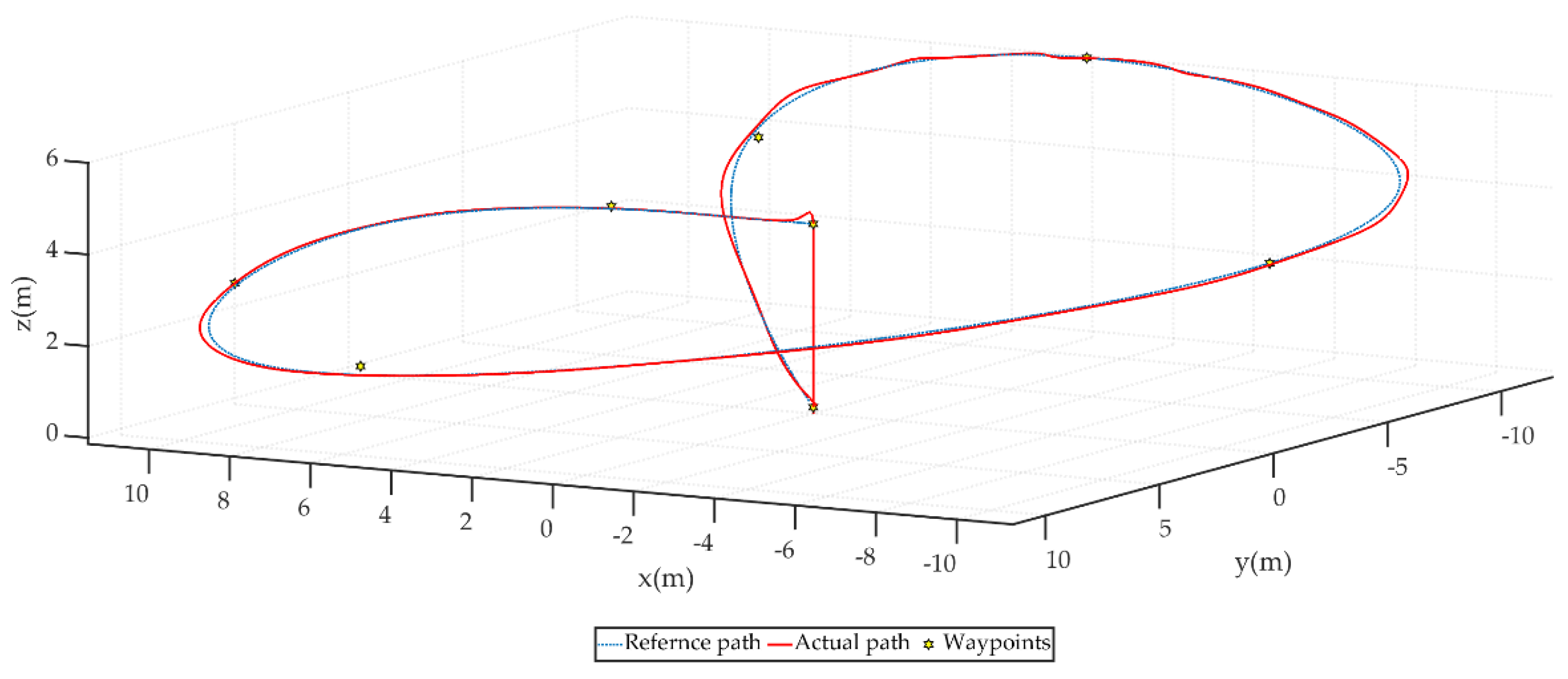
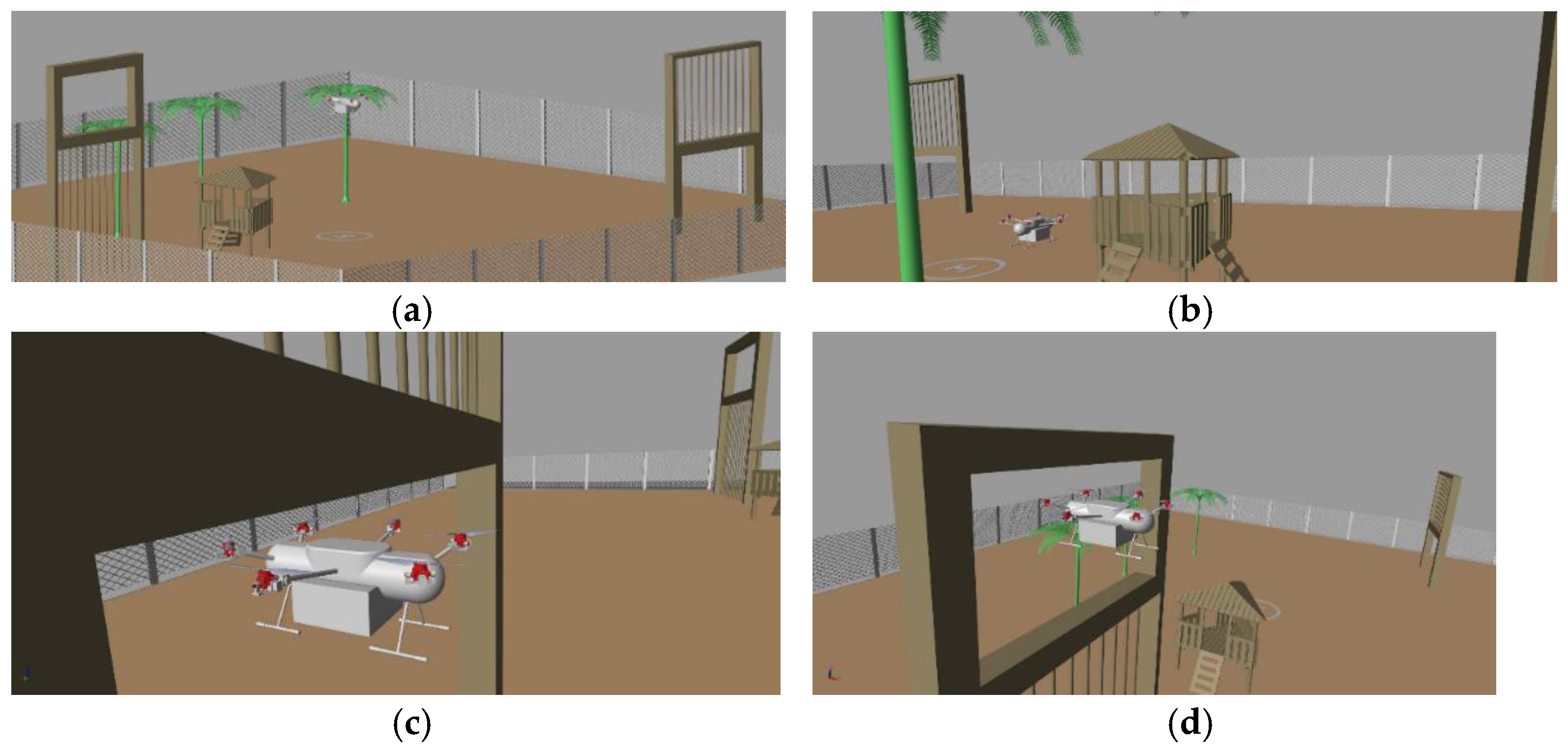
6.2. Simulation Result
6.2.1. Scenario 1
6.2.2. Scenario 2
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Appendix A. Position and Orientation Matrix Derivation

References
- Fourlas, G.K.; Karras, G.C. A Survey on Fault Diagnosis and Fault-Tolerant Control Methods for Unmanned Aerial Vehicles. Machines 2021, 9, 197. [Google Scholar] [CrossRef]
- Baldini, A.; Felicetti, R.; Freddi, A.; Longhi, S.; Monteriù, A. Actuator Fault-Tolerant Control Architecture for Multirotor Vehicles in Presence of Disturbances. J. Intell. Robotics Syst. 2020, 99, 859–874. [Google Scholar] [CrossRef]
- Pose, C.D.; Giribet, J.I.; Mas, I. Fault Tolerance Analysis for a Class of Reconfigurable Aerial Hexarotor Vehicles. IEEE/ASME Trans. Mechatron. 2020, 25, 1851–1858. [Google Scholar] [CrossRef]
- Schneider, T.; Bouabdallah, S.; Rudin, G.D.K. Fault-Tolerant Multirotor Systems. Master’s Thesis, ETH Zurich, Zürich, Switzerland, 2011. [Google Scholar]
- Michael, A.; Klaus, M.D.; Danie, G.; Jan, S. Design of a Multi Rotor MAV with regard to Efficiency, Dynamics and Redundancy. In Proceedings of the AIAA 2012-4779, AIAA Guidance, Navigation, and Control Conference, Minneapolis, MN, USA, 13–16 August 2012. [Google Scholar]
- Sanjuan, A.; Nejjari, F.; Sarrate, R. Reconfigurability Analysis of Multirotor UAVs under Actuator Faults. In Proceedings of the 2019 4th Conference on Control and Fault Tolerant Systems (SysTol), Casablanca, Morocco, 18–20 September 2019; pp. 26–31. [Google Scholar] [CrossRef]
- Yang, T.; Li, P.; Zhang, H.; Li, J.; Li, Z. Monocular Vision SLAM-Based UAV Autonomous Landing in Emergencies and Unknown Environments. Electronics 2018, 7, 73. [Google Scholar] [CrossRef] [Green Version]
- Wayne, D.; Kenneth, A.B.; Roger, B. Aircraft Control Allocation; Wiley: Chichester, UK, 2017. [Google Scholar]
- Wang, B.; Shi, W.; Miao, Z. Confidence Analysis of Standard Deviational Ellipse and Its Extension into Higher Dimensional Euclidean Space. PLoS ONE 2015, 10, e0118537. [Google Scholar] [CrossRef] [PubMed]
- Wolfgang, K.H.; Léopold, S. Applied Multivariate Statistical Analysis; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar] [CrossRef]
- Gong, J. Clarifying the Standard Deviational Ellipse. Geogr. Anal. 2002, 34, 155–167. [Google Scholar] [CrossRef]
- Jiang, G.; Richard, M.V. A nonparallel hexrotor UAV with faster response to disturbances for precision position keeping. In Proceedings of the 2014 IEEE International Symposium on Safety, Security, and Rescue Robotics, Hokkaido, Japan, 27–30 October 2014; pp. 1–5. [Google Scholar]
- Zhang, J.; Max, S.; Florian, H. Attainable Moment Set Optimization to Support Configuration Design: A Required Moment Set Based Approach. Appl. Sci. 2021, 11, 3685. [Google Scholar] [CrossRef]
- Wen, F.H.; Hsiao, F.Y.; Shiau, J.K. Analysis and Management of Motor Failures of Hexacopter in Hover. Actuators 2021, 10, 48. [Google Scholar] [CrossRef]
- Haicheng, L.; Rodney, T.; Peter, V.O.; Martijn, M. Executing convex polytope queries on nD point clouds. Int. J. Appl. Earth Obs. Geoinf. 2021, 105, 102625. [Google Scholar] [CrossRef]
- Weisstein, E.W. Point-Plane Distance. From MathWorld—A Wolfram Web Resource. Available online: https://mathworld.wolfram.com/Point-PlaneDistance.html (accessed on 9 May 2022).
- Denery, T.; Ghidella, J.; Mosterman, P.; Shenoy, R. Creating Flight Simulator Landing Gear Models Using Multidomain Modeling Tools. In Proceedings of the AIAA Meeting Papers on Disc, (2006-6821), Keystone, CO, USA, 21–24 August 2006; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2006. [Google Scholar]
- MathWorks Inc. Simscape MultibodyTM; MathWorks Inc.: Natick, MA, USA, 2020. [Google Scholar]
- Khurrum, M.; Norilmi, A.I. Application of multibody simulation tool for dynamical analysis of tethered aerostat. J. King Saud Univ. Eng. Sci. 2022, 34, 209–216. [Google Scholar] [CrossRef]
- Sun, W.; Zhang, X.; Lin, G.; Wang, H.; Han, J. Extreme Maneuvering Control and Planning of Multi-Rotor UAV for High-Speed Invading Target Avoidance. In Proceedings of the 2021 IEEE International Conference on Real-Time Computing and Robotics (RCAR), Xining, China, 15–19 July 2021; pp. 387–392. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, J.; Zhang, D.; Shen, L. Control and flight test of a tiltrotor unmanned aerial vehicle. Int. J. Adv. Robot. Syst. 2017, 14, 172988141667814. [Google Scholar] [CrossRef]
- Hussein, H. Fault-Tolerant Control of a Multirotor Unmanned Aerial Vehicle under Hardware and Software Failures. Ph.D. Thesis, Université Libanaise, Beirut, Lebanon, 2020. [Google Scholar]
- Vey, D.; Lunze, J. Structural reconfigurability analysis of multirotor UAVs after actuator failures. In Proceedings of the 2015 54th IEEE Conference on Decision and Control (CDC), Osaka, Japan, 15–18 December 2015; pp. 5097–5104. [Google Scholar] [CrossRef]
- Merheb, A.; Noura, H.; Bateman, F. Emergency Control of AR Drone Quadrotor UAV Suffering a Total Loss of One Rotor. IEEE/ASME Trans. Mechatron. 2017, 22, 961–971. [Google Scholar] [CrossRef]
- Giribet, J.I.; Sanchez, R.S.; Ghersin, A.S. Analysis and design of a tilted rotor hexacopter for fault tolerance. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 1555–1567. [Google Scholar] [CrossRef]
- Giribet, J.I.; Pose, C.D.; Ghersin, A.S.; Mas, I. Experimental Validation of a Fault-Tolerant Hexacopter with Tilted Rotors. Int. J. Electr. Electron. Eng. Telecommun. 2018, 7, 58–65. [Google Scholar] [CrossRef] [Green Version]
- Michieletto, G.; Ryll, M.; Franchi, A. Control of statically hoverable multi-rotor aerial vehicles and application to rotor-failure robustness for hexacopters. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 2747–2752. [Google Scholar] [CrossRef] [Green Version]
- Gauthier, R.; Cristina, S.M.; Sihem, T.; Mathieu, B.; Nicolas, M. Minimum-time B-spline trajectories with corridor constraints. Application to cinematographic quadrotor flight plans. Control Eng. Pract. 2019, 89, 190–203. [Google Scholar] [CrossRef] [Green Version]







| Dimensionality (n) | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | 0.6827 | 0.9545 | 0.9973 | 0.9999 | 1.0000 | 1.0000 |
| 2 | 0.3935 | 0.8647 | 0.9889 | 0.9997 | 1.0000 | 1.0000 |
| 3 | 0.1987 | 0.7385 | 0.9707 | 0.9989 | 1.0000 | 1.0000 |
| 4 | 0.0902 | 0.5940 | 0.9389 | 0.9970 | 0.9999 | 1.0000 |
| Fault Condition | Parameters (Angles in Degree) | Cost Function | |
|---|---|---|---|
| Initial Value | Optimization | ||
| Actuator 1 failed | 3.8862 | ||
| Actuator 2 failed | 3.8862 | ||
| Actuator 3 failed | 3.5078 | ||
| Actuator 4 failed | 3.4718 | ||
| Actuator 5 failed | 3.6263 | ||
| Actuator 6 failed | 3.5029 | ||
| Fault Condition | Parameters (Angles in Degree) | Cost Function | |
|---|---|---|---|
| Initial Value | Optimization | ||
| Actuator 1 failed | 7.747 | ||
| Actuator 2 failed | 8.416 | ||
| Actuator 3 failed | 8.595 | ||
| Actuator 4 failed | 8.101 | ||
| Actuator 5 failed | 8.173 | ||
| Actuator 6 failed | 6.751 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Debele, Y.; Shi, H.-Y.; Wondosen, A.; Kim, J.-H.; Kang, B.-S. Multirotor Unmanned Aerial Vehicle Configuration Optimization Approach for Development of Actuator Fault-Tolerant Structure. Appl. Sci. 2022, 12, 6781. https://doi.org/10.3390/app12136781
Debele Y, Shi H-Y, Wondosen A, Kim J-H, Kang B-S. Multirotor Unmanned Aerial Vehicle Configuration Optimization Approach for Development of Actuator Fault-Tolerant Structure. Applied Sciences. 2022; 12(13):6781. https://doi.org/10.3390/app12136781
Chicago/Turabian StyleDebele, Yisak, Ha-Young Shi, Assefinew Wondosen, Jin-Hee Kim, and Beom-Soo Kang. 2022. "Multirotor Unmanned Aerial Vehicle Configuration Optimization Approach for Development of Actuator Fault-Tolerant Structure" Applied Sciences 12, no. 13: 6781. https://doi.org/10.3390/app12136781
APA StyleDebele, Y., Shi, H.-Y., Wondosen, A., Kim, J.-H., & Kang, B.-S. (2022). Multirotor Unmanned Aerial Vehicle Configuration Optimization Approach for Development of Actuator Fault-Tolerant Structure. Applied Sciences, 12(13), 6781. https://doi.org/10.3390/app12136781






