Target Localization and Sensor Movement Trajectory Planning with Bearing-Only Measurements in Three Dimensional Space
Abstract
:1. Introduction
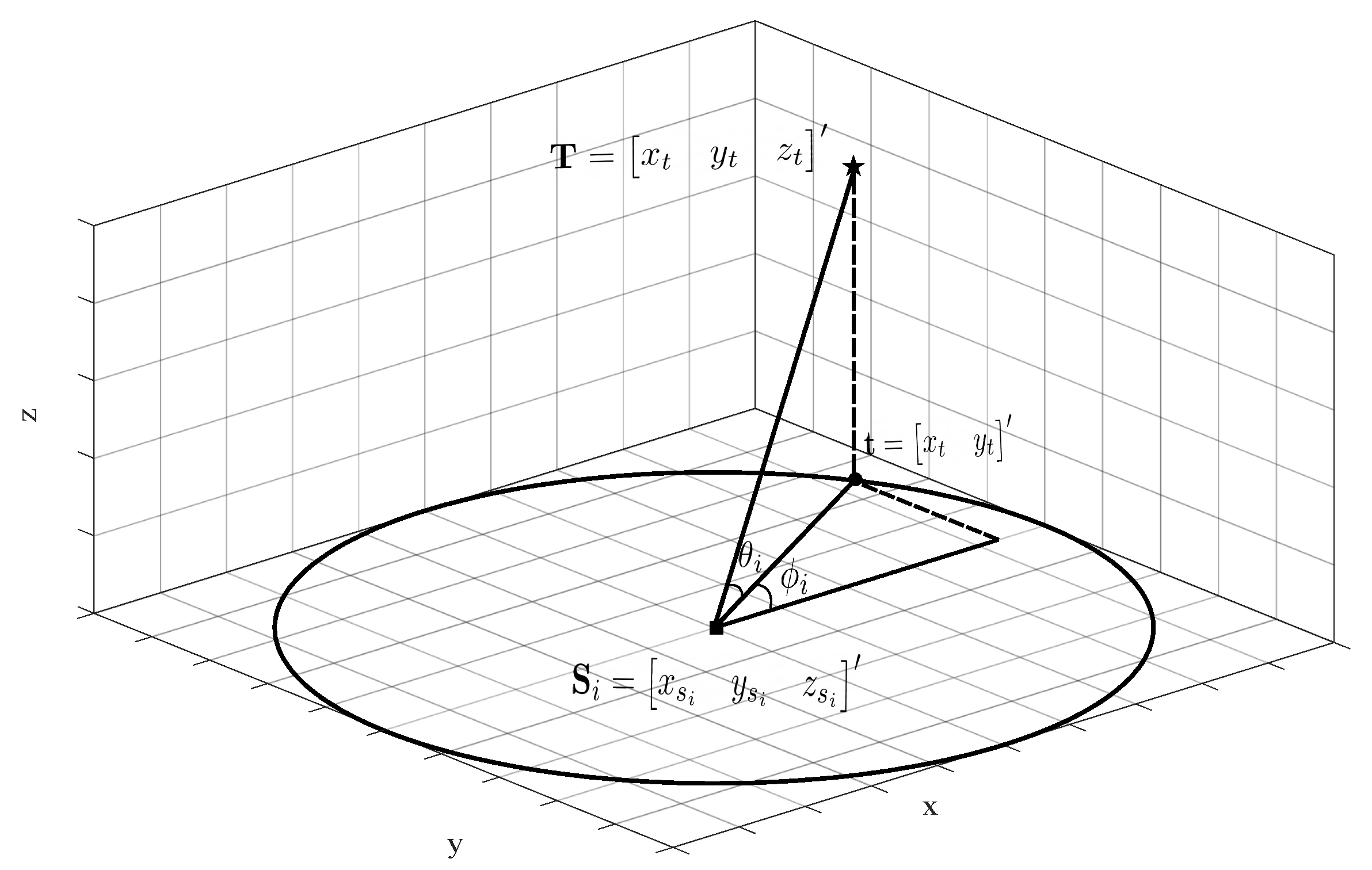
2. Bearing-Only Localization in 3D Space
3. Bias Compensation Estimator for Localization in 3D Space
3.1. Bias Compensation Localization in 2D Space
3.2. Bias Compensation Method in Z-Axis
3.3. BC-WIV Estimator in 3D Space
4. Sensor Trajectory Design
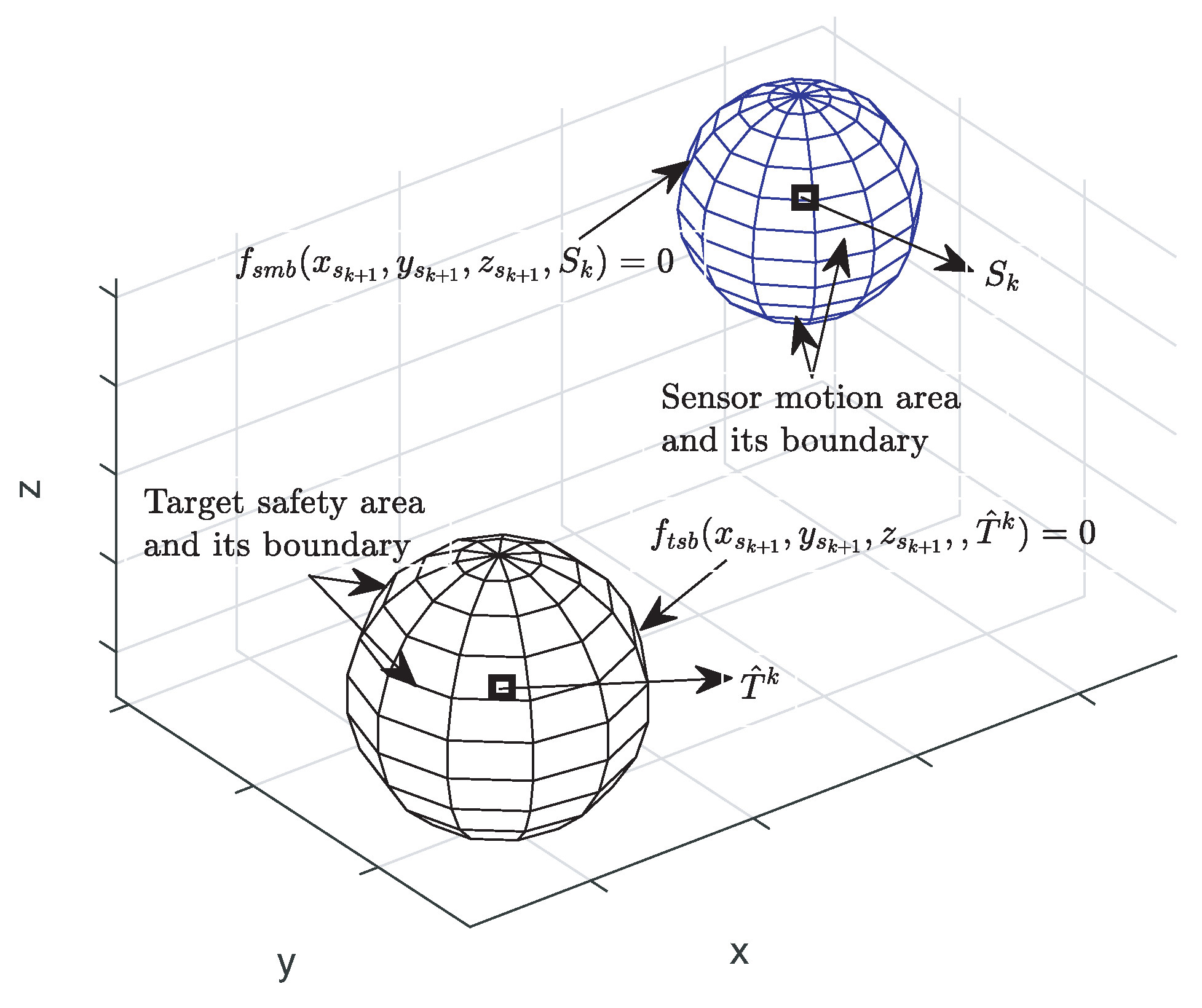
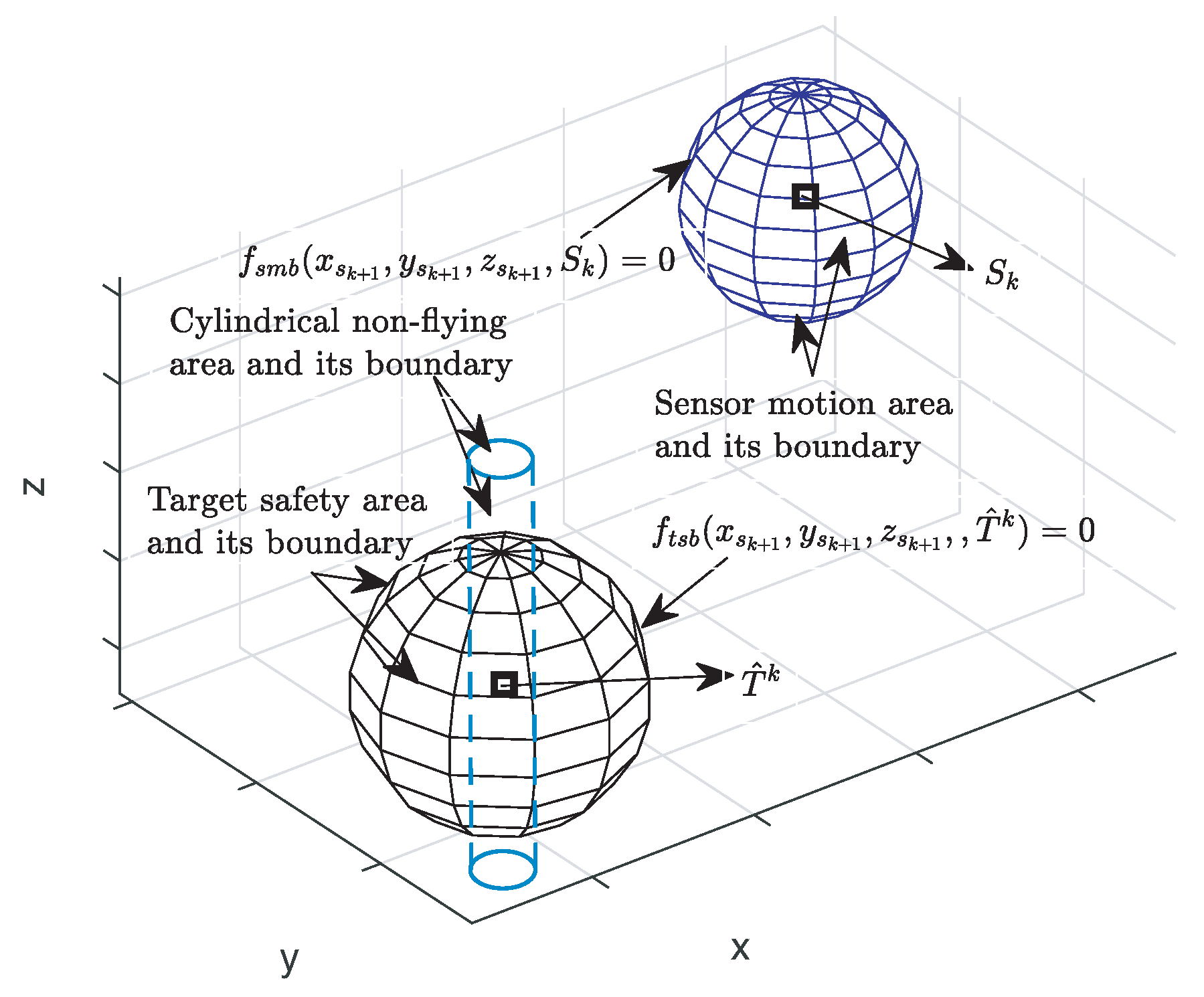
4.1. Constraints
4.2. Sensor Trajectory Planning Strategies
4.3. Optimal Solution Region
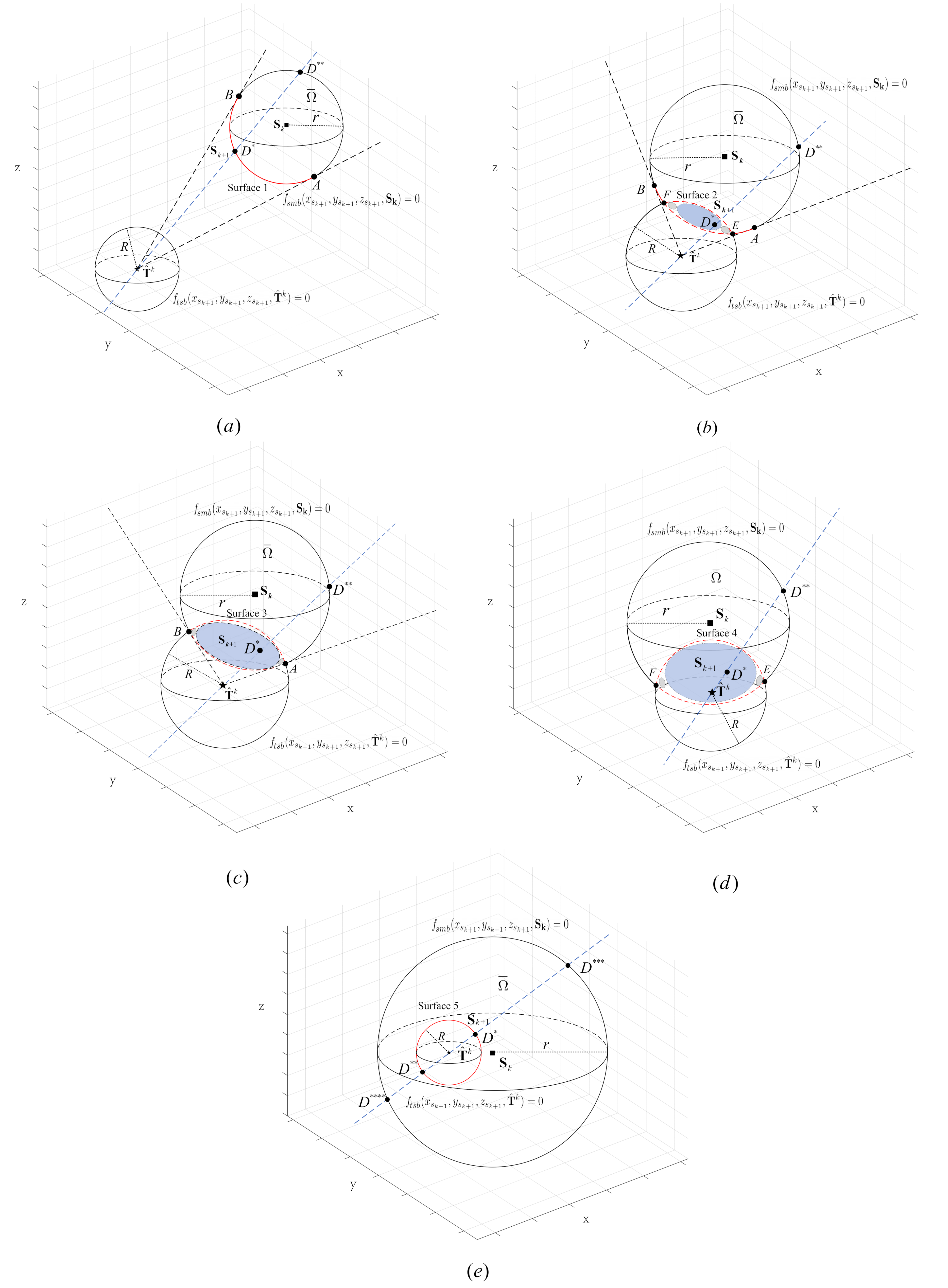
- When the sensor motion area and the target safety area are separated, define the boundary part of the sensor motion area inside as surface 1 in Figure 3a. The feasible region is the sensor motion area;
- When the sensor motion area intersects with the target safety area, the feasible region is the sensor motion area where the part inside the target safety area is excluded, and the surface is where part of the target safety boundary is inside the sensor motion area. According to the position of , it can be divided into three sub-cases: (i) when is outside the sensor motion area and is not contained by the target safety area, define the part of the sensor motion boundary inside with the section inside the target safety area replaced by the section of the target safety boundary inside the sensor movement area, such as surface 2 in Figure 3b. E and F (E and F are symmetrically distributed) are the points where the two spheres intersect; (ii) when the is outside the sensor motion area and if is contained by the target safety area, define the part of the target safety boundary inside the sensor motion area as surface 3 in Figure 3c; (iii) when the is inside the sensor motion area, define the part of the target safety boundary inside the sensor motion area as surface 4 in Figure 3d;
- when the sensor motion area contains the target safety area, the feasible region is the sensor motion area where the interior section of the target safety area is excluded. The target safety boundary is defined as surface 5 in Figure 3e.
4.4. Analytical Derivation for the Global Maximizer
4.5. Single Sensor Trajectory Design Procedure
- Generate through the maximization of (69) or (72). The maximizer of (69) or (72) can be produced in an analytical way described in Section 4.4;
- Gather the measurement information , , and from the sensor at ;
- Use localization technique to generate ;
- .
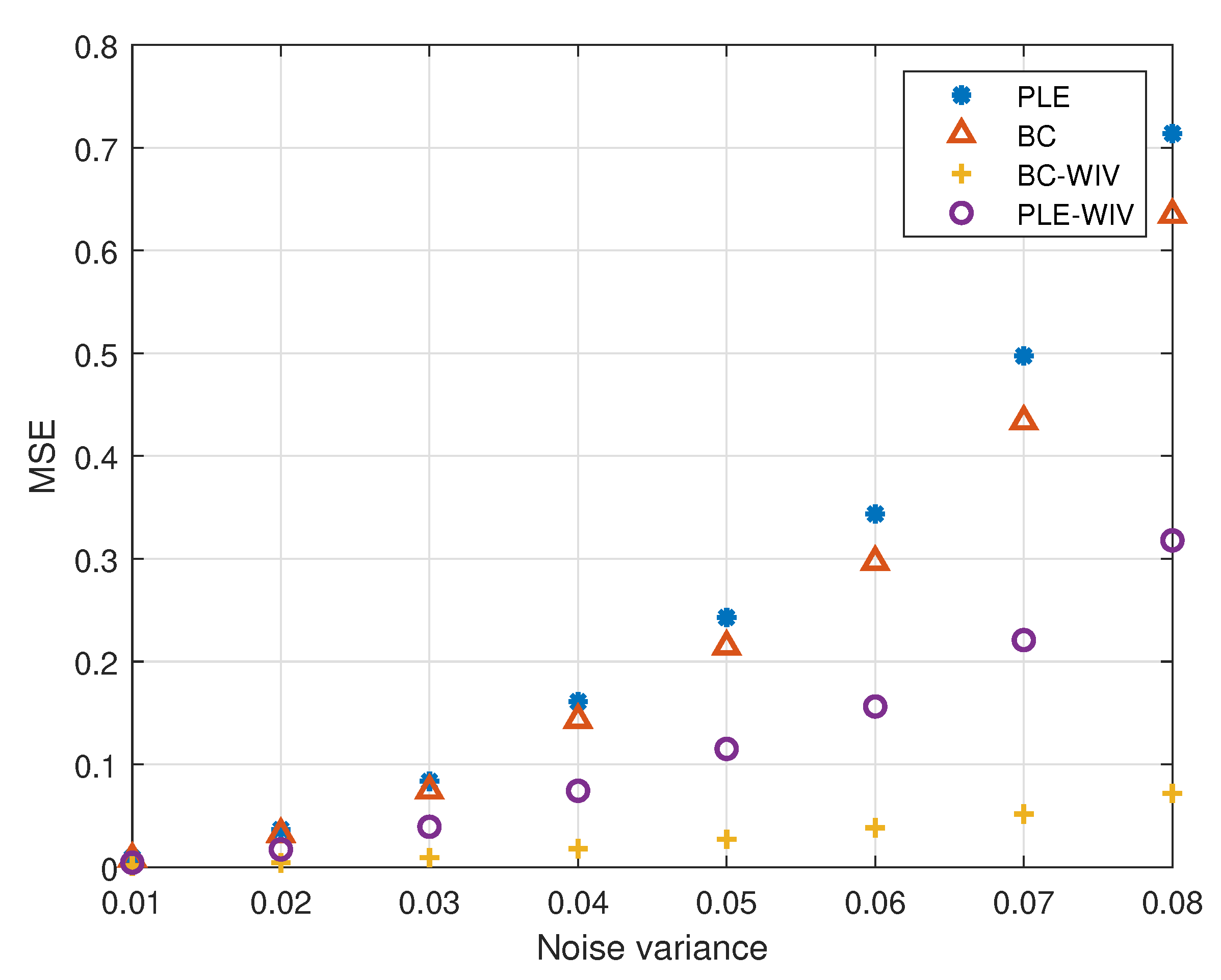
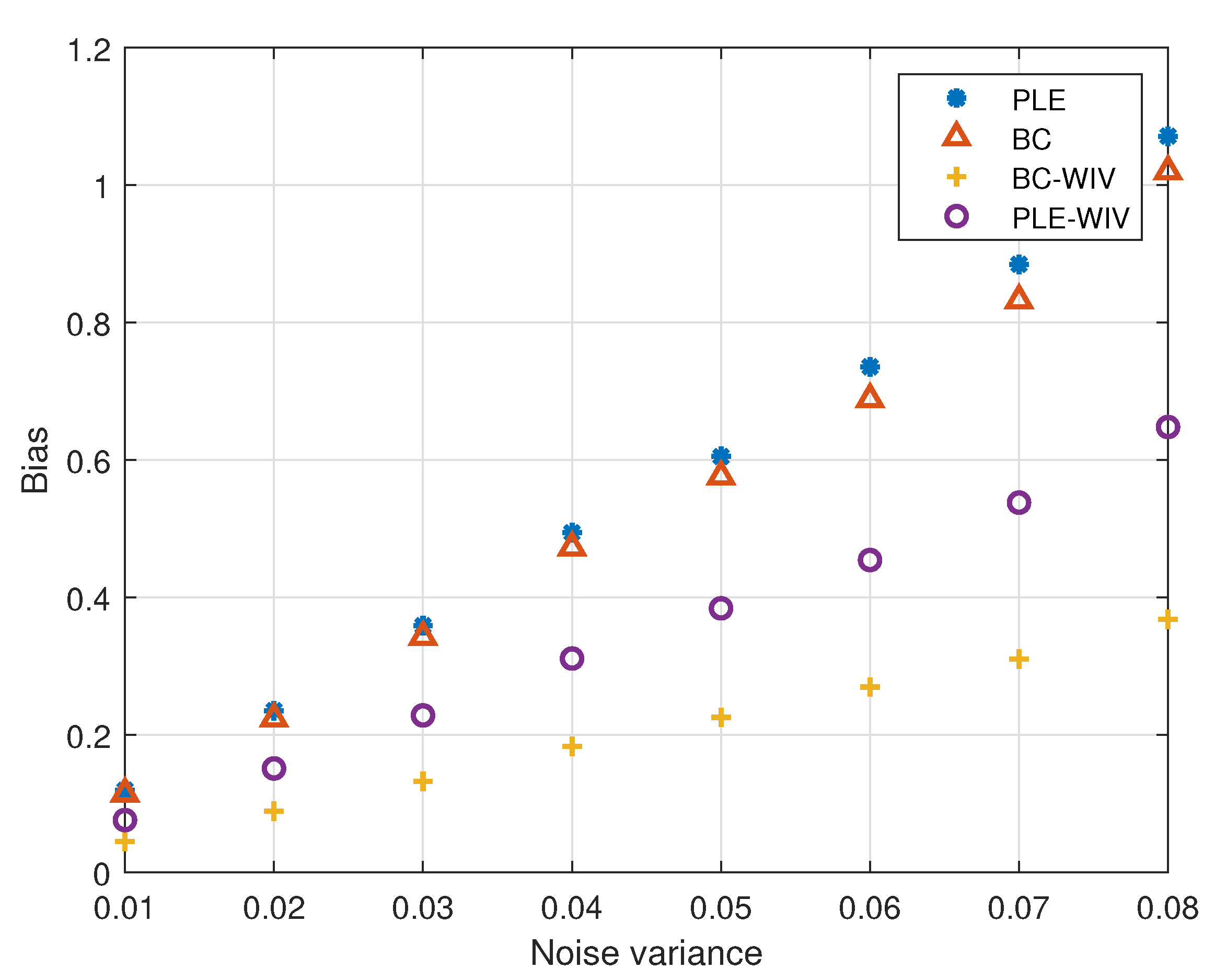
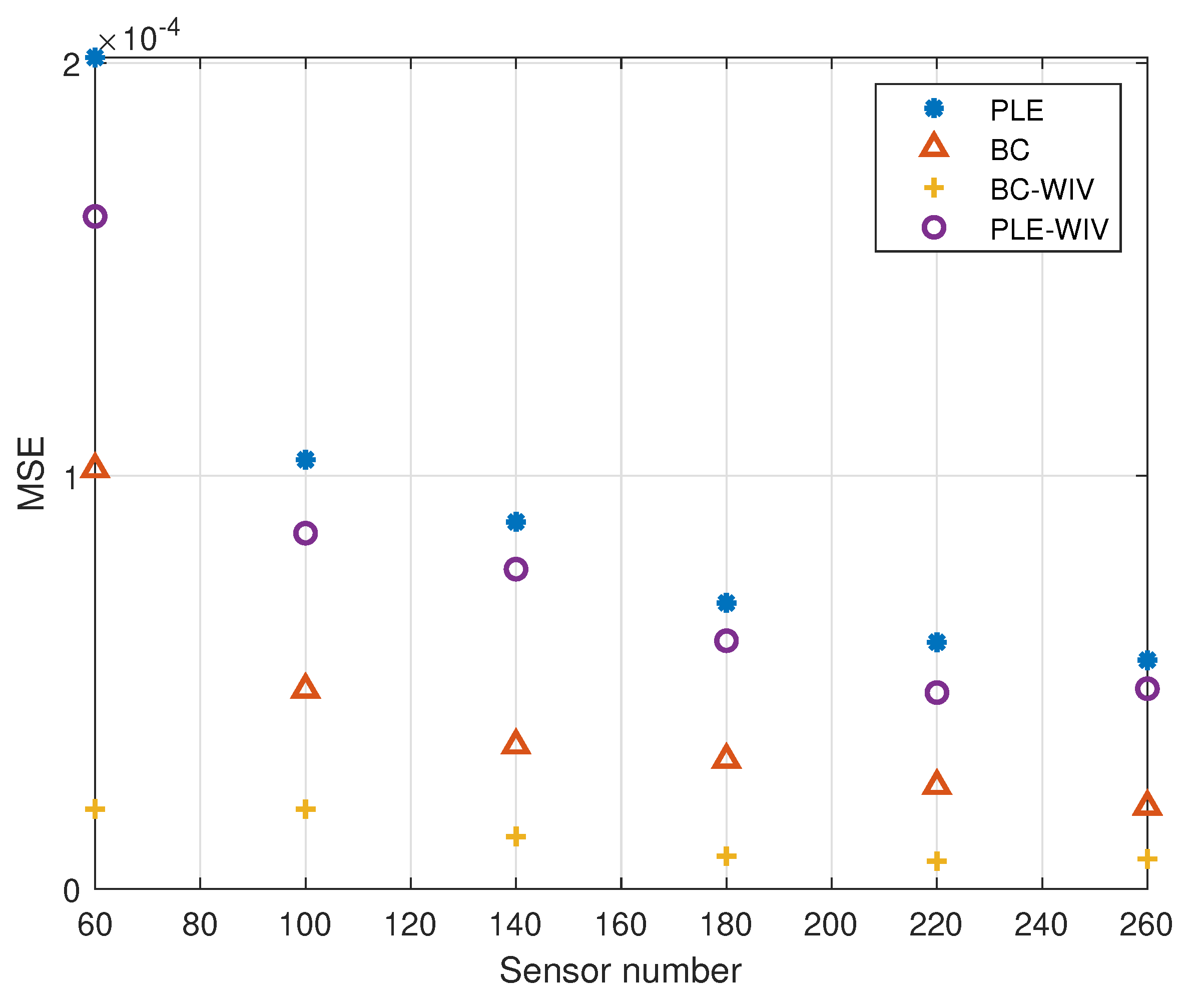
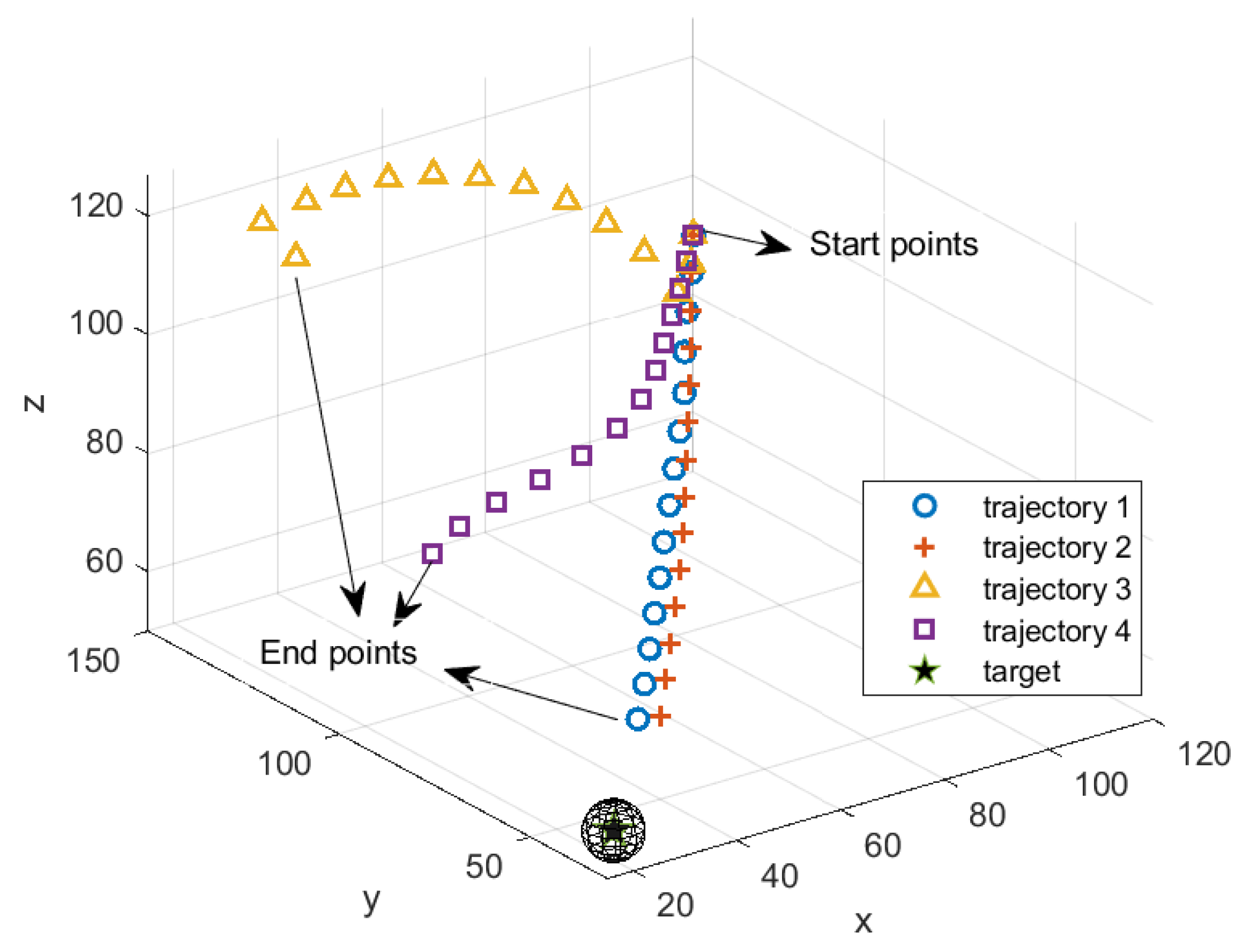
5. Simulation
5.1. Example 1
5.2. Example 2
6. Conclusions and Future Works
7. Patents
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FIM | Fisher information matrix |
| AOA | Angle of arrival |
| 2D | Two dimensional |
| 3D | Three dimensional |
| MSE | Mean square error |
| IV | Instrumental variable |
| CRLB | Cramér-Rao lower bound |
| UAV | Unmanned aerial vehicle |
| BC | Bias compensation |
| BC-WIV | Bias compensation weighted instrumental variable |
| PLE | Pseudo-linear estimator |
References
- Jatoi, M.A.; Kamel, N.; Malik, A.S.; Faye, I.; Begum, T. A survey of methods used for source localization using EEG signals-ScienceDirect. Biomed. Signal Process. Control 2014, 11, 42–52. [Google Scholar] [CrossRef]
- Dogançay, K. UAV Path Planning for Passive Emitter Localization. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 1150–1166. [Google Scholar] [CrossRef]
- Anup, P.; Takuro, S. Localization in Wireless Sensor Networks: A Survey on Algorithms, Measurement Techniques, Applications and Challenges. J. Sens. Actuator Netw. 2017, 6, 24. [Google Scholar]
- Bishop, A.N.; Fidan, B.; Anderson, B.D.; Doğançay, K.; Pathirana, P.N. Optimality analysis of sensor-target localization geometries. Automatica 2010, 46, 479–492. [Google Scholar] [CrossRef]
- Kim, Y.; Bang, H. Introduction to Kalman Filter and Its Applications. Introd. Implement. Kalman Filter 2018, 1, 1–16. [Google Scholar]
- Aidala, V.J. Kalman Filter Behavior in Bearings-Only Tracking Applications. IEEE Trans. Aerosp. Electron. Syst. 2007, 15, 29–39. [Google Scholar] [CrossRef]
- Aidala, V.; Hammel, S. Utilization of modified polar coordinates for bearings-only tracking. IEEE Trans. Autom. Control 1983, 28, 283–294. [Google Scholar] [CrossRef] [Green Version]
- Zhan, R.; Wan, J. Iterated Unscented Kalman Filter for Passive Target Tracking. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 1155–1163. [Google Scholar] [CrossRef]
- Nguyen, N.H.; Dogançay, K. 3D AOA Target Tracking with Two-step Instrumental-variable Kalman Filtering. In Proceedings of the ICASSP 2019—2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) IEEE, Brighton, UK, 12–17 May 2019; pp. 4390–4394. [Google Scholar]
- Dogançay, K.; Ibal, G. Instrumental Variable Estimator for 3D Bearings-Only Emitter Localization. In Proceedings of the 2005 International Conference on Intelligent Sensors, Sensor Networks and Information Processing, Melbourne, Australia, 5–8 December 2005; pp. 63–68. [Google Scholar]
- Nardone, S.C.; Lindgren, A.G.; Gong, K.F. Fundamental properties and performance of conventional bearings-only target motion analysis. IEEE Trans. Autom. Control 1984, 29, 775–787. [Google Scholar] [CrossRef]
- Badriasl, L.; Dogançay, K. Three-dimensional target motion analysis using azimuth/elevation angles. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 3178–3194. [Google Scholar] [CrossRef]
- Dogançay, K. Bias compensation for the bearings-only pseudolinear target track estimator. IEEE Trans. Signal Process. 2005, 54, 59–68. [Google Scholar] [CrossRef]
- Dogançay, K. 3D Pseudolinear Target Motion Analysis From Angle Measurements. IEEE Trans. Signal Process. 2015, 63, 1. [Google Scholar] [CrossRef]
- Adib, N.; Douglas, S.C. Extending the Stansfield Algorithm to Three Dimensions: Algorithms and Implementations. IEEE Trans. Signal Process. 2018, 66, 1106–1117. [Google Scholar] [CrossRef]
- Zhao, S.; Chen, B.M.; Lee, T.H. Optimal sensor placement for target localization and tracking in 2D and 3D. Int. J. Control 2015, 86, 1687–1704. [Google Scholar] [CrossRef]
- He, S.; Shin, H.S.; Tsourdos, A. Trajectory Optimization for Target Localization With Bearing-Only Measurement. IEEE Trans. Robot. 2019, 35, 653–668. [Google Scholar] [CrossRef] [Green Version]
- Dogançay, K.; Hmam, H. Optimal angular sensor separation for AOA localization. Signal Process. 2008, 88, 1248–1260. [Google Scholar] [CrossRef]
- Xu, S.; Dogançay, K. Optimal Sensor Placement for 3-D Angle-of-Arrival Target Localization. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 1196–1211. [Google Scholar] [CrossRef]
- Oshman, Y.; Davidson, P. Optimization of observer trajectories for bearings-only target localization. IEEE Trans. Aerosp. Electron. Syst. 1999, 35, 892–902. [Google Scholar] [CrossRef]
- Sheng, X.; Dogançay, K. Optimal sensor deployment for 3D AOA target localization. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), South Brisbane, Australia, 19–24 April 2015; pp. 2544–2548. [Google Scholar]
- Sheng, X.; Dogançay, K.; Hmam, H. 3D pseudolinear Kalman filter with own-ship path optimization for AOA target tracking. In Proceedings of the 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20–25 March 2016; pp. 3136–3140. [Google Scholar]
- Xu, S.; Dogançay, K.; Hmam, H. Distributed pseudolinear estimation and UAV path optimization for 3D AOA target tracking. Signal Process. 2017, 133, 64–78. [Google Scholar] [CrossRef]
- Nguyen, N.H.; Dogançay, K. Single-platform passive emitter localization with bearing and Doppler-shift measurements using pseudolinear estimation techniques. Signal Process. 2016, 125, 336–348. [Google Scholar] [CrossRef]
- Logothetis, A.; Isaksson, A.; Evans, R.J. Comparison of suboptimal strategies for optimal own-ship maneuvers in bearings-only tracking. In Proceedings of the 1998 American Control Conference, Philadelphia, PA, USA, 26 June 1998; Volume 6, pp. 3334–3338. [Google Scholar]
- Gavish, M.; Weiss, A.J. Performance analysis of bearing-only target location algorithms. IEEE Trans. Aerosp. Electron. Syst. 1992, 28, 817–828. [Google Scholar] [CrossRef]
- Dogançay, K. Bearings-only target localization using total least squares. Signal Process. 2005, 85, 1695–1710. [Google Scholar] [CrossRef]
- Bai, E. Parameter convergence in source localization. In Proceedings of the 2016 IEEE Conference on Control Applications (CCA), Buenos Aires, Argentina, 19–22 September 2016; pp. 929–933. [Google Scholar]
- Zhou, K. Roumeliotis S. Multirobot Active Target Tracking With Combinations of Relative Observations. IEEE Trans. Robot. 2011, 27, 678–695. [Google Scholar] [CrossRef]
- Bu, S.; Meng, A.; Zhou, G. A New Pseudolinear Filter for Bearings-Only Tracking without Requirement of Bias Compensation. Sensors 2021, 21, 5444. [Google Scholar] [CrossRef]
- Pillonetto, G.; Dinuzzo, F.; Chen, T.; De Nicolao, G.; Ljung, L. Kernel methods in system identification, machine learning and function estimation: A survey. Automatica 2014, 50, 657–682. [Google Scholar] [CrossRef] [Green Version]


| Observation Point | |||
|---|---|---|---|
| k = 10 | 98/100 | 96/100 | 3/100 |
| k = 15 | 99/100 | 96/100 | 2/100 |
| Trajectory 1 | Trajectory 2 | Trajectory 3 | Trajectory 4 | |
|---|---|---|---|---|
| mean of | 91.16 | 90.58 | 89.62 | 90.49 |
| mean of | 93.42 | 92.86 | 88.85 | 90.99 |
| Trajectory 1 | Trajectory 2 | Trajectory 3 | Trajectory 4 | |
|---|---|---|---|---|
| runtime(s) | 0.5558 | 0.5240 | 0.6996 | 0.5899 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, Y.; Gao, B.; Tang, X.; Yu, L. Target Localization and Sensor Movement Trajectory Planning with Bearing-Only Measurements in Three Dimensional Space. Appl. Sci. 2022, 12, 6739. https://doi.org/10.3390/app12136739
Zou Y, Gao B, Tang X, Yu L. Target Localization and Sensor Movement Trajectory Planning with Bearing-Only Measurements in Three Dimensional Space. Applied Sciences. 2022; 12(13):6739. https://doi.org/10.3390/app12136739
Chicago/Turabian StyleZou, Yiqun, Bilu Gao, Xiafei Tang, and Lingli Yu. 2022. "Target Localization and Sensor Movement Trajectory Planning with Bearing-Only Measurements in Three Dimensional Space" Applied Sciences 12, no. 13: 6739. https://doi.org/10.3390/app12136739
APA StyleZou, Y., Gao, B., Tang, X., & Yu, L. (2022). Target Localization and Sensor Movement Trajectory Planning with Bearing-Only Measurements in Three Dimensional Space. Applied Sciences, 12(13), 6739. https://doi.org/10.3390/app12136739






