Analysis of the Mode Shapes of Kaplan Runners
Abstract
:1. Introduction
2. Numerical and Experimental Modal Analysis
- ωr is the natural frequency of the corresponding vibration mode.
- θr is the damping factor of the structure.
- {θ}r is the vibration mode shape that dominates the structure near a resonance condition (ωexcitation = ωr).
- Qr is the scaling factor, which is a constant value for each mode shape.
- Receptance function: relation between the displacement and the excitation force.
- Mobility function: relation between the velocity and the excitation force.
- Inertance function: relation between the acceleration and the excitation force.
3. Natural Frequencies and Mode Shapes of Simplified Structures
3.1. Modal Characteristics of a Disk-like Structure
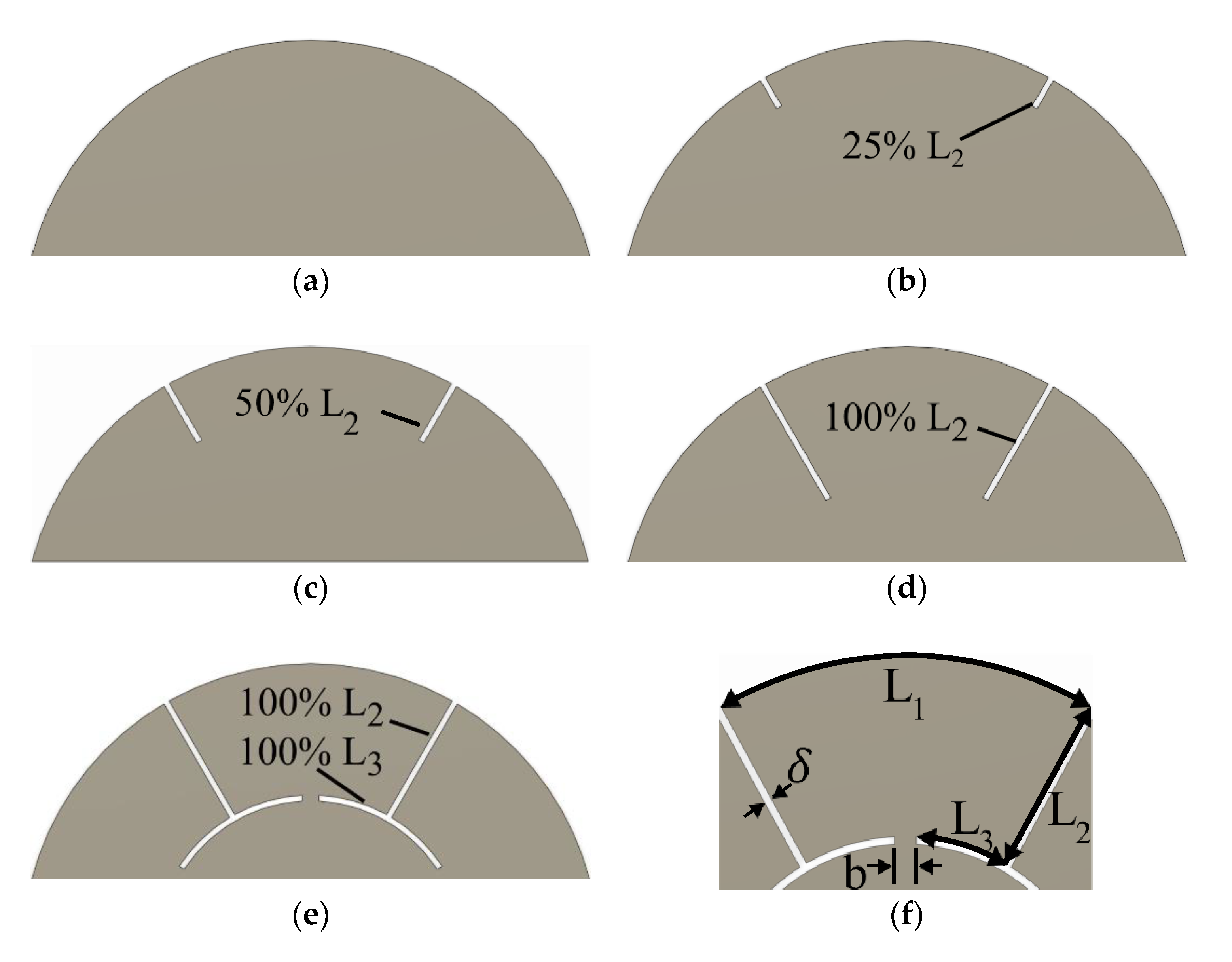
3.2. Transition from a Disk to a Bladed Structure
3.3. Influence of the Blade Number on the Mode Shapes
3.3.1. Mode Shapes Due to the Clamping
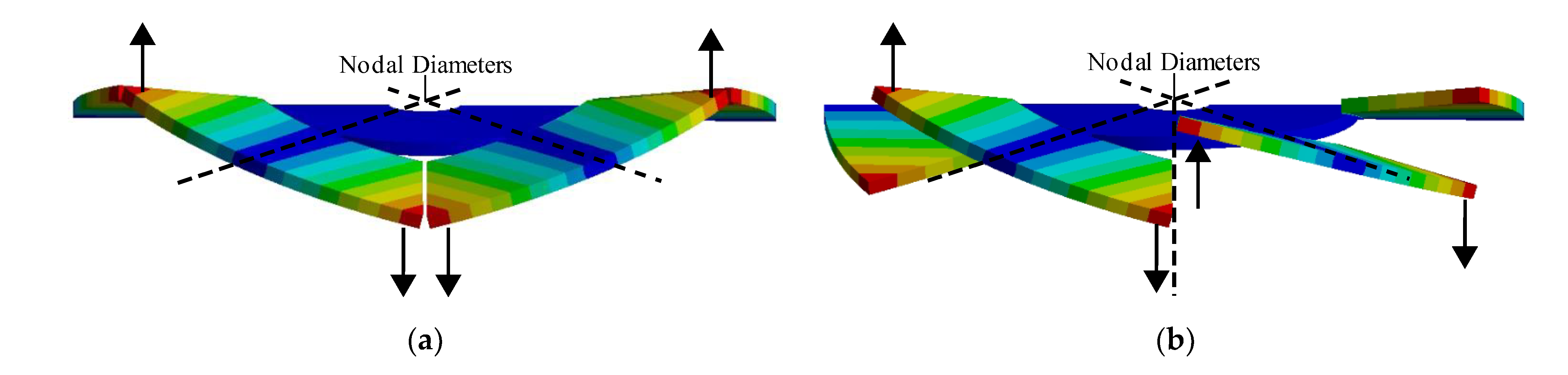
3.3.2. Diametrical Mode Shapes of Bladed Disks
3.3.3. Circular Mode Shapes of Bladed Disks
3.4. Mode Shapes Classification
4. Modal Characteristics of a Kaplan Runner
Runner Mode Shapes and their Classifications
5. Experimental Modal Analysis of a Kaplan Runner
5.1. Instrumentation
5.2. Runner Mode Shapes
5.3. Local Mode Shapes
5.4. Variation of Stiffness
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Detailed Geometries of Bladed Disk and Its Transitions
| Z | Transition 1 | Transition 2 | Transition 3 | Final Model |
|---|---|---|---|---|
| 4 |  |  |  |  |
| 5 |  |  |  |  |
| 6 |  |  |  |  |
| 7 |  |  |  |  |
Appendix B. Mode (1,0), (2,0) and (3,0) for All Transition Geometries and Bladed Disks
| Z | Transition 1 | Transition 2 | Transition 3 | Final Model |
|---|---|---|---|---|
| 4 | 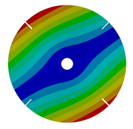 | 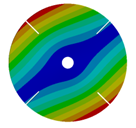 |  | 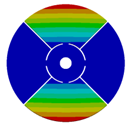 |
| 167.55 | 166.92 | 150.75 | 104.52 | |
| 5 | 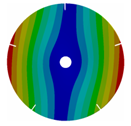 | 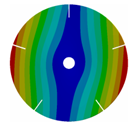 | 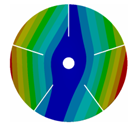 | 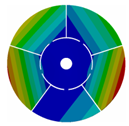 |
| 167.47 | 167.36 | 158.63 | 118.19 | |
| 6 |  | 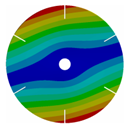 |  | 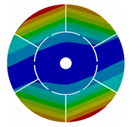 |
| 167.57 | 167.43 | 162.73 | 133.65 | |
| 7 | 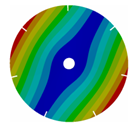 | 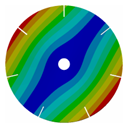 | 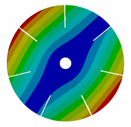 | 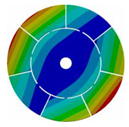 |
| 167.62 | 167.66 | 164.79 | 145.46 |
| Z | Transition 1 | Transition 2 | Transition 3 | Final Model |
|---|---|---|---|---|
| 4 | 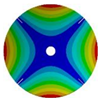 | 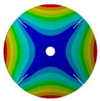 |  |  |
| 264.98 Hz | 245.03 Hz | 152.50 Hz | 101.26 Hz | |
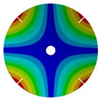 | 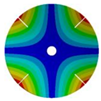 |  | 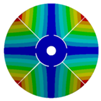 | |
| 266.55 Hz | 254.25 Hz | 216.49 Hz | 144.87 Hz | |
| 5 | 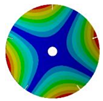 | 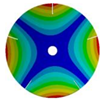 | 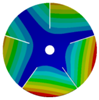 | 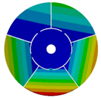 |
| 268.07 Hz | 257.62 Hz | 188.58 Hz | 120.32 Hz | |
 |  | 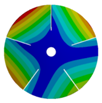 | 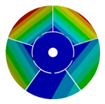 | |
| 268.07 Hz | 257.62 Hz | 188.59 Hz | 120.31 Hz | |
| 6 | 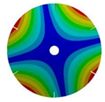 |  | 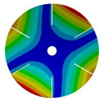 |  |
| 267.42 Hz | 254.97 Hz | 208.35 Hz | 143.41 Hz | |
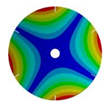 | 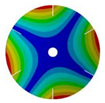 | 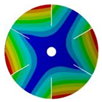 | 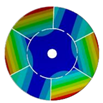 | |
| 267.42 Hz | 254.97 Hz | 208.35 Hz | 143.41 Hz | |
| 7 | 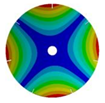 |  |  | 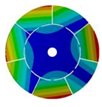 |
| 268.08 Hz | 257.89 Hz | 220.39 Hz | 163.58 Hz | |
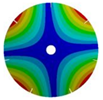 |  | 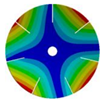 | 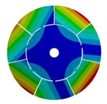 | |
| 268.08 Hz | 257.90 Hz | 220.38 Hz | 163.58 Hz |
| Z | Transition 1 | Transition 2 | Transition 3 | Final Model |
|---|---|---|---|---|
| 4 | 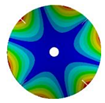 | 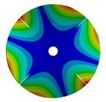 |  | 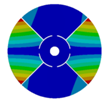 |
| 576.89 Hz | 507.55 Hz | 283.68 | 154.12 Hz | |
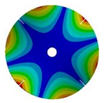 | 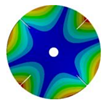 | 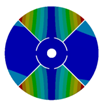 | 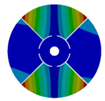 | |
| 577.27 Hz | 510.25 Hz | 283.67 Hz | 154.13 Hz | |
| 5 |  | 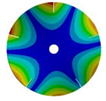 | 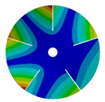 | 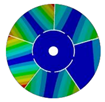 |
| 586.92 Hz | 541.60 Hz | 336.81 Hz | 177.91 Hz | |
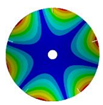 |  | 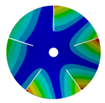 | 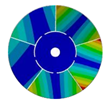 | |
| 586.93 Hz | 541.60 Hz | 336.80 Hz | 177.91 Hz | |
| 6 | 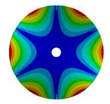 | 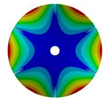 | 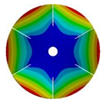 | 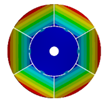 |
| 583.52 Hz | 520.45 Hz | 313.76 Hz | 163.84 Hz | |
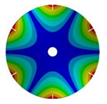 | 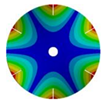 |  | 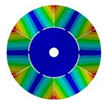 | |
| 583.99 Hz | 539.40 Hz | 430.09 Hz | 224.71 Hz | |
| 7 | 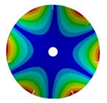 | 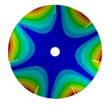 | 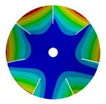 | 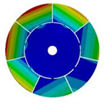 |
| 586.53 Hz | 541.55 Hz | 382.78 Hz | 206.30 Hz | |
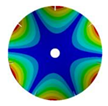 | 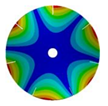 |  |  | |
| 586.53 Hz | 541.54 Hz | 382.78 Hz | 206.31 Hz |
References
- IEA. Global Energy Review 2021; IEA: Paris, France, 2021; Available online: https://www.iea.org/reports/global-energy-review-2021 (accessed on 26 June 2022).
- IRENA. Renewable Energy Statistics 2021; The International Renewable Energy Agency: Abu Dhabí, United Arab Emirates, 2021. [Google Scholar]
- Deschênes, C.; Fraser, R.; Fau, J.-P. New trends in turbine modelling and new ways of partnership. In Proceedings of the International Group of Hydraulic Efficiency Measurement (IGHEM), Toronto, ON, Canada, 17–19 July 2002; pp. 1–12. [Google Scholar]
- Valentín, D.; Presas, A.; Valero, C.; Egusquiza, M.; Egusquiza, E. Detection of Hydraulic Phenomena in FrancisTurbines with Different Sensors. Sensors 2019, 19, 4053. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Egusquiza, E.; Valero, C.; Valentin, D.; Presas, A.; Rodriguez, C.G. Condition monitoring of pump-turbines. New challenges. Meas. J. Int. Meas. Confed. 2015, 67, 151–163. [Google Scholar] [CrossRef] [Green Version]
- Valero, C.; Egusquiza, M.; Egusquiza, E.; Presas, A.; Valentin, D.; Bossio, M. Extension of Operating Range in Pump-Turbines. Influence of Head and Load. Energies 2017, 10, 2178. [Google Scholar] [CrossRef] [Green Version]
- Trivedi, C.; Gandhi, B.; Cervantes, M. Effect of transients on Francis turbine runner life: A review. J. Hydraul. Res. 2013, 51. [Google Scholar] [CrossRef]
- Zhang, M.; Valentín, D.; Valero, C.; Egusquiza, M.; Egusquiza, E. Failure investigation of a Kaplan turbine blade. Eng. Fail. Anal. 2019, 97, 690–700. [Google Scholar] [CrossRef]
- Luo, Y.; Wang, Z.; Zeng, J.; Lin, J. Fatigue of piston rod caused by unsteady, unbalanced, unsynchronized blade torques in a Kaplan turbine. Eng. Fail. Anal. 2010, 17, 192–199. [Google Scholar] [CrossRef]
- Wang, Z.W.; Luo, Y.Y.; Zhou, L.J.; Xiao, R.F.; Peng, G.J. Computation of dynamic stresses in piston rods caused by unsteady hydraulic loads. Eng. Fail. Anal. 2008, 15, 28–37. [Google Scholar] [CrossRef]
- Liang, Q.W.; Rodríguez, C.G.; Egusquiza, E.; Escaler, X.; Avellan, F. Numerical Modal Analysis on a Francis Turbine Runner With Finite Element Method Considering Added Mass Effect. 2005. Available online: https://www.semanticscholar.org/paper/1-Numerical-modal-analysis-on-a-Francis-turbine-Liang-Rodr%C3%ADguez/69fe05340c0ed131fbeb83236ffe56f5633a6154 (accessed on 26 June 2022).
- Rodriguez, C.G.; Egusquiza, E.; Escaler, X.; Liang, Q.W.; Avellan, F. Experimental investigation of added mass effects on a Francis turbine runner in still water. J. Fluids Struct. 2006, 22, 699–712. [Google Scholar] [CrossRef]
- Singhal, R.K.; Guan, W.; Williams, K. Modal analysis of a thick-walled circular cylinder. Mech. Syst. Signal Process. 2002, 16, 141–153. [Google Scholar] [CrossRef]
- Huang, X.X.; Egusquiza, E.; Valero, C.; Presas, A. Dynamic behaviour of pump-turbine runner: From disk to prototype runner. IOP Conf. Ser. Mater. Sci. Eng. 2013, 52, TOPIC 2. [Google Scholar] [CrossRef]
- Presas, A.; Valentin, D.; Egusquiza, E.; Valero, C.; Seidel, U. On the detection of natural frequencies and mode shapes of submerged rotating disk-like structures from the casing. Mech. Syst. Signal Process. 2015, 60, 547–570. [Google Scholar] [CrossRef] [Green Version]
- Valentin, D.; Presas, A.; Egusquiza, E. Influence of Non-Rigid Sufaces on the Dynamic Response of a Submerged and Confined Disk. In Proceedings of the 6th IAHR International Meeting of the Workgroup on Cavitation and Dynamic Problems in Hydraulic Machinery and Systems, Ljubljana, Slovenia, 9–11 September 2015. [Google Scholar]
- Louyot, M.; Nennemann, B.; Monette, C.; Gosselin, F.P. Modal analysis of a spinning disk in a dense fluid as a model for high head hydraulic turbines. J. Fluids Struct. 2019, 94, 102965. [Google Scholar] [CrossRef] [Green Version]
- Muhsen, A.A.; Al-Malik, A.A.R.; Attiya, B.H.; Al-Hardanee, O.F.; Abdalazize, K.A. Modal analysis of Kaplan turbine in Haditha hydropower plant using ANSYS and SolidWorks. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1105, 012056. [Google Scholar] [CrossRef]
- Vialle, J.-P.; Lowys, P.-Y.; Dompierre, F.; Sabourin, M. Prediction of natural frequencies in water-Application to a Kaplan runner. In Proceedings of the HydroVision 2008, Sacremento, CA, USA, 14–18 July 2008; p. 252. [Google Scholar]
- Zhang, M.; Chen, Q.G. Numerical Model on the Dynamic Behavior of a Prototype Kaplan Turbine Runner. Math. Probl. Eng. 2021, 2021, 4421340. [Google Scholar] [CrossRef]
- Zhang, M. On the Changes in Dynamic Behavior Produced by the Hydraulic Turbine Runner Damage. Tesi Doctoral, UPC, Departament de Mecànica de Fluids, Barcelona. 2019. Available online: http://hdl.handle.net/2117/166975 (accessed on 26 June 2022).
- Cao, J.; Luo, Y.; Presas, A.; Ahn, S.H.; Wang, Z.; Huang, X.; Liu, Y. Influence of rotation on the modal characteristics of a bulb turbine unit rotor. Renew. Energy 2022, 187, 887–895. [Google Scholar] [CrossRef]
- Modal Analysis Theory. In Noise and Vibration Analysis; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2011; pp. 119–146. [CrossRef]
- Heylen, W.; Lammens, S.; Sas, P. Modal Analysis Theory and Testing; Katholieke Universiteit Leuven: Leuven, Belgium, 2007. [Google Scholar]
- Southwell, R.V. On the Free Transverse Vibrations of a Uniform Circular Disc Clamped at Its Centre; and on the Effects of Rotation. Proc. R. Soc. London. Ser. A Contain. Pap. A Math. Phys. Character 1922, 101, 133–153. [Google Scholar]
- Leissa, A.W. Vibration of Plates; Scientific and Technical Information Division, National Aeronautics and Space Administration: Washington, DC, USA, 1969. [Google Scholar]
- Braun, S.; Diego, S.; Francisco, S.; York, N.; London, B.; Tokyo, S. Encyclopedia of Vibration; Academic Press: Cambridge, MA, USA, 2001. [Google Scholar] [CrossRef]
- Presas, A.; Valentin, D.; Valero, C.; Egusquiza, M.; Egusquiza, E. Experimental measurements of the natural frequencies and mode shapes of rotating disk-blades-disk assemblies from the stationary frame. Appl. Sci. 2019, 9, 3864. [Google Scholar] [CrossRef] [Green Version]
- Berger, S.; Aubry, E.; Marquet, F.; Thomann, G. Experimental Modal Shape Identification Of A Rotating Asymmetric Disk Subjected To Multiple-Frequency Excitatoin: Use Of Finite Impulse Response (FIR) Filters. Soc. Exp. Mech. 2003, 27, 44–48. [Google Scholar] [CrossRef]
- Oldac, O.; Tufekci, M.; Genel, O.E.; Tufekci, E. Free Bending Vibrations of Rotating Disks With A Concentric Hole. Int. J. Technol. Eng. Stud. 2017, 3, 253–263. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, Y.; Jiang, B. A Study on Mode Shape and Natural Frequency of Rotating Flexible Cracked Annular Thin Disk. Shock Vibrat. 2021, 2021, 6533487. [Google Scholar] [CrossRef]
- Blevins, R.D. Formulas for Natural Frequency and Mode Shape/Robert D. Blevins; Van Nostrand Reinhold Co.: New York, NY, USA, 1979. [Google Scholar]



| D | 0 | 1 | 2 | 3 | … | m | |
|---|---|---|---|---|---|---|---|
| C | |||||||
| 0 |  | 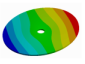 | 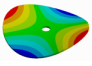 | 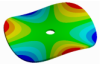 | … | (m, 0) | |
| 1 | 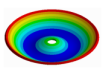 |  | 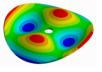 | 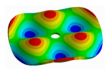 | … | (m, 1) | |
| n | (0, n) | (1, n) | (2, n) | (3, n) | … | (m, n) | |
| Disk | Transition 1 | Transition 2 | Transition 3 | Final Model |
|---|---|---|---|---|
 |  |  |  |  |
| Disk | Z = 4 | Z = 5 | Z = 6 | Z = 7 |
|---|---|---|---|---|
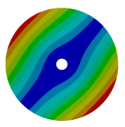 | 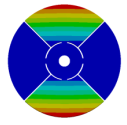 | 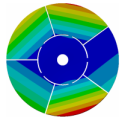 | 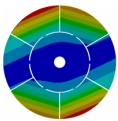 | 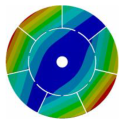 |
| 167.00 | 104.52 | 118.19 | 133.65 | 145.46 |
| Disk | Z = 4 | Z = 5 | Z = 6 | Z = 7 |
|---|---|---|---|---|
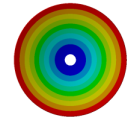 | 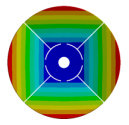 |  | 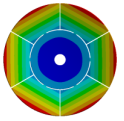 |  |
| 205.64 | 107.81 | 123.72 | 144.19 | 160.87 |
| Disk | Transition 1 | Transition 2 | Transition 3 | Bladed Disk |
|---|---|---|---|---|
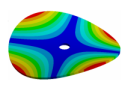 | 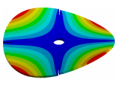 | 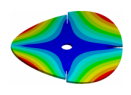 | 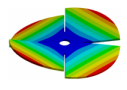 |  |
| 270.9 Hz | 264.98 Hz | 245.03 Hz | 152.5 Hz | 101.26 Hz |
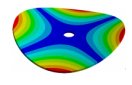 | 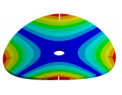 | 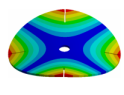 | 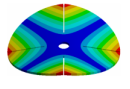 | 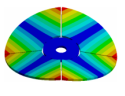 |
| 270.9 Hz | 266.55 Hz | 254.25 Hz | 216.49 Hz | 144.87 Hz |
| Disk | Transition 1 | Transition 2 | Transition 3 | Bladed Disk |
|---|---|---|---|---|
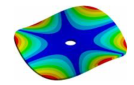 |  | 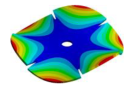 |  | 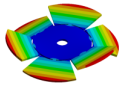 |
| 600.80 Hz | 583.52 Hz | 520.45 Hz | 313.16 | 162.84 Hz |
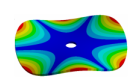 | 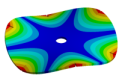 | 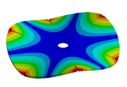 | 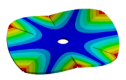 |  |
| 600.80 Hz | 583.99 Hz | 539.40 Hz | 430.09 Hz | 224.71 Hz |
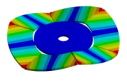
| Disk | Transition 1 | Transition 2 | Transition 3 | Bladed Disk |
|---|---|---|---|---|
 | 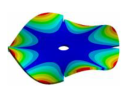 | 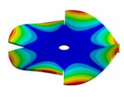 | 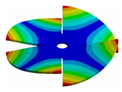 | 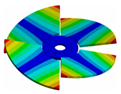 |
| 1050.00 Hz | 985.55 Hz | 778.21 Hz | 335.10 Hz | 160.50 Hz |
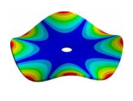 | 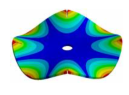 | 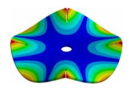 | 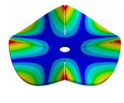 |  |
| 1050.00 Hz | 995.04 Hz | 896.11 Hz | 747.68 Hz | 652.96 Hz |
| Disk | Transition 1 | Transition 2 | Transition 3 | Bladed Disk |
|---|---|---|---|---|
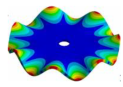 | 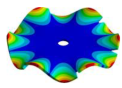 | 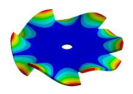 | 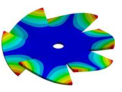 | 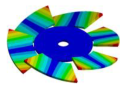 |
| 2259.10 Hz | 2099.6 Hz | 1572.40 Hz | 772.65 Hz | 254.37 Hz |
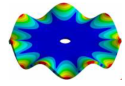 | 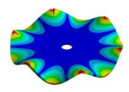 | 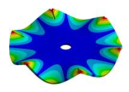 | 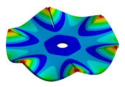 |  |
| 2259.10 Hz | 2131.30 Hz | 1913.30 Hz | 1694.40 Hz | 1447.6 Hz |
| Disk | Transition 1 | Transition 2 | Transition 3 | Bladed Disk |
|---|---|---|---|---|
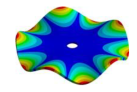 | 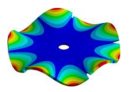 | 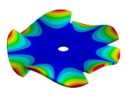 |  | 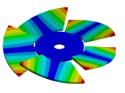 |
| 1604.30 Hz | 1532.00 Hz | 1261.80 Hz | 524.68 Hz | 200.53 Hz |
 | 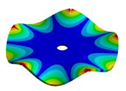 |  | 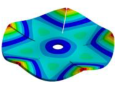 | 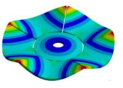 |
| 1604.30 | 1540.70 Hz | 1421.50 Hz | 1315.60 Hz | 1185.30 Hz |
| Disk | Transition 1 | Transition 2 | Transition 3 | Bladed Disk |
|---|---|---|---|---|
 | 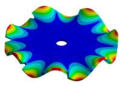 |  | 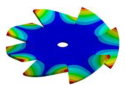 |  |
| 3010.90 Hz | 2797.8 Hz | 2107.70 Hz | 1060.60 Hz | 319.08 Hz |
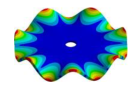 | 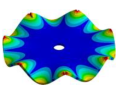 | 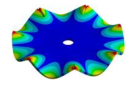 |  | 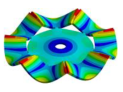 |
| 3010.90 Hz | 2840.2 Hz | 2545.90 Hz | 2207.40 Hz | 1748.70 Hz |
| Disk | Z = 4 | Z = 5 | Z = 6 | Z = 7 |
|---|---|---|---|---|
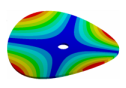 |  | 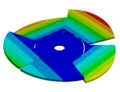 | 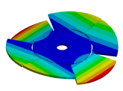 | 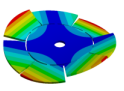 |
| 270.9 Hz | 101.26 Hz | 120.32 Hz | 143.41 Hz | 163.58 Hz |
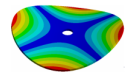 | 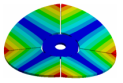 | 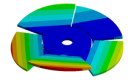 |  | 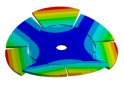 |
| 270.9 Hz | 144.78 Hz | 120.31 Hz | 143.41 Hz | 163.58 Hz |
| Disk | Z = 4 | Z = 5 | Z = 6 | Z = 7 |
|---|---|---|---|---|
 | 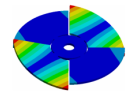 |  | 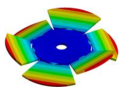 | 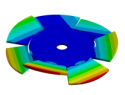 |
| 600.80 Hz | 154.13 Hz | 177.96 Hz | 163.84 Hz | 206.3 Hz |
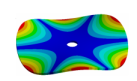 | 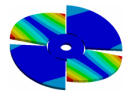 | 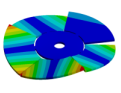 | 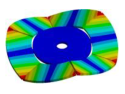 |  |
| 600.80 Hz | 154.12 Hz | 177.91 Hz | 224.71 Hz | 206.31 Hz |
| Disk | Z = 4 | Z = 5 | Z = 6 | Z = 7 |
|---|---|---|---|---|
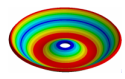 | 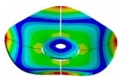 | 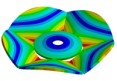 | 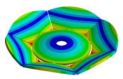 | 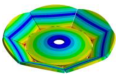 |
| 1212.10 Hz | 1073.90 Hz | 745.33 Hz | 724.85 Hz | 721.68 Hz |
| Mode | (2,0)1B | (2,0)1T | (4,0)1T | (4,0)2T |
|---|---|---|---|---|
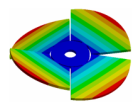 | 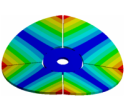 | 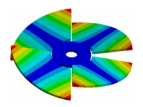 | 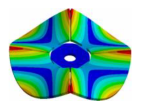 | |
| ND | 0 | 2 | 2 | 4 |
| cPD | 2 | 0 | 2 | 0 |
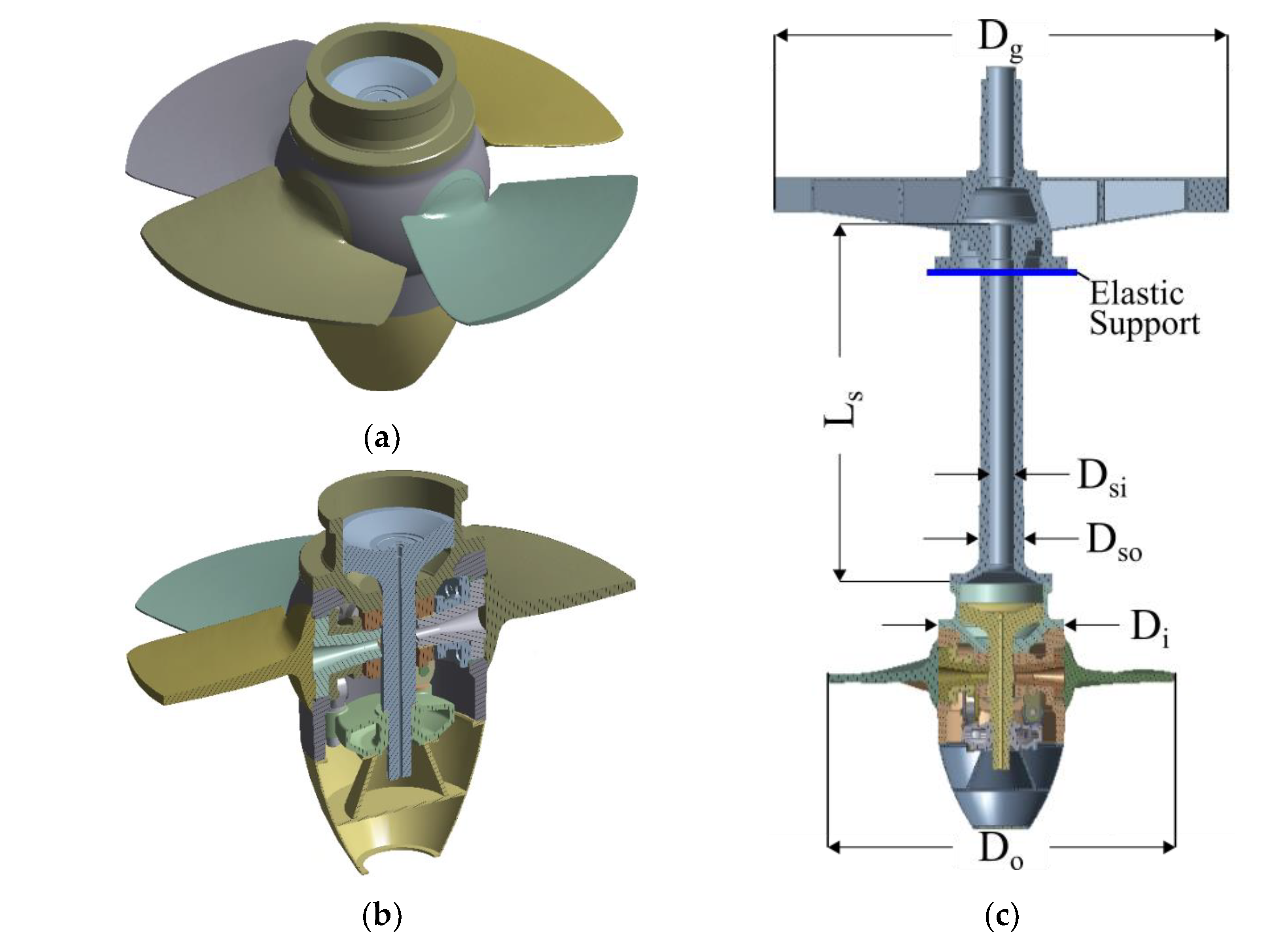
| Dimension | Symbol | Percentage of Do [%] |
|---|---|---|
| Runner Outer Diameter | Do | 100 |
| Runner Inner Diameter | Di | 42 |
| Shaft Outer Diameter | Dso | 12.38 |
| Shaft Inner Diameter | Dsi | 6.99 |
| Shaft Length | Ls | 96.18 |
| Generator Diameter | Dg | 131.15 |
| Shaft Dominated Mode shape | 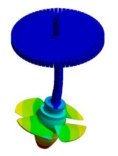 |  | |||
| 5.852 Hz | 22.138 Hz | ||||
| Generator Dominated Mode Shapes |  | 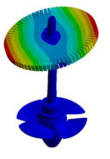 | 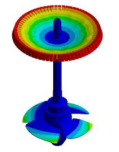 | 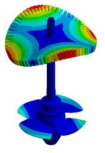 |  |
| 28.654 Hz | 28.785 Hz | 41.959 Hz | 44.135 Hz | 44.234 Hz | |
| Runner Dominated Mode Shapes |  | 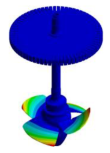 | 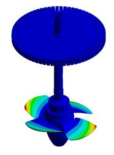 |  | 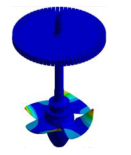 |
| 34.945 Hz | 38.443 Hz | 38.751 Hz | 44.298 Hz | 49.992 Hz | |
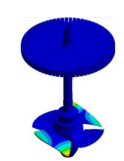 |  |  | 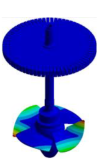 | ||
| 51.120 Hz | 51.269 Hz | 53.140 Hz | 53.444 Hz |
| Mode | Bladed Disk | Kaplan Runner | Mode | Bladed Disk | Kaplan Runner |
|---|---|---|---|---|---|
| (0,0)1B | 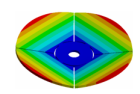 | 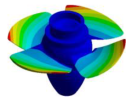 | (3,0)1T-1 | 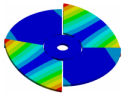 | 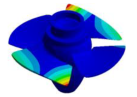 |
| (2,0)1B | 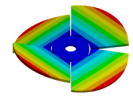 | 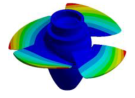 | (3,0)1T-2 | 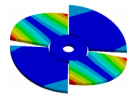 | 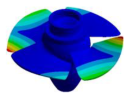 |
| (1,0)1B | - |  | (4,0)1T-1 | - | 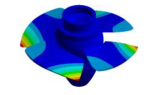 |
| (2,0)1T | 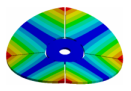 | 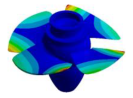 | (4,0)1T-2 | 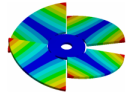 | 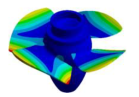 |
| (3,0)1T1B | - |  |
| Mode | FEM model | Real Runner | Mode | FEM Model | Real Runner |
|---|---|---|---|---|---|
| (0,0)1B | 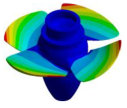 |  | (3,0)1T | Not extracted |  |
| 34.945 Hz | 39.375 Hz | 45.625 Hz | |||
| (2,0)1B | 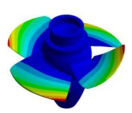 | 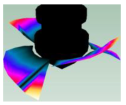 | (3,0)1T-1 | 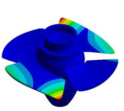 | Not Detected |
| 38.443 Hz | 36.625 Hz | 51.120 Hz | |||
| (1,0)1B | 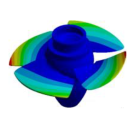 | Not Detected | (3,0)1T-2 | 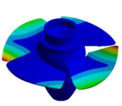 | Not Detected |
| 38.751 Hz | 53.444 Hz | ||||
| (2,0)1T | 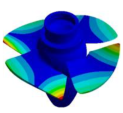 | 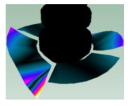 | (4,0)1T-1 |  | Not detected |
| 51.269 Hz | 49.625 Hz | 49.992 Hz | |||
| (3,0)1T1B | 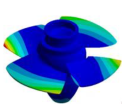 | Not Detected | (4,0)1T-2 | 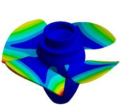 | 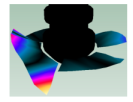 |
| 44.298 Hz | 53.140 Hz | 50.375 Hz |
| Mode | 1Tb1-1 | 1Tb1-2 | 2Tb1,2 | 2Tb1 |
|---|---|---|---|---|
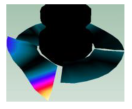 |  |  |  | |
| 54.125 Hz | 68.750 Hz | 87.625 Hz | 91.500 Hz |
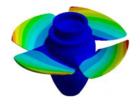 |  | 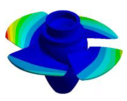 |  | 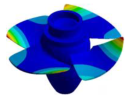 |
| 34.593 Hz | 37.977 Hz | 38.391 Hz | 43.913 Hz | 49.393 Hz |
 |  | 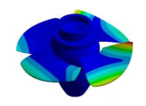 |  | |
| 50.498 Hz | 50.554 Hz | 52.438 Hz | 52.712 Hz |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moraga, G.; Egusquiza, M.; Valentín, D.; Valero, C.; Presas, A. Analysis of the Mode Shapes of Kaplan Runners. Appl. Sci. 2022, 12, 6708. https://doi.org/10.3390/app12136708
Moraga G, Egusquiza M, Valentín D, Valero C, Presas A. Analysis of the Mode Shapes of Kaplan Runners. Applied Sciences. 2022; 12(13):6708. https://doi.org/10.3390/app12136708
Chicago/Turabian StyleMoraga, Greco, Mònica Egusquiza, David Valentín, Carme Valero, and Alexandre Presas. 2022. "Analysis of the Mode Shapes of Kaplan Runners" Applied Sciences 12, no. 13: 6708. https://doi.org/10.3390/app12136708
APA StyleMoraga, G., Egusquiza, M., Valentín, D., Valero, C., & Presas, A. (2022). Analysis of the Mode Shapes of Kaplan Runners. Applied Sciences, 12(13), 6708. https://doi.org/10.3390/app12136708








