Modal Decomposition of the Precessing Vortex Core in a Hydro Turbine Model
Abstract
:1. Introduction
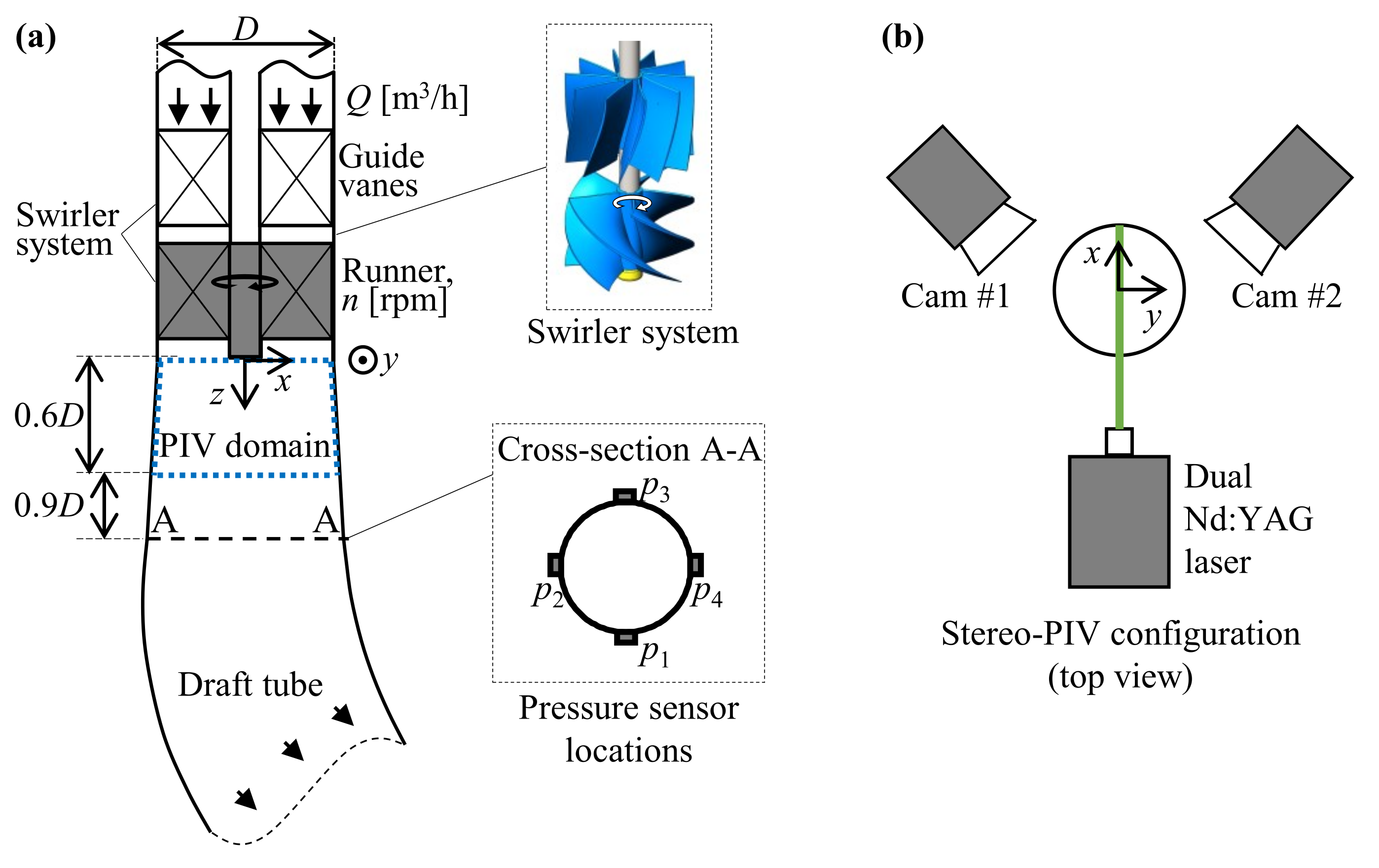
2. Experimental Set-Up and Measurements
2.1. Test Section
2.2. Wall Pressure Measurements
2.3. Stereo-PIV Measurements
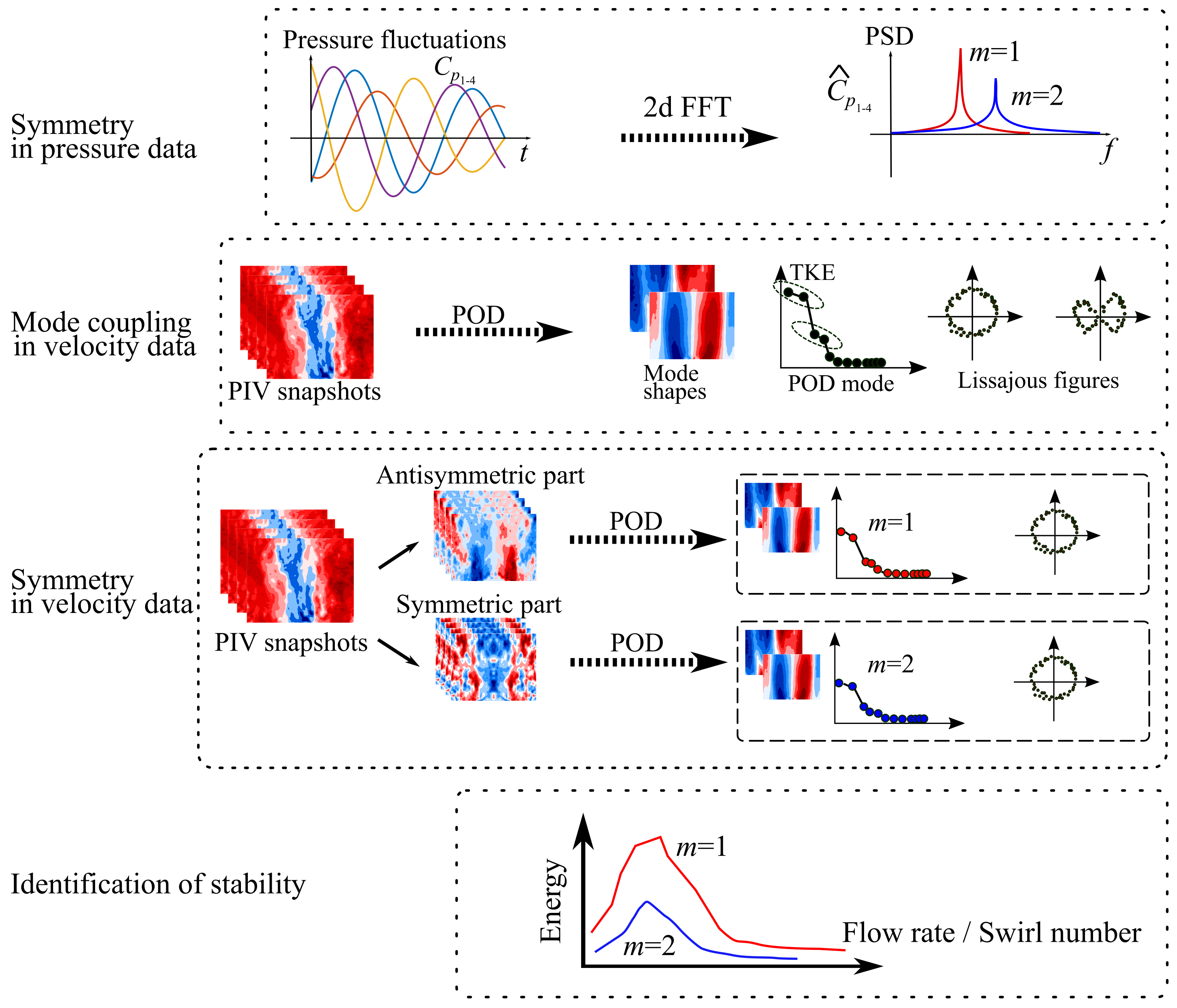
3. Post-Processing Routines
3.1. Spatial Fourier Mode Decomposition
3.2. Proper Orthogonal Decomposition (POD)
3.3. Symmetric and Antisymmetric Decomposition of the Velocity Fields
3.4. Outline of Applied Methods
- -
- Extract symmetry properties from the four signals of pressure fluctuations by using the spatial Fourier mode decomposition;
- -
- Find a mode coupling in the velocity data by classical POD analysis;
- -
- Extract symmetry properties from POD of the symmetric/antisymmetric decomposed velocity data;
- -
- Track modes as a function of operating condition and identify the onset of instabilities.
4. Results and Discussion
4.1. Wall Pressure Fluctuations
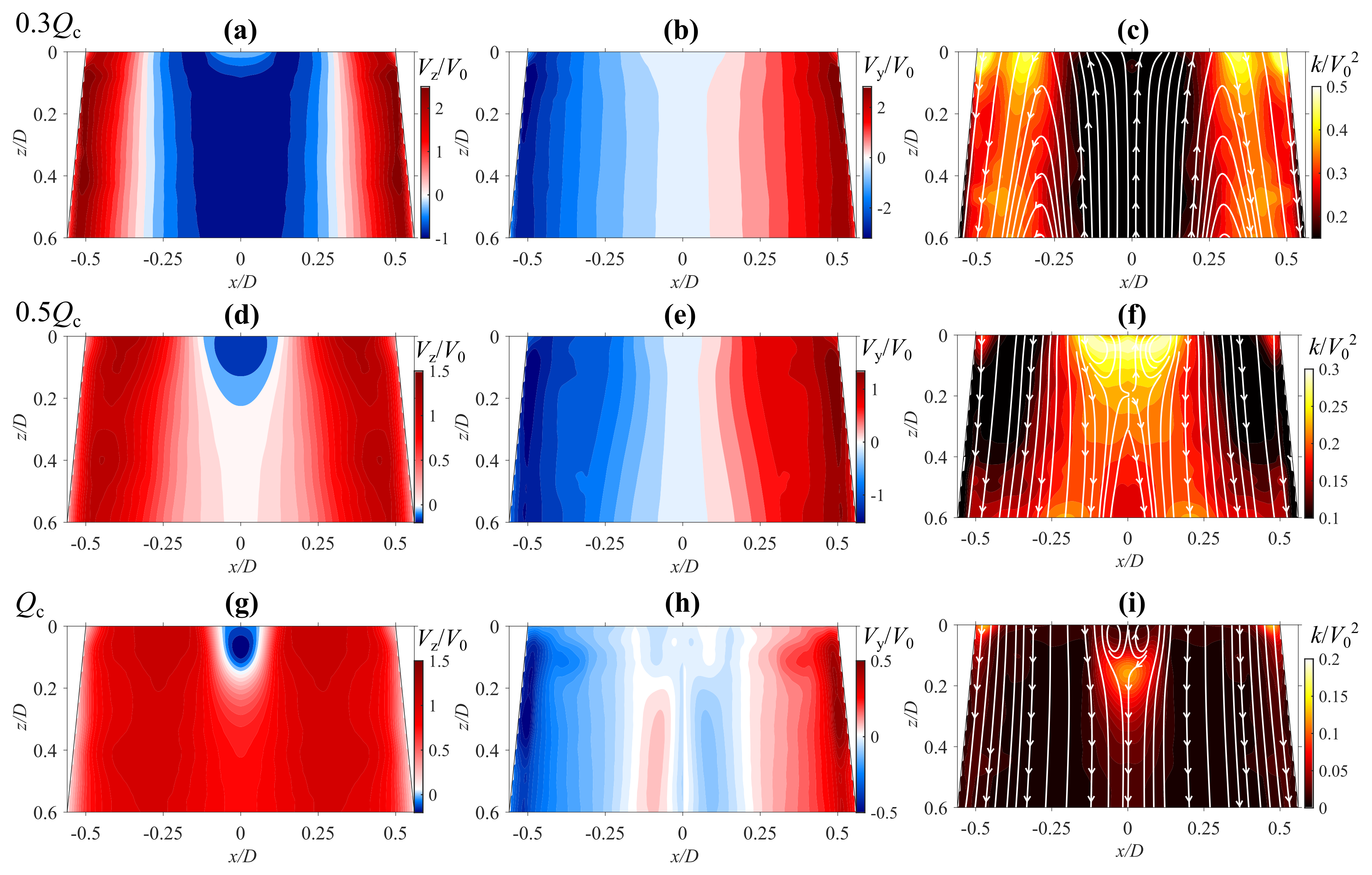
4.2. Mean Velocity Distributions
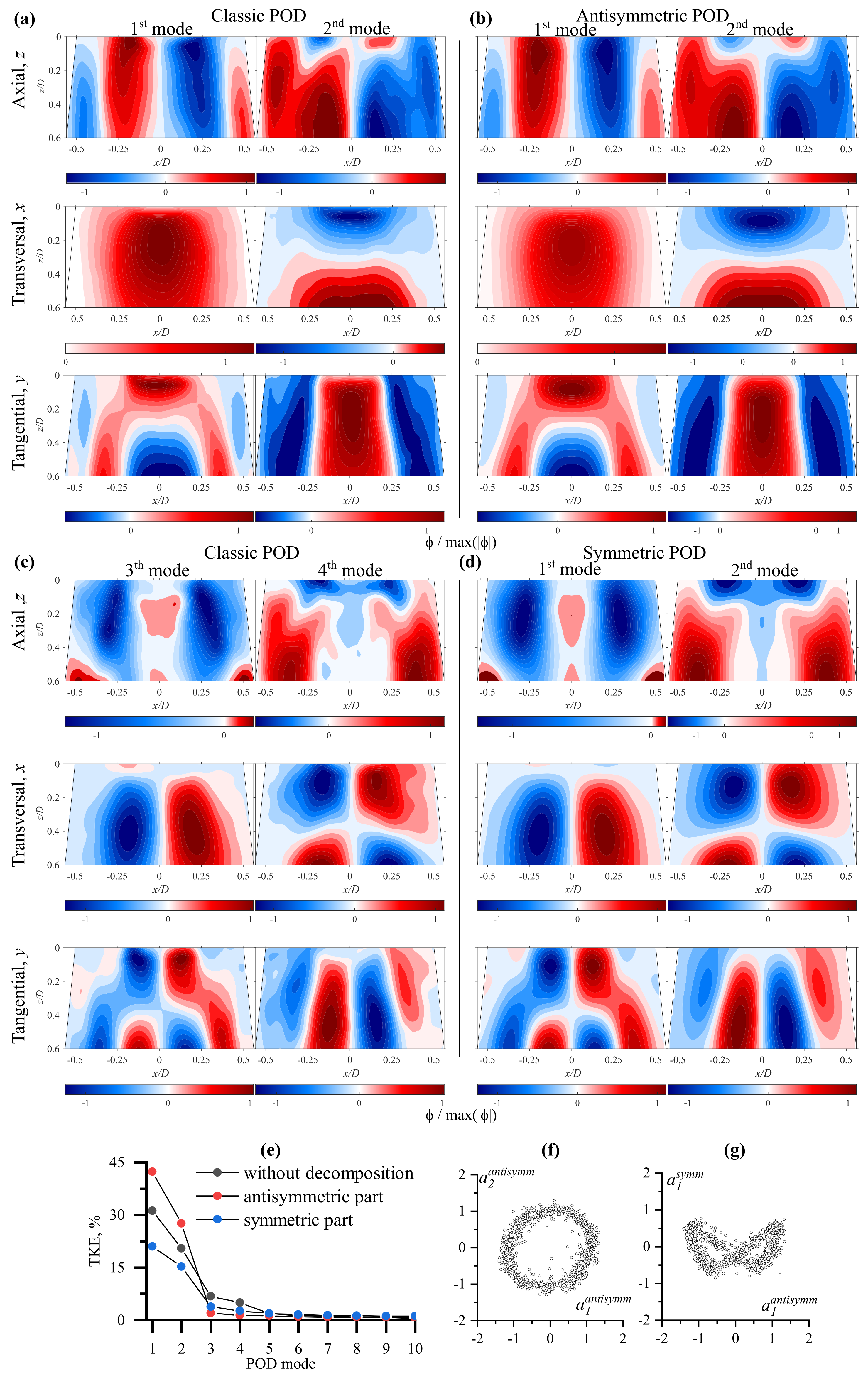
4.3. Classic POD at Part-Load Regime
4.4. Symmetric/Antisymmetric POD at Various Flow Regimes
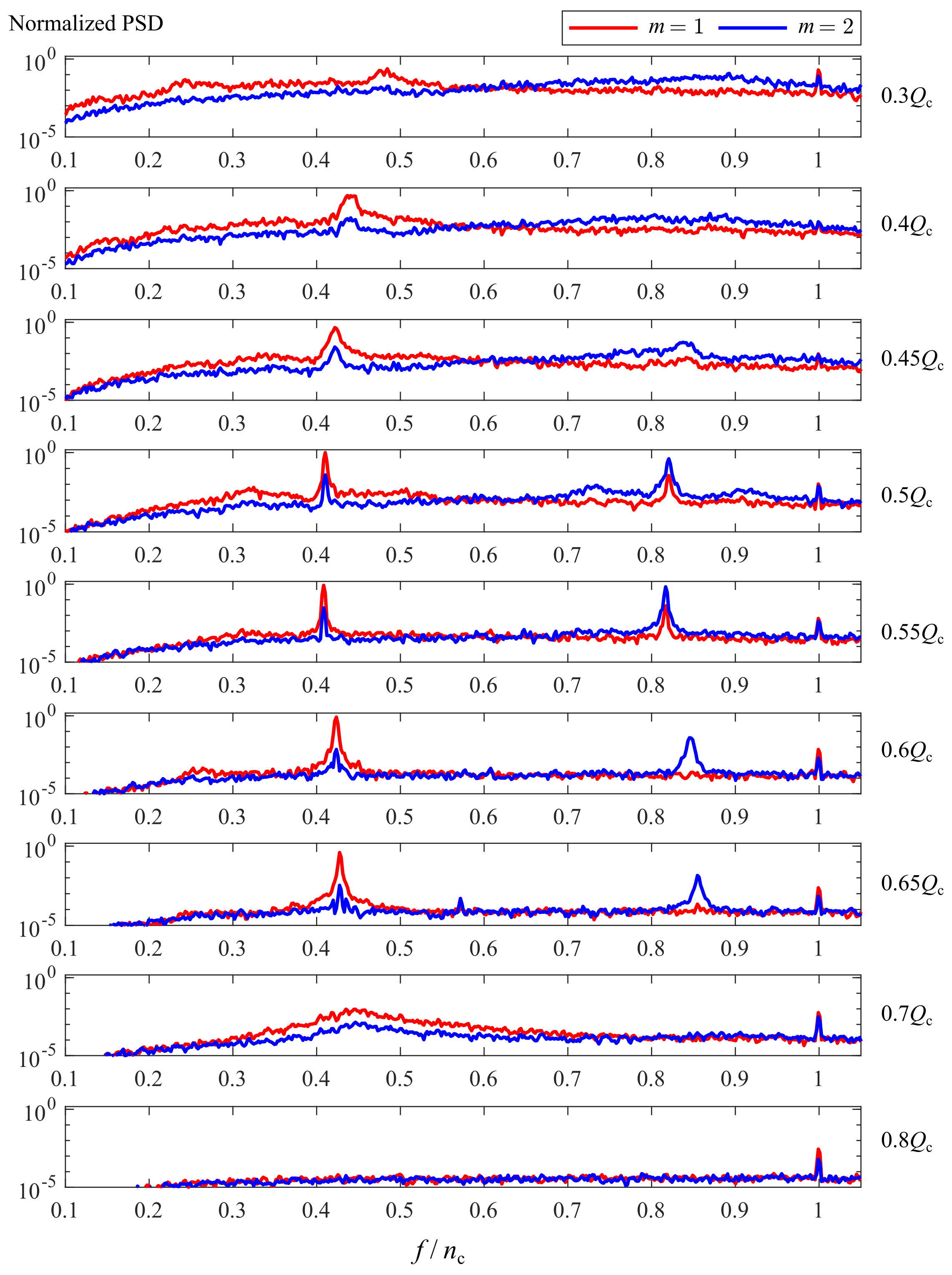
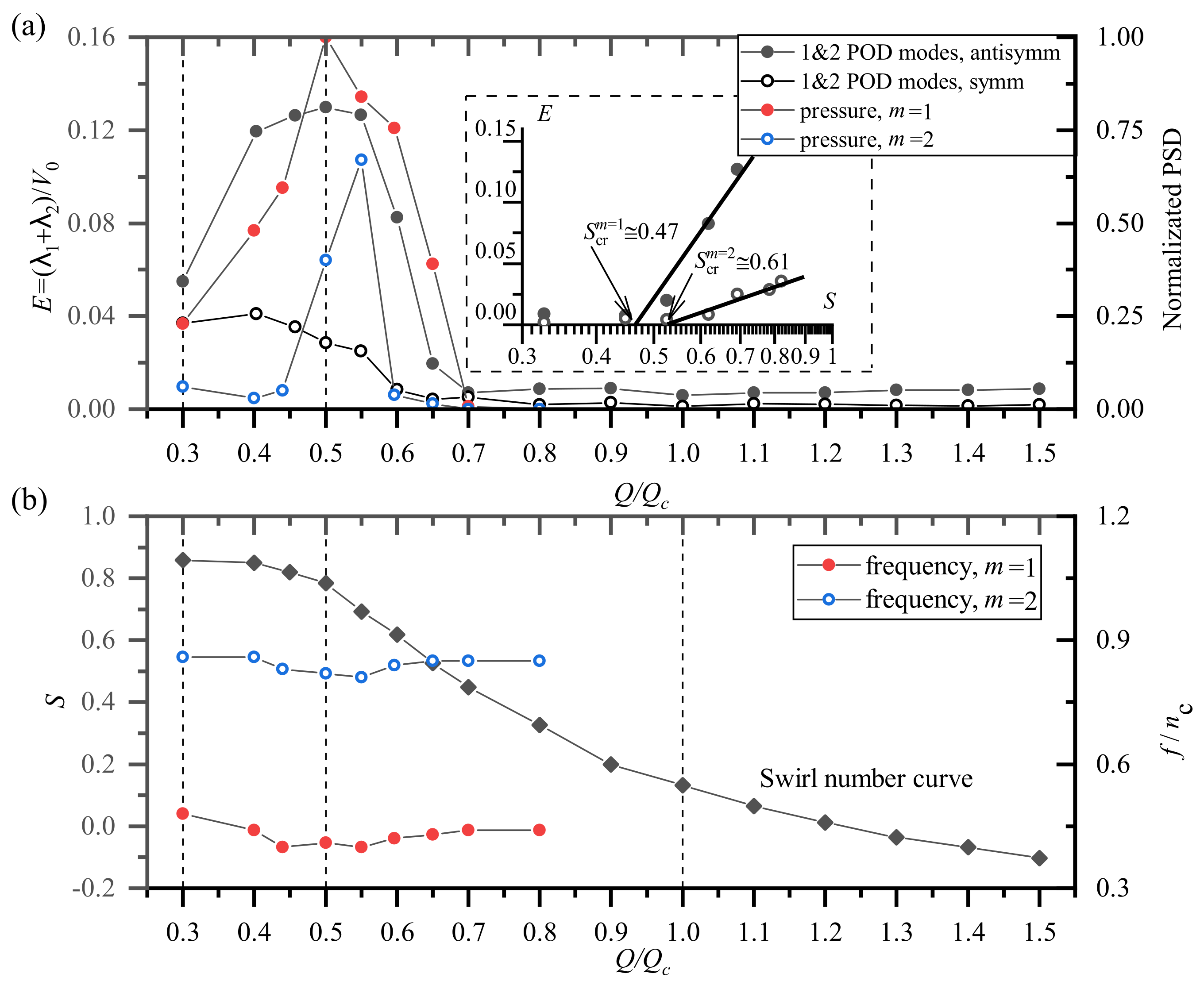
4.5. Identification of Stability
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Swirl Number Definition
References
- Liang, H.; Maxworthy, T. An experimental investigation of swirling jets. J. Fluid Mech. 2005, 525, 115–159. [Google Scholar] [CrossRef]
- Gupta, K.; Lilley, D.; Syred, N. Swirl Flows; Abacus Press: Kent, UK, 1984. [Google Scholar]
- Syred, N. A review of oscillation mechanisms and the role of the precessing vortex core (PVC) in swirl combustion systems. Prog. Energy Combust. Sci. 2006, 32, 93–161. [Google Scholar] [CrossRef]
- Dörfler, P.; Sick, M.; Coutu, A. Flow-Induced Pulsation and Vibration in Hydroelectric Machinery: Engineer’s Guidebook for Planning, Design and Troubleshooting; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Favrel, A.; Gomes Pereira Junior, J.; Müller, A.; Landry, C.; Yamamoto, K.; Avellan, F. Swirl number based transposition of flow-induced mechanical stresses from reduced scale to full-size Francis turbine runners. J. Fluids Struct. 2020, 94, 102956. [Google Scholar] [CrossRef]
- Kumar, S.; Cervantes, M.J.; Gandhi, B.K. Rotating vortex rope formation and mitigation in draft tube of hydro turbines—A review from experimental perspective. Renew. Sustain. Energy Rev. 2021, 136, 110354. [Google Scholar] [CrossRef]
- Trivedi, C.; Cervantes, M.J.; Gunnar Dahlhaug, O. Numerical techniques applied to hydraulic turbines: A perspective review. Appl. Mech. Rev. 2016, 68, 010802. [Google Scholar] [CrossRef]
- Tiwari, G.; Kumar, J.; Prasad, V.; Patel, V.K. Utility of CFD in the design and performance analysis of hydraulic turbines—A review. Energy Rep. 2020, 6, 2410–2429. [Google Scholar] [CrossRef]
- Goyal, R.; Gandhi, B.K. Review of hydrodynamics instabilities in Francis turbine during off-design and transient operations. Renew. Energy 2018, 116, 697–709. [Google Scholar] [CrossRef]
- Trivedi, C.; Dahlhaug, O.G. A comprehensive review of verification and validation techniques applied to hydraulic turbines. Int. J. Fluid Mach. Syst. 2019, 12, 345–367. [Google Scholar] [CrossRef]
- Valentín, D.; Presas, A.; Valero, C.; Egusquiza, M.; Egusquiza, E.; Gomes, J.; Avellan, F. Transposition of the mechanical behavior from model to prototype of Francis turbines. Renew. Energy 2020, 152, 1011–1023. [Google Scholar] [CrossRef]
- Ciocan, G.D.; Iliescu, M.S.; Vu, T.C.; Nennemann, B.; Avellan, F. Experimental Study and Numerical Simulation of the FLINDT Draft Tube Rotating Vortex. J. Fluids Eng. 2007, 129, 146–158. [Google Scholar] [CrossRef]
- Kirschner, O.; Ruprecht, A.; Göde, E.; Riedelbauch, S. Experimental investigation of pressure fluctuations caused by a vortex rope in a draft tube. Proc. IOP Conf. Ser. Earth Environ. Sci. 2012, 15, 062059. [Google Scholar] [CrossRef]
- Trivedi, C.; Cervantes, M.J.; Gandhi, B.K.; Dahlhaug, O.G. Experimental and numerical studies for a high head Francis turbine at several operating points. J. Fluids Eng. 2013, 135, 111102. [Google Scholar] [CrossRef]
- Favrel, A.; Müller, A.; Landry, C.; Yamamoto, K.; Avellan, F. Study of the vortex-induced pressure excitation source in a Francis turbine draft tube by particle image velocimetry. Exp. Fluids 2015, 56, 1–15. [Google Scholar] [CrossRef]
- Favrel, A.; Müller, A.; Landry, C.; Yamamoto, K.; Avellan, F. LDV survey of cavitation and resonance effect on the precessing vortex rope dynamics in the draft tube of Francis turbines. Exp. Fluids 2016, 57, 1–16. [Google Scholar] [CrossRef]
- Favrel, A.; Gomes Pereira Junior, J.; Landry, C.; Müller, A.; Nicolet, C.; Avellan, F. New insight in Francis turbine cavitation vortex rope: Role of the runner outlet flow swirl number. J. Hydraul. Res. 2018, 56, 367–379. [Google Scholar] [CrossRef]
- Susan-Resiga, R.; Muntean, S.; Bosioc, A. Blade design for swirling flow generator. In Proceedings of the 4th German–Romanian Workshop on Turbomachinery Hydrodynamics (GRoWTH), Stuttgart, Germany, 12–15 June 2008. [Google Scholar]
- Muntean, S.; Bosioc, A.; Stanciu, R.; Tanasa, C.; Susan-Resiga, R.; Vekas, L. 3D numerical analysis of a swirling flow generator. In Proceedings of the 4th IAHR International Meeting of the Workgroup on Cavitation and Dynamic Problems in Hydraulic Machinery and Systems, Belgrade, Serbia, 26–28 October 2011; pp. 115–125. [Google Scholar]
- Alekseenko, S.V.; Kuibin, P.A.; Shtork, S.I.; Skripkin, S.G.; Tsoy, M.A. Vortex reconnection in a swirling flow. JETP Lett. 2016, 103, 455–459. [Google Scholar] [CrossRef]
- Skripkin, S.; Tsoy, M.; Shtork, S.; Hanjalić, K. Comparative analysis of twin vortex ropes in laboratory models of two hydro-turbine draft-tubes. J. Hydraul. Res. 2016, 54, 450–460. [Google Scholar] [CrossRef]
- Skripkin, S.G.; Tsoy, M.A.; Kuibin, P.A.; Shtork, S.I. Study of Pressure Shock Caused by a Vortex Ring Separated From a Vortex Rope in a Draft Tube Model. J. Fluids Eng. 2017, 139. [Google Scholar] [CrossRef]
- Štefan, D.; Rudolf, P.; Hudec, M.; Uruba, V.; Procházka, P.; Urban, O. Experimental investigation of vortex ring formation as a consequence of spiral vortex re-connection. Proc. IOP Conf. Ser. Earth Environ. Sci. 2019, 405, 012033. [Google Scholar] [CrossRef] [Green Version]
- Sentyabov, A.; Platonov, D.; Minakov, A.; Lobasov, A. Numerical study of the vortex breakdown and vortex reconnection in the flow path of high-pressure water turbine. Proc. J. Phys. Conf. Ser. 2021, 2088, 012040. [Google Scholar] [CrossRef]
- Tǎnasǎ, C.; Bosioc, A.I.; Susan-Resiga, R.F.; Muntean, S. Experimental investigations of the swirling flow in the conical diffuser using flow-feedback control technique with additional energy source. Proc. IOP Conf. Ser. Earth Environ. Sci. 2012, 15, 062043. [Google Scholar] [CrossRef]
- Bosioc, A.I.; Susan-Resiga, R.; Muntean, S.; Tanasa, C. Unsteady pressure analysis of a swirling flow with vortex rope and axial water injection in a discharge cone. J. Fluids Eng. 2012, 134, 081104. [Google Scholar] [CrossRef]
- Tănasă, C.; Muntean, S.; Bosioc, A.I.; Susan-Resiga, R.; Ciocan, T. Influence of the air admission on the unsteady pressure field in a decelerated swirling flow. UPB Sci. Bull. Ser. D 2016, 78, 161–170. [Google Scholar]
- Tănasă, C.; Bosioc, A.; Muntean, S.; Susan-Resiga, R. A novel passive method to control the swirling flow with vortex rope from the conical diffuser of hydraulic turbines with fixed blades. Appl. Sci. 2019, 9, 4910. [Google Scholar] [CrossRef] [Green Version]
- Bosioc, A.I.; Tănasă, C. Experimental study of swirling flow from conical diffusers using the water jet control method. Renew. Energy 2020, 152, 385–398. [Google Scholar] [CrossRef]
- Cassidy, J.J. Experimental Study and Analysis of Draft-Tube Surging; BUR Reclam REP HYD-591; Bureau of Reclamation: Denver, CO, USA, 1969; p. 31. [Google Scholar]
- Sonin, V.; Ustimenko, A.; Kuibin, P.; Litvinov, I.; Shtork, S. Study of the velocity distribution influence upon the pressure pulsations in draft tube model of hydro-turbine. Proc. IOP Conf. Ser. Earth Environ. Sci. 2016, 49, 82020. [Google Scholar] [CrossRef]
- Litvinov, I.; Shtork, S.; Gorelikov, E.; Mitryakov, A.; Hanjalic, K. Unsteady regimes and pressure pulsations in draft tube of a model hydro turbine in a range of off-design conditions. Exp. Therm. Fluid Sci. 2018, 91, 410–422. [Google Scholar] [CrossRef]
- Liu, Z.; Favrel, A.; Miyagawa, K. Effect of the conical diffuser angle on the confined swirling flow induced Precessing Vortex Core. Int. J. Heat Fluid Flow 2022, 95, 108968. [Google Scholar] [CrossRef]
- Nobach, H. Limits in Planar PIV Due to Individual Variations of Particle Image Intensities; OCLC: 884225910; INTECH Open Access Publisher: London, UK, 2012. [Google Scholar]
- Goyal, R.; Gandhi, B.; Cervantes, M.J. PIV measurements in Francis turbine—A review and application to transient operations. Renew. Sustain. Energy Rev. 2018, 81, 2976–2991. [Google Scholar] [CrossRef]
- Štefan, D.; Hudec, M.; Uruba, V.; Procházka, P.; Urban, O.; Rudolf, P. Experimental investigation of swirl number influence on spiral vortex structure dynamics. IOP Conf. Ser. Earth Environ. Sci. 2021, 774, 012085. [Google Scholar] [CrossRef]
- Kumar, S.; Khullar, S.; Cervantes, M.J.; Gandhi, B.K. Proper orthogonal decomposition of turbulent swirling flow of a draft tube at part load. IOP Conf. Ser. Earth Environ. Sci. 2021, 774, 012091. [Google Scholar] [CrossRef]
- Goyal, R.; Cervantes, M.J.; Gandhi, B.K. Characteristics of Synchronous and Asynchronous modes of fluctuations in Francis turbine draft tube during load variation. Int. J. Fluid Mach. Syst. 2017, 10, 164–175. [Google Scholar] [CrossRef]
- Oberleithner, K.; Sieber, M.; Nayeri, C.N.; Paschereit, C.O.; Petz, C.; Hege, H.C.; Noack, B.R.; Wygnanski, I. Three-dimensional coherent structures in a swirling jet undergoing vortex breakdown: Stability analysis and empirical mode construction. J. Fluid Mech. 2011, 679, 383–414. [Google Scholar] [CrossRef] [Green Version]
- Pasche, S.; Avellan, F.; Gallaire, F. Part Load Vortex Rope as a Global Unstable Mode. J. Fluids Eng. 2017, 139, 051102. [Google Scholar] [CrossRef]
- Müller, J.S.; Lückoff, F.; Oberleithner, K. Guiding Actuator Designs for Active Flow Control of the Precessing Vortex Core by Adjoint Linear Stability Analysis. J. Eng. Gas Turbines Power 2019, 141, 041028. [Google Scholar] [CrossRef]
- Müller, J.S.; Lückoff, F.; Paredes, P.; Theofilis, V.; Oberleithner, K. Receptivity of the turbulent precessing vortex core: Synchronization experiments and global adjoint linear stability analysis. J. Fluid Mech. 2020, 888, A3. [Google Scholar] [CrossRef] [Green Version]
- Palde, U.J. Influence of Draft Tube Shape on Surging Characteristics of Reaction Turbines; Hydraulics Branch, Division of General Research, Engineering and Research Center, US Department of the Interior, Bureau of Reclamation: Washinton, DC, USA, 1972. [Google Scholar]
- Cervantes, M.; Trivedi, C.H.; Dahlhaug, O.G.; Nielsen, T. Francis-99 Workshop 1: Steady operation of Francis turbines. Proc. J. Phys. Conf. Ser. 2015, 579, 011001. [Google Scholar] [CrossRef] [Green Version]
- Lückoff, F.; Oberleithner, K. Excitation of the precessing vortex core by active flow control to suppress thermoacoustic instabilities in swirl flames. Int. J. Spray Combust. Dyn. 2019, 11, 175682771985623. [Google Scholar] [CrossRef]
- Vanierschot, M.; Müller, J.S.; Sieber, M.; Percin, M.; van Oudheusden, B.W.; Oberleithner, K. Single-and double-helix vortex breakdown as two dominant global modes in turbulent swirling jet flow. J. Fluid Mech. 2020, 883. [Google Scholar] [CrossRef]
- Holmes, P.; Lumley, J.L.; Berkooz, G.; Rowley, C.W. Turbulence, Coherent Structures, Dynamical Systems and Symmetry; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Stöhr, M.; Sadanandan, R.; Meier, W. Phase-resolved characterization of vortex–flame interaction in a turbulent swirl flame. Exp. Fluids 2011, 51, 1153–1167. [Google Scholar] [CrossRef] [Green Version]
- Gurka, R.; Liberzon, A.; Hetsroni, G. POD of vorticity fields: A method for spatial characterization of coherent structures. Int. J. Heat Fluid Flow 2006, 27, 416–423. [Google Scholar] [CrossRef]
- Dulin, V.M.; Lobasov, A.S.; Chikishev, L.M.; Markovich, D.M.; Hanjalic, K. On Impact of Helical Structures on Stabilization of Swirling Flames with Vortex Breakdown. Flow Turbul. Combust. 2019, 103, 887–911. [Google Scholar] [CrossRef]
- Rukes, L.; Sieber, M.; Paschereit, C.O.; Oberleithner, K. Effect of initial vortex core size on the coherent structures in the swirling jet near field. Exp. Fluids 2015, 56, 197. [Google Scholar] [CrossRef]
- Stöhr, M.; Boxx, I.; Carter, C.D.; Meier, W. Experimental study of vortex-flame interaction in a gas turbine model combustor. Spec. Issue Turbul. Combust. 2012, 159, 2636–2649. [Google Scholar] [CrossRef] [Green Version]
- Oberleithner, K.; Paschereit, C.O.; Wygnanski, I. On the impact of swirl on the growth of coherent structures. J. Fluid Mech. 2014, 741, 156–199. [Google Scholar] [CrossRef] [Green Version]
- Gallaire, F.; Ruith, M.; Meiburg, E.; Chomaz, J.M.; Huerre, P. Spiral vortex breakdown as a global mode. J. Fluid Mech. 2006, 549, 71. [Google Scholar] [CrossRef] [Green Version]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Litvinov, I.; Sharaborin, D.; Gorelikov, E.; Dulin, V.; Shtork, S.; Alekseenko, S.; Oberleithner, K. Modal Decomposition of the Precessing Vortex Core in a Hydro Turbine Model. Appl. Sci. 2022, 12, 5127. https://doi.org/10.3390/app12105127
Litvinov I, Sharaborin D, Gorelikov E, Dulin V, Shtork S, Alekseenko S, Oberleithner K. Modal Decomposition of the Precessing Vortex Core in a Hydro Turbine Model. Applied Sciences. 2022; 12(10):5127. https://doi.org/10.3390/app12105127
Chicago/Turabian StyleLitvinov, Ivan, Dmitriy Sharaborin, Evgeny Gorelikov, Vladimir Dulin, Sergey Shtork, Sergey Alekseenko, and Kilian Oberleithner. 2022. "Modal Decomposition of the Precessing Vortex Core in a Hydro Turbine Model" Applied Sciences 12, no. 10: 5127. https://doi.org/10.3390/app12105127
APA StyleLitvinov, I., Sharaborin, D., Gorelikov, E., Dulin, V., Shtork, S., Alekseenko, S., & Oberleithner, K. (2022). Modal Decomposition of the Precessing Vortex Core in a Hydro Turbine Model. Applied Sciences, 12(10), 5127. https://doi.org/10.3390/app12105127





