Hybrid Heuristic for Vehicle Routing Problem with Time Windows and Compatibility Constraints in Home Healthcare System

Abstract

This work involves a heuristic for solving vehicle routing problems with time windows (VRPTW) with general compatibility-matching between customer/patient and server/caretaker constraints to capture the nature of systems such as caretakers’ home visiting systems or home healthcare (HHC) systems. Since any variation of VRPTW is more complicated than regular VRP, a specific, custom-made heuristic is needed to solve the problem. The heuristic proposed in this work is an efficient hybrid of a novice Local Search (LS), Ruin and Recreate procedure (R&R) and Particle Swarm Optimization (PSO). The proposed LS acts as the initial solution finder as well as the engine for finding a feasible/local optimum. While PSO helps in moving from current best solution to the next best solution, the R&R part allows the solution to be over-optimized and LS moves the solution back on the feasible side. To test our heuristic, we solved 56 benchmark instances of 25, 50, and 100 customers and found that our heuristics can find 52, 21, and 18 optimal cases, respectively. To further investigate the proficiency of our heuristic, we modified the benchmark instances to include compatibility constraints. The results show that our heuristic can reach the optimal solutions in 5 out of 56 instances.

1. Introduction

In the year 2020, the proportion of the Thai population aged over 65 was 19.8%, more than double the global average of 9.3%. This figure is expected to increase to 29.6% over the next 30 years [1]. This means that in a short period of time Thailand will become a Super Aged country, defined as a country where more than 28% of the population is over 60 years of age. As projected by the Office of the National Economic and Social Development Board, Office of the Prime Minister, Bangkok, Thailand [2], the number of elderly people living alone with health problems will also increase. Home healthcare (HHC), which plays a major role in a proactive healthcare system, is essential for this population group, especially those with chronic diseases and bedridden patients requiring long-term care [3]. Caring for these people may involve injections, wound dressing, physical therapy, and other rehabilitation procedures, as well as health-related advice-giving to ensure the sustainability and improved life quality of the coming Aged Society. For the elderly, home visits represent more efficient management of human resources than having them visit the hospital individually.

In attempting to manage home visits in an HHC system, the following need to be considered: (1) compatibility matching of patients/customers and physicians, experts, or healthcare staff; (2) best routing for healthcare personnel to visit their customers; (3) meeting applicable service conditions, and (4) minimizing the cost of the whole system. The second consideration together with the fourth bear similarities to a regular VRP, and if the third is also considered, the problem becomes a vehicle routing problem with time windows (VRPTW). In this work, we will also integrate the first aspect into the VRPTW to better capture the nature of the HHC system. When all these aspects are taken into consideration, the problem becomes even more complicated and requires a custom-made heuristic to find a solution.

Most of the VRPTWs showcased in the literature already consider minimizing distance traveled as the main objective. The model we constructed can also deal with minimizing the total cost, with main objectives ranging from total distance traveled to completion time. This, along with the new general set of compatibility constraints, will make it more relevant for real-world applications, as patient-caretaker compatibility matching is sometimes necessary and minimizing waiting time and balancing job numbers per vehicle are a more important issue in VRPTWs that are similar to HHC systems.

The work process in this study goes as follows: First, a VRPTW with compatibility matching constraints is formulated. Subsequently, a hybrid heuristic combining local search (LS), Ruin and Recreate procedure (R&R), and particle swarm optimization (PSO) is proposed for solving the problem, which is NP-hard in nature. Finally, simulation results tested on best known benchmark instances, namely Solomon’s instances, are presented to show our heuristic’s efficiency in solving VRPTW problems with and without compatibility matching constraints.

This paper is organized as follows: Section 2 provides a review of literature on VRPTW. Section 3 presents a mathematical formulation of the problem. Section 4 describes the solution approach. Computational experiments on Solomon’s instances and conclusions are presented in Section 5 and Section 6, respectively.

2. Materials and Methods

As mentioned earlier, managing home visits in HHC systems can be viewed as a variety of VRPTW. In addition to minimizing the arrival time, finishing time, or processing time in caretaker-customer matching, the models may require further constraints to better suit the problems. Some existing works consider the travel cost, penalty cost, fixed cost, and overtime cost of the healthcare worker in their objective function. Wirnitzer et al. [4] find the minimum staff numbers including minimum number per hour and per customer and the number of staff replacing/switching times per customer. Braekers et al. [5] minimize the weighted sum costs while maximizing service level; therefore, the costs considered comprise the total costs and penalty costs that arise when customers find it inconvenient to receive service. Putting compatibility in the objective function, Ait Haddadene et al. [6] minimize total travel time as well as non-preferences between caretakers and patients to maximize compatibility while adding synchronization constraints, as some patients may need multiple services at the same time. Polnik et al. [7], also with synchronized visits to a home, construct a heuristic to solve the problem where each stop has only one task that might need multiple caretakers. Considering compatibility in the constraints, Yu et al. [8] minimize maximum traveling time with the vehicle allowed to visit only compatible nodes. Riazi et al. [9] consider minimizing total distance traveled but with caretaker qualification requirements in the constraints. In another work, Kandakoglu et al. [10] consider the weighted sum of total distance traveled, total travel cost, overtime wages and number of working staff; their notable constraints include the lunch break of the nurses. Nasir and Kuo [11] only consider the minimum total travel cost of staff but have synchronization constraints between nurses and vehicles as they consider the travel costs of the two separately. Cissé et al. [12] and Mascolo et al. [13] give the most recent extended review of literature in HHC routing and scheduling problems with variety of constraints to date.

Of the recently proposed heuristics for solving VRPTW that are more complicated than an NP-hard VRP, most are metaheuristics. The benchmark instances given in [14], known as Solomon’s instances, can be used to assess constructed heuristics.

Table 1. The best objective function values obtained in literature on Solomon’s instances.

Problem	Best-Known Solution		References
	Number of Vehicles	Total Distance
C101	10	827.30 *	[15,16]
C102	10	827.30 *	[15,16]
C103	10	826.30 *	[15,16]
C104	10	822.90 *	[15,16]
C105	10	827.30 *	[15,16]
C106	10	827.30 *	[15,16]
C107	10	827.30 *	[15,16]
C108	10	827.30 *	[15,16]
C109	10	827.30 *	[15,16]
C201	3	589.10 *	[16,17]
C202	3	589.10 *	[16]
C203	3	588.70 *	[16]
C204	3	590.60	[18,19,20,21,22]
C205	**	586.40 *	[17]
C206	**	586.00 *	[17]
C207	**	585.80 *	[17]
C208	3	585.80 *	[16]
R101	20	1637.7 *	[15,16,17]
R102	18	1466.6 *	[15,16,17]
R103	14	1208.7 *	[15,16,17]
R104	11	976.61	[22,23]
R105	15	1355.3 *	[15,16,17]
R106	13	1234.6 *	[15,16,17]
R107	11	1064.6 *	[15,16,17]
R108	10	938.20	[22]
R109	13	1146.9 *	[16,17]
R110	12	1068.0 *	[16,17]
R111	12	1048.7 *	[16,17]
R112	10	953.63	[18,23]
R201	8	1143.2 *	[16]
R202	8	1034.4	[23]
R203	6	874.87	[22,23]
R204	5	735.80	[22]
R205	5	954.16	[19,22]
R206	4	879.86	[23]
R207	4	797.99	[22]
R208	4	705.33	[22]
R209	5	859.39	[23]
R210	6	905.21	[22]
R211	4	753.15	[22]
RC101	14	1619.8 *	[16,17]
RC102	14	1457.4 *	[17]
RC103	11	1258.0 *	[17]
RC104	10	1135.5 *	[21]
RC105	15	1513.7 *	[16,17]
RC106	13	1378.0	[22]
RC107	12	1212.8	[20,22,23]
RC108	11	1117.5	[20,23]
RC201	9	1261.8 *	[16]
RC202	8	1095.6	[22,23]
RC203	5	926.82	[22]
RC204	4	786.38	[23]
RC205	7	1157.6	[22,23]
RC206	7	1054.6	[22,23]
RC207	6	966.08	[23]
RC208	4	778.93	[22]

* results claimed as optimal in the references. ** information not given in the references.

shows the objective function values studied in the most recent literature. Note that only works that consider hard time windows, i.e., where the service providers need to wait for customers to become available, are presented in the table.

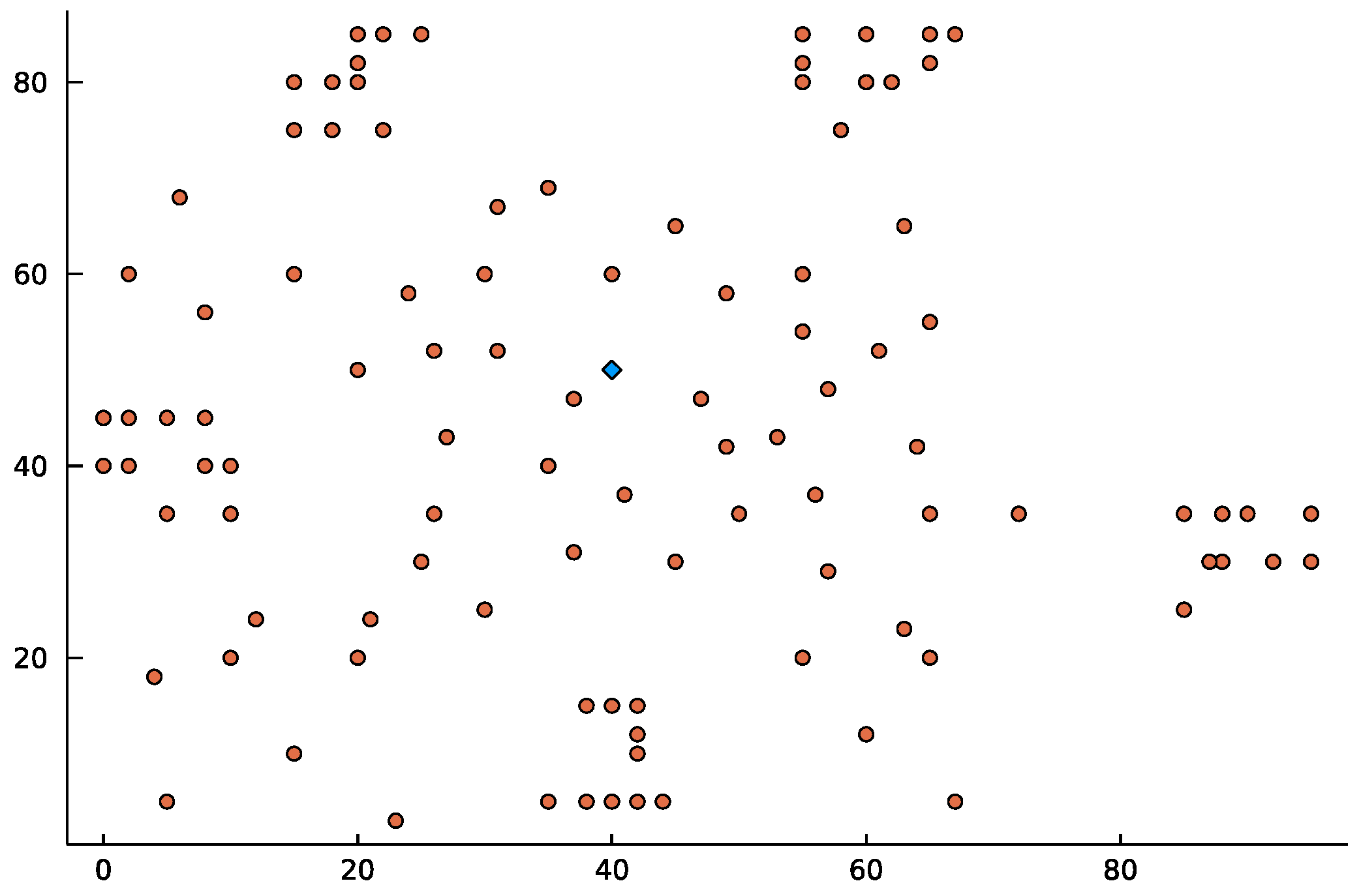
There are three groups of Solomon’s instances. After plotting these instances, we can see that the customers in Group C instances appear to be scattered in groups or clusters, as seen in Figure 1. These instances are similar to real-world problems where customers live in geographically scattered villages. The customers in Group R instances (Figure 2) are relatively randomly placed, corresponding to customers living in a big city. The customers in Group RC (Figure 3) are randomly clustered, that is, they appear in groups, but within these groups, they are more or less randomly placed. This system can also be found in a typical real-world system as well. Since VRPTW is very applicable and useful for real-world problems, heuristics for solving VRPTW have been widely studied and still attract many researchers in the field. The relevant recent works are summarized in

Table 2. Literature review for VRPTW with various objective functions and their proposed algorithms.

Objective	Proposed Algorithms	Reference
Total cost	Insertion and saving heuristic	[24]
	Adaptive large neighborhood search with removal and insertion operator	[25]
	Adaptive genetic algorithm with 2-opt procedure	[26]
	Particle swarm optimization with simulated annealing	[27]
Total distance	Probabilistic tabu search	[18]
	Branch and bound algorithm with greedy algorithm and large neighborhood search	[28]
	Large neighborhood search with ruin and recreate procedure	[29]
	Parallel cutting plane of branch and bound	[17]
	Parallel strategy of branch and bound	[15]
	Simulated annealing with ruin and recreate procedure	[30]
	Lagrangian relaxation and Column generation	[16]
	Genetic algorithm	[23]
	Variable neighborhood search with pruning and propagation techniques of constraint	[31]
	Simulated annealing with K-restart	[32]
	Parallel hybrid genetic algorithm with evolution function	[33]
	Two-phase set partitioning and genetic algorithm	[20]
	Multi-parametric mutation procedure with 1 + 1 evolution strategies algorithm	[34]
	Adaptive large neighborhood search	[35]
	Parallel simulated annealing	[21]
	Particle swarm optimization with adaptive strategies	[36]
Bi-level Minimizing the number of vehicles and total distance	Two evolutionary strategies algorithm with representation and mutation operators	[37]
	Simulated annealing (for solving primary) and large neighborhood search (for solving secondary)	[38]
	Genetic algorithm with Pareto ranking technique	[19]
	Arc-guided evolution strategies	[39]
Bi-level Minimizing cost and maximizing path length	Iterated local search and decomposition	[40]
Multiple problems: - Minimize number of vehicles - Minimize total distance	Multiple ant colony system (one for number of vehicles and one for total distance)	[41]
Multiple problems: - Minimizing total waiting time - Minimizing average waiting time - Maximizing slack time	Greedy randomized adaptive search and Variable neighborhood search	[42]
Multiple problems: - Minimizing total distance - Minimizing number of vehicles	Genetic algorithm with ruin and recreate procedure	[22]
The combination of total distance and lateness penalty (soft time windows)	Tabu search with multiple exchange procedures	[43]

.

3. Mathematical Modeling

As mentioned earlier, home visiting in a HHC system can be formulated as a VRPTW problem, which can then be written as a complete graph, $G=\left(N,E\right)$ having $N=\left\{0,1,\dots ,n\right\}$ being customers (or patients) where $0$ is the starting point of the route. The set $E$, the edges in the graph, represents the travelling connections between nodes. The travel times between points and service time at each point are given. Since the medical needs of patients or customers are unique and may be time-bound, if the service providers (or caretakers) arrive before the specified time window, they will have to wait until the appropriate time. This problem is considered a hard time windows problem. The model constructed here has the objective to minimize total travel costs with the constraints to meet all the traveling/service/matching conditions. The proposed model can be described as follows:

Indices:

$0$:

the starting point of the route (called the origin or the health center)

$i,j$:

patients $\left(1,2,\dots ,n\right)$

$k$:

the caretaker $\left(1,2,\dots ,m\right)$

Parameters:

$d_{ij}$:

the travel time from patient $i$ to patient $j$

$p_j^k$:

the service time of caretaker $k$ at patient $j$

$e_j$:

the earliest starting time (or availability time) of patient $j$

$l_j$:

the latest start time of patient $j$

$q_j$:

the demand of patient $j$

$Q$:

the capacity of all vehicles

$[r_{jk}]$:

 a compatible matching matrix $\left(n\times m\right)$ whose element $r_{jk}=1$ means patient $j$ can be treated by caretaker $k$ otherwise $r_{jk}=0$

$M$:

a large number

Variables:

$x_{0j}^k$:

equal to 1 if caretaker $k$ travels from the origin to patient $j$; otherwise, 0

$x_{ij}^k$:

equal to 1 if caretaker $k$ travels from node $i$ to patient $j$; otherwise, 0

$x_{j0}^k$:

equal to 1 if patient $j$ is the last patient visited by caretaker $k$; otherwise, 0

$u_j$:

variables for subtour elimination

$t_j$:

the starting time of patient $j$

$c_{ij}$:

the traveled cost between patient $i$ and patient $j$

Mathematical Model

Given a set of patients $N=\left\{0,1,2,\dots ,n\right\}$ where $0$ represents depot node, a set of caretakers $K=\left\{1, 2, \dots , m\right\}$ and a set of time windows corresponding to the caretakers, the objective is to find a route for each caretaker to start and return to the origin, with all patients needing to be visited only once with a minimum total cost. Each caretaker must start the job within the time window. This HHC problem can be formulated as a mixed-integer linear programming (MILP):

$$\mathrm{minimize} {\displaystyle \sum }_{j=0}^n{\displaystyle \sum }_{i=0, i\ne j}^n{c}_{ij}{x}_{ij}^k$$

subject to

$${\displaystyle \sum }_{j=1}^n{x}_{0j}^k=1, \forall k\in K$$

(1)

$${\displaystyle \sum }_{j=1}^n{x}_{j0}^k=1, \forall k\in K$$

(2)

$${\displaystyle \sum }_{k=1}^m{\displaystyle \sum }_{i=0,i\ne j}^n{x}_{ij}^k=1, \forall j\in N\backslash \left\{0\right\}$$

(3)

$${\displaystyle \sum }_{k=1}^m{\displaystyle \sum }_{j=0,i\ne j}^n{x}_{ij}^k=1, \forall i\in N\backslash \left\{0\right\}$$

(4)

$${\displaystyle \sum }_{i=0,i\ne j}^n{x}_{ij}^k-{\displaystyle \sum }_{l=0,l\ne j}^n{x}_{jl}^k=0, \forall j\in N\backslash \left\{0\right\}, \forall k\in K$$

(5)

$${\displaystyle \sum }_{i=0,i\ne j}^n{x}_{ij}^k\le r_{jk}, \forall j\in N, \forall k\in K$$

(6)

$$u_i-u_j+q_j\le Q\left(1-x_{ij}^k\right), \forall i,j\in N\backslash \left\{0\right\}, i\ne j, \forall k\in K$$

(7)

$$q_j\le u_j\le Q, \forall j\in N\backslash \left\{0\right\}$$

(8)

$$t_i+p_i^k+d_{ij}-M\left(1-x_{ij}^k\right)\le t_j, \forall i\in N, i\ne j, \forall j\in N, \forall k\in K$$

(9)

$$e_j\le t_j\le l_j, \forall j\in N$$

(10)

$$x_{ij}^k\in \left\{0,1\right\}, \forall i,j\in N, i\ne j, \forall k\in K$$

(11)

With the objective function being to minimize total costs, constraints (1) and (2) are to make sure that each caretaker starts and ends their route at the origin. Constraints (3) and (4) make sure that, for each patient, there is only one caretaker visit and departure. Similarly, constraints (5) ensure that a caretaker leaves a patient for the next one after completing service to the first patient. Constraints (6) are the compatibility constraints to guarantee that only a caretaker compatible with the patient will travel and take care of that patient. Constraints (7) and (8) are the subtour elimination constraint together with capacity constraints. Constraints (9) will activate when caretaker $k$ travels from patient $i$ to patient $j$ ($x_{ij}^k=1$). The completion time of patient $i$ (sum of starting time, service duration and travel time) must be less than the starting time of patient $j$. Constraints (10) are time window constraints. Constraints (11) ensure integrality of variables. Finally, $M$ is a sufficiently large number.

4. Algorithms

VRPTW is complicated and becomes even more so when some specific constraints, in this case compatibility-matching constraints, are added. We therefore construct a local search to use along with the help of PSO and R&R to solve the problem. Given the discrete nature of our problem, the moving directions in the PSO initially used to solve the continuous optimization problem can be adapted using our developed local search, R&R, and PSO (path relinking procedure). The local search and R&R represent the effect of the individual particle’s cognitive behavior, while the path relinking describes the impact of global social learning behavior which allows a jump out of the local optimum.

Note that the feasibility of solution (particle) can be checked by substituting the particle’s binary representation into the proposed mathematical model. Due to the complexity caused by the presence of time windows, it is difficult to randomly generate a feasible solution (particle). To solve this issue, after the random solution (which is probably infeasible) is obtained, the patients that cause solution infeasibility (arrival time lies outside the time window) are removed. Then the Inserting procedure, described below, is applied to reinsert the patients. The removed patients are added to each caretaker until there is no available place left. If there is still a patient left, a new caretaker is deployed, and the Inserting procedure is applied until there is no patient left to schedule.

Note that the constructed heuristic can be applied, with only slight modifications, to any VRPTW. All steps in the proposed heuristic remain the same, but the feasibility check is based on the characteristics of the new problem. In a similar manner to the feasibility check, the calculation of objective value can be adjusted to satisfy the new problem.

The main algorithm along with all sub-procedures are given in detail below.

4.1. Main Algorithm

PSO is a population-based algorithm for solving an optimization problem which simulates the social behavior of the birth flock. Each individual, called a particle, represents a feasible solution. The particles try to find a direction to the best new solution iteratively around the search space using the information guided by themselves and the best-known best solution.

Let $n$ be the population size, $r$ be the number of R&R runs, $Ite{r}_{\max }$ be the maximum number of iterations, $P=\left\{p_1, p_2, \dots , p_n\right\}$ be the set of all particles, and $f\left(p_i\right)$ be the objective value (i.e., total cost) of particle $p_i$, for $i=1,2,\dots ,n$. The pseudocode of the main algorithm based on PSO is given below.

Main Algorithm
1.	Set parameters: $\mathrm{population} \mathrm{size} \left(n\right)$, the number of R&R runs ($r$), and maximum number of iterations $\left(Ite{r}_{max}\right)$
2.	Initial step:$\mathrm{Generate} n$$\mathrm{initial} \mathrm{particles}, \mathrm{set} \mathrm{as} P=\left\{p_1, p_2, \dots , p_n\right\}$
3.		For $p_i\in P$ do
4.			If $p_i$ is infeasible do
5.				$\mathrm{Remove} \mathrm{all} \mathrm{patients} \mathrm{from} p_i$ that make the schedule infeasible
6.				Insert the removed patients into the remaining schedule using the Inserting procedure
7.			End If
8.		End For
9.	End Initial step
10.	Calculate best-known solution (particle), $p_{best}=\arg \underset{p_{\mathrm{i}}\in P}{\min }\left(f\left(p_i\right)\right)$
11.	While$iteration<Ite{r}_{max}$ and the best particle does not change for 10 iterations
12.		Apply Local search procedure to each particle $\left(p_i\right)$
13.		Apply Path relinking procedure to each particle $\left(p_i\right)$
14.		$\mathrm{Calculate} \mathrm{the} \mathrm{new} p_{best}$ (line 10)
15.		If $p_{best}$ does not change for $r$ iterations do
16.			Apply the R&R procedure
17.		End If
18.	End While
19.	Return $p_{best}$

4.2. Path Relinking Procedure

Path relinking is a search strategy guided by the other solution based on the idea that quality solutions may share similar properties [44]. The guide solution is selected from the current best solution.

Path relinking aims to create a new solution that shares information from the original and the guided solutions. In the context of VRPTW, the good solutions may retain some routes as the current best solution. Route-based path relinking is therefore considered in this study: the new solution will have one of the routes as the guided solution. The path relinking contains two steps. The first step is to select a guided route (any route) from the guided solution and then remove all patients corresponding to the guided route from the current solution. The next step is to insert the removed patients into the current solution using the Inserting procedure. Suppose, for example, that the current solution contains 3 routes arranged as follows: O-A1-A2-A3-A4-O, O-B1-B2-B3-O, O-C1-C2-C3-C4-C5-O, and the guided route is O-A2-B3-A3-C5-O. The result will contain 4 routes: O-A2-B3-A3-C5-O (the guided route), O-A1-A4-O, O-B1-B2-O, and O-C1-C2-C3-C4-O. The procedure can be summarized as follows:

Path Relinking Procedure
1.	Input: the current solution, set to $p$ and guided solution (current best solution), set to $p_{best}$
2.	Randomly choose any route in $p_{best}$$, \mathrm{set} \mathrm{to} r_0$
3.	Remove all jobs corresponding to route $r_0$$\mathrm{from} p$. If the remaining schedule is infeasible, move the infeasible patient to $r_0$.
4.	Apply the Inserting procedure to insert all jobs in $r_0$ $\mathrm{to} p$

4.3. Inserting Procedure

The aim of this procedure is to arrange patients, one by one, between pairs of already assigned patients where none of the assigned patients are served late. In the iteration process, if the inserted patient cannot be treated immediately after the completion time of the directly preceding patient, that caretaker will wait until the lower time window of the patient is reached. A patient that cannot be inserted into any position will be considered a tardy (late) patient.

Let $J$ be a set of assigned patients, $J_w$ be a set of tardy patients, $J_c$ be a set of remaining unattended patients and let $J\left(j\right)$ be a set of all assignments obtained by inserting patient $j$ between every pair of patients in the assignment $J$, iteratively. The inserting procedure can be described as follows:

Inserting Procedure
1.	Input: A set of assigned patients, set to $J$, and a set of patients (waiting to be scheduled), set to $J_c$
2.	Set$J_w=\varnothing$ and arrange the patients in $J_c$ according to their upper time windows in ascending order
3.	While $J_c\ne \varnothing$ do
4.		Choose the first patient in $J_c$$, \mathrm{say} j$$. \mathrm{Remove} j$$\mathrm{from} J_c$
5.		Consider the set of assignments $J\left(j\right)$
6.		If there is more than one assignment and all patients are not late do
7.			Choose the case that has the minimum completion time, set to $J$
8.		Else If there is a tardy patient in every assignment in $J\left(j\right)$ do
9.			Choose the assignment with only one late patient, set as $J$$, \mathrm{and} \mathrm{whose} \mathrm{assignment} \mathrm{completion} \mathrm{time} \mathrm{after} \mathrm{removing} \mathrm{that} \mathrm{patient} \mathrm{is} \mathrm{the} \mathrm{smallest}. \mathrm{Add} \mathrm{the} \mathrm{late} \mathrm{patient} \mathrm{to} J_w$
10.		Else If $\mathrm{every} \mathrm{assignment} J\left(j\right)$ has more than two tardy patients do
11.			$\mathrm{Add} \mathrm{the} \mathrm{patient} j$$\mathrm{to} \mathrm{the} \mathrm{set} J_w$
12.		End If
13.	End While
14.	While $J_w\ne \varnothing$ do
15.		Add a new caretaker. Repeat all steps in the While loop with $J_w$$, \mathrm{instead} \mathrm{of} J_c$, until there is no change in $J$.
16.	End While

4.4. Local Search Procedure

The aim of the proposed Local Search is to improve the solution. Some patients, if served by a different caretaker, could result in reduced objective value. Since there are many candidates to consider, it is more convenient to generate a priority list of every pair of jobs. The List is sorted using the traveling times between pairs of patients in ascending order.

We developed three improving procedures: Swapping procedure (Section 4.4.1), Moving procedure (Section 4.4.2), and 2-opt procedure (Section 4.4.3). In the first step of Local Search, the procedure will generate a priority list containing all candidates for swapping, moving, and 2-opt. It will then apply Swapping, Moving and 2-opt procedures accordingly. The procedures are explained in detail below.

4.4.1. Swapping Procedure

The swapping procedure aims to switch the order of a pair of jobs on the List in order to make the solution better, or to reduce the objective value. For our purpose, the List is generated by sorting travel times between pairs of patients. This procedure will be applied multiple times until the solution can no longer be improved.

Swapping Procedure
1.	For (job1, job2) in List do
2.		swap the routing position between job1 and job2 if it reduces the total routing cost and the routing is still feasible.
3.	End For

4.4.2. Moving Procedure

This procedure uses the same idea as the swapping procedure: the chosen patient is moved to another position. The patient moves when the objective value is reduced; otherwise, the patient will maintain his/her position. This procedure also uses the same List as the swapping procedure.

Moving Procedure
1.	For (job1, job2) in List do
2.		Move job2 to process before or after job1 if it reduces the total routing cost and the routing is feasible. If both positions reduce cost, choose the one with more cost reduction.
3.	End For

4.4.3. 2-Opt Procedure

This is a local search procedure for solving the traveling salesman problem. It uses the same idea as the swapping procedure by swapping a pair of edges, instead of patients, from any route and reconnecting them with each other. In other words, the main idea is the crossover between two routes. The edge moves when the objective value is reduced; otherwise, all patients will maintain their positions. The List for this procedure contains all pairs of edges in random order. Suppose, for example, that we have two routes that start and end at the origin, denoted by “O”, and are arranged as follows: O-A1-A2-A3-A4-A5-O and O-B1-B2-B3-B4-B5-B6-O. Suppose the selected edges are (A1-A2) and (B4-B5). The result routes will be O-A1-B5-B6-O and O-B1-B2-B3-B4-A2-A3-A4-A5-O.

2-Opt Procedure
1.	For (A-B, C-D) in List do
2.		Define a path starting from depot to node A by OA, a path starting from B to depot by BO, a path starting from depot to node C by OC, and a path starting from D to depot by DO.
3.		Reconstruct a path as OA connected to DO and OC connected to BO only if the result is feasible and the total cost is reduced.
4.	End For

4.5. R&R Procedure

The main idea behind this procedure is to jump out to a new solution to avoid the local optimum [30]. In this procedure, one of the caretakers is randomly removed. The removed patients are then added to the remaining caretakers using the Inserting procedure. If some of the remaining patients cannot be inserted into any place, a new caretaker will be deployed by applying the Inserting procedure to the remaining patients.

R&R Procedure
1.	Input: Routing solution
2.	Randomly select a caretaker, set to $Removal$, and remove all patients belonging to that caretaker from the routing solution.
3.	For $patient\in Removal$ do
4.		$\mathrm{Insert} patient$ by applying the Inserting procedure to each caretaker; if there is no place to insert, deploy a new caretaker and apply the procedure again
5.	End For

5. Computational Results on Solomon’s Instances

To test our constructed heuristic, we apply it to solve the well-known benchmark instances called Solomon’s instances with 25, 50, and 100 customers. As mentioned earlier, there are 3 groups of instances, C (clustered), R (random) and RC (randomly clustered). The parameters used in all simulation results are: number of particles, set at 15 ($n=15$); number of R&R runs, which is 5 ($r=5$); and maximum iterations, set at 500 ($Iter\_max=500$). These parameters greatly affect the performance of the heuristic. For example, if the number of particles is high, the objective function value tends to be better. However, we will have to sacrifice the time needed to execute each iteration. Since a higher number of particles does not guarantee a better solution, we limit the number of particles to 15 where the running time is comparatively low. The number of R&R is set to 5 in an attempt to diversify particles when they have similar solutions or similar route. This normally occurs when the heuristic reaches a local optimum, since the path relinking process tends to move all particles that are similar to each other. As for the maximum number of iterations, in all problems tested this has never reached 500, hence the number is set to 500.

To illustrate the proposed heuristic’s performance, the heuristic is written in Julia’s language [45,46] and run on AMD Ryzen 9 12-Core processors with 3.8 GHz CPU and 64 GB of RAM. The results shown in

Table 3. Comparisons between the exact solutions and the results obtained by our heuristic on 25-customer Solomon instances.

Problem	Optimum			Our Best		%Gap	Execution Time (s)
	Number of Vehicles	Total Distance	Reference	Number of Vehicles	Total Distance
C101	3	191.3	[47]	3	191.3	0.000	17.13
C102	3	190.3	[47]	3	190.3	0.000	30.44
C103	3	190.3	[47]	3	190.3	0.000	16.38
C104	3	186.9	[47]	3	186.9	0.000	30.74
C105	3	191.3	[47]	3	191.3	0.000	25.25
C106	3	191.3	[47]	3	191.3	0.000	15.98
C107	3	191.3	[47]	3	191.3	0.000	16.48
C108	3	191.3	[47]	3	191.3	0.000	14.34
C109	3	191.3	[47]	3	191.3	0.000	21.45
C201	2	214.7	[17]	2	214.7	0.000	29.40
C202	2	214.7	[17]	2	214.7	0.000	26.66
C203	2	214.7	[17]	2	214.7	0.000	33.97
C204	2	213.1	[17]	2	214.5	0.657	47.89
C205	2	214.7	[17]	2	214.7	0.000	49.21
C206	2	214.7	[17]	2	214.7	0.000	41.50
C207	2	214.5	[17]	1	274.0	27.74	45.93
C208	2	214.5	[17]	1	229.1	6.807	42.62
R101	8	617.1	[47]	8	617.1	0.000	25.21
R102	7	547.1	[47]	7	547.1	0.000	23.50
R103	5	454.6	[47]	5	454.6	0.000	20.80
R104	4	416.9	[47]	4	416.9	0.000	26.97
R105	6	530.5	[47]	6	530.5	0.000	15.39
R106	3	465.4	[47]	5	465.4	0.000	23.06
R107	4	424.3	[47]	5	430.8	1.532	22.06
R108	4	397.3	[47]	4	397.3	0.000	19.90
R109	5	441.3	[47]	5	441.3	0.000	16.39
R110	4	444.1	[47]	5	444.1	0.000	23.13
R111	5	428.8	[47]	4	428.8	0.000	20.35
R112	4	393.0	[47]	4	393.0	0.000	18.15
R201	4	463.3	[17]	4	463.3	0.000	25.58
R202	4	410.5	[17]	4	410.5	0.000	18.46
R203	3	391.4	[17]	3	391.4	0.000	25.46
R204	2	355.0	[17]	2	355.0	0.000	27.90
R205	3	393.0	[17]	3	393.0	0.000	25.92
R206	3	374.4	[17]	3	374.4	0.000	27.84
R207	3	361.6	[16]	3	361.6	0.000	27.24
R208	1	328.2	[48]	1	328.2	0.000	19.03
R209	2	370.7	[16]	2	370.7	0.000	19.94
R210	3	404.6	[17]	3	404.6	0.000	26.32
R211	2	350.9	[16]	2	350.9	0.000	22.49
RC101	4	461.1	[47]	4	461.1	0.000	38.39
RC102	3	351.8	[47]	3	351.8	0.000	39.48
RC103	3	332.8	[47]	3	332.8	0.000	38.72
RC104	3	306.6	[47]	3	306.6	0.000	39.89
RC105	4	411.3	[47]	4	411.3	0.000	39.10
RC106	3	345.5	[47]	3	345.5	0.000	42.88
RC107	3	298.3	[47]	3	298.3	0.000	36.47
RC108	3	294.5	[47]	3	294.5	0.000	43.91
RC201	3	360.2	[17]	3	360.2	0.000	18.25
RC202	3	338.0	[17]	3	338.0	0.000	11.64
RC203	3	326.9	[48]	3	326.9	0.000	13.74
RC204	3	299.7	[49]	3	299.7	0.000	12.33
RC205	3	338.0	[15]	3	338.0	0.000	17.65
RC206	3	324.0	[16]	3	324.0	0.000	13.34
RC207	3	298.3	[16]	3	298.3	0.000	11.50
RC208	2	269.1	[49]	2	269.1	0.000	10.98

,

Table 4. Comparisons between the exact solution or best solutions (with “*”) and the results obtained by our heuristic on 50-customer Solomon instances.

Problem	Best-Known			Our Best		%Gap	Execution Time (s)
	Number of Vehicles	Total Distance	Reference	Number of Vehicles	Total Distance
C101	5	362.4	[47]	5	362.4	0.000	104.8
C102	5	361.4	[47]	5	361.4	0.000	104.1
C103	5	361.4	[47]	5	382.1	5.727	104.8
C104	5	358.0	[47]	5	361.1	0.8659	104.7
C105	5	362.4	[47]	5	362.4	0.000	98.30
C106	5	362.4	[47]	5	362.4	0.000	101.1
C107	5	362.4	[47]	5	362.4	0.000	97.12
C108	5	362.4	[47]	5	362.4	0.000	104.8
C109	5	362.4	[47]	5	362.4	0.000	95.53
C201	3	360.2	[17]	3	360.2	0.000	275.6
C202	3	360.2	[17]	3	360.2	0.000	207.4
C203	3	359.8	[17]	3	359.8	0.000	469.5
C204	2	350.1	[17]	2	357.6	2.142	472.4
C205	3	359.8	[17]	3	359.8	0.000	349.7
C206	3	359.8	[17]	3	359.8	0.000	427.4
C207	3	359.6	[17]	3	359.6	0.000	226.2
C208	2	350.5	[17]	2	350.5	0.000	458.7
R101	12	1044	[47]	12	1049	0.4789	124.4
R102	11	909.0	[47]	11	909.0	0.000	116.6
R103	9	772.9	[47]	9	772.9	0.000	128.6
R104	6	625.4	[47]	6	636.0	1.694	95.72
R105	9	899.3	[47]	11	922.4	2.568	105.3
R106	5	793.0	[47]	9	795.5	0.3153	128.5
R107	7	711.1	[47]	7	711.1	0.000	95.11
R108	6	617.7	[17]	6	623.7	0.9713	95.83
R109	8	786.8	[47]	8	792.0	0.6609	118.4
R110	7	697.0	[47]	8	718.5	3.084	127.7
R111	7	707.2	[17]	7	719.3	1.711	87.38
R112	6	630.2	[17]	6	650.3	3.189	97.39
R201	6	791.9	[17]	6	812.1	2.550	143.3
R202	5	698.5	[17]	6	715.4	2.419	140.3
R203	5	605.3	[48]	5	613.8	1.404	160.0
R204	2	506.4	[48]	3	512.7	1.244	153.2
R205	4	690.1	[48]	5	700.0	1.434	117.1
R206	4	632.4	[48]	5	643.4	1.739	153.7
R207	2 *	594.0 *	[50]	3	584.2	−1.649 *	133.4
R208	2 *	508.4 *	[50]	2	496.2	−2.399 *	189.5
R209	4	600.6	[48]	4	600.6	0.000	109.0
R210	4	645.6	[48]	5	655.5	1.533	167.3
R211	3	535.5	[48]	4	552.2	3.118	133.3
RC101	8	944.0	[47]	8	944.8	0.08475	183.0
RC102	7	822.5	[47]	8	838.9	1.993	215.5
RC103	6	710.9	[47]	7	754.5	6.133	224.9
RC104	5	545.8	[47]	5	552.2	1.172	234.0
RC105	8	855.3	[47]	9	889.0	3.940	211.2
RC106	6	723.2	[47]	7	769.0	6.333	234.9
RC107	6	642.7	[47]	6	670.2	4.278	229.3
RC108	6	598.1	[47]	6	598.1	0.000	210.5
RC201	5	684.8	[15]	5	684.8	0.000	139.1
RC202	5	613.6	[48]	5	613.6	0.000	139.3
RC203	4	555.3	[48]	4	566.2	1.962	154.1
RC204	3	444.2	[51]	3	447.2	0.6754	152.1
RC205	5	630.2	[48]	5	633.7	0.5554	130.9
RC206	5	610.0	[48]	5	610.1	0.01639	195.0
RC207	4	558.6	[49]	5	562.5	0.6982	139.5
RC208	2 *	498.8 *	[50]	4	490.6	−1.643 *	122.3

and

Table 5. Comparisons between the exact solution or best solutions (with “*”) and the results obtained by our heuristic on 100-customer Solomon instances.

Problem	Best-Known			Our Best		%Gap	Execution Time (s)
	Number of Vehicles	Total Distance	Reference	Number of Vehicles	Total Distance
C101	10	827.30	[47]	10	827.30	0.0000	533.12
C102	10	827.30	[47]	10	827.30	0.0000	794.94
C103	10	826.30	[47]	10	826.30	0.0000	1456.5
C104	10	822.90	[47]	10	822.90	0.0000	1524.0
C105	10	827.30	[47]	10	827.30	0.0000	1243.1
C106	10	827.30	[47]	10	827.30	0.0000	1010.7
C107	10	827.30	[47]	10	827.30	0.0000	1316.3
C108	10	827.30	[47]	10	827.30	0.0000	936.42
C109	10	827.30	[47]	10	827.30	0.0000	1692.4
C201	3	589.10	[17]	3	589.10	0.0000	1887.9
C202	3	589.10	[17]	3	589.10	0.0000	814.01
C203	3	588.70	[16]	3	588.70	0.0000	1806.4
C204	3	588.10	[17]	3	588.10	0.0000	1280.1
C205	3	586.40	[17]	3	586.40	0.0000	2014.4
C206	3	586.00	[17]	3	586.00	0.0000	2121.1
C207	3	585.80	[17]	3	585.80	0.0000	762.62
C208	3	585.80	[16]	3	585.80	0.0000	1697.6
R101	20	1637.7	[47]	20	1637.7	0.0000	1091.7
R102	18	1466.6	[47]	18	1467.7	0.07500	1826.4
R103	14	1208.7	[17]	15	1220.3	0.95971	1246.7
R104	11	971.50	[48]	10	984.50	1.3381	2208.1
R105	15	1355.3	[47]	16	1373.1	1.3134	1542.2
R106	13	1234.6	[17]	14	1259.3	2.0007	768.54
R107	11	1064.6	[17]	12	1084.6	1.8786	664.12
R108	9 *	938.20 *	[22]	11	952.30	1.5029 *	633.11
R109	13	1146.9	[17]	13	1165.9	1.6566	1143.8
R110	12	10,680	[17]	12	1091.2	2.1723	1761.7
R111	12	1048.7	[17]	12	1065.3	1.5829	1274.6
R112	10 *	953.60 *	[23]	11	971.80	1.9086 *	1961.3
R201	8	1143.2	[16]	8	1146.6	0.29741	1297.3
R202	8 *	1034.4 *	[23]	7	1035.8	0.13534 *	880.37
R203	6 *	874.90 *	[23]	6	877.00	0.24003 *	2108.4
R204	5 *	735.80 *	[22]	5	742.40	0.89698 *	2013.9
R205	5 *	954.20 *	[19]	5	957.20	0.31440 *	2050.3
R206	4 *	879.90 *	[23]	6	894.40	1.6479 *	1236.0
R207	4 *	798.00 *	[22]	5	808.60	1.3283 *	2164.1
R208	4 *	705.30 *	[22]	4	718.70	1.8999 *	871.52
R209	5 *	859.40 *	[23]	5	870.30	1.2683 *	1077.4
R210	6 *	905.20 *	[22]	6	916.00	1.1931 *	2154.1
R211	4 *	753.20 *	[22]	5	758.60	0.71694 *	1968.6
RC101	15	1619.8	[16]	16	1647.5	1.7101	2023.8
RC102	14	1457.4	[48]	14	1473.5	1.1047	868.49
RC103	11	1258.0	[17]	12	1282.5	1.9475	1585.9
RC104	10 *	1135.5 *	[21]	11	1159.2	2.0872 *	1363.0
RC105	15	1513.7	[47]	15	1554.9	2.7218	658.57
RC106	13 *	1368.0 *	[22]	14	1398.2	2.2076 *	1787.3
RC107	12	1207.8	[48]	12	1251.0	3.5768	1235.4
RC108	11	1114.2	[48]	11	1132.5	1.6424	1828.4
RC201	9	1261.8	[16]	9	1268.8	0.55476	1849.6
RC202	8	1092.3	[48]	8	1096.3	0.36620	506.41
RC203	5 *	926.80 *	[22]	5	934.40	0.82003 *	947.26
RC204	4 *	786.40 *	[23]	4	793.60	0.91556 *	664.77
RC205	7	1154.0	[48]	8	1162.7	0.75390	1385.4
RC206	7 *	1054.6 *	[23]	7	1070.2	1.4792 *	1334.3
RC207	6 *	966.10 *	[23]	6	967.70	0.1656 *	1641.8
RC208	4 *	778.90 *	[23]	4	778.90	0.0000 *	2208.1

compare the optimum objective function values and that obtained with our heuristic for the Solomon’s instances with 25, 50, and 100 customers, respectively. For those instances where the optimal solutions have not been found in the existing literature, we compare our results with the best solutions from the literature. The number of vehicles presented is equivalent to the number of caretakers. The customers presented can be seen as the patients. The “%Gap” is the percentage difference between the values obtained with our heuristic and the optimal values. With 52, 21, and 18 out of 56 cases that our heuristic can find the optimal solutions in 25, 50, and 100 customer instances, we can say that our heuristic performs better in smaller-size instances. In general, our heuristic performs better in C1 and C2 instances since the %Gap is smaller compared to the R1, R2, RC1, and RC2 instances. Moreover, in most cases the optimal solutions have yet to be found, and the %Gap is less than 5%.

Note that for all computations, the distance between each pair of nodes is truncated to 1 digit. It is also worth mentioning that the running time for each iteration on 25-customer instances is recorded at approximately 1 s for RC2 instances (at 20 total number of iterations), 2 s for all C1, R1, R2, and RC1 instances (at 10, 10, 12, and 20 iterations), and 3 s for C2 instances (at 15 iterations). The running times for each iteration on 50 customer instances are 4 s for C1 (at 25 iterations), 5 s for R2 and RC2 (at 25 and 30 iterations), and 6, 7, and 10 s for R1, RC1, and C2 instances (at 20, 25, and 30 iterations), respectively. For those instances with 100 customers, the running time for each iteration is recorded at approximately 30 s for all C1 instances, and 1 min for C2, R1, R2, RC1, and RC2 instances. Note that the running time depends on the number of particles and maximum iterations set. However, for each instance, the heuristic executes with the indicated solution after only a few iterations (for the worst case, up to 30 iterations or up to 30 min for each instance).

To further analyze the performance of our heuristic, we modify Solomon’s instances to contain compatibility between patients and caretakers. The solutions obtained with our heuristic are shown in

Table 6. Comparison between the exact solution of Solomon’s instances with and without compatibility, and the solution with compatibility obtained with our algorithm.

Problem	Optimum without Compatibility		Optimum with Compatibility			Our Algorithm with Compatibility		%Gap
	Number of Vehicles	Total Distance	Number of Vehicles	Total Distance	%Gap	Number of Vehicles	Total Distance
C101	3	191.3	3	253.3	0.0	4	228.3	−9.870
C102	3	190.3	3	244.1	0.0	3	267.3	9.504
C103	3	190.3	3	236.8	0.0	3	247.6	4.561
C104	3	186.9	3	261.3	0.0	3	263.6	0.8802
C105	3	191.3	3	228.9	0.0	3	243.5	6.378
C106	3	191.3	3	253.3	0.0	3	256.7	1.342
C107	3	191.3	3	232.1	0.0	3	246.7	6.290
C108	3	191.3	3	231.9	0.0	3	237.3	2.329
C109	3	191.3	3	231.9	0.0	3	246.5	6.300
C201	2	214.7	3	356.2	0.0	2	386.6	8.534
C202	2	214.7	2	244.8	0.0	2	244.8	0.000
C203	2	214.7	2	244.8	0.0	2	247.4	1.062
C204	2	213.1	2	235.8	0.0	2	244.8	3.817
C205	2	214.7	2	261.4	0.0	2	267.0	2.142
C206	2	214.7	2	259.1	0.0	2	263.0	1.505
C207	2	214.5	2	252.4	0.0	2	261.2	3.486
C208	2	214.5	2	251.8	0.0	2	251.8	0.000
R101	8	617.1	8	623.9	0.0	9	643.7	3.174
R102	7	547.1	7	553.6	0.0	7	585.7	5.798
R103	5	454.6	5	454.6	0.0	5	474.0	4.268
R104	4	416.9	4	416.9	0.0	4	416.9	0.000
R105	6	530.5	5	555.6	0.0	6	582.2	4.788
R106	3	465.4	5	465.4	0.0	5	475.2	2.106
R107	4	424.3	4	432.5	0.0	4	440.3	1.804
R108	4	397.3	4	407.9	0.0	4	408.3	0.09810
R109	5	441.3	5	446.9	0.0	4	481.0	7.630
R110	4	444.1	4	444.7	0.0	5	457.1	2.788
R111	5	428.8	4	437.8	0.0	4	477.1	8.977
R112	4	393.0	4	403.3	0.0	4	415.2	2.951
R201	4	463.3	3	463.3	0.0	3	503.9	8.763
R202	4	410.5	3	421.0	0.0	3	457.5	8.670
R203	3	391.4	3	412.0	0.0	2	444.5	7.888
R204	2	355.0	3	369.5	0.0	3	393.9	6.603
R205	3	393.0	2	418.8	0.0	2	418.8	0.000
R206	3	374.4	3	375.9	0.0	3	405.0	7.741
R207	3	361.6	3	375.9	0.0	3	400.7	6.598
R208	1	328.2	3	369.5	0.0	3	385.5	4.330
R209	2	370.7	3	390.5	0.0	3	409.8	4.942
R210	3	404.6	3	423.4	0.0	3	452.6	6.897
R211	2	350.9	3	381.3	0.0	3	413.6	8.471
RC101	4	461.1	4	464.9	0.0	5	488.2	5.0118
RC102	3	351.8	4	405.4	0.0	4	420.7	3.7741
RC103	3	332.8	4	386.4	0.0	4	386.4	0.0000
RC104	3	306.6	4	367.8	0.0	4	372.6	1.3051
RC105	4	411.3	4	458.9	0.0	5	481.4	4.9030
RC106	3	345.5	4	399.2	0.0	4	406.3	1.7786
RC107	3	298.3	4	365.9	0.0	4	368.3	0.6559
RC108	3	294.5	4	361.6	0.0	4	367.8	1.7146
RC201	3	360.2	3	524.5	0.0	3	574.5	9.5329
RC202	3	338.0	2	436.0	0.0	2	437.0	0.2294
RC203	3	326.9	3	356.6	0.0	4	362.9	1.7667
RC204	3	299.7	3	327.5	2.8	3	330.9	1.0382
RC205	3	338.0	3	498.7	7.4	3	547.8	9.8456
RC206	3	324.0	2	409.5	0.0	2	444.1	8.4493
RC207	3	298.3	4	672.3	0.0	4	701.7	4.3730
RC208	2	269.1	4	559.3	0.0	4	613.3	9.6549

along with the optimal solutions. Note the negative %Gap in the first instance: this is because our heuristic cannot find a feasible solution with 3 vehicles. The optimal solutions can be found for only 5 out of 56 cases. This indicates that the difficulty level of the problem has increased dramatically. Note that the computation time of the instances with compatibility is the same as without compatibility constraints.

6. Conclusions

In this paper, we formulated mathematical modeling and a heuristic for solving a home healthcare routing and scheduling problem in which caretakers must visit specific patients within a specific time frame. This problem can be formulated into a vehicle routing problem with time windows (VRPTW) and compatibility constraints.

Due to the NP-hard nature of the problem, we presented a new heuristic combining particle swarm optimization, inserting procedure, local search, path relinking, and ruin-and-recreate (R&R) procedures. In particular, the inserting procedure is used to generate initial solutions and restore the feasibility of the solution. The constructed local search procedure representing the particle’s movement to the local space is used to improve the solutions. Path relinking represents the global search movement of particles; at each iteration, the procedure is used to improve the current solution by integrating the current solution with the current best solution. R&R is deployed in cases where leaping out of the local optimum is necessary.

To test the performance of the heuristic, we applied it to Solomon’s instances with 25, 50 and 100 customers and compared objective values obtained with our heuristic and the optimum values collected from published literature. Computational results show that our proposed heuristic performs better on smaller instances and in all clustered problems (C1 and C2 instances). Further investigation with compatibility constraints included in the model shows that our proposed heuristic also performed very well on 25 customer instances yielding solutions with less than 10% optimality gap. However, only 5 optimal solutions are found in the model with compatibility constraints compared with 52 optimal solutions found in the model without the constraints. This also suggests that the problem is much more difficult compared with regular VRPTW.

The parameters in this study are experimentally selected to balance the computation time and solution quality. This does not guarantee the best performance of the algorithm. Moreover, as searching for the parameters is very time-consuming, one could consider the parameterized metaheuristic as presented in [52].