A Proactive Approach to Extended Vehicle Routing Problem with Drones (EVRPD)
Abstract
:1. Introduction
2. Vehicle Routing Problem with Drones-Literature Review
- (a)
- Area coverage where sensor or camera drones should monitor (cover) an area that may take various shapes. This problem occurs in disaster management (assessment of the damage after an earthquake, flood, tornado, etc.), agriculture (observing vegetation indexes and creating digital maps of the crop area), aerial archeology, etc. [15]
- (b)
- Search operations where drones need to find a stationary or moving object. In a drone search, this problem is easily observed in wildlife monitoring and search and rescue applications. You need to define a search path for one or more drones to find an object in an unknown location.
- (c)
- Routing for a set of locations where drones must visit a specific and finite set of addresses. In many surveillance and delivery applications, drones must tour a certain set of locations starting and ending at the depot. The resulting planning problems can be modeled as generalized versions of one of the underlying routing problems, such as a TSP [16,17], multiple TSPs [18,19,20,21,22,23,24,25], or a VRP [26,27,28,29,30].
- (d)
- Data collection and charging on wireless sensor networks (WSNs) where drones must collect information from a specific or given set of locations while considering the communication schedule and limited memory capacity.
- (e)
- Allocating communication links and computing power to mobile devices with set (or redirected) drones to provide communication links with mobile devices of sufficient quality.
3. Problem Statement and Mathematical Model
3.1. Problem Statement
- Recipients (customers) were defined (the location of each recipient was known, which translated into the determination of the distance–cost grid (network) between recipients and the travel time from recipient to recipient);
- Shipments (parcels) must be delivered or picked up from the customer;
- Several shipments (parcels) could be addressed to a customer (parcels should be delivered at once; if there are too many of them, e.g., the capacity of the drone was reached, we replaced one customer with two or more (we introduced the so-called virtual customers who had the same location)), which created significant novelty in relation to the VRPD;
- Various types of shipment were considered;
- Mobile points (mobile hubs—MHs) were used for drone take-offs;
- Drones and vehicles (i.e., trucks) were used to transport shipments (trucks to deliver drones to MHs and drones to deliver shipments to customers);
- The number of MHs was limited;
- Locations for MHs were known;
- The selection of MHs was optimized for a given set of shipments which created novelty in relation to VRPD;
- The number of drones and trucks was limited;
- Each drone was characterized by:
- ○
- Load capacity (which determined the number of shipments (parcels) it could carry);
- ○
- The maximum range (which determined the time in which the parcels must be delivered);
- In general, a drone could visit several clients, which was especially useful for a network of clients, e.g., a network of pharmacies, a network of car repair shops, etc.;
- The delivery route for all drones was minimized;
- The allocation of shipments to drones and drones to vehicles was determined, which introduced novelty in relation to the VRPD;
- If it was impossible to deliver a set of shipments, the shipments preventing delivery were found;
- Situations where a specific drone dx was damaged or unavailable and could not take part in deliveries were also considered.
3.2. Mathematical Model
4. Materials and Methods—Implementation of the EVRPD Model
4.1. AMPL and Mathematical Programming
4.2. Dedicated Genetic Algorithm
4.2.1. Dedicated Representation of Individuals for the EVRPD
4.2.2. Initiation—Selection of the Initial Population
4.2.3. Evaluation Procedure
- Step 1: The traveling salesman problem (TSP) was solved for each MH starting point and each drone. The route was determined in such a way that the cost of delivery was the lowest, and the delivery time was within the set time.
- Step 2: The MH starting points were selected in such a way that the total cost of deliveries was as low as possible and that the number of allowed starting points was not exceeded. This step also ensured that constraint (14) was satisfied.
4.2.4. Constraint Handling Procedure
4.2.5. Genetic Operators
5. Computational Examples
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. AMPL Model for the EVRPD (Files Ready to Use for the Gurobi Solver)
Appendix B. Data for EVRPD
| k | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Vkk | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| UAk | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| k | 1 | 2 | 3 | 4 |
| VCd | 10 | 10 | 10 | 10 |
| WAk,o | o | |||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | ||
| k | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 3 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 4 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | |
| 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | |
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | |
| 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | |
| FAo,j | j | |||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | ||
| o | 1 | 0 | 2 | 4 | 3 | 6 | 7 | 5 | 3 | 1 | 5 | 3 | 4 | 3 |
| 2 | 2 | 0 | 5 | 4 | 5 | 9 | 6 | 5 | 1 | 7 | 4 | 2 | 3 | |
| 3 | 4 | 5 | 0 | 4 | 7 | 3 | 5 | 4 | 5 | 2 | 2 | 7 | 6 | |
| 4 | 3 | 4 | 4 | 0 | 8 | 7 | 2 | 1 | 3 | 4 | 5 | 5 | 3 | |
| 5 | 6 | 5 | 7 | 8 | 0 | 8 | 10 | 8 | 6 | 9 | 4 | 7 | 8 | |
| 6 | 7 | 9 | 3 | 7 | 8 | 0 | 8 | 7 | 8 | 3 | 4 | 10 | 9 | |
| 7 | 5 | 6 | 5 | 2 | 10 | 8 | 0 | 2 | 5 | 5 | 7 | 7 | 4 | |
| 8 | 3 | 5 | 4 | 1 | 8 | 7 | 2 | 0 | 4 | 4 | 5 | 5 | 3 | |
| 9 | 1 | 1 | 5 | 3 | 6 | 8 | 5 | 4 | 0 | 6 | 5 | 2 | 2 | |
| 10 | 5 | 7 | 2 | 4 | 9 | 3 | 5 | 4 | 6 | 0 | 4 | 9 | 7 | |
| 11 | 3 | 4 | 2 | 5 | 4 | 4 | 7 | 5 | 5 | 4 | 0 | 7 | 6 | |
| 12 | 4 | 2 | 7 | 5 | 7 | 10 | 7 | 5 | 2 | 9 | 7 | 0 | 3 | |
| 13 | 3 | 3 | 6 | 3 | 8 | 9 | 4 | 3 | 2 | 7 | 6 | 3 | 0 | |
| TAo,j | o | |||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | ||
| j | 1 | 0 | 1 | 2 | 1 | 3 | 3 | 2 | 1 | 1 | 3 | 2 | 2 | 1 |
| 2 | 1 | 0 | 3 | 2 | 2 | 4 | 3 | 2 | 1 | 4 | 2 | 1 | 2 | |
| 3 | 2 | 3 | 0 | 2 | 3 | 2 | 3 | 2 | 2 | 1 | 1 | 4 | 3 | |
| 4 | 1 | 2 | 2 | 0 | 4 | 4 | 1 | 0 | 2 | 2 | 3 | 2 | 1 | |
| 5 | 3 | 2 | 3 | 4 | 0 | 4 | 5 | 4 | 3 | 4 | 2 | 3 | 4 | |
| 6 | 3 | 4 | 2 | 4 | 4 | 0 | 4 | 3 | 4 | 1 | 2 | 5 | 5 | |
| 7 | 2 | 3 | 3 | 1 | 5 | 4 | 0 | 1 | 3 | 2 | 3 | 3 | 2 | |
| 8 | 1 | 2 | 2 | 0 | 4 | 3 | 1 | 0 | 2 | 2 | 2 | 3 | 2 | |
| 9 | 1 | 1 | 2 | 2 | 3 | 4 | 3 | 2 | 0 | 3 | 2 | 1 | 1 | |
| 10 | 3 | 4 | 1 | 2 | 4 | 1 | 2 | 2 | 3 | 0 | 2 | 4 | 4 | |
| 11 | 2 | 2 | 1 | 3 | 2 | 2 | 3 | 2 | 2 | 2 | 0 | 3 | 3 | |
| 12 | 2 | 1 | 4 | 2 | 3 | 5 | 3 | 3 | 1 | 4 | 3 | 0 | 1 | |
| 13 | 1 | 2 | 3 | 1 | 4 | 5 | 2 | 2 | 1 | 4 | 3 | 1 | 0 | |
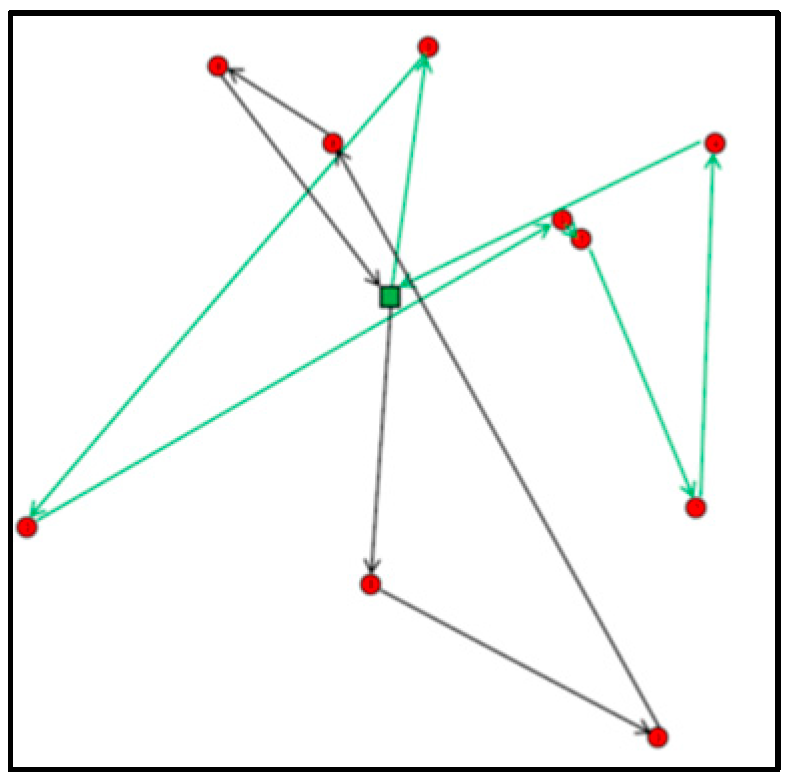
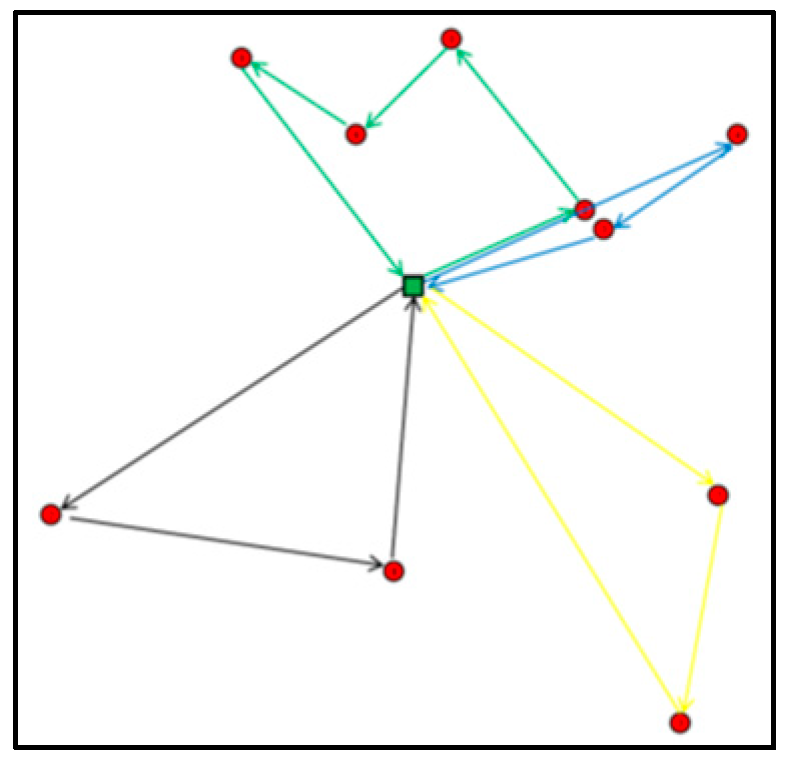
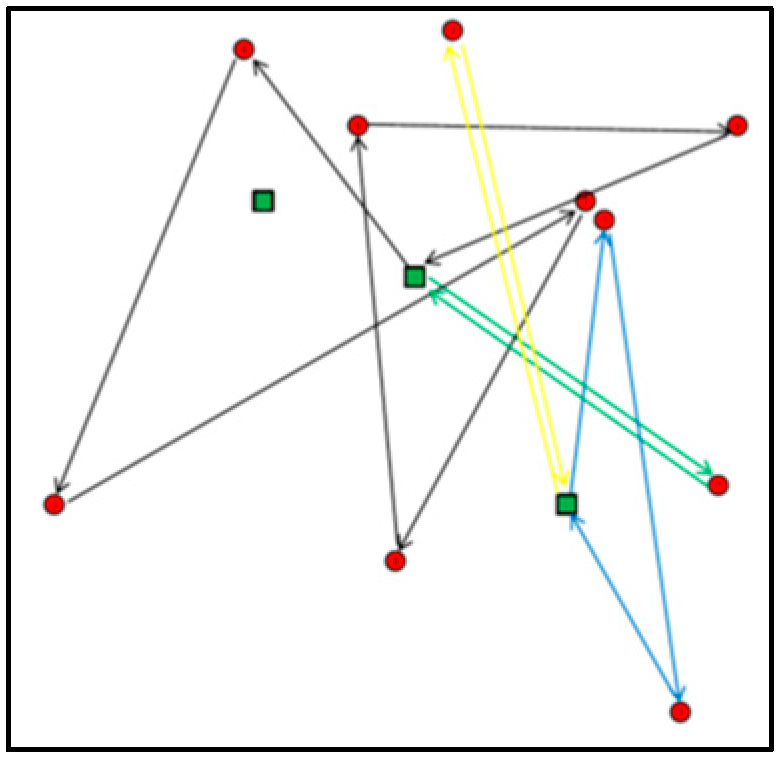
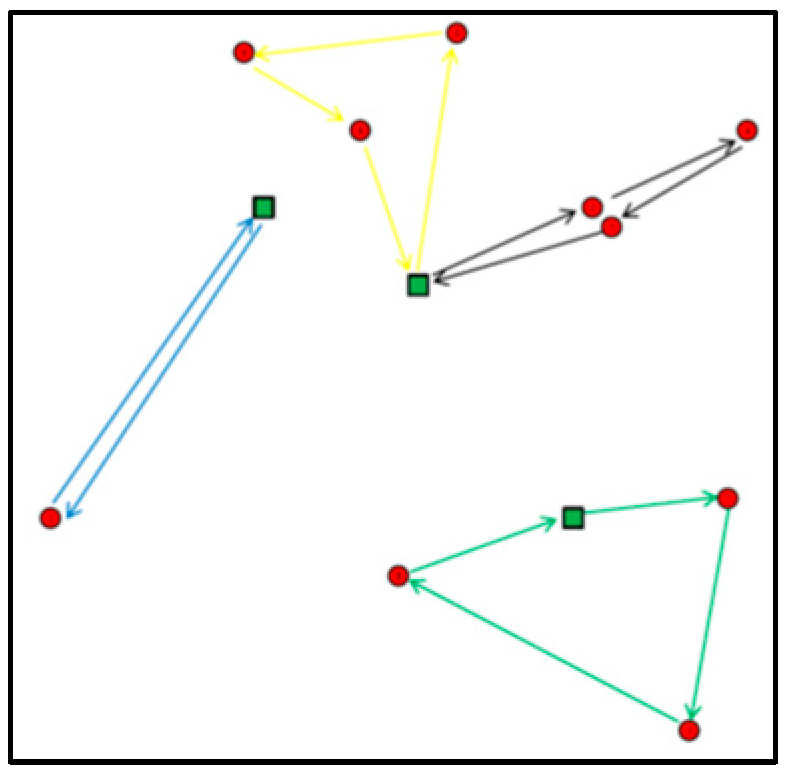
Appendix C. Obtained Routes for Experiments E01, E05, E07, E09, E12 and E16


References
- Aurambout, J.P.; Gkoumas, K.; Ciuffo, B. Last mile delivery by drones: An estimation of viable market potential and access to citizens across European cities. Eur. Transp. Res. Rev. 2019, 11, 30. [Google Scholar] [CrossRef]
- Singireddy, S.R.R.; Daim, T.U. Technology Roadmap: Drone Delivery—Amazon Prime Air. In Infrastructure and Technology Management. Innovation, Technology, and Knowledge Management; Daim, T., Chan, L., Estep, J., Eds.; Springer: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- ConnCarProjectReport-1.pdf (berkeley.edu). Available online: https://scet.berkeley.edu/wp-content/uploads/ConnCarProjectReport-1.pdf (accessed on 10 July 2021).
- Merkert, R.; Bushell, J. Managing the drone revolution: A systematic literature review into the current use of airborne drones and future strategic directions for their effective control. J. Air Transp. Manag. 2020, 89, 101929. [Google Scholar] [CrossRef] [PubMed]
- Hern, A. DHL Launches First Commercial Drone ‘Parcelcopter’ Delivery Service. Available online: https://www.theguardian.com/technology/2014/sep/25/german-dhl-launches-first-commercial-drone-delivery-service (accessed on 10 July 2021).
- Drones Are Legit Delivering Pizza Right Now in New Zealand. Available online: https://www.inc.com/will-yakowicz/drone-pizza-delivery-flirtey-dominos.html (accessed on 10 July 2021).
- Amorosi, L.; Puerto, J.; Valverde, C. Coordinating drones with mothership vehicles: The mothership and drone routing problem with graphs. Comput. Oper. Res. 2021, 136, 105445. [Google Scholar] [CrossRef]
- Thibbotuwawa, A.; Bocewicz, G.; Nielsen, P.; Banaszak, Z. Unmanned Aerial Vehicle Routing Problems: A Literature Review. Appl. Sci. 2020, 10, 4504. [Google Scholar] [CrossRef]
- Apt, K.; Wallace, M. Constraint Logic Programming using Eclipse; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Home AMPL. Available online: https://ampl.com/ (accessed on 10 July 2021).
- Sitek, P.; Wikarek, J.; Bocewicz, G.; Nielsen, I. A decision support model for handling customer orders in business chain. Neurocomputing 2021, 482, 298–309. [Google Scholar] [CrossRef]
- Dell’Amico, M.; Montemanni, R.; Novellani, S. Drone-assisted deliveries: New formulations for the flying sidekick traveling salesman problem. Optim. Lett. 2021, 15, 1617–1648. [Google Scholar] [CrossRef]
- Kim, S.; Moon, I. Traveling salesman problem with a drone station. IEEE Trans. Syst. Man Cybern. Syst. 2018, 49, 42–52. [Google Scholar] [CrossRef]
- Otto, A.; Agatz, N.; Campbell, J.; Golden, B.; Pesch, E. Optimization approaches for civil applications of unmanned aerial vehicles (UAVs) or aerial drones: A survey. Networks 2018, 72, 411–458. [Google Scholar] [CrossRef]
- Park, Y.; Nielsen, P.; Moon, I. Unmanned aerial vehicle set covering problem considering fixed-radius coverage constraint. Comput. Oper. Res. 2020, 119, 104936. [Google Scholar] [CrossRef]
- Phung, M.D.; Quach, C.H.; Dinh, T.H.; Ha, Q. Enhanced discrete particle swarm optimization path planning for UAV vision-based surface inspection. Autom. Constr. 2017, 81, 25–33. [Google Scholar] [CrossRef]
- Sanci, S.; Isler, V. A parallel algorithm for UAV flight route planning on GPU. Int. J. Parallel Program. 2011, 39, 809–837. [Google Scholar] [CrossRef]
- Alidaee, B.; Gao, H.; Wang, H. A note on task assignment of several problems. Comput. Ind. Eng. 2010, 59, 1015–1018. [Google Scholar] [CrossRef]
- Bae, J.; Rathinam, S. Approximation algorithm for a heterogeneous vehicle routing problem. Int. J. Adv. Robot. Syst. 2015, 12. [Google Scholar] [CrossRef]
- Bellingham, J.; Tillerson, M.; Richards, A.; How, J.P. Multi-task allocation and path planning for cooperating UAVs. In Cooperative Control: Models, Applications and Algorithms; Butenko, S., Murphey, R., Pardalos, P.M., Eds.; Springer: Boston, MA, USA, 2003; pp. 23–41. [Google Scholar] [CrossRef]
- Manyam, S.G.; Rathinam, S.; Darbha, S. Computation of lower bounds for a multiple depot, multiple vehicle routing problem with motion constraints. J. Dyn. Syst. Meas. Control 2015, 137, 2378–2383. [Google Scholar] [CrossRef]
- Rathinam, S.; Sengupta, R. Lower and upper bounds for a multiple depot UAV routing problem. In Proceedings of the 45th IEEE Conference on Decision and Control, San Diego, CA, USA, 13–15 December 2006; pp. 5287–5292. [Google Scholar] [CrossRef]
- Sundar, K.; Rathinam, S. Algorithms for heterogeneous, multiple depot, multiple unmanned vehicle path planning problems. J. Intell. Robot. Syst. 2017, 88, 513–526. [Google Scholar] [CrossRef]
- Venkatachalam, S.; Sundar, K.; Rathinam, S. Two-stage stochastic programming model for routing multiple drones with fuel constraints. arXiv 2017, arXiv:1711.04936. [Google Scholar]
- Vilar, R.G.; Shin, H.S. Communication-aware task assignment for UAV cooperation in urban environments. IFAC Proc. 2013, 46, 352–359. [Google Scholar] [CrossRef]
- Gottlieb, Y.; Shima, T. UAVs task and motion planning in the presence of obstacles and prioritized targets. Sensors 2015, 15, 29734–29764. [Google Scholar] [CrossRef]
- Jiang, X.; Zhou, Q.; Ye, Y. Method of task assignment for UAV based on particle swarm optimization in logistics. In Proceedings of the 2017 International Conference on Intelligent Systems, Metaheuristics & Swarm Intelligence, Hong Kong, China, 25–27 March 2017; pp. 113–117. [Google Scholar] [CrossRef]
- Kim, S.J.; Lim, G.J.; Cho, J.; Côté, M.J. Drone-aided healthcare services for patients with chronic diseases in rural areas. J. Intell. Robot. Syst. 2017, 88, 163–180. [Google Scholar] [CrossRef]
- Liu, X.F.; Guan, Z.-W.; Song, Y.-Q.; Chen, D.-S. An optimization model of UAV route planning for road segment surveillance. J. Cent. South Univ. 2014, 21, 2501–2510. [Google Scholar] [CrossRef]
- Phan, D.H.; Suzuki, J. Evolutionary multiobjective optimization for the pickup and delivery problem with time windows and demands. Mob. Netw. Appl. 2016, 21, 175–190. [Google Scholar] [CrossRef]
- Wang, Z.; Sheu, J.B. Vehicle routing problem with drones. Transp. Res. Part B Methodol. 2019, 122, 350–364. [Google Scholar] [CrossRef]
- Murray, C.C.; Chu, A.G. The flying sidekick traveling salesman problem: Optimization of drone-assisted parcel delivery. Transp. Res. Part C Emerg. Technol. 2015, 54, 86–109. [Google Scholar] [CrossRef]
- Murray, C.C.; Raj, R. The multiple flying sidekicks traveling salesman problem: Parcel delivery with multiple drones. Transp. Res. Part C Emerg. Technol. 2020, 110, 368–398. [Google Scholar] [CrossRef]
- Phan, C.; Liu, H.H.T. A cooperative UAV/UGV platform for wildfire detection and fighting. In Proceedings of the 2008 Asia Simulation Conference—7th International Conference on System Simulation and Scientific Computing, Beijing, China, 10–12 October 2008; pp. 494–498. [Google Scholar] [CrossRef]
- Viguria, A.; Maza, I.; Ollero, A. Distributed service-based cooperation in aerial/ground robot teams applied to fire detection and extinguishing missions. Adv. Robot. 2010, 24, 1–23. [Google Scholar] [CrossRef]
- Wu, G.; Pedrycz, W.; Li, H.; Ma, M.; Liu, J. Coordinated planning of heterogeneous Earth observation resources. IEEE Trans. Syst. Man Cybern. Syst. 2016, 46, 109–125. [Google Scholar] [CrossRef]
- Puerto, J.; Valverde, C. Routing for unmanned aerial vehicles: Touring dimensional sets. Eur. J. Oper. Res. 2022, 298, 118–136. [Google Scholar] [CrossRef]
- Rojas, V.; Solano-Charris, E.; Muñoz-Villamizar, A.; Montoya-Torres, J.R. Unmanned aerial vehicles/drones in vehicle routing problems: A literature review. Int. Trans. Oper. Res. 2021, 28, 1626–1657. [Google Scholar] [CrossRef]
- Sujit, P.B.; Sousa, J.; Pereira, F.L. UAV and AUVs coordination for ocean exploration. In Proceedings of the OCEANS 2009-EUROPE, Bremen, Germany, 11–14 May 2009; pp. 1–7. [Google Scholar] [CrossRef]
- Tokekar, P.; Hook, J.V.; Mulla, D.; Isler, V. Sensor planning for a symbiotic UAV and UGV system for precision agriculture. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2016; Volume 32, pp. 1498–1511. [Google Scholar] [CrossRef]
- Jia, S.; Zhang, L. Modelling unmanned aerial vehicles base station in ground-to-air cooperative networks. IET Commun. 2017, 11, 1187–1194. [Google Scholar] [CrossRef]
- Ladosz, P.; Oh, H.; Chen, W.H. Trajectory planning for communication relay unmanned aerial vehicles in urban dynamic environments. J. Intell. Robot. Syst. 2018, 89, 7–25. [Google Scholar] [CrossRef]
- Oh, H.; Shin, H.S.; Kim, S.; Tsourdos, A.; White, B.A. Cooperative mission and path planning for a team of UAVs. In Handbook of Unmanned Aerial Vehicles; Valavanis, K.P., Vachtsevanos, G.J., Eds.; Springer: Dordrecht, The Netherlands, 2015; pp. 1509–1545. [Google Scholar]
- Sharma, V.; Srinivasan, K.; Kumar, R.; Chao, H.-C.; Hua, K.-L. Efficient cooperative relaying in flying ad hoc networks using fuzzy-bee colony optimization. J. Supercomput. 2017, 73, 3229–3259. [Google Scholar] [CrossRef]
- Dyrkoren, E.; Berg, T. Norwegian work on search and rescue in Barents Sea. In Proceedings of the 33rd International Conference on Offshore Mechanics and Arctic Engineering, Volume 10: Polar and Arctic Science and Technology, San Francisco, CA, USA, 8–13 June 2014. [Google Scholar] [CrossRef]
- Wang, X.; Poikonen, S.; Golden, B. The vehicle routing problem with drones: Several worst-case results. Optim. Lett. 2016, 11, 679–697. [Google Scholar] [CrossRef]
- Poikonen, S.; Wang, X.; Golden, B. The Vehicle Routing Problem with Drones: Extended Models and Connections. Networks 2017, 70, 34–43. [Google Scholar] [CrossRef]
- Ulmer, M.; Thomas, B. Same-Day Delivery with a Heterogeneous Fleet of Drones and Vehicles. Networks 2018, 72, 475–505. [Google Scholar] [CrossRef]
- Dorling, K.; Heinrichs, J.; Messier, G.G.; Magierowski, S. Vehicle Routing Problems for Drone Delivery. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 70–85. [Google Scholar] [CrossRef]
- Luo, H.; Liang, Z.; Zhu, M.; Hu, X.; Wang, G. Integrated optimization of unmanned aerial vehicle task allocation and path planning under steady wind. PLoS ONE 2018, 13, e0194690. [Google Scholar] [CrossRef]
- Gurobi—The Fastest Solver. Available online: https://www.gurobi.com/ (accessed on 10 July 2021).
- LINGO and Optimization Modeling. Available online: https://www.lindo.com/index.php/products/lingo-and-optimization-modeling (accessed on 10 July 2021).
- Zhou, Y.; Lee, G.M. A Bi-Objective Medical Relief Shelter Location Problem Considering Coverage Ratios. Int. J. Ind. Eng. Theory Appl. Pract. 2021, 27, 971–988. [Google Scholar] [CrossRef]
- Zenodo—Research. Available online: https://zenodo.org/record/2572764#.YYvxmmDMKUk (accessed on 10 July 2022).
- Wehbi, X.L.; Bektaş, T.; Iris, C. Optimising vehicle and on-foot porter routing in urban logistics. Transp. Res. Part D Transp. Environ. 2022, 109, 103371. [Google Scholar] [CrossRef]
- Caggiani, Y.L.; Colovic, A.; Prencipe, L.P.; Ottomanelli, M. A green logistics solution for last-mile deliveries considering e-vans and e-cargo bikes. Transp. Res. Procedia 2021, 52, 75–82. [Google Scholar] [CrossRef]
- Sacramento, Z.D.; Pisinger, D.; Ropke, S. An adaptive large neighborhood search metaheuristic for the vehicle routing problem with drones. Transp. Res. Part C Emerg. Technol. 2019, 102, 289–315. [Google Scholar] [CrossRef]



| (A) | ||||
| Symbol | Description | P/R | ||
| Q1 | Is it possible to make deliveries? | P/R | ||
| Q2 | What is the minimum cost of deliveries? | P/R | ||
| Q3 | Is it possible to make deliveries within the given time T? | P/R | ||
| Q4 | What is the minimum cost of deliveries in the given time T? | P/R | ||
| Q5 | What is the minimum number of mobile points (mobile hubs—MHs) required to make deliveries? | P | ||
| Q6 | What is the minimum number of drones needed to make deliveries? | P | ||
| Q7 | Can deliveries be made if the drone dx is damaged? | P | ||
| Q8 | Is it possible to make deliveries if it is not possible to use the mobile point mx? | P | ||
| P/R—proactive/reactive | ||||
| (B) | ||||
| Question | Set of constraints | Problem type | Model type | Decision Variable |
| Q1 | (2)–(8) and (10)–(15) | feasible | CSP | Rs |
| Q2 | (1a) and (2)–(8) and (10)–(15) | optimal | BIP | Xh,d,c,j, Rs |
| Q3 | (2)–(15) | feasible | CSP | Rs |
| Q4 | (1a) and (2)–(15) | optimal | BIP | Xh,d,c,j, Rs |
| Q5 | (2)–(8) and (10)–(15) and min MS | optimal | BIP | Zh |
| Q6 | (1b) and (2)–(8) and (10)–(15) | optimal | BIP | Yh,d,c,j,s |
| Q7 | (2)–(8) and (10)–(15) and VCdi = 0 | feasible | CSP | Rs, Yh,d,c,j,s |
| Q8 | (2)–(8) and (10)–(15) and VKmx = 0 | feasible | CSP | Zh, Xh,d,c,j |
| Symbol | Description |
|---|---|
| Indices and Sets | |
| C | The set of customers |
| S | The set of all items (shipments, parcels) |
| D | The set of all drones |
| H | A set of possible locations for mobile points (mobile hubs—MHs) |
| c, j | Delivery point (customer) index (c, j ∈ C) |
| s | Shipment index (s∈S) |
| d | Drone index (d∈D) |
| h | Mobile point index (h∈K) |
| Parameters | |
| VSs | Parcel volume (volumetric weight) s (s∈S) |
| VCd | Drone’s d payload (d∈D) |
| RAs,c | If parcel k should be delivered to customer o, then RAs,c = 1, otherwise RAs,c = 0 (s∈S, c∈C) |
| FAc,j | Cost of travel between customers c and j (c, j ∈ C ∪ M)—average values include 2D and 3D |
| TAc,j | Transfer time between customers c and j (c, j ∈ C ∪ M)—average values include 2D and 3D |
| TX | Time within which the delivery should be made |
| MS | Maximum number of mobile points (mobile hubs—MHs) |
| ST | A large constant |
| UAs | If parcel s was delivered from the mobile point (MH) to the customer, then UAs = 1; otherwise, UAs = 0 (s∈S). The parameter value determined the delivery direction. |
| Decision variables | |
| Xh,d,c,j | If a drone d traveled from customer c to customer j and took off from MH, h then Xh,d,c,j = 1, otherwise Xh,d,c,j = 0, (h∈H, d∈D, c,j∈C∪M). |
| Yh,d,c,j,s | If a drone d traveled from customer c to customer j and took off from MH, h carrying parcel s, then Yh,d,c,j,s = 1, otherwise Yh,d,c,j,s = 0, (h∈H, d∈D, c, j∈C∪M). |
| Rs | If parcel s could not be delivered, then Rs = 1 otherwise Rs = 0 (s∈S). (The introduction of this decision variable meant that the model will always be solvable.) |
| Zh | If there were take-offs from mobile point h, then Zh = 1; otherwise, Zh = 0. |
| Constraints | Description |
|---|---|
| (1a) | Delivery cost (for Q2 and Q4, it is an objective function (FC1) and is minimized) |
| (1b) | Number of drones used (for Q6, it is an objective function (FC2) and is minimized) |
| (2) | Determined the arrival and departure of the drone at and from the delivery point (customer) |
| (3) | If no items were to be carried on the route, then a drone did not travel that route. |
| (4) | If a drone did not travel along a route, no items were to be carried on that route. |
| (5) | In no route segment could a drone carry more parcels than its payload. |
| (6) | Items were delivered to and from mobile points, h∈H. |
| (7) | Ensured a single run of the drone |
| (8) | Items were picked up or delivered to customers. This constraint prevented sub-tours. |
| (9) | Runs were executed within the required time. |
| (10) | Each drone picked up or delivered parcels from or to a source (MH); the first component of the constraint was responsible for the delivery of parcels to the customer, while the second was responsible for the pick up from the customer. |
| (11) | Ensured the drone was at a point only once (no returns). |
| (12) | Ensured the drone took off and returned to the MH point. (We excluded the possibility that the drone left the parcel with a given customer and another took it to the next customer). |
| (13) | Determined the value of the decision variable Zh. This variable determined mobile point h∈H from the drone take-off point (in this version of the model, we did not introduce capacity limits for trucks, so Zh = 1 determined both the MH point and the truck). |
| (14) | Drone take-offs could not take place from more mobile points h∈H than the number of vehicles (trucks). |
| (15) | Binarity |
| E | Q | N_MH | ST | MI (MO) | SC | TR | AMPL+Gurobi | DGA | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TX | V | T | FC | TX | T | FC | |||||||
| E01 | Q1 | 1 | 1 | 10 (10) | 1 | 30 | 26 | 1211 | 1 | 56 | 22 | 2 | 48 |
| E02 | Q2 | 1 | 1 | 10 (10) | 1 | 30 | 16 | 1211 | 1 | 34 | 16 | 25 | 34 |
| E03 | Q3 | 1 | 1 | 10 (10) | 1 | 16 | 16 | 1221 | 1 | 42 | 16 | 4 | 35 |
| E04 | Q4 | 1 | 1 | 10 (10) | 1 | 16 | 16 | 1211 | 1 | 34 | 16 | 25 | 34 |
| E05 | Q1 | 1 | 1 | 10 (10) | 4 | 30 | 15 | 4841 | 2 | 55 | 18 | 1 | 51 |
| E06 | Q2 | 1 | 1 | 10 (10) | 4 | 30 | 16 | 4841 | 2 | 34 | 16 | 24 | 34 |
| E07 | Q3 | 1 | 1 | 10 (10) | 4 | 10 | 7 | 4841 | 15 | 52 | 7 | 3 | 52 |
| E08 | Q4 | 1 | 1 | 10 (10) | 4 | 10 | 9 | 4841 | 35 | 40 | 9 | 25 | 40 |
| E09 | Q1 | 3 | 2 | 10 (10) | 4 | 30 | 19 | 17,427 | 3 | 75 | 18 | 4 | 66 |
| E10 | Q2 | 3 | 2 | 10 (10) | 4 | 30 | 15 | 17,427 | 3 | 33 | 15 | 25 | 33 |
| E11 | Q3 | 3 | 2 | 10 (10) | 4 | 10 | 6 | 17,427 | 67 | 41 | 6 | 8 | 41 |
| E12 | Q4 | 3 | 2 | 10 (10) | 4 | 10 | 7 | 17,427 | 85 | 37 | 7 | 25 | 37 |
| E13 | Q1 | 3 | 3 | 10 (10) | 4 | 30 | 18 | 17,427 | 2 | 42 | 15 | 10 | 38 |
| E14 | Q2 | 3 | 3 | 10 (10) | 4 | 30 | 15 | 17,427 | 7 | 33 | 15 | 25 | 33 |
| E15 | Q3 | 3 | 3 | 10 (10) | 4 | 8 | 7 | 17,427 | 8 | 52 | 5 | 12 | 50 |
| E16 | Q4 | 3 | 3 | 10 (10) | 4 | 8 | 5 | 17,427 | 12 | 40 | 5 | 25 | 40 |
| E17 | Q5 | 1 | 1 | 10 (10) | 1 | 30 | --- | 1211 | 2 | 1 | --- | 2 | 1 |
| E18 | Q6 | 1 | 1 | 10 (10) | 1 | 30 | --- | 1211 | 2 | 1 | --- | 2 | 1 |
| E19 | Q5 | 1 | 1 | 10 (10) | 1 | 16 | --- | 1211 | 2 | 1 | --- | 2 | 1 |
| E20 | Q6 | 1 | 1 | 10 (10) | 1 | 16 | --- | 1211 | 2 | 1 | --- | 2 | 1 |
| E21 | Q5 | 1 | 1 | 10 (10) | 4 | 30 | --- | 4841 | 2 | 1 | --- | 2 | 1 |
| E22 | Q6 | 1 | 1 | 10 (10) | 4 | 30 | --- | 4841 | 2 | 1 | --- | 2 | 1 |
| E23 | Q5 | 1 | 1 | 10 (10) | 4 | 16 | --- | 4841 | 4 | 1 | --- | 4 | 1 |
| E24 | Q6 | 1 | 1 | 10 (10) | 4 | 16 | --- | 4841 | 34 | 2 | --- | 27 | 2 |
| E25 | Q5 | 3 | 2 | 10 (10) | 4 | 30 | --- | 17,427 | 3 | 1 | --- | 3 | 1 |
| E26 | Q6 | 3 | 2 | 10 (10) | 4 | 30 | --- | 17,427 | 4 | 1 | --- | 4 | 1 |
| E27 | Q5 | 3 | 2 | 10 (10) | 4 | 30 | --- | 17,427 | 48 | 2 | --- | 23 | 2 |
| E28 | Q6 | 3 | 2 | 10 (10) | 4 | 30 | --- | 17,427 | 92 | 3 | --- | 25 | 3 |
| E29 | Q5 | 3 | 3 | 10 (10) | 4 | 30 | --- | 17,427 | 3 | 1 | --- | 3 | 1 |
| E30 | Q6 | 3 | 3 | 10 (10) | 4 | 30 | --- | 17,427 | 1 | 1 | --- | 1 | 1 |
| E31 | Q5 | 3 | 3 | 10 (10) | 4 | 30 | --- | 17,427 | 34 | 2 | --- | 24 | 2 |
| E32 | Q6 | 3 | 3 | 10 (10) | 4 | 30 | --- | 17,427 | 67 | 4 | --- | 28 | 4 |
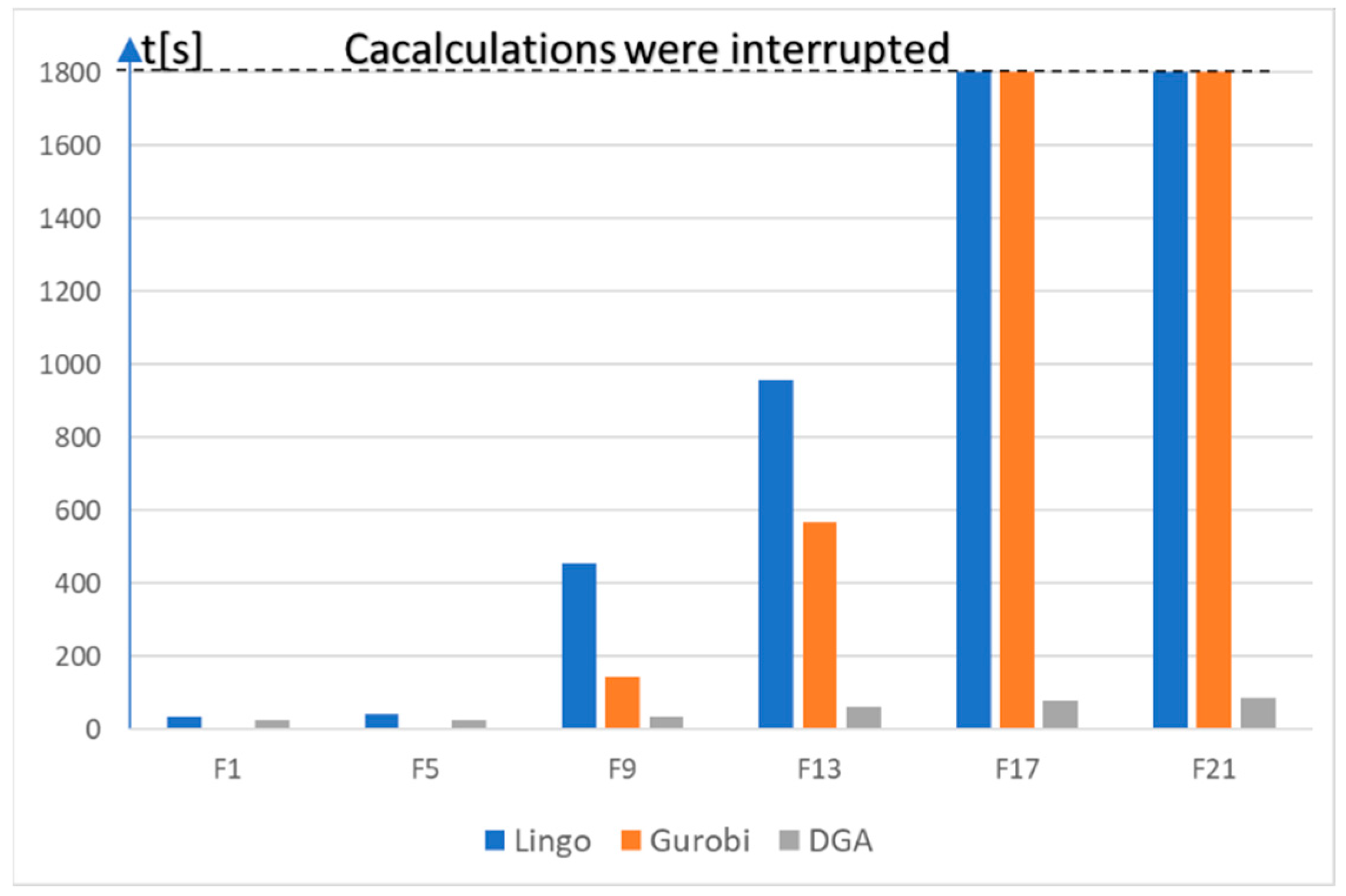
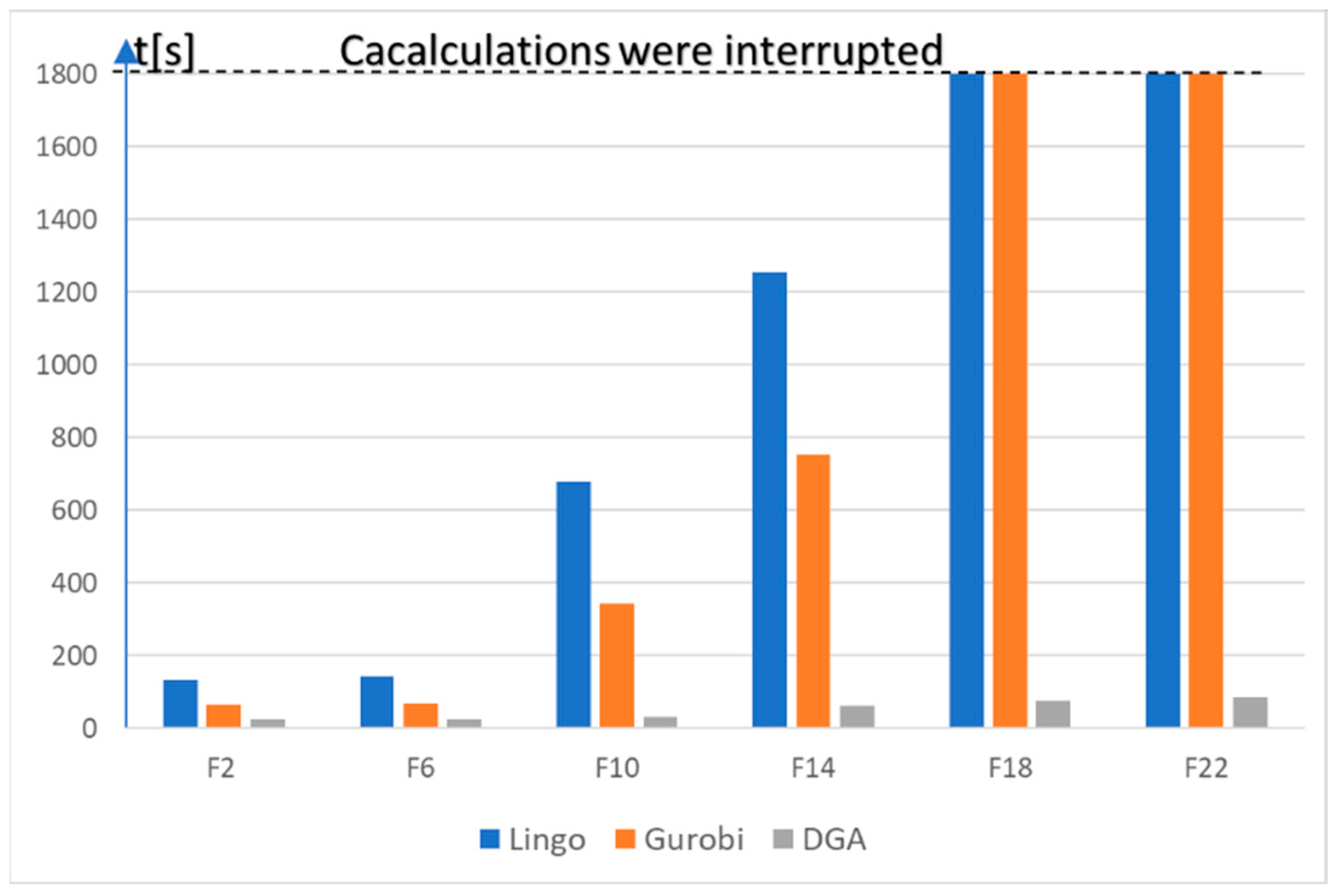
| F (Instance) | Q | MI (MO) | SC | TR | AMPL+Gurobi | AMPL+LINGO | DGA | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| V | TX | T | FC | T | FC | TX | T | FC | |||||
| F1 (10.10.1.txt) | Q2 | 10 (10) | 4 | 30 | 17,427 | 15 | 3 | 33 | 34 | 33 | 15 | 25 | 33 |
| F2 (10.10.1.txt) | Q4 | 10 (10) | 4 | 8 | 17,427 | 7 | 67 | 37 | 134 | 37 | 7 | 25 | 37 |
| F3 (10.10.1.txt) | Q5 | 10 (10) | 4 | 8 | 17,427 | --- | 4 | 1 | 35 | 1 | --- | 8 | 1 |
| F4 (10.10.1.txt) | Q6 | 10 (10) | 4 | 8 | 17,427 | --- | 54 | 1 | 145 | 1 | --- | 14 | 1 |
| F5 (10.10.3.txt) | Q2 | 10 (10) | 4 | 30 | 17,427 | 14 | 6 | 29 | 41 | 29 | 14 | 24 | 29 |
| F6 (10.10.3.txt) | Q4 | 10 (10) | 4 | 10 | 17,427 | 7 | 68 | 36 | 145 | 36 | 7 | 25 | 36 |
| F7 (10.10.3.txt) | Q5 | 10 (10) | 4 | 10 | 17,427 | --- | 6 | 1 | 45 | 1 | --- | 10 | 1 |
| F8 (10.10.3.txt) | Q6 | 10 (10) | 4 | 10 | 17,427 | --- | 3 | 1 | 189 | 1 | --- | 13 | 1 |
| F9 (12.10.1.txt) | Q2 | 12 (12) | 4 | 30 | 28,395 | 16 | 145 | 32 | 456 | 32 | 16 | 34 | 32 |
| F10 (12.10.1.txt) | Q4 | 12 (12) | 4 | 10 | 28,395 | 10 | 345 | 35 | 678 | 35 | 10 | 33 | 35 |
| F11 (12.10.1.txt) | Q5 | 12 (12) | 4 | 10 | 28,395 | --- | 67 | 2 | 189 | 2 | --- | 23 | 2 |
| F12 (12.10.1.txt) | Q6 | 12 (12) | 4 | 10 | 28,395 | --- | 345 | 2 | 867 | 2 | --- | 34 | 2 |
| F13 (20.10.1.txt) | Q2 | 20 (20) | 4 | 30 | 116,424 | 18 | 567 | 67 | 956 | 67 | 18 | 61 | 67 |
| F14 (20.10.1.txt) | Q4 | 20 (20) | 4 | 12 | 116,424 | 10 | 754 | 82 | 1256 | 82 | 10 | 62 | 82 |
| F15 (20.10.1.txt) | Q5 | 20 (20) | 4 | 12 | 116,424 | --- | 134 | 2 | 565 | 2 | --- | 55 | 2 |
| F16 (20.10.1.txt) | Q6 | 20 (20) | 4 | 12 | 116,424 | --- | 534 | 3 | 987 | 3 | --- | 57 | 3 |
| F17 (50.10.1.txt) | Q2 | 50 (50) | 4 | 30 | 1,727,485 | 28 | 1800 * | 132 | 1800 * | NFSF | 26 | 78 | 128 |
| F18 (50.10.1.txt) | Q4 | 50 (50) | 4 | 25 | 1,727,485 | 24 | 1800 * | 156 | 1800 * | NFSF | 24 | 76 | 141 |
| F19 (50.10.1.txt) | Q5 | 50 (50) | 4 | 25 | 1,727,485 | --- | 1800 * | 2 | 1800 * | NFSF | --- | 77 | 2 |
| F20 (50.10.1.txt) | Q6 | 50 (50) | 4 | 25 | 1,727,485 | --- | 1800 * | 3 | 1800 * | NFSF | --- | 79 | 3 |
| F21 (100.10.1.txt) | Q2 | 100 (100) | 6 | 35 | 19,318,893 | - | 1800 * | NFSF | 1800 * | NFSF | 34 | 87 | 194 |
| F22 (100.10.1.txt) | Q4 | 100 (100) | 6 | 30 | 19,318,893 | - | 1800 * | NFSF | 1800 * | NFSF | 28 | 89 | 210 |
| F23 (100.10.1.txt) | Q5 | 100 (100) | 6 | 30 | 19,318,893 | --- | 1800 * | NFSF | 1800 * | NFSF | --- | 86 | 1 |
| F24 (100.10.1.txt) | Q6 | 100 (100) | 6 | 30 | 19,318,893 | --- | 1800 * | NFSF | 1800 * | NFSF | --- | 85 | 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sitek, P.; Wikarek, J.; Jagodziński, M. A Proactive Approach to Extended Vehicle Routing Problem with Drones (EVRPD). Appl. Sci. 2022, 12, 8255. https://doi.org/10.3390/app12168255
Sitek P, Wikarek J, Jagodziński M. A Proactive Approach to Extended Vehicle Routing Problem with Drones (EVRPD). Applied Sciences. 2022; 12(16):8255. https://doi.org/10.3390/app12168255
Chicago/Turabian StyleSitek, Paweł, Jarosław Wikarek, and Mieczysław Jagodziński. 2022. "A Proactive Approach to Extended Vehicle Routing Problem with Drones (EVRPD)" Applied Sciences 12, no. 16: 8255. https://doi.org/10.3390/app12168255
APA StyleSitek, P., Wikarek, J., & Jagodziński, M. (2022). A Proactive Approach to Extended Vehicle Routing Problem with Drones (EVRPD). Applied Sciences, 12(16), 8255. https://doi.org/10.3390/app12168255







