A Two-Objective ILP Model of OP-MATSP for the Multi-Robot Task Assignment in an Intelligent Warehouse
Abstract
:1. Introduction
- This paper regards the multi-robot task assignment in an intelligent warehouse as an open-path multi-depot asymmetric traveling salesman problem (OP-MATSP). Moreover, the OP-MATSP is proposed for the first time in this paper.
- A two-objective integer linear programming (ILP) model of OP-MATSP is established. Through this ILP model, we solve small-scale multi-robot task assignment problems using the Gurobi solver.
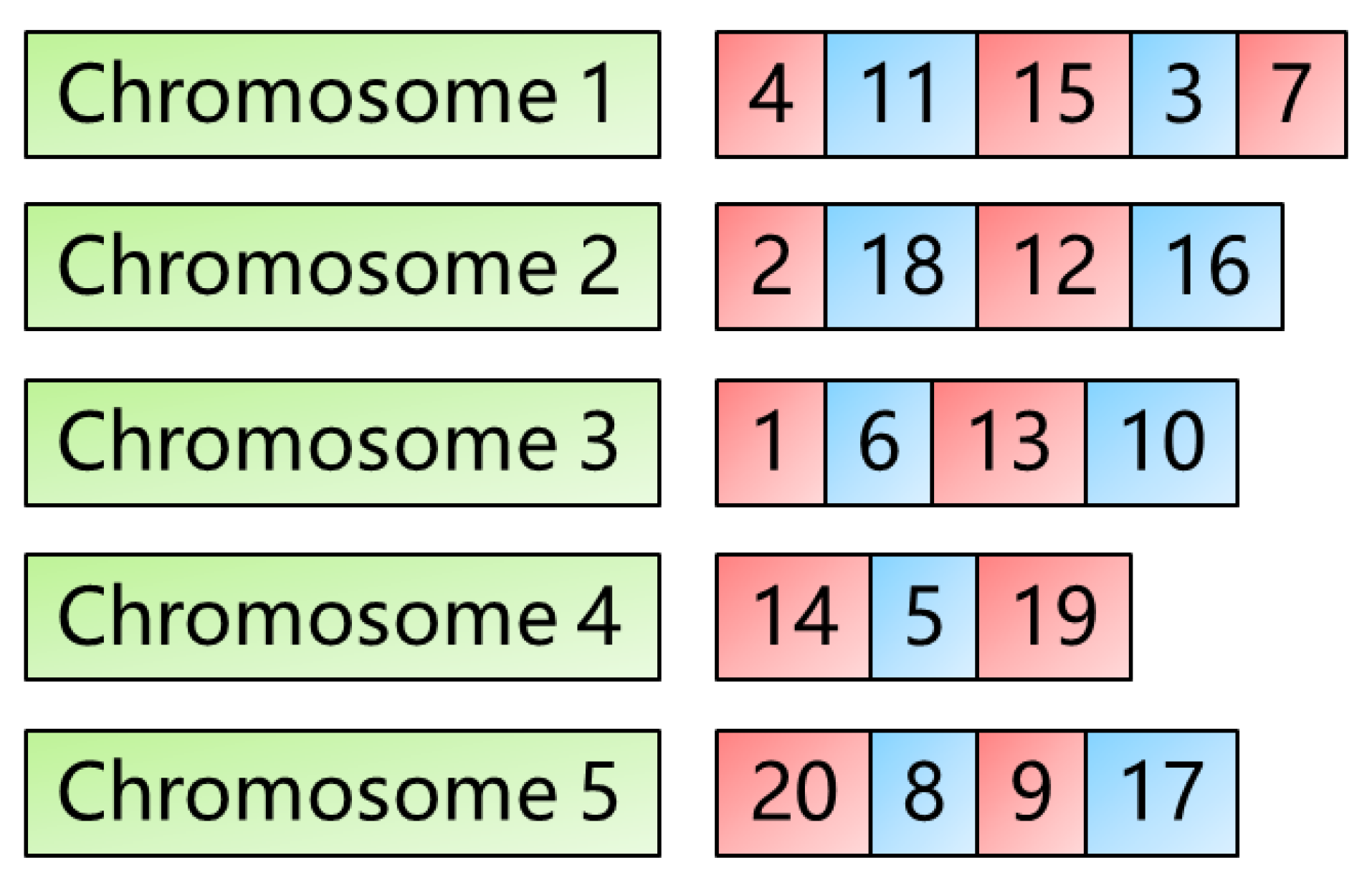
- Multi-chromosome coding-based genetic algorithms are implemented to solve large-scale multi-robot task assignment problems.
2. Methods
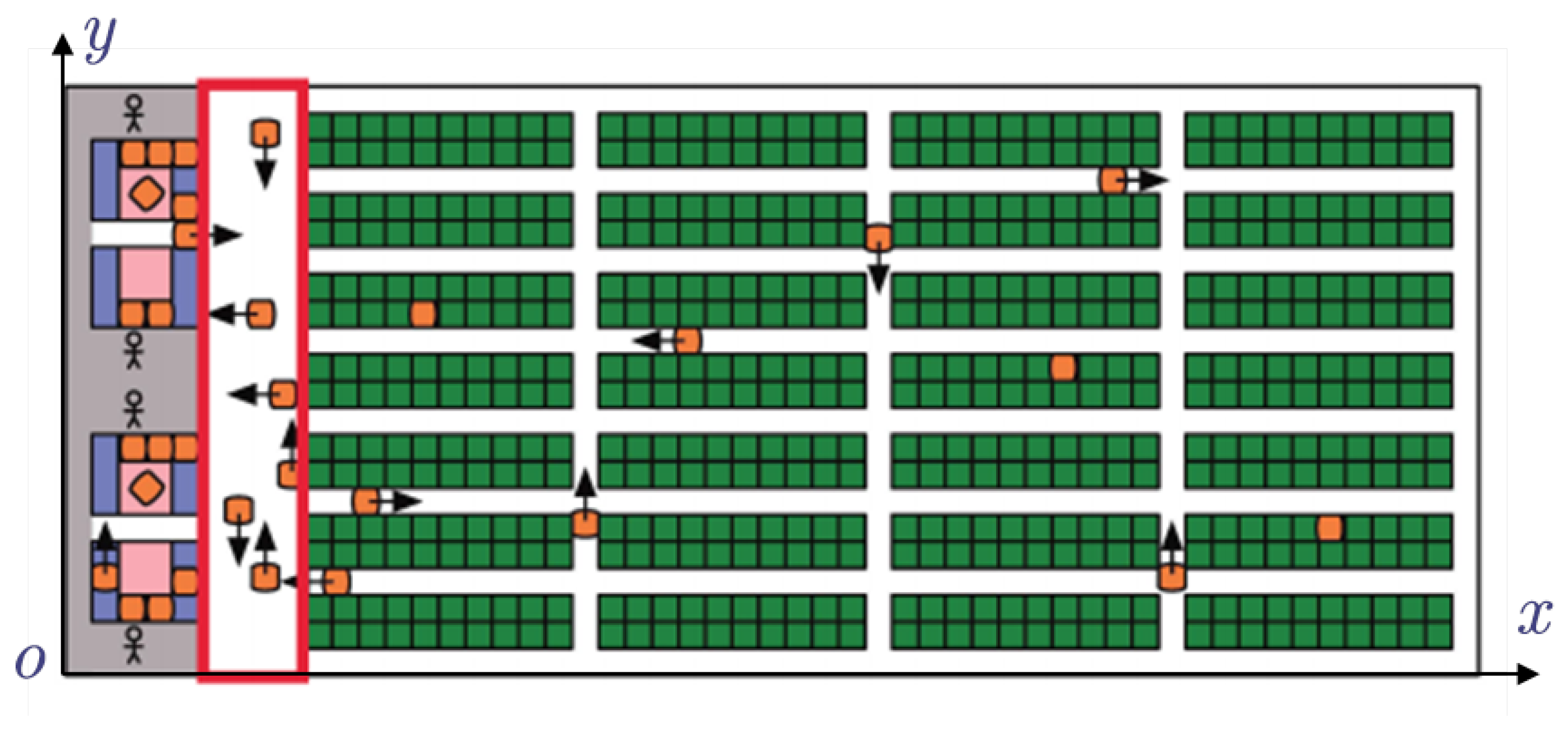
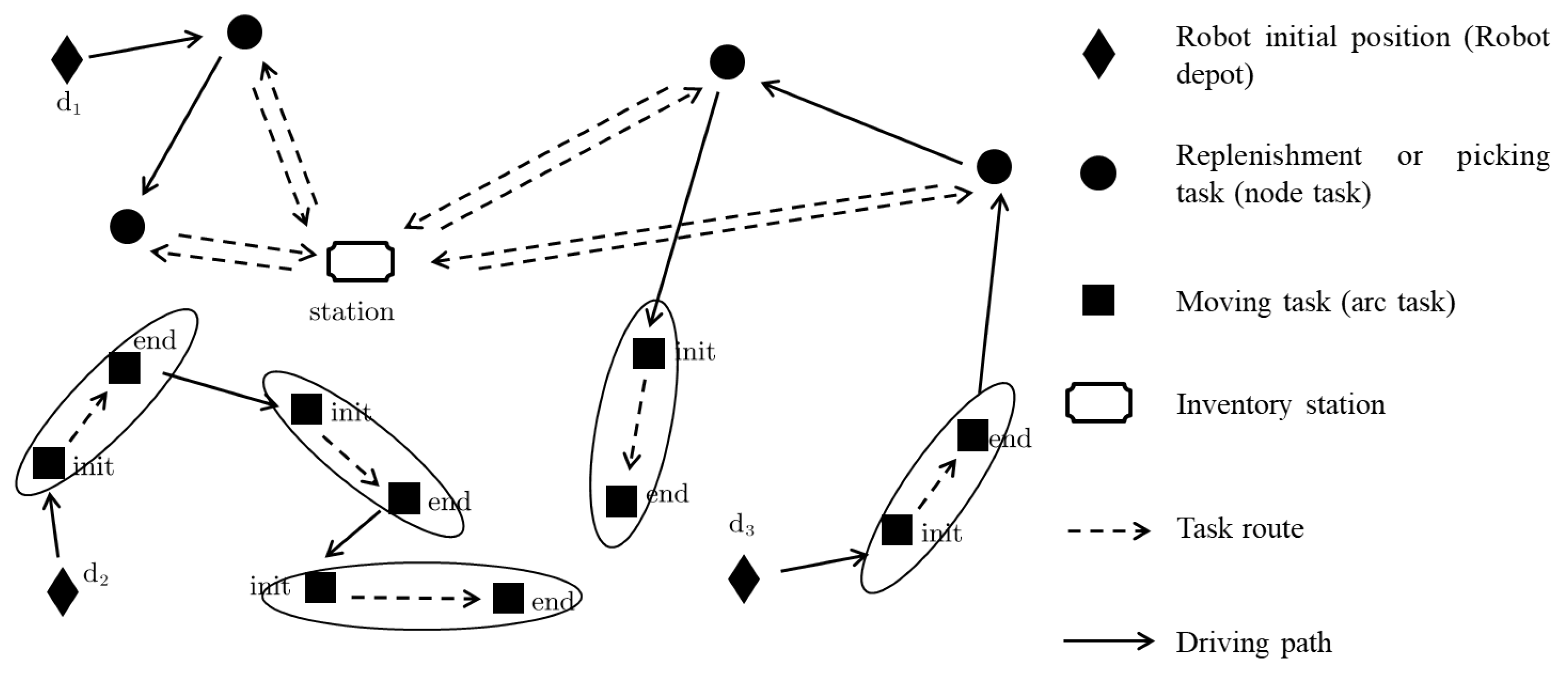
2.1. Task Definition
2.2. Multi-Robot Task Assignment in an Intelligent Warehouse
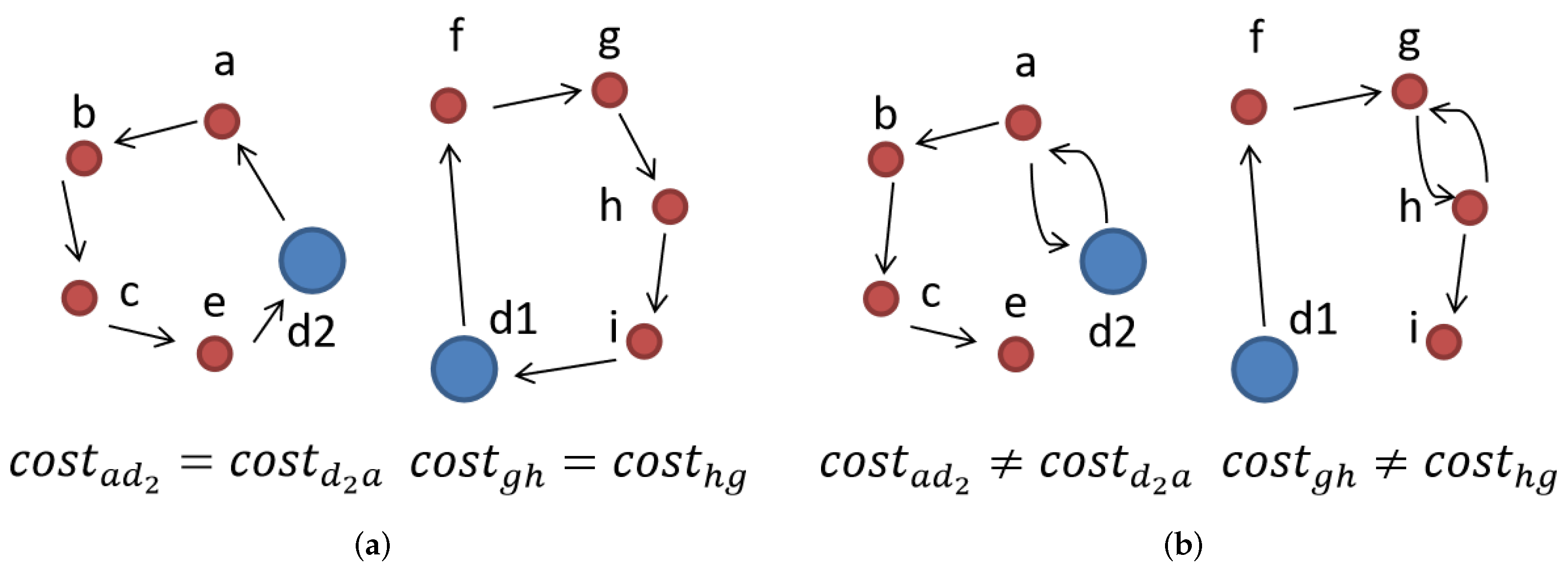
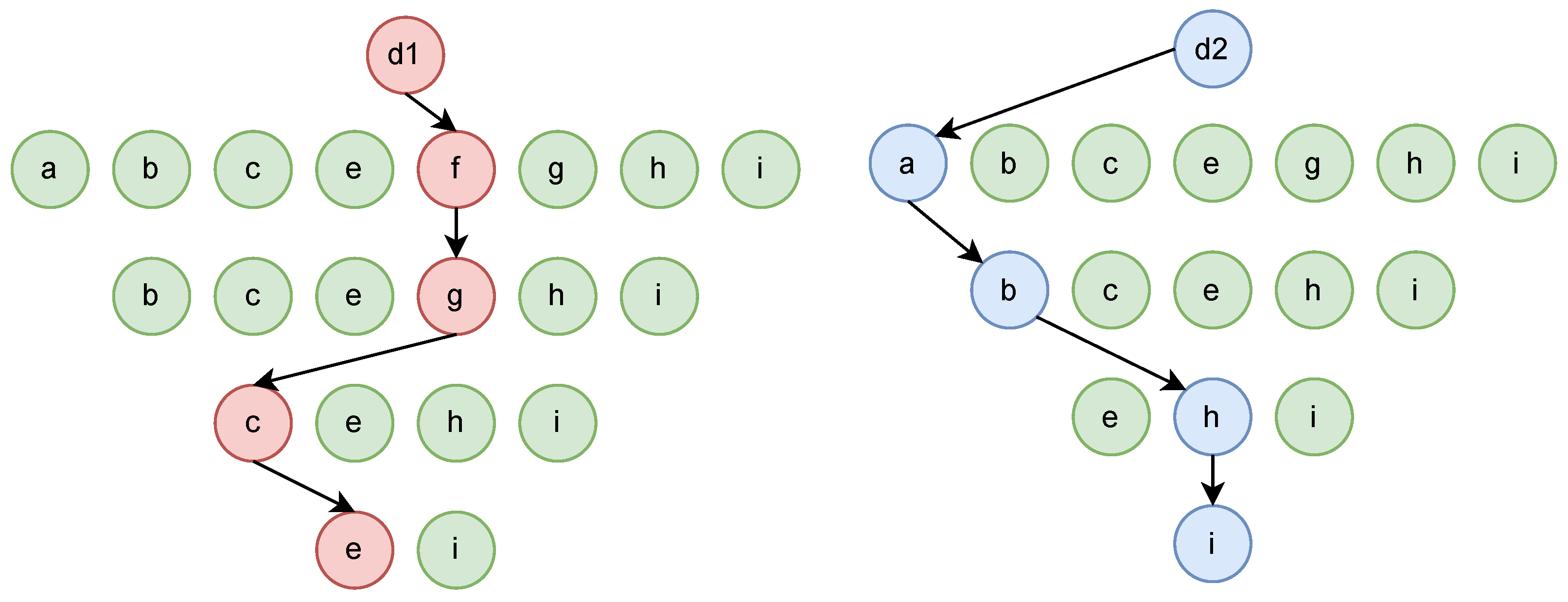
2.3. Open-Path Multi-Depot Asymmetric Traveling Salesman Problem (OP-MATSP)
2.4. Formulation of the Two-Objective ILP Model
- (1)
- Sets: the city node set.: the depot node set. Since each traveling salesman starts from a unique depot node, we assume that the set of traveling salesmen is equal to the depot node set .V: the city and depot node set.
- (2)
- Parameters: the cost from node i to node j.: the own cost of city node i.
- (3)
- Decision variables: if mth traveling salesman visits the node i and moves to the next node j, then ; otherwise, , , .: if mth traveling salesman visits the node i, then ; otherwise, , , .
- (4)
- Constraints
- (a)
- The mth traveling salesman can only visit the city node from the mth depot node, but not other depot nodes. To guarantee the above assumptions, we set the following constraints:
- (b)
- To prevent the traveling salesman from repeatedly visiting the same city node or depot node, the following constraint is established:
- (c)
- The relationship between decision variables and can be expressed as:
- (d)
- The number of node sequences is the same as the number of traveling salesmen. To ensure each traveling salesman visits only one node sequence, we add the following constraints:
- (e)
- The city node can only be visited by one traveling salesman. To prevent one city node from being repeatedly visited by different traveling salesmen, the following constraints are established:
- (f)
- To prevent the traveling salesman from visiting the previous node after visiting the current node, we establish the following constraints:
- (g)
- To ensure the continuity of node sequence and avoid the fracture of node sequence, the following flow balance constraint is established:
- (h)
- We need to ensure that every node is visited and each traveling salesman’s route forms a Hamiltonian cycle. To prevent sub-tours in the traveling salesman’s routing, we have to add sub-tour elimination constraints (SECs). The SECs for the MATSP in this paper are Danzig–Fulkerson–Johnson (DFJ) [24]:where represents the cardinality of subset , and represents the cardinality of set V. In each subset , sub-tours are prevented.
- (i)
- To ensure that each traveling salesman starts from the depot node and visits at least one city node, we add the following constraints:
- (5)
- Objective optimization functionsWe will first propose two objective optimization functions based on MATSP. Sum-of-cost consists of two parts: the sum of the costs of all city nodes and the sum of the costs between nodes in the node sequence . Because is a constant, the expression of sum-of-cost (SOC) can be simplified as:Makespan is the maximum value of the total cost of each node sequence. Makespan also includes two parts: the sum of the costs of all city nodes in the sequence and the sum of the costs between nodes in the node sequence . We define the makespan as:Finally, we obtain the objective optimization function of OP-MATSP by changing the two objective functions of MATSP. The difference between OP-MATSP and MATSP is whether all traveling salesmen return to the depot after visiting all city nodes. Therefore, we can get two objective optimization functions of OP-MATSP by subtracting the cost of the traveling salesman returning the depot from the last city node in Equations (17) and (18).The sum-of-cost of OP-MATSP can be expressed as:where represents the cost from the last city node to the depot of all traveling salesmen.The makespan of OP-MATSP can be expressed as:where represents the cost of the mth traveling salesman routing from the last city node to the depot.
- (6)
- The two-objective ILP modelIn conclusion, a two-objective ILP model of OP-MATSP is established, through which we can solve the multi-robot task assignment in an intelligent warehouse. The entire two-objective ILP model is:
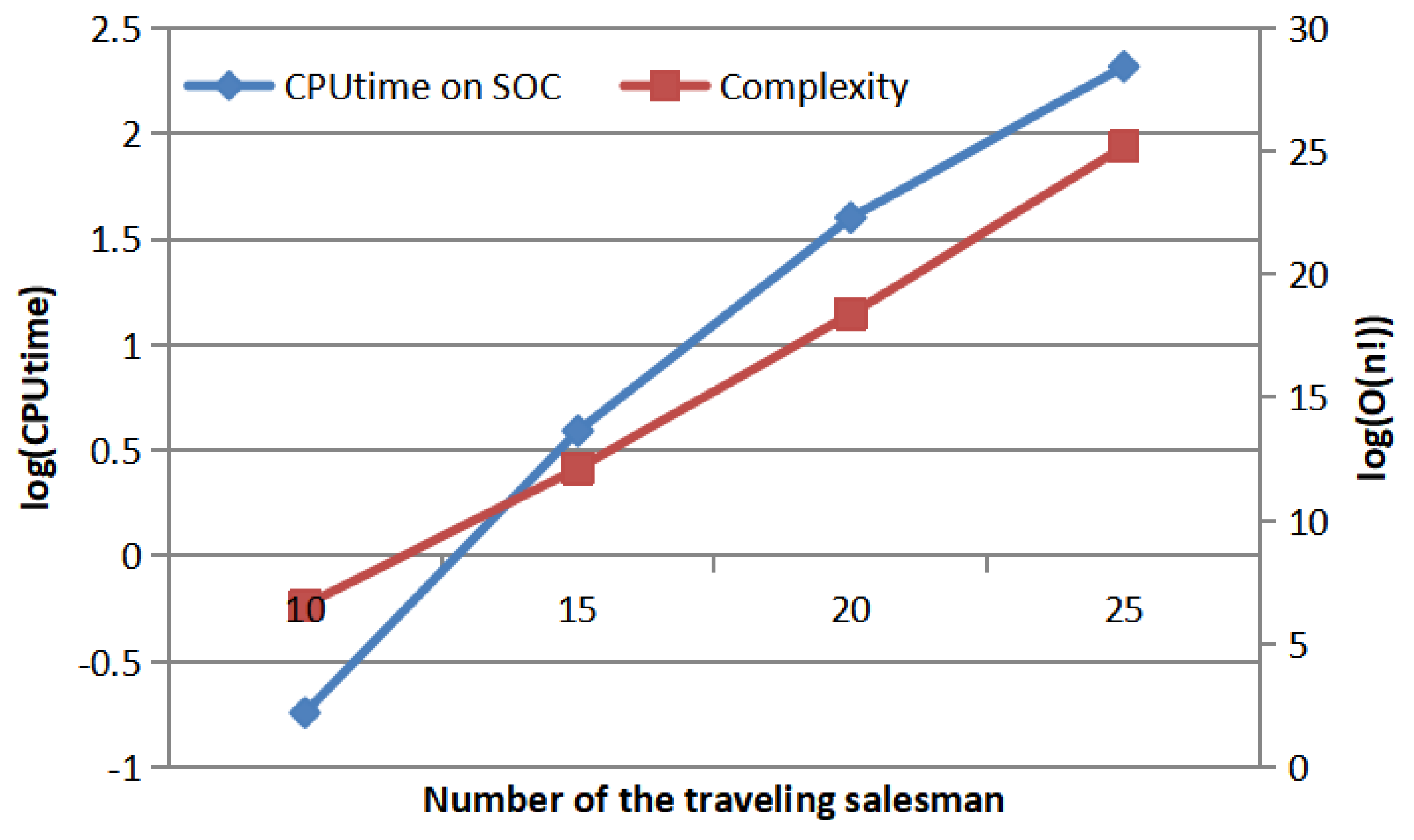
2.5. Analysis of Computational Time Complexity
3. Results and Discussion
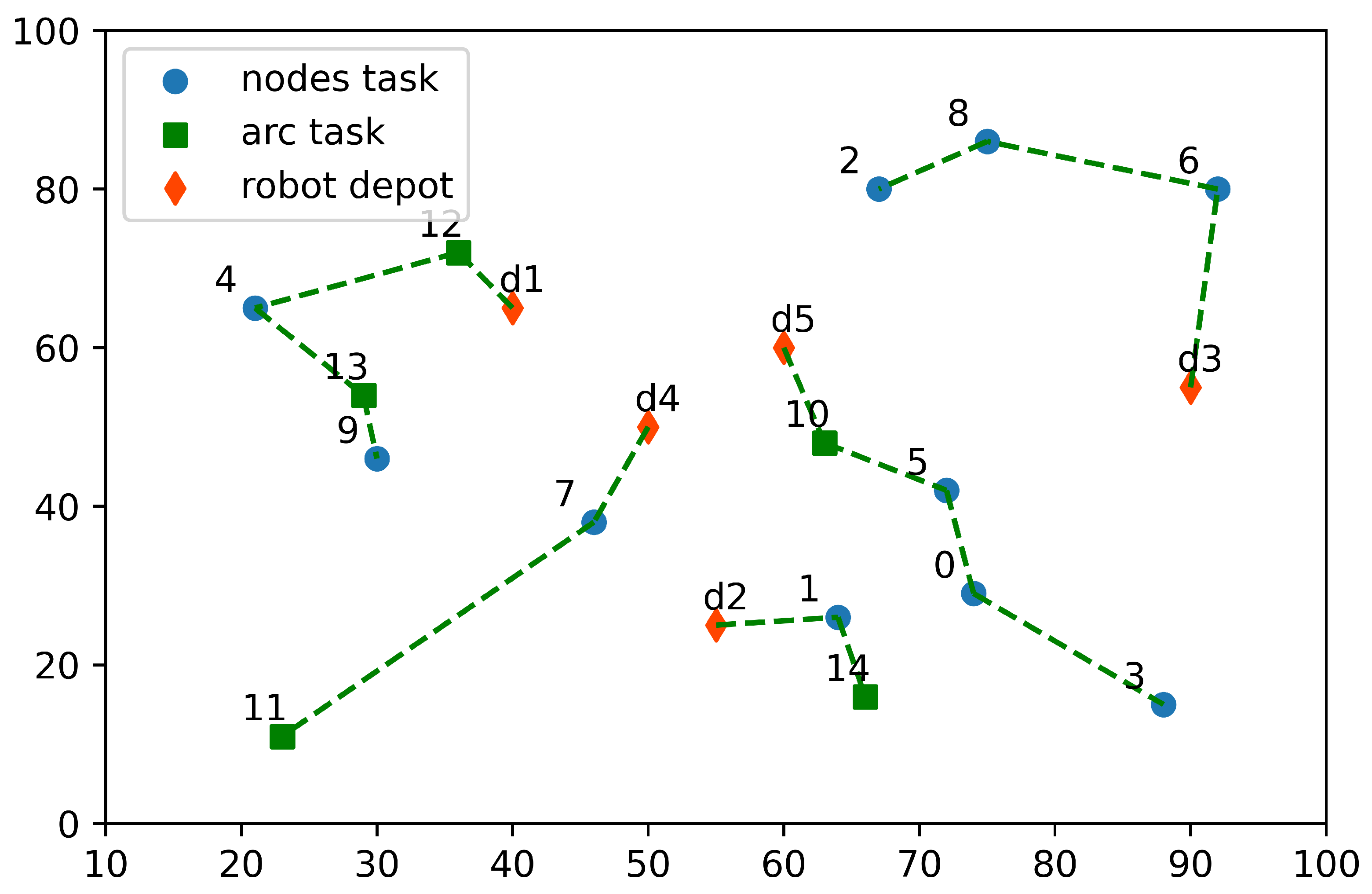
3.1. Setting and Instance Generation
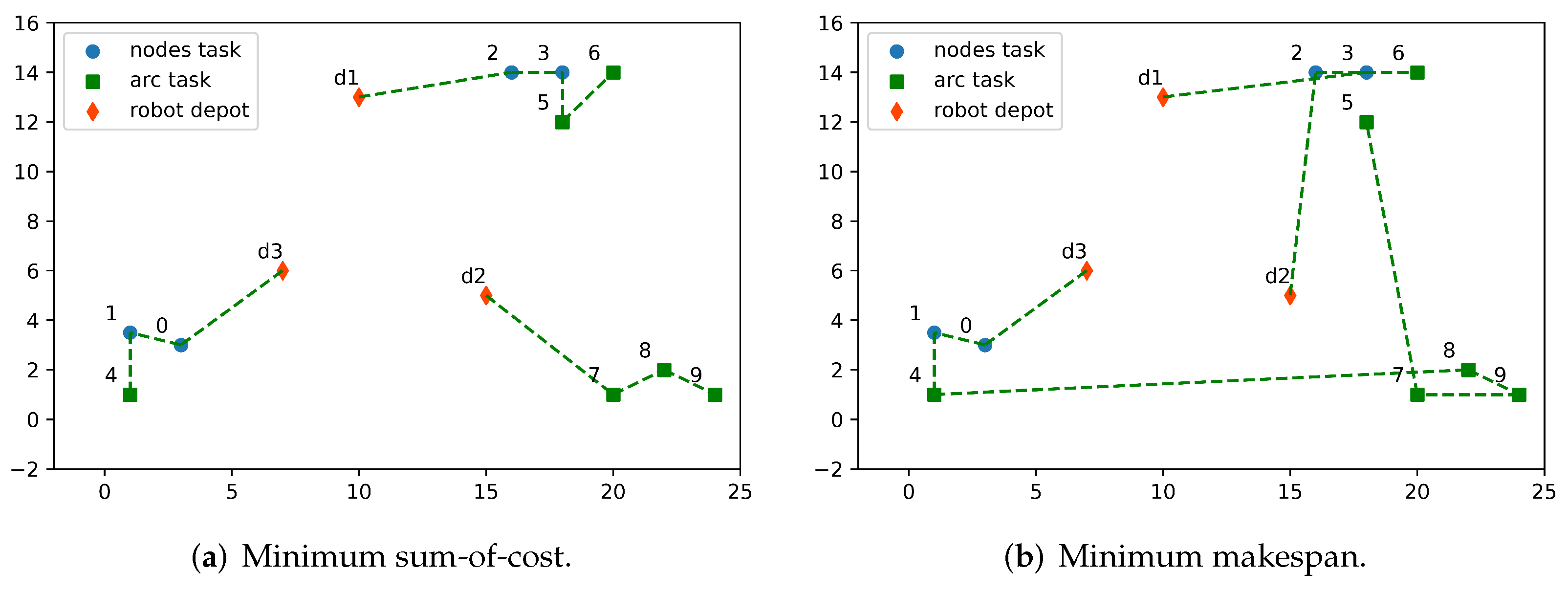
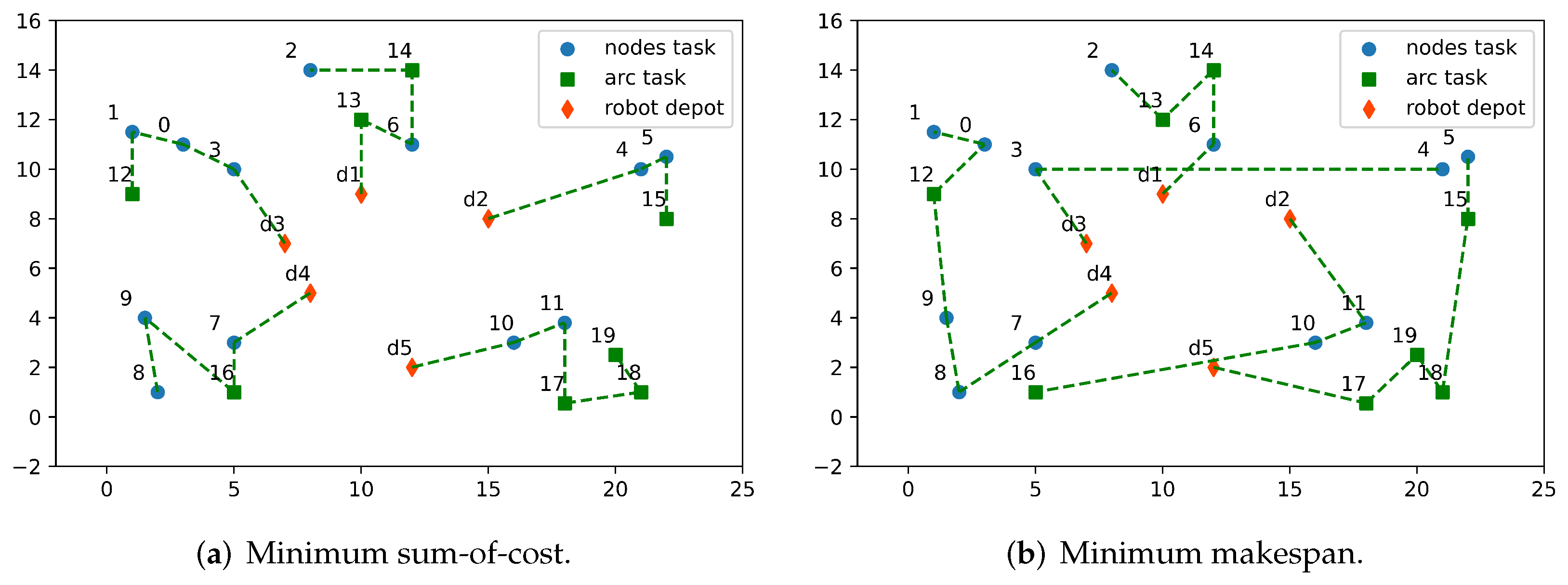
3.2. Small-Scale Problems Solved by Gurobi
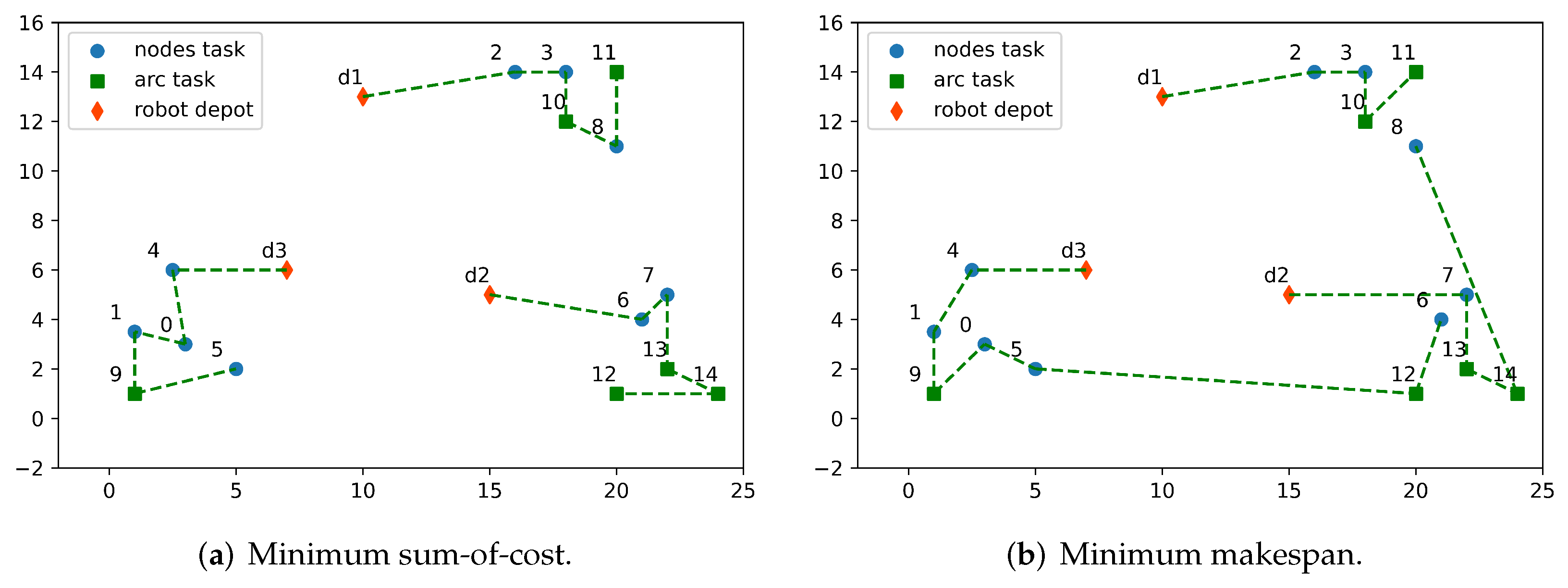
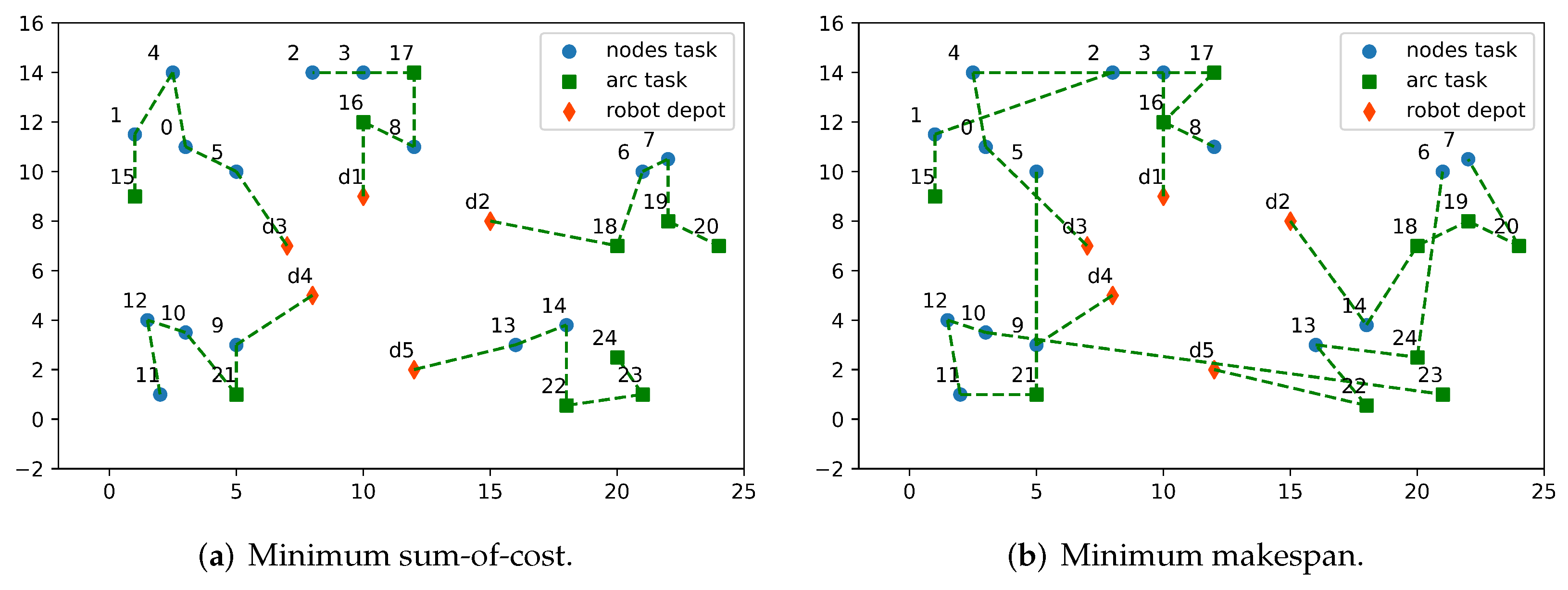
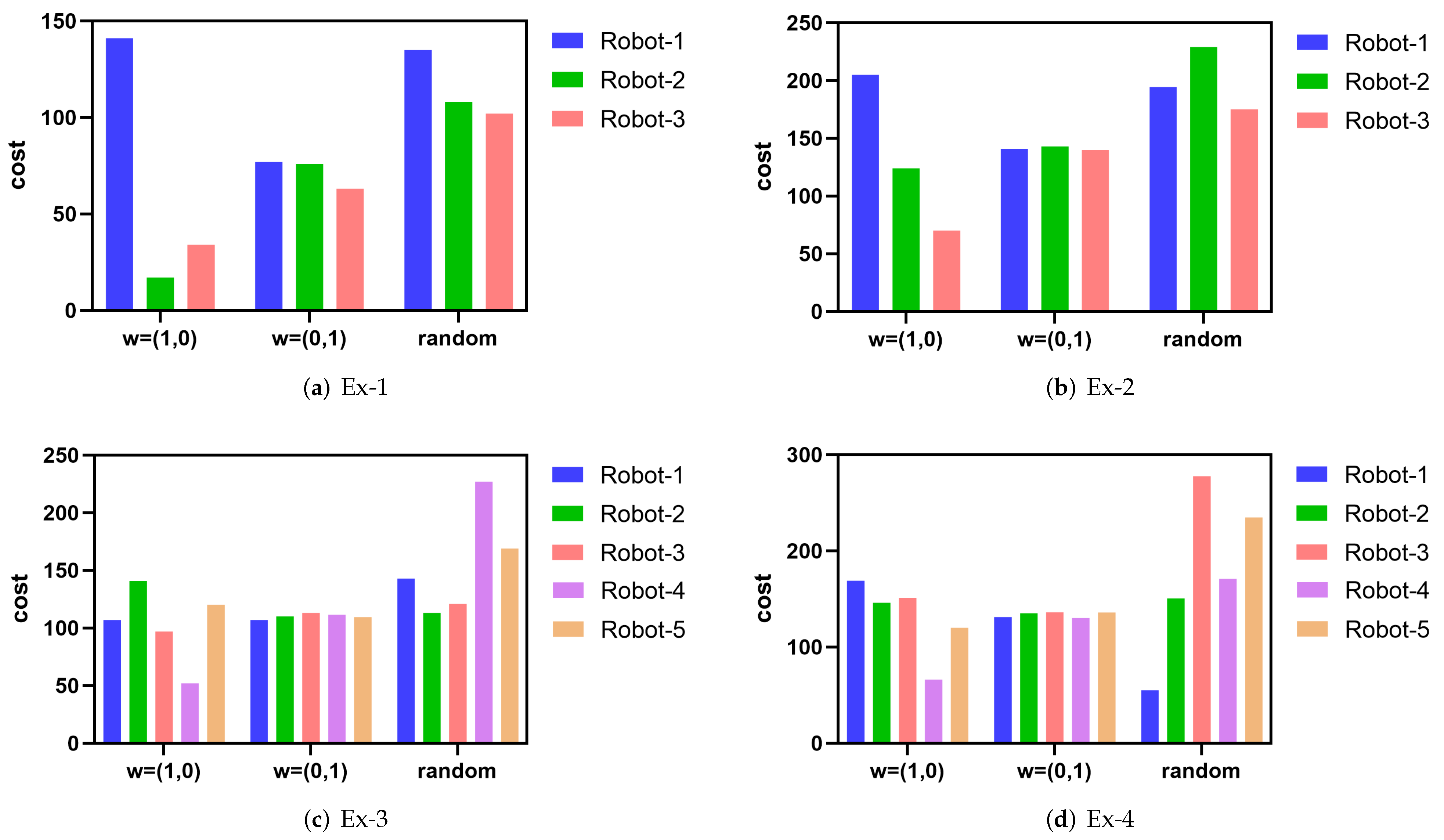
3.3. Large-Scale Problems Solved by the Multi-Chromosome Coding-Based Genetic Algorithm
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- de Koster, R. Automated and Robotic Warehouses: Developments and Research Opportunities. Logist. Transp. 2018, 38, 33–40. [Google Scholar] [CrossRef]
- Farinelli, A.; Boscolo, N.; Zanotto, E.; Pagello, E. Advanced approaches for multi-robot coordination in logistic scenarios. Robot. Auton. Syst. 2017, 90, 34–44. [Google Scholar] [CrossRef]
- Wurman, R.P.; D’Andrea, R.; Mountz, M. Coordinating hundreds of cooperative, autonomous vehicles in warehouses. AI Mag. 2007, 29, 1752–1759. [Google Scholar]
- NZanywayingoma, F.; Yang, Y. Effective task scheduling and dynamic resource optimization based on heuristic algorithms in cloud computing environment. KSII Trans. Internet Inf. Syst. 2017, 11, 5780–5802. [Google Scholar]
- Erdmann, M.; Lozano-Perez, T. On multiple moving objects. In Proceedings of the 1986 IEEE International Conference on Robotics and Automation, San Francisco, CA, USA, 7–10 April 1986; Volume 3, pp. 1419–1424. [Google Scholar] [CrossRef]
- Wagner, G.; Choset, H.; Ayanian, N. Subdimensional Expansion and Optimal Task Reassignment. In SOCS, Proceedings of the 5th Annual Symposium on Combinatorial, Niagara Falls, ON, Canada, 19–21 July 2012; Association for the Advancement of Artificial Intelligence: Palo Alto, CA, USA, 2012. [Google Scholar]
- Khamis, A.; Hussein, A.; Elmogy, A. Multi-robot task allocation: A review of the state-of-the-art. Coop. Robot. Sens. Netw. 2015, 2015, 31–51. [Google Scholar]
- Liu, Y.; Ji, S.; Su, Z.; Guo, D. Multi-objective AGV scheduling in an automatic sorting system of an unmanned (intelligent) warehouse by using two adaptive genetic algorithms and a multi-adaptive genetic algorithm. PLoS ONE 2019, 14, e0226161. [Google Scholar] [CrossRef]
- Pan, X.Y.; Wu, J.; Zhang, Q.W.; Lai, D.; Xie, H.L.; Zhang, C. A case study of AGV scheduling for production material handling. Appl. Mech. Mater. 2013, 411, 2351–2354. [Google Scholar] [CrossRef]
- Zheng, Y.; Xiao, Y.; Seo, Y. A tabu search algorithm for simultaneous machine/AGV scheduling problem. Int. J. Prod. Res. 2014, 52, 5748–5763. [Google Scholar] [CrossRef]
- Mousavi, M.; Yap, H.J.; Musa, S.N.; Tahriri, F.; Md Dawal, S.Z. Multi-objective AGV scheduling in an FMS using a hybrid of genetic algorithm and particle swarm optimization. PLoS ONE 2017, 12, e0169817. [Google Scholar] [CrossRef] [Green Version]
- Su-yan, T.; Yi-fan, Z.; Li, Q.; Yong-lin, L. Survey of task allocation in multi Agent systems. Xi Tong Gong Cheng Yu Dian Zi Ji Shu [Syst. Eng. Electron.] 2010, 32, 2155–2161. [Google Scholar]
- Axsäter, S. On the first come–first served rule in multi-echelon inventory control. Nav. Res. Logist. 2007, 54, 485–491. [Google Scholar] [CrossRef]
- Shi, J.; Bao, Y.; Leng, F.; Yu, G. Priority-Based Balance Scheduling in Real-Time Data Warehouse. In Proceedings of the 2009 Ninth International Conference on Hybrid Intelligent Systems, Shenyang, China, 12–14 August 2009; Volume 3, pp. 301–306. [Google Scholar] [CrossRef]
- Bolu, A.; Korçak, Ö. Adaptive task planning for multi-robot smart warehouse. IEEE Access 2021, 9, 27346–27358. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, F.; Weng, X. A building-block-based genetic algorithm for solving the robots allocation problem in a robotic mobile fulfilment system. Math. Probl. Eng. 2019, 2019, 6153848. [Google Scholar] [CrossRef] [Green Version]
- Vivaldini, K.; Rocha, L.; Fróes, N.; Becker, M.; Moreira, A. Integrated tasks assignment and routing for the estimation of the optimal number of AGVS. Int. J. Adv. Manuf. Technol. 2015, 82, 719–736. [Google Scholar] [CrossRef]
- Lenstra, J.K.; Kan, A.R. Some simple applications of the travelling salesman problem. J. Oper. Res. Soc. 1975, 26, 717–733. [Google Scholar] [CrossRef]
- De Koster, R.; Le-Duc, T.; Roodbergen, K.J. Design and control of warehouse order picking: A literature review. Eur. J. Oper. Res. 2007, 182, 481–501. [Google Scholar] [CrossRef]
- Theys, C.; Bräysy, O.; Dullaert, W.; Raa, B. Using a TSP heuristic for routing order pickers in warehouses. Eur. J. Oper. Res. 2010, 200, 755–763. [Google Scholar] [CrossRef]
- Azadnia, H.A.; Taheri, S.; Ghadimi, P.; Saman, Z.M.M.; Wong, Y.K. Order batching in warehouses by minimizing total tardiness: A hybrid approach of weighted association rule mining and genetic algorithms. Sci. World J. 2013, 2013, 246578. [Google Scholar] [CrossRef]
- Tsiropoulou, E.E.; Paruchuri, S.T.; Baras, J.S. Interest, energy and physical-aware coalition formation and resource allocation in smart IoT applications. In Proceedings of the 2017 51st Annual Conference on Information Sciences and Systems (CISS), Baltimore, MD, USA, 22–24 March 2017; pp. 1–6. [Google Scholar]
- Benavent, E.; Martínez, A. Multi-depot multiple TSP: A polyhedral study and computational results. Ann. Oper. Res. 2013, 207, 7–25. [Google Scholar] [CrossRef]
- Dantzig, G.; Fulkerson, R.; Johnson, S. Solution of a large-scale traveling-salesman problem. J. Oper. Res. Soc. Am. 1954, 2, 393–410. [Google Scholar] [CrossRef] [Green Version]
- Odili, J.B.; Noraziah, A.; Zarina, M. A Comparative Performance Analysis of Computational Intelligence Techniques to Solve the Asymmetric Travelling Salesman Problem. Comput. Intell. Neurosci. 2021, 2021, 6625438. [Google Scholar] [CrossRef] [PubMed]
- Bixby, B. The gurobi optimizer. Transp. Res. Part B 2007, 41, 159–178. [Google Scholar]
- Liu, Z.; Liu, G.; Wang, H.; He, F. The linear weighting method for solving a class of non-differentiable multiobjective programming problem. In Proceedings of the 2011 International Conference on Multimedia Technology, Hangzhou, China, 26–28 July 2011; pp. 3273–3276. [Google Scholar]
- Ronald, S.; Kirkby, S.; Eklund, P. Multi-chromosome mixed encodings for heterogeneous problems. In Proceedings of the 1997 IEEE International Conference on Evolutionary Computation (ICEC’97), Indianapolis, IN, USA, 13–16 April 1997; pp. 37–42. [Google Scholar] [CrossRef]
- Ciesielski, V.; Scerri, P. Compound optimisation. Solving transport and routing problems with a multi-chromosome genetic algorithm. In Proceedings of the 1998 IEEE International Conference on Evolutionary Computation Proceedings. IEEE World Congress on Computational Intelligence (Cat. No. 98TH8360), Anchorage, AK, USA, 4–9 May 1998; pp. 365–370. [Google Scholar] [CrossRef]
- Ye, D.; Liu, G.; He, B. Multi-chromosome Genetic Algorithm for Multiple Traveling Salesman Problem. J. Syst. Simul. 2019, 31, 36–42. [Google Scholar]
- Khatib, W.; Fleming, P.J. The stud GA: A mini revolution? In Proceedings of the International Conference on Parallel Problem Solving from Nature, Amsterdam, The Netherlands, 27–30 September 1998. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]
- Deb, K.; Jain, H. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I: Solving Problems with Box Constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
| Item | Ex-1 | Ex-2 | Ex-3 | Ex-4 |
|---|---|---|---|---|
| 0.18 | 3.9 | 39.97 | 208.45 | |
| 1.08 | 362.08 | 900.57 1 | 900.4 1 | |
| 10! | 15! | 20! | 25! |
| Index | Item | Ex-1 | Ex-2 | Ex-3 | Ex-4 |
|---|---|---|---|---|---|
| SOC | STA | 345 | 598.5 | 773 | 889.05 |
| ILP model | 192 | 399 | 517.1 | 622.1 | |
| 44.3% | 33.3% | 33.1% | 30% | ||
| MS | STA | 135 | 229 | 227 | 277.6 |
| ILP model | 77 | 143 | 113 | 139 | |
| 43% | 37.6% | 50.2% | 49.9% |
| Type | Templet | Selection | Crossover | Mutation |
|---|---|---|---|---|
| Single-obj | soea_psy_EGA_templet 1 | Tournament | partial matching () | Invertion () |
| soea_psy_SEGA_templet 2 | Tournament | partial matching () | Invertion () | |
| soea_psy_SGA_templet 3 | Roulette Wheel | partial matching () | Invertion () | |
| soea_psy_studGA_templet [31] | Tournament | partial matching () | Invertion () | |
| Multi-obj | moea_psy_awGA_templet 4 | Tournament | partial matching () | Invertion () |
| moea_psy_NSGA2_templet [32] | Tournament | partial matching () | Invertion () | |
| moea_psy_NSGA2_archive_templet 5 | Tournament | partial matching () | Invertion () | |
| moea_psy_NSGA3_templet [33] | unconstrained random | partial matching () | Invertion () |
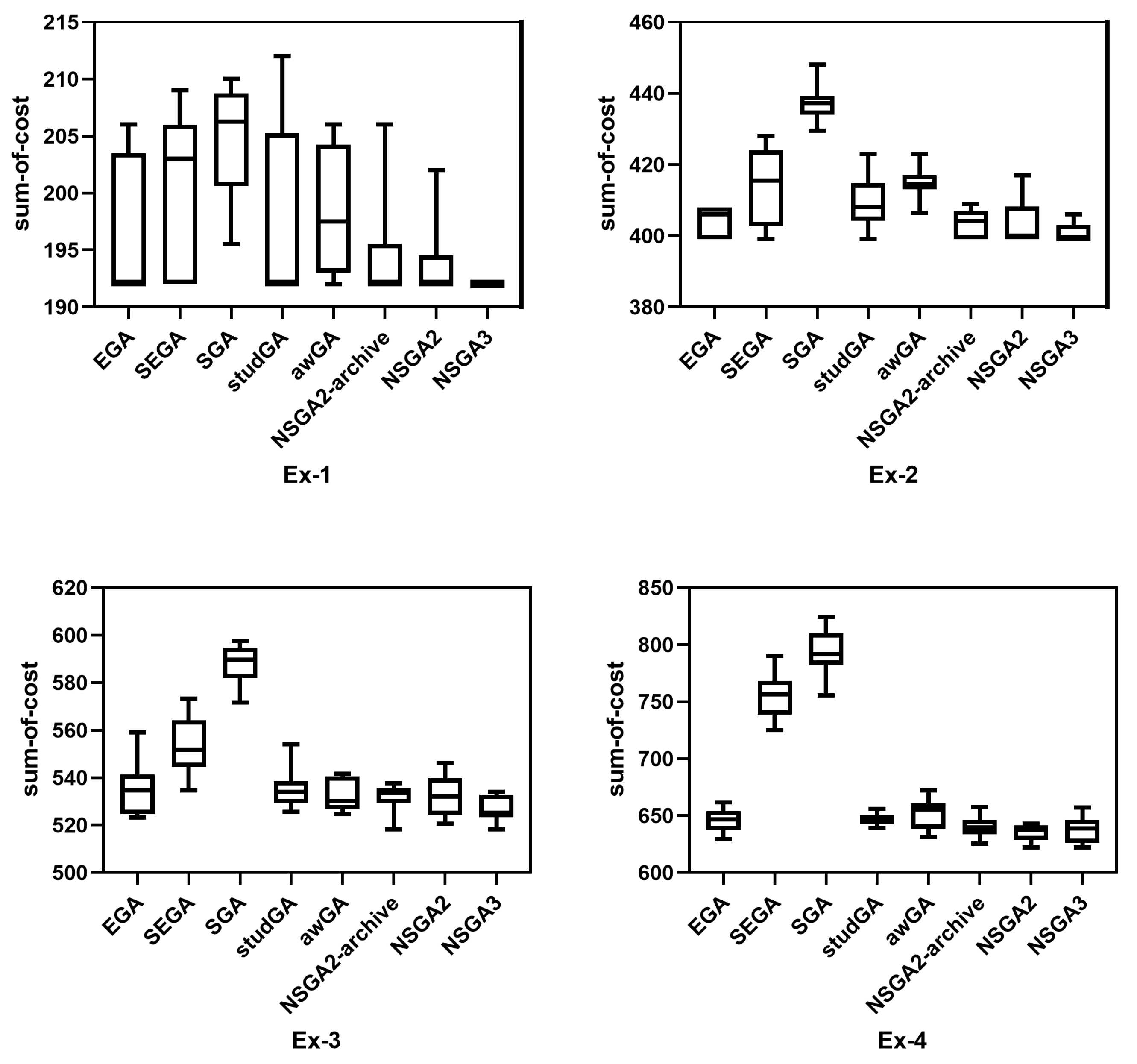
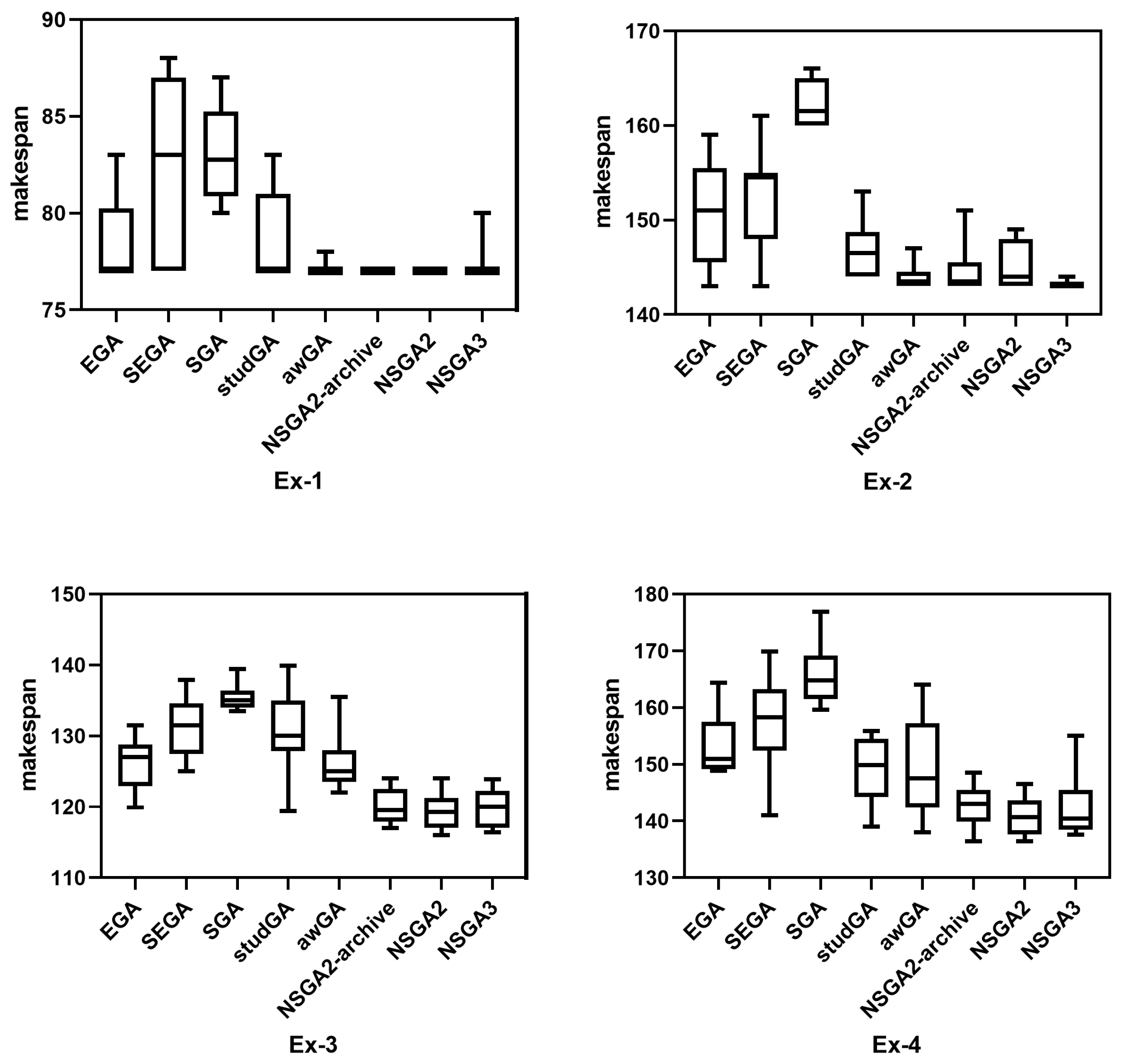
| Ex | Index | soea-EGA | soea-SEGA | soea-SGA | soea-studGA | moea-awGA | moea-NSGA2-archive | moea-NSGA2 | moea-NSGA3 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Best | Aveg | Best | Aveg | Best | Aveg | Best | Aveg | Best | Aveg | Best | Aveg | Best | Aveg | Best | Aveg | ||
| Ex-1 | SOC | 192 | 195.8 | 192 | 200.1 | 195.5 | 204.6 | 192 | 196.7 | 192 | 198.2 | 192 | 194.6 | 192 | 196.5 | 192 | 192 |
| 0% | 1.94% | 0% | 4.05% | 1.79% | 6.16% | 0% | 2.39% | 0% | 3.13% | 0% | 1.34% | 0% | 1.03% | 0% | 0% | ||
| MS | 77 | 78.6 | 77 | 82.1 | 80 | 83 | 77 | 78.7 | 77 | 77.1 | 77 | 77 | 77 | 77 | 77 | 77.3 | |
| 0% | 2.04% | 0% | 6.21% | 3.75% | 7.23% | 0% | 2.16% | 0% | 0.13% | 0% | 0% | 0% | 0% | 0% | 0.39% | ||
| Ex-2 | SOC | 399 | 403.9 | 399 | 414.1 | 429.5 | 437.4 | 399 | 409.1 | 406.5 | 414.7 | 399 | 403.65 | 399 | 403.7 | 399 | 400.7 |
| 0% | 1.21% | 0% | 3.65% | 7.1% | 8.78% | 0% | 2.47% | 1.85% | 3.79% | 0% | 1.15% | 0% | 1.16% | 0% | 0.42% | ||
| MS | 143 | 150.6 | 143 | 152.2 | 160 | 162.3 | 144 | 146.9 | 143 | 144 | 143 | 144.6 | 143 | 145.09 | 143 | 143.2 | |
| 0% | 5.05% | 0% | 6.04% | 10.63% | 11.89% | 0.69% | 2.65% | 0% | 0.69% | 0% | 1.11% | 0% | 1.58% | 0% | 0.14% | ||
| Ex-3 | SOC | 523.25 | 535.12 | 534.6 | 552.99 | 571.6 | 588.21 | 525.5 | 534.92 | 524.6 | 531.98 | 518.1 | 532.15 | 520.6 | 531.93 | 518.1 | 526.97 |
| 1.18% | 3.37% | 3.27% | 6.49% | 9.53% | 12.09% | 1.6% | 3.33% | 1.43% | 2.8% | 0.19% | 2.83% | 0.67% | 2.79% | 0.19% | 1.87% | ||
| MS | 119.9 | 126.17 | 125 | 131.33 | 133.5 | 135.53 | 119.4 | 130.93 | 122 | 126.25 | 117 | 120.05 | 116 | 119.36 | 116.4 | 120 | |
| 5.75% | 10.44% | 9.6% | 13.96% | 15.36% | 16.62% | 5.36% | 13.69% | 7.38% | 10.5% | 3.42% | 5.87% | 2.59% | 5.33% | 2.92% | 5.38% | ||
| Ex-4 | SOC | 629 | 645.53 | 725 | 755.09 | 755.6 | 793.1 | 639.1 | 647.16 | 631.1 | 652.01 | 625.5 | 640.31 | 622.1 | 635.6 | 622.1 | 637.89 |
| 1.1% | 3.63% | 14.19% | 17.61% | 17.67% | 21.56% | 2.66% | 3.87% | 1.43% | 4.59% | 0.54% | 2.84% | 0% | 2.12% | 0% | 2.48% | ||
| MS | 148.9 | 153.5 | 141 | 157.29 | 159.6 | 165.84 | 139 | 149.13 | 138 | 149.8 | 136.4 | 142.63 | 136.4 | 140.73 | 137.6 | 142.44 | |
| 6.65% | 9.45% | 1.42% | 11.63% | 12.91% | 16.18% | 0% | 6.79% | −0.72% | 7.21% | −1.91% | 2.55% | −1.91% | 1.23% | −1.02% | 2.42% | ||
| Index | Interation | EGA | NSGA3 | ||
|---|---|---|---|---|---|
| Best | Aveg | Best | Aveg | ||
| SOC | 5000 | 186,274 | 188,044 | 183,507 | 185,334 |
| 20,000 | 182,712 | 184,076 | 182,074 | 184,494 | |
| 1.91% | 2.11% | 0.78% | 0.45% | ||
| MS | 5000 | 40,410 | 42,021 | 37,241 | 37,836.2 |
| 20,000 | 39,552 | 40,455.3 | 37,272 | 37,795.7 | |
| 2.12% | 3.73% | −0.08% | 0.11% | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, J.; Li, Y.; Xu, Y.; Lv, S. A Two-Objective ILP Model of OP-MATSP for the Multi-Robot Task Assignment in an Intelligent Warehouse. Appl. Sci. 2022, 12, 4843. https://doi.org/10.3390/app12104843
Gao J, Li Y, Xu Y, Lv S. A Two-Objective ILP Model of OP-MATSP for the Multi-Robot Task Assignment in an Intelligent Warehouse. Applied Sciences. 2022; 12(10):4843. https://doi.org/10.3390/app12104843
Chicago/Turabian StyleGao, Jianqi, Yanjie Li, Yunhong Xu, and Shaohua Lv. 2022. "A Two-Objective ILP Model of OP-MATSP for the Multi-Robot Task Assignment in an Intelligent Warehouse" Applied Sciences 12, no. 10: 4843. https://doi.org/10.3390/app12104843
APA StyleGao, J., Li, Y., Xu, Y., & Lv, S. (2022). A Two-Objective ILP Model of OP-MATSP for the Multi-Robot Task Assignment in an Intelligent Warehouse. Applied Sciences, 12(10), 4843. https://doi.org/10.3390/app12104843






