Transient Response of Bridge Piers to Structure Separation under Near-Fault Vertical Earthquake
Abstract
1. Introduction
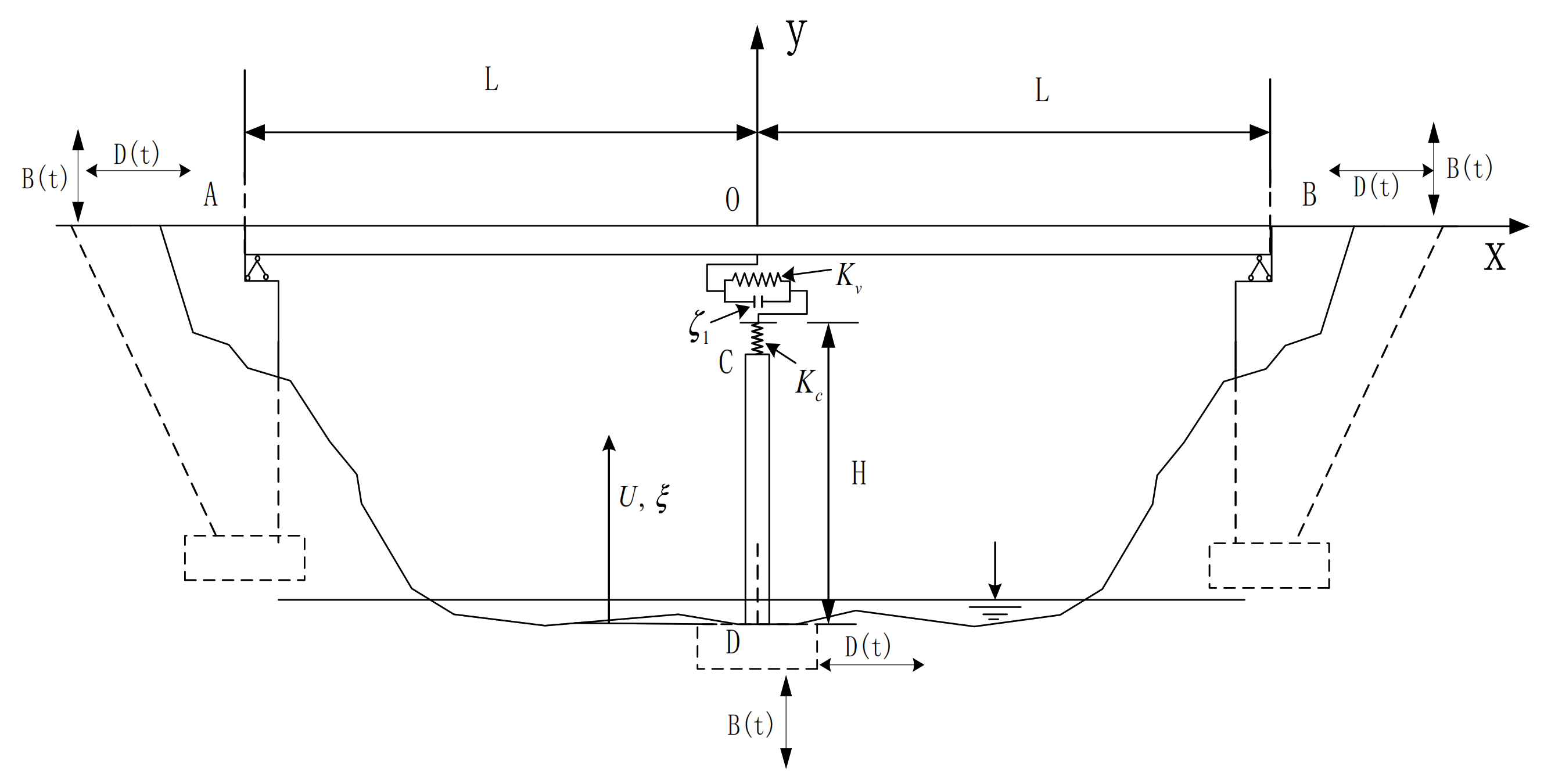
2. Theoretical Model and Vertical Displacement Calculation
- (1)
- In order to simplify the calculation, linear elastic calculation is adopted for the material of the model, ignoring the nonlinearity of the structure;
- (2)
- Ignore the possible bearing shear failure caused by a horizontal earthquake;
- (3)
- During seismic action, there are often stops in the lateral direction. This study only considers the coupling of vertical and longitudinal seismic activities;
- (4)
- Ignore the difference in the arrival time of the horizontal and vertical seismic waves, assuming that the earthquakes in both directions are excited at the same time.
2.1. Vertical Seismic Response Spectrum
2.2. Theoretical Solution of Displacement Response of Bridge in Vertical Contact Stage
2.3. Corresponding Theoretical Solution of Bridge Vertical Separation Stage Displacement
2.4. Corresponding Theoretical Solution of Bridge Vertical Impact Stage Displacement
3. Calculation of Horizontal Displacement Response of Bridge
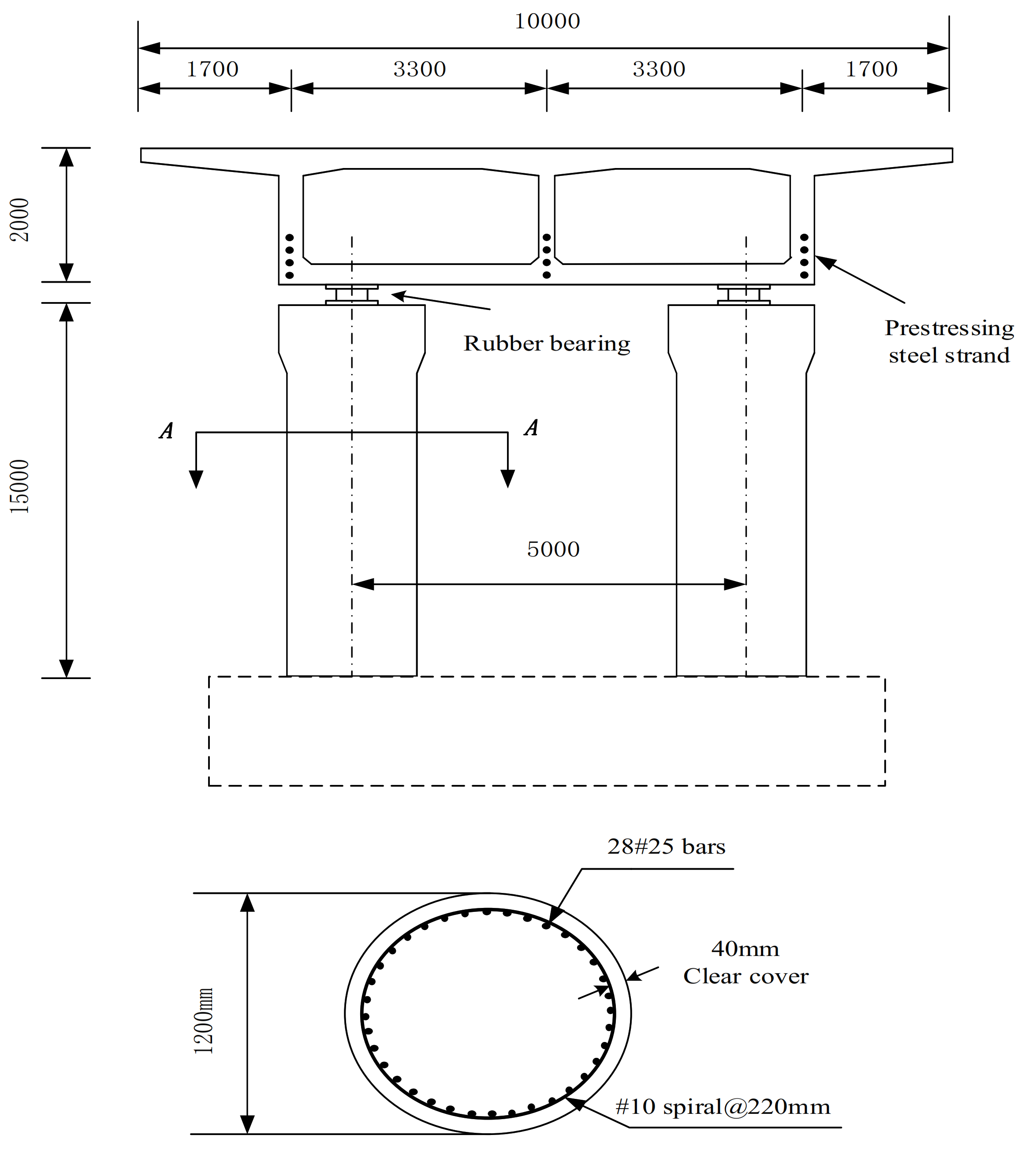
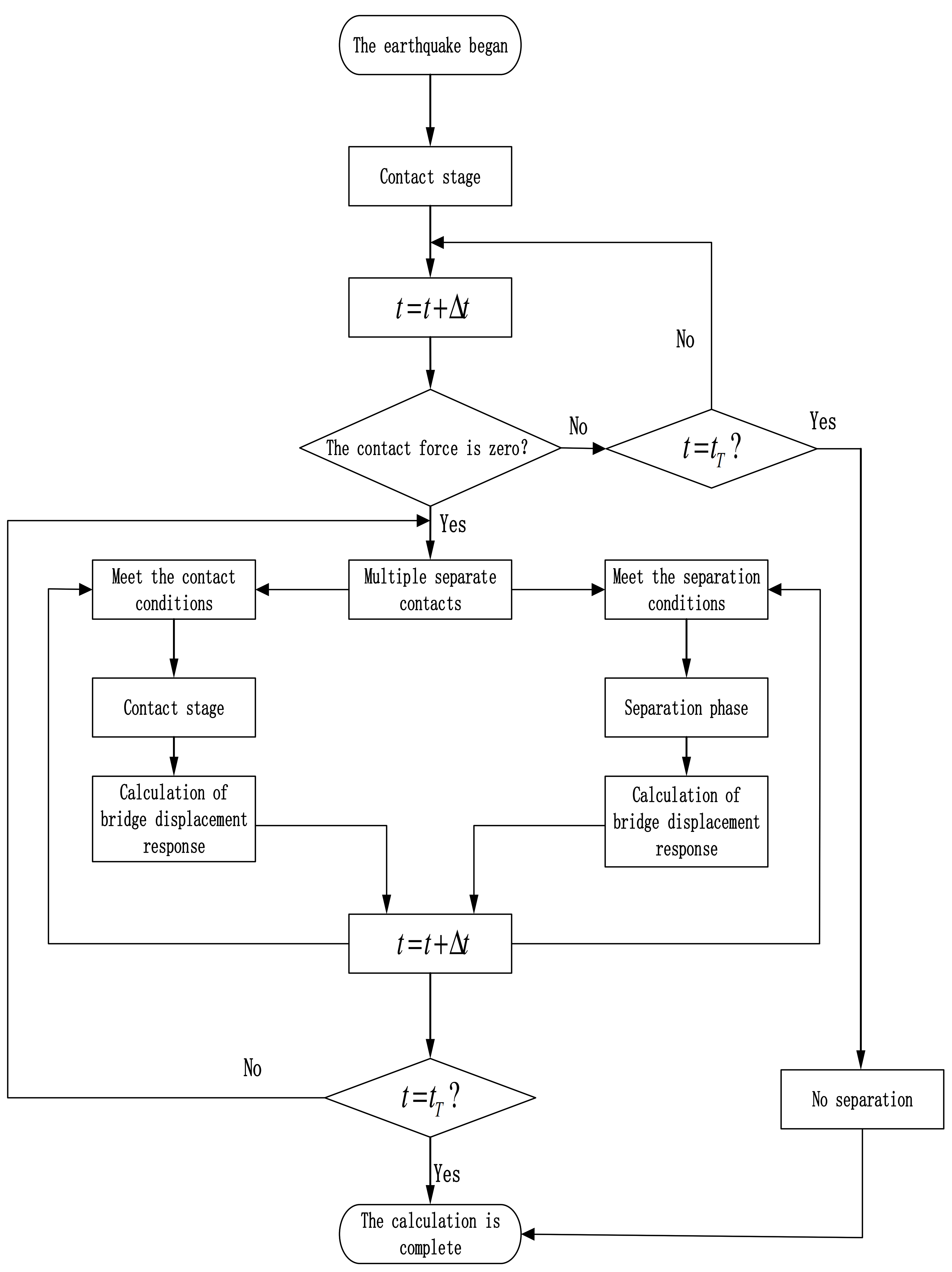
4. Numerical Simulation and Analysis
- (1)
- When the bridge is forced to resonate, the structural force and displacement response are always calculated by elastic deformation;
- (2)
- Ignore the possible bearing shear failure caused by a horizontal earthquake;
- (3)
- During seismic action, there are often stops in the lateral direction. This study only considers the coupling of vertical and longitudinal seismic activities;
- (4)
- Ignore the difference in the arrival time of the horizontal and vertical seismic waves, assuming that the earthquakes in both directions are excited at the same time.
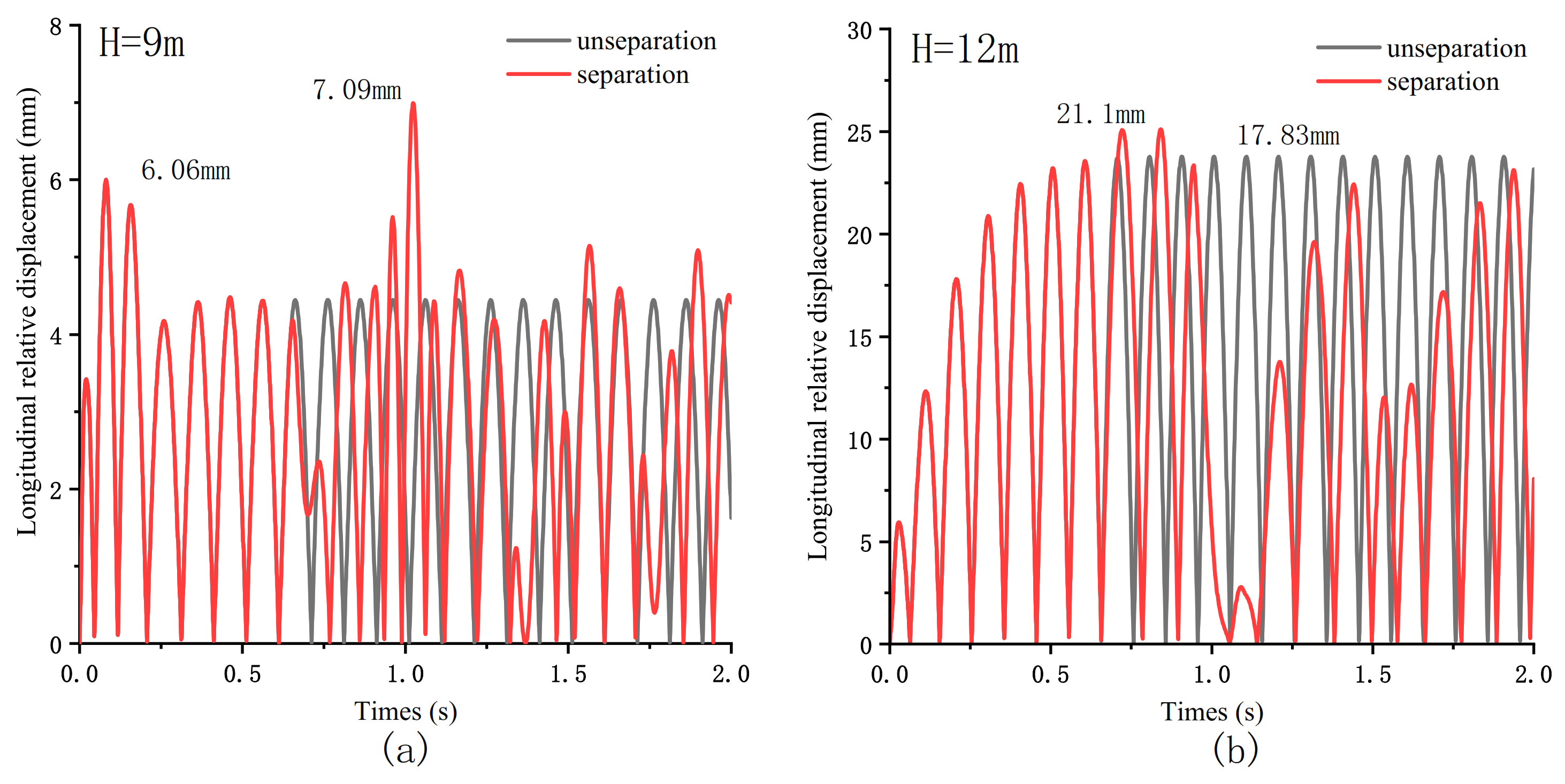
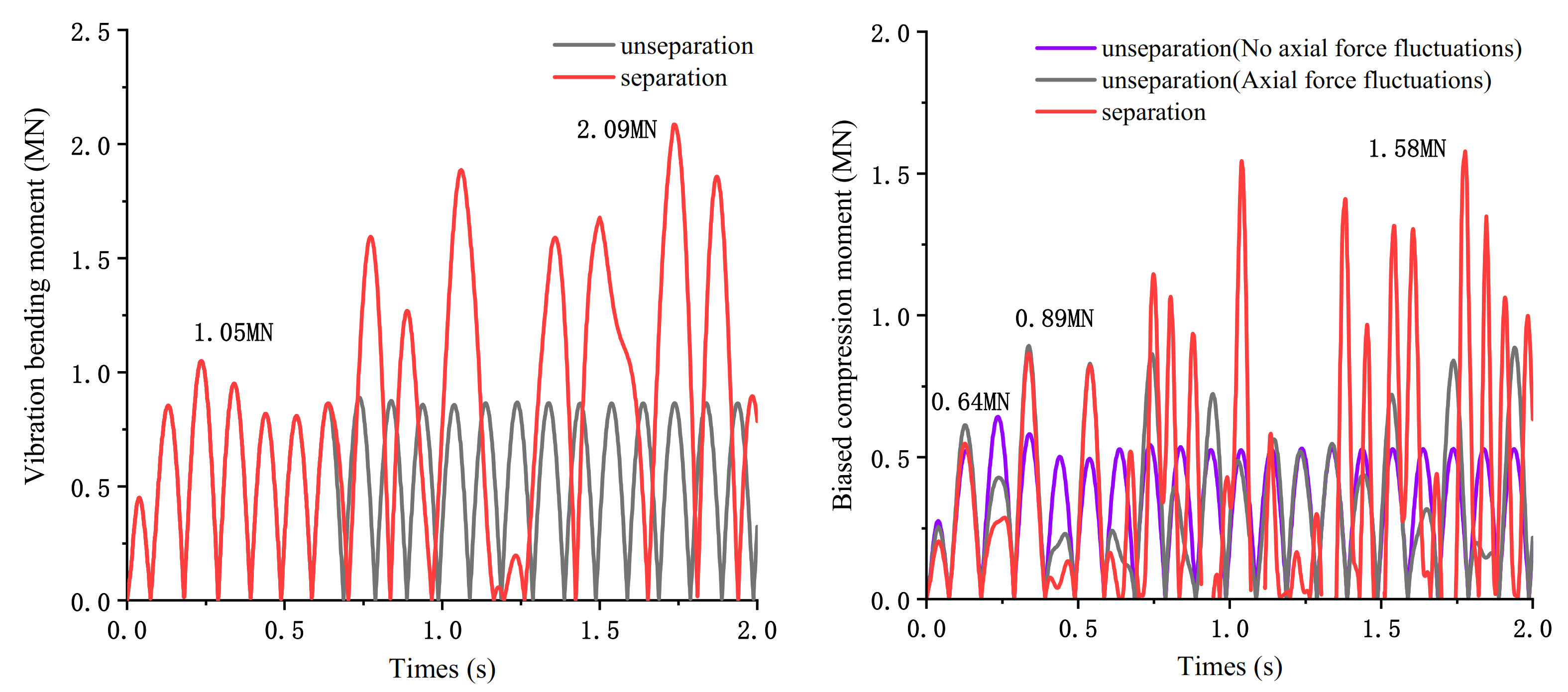
4.1. The Influence of Near-Field Vertical Seismic Acceleration on the Structure
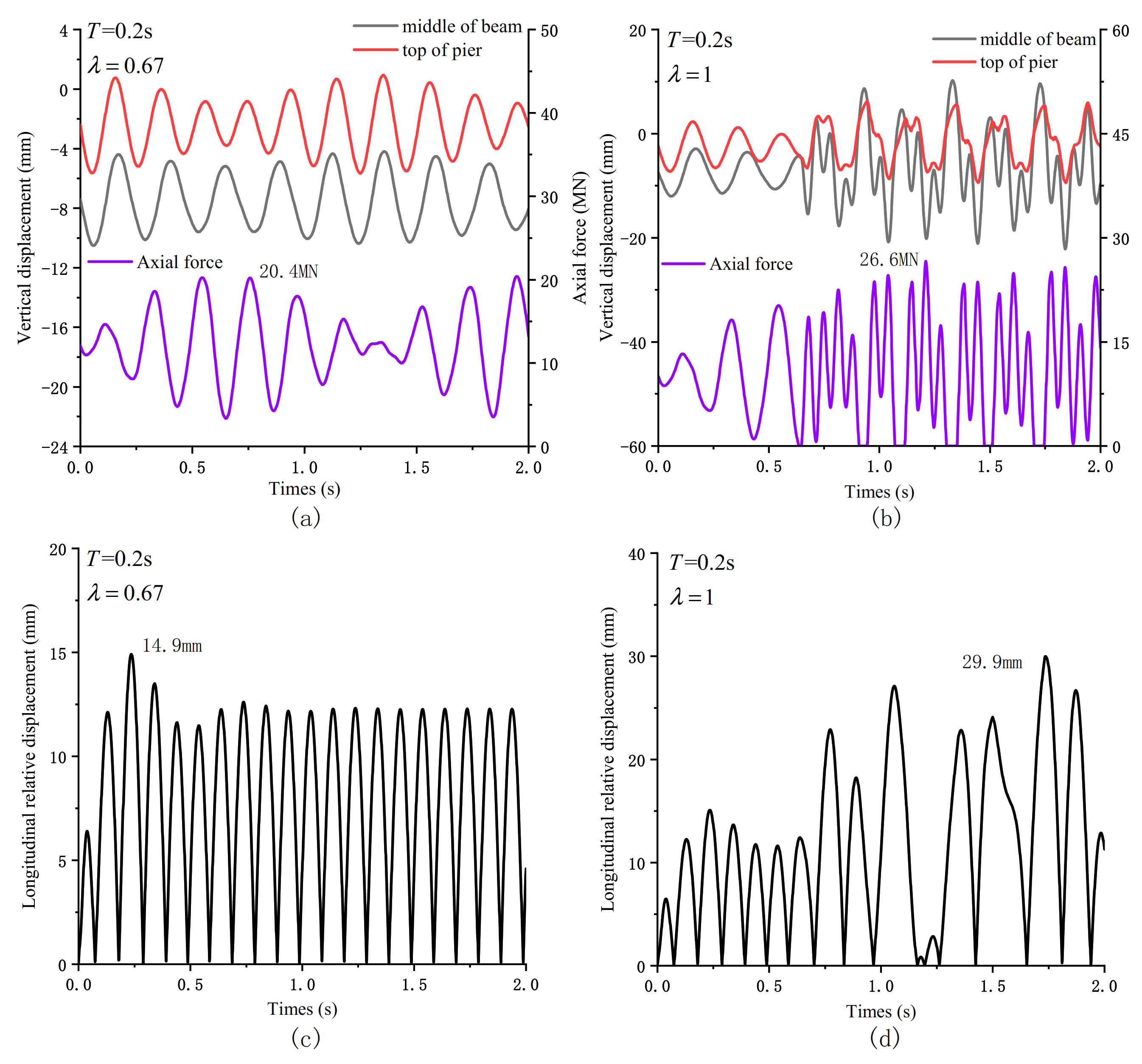
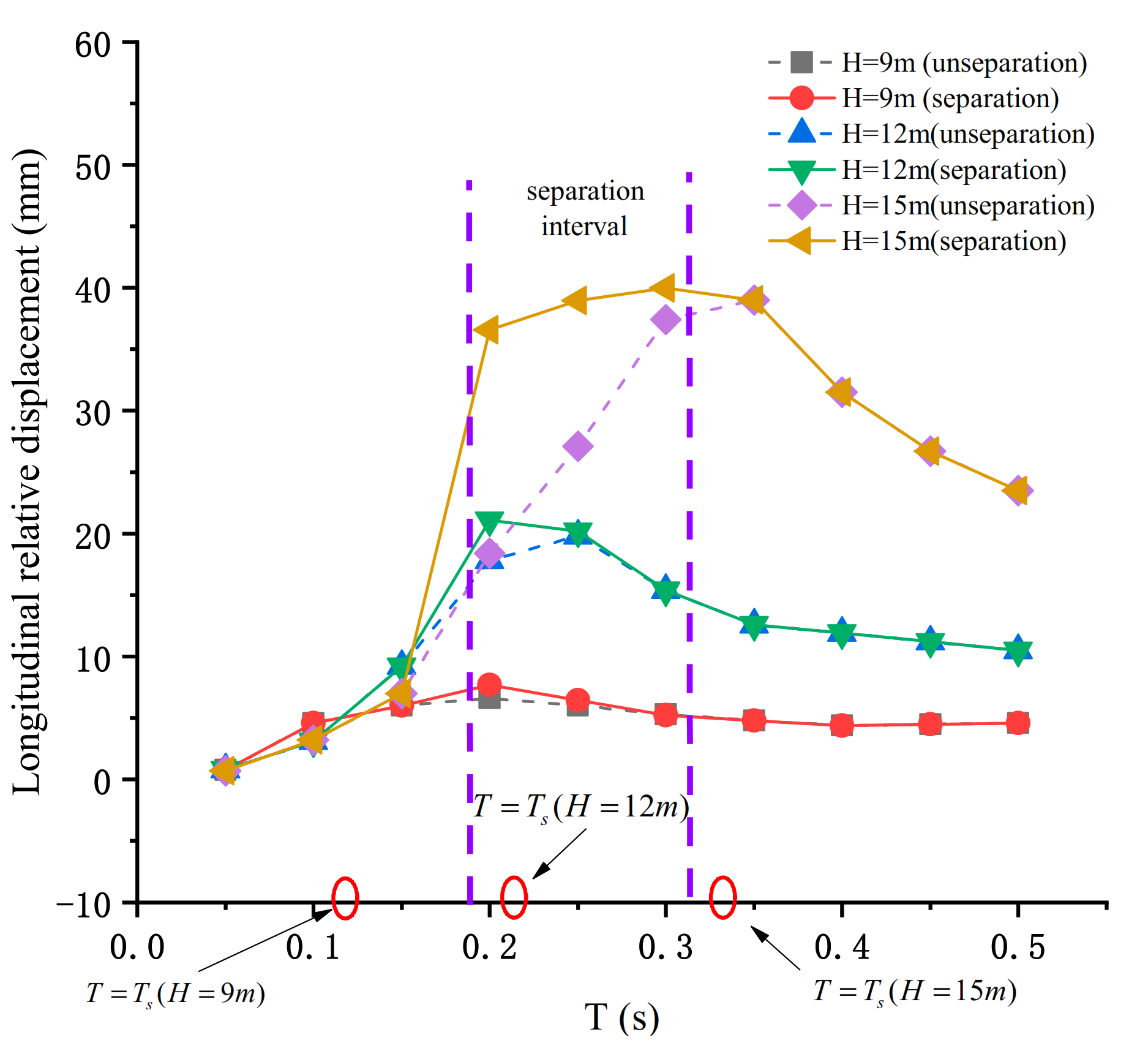
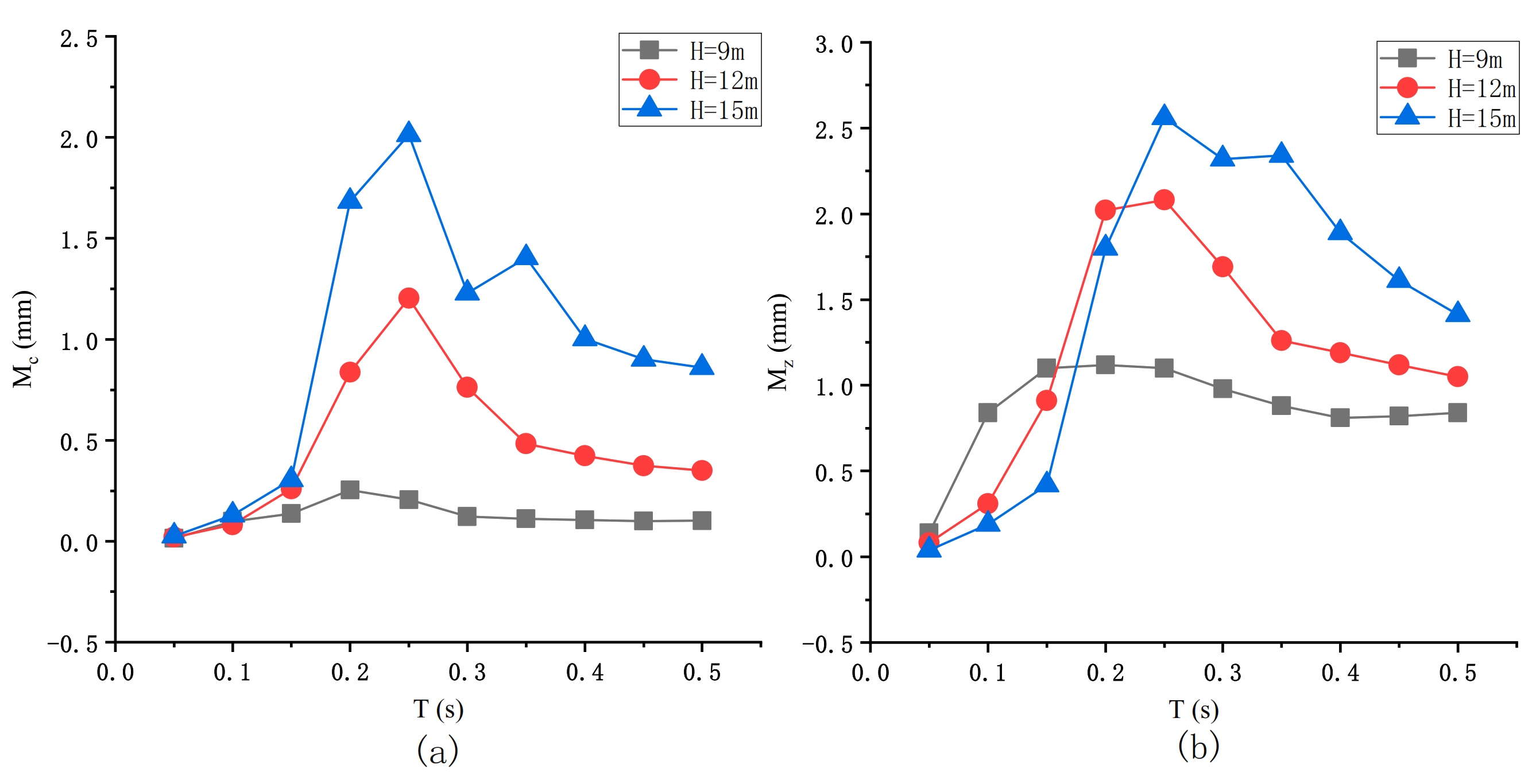
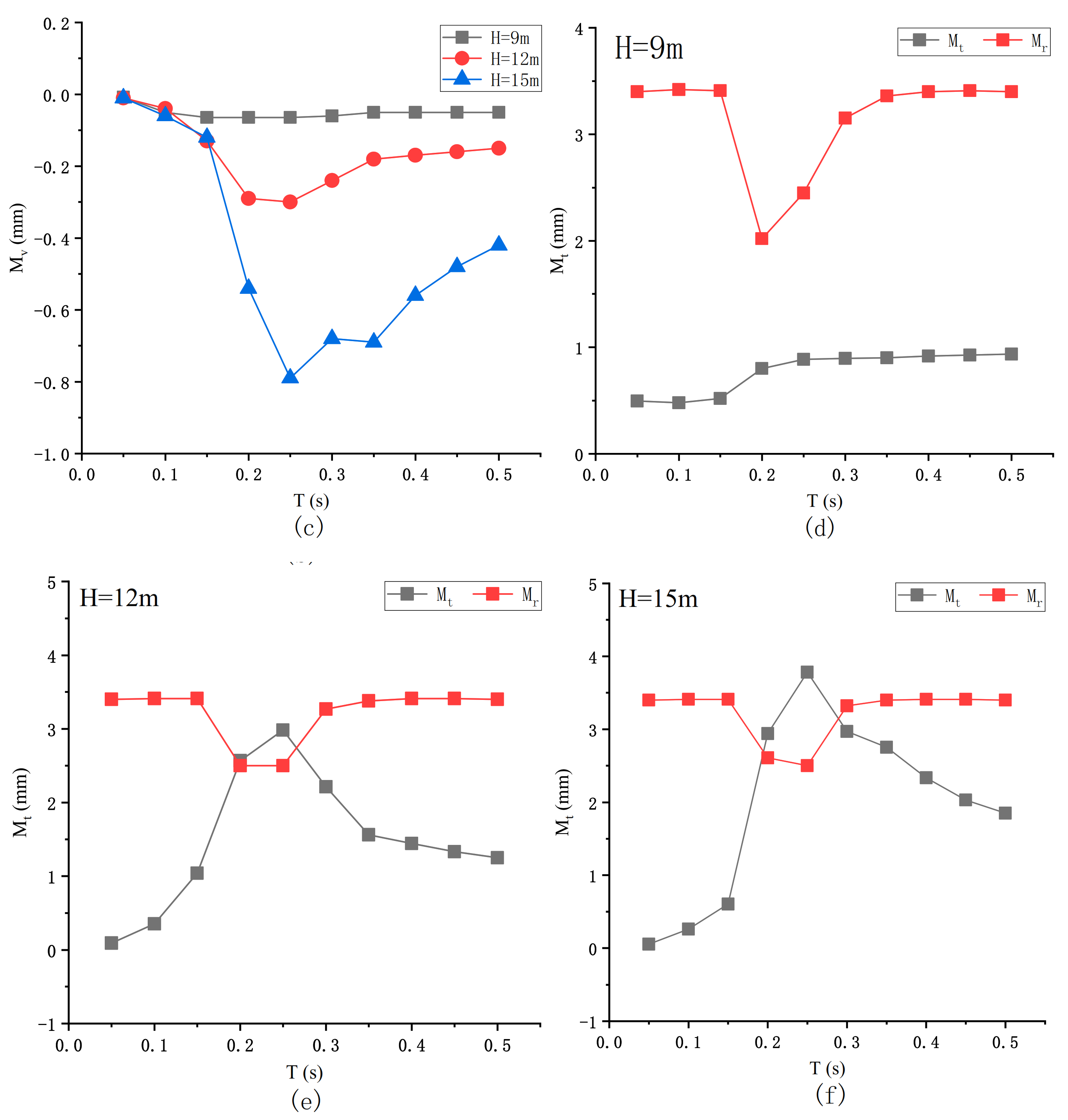
4.2. Seismic Response of Bridge Pier under Different Excitation Periods
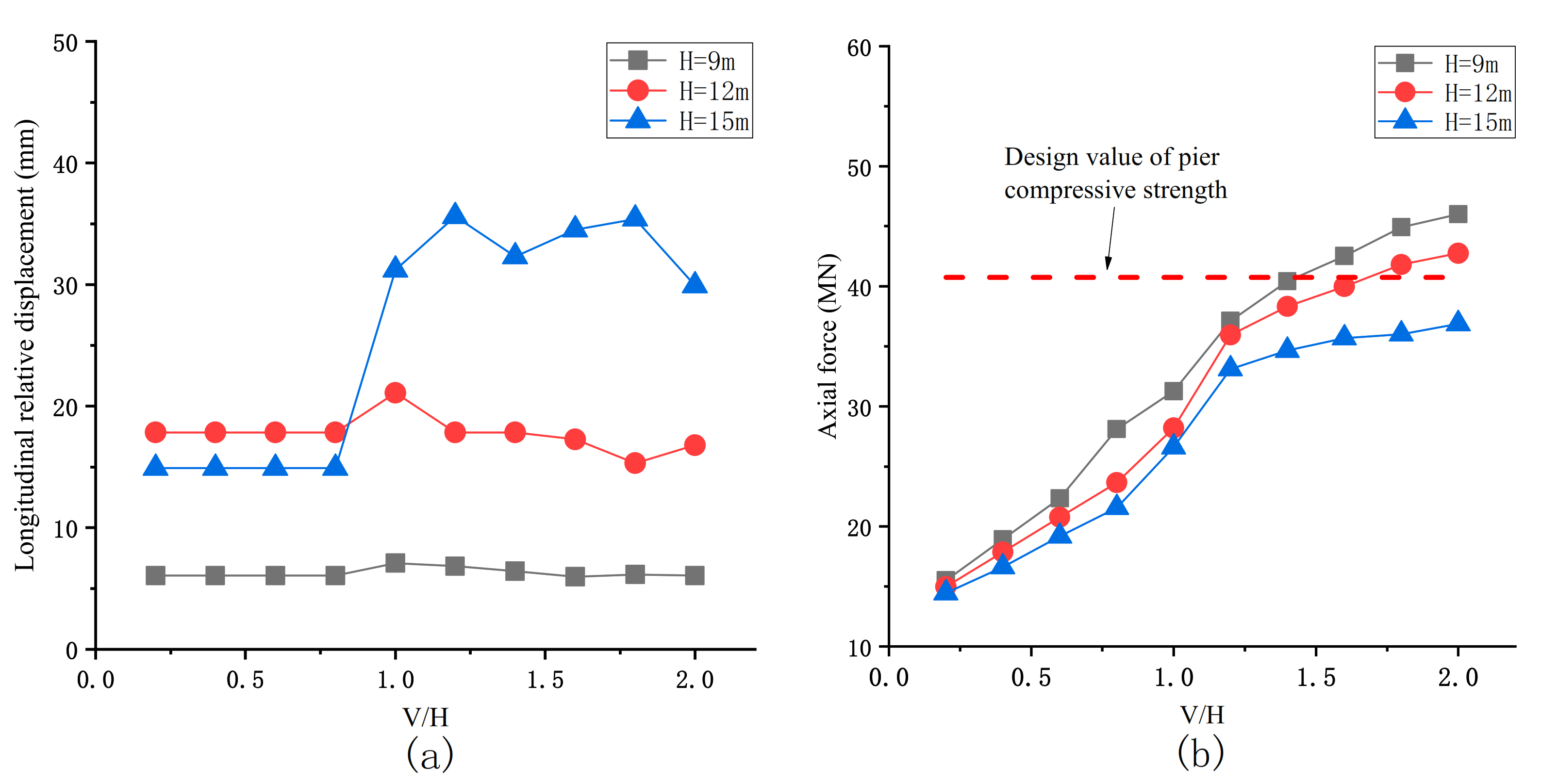
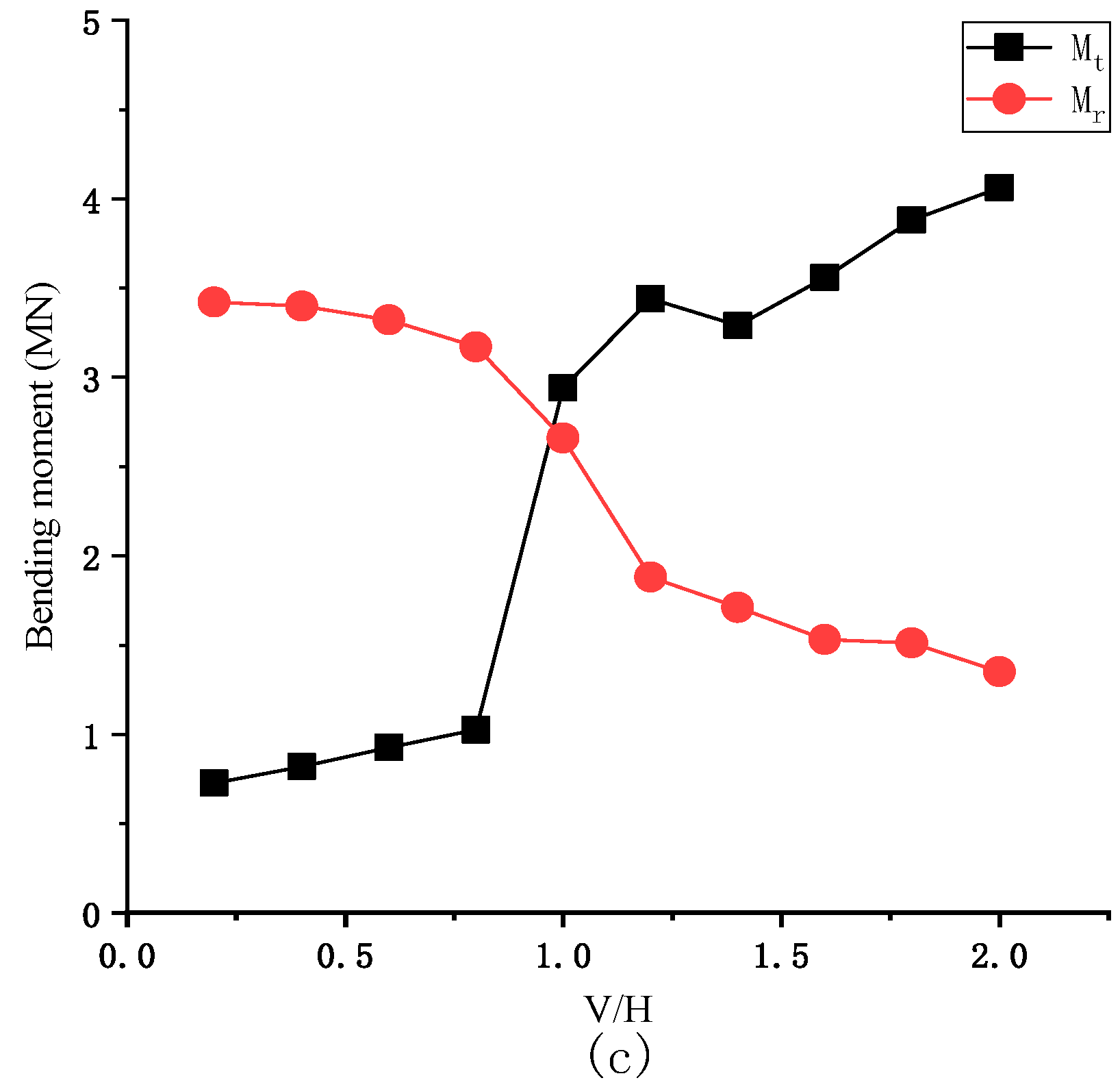
4.3. Seismic Response of Bridge Piers under Different Vertical Excitation Amplitudes
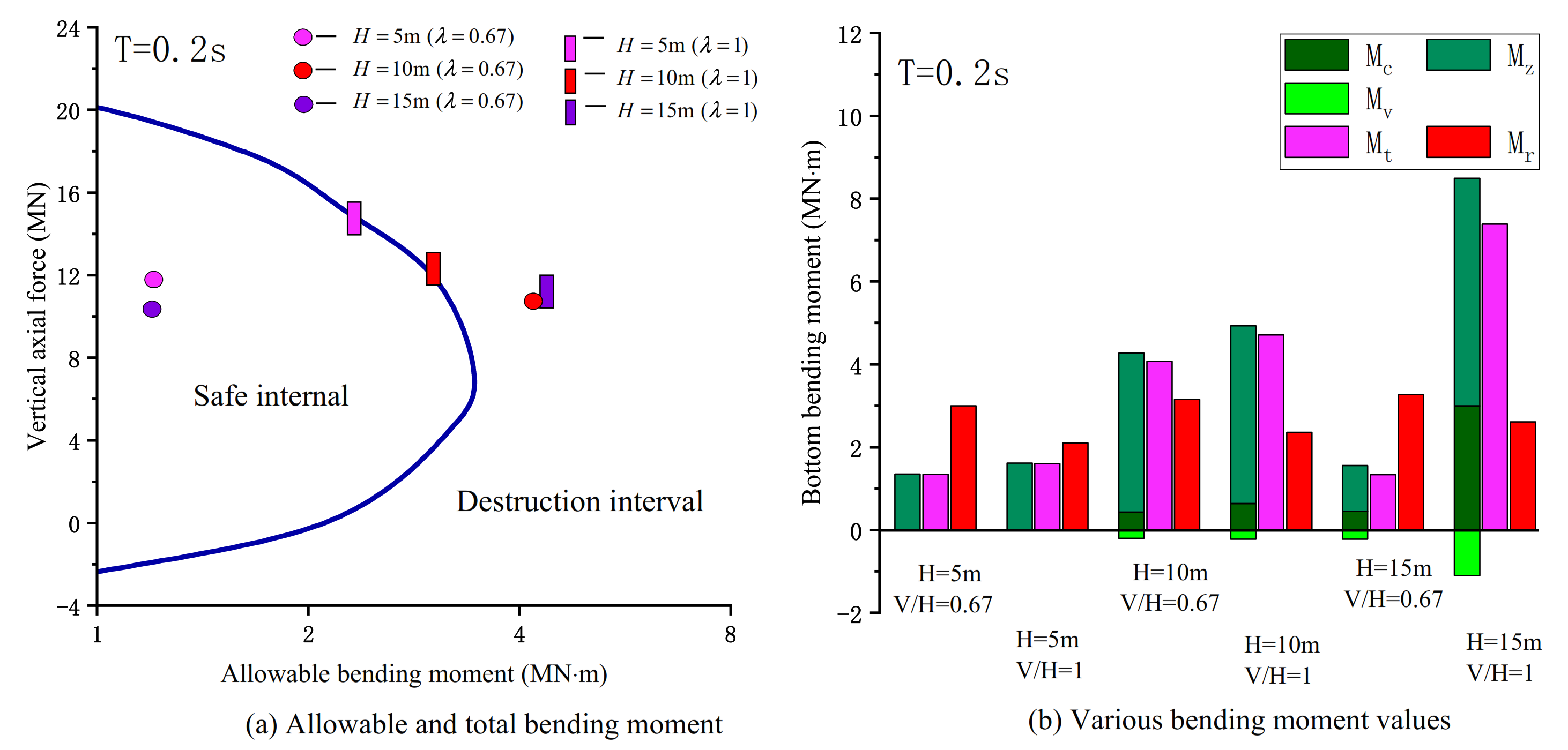
5. Discussion
6. Conclusions
- For medium- and small-span rubber bearing bridges, when the designed piers were high ( > ), the change of longitudinal displacement caused by separation will affect the bending failure of bridge piers.
- Only when the excitation period was close to the vertical natural vibration period can the structure separation occur, and the allowable moment of pier is the lowest. There may be two peaks in the total bending moment of pier. The excitation period was close to the longitudinal natural vibration period, and the other is when the structure is separated.
- With the increase of V/H, the total bending moment at the bottom of pier increased slowly, the allowable bending moment decreased gradually, and the pier is damaged.
- When V/H exceeded a specific range, the structure will be separated and a large vertical impact force will be produced. The impact force will cause the pier axial compression failure.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Nomenclature
| the magnitude of V/H | |
| α | the peak value of V/H |
| β | the linear attenuation coefficient |
| density of structure | |
| modulus of elasticity of main girder | |
| main girder section coefficient | |
| main girder section area | |
| modulus of elasticity of pier | |
| pier section coefficient | |
| pier section area | |
| q | uniform load of main beam |
| the deflection of the beam (i = 1,2) | |
| static displacement of the beam (i = 1,2) | |
| dynamic deformation part of the beam | |
| the deflection of the pier (i = 1,2) | |
| static displacement of the pier (i = 1,2) | |
| dynamic deformation part of the pier | |
| axial pressure of the initial girder and the support | |
| equation includes the bending wave function of the girder at contact time (i = 1,2) | |
| the longitudinal wave functionof the pier at contact time | |
| equation includes the bending wave function of the girder at separation of time (i = 1,2) | |
| the longitudinal wave functionof the pier at separation of time | |
| natural vibration frequency of the structure at contact time | |
| main beam seismic frequency at contact time | |
| pier seismic frequency at contact time | |
| natural frequency of the vibration considering the damping effect | |
| bearing damping | |
| structural self-damping | |
| wave numbers of flexural wave at contact time (longitudinal direction is wave numbers of longitudinal wave) | |
| wave numbers of longitudinal wave at contact time (longitudinal direction is wave numbers of flexural wave) | |
| wave numbers of flexural wave at separation time (longitudinal direction is wave numbers of longitudinal wave) | |
| wave numbers of longitudinal wave at separation time (longitudinal direction is wave numbers of flexural wave) | |
| time function of the bridge | |
| time function of the main beam | |
| time function of the pier | |
| impulse response function of the main beam | |
| impulse response function of the pier | |
| modal masses of the main beam | |
| modal masses of the pier |
References
- Li, H.N.; Xiao, S.Y.; Huo, L.S. Damage investigation and analysis of Engineering structures in the Wenchuan earthquake. J. Build. Struct. 2008, 29, 10–19. [Google Scholar]
- Zhuang, W.L.; Liu, Z.; Jiang, J. Earthquake-induced damage analysis of highway bridges in Wenchuan earthquake and countermeasures. Chin. J. Rock Mech. Eng. 2009, 28, 1377–1387. [Google Scholar]
- Xu, S.Y.; Zhang, J. Axial–shear–flexure interaction hysteretic model for RC columns under combined actions. Eng. Struct. 2012, 34, 548–563. [Google Scholar] [CrossRef]
- Ghannoum, W.M.; Mohle, J.P. Rotation-Based Shear Failure Model for Lightly Confined RC Columns. J. Struct. Eng. 2012, 138, 1267–1278. [Google Scholar] [CrossRef]
- Elwood, K.J. Modeling failures in existing reinforced concrete. Can. J. Civ. Eng. 2004, 31, 846–859. [Google Scholar] [CrossRef]
- Button, M.R.; Cronin, C.J.; Mayes, R.L. Effect of Vertical Motions on Seismic Response of Highway Bridges. J. Struct. Eng. 2002, 128, 1551–1564. [Google Scholar] [CrossRef]
- Huang, F.; Cao, Z.; Jiang, S.H.; Zhou, C.; Huang, J.; Guo, Z. Landslide susceptibility prediction based on a semi-supervised multiple-layer perceptron model. Landslides 2020, 17, 2919–2930. [Google Scholar] [CrossRef]
- Li, W.; Fan, X.; Huang, F.; Chen, W.; Hong, H.; Huang, J.; Guo, Z. Uncertainties analysis of collapse susceptibility prediction based on remote sensing and GIS: Influences of different data-based models and connections between collapses and environmental factors. Remote Sens. 2020, 12, 4134. [Google Scholar] [CrossRef]
- Zhu, L.; Huang, L.; Fan, L.; Huang, J.; Huang, F.; Chen, J.; Zhang, Z.; Wang, Y. Landslide Susceptibility Prediction Modeling Based on Remote Sensing and a Novel Deep Learning Algorithm of a Cascade-Parallel Recurrent Neural Network. Sensors 2020, 20, 1576. [Google Scholar] [CrossRef]
- Wilson, T.; Chen, S.; Mahmoud, H. Analytical case study on the seismic performance of a curved and skewed reinforced concrete bridge under vertical ground motion. Eng. Struct. 2015, 100, 128–136. [Google Scholar] [CrossRef]
- Kunnath, S.K.; Erduran, E.; Chai, Y.H.; Yashinsky, M. Effect of near-fault vertical ground motions on seismic response of high overcrossings. J. Bridge Eng. 2008, 13, 282–290. [Google Scholar] [CrossRef]
- Yu, C.P. Effect of Vertical Earthquake Components on Bridge Response. Ph.D. Thesis, University of Texas, Austin, TX, USA, 1998. [Google Scholar]
- Papazoglou, A.J.; Elnashai, A.S. Analytical and field evidence of the damaging effect of vertical earthquake ground motion. Earthq. Eng. Struct. Dyn. 1996, 25, 1109–1137. [Google Scholar] [CrossRef]
- Varecac, D.; Draganic, H.; Gazic, G. Influence of the Vertical Component of Earthquake on Large Span Rc Beams. Teh. Vjesn. Tech. Gaz. 2010, 17, 357–366. [Google Scholar]
- Kim, S.J.; Holub, C.J.; Elnashai, A.S. Experimental investigation of the behavior of RC bridge piers subjected to horizontal and vertical earthquake motion. Eng. Struct. 2011, 33, 2221–2235. [Google Scholar] [CrossRef]
- Güllü, H.; Jaf, H.S. Full 3D nonlinear time history analysis of dynamic soil structure interaction for a historical masonry arch bridge. Environ. Earth Sci. 2016, 75, 1–17. [Google Scholar] [CrossRef]
- Zheng, W.; Leonardo, D.O.; Jamie, E.P. Seismic response of a bridge-soil-foundation system under the combined effect of vertical and horizontal ground motions. Earthq. Eng. Struct. Dyn. 2012, 4, 545–564. [Google Scholar]
- Rezaei Rad, A.; Banazadeh, M. Probabilistic Risk-Based Performance Evaluation of Seismically Base-Isolated Steel Structures Subjected to Far-Field Earthquakes. Buildings 2018, 8, 128. [Google Scholar] [CrossRef]
- Sharma, A.; Jangid, R.S. Seismic Response of Base-Isolated Benchmark Building with Variable Sliding Isolators. J. Earthq. Eng. 2010, 14, 1063–1091. [Google Scholar] [CrossRef]
- Bozorgnia, Y.; Niazi, M.; Campbell, K.W. Characteristic of free-field vertical ground motion during the Northridge earthquake. Earthq. Spectra 1995, 11, 515–526. [Google Scholar] [CrossRef]
- Wang, G.-Q.; Zhou, X.-Y.; Zhang, P.-Z.; Igel, H. Characteristics of amplitude and duration for near fault strong ground motion from the 1999 Chi-Chi, Taiwan earthquake. Soil Dyn. Earthq. Eng. 2002, 22, 73–96. [Google Scholar] [CrossRef]
- Wang, D.; Xie, L. Attenuation of peak ground accelerations from the great Wenchuan earthquake. Earthq. Eng. Eng. Vib. 2009, 8, 179–188. [Google Scholar] [CrossRef]
- Wang, C.J.; Shih, M.H. Performance study of a bridge involving sliding decks and pounded abutment during a violent earthquake. Eng. Struct. 2007, 29, 802–812. [Google Scholar] [CrossRef]
- Zuo, Y.; Sun, G.J.; Li, H.J. Comparison and Research of Unseating Prevention Measures in Seismic Codes of China and Foreign Countries. J. Disaster Prev. Mitig. Eng. 2016, 36, 617–623, 639. [Google Scholar]
- Han, W.; Song, C.; Li, Q. Strong ground motion at meizoseisal area & safety of important engineering projects at potential earthquake region. J. Eng. Geol. 2004, 12, 346–353. [Google Scholar]
- Tanimura, S.; Mimura, K.; Nonaka, T.; Zhu, W. Dynamic failure of structures due to the great Hanshin-Awaji earthquake. Int. J. Impact Eng. 2000, 24, 583–596. [Google Scholar] [CrossRef]
- Kim, S.H.; Shinozuka, M. Effects of Seismically Induced Pounding at Expansion Joints of Concrete Bridges. J. Eng. Mech. 2003, 129, 1225–1234. [Google Scholar] [CrossRef]
- Li, S.; Guo, A.; Cui, L. Pounding-induced stress wave analysis and mitigation of highway bridges under earthquake. In Proceedings of the 11th International Conference in Experimental Structural Engineering, University of Illinois Urbana-Champaign, Chmapaign, IL, USA, 1–2 August 2015. [Google Scholar]
- DesRoches, R.; Delemont, M. Seismic retrofit of simply supported bridges using shape memory alloys. Eng. Struct. 2002, 24, 325–332. [Google Scholar] [CrossRef]
- Yang, H.B.; Yin, X.C.; Hao, H. Theoretical Investigation of Bridge Seismic Responses with Pounding under Near-Fault Vertical Ground Motions. Adv. Struct. Eng. 2015, 18, 452–468. [Google Scholar] [CrossRef]
- Yang, H.B.; Yin, X.C. Transient responses of girder bridges with vertical poundings under near-fault vertical earthquake. Earthq. Eng. Struct. Dyn. 2015, 44, 2637–2657. [Google Scholar] [CrossRef]
- Xing, Y.F.; Wang, L.J. Analysis of wave propagation in the built-up structures of rod-beam and beam-beam. J. Beijing Univ. Aeronaut. Astronaut. 2013, 30, 520–523. [Google Scholar]
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. CJJ 166-2011. Code for Seismic Design of Urban Bridges; Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2011. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
An, W.; Song, G. Transient Response of Bridge Piers to Structure Separation under Near-Fault Vertical Earthquake. Appl. Sci. 2021, 11, 4068. https://doi.org/10.3390/app11094068
An W, Song G. Transient Response of Bridge Piers to Structure Separation under Near-Fault Vertical Earthquake. Applied Sciences. 2021; 11(9):4068. https://doi.org/10.3390/app11094068
Chicago/Turabian StyleAn, Wenjun, and Guquan Song. 2021. "Transient Response of Bridge Piers to Structure Separation under Near-Fault Vertical Earthquake" Applied Sciences 11, no. 9: 4068. https://doi.org/10.3390/app11094068
APA StyleAn, W., & Song, G. (2021). Transient Response of Bridge Piers to Structure Separation under Near-Fault Vertical Earthquake. Applied Sciences, 11(9), 4068. https://doi.org/10.3390/app11094068





