Abstract
Currently, optimization models for the safe and reliable operation of power systems deal with two major challenges: the first one is the reduction of the computational load when considering contingencies; the second one is the adequate modeling of the uncertainty of intermittent generation and demand. This paper proposes a new affinely adjustable robust model to solve the security constrained unit commitment problem considering these sources of uncertainty. Linear decision rules, which take into account the forecasts and forecast errors of the different sources of uncertainty, are used for the affine formulation of the dispatch variables, thus allowing the tractability of the model. Another major novelty is that the evaluation of the security constraints is performed by incorporating a novel method, proposed in the literature, based on the user-cuts concept. This method efficiently and dynamically adds only the binding security constraints, increasing the computational efficiency of the model when transmission line contingencies are considered. Finally, Monte Carlo simulations on the post-optimization results were run to demonstrate the effectiveness, feasibility and robustness of the solutions provided by the proposed model.
1. Introduction
Nowadays, the planning and operation of power generation systems worldwide relies on optimization models. Particularly, unit commitment (UC) aims at meeting forecasted energy demand at minimum cost in an hour-by-hour daily horizon while meeting different physical and operational constraints. Moreover, market regulation and system reliability requirements lead to additional constraints. An updated overview of the UC is given at [1], whereas Knueven et al. [2] provide a comprehensive review of mixed integer programming models of the UC.
Today, a key aspect in the expansion of power systems is the high penetration of non-conventional renewable energy sources, such as wind and solar generation. Nonetheless, the intermittent nature of these energy sources increases the uncertainty in the operation and planning of the system. The authors in [3] define three categories of uncertainty within power systems: (1) uncertainty of generation resources (fuel prices, generator outages, intermittent generation output power, etc.); (2) uncertainty on the demand side; and (3) uncertainty in the transmission of energy (contingencies in lines). Meanwhile, other authors such as [4] have developed a computational framework to integrate the uncertainties of wind, demand, and the operating outputs of generators and transmission lines. These uncertainties may arise at any time and produce disturbances in the normal operation and balance of the system. In order to mitigate the negative effects of uncertainty, new mathematical optimization models focus on incorporating the dynamic and unexpected variability of power systems. Conventional procedures and methods for the UC solution, under different conditions of uncertainty, have been widely applied by researchers [5,6].
Dealing with the uncertainties of the UC problem through deterministic optimization (as in [7,8]), where load and intermittent generation sources are based solely on forecasts, may not be adequate to correctly address the reliable balance between this type of sources and demand. Although this approach may be easy to implement and computationally more efficient, its greatest drawback lies in the overestimation of generation reserves, a circumstance that turns out to be economically inefficient for the system.
On the other hand, stochastic optimization models for the UC (SOUC) address the behavior of the corresponding random variables through probability distributions that are modeled by a finite set of scenarios, each one with a given probability. This approach overcomes some of the drawbacks of deterministic formulations. However, considering a large number of scenarios in the SOUC hinders the computational tractability of the underlying mathematical models. Dyer and Stougie [9] discuss in detail the computational complexity of the SOUC. As an alternative, different techniques have been used to solve the SOUC efficiently (i.e., shortening the required solution times). These techniques include: Lagrangian relaxation—LR [5,10,11,12,13], Benders decomposition—BD [12,14,15,16,17], strong valid inequalities embedded in cutting plane approaches [18,19], column generation [20,21], and progressive hedging algorithms [22,23,24,25,26,27,28,29,30]. Likewise, the parallel implementation of the above techniques is also an alternative, e.g., LR [10] and BD [31].
The other major drawback of SOUC approaches is the difficulty that arises when trying to estimate the probability distribution of the stochastic variables. Alternatively, robust optimization of the UC (ROUC) does not require the definition of scenarios or the estimation of their realization probabilities. Instead, it defines an uncertainty set to optimize the response of the system over all possible realizations of the random variables, particularly the worst one [1]. Several authors have tackled the UC from the robust optimization perspective [32,33,34,35,36]. However, one major drawback appears, as a direct consequence of protecting the system against an improbable worst-case scenario: the obtained solution can be over-conservative [37]. Several strategies have been proposed to reduce the conservatism of the ROUC approach. For instance, min-max regret optimization [38], a unifying approach combining the elements and advantages of the SOUC and the ROUC [39], and a so-called non-conservative robust (security constrained) UC [38].
Remarkably, adaptive robust optimization of the UC (AROUC) produces a less conservative and more stable solution than ROUC approaches [40,41,42,43]. This result is obtained due to adjustable decision variables (also known as wait-and-see variables) that are calculated when some of the uncertain data are known at a given period (by considering information of past realizations of the random variables) [44,45]. However, a known drawback of adaptive robust optimization (ARO) is the intractability that may occur for large scale problems given the NP-hardness of the problems [45]. The solution of this drawback results in the use of affinely adjustable robust optimization (AARO) approaches where adjustable variables are constrained to affine policies (AP), also known as affine arithmetic (AA) [45]. Xiong and Jirutitijaroen [46] pioneered the combination of AA and ARO for the solution of the energy and reserve dispatch problem. The effectiveness of AA stimulates the use of this approach to tackle the uncertainty in optimal power flow problems [47,48,49,50,51,52,53], and UCs in power systems [54] and isolated micro-grids [55].
In recent years, some researchers have proposed including the affinely adjustable robust optimization within the UC (AAROUC), considering different sources of uncertainty. It was found that the AAROUC provides better results compared to conventional optimization methods when dealing with uncertainty in power systems. Shahidehpour et al. [56] presented a distributionally robust optimization (DRO) model for UC in coordinated electricity and district heating networks. Simplified affine policies were used to improve the computational tractability of the model. Zugno et al. [57] introduced a model based on AARO to solve the UC problem and dispatch of generation units participating in electricity and heat markets.
Xiong et al. [58] propose a DRO model to solve the UC (DROUC) considering only the volatility of wind power generation. DROUC produces less conservative solutions than ROUC. They applied formulations based on linear decision rules for the dispatch variables to improve computation time. Finally, Lorca et al. [42] presented a multistage adaptive robust optimization model for the UC only considering the uncertainty of the load. Simplified affine policies based on linear decision rules were explored to deal with large-scale power systems. The interested reader may refer to [45,59] for the theoretic background regarding AARO. Researchers have concluded that AAROUC models (that incorporate the realization of the uncertain parameters in previous periods) significantly reduce the operational cost of the system when compared with UC models based on conventional deterministic, stochastic, and robust optimization models [42,56].
Although AARO models have been proposed for the UC problem in the past [42,46,56,58]. Previous works examined only one uncertainty source at a time when non-conventional renewable sources are considered. For instance, Ref. [42] only contemplates demand uncertainty, whereas Ref. [58] only includes wind generation uncertainty. In Ref. [56], the authors include wind and solar generation uncertainty but not demand uncertainty. Moreover, to the best of our knowledge, security constraints are seldom studied in this context. Therefore, the contributions of this paper are threefold. First, we introduce a new AAROUC model where uncertainties in load, wind, and solar generation are simultaneously considered. This model relies on forecasts and forecast errors of the different sources of uncertainty to restrict the wait-and-see or adjustable variables of the model. Second, the model includes security constraints, resulting in an AARO-SCUC model that, (to the best of our knowledge), has not been studied before in the literature. Third, the evaluation of the security constraints is based on the concept of user cuts (as proposed in [60,61]). This method efficiently and dynamically adds only the binding security constraints, increasing the computational efficiency of the model when transmission line contingencies are contemplated.
The rest of this paper is organized as follows: Section 2 presents the theoretical background of AARO and security constrained UC. Section 3 describes the deterministic formulation of the security constrained UC. Section 4 introduces the AARO reformulation of the security constrained UC. Section 5 discusses the results of computational experiments conducted on benchmark power systems from the literature. Finally, Section 6 summarizes the main conclusions and future research possibilities that arise with the use of AARO for the solution of the security constrained UC.
2. Theorical Background
To set the theoretical background needed for the AARO formulation of the security constrained UC, this section discusses the basics of affine arithmetic, and affinely adjustable robust optimization.
2.1. Affine Arithmetic
Affine arithmetic is a numerical computation model for interval methods that overcomes one of the main obstacles of traditional interval arithmetic (the dependency problem). That is, standard interval arithmetic procedures tend to overestimate the range of a function (f) defined over intervals, and with an increase of the magnitude of the problem as f becomes more complex. AA is a self-validated numerical computation model that relies on first order correlations between computed and input quantities. This allows the computation of the numerical error of a given quantity, something that is very useful when lower and upper bounds of a given function are analyzed. de Figueiredo and Stolfi [62] present the main concepts of AA. We follow their notation and definitions in this paper.
In AA, a quantity (or ideal variable) x is represented by a first order polynomial (i.e., an affine form) given in Equation (1). In this equation, represents the central value. Noise symbols represent independent components of the total uncertainty of variable x, whose values are unknown but restricted to the interval [−1, +1]. Finally, are the partial deviations associated with each term. These terms represent the magnitude of the uncertainty of the corresponding component:
For instance, Equation (2) corresponds to the AA representation () of the output of a generation unit while considering both the uncertainty of wind generation and demand. In this equation, is the central value of the generation variable , whereas are the deviations of the variable due to demand forecasting errors (), and are the deviations of the variable caused by forecasting errors of wind generation ():
It is worth noting that affine forms enable the computation of interval bounds. Therefore, a quantity or variable x represented in the affine form of Equation (1) is bounded in the interval , where the total deviation is defined as .
2.2. Affinely Adjustable Robust Optimization (AARO)
There are two types of variables within AARO: adjustable and non-adjustable. In this case, the non-adjustable variables are those sided with the UC constraints, while the adjustable ones are those that belong to the dispatch constraints. One of the most important features when using AARO is that the adjustable variables can be tuned by themselves (considering the deviation produced in past periods), based on the known uncertainty data which is fundamental in multi-period problems [45].
The first step in developing a formulation using AARO is to establish a linear decision rule (LDR) through affine rules. For example, allowing be a linear function of the demand where
where and , , are new decision variables introduced to define the LDR. In AARO, the optimal values of and are computed instead of computing [45].
The second step consists of defining an uncertainty set for the objective function, and for each constraint of the problem, which could be a polyhedral or ellipsoidal set. It is important to select a set of uncertainties that allows the AARO model to be solved efficiently. For example, it is not possible to know the future value of the demand variable , but it is possible to know that:
where is the nominal value of the demand for each period t, and is the uncertainty level. Thus, probability distributions are not necessary to define the uncertain parameters within the model.
Without loss of generality, the following equivalences are used to reformulate the LDR (3), considering the uncertainty set (4):
where b is a real number.
Finally, in order to eliminate the absolute value in (6), it is necessary to introduce a linear decision variable , to guarantee the linearity of the decision rule. In this way, the AARO formulation is obtained for an adjustable variable limited by an uncertainty set:
In this expression, signs of term depend on the side of the inequality where the adjustable variable is.
3. Deterministic Model for Security Constrained Unit Commitment
The deterministic Security Constrained Unit Commitment is formulated as a mixed-integer linear programming (MILP) problem, minimizing the operating cost of the power system subject to system network constraints, under both normal and contingency () operation conditions, given by Equations (8) to (19) as shown below. The notation of the model is given in Appendix A:
Subject to:
Binary variable logic:
Initial on-off status of generator i at (11), minimum up (12) and down time constraints (13):
where:
Minimum and maximum generator output constraint:
Ramping constraints:
Net power balance constraints:
Power flow constraint under normal condition (18):
Power flow constraint under contingency () conditions (19):
parameter is the sensitivity factor between line l and generator bus s when line k was opened. It is computed as follows:
In this equation, is the power transfer distribution factor of the line l given a power injection in bus s. Likewise, is a power transfer distribution factor of the opened line k given a power injection in bus s. Finally, is line outage distribution factor of the line l when line k is opened.
4. AARO Model for Security Constrained Unit Commitment (SCUC)
Section 3 presented a deterministic formulation of the SCUC. This formulation works under the assumption that all parameters supporting the decision-making in each period are known. Nonetheless, this assumption is not adequate to deal with uncertainty as previously stated in Section 1. In order to consider the effect of uncertainty on the safe, economical and reliable operation of power systems, this section presents a new AARO formulation for SCUC.
4.1. AARO Formulation to Solve the SCUC Problem
In this formulation, the non-adjustable variables are those binary variables belonging to Equations (9)–(13) (fist stage decisions), while the adjustable variables belong to the dispatch Equations (14)–(19).
Dispatch decisions, which are being taken every hour, depend on the knowledge of the uncertainty parameters up to the current operating time. Therefore, dispatch decisions are non-anticipative variables. The AAROUC perfectly models this condition, since it allows considering Automatic Generation Control (AGC) actions where hydro-thermal generators can correct errors only at the current time.
In Equation (21), represents the affine form of the power dispatch variable for each generator , being its central value, and determines the non-anticipativity condition. , represent the deviation variables and forecast errors related to the uncertainty of wind generation, solar generation, and demand, respectively. Forecast errors belong to the uncertainty set bounded by the a maximum level of uncertainty as shown in Section 4.2:
Finally, in consideration of the theoretical background provided in Section 2, the deterministic model presented in Section 3, the uncertainty of demand and that of renewable energy sources (i.e., wind and solar generation), a new AARO model to solve the SCUC is presented below:
Suject to:
Binary constraints of the UC. On–off status and minimum up and down time constraints given in Equations (9)–(13).
Dispatching cost. The constraint given by (23) represents the cost of dispatch. The additional variable sets an upper bond by denoting the highest cost for the dispatch problem. Constraints (24)–(26) are the absolute values of the deviations (related to the objective function) generated by the uncertainties of wind and photovoltaic generation, as well as the load, respectively:
Variables represent the adjustment of the hydro-thermal generator (i) at time t and past period , given the deviation of forecast errors of the wind generator (w), solar generator (p) and total demand, respectively. Likewise, auxiliary linear variables ensure the linearity of the decision rule for affine policies of the objective function, given the deviation of forecast errors of the wind generator (w), solar generator (p) and total demand, correspondingly, at time t and past period .
Generation limits. Constraints (27) and (28) correspond to the AARO formulation for constraint (14) establishing minimum and maximum generation limits, respectively. Constraints (29)–(31) are the absolute values of the deviations produced by the uncertainties of wind and solar generation as well as demand, correspondingly, related to the variable of power dispatched by each hydro-thermal generator:
Auxiliary linear variables ensure the linearity of the decision rule for affine policies of the operational limits of hydro-thermal generator (i), given the deviation of forecast errors of the wind generator (w), solar generator (p) and total demand, respectively, at time t and past period .
Ramp limits. Equations (32) and (33) correspond to the AARO formulation for constraint (15). These indicate up and down ramp limits. Constraints (34)–(36) are the absolute values of the deviations produced by the uncertainties of wind and solar generation as well as demand, respectively. These are linked with the ramping conditions for each generator.
Auxiliary linear variables ensure the linearity of the decision rule for affine policies of the ramp limits of hydro-thermal generator (i), given the deviation of forecast errors of the wind generator (w), solar generator (p), and total demand, respectively, at time t and past period .
Power balance. Bearing in mind that both the equality constraints with non-uncertain variables do not generate inconveniences for AARO formulations [59] and the affine formulation of constratints (16), it is possible to express the power balance constraints within the AARO formulation as indicated by Equations (37)–(41):
Line operation limits (normal operation). Constraints (42) and (43) correspond to the AARO formulation and constraint (18) is the maximum operative limit of lines under normal operation. Constraints (44)–(46) are the absolute values of the deviations, produced by the uncertainties of wind, solar and demand generation, respectively, related to the power flow variable under normal operating conditions.
Auxiliary linear variables ensure the linearity of the decision rule for affine policies of the limits of transmission line (l) under normal operating conditions, given the deviation of forecast errors of the wind generator (w), solar generator (p), and demand at bus (s), respectively, at time t and past period .
Line operation limits (contingency operations). Equations (47) and (48) correspond to the AARO formulation of constraint (19) establishing the maximum operating limit of lines under network contingencies. Constraints (49)–(51) establish the absolute values of the deviations, produced by the uncertainties of wind and solar generation and demand, correspondingly, linked with the power flow variable under contingency conditions.
Auxiliary linear variables ensure the linearity of the decision rule for affine policies of the limits of transmission line (l) under contingency of the line (k), given the deviation of forecast errors of the wind generator (w), solar generator (p) and demand at bus (s), respectively, at time t and past period .
In these equations, the OTDF allows for efficiently modeling and computing the contingencies of the transmission system for the SCUC problem. However, SCUC carries great computational times when dealing with large-scale systems, given the nature of the variables involved. Many works have approached this challenge from different procedures [61,63,64,65,66]. It is not computationally necessary to consider all possible contingencies of the network, since some of them do not generate violations of the maximum operating limits in the rest of the lines of the system. Therefore, to solve this challenge, a strategy, based on the work presented in [60,61], was implemented in our model. Algorithm 1, presents the strategy that works with user cuts, which could be seen as cutting planes or linear constraints, which are strategically added within the model through user-defined rules [67].
| Algorithm 1: Method for Adding N − 1 Security Constraints as user cuts |
 |
Algorithm 1 iteratively defines the feasible region of the SCUC, by adding only the binding security constraints. In this way, it is possible to compact the model and considerably reduce its computation times. Step 1 is where the iterative process is started. Step 2 solves AAROUC model defined by Equations (22)–(46) (contingencies are not considered) only at the first iteration; after the first iteration, it also solves the AARO-SCUC model defined by Equations (22)–(51), considering only the binding security constraints added in step 13. Post-optimization values of the wind (), solar () and demand () deviations related to the power dispatched by each generator are obtained in every iteration. Steps 4–8 estimate the absolute values of the wind (), solar () and demand ( deviations of the power flow under contingency conditions estimated in step 9. Steps 11–16 establish the rules for selecting and adding (step 13) those security constraints (47)–(51) that define the feasible region of the model. Finally, the iterative process ends when the total system overload factor is less than the tolerance (in this case, ). This procedure could be seen as a computational novelty of our approach.
4.2. Uncertainty Sets
A brief description of the uncertainty sets used in our model is introduced in this section. The interested reader may consult [45,59] for an in-depth explanation on this topic. As previously stated, in Section 4.1, an uncertainty set can be polyhedral or ellipsoidal. For instance, Tian et al. [68] adopted an ellipsoidal uncertainty set within the AAROUC model to fit the spatial–temporal correlated wind power. Additionally, they proposed and tested a new criterion to select the value of the level of uncertainty. Conversely, we use uncertainty boxes (i.e., a polyhedral uncertainty set) for each one of the sources of uncertainty considered in our AAROUC model;
Equations (52)–(54) represent the intervals for each uncertainty variable: realized wind forecast error , materialized solar forecast error and materialized demand forecast error . These intervals are symmetric and zero-centered, that is, realizations of uncertainty variables could be zero (i.e., ). Likewise, are the maximum uncertainty level forecasts that limit each interval. These quantities, also known as the budget value of the uncertainty set, are generally input data.
5. Tests and Results
The proposed model was written in the General Algebraic Modeling System (GAMS, version 24.8.5), using CPLEX (version 12.6.1) as an optimization engine. To illustrate the applicability and effectiveness of the proposed model, two power systems were used, namely: a didactic 6-bus power system [69] and the IEEE RTS 24-bus power system. A time horizon of 24 h was used for both systems. Experiments on the 6-bus power system were run in a desktop computer with an Intel core i5-5200 processor running at GHz, 16 GB RAM, whereas experiments for the 24-bus power system were performed on a computing server with an Intel Xeon Platinum 8160 with 96 processors running at Ghz.
Two numerical experiments were performed. The first one captures the behavior of the objective function (OF) and running time based on known uncertainties of past time periods, considered in our AARO-SCUC model. The main idea of this numerical experiment is to determine the impact of known uncertain parameters of past time periods on the cost of the system. In this way, it is possible to perform a trade-off analysis between the quality and robustness of the solution and the model computing time. This would allow for determining computationally effective and reliable solutions when dealing with large-scale systems.
The second experiment is a post-hoc analysis of the robustness of the solutions obtained with our AARO-SCUC formulation. In this case, Monte Carlo Simulations (MCS) were carried out considering 100 replications and 300 random scenarios, which were generated using uniform distribution for each random variable. In the second experiment, the level of uncertainty of the random variables was increased up to 200% of its original value, using steps of 2%. Figure 1 illustrates the increase in the level of uncertainty associated with the random variables (blue dots) with respect to the defined uncertainty set (red box, representing the maximum uncertainty level of the variable). In the first rightmost box, the uncertainty level goes up to 50% of the maximum uncertainty level. Later, in the second box, this level reaches up to 100% of the maximum level. From 0% to 100% of the maximum uncertainty level, our AARO-SCUC model must always yield feasible solutions. That is, the number of violated constraints must be zero. Finally, in the third rightmost set, there are values of the uncertainty outside the maximum level, resulting in a number of violated constraints produced by these values. As a robustness measure of the solution, in this experiment, when a given scenario produces an infeasible solution, the number of violated constraints per replication is registered.
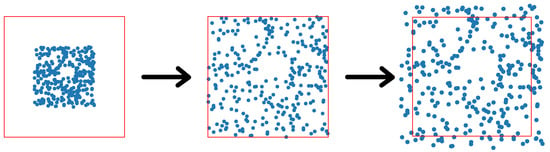
Figure 1.
Numerical experiments for the uncertainty sets.
5.1. 6-Bus System
The system shown in Figure 2 has six buses, seven lines and three generation units (two thermal units and one hydro unit). Renewable Energies Sources (RES) are located at buses 1 (PV, 20 MW) and 3 (wind, 200 MW), respectively. Meanwhile, the total load is distributed at buses 3, 4, and 5. The maximum uncertainty levels of load and RES error forecasting are set at and , respectively. The input data and the model can be found on GitHub [70].
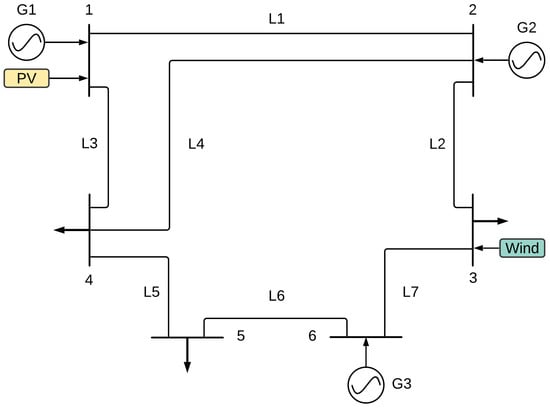
Figure 2.
6 bus test system.
Figure 3 shows the value of the operating cost of the power system on the left axis (blue bars), run time using Algorithm 1 to solve the AARO-SCUC (dashed orange line), and run time of the AARO-SCUC solution without using Algorithm 1 (dashed magenta line) on the right axis. This figure shows the behavior of the OF and running time when different numbers of past time periods are considered in the AARO model for the known uncertainty parameters. This analysis was performed by adding the logical condition into the model, with n being the number of past time periods containing known uncertainty data (with ).
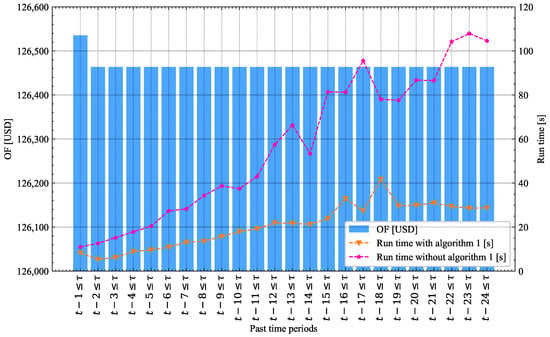
Figure 3.
OF value and solution time vs. number of past time information, 6-bus system.
Figure 3 reveals that using Algorithm 1 brings computational advantages to the proposed AARO-SCUC model, when more known uncertain information from past periods is desired. That is, the execution times of the model using such algorithm (dashed orange line) are much shorter compared to the times it takes for the model without using it (dashed magenta line). For example, if it is desirable to take into account the uncertain information disclosed from 23 past periods including the current period (), the solution of the AARO-SCUC model takes 30 s when Algorithm 1 is used, whereas it takes 105 s without using it. That is, Algorithm 1 provides a 2.5 speed-up factor when solving the proposed AARO-SCUC model. These results are in line with [60], which have proven the effectiveness of this computational approach for reducing the solution times of SCUC as the complexity and size of the power system increases.
Furthermore, Figure 3 shows that, when considering the revealed uncertainty of only a past period (), the operating cost of the system is 0.12654 MUSD, while the cost of the system for decreases to 0.12646 MUSD. This value represents a negligible decrease of 0.0567% in the OF that comes at the price of multiplying the run time by a factor of six. Furthermore, from to , the cost does not change, but the run time has an increasing behavior. This results shows that it is possible to obtain good quality solution in short running times by considering only the information from a few past periods. It is noteworthy that, in this case, the optimality gap was zero for all runs.
Once the computational effectiveness of the proposed approach is illustrated, it is also important to verify the robustness and stability of the solutions provided by the AARO-SCUC model. For this purpose, a post-hoc analysis using MCS was executed. Figure 4 shows the feasibility behavior of the solutions of the AARO-SCUC model for different values of n in expression (i.e., more () or less () information about past realizations of the uncertain variables are considered) after evaluating a large number of realizations (scenarios) of the uncertain variables inside and outside the uncertainty sets generated through MCS (represented in the horizontal axis of this figure). This figure shows that the number of violated constraints is zero for those realizations of the uncertain variables that are within the range 0% to 100% of the maximum uncertainty level. As expected, the solutions of the model are robust, generating feasible solutions (valid operating points) for all realizations of uncertain variables within the box. For values outside the box, (i.e., greater than 100%), the behavior of the obtained solution may vary depending on the value of n. That is, if less revealed uncertainty from past periods is considered (smaller values of n), there is a greater number of violated constraints. A detailed analysis of this behavior follows.
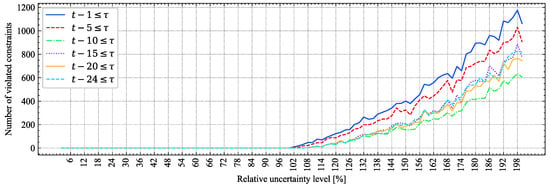
Figure 4.
Number of violated constraints vs. materialization of forecast errors, 6-bus system.
Figure 5 zooms in Figure 4. This figure shows that, for realizations that are 104% of the size of the uncertainty box, the number of violated constraints is approximately 20 when (i.e., if only the information on current uncertain parameters and those revealed a period ago is considered). On the other hand, this number drops to 0 if for the same realization value (104%). Similarly, for realizations of 120% of the size of the uncertainty set, the number of violated constraints is close to 90 for , whereas it decreases to 30 if n increases to 24. In summary, when more information on the uncertainty values revealed from past times are taken into account in the AARO-SCUC model (i.e., larger values of n in expression ), more stable solutions may be obtained for realizations of the uncertain variables that slightly surpass the maximum uncertainty level. However, increasing the value of n increases the run time. This result exhibits a clear trade-off between solution robustness and running time.
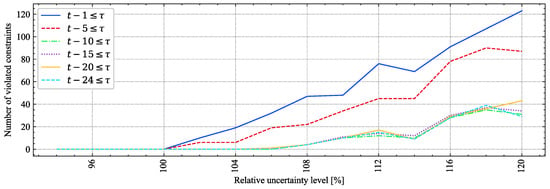
Figure 5.
Zoom of Figure 4.
5.2. IEEE RTS 24-Bus Power System
To further explore the performance of the proposed AARO-SCUC model, several experiments were performed with the IEEE RTS 24-bus power system. This system comprises 24 buses of which 17 are demand buses, 26 conventional generators, nine wind generators and five solar generators that are connected to 31 transmission lines. The data for this test system are also available in GitHub [70]. The maximum levels of uncertainty considered for the model were set at for demand, and for wind and solar generation.
Figure 6 shows the behavior of the optimality gap (blue bars) and the computation time of Algorithm 1 (dashed orange line) based on the amount of uncertain information disclosed from different periods in the past (n). For the sake of conciseness and based on the results presented in Section 5.1, this figure only includes the results from to . In this case, both the computation times and the optimality gap tend to increase as more uncertain information revealed from past periods (n) increases.
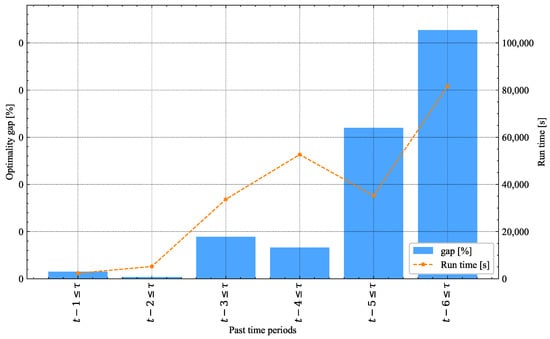
Figure 6.
OF value and solution time vs. amount of past time information, 24-bus system.
For all the experiments, the dual solution (i.e., the lower bound of the cost) was 0.49430 MUSD. Initially, the differences in the optimality gap and computation times when comparing the results for and are very small. By contrast, in , the optimality gap is 0.0149%, obtained with an MILP solution of 0.494373 MUSD of cost; meanwhile, for , the gap is 0.5200%, obtained with a solution of 0.496880 MUSD of cost. The solution with produces a solution with a 0.508% cost increase when compared to the cost of the system for . Furthermore, the computation times of Algorithm 1 vary considerably as n increases. It takes 1417 s for , whereas it takes 81,000 s for , the computation time at being 57 times the computation time it takes to solve the model for . This confirms the results of Section 5.1, that is, high quality solutions can be obtained in short running times with uncertain information revealed from very few past periods.
Long computing times are obtained in this system for because we assume that all buses have uncertain loads, something that considerably increases the computational complexity of the AARO-SCUC model. For instance, this feature renders the solution of the AARO-SCUC model impossible for this system without the dynamic generation of security constraints of Algorithm 1.
Note, however, that the solution of the AARO-SCUC model using Algorithm 1 may work well in large-scale systems by exploiting one of the advantages of affine policies. In that case, linear decision rules precisely allow the tractability of these kind of systems by taking into account some practical considerations. For instance, one should define, within the affine policies, a subset of only those hydrothermal generators that have sufficient technical capacities to respond to uncertainty deviations. Likewise, one can define in the affine policies, only the subset of buses with uncertain loads. These considerations decrease the computational burden of the model and allow for obtaining proper solutions.
The next step is to verify that such solutions are robust using again the post-hoc analysis with MCS described in Section 5.1. Figure 7, as well as the results presented in Section 5.1, show that realizations of the uncertain variables within the uncertainty box do not generate violated constraints (infeasible unfeasible solutions). On the contrary, for realizations of the uncertain variables greater than 100% (values outside the uncertain box), the number of violated constraints is greater than zero. This means that at least one constraint is violated when evaluating the solution of the AARO-SCUC model. Moreover, this number is higher as the size of realizations outside the uncertainty set increases when compared against the one that was used in the optimization model. Nonetheless, Figure 8 shows that the number of violated constraints are lower as more uncertain information revealed from past periods is considered, a behavior similar to the one observed in Section 5.1.
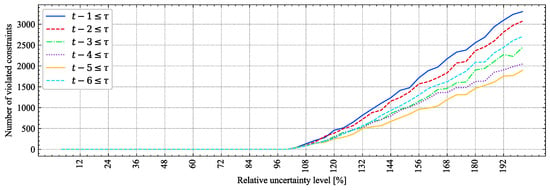
Figure 7.
Number of violated constraints vs. materialization of forecast errors, 24-bus system.
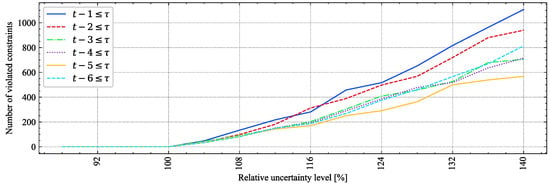
Figure 8.
Zoom of Figure 7.
6. Conclusions
This paper presented a new affinely adjustable robust model to solve the security constrained unit commitment problem considering uncertainty of intermittent generation sources and demand. The affine policies were only applied for the variables of the dispatch as adjustable variables in the event of the realization of uncertain variables. This approach keeps the non-anticipativity condition (), i.e., only uncertain information known from past periods and the current period is considered. In addition, a user-cut based algorithm was implemented to generate security constraints in the solution of the model. This algorithm merges the linear sensitivity factors (PTDF, LODF, and OTDF) and some logical and functional rules that allow for defining the feasible region of the problem only with the binding constraints—a feature that improves the computational efficiency for the proposed model.
Computational experiments showed that (1) the algorithm proposed in this paper, based on user cuts, is computationally efficient for evaluating security constraints within the proposed AARO-SCUC model; (2) high quality solutions can be obtained in short run times by considering only information revealed from the current period and few periods in the past ( or ). That is, it is not necessary to consider, for example, uncertain information disclosed for 23 past periods and the current one () to obtain good solutions. This behavior could be determined mainly by the non-anticipativity condition of the dispatch variables. Furthermore, through the AGC, power systems have the particularity of correcting the inconveniences produced by the deviations of the forecast errors just at the instant t. (3) A post-hoc analysis using Monte Carlo simulations shows that all the solutions of the model are robust for any condition where the realizations of the uncertainty variables are less than or equal to the maximum level of uncertainty used within the optimization process. In addition, there seems to be an inverse relationship between the level of uncertainty revealed of past periods considered and the number of violated constraints for variable realizations outside the maximum level of uncertainty.
The proposed model was optimized under uncertainty boxes bounded by maximum uncertainty levels. An important topic for future work is to consider unbounded uncertainty sets in order to always obtain a good performance of the model solution (feasible solutions) for realizations of the uncertain variable outside the uncertainty set. To reach this goal, a potential procedure based on global robust optimization may be implemented.
Another important research opportunity for the reduction of the conservatism of the solution is to consider ellipsoidal uncertainty sets, using the criterion proposed by [68]. This also allows for the modeling of spatio-temporal dependencies of solar and wind generators. This, however, will change the structure of the AAROUC model since it results in nonlinear decision rules requiring the solution of mixed-integer second-order cone programming models.
Author Contributions
Conceptualization, C.C.M.-C., J.E.S.-A. and Á.J.-D.; Data curation, J.E.S.-A. and C.C.M.-C.; Formal analysis, C.C.M.-C., J.E.S.-A., J.M.L.-L., Á.J.-D. and J.G.V.; Funding acquisition, Á.J.-D., J.M.L.-L. and J.G.V.; Investigation, C.C.M.-C. and J.E.S.-A.; Methodology, C.C.M.-C.; Project administration, Á.J.-D., J.M.L.-L. and J.G.V.; Resources, C.C.M.-C., J.E.S.-A., Á.J.-D., J.M.L.-L. and J.G.V.; Software, J.E.S.-A. and C.C.M.-C.; Supervision, Á.J.-D., J.M.L.-L. and J.G.V.; Validation, C.C.M.-C. and J.E.S.-A.; Visualization, C.C.M.-C. and J.E.S.-A.; Writing—original draft, C.C.M.-C. and J.E.S.-A.; Writing—review and editing, Á.J.-D., J.M.L.-L. and J.G.V.; All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Minciencias, Colombia. Project code 1115-745-54929; contract 056-2017; project name: “Despacho Económico Multiperiodo Integrando Energías Renovables Intermitentes”.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Some of the data and the model used in the computational experiment are available at [70].
Acknowledgments
The authors gratefully acknowledge the support from Universidad de Antioquia.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| AA | Affine arithmetic |
| AARO | Affinely adjustable robust optimization |
| AAROUC | Affinely adjustable robust optimization unit commitment |
| AGC | Automatic generation control |
| BD | Benders decomposition |
| DRO | Distributionally robust optimization |
| LODF | Line outage distribution factor |
| LR | Lagrangian relaxation |
| LSF | Linear sensitivity factors |
| MCS | Monte Carlo Simulations |
| MILP | Mixed-integer linear programming |
| OF | Objective function |
| OTDF | Outage transfer distribution factors |
| PTDF | Power transfer distribution factor |
| SCUC | Security constrained unit commitment |
| ROUC | Robust optimization of the UC |
| SOUC | Stochastic optimization for the unit commitment |
| SSCUC | Stochastic security constraint unit commitment |
| UC | Unit commitment |
Appendix A. Nomenclature
The nomenclature used through the paper is provided here for quick reference:
Appendix A.1. Indexes and Notations
| i | Index of conventional generators, 1 to I |
| w | Index of Wind generators, 1 to W |
| p | Index of PV generators, 1 to P |
| l, k | Index of lines and contingencies, respectively, 1 to L |
| s, ss | Index of buses, 1 to S |
| t, tt, | Index of time periods, 1 to T |
Appendix A.2. Parameters
| Generation map for conventional generators | |
| Generation map for wind generators | |
| Generation map for PV generators | |
| Fixed production cost of thermal generator [USD] | |
| Operating variable cost of generator [USD] | |
| Startup cost of conventional generator [USD] | |
| Shut down cost of thermal generator [USD] | |
| Demand in bus s at time t [MW] | |
| Minimum down time of thermal generator i [h] | |
| Minimum up time of thermal generator i [h] | |
| Time that thermal generator i has been down before [h] | |
| Time that thermal generator i has been up before [h] | |
| Rated capacity of thermal generator i [MW] | |
| Minimum output of thermal generator i [MW] | |
| On-Off status of generator i at (equal to 1 if | |
| and 0 otherwise) | |
| Power Forecast of wind generator w, at time t | |
| Power Forecast of PV generator p, at time t | |
| Load Forecast of demand at bus s, at time t | |
| Maximum Capacity of the line l [MW] | |
| Transmission capacity factor of the line l | |
| Length of time the thermal generator i has to be off at the start | |
| time of the planning horizon [h] | |
| Length of time the thermal generator i has to be on at the start | |
| time of the planning horizon [h] | |
| Ramp-down limit of thermal generator i [MW/h] | |
| Ramp-up limit of thermal generator i [MW/h] | |
| Matrix of Power transfer distribution factors | |
| Matrix of Line Outage distribution factors | |
| Matrix of Outage transfer distribution factors | |
| Materialized forecast error of the wind generator w, at time t [MW] | |
| Materialized forecast error of the PV generator p, at time t [MW] | |
| Materialized forecast error of the the demand located at bus s, | |
| at time t [MW] | |
| Maximum forecast error of the wind generator w, at time t [MW] | |
| Maximum forecast error of the PV generator p, at time t [MW] | |
| Maximum forecast error of the demand located at bus s, at time | |
| t [MW] |
Appendix A.3. Variables
| Conventional generator power output, of the generator i at time t [MW] | |
| Binary variable equal to 1 if the thermal generator i is producing at time | |
| t, and 0 otherwise | |
| Binary variable equal to 1 if the thermal generator i is started at the | |
| beginning of time t and 0 otherwise | |
| Binary variable equal to 1 if the thermal generator i is shutdown at the | |
| beginning of time t and 0 otherwise | |
| Net power injection in bus s, at time t [MW] | |
| Power flow of the line l, at time t, under normal operation [MW] | |
| Power flow of line l under the contingency k, at time t [MW] | |
| Central value of power output, of the generator i at time t [MW] | |
| Central value for net power injection in bus s, at time t [MW] | |
| Upper bound of the highest cost for the dispatch problem [USD] | |
| Adjustment of the generator i at time t given by the deviation of forecast | |
| error of the wind generator w in the past periods [p.u.] | |
| Adjustment of the generator i at time t given by the deviation of forecast | |
| error of the PV generator p in the past periods [p.u.] | |
| Adjustment of the generator i at time t given by the deviation | |
| of forecast error of total demand in the past periods [p.u.] | |
| Adjust variable for the objective function given by the deviation of | |
| forecast error of the wind generator w at time t [USD/MW] | |
| Adjust variable for the objective function given by | |
| the deviation of forecast error of the PV generator p at time t | |
| Adjust variable for the objective function given by | |
| the deviation of forecast error of the total demand at time t [USD/MW]. | |
| Adjust variable for power limits of the generator i at time t given by | |
| the deviation of forecast error of the wind generator w in the past | |
| periods [p.u.] | |
| Adjust variable for power limits of the generator i at time t given by | |
| the deviation of forecast error of the PV generator p in the past | |
| periods [p.u.] | |
| Adjust variable for power limits of the generator i at time t given by | |
| the deviation of forecast error of total demand in the past periods [p.u.] | |
| Adjust variable for ramping limits of the generator i at time t given by | |
| the deviation of forecast error of the wind generator w in the past | |
| periods [p.u.] | |
| Adjust variable for ramping limits of the generator i at time t given by | |
| the deviation of forecast error of PV generator p in the past | |
| periods [p.u.] | |
| Adjust variable for ramping limits of the generator i at time t given by | |
| the deviation of forecast error of the total demand in the past | |
| periods [p.u.] | |
| Adjust variable for power flow limits of the line l at time t given by the | |
| deviation of forecast error of the wind generator w in the past | |
| periods [p.u.] | |
| Adjust variable for power flow limits of the line l at time t given by the | |
| deviation of forecast error of the PV generator p in the past | |
| periods [p.u.] |
| Adjust variable for power flow limits of the line l at time t given by | |
| deviation of forecast the demand at bus s in the past periods [p.u.] | |
| Adjust variable for power flow limits of the line l under contingency of | |
| the line k at time t given by the deviation of forecast error of the wind | |
| generator w in the past periods [p.u.] | |
| Adjust variable for power flow limits of the line l under contingency of | |
| line k at time t given by the deviation of forecast error of the PV generator | |
| p in the past periods [p.u.] | |
| Adjust variable for power flow limits of the line l under contingency of | |
| line k at time t given by the deviation of forecast error of the demand | |
| at bus s in the past periods [p.u.] |
References
- Anjos, M.F.; Conejo, A.J. Unit Commitment in Electric Energy Systems. Found. Trends Electr. Energy Syst. 2017, 1, 220–310. [Google Scholar] [CrossRef]
- Knueven, B.; Ostrowski, J.; Watson, J.P. On mixed-integer programming formulations for the unit commitment problem. INFORMS J. Comput. 2020, 32, 857–876. [Google Scholar] [CrossRef]
- Huang, Y.; Pardalos, P.M.; Zheng, Q.P. Electrical Power Unit Commitment—Deterministic and Two-Stage Stochastic Programming Models and Algorithms; Springer: New York, NY, USA, 2017. [Google Scholar] [CrossRef]
- Quan, H.; Srinivasan, D.; Khambadkone, A.; Khosravi, A. A computational framework for uncertainty integration in stochastic unit commitment with intermittent renewable energy sources. Appl. Energy 2015, 152, 71–82. [Google Scholar] [CrossRef]
- Zheng, Q.P.; Wang, J.; Liu, A.L. Stochastic Optimization for Unit Commitment: A Review. IEEE Trans. Power Syst. 2015, 30, 1913–1924. [Google Scholar] [CrossRef]
- Tahanan, M.; Ackooij, W.v.; Frangioni, A.; Lacalandra, F. Large-scale Unit Commitment under uncertainty. 4OR 2015, 13, 115–171. [Google Scholar] [CrossRef]
- Restrepo, J.F.; Galiana, F.D. Assessing the Yearly Impact of Wind Power Through a New Hybrid Deterministic/Stochastic Unit Commitment. IEEE Trans. Power Syst. 2011, 26. [Google Scholar] [CrossRef]
- Aminifar, F.; Fotuhi-Firuzabad, M.; Shahidehpour, M. Unit Commitment With Probabilistic Spinning Reserve and Interruptible Load Considerations. IEEE Trans. Power Syst. 2009, 24. [Google Scholar] [CrossRef]
- Dyer, M.; Stougie, L. Computational complexity of stochastic programming problems. Math. Program. 2006, 106, 423–432. [Google Scholar] [CrossRef]
- Wang, C.; Fu, Y. Fully Parallel Stochastic Security-Constrained Unit Commitment. IEEE Trans. Power Syst. 2016, 31, 3561–3571. [Google Scholar] [CrossRef]
- Tuohy, A.; Meibom, P.; Denny, E.; O’Malley, M. Unit Commitment for Systems With Significant Wind Penetration. IEEE Trans. Power Syst. 2009, 24, 592–601. [Google Scholar] [CrossRef]
- Cerisola, S.; Baíllo, A.; Ramos, A.; Gollmer, R. Stochastic Power Generation Unit Commitment in Electricity Markets: A Novel Formulation and a Comparison of Solution Methods. Oper. Res. 2009, 57, 32–46. [Google Scholar] [CrossRef]
- Carpentier, P.; Gohen, G.; Culioli, J.C.; Renaud, A. Stochastic optimization of unit commitment: A new decomposition framework. IEEE Trans. Power Syst. 1996, 11, 1067–1073. [Google Scholar] [CrossRef]
- Huang, Y.; Zheng, Q.P.; Wang, J. Two-stage stochastic unit commitment model including non-generation resources with conditional value-at-risk constraints. Electr. Power Syst. Res. 2014, 116, 427–438. [Google Scholar] [CrossRef]
- Ningyu, Z.; Jiankun, L.; Qian, Z. Two-stage stochastic model of unit commitment with wind farm. In Proceedings of the 2014 China International Conference on Electricity Distribution (CICED), Shenzhen, China, 23–26 September 2014; pp. 1080–1084. [Google Scholar] [CrossRef]
- Wang, J.; Wang, J.; Liu, C.; Ruiz, J.P. Stochastic unit commitment with sub-hourly dispatch constraints. Appl. Energy 2013, 105, 418–422. [Google Scholar] [CrossRef]
- Wang, J.; Shahidehpour, M.; Li, Z. Security-Constrained Unit Commitment With Volatile Wind Power Generation. IEEE Trans. Power Syst. 2008, 23. [Google Scholar] [CrossRef]
- Pan, K.; Guan, Y. Strong Formulations for Multistage Stochastic Self-Scheduling Unit Commitment. Oper. Res. 2016, 64, 1482–1498. [Google Scholar] [CrossRef]
- Jiang, R.; Guan, Y.; Watson, J.P. Cutting planes for the multistage stochastic unit commitment problem. Math. Program. 2016, 157, 121–151. [Google Scholar] [CrossRef]
- Papavasiliou, A.; Oren, S.S. Multiarea Stochastic Unit Commitment for High Wind Penetration in a Transmission Constrained Network. Oper. Res. 2013, 61. [Google Scholar] [CrossRef]
- Shiina, T.; Birge, J.R. Stochastic unit commitment problem. Int. Trans. Oper. Res. 2004, 11, 19–32. [Google Scholar] [CrossRef]
- Gade, D.; Hackebeil, G.; Ryan, S.M.; Watson, J.P.; Wets, R.J.B.; Woodruff, D.L. Obtaining lower bounds from the progressive hedging algorithm for stochastic mixed-integer programs. Math. Program. 2016, 157, 47–67. [Google Scholar] [CrossRef]
- Ordoudis, C.; Pinson, P.; Zugno, M.; Morales, J.M. Stochastic unit commitment via Progressive Hedging—Extensive analysis of solution methods. In Proceedings of the 2015 IEEE Eindhoven PowerTech, Eindhoven, The Netherlands, 29 June–2 July 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Guo, G.; Hackebeil, G.; Ryan, S.M.; Watson, J.P.; Woodruff, D.L. Integration of progressive hedging and dual decomposition in stochastic integer programs. Oper. Res. Lett. 2015, 43, 311–316. [Google Scholar] [CrossRef]
- Li, C.; Zhang, M.; Hedman, K.W. N-1 Reliable Unit Commitment via Progressive Hedging. J. Energy Eng. 2015, 141, B4014004. [Google Scholar] [CrossRef]
- Ryan, S.M.; Wets, R.J.; Woodruff, D.L.; Silva-Monroy, C.; Watson, J. Toward scalable, parallel progressive hedging for stochastic unit commitment. In Proceedings of the 2013 IEEE Power Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013; pp. 1–5. [Google Scholar] [CrossRef]
- Gonçalves, R.E.C.; Finardi, E.C.; Silva, E.L.D. Applying different decomposition schemes using the progressive hedging algorithm to the operation planning problem of a hydrothermal system. Electr. Power Syst. Res. 2012, 83, 19–27. [Google Scholar] [CrossRef]
- Watson, J.P.; Woodruff, D.L. Progressive hedging innovations for a class of stochastic mixed-integer resource allocation problems. Comput. Manag. Sci. 2011, 8, 355–370. [Google Scholar] [CrossRef]
- Takriti, S.; Birge, J.R.; Long, E. A stochastic model for the unit commitment problem. IEEE Trans. Power Syst. 1996, 11. [Google Scholar] [CrossRef]
- Rockafellar, R.T.; Wets, R.J.B. Scenarios and Policy Aggregation in Optimization Under Uncertainty. Math. Oper. Res. 1991, 16. [Google Scholar] [CrossRef]
- Papavasiliou, A.; Oren, S.S. A comparative study of stochastic unit commitment and security-constrained unit commitment using high performance computing. In Proceedings of the 2013 European Control Conference (ECC), Zurich, Switzerland, 17–19 July 2013; pp. 2507–2512. Available online: https://perso.uclouvain.be/anthony.papavasiliou/public_html/ECC.pdf (accessed on 12 December 2018).
- Wang, C.; Liu, F.; Wang, J.; Qiu, F.; Wei, W.; Mei, S.; Lei, S. Robust Risk-Constrained Unit Commitment With Large-Scale Wind Generation: An Adjustable Uncertainty Set Approach. IEEE Trans. Power Syst. 2017, 32, 723–733. [Google Scholar] [CrossRef]
- Kory, W.H.; Akshay, S.K.; Zhang, M.; Gregory, T.; Alejandro, D.-G.; Jiang, X. The Application of Robust Optimization in Power Systems; Final Report (Project S-51); The Power Systems Engineering Research Center (PSERC): Tempe, AZ, USA, 2014. [Google Scholar]
- Guan, Y.; Wang, J. Uncertainty Sets for Robust Unit Commitment. IEEE Trans. Power Syst. 2014, 29. [Google Scholar] [CrossRef]
- Jiang, H.; Zhang, S.; Hu, Z.; Song, Y.; Chiwei, Y. Robust optimization method for unit commitment with network losses considering wind uncertainties. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–5. [Google Scholar] [CrossRef]
- Zhang, S.; Song, Y.; Hu, Z.; Yao, L. Robust optimization method based on scenario analysis for unit commitment considering wind uncertainties. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–7. [Google Scholar] [CrossRef]
- Morales, G.A. Unit Commitment Computational Performance, System Representation and Wind Uncertainty Management. Ph.D. Thesis, Universidad Pontificia Comillas ICAI-ICADE, Madrid, Spain, 2014. [Google Scholar]
- Jiang, R.; Wang, J.; Zhang, M.; Guan, Y. Two-Stage Minimax Regret Robust Unit Commitment. IEEE Trans. Power Syst. 2013, 28. [Google Scholar] [CrossRef]
- Zhao, C.; Guan, Y. Unified Stochastic and Robust Unit Commitment. IEEE Trans. Power Syst. 2013, 28, 3353–3361. [Google Scholar] [CrossRef]
- Yorino, N.; Abdillah, M.; Sasaki, Y.; Zoka, Y. Robust Power System Security Assessment Under Uncertainties Using Bi-Level Optimization. IEEE Trans. Power Syst. 2018, 33, 352–362. [Google Scholar] [CrossRef]
- Li, Y.Z. Discussion of “Adaptive Robust Optimization for the Security Constrained Unit Commitment Problem”. IEEE Trans. Power Syst. 2014, 29, 996. [Google Scholar] [CrossRef]
- Lorca, A.; Sun, X.A.; Litvinov, E.; Zheng, T. Multistage Adaptive Robust Optimization for the Unit Commitment Problem. Oper. Res. 2016, 64, 32–51. [Google Scholar] [CrossRef]
- Bertsimas, D.; Litvinov, E.; Sun, X.A.; Zhao, J.; Zheng, T. Adaptive Robust Optimization for the Security Constrained Unit Commitment Problem. IEEE Trans. Power Syst. 2013, 28, 52–63. [Google Scholar] [CrossRef]
- Gorissen, B.L.; Yanıkoğlu, I.; Hertog, D.D. A Practical Guide to Robust Optimization. Omega 2015, 53, 124–137. [Google Scholar] [CrossRef]
- Ben-Tal, A.; Goryashko, A.; Guslitzer, E.; Nemirovski, A. Adjustable robust solutions of uncertain linear programs. Math. Program. 2004, 99. [Google Scholar] [CrossRef]
- Xiong, P.; Jirutitijaroen, P. A linear decision rule approach for robust unit commitment considering wind power generation. In Proceedings of the 2014 Power Systems Computation Conference, Wrocław, Poland, 18–22 August 2014; pp. 1–7. [Google Scholar] [CrossRef]
- Vaccaro, A.; Petrelli, M.; Berizzi, A. Robust Optimization and Affine Arithmetic for Microgrid Scheduling under Uncertainty. In Proceedings of the 2019 IEEE International Conference on Environment and Electrical Engineering and 2019 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I CPS Europe), Genova, Italy, 11–14 June 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Romero-Quete, D.; Garcia, J.R. An affine arithmetic-model predictive control approach for optimal economic dispatch of combined heat and power microgrids. Appl. Energy 2019, 242, 1436–1447. [Google Scholar] [CrossRef]
- Luo, L.; Gu, W.; Wang, Y.; Chen, C. An Affine Arithmetic-Based Power Flow Algorithm Considering the Regional Control of Unscheduled Power Fluctuation. Energies 2017, 10, 1794. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, H.; Guo, M.; Lei, J.; Ge, H.; Wan, C. A mixed interval power flow analysis based on affine arithmetic. In Proceedings of the 2016 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Xi’an, China, 25–28 October 2016; pp. 758–762. [Google Scholar] [CrossRef]
- Pirnia, M.; Canizares, C.A.; Bhattacharya, K.; Vaccaro, A. A Novel Affine Arithmetic Method to Solve Optimal Power Flow Problems With Uncertainties. IEEE Trans. Power Syst. 2014, 29, 2775–2783. [Google Scholar] [CrossRef]
- Warrington, J.; Hohl, C.; Goulart, P.J.; Morari, M. Optimal unit commitment accounting for robust affine reserve policies. In Proceedings of the 2014 American Control Conference, Portland, OR, USA, 4–6 June 2014; pp. 5049–5055. [Google Scholar] [CrossRef]
- Pirnia, M.; Canizares, C.A.; Bhattacharya, K.; Vaccaro, A. An Affine Arithmetic method to solve the stochastic power flow problem based on a mixed complementarity formulation. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–7. [Google Scholar] [CrossRef]
- Romero-Quete, D.F.; Canizares, C. Affine Arithmetic Formulation of the Unit Commitment Problem Under Uncertainty. In Proceedings of the IREP’2017 Symposium, Espinho, Portugal, 28 August 2017; p. 9. [Google Scholar]
- Romero-Quete, D.; Canizares, C.A. An Affine Arithmetic-Based Energy Management System for Isolated Microgrids. IEEE Trans. Smart Grid 2018. [Google Scholar] [CrossRef]
- Shahidehpour, M.; Zhou, Y.; Wei, Z.; Sun, G.; Chen, S.; Li, Z. Distributionally Robust Unit Commitment in Coordinated Electricity and District Heating Networks. IEEE Trans. Power Syst. 2019. [Google Scholar] [CrossRef]
- Zugno, M.; Morales, J.M.; Madsen, H. Commitment and dispatch of heat and power units via affinely adjustable robust optimization. Comput. Oper. Res. 2016, 75, 191–201. [Google Scholar] [CrossRef]
- Xiong, P.; Jirutitijaroen, P.; Singh, C. A Distributionally Robust Optimization Model for Unit Commitment Considering Uncertain Wind Power Generation. IEEE Trans. Power Syst. 2017, 32, 39–49. [Google Scholar] [CrossRef]
- Ben-Tal, A.; Nemirovski, A. Selected topics in robust convex optimization. Math. Program. 2008, 112, 125–158. [Google Scholar] [CrossRef]
- Marín-Cano, C.C.; Sierra-Aguilar, J.E.; López-Lezama, J.M.; Jaramillo-Duque, A.; Villegas, J.G. A Novel Strategy to Reduce Computational Burden of the Stochastic Security Constrained Unit Commitment Problem. Energies 2020, 13, 3777. [Google Scholar] [CrossRef]
- Marín-Cano, C.C.; Sierra-Aguilar, J.E.; López-Lezama, J.M.; Jaramillo-Duque, A.; Villa-Acevedo, W.M. Implementation of User Cuts and Linear Sensitivity Factors to Improve the Computational Performance of the Security-Constrained Unit Commitment Problem. Energies 2019, 12, 1399. [Google Scholar] [CrossRef]
- De Figueiredo, L.H.; Stolfi, J. Affine Arithmetic: Concepts and Applications. Numer. Algor. 2004, 37, 147–158. [Google Scholar] [CrossRef]
- Zhai, Q.; Guan, X.; Cheng, J.; Wu, H. Fast Identification of Inactive Security Constraints in SCUC Problems. IEEE Trans. Power Syst. 2010, 25, 1946–1954. [Google Scholar] [CrossRef]
- Wu, H.; Guan, X.; Zhai, Q.; Ye, H. A Systematic Method for Constructing Feasible Solution to SCUC Problem With Analytical Feasibility Conditions. IEEE Trans. Power Syst. 2012, 27. [Google Scholar] [CrossRef]
- Ardakani, A.J.; Bouffard, F. Identification of umbrella constraints in DC-based security-constrained optimal power flow. In Proceedings of the 2014 IEEE PES General Meeting|Conference & Exposition, National Harbor, MD, USA, 27–31 July 2014. [Google Scholar] [CrossRef]
- Tejada-Arango, D.A.; Sánchez-Martın, P.; Ramos, A. Security Constrained Unit Commitment Using Line Outage Distribution Factors. IEEE Trans. Power Syst. 2018, 33, 329–337. [Google Scholar] [CrossRef]
- IBM®-IBM Knowledge Center. Differences between User Cuts and Lazy Constraints. 2014. Available online: https://www.ibm.com/support/knowledgecenter/SSSA5P12.7.0/ilog.odms.cplex.help/CPLEX/UsrMan/topics/progradv/usrcutlazyconstr/02defn.html (accessed on 3 April 2019).
- Tian, Y.; Wu, W.; Wang, K.; Fu, Y.; Li, G. Robust transmission constrained unit commitment under wind power uncertainty with adjustable conservatism. Trans. Distrib. IET Gener. 2020, 14, 824–832. [Google Scholar] [CrossRef]
- Wu, L.; Shahidehpour, M.; Li, T. Stochastic Security-Constrained Unit Commitment. IEEE Trans. Power Syst. 2007, 22, 800–811. [Google Scholar] [CrossRef]
- DEMIERI-Project. A New Affinely Adjustable Robust Model for Security Constrained Unit Commitment under Uncertainty. Available online: https://github.com/IceMerman/AARC-6bus (accessed on 17 February 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).