Fractal-Stereometric Correlation of Nanoscale Spatial Patterns of GdMnO3 Thin Films Deposited by Spin Coating
Abstract
1. Introduction
2. Materials and Methods
2.1. Material and Sample Preparation
2.2. Structure Analysis
2.3. SEM and AFM Measurements
2.4. Surface Analysis
2.5. Statistical Analysis
3. Results
3.1. Structural Evaluation
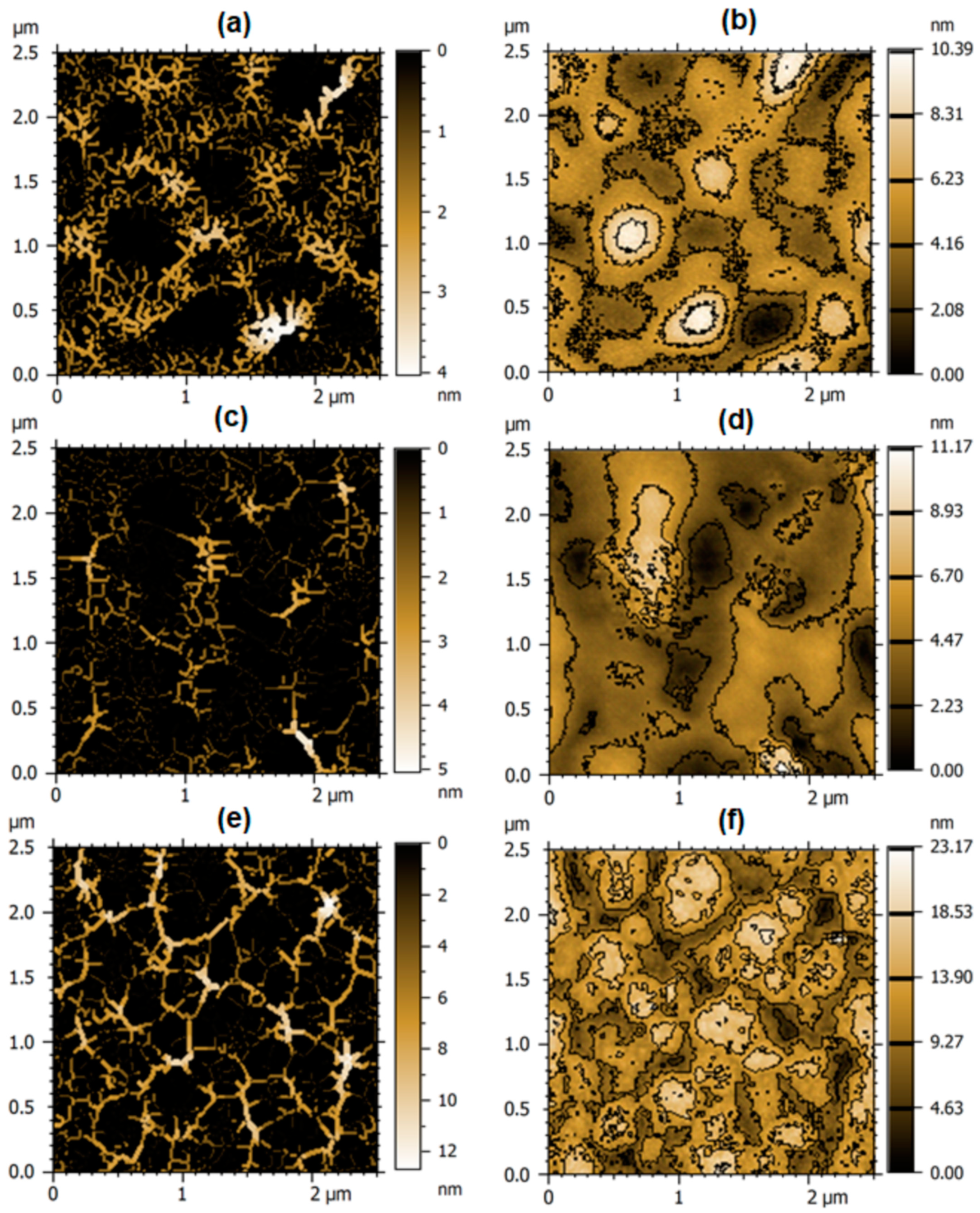
3.2. Surface Morphology Analysis
3.3. Advanced Stereometric Evaluation
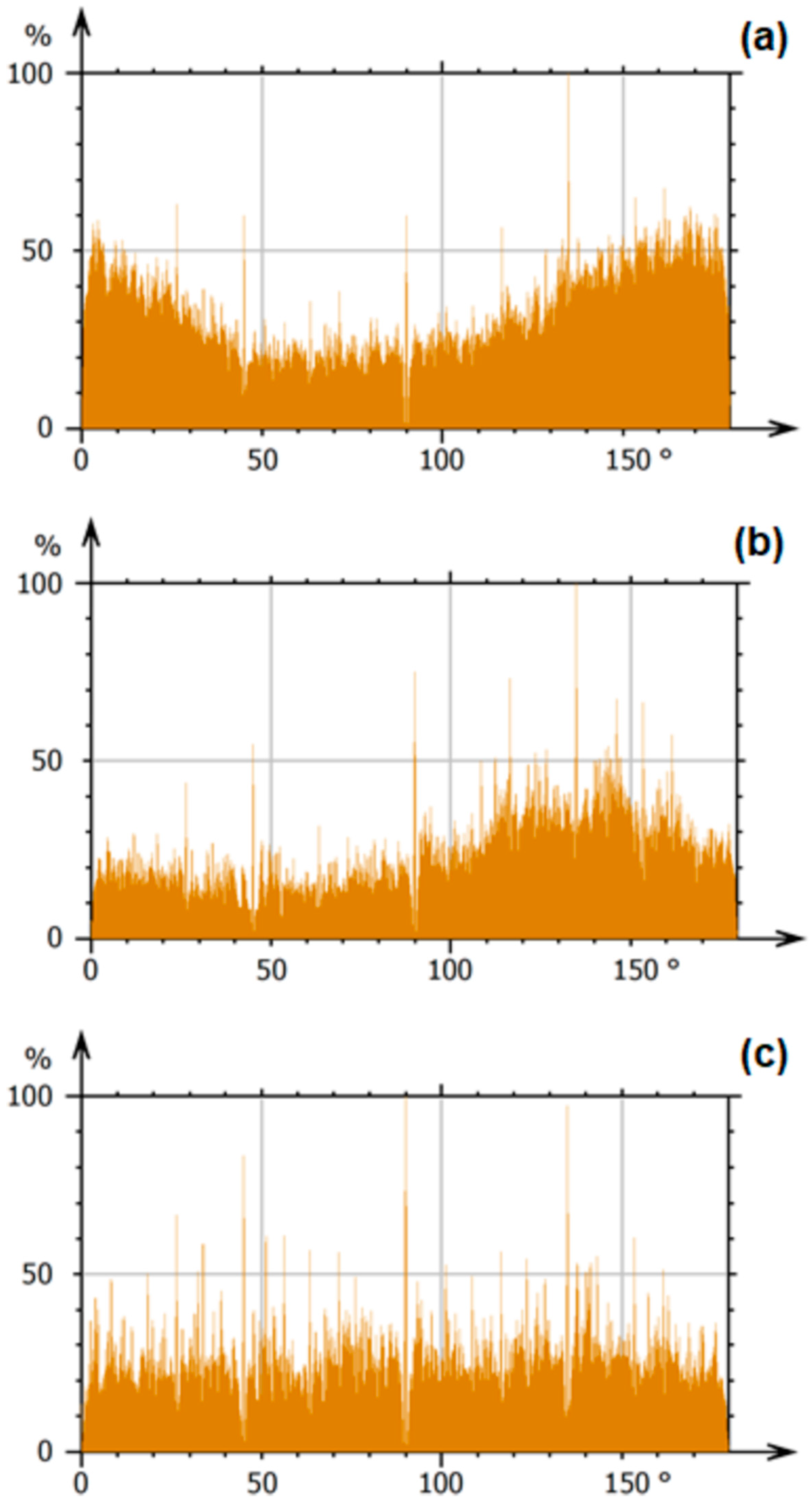
3.4. Microtexture Analysis
3.5. Fractal Characterization
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Marti, X.; Fina, I.; Frontera, C.; Liu, J.; Wadley, P.; He, Q.; Paull, R.J.; Clarkson, J.D.; Kudrnovský, J.; Turek, I.; et al. Room-temperature antiferromagnetic memory resistor. Nat. Mater. 2014, 13, 367–374. [Google Scholar] [CrossRef] [PubMed]
- Bibes, M.; Barthélémy, A. Towards a magnetoelectric memory. Nat. Mater. 2008, 7, 425–426. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.; Yang, S.M.; Kim, T.H.; Jeon, B.C.; Kim, Y.S.; Yoon, J.-G.; Lee, H.N.; Baek, S.H.; Eom, C.B.; Noh, T.W. Multilevel Data Storage Memory Using Deterministic Polarization Control. Adv. Mater. 2012, 24, 402–406. [Google Scholar] [CrossRef]
- Béa, H.; Gajek, M.; Bibes, M.; Barthélémy, A. Spintronics with multiferroics. J. Phys. Condens. Matter. 2008, 20, 434221. [Google Scholar] [CrossRef]
- Rajendran, S.; Qin, J.; Gracia, F.; Lichtfouse, E. Metal and Metal Oxides for Energy and Electronics; Springer International Publishing: Cham, Switzerland, 2021; Volume 5. [Google Scholar]
- Tachibana, M.; Shimoyama, T.; Kawaji, H.; Atake, T.; Takayama-Muromachi, E. Jahn-Teller distortion and magnetic transitions in perovskite RMnO3(R = Ho, Er, Tm, Yb, and Lu). Phys. Rev. B 2007, 75, 144425. [Google Scholar] [CrossRef]
- Liu, S.; Yan, S.; Luo, H.; Yao, L.; Hu, Z.; Huang, S.; Deng, L. Enhanced magnetoelectric coupling in La-modified Bi5Co0.5Fe0.5Ti3O15 multiferroic ceramics. J. Mater. Sci. 2018, 53, 1014–1023. [Google Scholar] [CrossRef]
- Asamitsu, A.; Moritomo, Y.; Tomioka, Y.; Arima, T.; Tokura, Y. A structural phase transition induced by an external magnetic field. Nature 1995, 373, 407–409. [Google Scholar] [CrossRef]
- Tiwari, A.; Rajeev, K.P. Electron tunneling experiments on La0.7A0.3MnO3 (A = Ca, Sr, Ba). Phys. Rev. B 1999, 60, 10591–10593. [Google Scholar] [CrossRef]
- Romaguera-Barcelay, Y.; Moreira, J.A.; Almeida, A.; Araújo, J.P.; de la Cruz, J.P. Dimensional effects on the structure and magnetic properties of GdMnO3 thin films. Mater. Lett. 2012, 70, 167–170. [Google Scholar] [CrossRef]
- Rasras, A.; Hamdi, R.; Mansour, S.; Samara, A.; Haik, Y. Study of the magnetocaloric effect in single-phase antiferromagnetic GdMnO3. J. Phys. Chem. Solids 2021, 149, 109798. [Google Scholar] [CrossRef]
- Ye, F.; Dai, H.; Wang, M.; Chen, J.; Li, T.; Chen, Z. The structural, dielectric, and magnetic properties of GdMnO3 multiferroic ceramics. J. Mater. Sci. Mater. Electron. 2020, 31, 3590–3597. [Google Scholar] [CrossRef]
- Noda, K.; Nakamura, S.; Nagayama, J.; Kuwahara, H. Magnetic field and external-pressure effect on ferroelectricity in manganites: Comparison between GdMnO3 and TbMnO3. J. Appl. Phys. 2005, 97, 10C103. [Google Scholar] [CrossRef]
- Peña, O.; Antunes, A.B.; Martínez, G.; Gil, V.; Moure, C. Inter-network magnetic interactions in GdMexMn1−xO3 perovskites (Me = transition metal). J. Magn. Magn. Mater. 2007, 310, 159–168. [Google Scholar] [CrossRef]
- Negi, P.; Dixit, G.; Agrawal, H.M.; Kumar, H.; Srivastava, R.C.; Sati, P.C.; Gupta, V.; Asokan, K. Tuning of structural and optical properties by sintering of multiferroic GdMnO3 precursor. Ferroelectrics 2017, 519, 200–208. [Google Scholar] [CrossRef]
- Negi, P.; Agrawal, H.M.; Singh, J.P.; Kumar, H.; Srivastava, R.C.; Asokan, K.; Chae, K.H. Magnetic Behaviour of Granular GdMnO3 Film. J. Supercond. Nov. Magn. 2017, 30, 1419–1425. [Google Scholar] [CrossRef]
- Negi, P.; Dixit, G.; Agrawal, H.M.; Srivastava, R.C. Structural, Optical and Magnetic Properties of Multiferroic GdMnO3 Nanoparticles. J. Supercond. Nov. Magn. 2013, 26, 1611–1615. [Google Scholar] [CrossRef]
- Ben, H.H.; Hoffmann, M.; Adeagbo, W.A.; Ernst, A.; Hergert, W. Magnetic Structure of Bulk GdMnO3: Influence of Strain. Phys. Status Solidi 2020, 257, 1900632. [Google Scholar]
- Ţălu, Ş.; Achour, A.; Solaymani, S.; Nikpasand, K.; Dalouji, V.; Sari, A.; Rezaee, S.; Nezafat, N.B. Micromorphology analysis of TiO2 thin films by atomic force microscopy images: The influence of postannealing. Microsc. Res. Tech. 2020, 282, 162–174. [Google Scholar] [CrossRef] [PubMed]
- Fattahi, M.; Nezafat, N.B.; Ţălu, Ş.; Solaymani, S.; Ghoranneviss, M.; Elahi, S.M.; Shafiekhani, A.; Rezaee, S. Topographic characterization of zirconia-based ceramics by atomic force microscopy: A case study on different laser irradiations. J. Alloys Compd. 2020, 831, 154763. [Google Scholar] [CrossRef]
- Barcelay, Y.R.; Moreira JA, G.; de Jesus Monteiro Almeida, A.; Brito, W.R.; Matos, R.S.; da Fonseca Filho, H.D. Nanoscale stereometric evaluation of BiZn0.5Ti0.5O3 thin films grown by RF magnetron sputtering. Mater. Lett. 2020, 279, 128477. [Google Scholar] [CrossRef]
- Anon Evaluation of nanostructured BiZn0.5Ti0.5O3 thin films deposited by RF magnetron sputtering. Mater. Sci. Eng. B 2021, 267, 115090. [CrossRef]
- Ramos, G.Q.; da Costa, Í.C.; Maia da Costa, M.E.H.; Pinto, E.P.; Matos, R.S.; da Fonseca, F.H.D. Stereometric analysis of Amazon rainforest Anacardium occidentale L. Leaves. Planta 2021, 253, 6. [Google Scholar] [CrossRef]
- Yadav, R.P.; Dwivedi, S.; Mittal, A.K.; Kumar, M.; Pandey, A.C. Fractal and multifractal analysis of LiF thin film surface. Appl. Surf. Sci. 2021, 261, 547–553. [Google Scholar] [CrossRef]
- Shakoury, R.; Rezaee, S.; Mwema, F.; Luna, C.; Ghosh, K.; Jurečka, S.; Ţălu, Ş.; Arman, A.; Grayeli, K.A. Multifractal and optical bandgap characterization of Ta2O5 thin films deposited by electron gun method. Opt. Quantum Electron. 2020, 52, 1–13. [Google Scholar] [CrossRef]
- Ţălu, Ş.; Stach, S.; Valedbagi, S.; Bavadi, R.; Elahi, S.M.; Ţălu, M. Multifractal characteristics of titanium nitride thin films. Mater. Sci. 2015, 33, 541–548. [Google Scholar] [CrossRef]
- Guariglia, E.; Silvestrov, S. Fractional-Wavelet Analysis of Positive Definite Distributions and Wavelets on D’ (C); Springer: Berlin/Heidelberg, Germany, 2016; pp. 337–353. [Google Scholar]
- Senthilkumar, M.; Sahoo, N.K.; Thakur, S.; Tokas, R.B. Characterization of microroughness parameters in gadolinium oxide thin films: A study based on extended power spectral density analyses. Appl. Surf. Sci. 2005, 252, 1608–1619. [Google Scholar] [CrossRef]
- Arman, A.; Ţălu, Ş.; Luna, C.; Ahmadpourian, A.; Naseri, M.; Molamohammadi, M. Micromorphology characterization of copper thin films by AFM and fractal analysis. J. Mater. Sci. Mater. Electron. 2015, 26, 9630–9639. [Google Scholar] [CrossRef]
- Romaguera-Barcelay, Y.; Moreira, J.A.; González-Aguilar, G.; Almeida, A.; Araujo, J.P.; Pérez de la Cruz, J. Synthesis of orthorhombic rare-earth manganite thin films by a novel chemical solution route. J. Electroceram. 2011, 26, 44–55. [Google Scholar] [CrossRef]
- Romaguera-Barcelay, Y.; Agostinho Moreira, J.; Almeida, A.; Tavares, P.B.; Pérez de la Cruz, J. Structural, electrical and magnetic properties of magnetoelectric GdMnO3 thin films prepared by a sol–gel method. Thin Solid Films 2014, 564, 419–425. [Google Scholar] [CrossRef]
- Rodríquez-Carvajal, J.; Roisnel, T. Line Broadening Analysis Using FullProf*: Determination of Microstructural Properties. Mater. Sci. Forum 2004, 443–444, 123–126. [Google Scholar] [CrossRef]
- Franco, L.A.; Sinatora, A. 3D surface parameters (ISO 25178–2): Actual meaning of Spk and its relationship to Vmp. Precis. Eng. 2015, 40, 106–111. [Google Scholar] [CrossRef]
- Blateyron, F. Characterisation of Areal Surface Texture; Springer: Berlin/Heidelberg, Germany, 2013; Volume 9783642364. [Google Scholar]
- Blateyron, F. The Areal Field Parameters Characterisation of Areal Surface Texture; Springer: Berlin/Heidelberg, Germany, 2013; Volume 9783642364, pp. 15–43. [Google Scholar]
- Matos, R.S.; Pinto, E.P.; Ramos, G.Q.; Fonseca de Albuquerque, M.D.; Fonseca Filho, H.D. Stereometric characterization of kefir microbial films associated with Maytenus rigida extract. Microsc. Res. Tech. 2020, 83, 1401–1410. [Google Scholar] [CrossRef] [PubMed]
- Berry, M.V.; Lewis, N.J.F. On the Weierstrass-Mandelbrot fractal function. Proc. R. Soc. Lond. A Math. Phys. Sci. 1980, 370, 459–484. [Google Scholar]
- Guariglia, E. Primality, Fractality, and Image Analysis. Entropy 2019, 21, 304. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Su, H.; Zhong, C.; Meng, Z.; Luo, H.; Li, X.; Tang, Y.Y.; Lu, Y. Hyperspectral image classification using wavelet transform-based smooth ordering. Int. J. Wavelets Multiresolut. Inf. Process. 2019, 17, 1950050. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Wheeler, J.A. The Fractal Geometry of Nature. Am. J. Phys. 1983, 51, 286–287. [Google Scholar] [CrossRef]
- Omar, M.; Salcedo, C.; Ronald, R.; Zamora, M.; Tavares, C. Study fractal leaf surface of the plant species Copaifera sp. using the Microscope Atomic-Force-AFM. Rev. ECIPerú 2016, 13, 10–16. [Google Scholar]
- Ţălu, Ş.; Abdolghaderi, S.; Pinto, E.P.; Matos, R.S.; Salerno, M. Advanced fractal analysis of nanoscale topography of Ag/DLC composite synthesized by RF-PECVD. Surf. Eng. 2020, 36, 713–719. [Google Scholar] [CrossRef]
- Jacobs TD, B.; Junge, T.; Pastewka, L. Quantitative characterization of surface topography using spectral analysis. Surf. Topogr. Metrol. Prop. 2017, 5, 13001. [Google Scholar] [CrossRef]
- Horcas, I.; Fernández, R.; Gómez-Rodríguez, J.M.; Colchero, J.; Gómez-Herrero, J.; Baro, A.M. WSXM: A software for scanning probe microscopy and a tool for nanotechnology. Rev. Sci. Instrum. 2007, 78, 13705. [Google Scholar] [CrossRef]
- De Melo RH, C.; Conci, A. Succolarity: Defining a method to calculate this fractal measure. In Proceedings of the 15th International Conference on Systems, Signals and Image Processing (IEEE), Bratislava, Slovakia, 25–28 June 2008; pp. 291–294. [Google Scholar]
- Nosonovsky, M. Entropy in tribology: In the search for applications. Entropy 2010, 12, 1345–1390. [Google Scholar] [CrossRef]
- Zheng, X.; Tang, Y.Y.; Zhou, J. A Framework of Adaptive Multiscale Wavelet Decomposition for Signals on Undirected Graphs. IEEE Trans. Signal. Process. 2019, 67, 1696–1711. [Google Scholar] [CrossRef]
- Matos, R.S.; Lopes GA, C.; Ferreira, N.S.; Pinto, E.P.; Carvalho JC, T.; Figueiredo, S.S.; Oliveira, A.F.; Zamora RR, M. Superficial Characterization of Kefir Biofilms Associated with Açaí and Cupuaçu Extracts. Arab. J. Sci. Eng. 2018, 43, 3371–3379. [Google Scholar] [CrossRef]
- Mori, T.; Kamegashira, N.; Aoki, K.; Shishido, T.; Fukuda, T. Crystal growth and crystal structures of the LnMnO3 perovskites: Ln = Nd, Sm, Eu and Gd. Mater. Lett. 2002, 54, 238–243. [Google Scholar] [CrossRef]
- Ferreira, N.S.; Sasaki, J.M.; Silva, J.R.R.S.; Attah-Baah, J.M.; Macêdo, M.A. Visible-Light-Responsive Photocatalytic Activity Significantly Enhanced by Active [VZn + VO+] Defects in Self-Assembled ZnO Nanoparticles. Inorg. Chem. 2021. [Google Scholar] [CrossRef] [PubMed]
- Negi, P.; Agrawal, H.M.; Srivastava, R.C.; Asokan, K. Fabrication of Multiferroic GdMnO3 Thin Film by Pulsed Laser Deposition Techniqu. IP Conf. Proc. 2012, 1451, 169–171. [Google Scholar]
- Yu, N.; Polycarpou, A.A. Contact of rough surfaces with asymmetric distribution of asperity heights. J. Tribol. 2002, 124, 367–376. [Google Scholar] [CrossRef]
- De Oliveira, L.M.; Matos, R.S.; Campelo, P.H.; Sanches, E.A.; da Fonseca Filho, H.D. Evaluation of the nanoscale surface applied to biodegradable nanoparticles containing Allium sativum essential oil. Mater. Lett. 2020, 275, 128111–128115. [Google Scholar] [CrossRef]
- Abbott, E.J.; Firestone, F.A. Specifying surface quality. Mech. Eng. 1993, 55, 569–572. [Google Scholar]
- Ţălu, Ş.; Janus, K.; Stach, S.; Preparation, A.S. Nanoscale patterns in carbon–Nickel nanocomposite thin films investigated by AFM and stereometric analysis. Int. J. Mater. 2017, 4, 54–62. [Google Scholar]
- Ito, R.M.; de Souza, C.C.; Gandarilla AM, D.; de Oliveira, L.M.; Brito, W.R.; Sanches, E.A.; Matos, R.S.; da Fonseca Filho, H.D. Micromorphology and microtexture evaluation of poly(o-ethoxyaniline) films using atomic force microscopy and fractal analysis. J. Polym. Res. 2020, 27, 299. [Google Scholar] [CrossRef]
- Ramos, G.Q.; Matos, R.S.; da Fonseca Filho, H.D. Advanced Microtexture Study of Anacardium occidentale L. Leaf Surface from the Amazon by Fractal Theory. Microsc. Microanal. 2020, 26, 989–996. [Google Scholar] [CrossRef] [PubMed]
- Matos, R.S.; Gonçalves EC, M.; Pinto, E.P.; Lopes GA, C.; Ferreira, N.S.; Resende, C.X. Nanoscale morphology, structure and fractal study of kefir microbial films grown in natura. Polímeros 2020, 30, e2020033–e2020043. [Google Scholar] [CrossRef]
- Țălu, Ș.; Ghaderi, A.; Stępień, K.; Mwema, F.M. Advanced Micromorphology Analysis of Cu/Fe NPs Thin Films. IOP Conf. Ser. Mater. Sci. Eng. 2019, 611, 12016. [Google Scholar] [CrossRef]
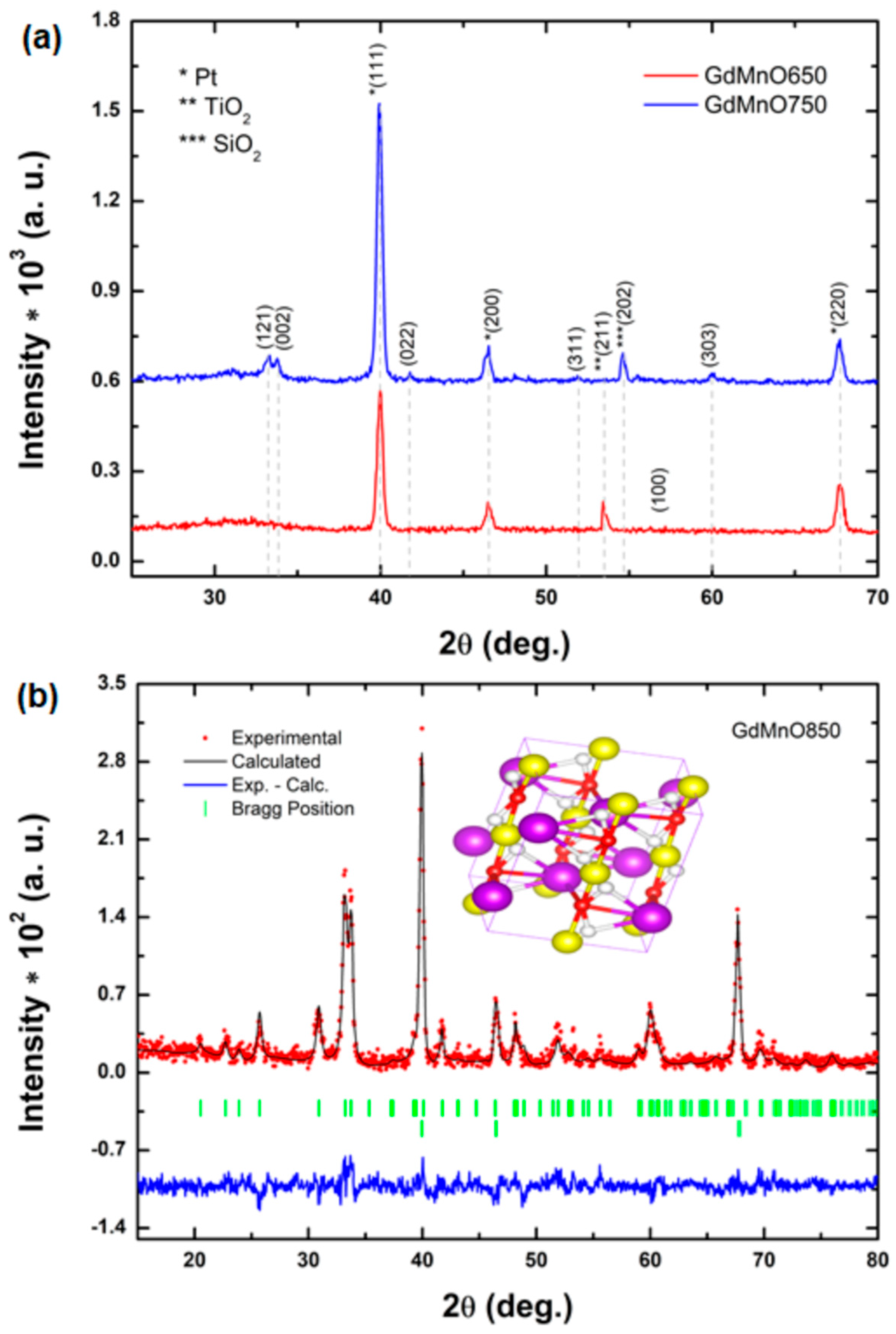


| Sample | a (Å) | b (Å) | c (Å) | Vc (Å3) | D(xrd) (nm) | ε | Δ (1/D2(xrd)) |
| GdMnO850 | 5.31715(2) | 5.78694(3) | 7.44901(6) | 229.206(6) | 14.227(7) | 7.1264(4) | 0.00494(1) |
| Parameter | Unit | GdMnO650 | GdMnO750 | GdMnO850 |
|---|---|---|---|---|
| Height | ||||
| Sq | (nm) | 1.58 ± 0.25 | 1.65 ± 0.22 | 3.63 ± 0.30 |
| Ssk | (-) | 0.44 ± 0.21 | 0.15 ± 0.27 | −0.08 ± 0.08 |
| Sku | (-) | 3.61 ± 0.42 | 3.48 ± 0.23 | 2.63 ± 0.04 |
| Sp | (nm) | 7.80 ± 2.39 | 6.58 ± 1.42 | 17.12 ± 5.49 |
| Sv | (nm) | 4.49 ± 0.25 | 5.31 ± 0.81 | 12.11 ± 0.51 |
| Sz | (nm) | 12.28 ± 2.34 | 11.88 ± 1.59 | 29.22 ± 5.59 |
| Sa | (nm) | 1.23 ± 0.21 | 1.28 ± 0.15 | 2.97 ± 0.26 |
| Parameter | Unit | GdMnO650 | GdMnO750 | GdMnO850 |
|---|---|---|---|---|
| Functional | ||||
| Smc | (nm) | 2.07 ± 0.42 | 2.01 ± 0.27 | 4.67 ± 0.42 |
| Sxp | (nm) | 2.72 ± 0.12 | 3.29 ± 0.51 | 7.09 ± 0.36 |
| Sk | (nm) | 3.58 ± 0.69 | 3.88 ± 0.31 | 10.05 ± 90.01 |
| Spk * | (nm) | 2.17 ± 0.51 | 2.11 ± 0.59 | 2.64 ± 0.30 |
| Svk | (nm) | 1.33 ± 0.21 | 1.75 ± 0.47 | 2.93 ± 0.25 |
| Smr1 | (%) | 14.02 ± 1.55 | 10.47 ± 1.08 | 7.64 ± 0.52 |
| Smr2 * | (%) | 90.95 ± 2.01 | 89.20 ± 2.07 | 90.28 ± 0.38 |
| Vmp * | (µm3/µm2) | 1.04 × 10−4 ± 2.15 × 10−5 | 1.03 × 10−4 ± 2.79 × 10−5 | 1.41 × 10−4 ± 1.63 × 10−5 |
| Vmc | (µm3/µm2) | 1.31 × 10−3 ± 2.38 × 10−4 | 1.38 × 10−3 ± 1.53 × 10−4 | 3.52 × 10−3 ± 3.45 × 10−4 |
| Vvc | (µm3/µm2) | 2.02 × 10−3 ± 4.44 × 10−4 | 1.92 × 10−3 ± 2.60 × 10−4 | 4.43 × 10−3 ± 4.24 × 10−4 |
| Vvv | (µm3/µm2) | 1.54 × 10−4 ± 8.26 × 10−6 | 1.96 × 10−4 ± 4.23 × 10−5 | 3.80 × 10−4 ± 1.50 × 10−5 |
| Feature | ||||
| Spd * | (1/µm2) | 31.00 ± 17.93 | 10.00 ± 0.43 | 20.44 ± 10.62 |
| Spc * | (1/µm2) | 11.86 ± 2.56 | 8.00 ± 1.00 | 10.98 ± 2.70 |
| Hybrid | ||||
| Sdq | (-) | 0.04 ± 0.00 | 0.03 ± 0.01 | 0.085 ± 0.002 |
| Sdr | (%) | 0.07 ± 0.01 | 0.05 ± 0.01 | 0.35 ± 0.01 |
| Parameter | Unit | GdMnO650 | GdMnO750 | GdMnO850 |
|---|---|---|---|---|
| Furrows | ||||
| Maximum depth | (nm) | 3.38 ± 0.43 | 4.16 ± 0.56 | 12.24 ± 0.52 |
| Mean depth | (nm) | 1.51 ± 0.13 | 1.34 ± 0.19 | 4.60 ± 0.34 |
| Mean density | (cm/cm2) | 86,382.81 ± 4997.06 | 78,881.94 ± 1442.56 | 81,635.01 ± 564.91 |
| Texture | ||||
| TI | (%) | 63.58 ± 10.78 | 40.45 ± 15.08 | 65.44 ± 7.54 |
| Str | (-) | 0.64 ± 0.11 | 0.40 ± 0.15 | 0.65 ± 0.08 |
| Std | (°) | 169.75 ± 4.68 | 141.19 ± 7.05 | 120.62 ± 19.88 |
| Parameter | Unit | GdMnO650 | GdMnO750 | GdMnO850 |
|---|---|---|---|---|
| FD | (-) | 2.242 ± 0.034 | 2.207 ± 0.007 | 2.281 ± 0.025 |
| HC | (-) | 0.169 ± 0.172 | 0.357 ± 0.023 | 0.813 ± 0.038 |
| |β| | (-) | 4.02 × 10−7 ± 1.58 × 10−7 | 4.09 × 10−7 ± 1.82 × 10−7 | 8.45 × 10−8 ± 3.15 × 10−8 |
| FS | (-) | 0.536 ± 0.022 | 0.500 ± 0.024 | 0.483 ± 0.009 |
| E | (-) | 0.962 ± 0.019 | 0.967 ± 0.017 | 0.996 ± 0.003 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Romaguera-Barcelay, Y.; Ţălu, Ş.; Matos, R.S.; Oliveira, R.M.P.B.; Moreira, J.A.; de Cruz, J.P.; da Fonseca Filho, H.D. Fractal-Stereometric Correlation of Nanoscale Spatial Patterns of GdMnO3 Thin Films Deposited by Spin Coating. Appl. Sci. 2021, 11, 3886. https://doi.org/10.3390/app11093886
Romaguera-Barcelay Y, Ţălu Ş, Matos RS, Oliveira RMPB, Moreira JA, de Cruz JP, da Fonseca Filho HD. Fractal-Stereometric Correlation of Nanoscale Spatial Patterns of GdMnO3 Thin Films Deposited by Spin Coating. Applied Sciences. 2021; 11(9):3886. https://doi.org/10.3390/app11093886
Chicago/Turabian StyleRomaguera-Barcelay, Yonny, Ştefan Ţălu, Robert Saraiva Matos, Rosane Maria Pessoa Betânio Oliveira, Joaquim Agostinho Moreira, Javier Perez de Cruz, and Henrique Duarte da Fonseca Filho. 2021. "Fractal-Stereometric Correlation of Nanoscale Spatial Patterns of GdMnO3 Thin Films Deposited by Spin Coating" Applied Sciences 11, no. 9: 3886. https://doi.org/10.3390/app11093886
APA StyleRomaguera-Barcelay, Y., Ţălu, Ş., Matos, R. S., Oliveira, R. M. P. B., Moreira, J. A., de Cruz, J. P., & da Fonseca Filho, H. D. (2021). Fractal-Stereometric Correlation of Nanoscale Spatial Patterns of GdMnO3 Thin Films Deposited by Spin Coating. Applied Sciences, 11(9), 3886. https://doi.org/10.3390/app11093886











