Statistical Analysis of Nanofiber Mat AFM Images by Gray-Scale-Resolved Hurst Exponent Distributions
Abstract
1. Introduction
2. Materials and Methods
3. Results
- -
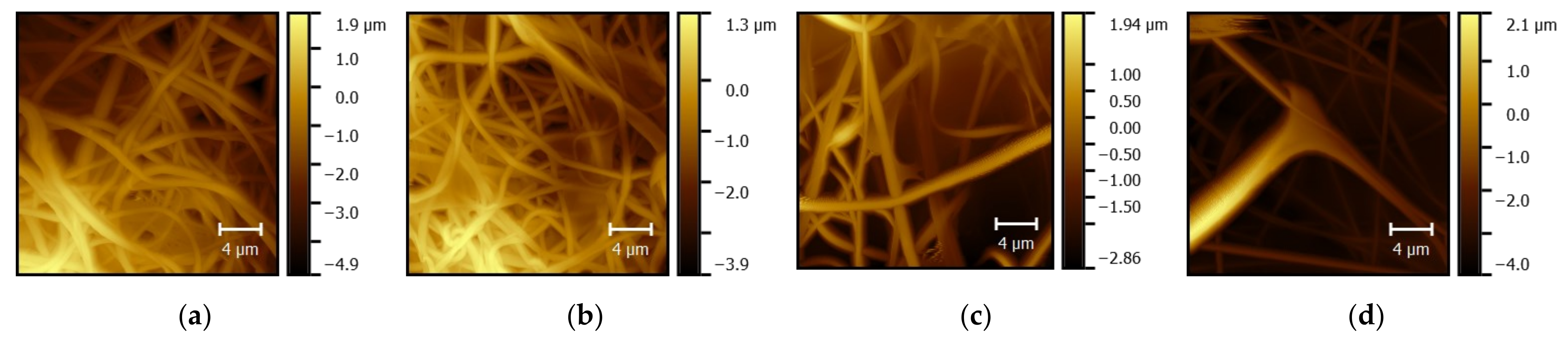
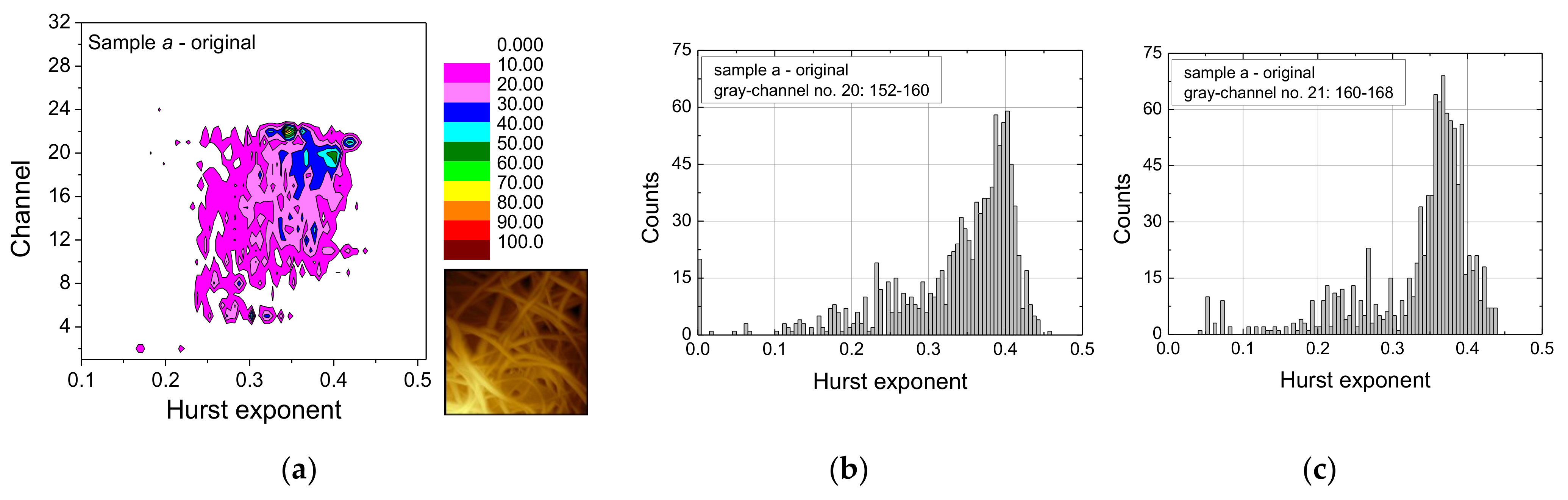
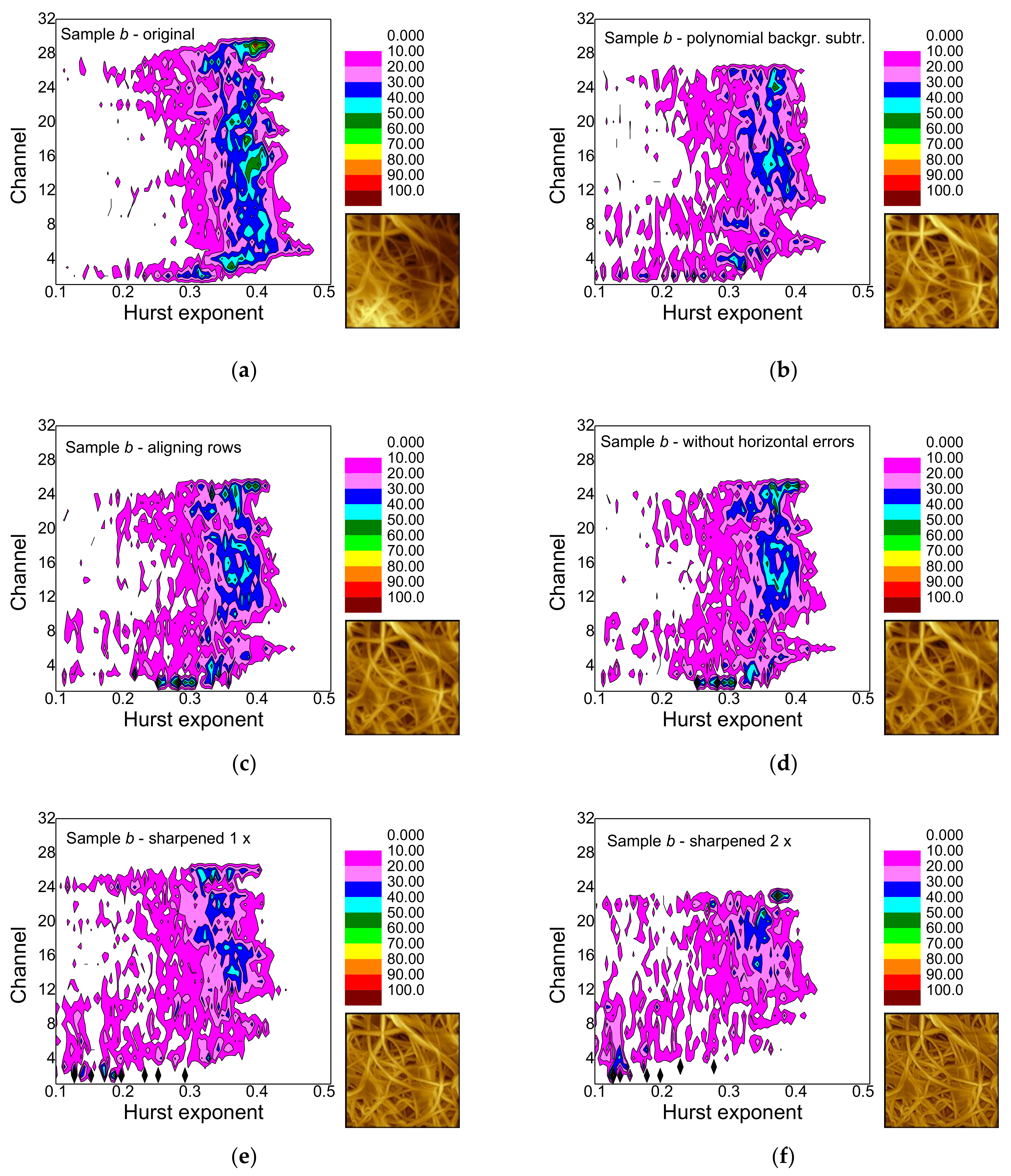
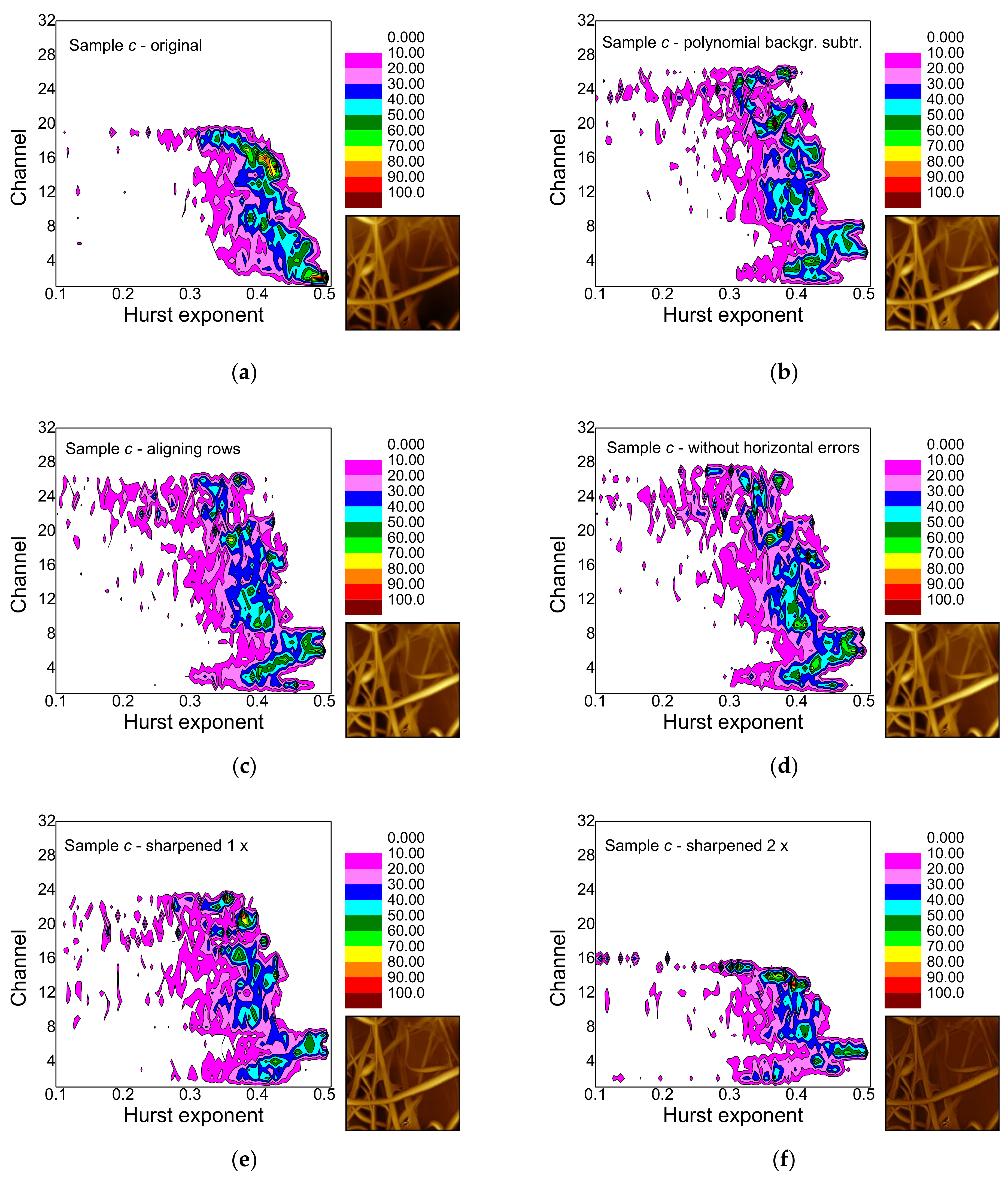
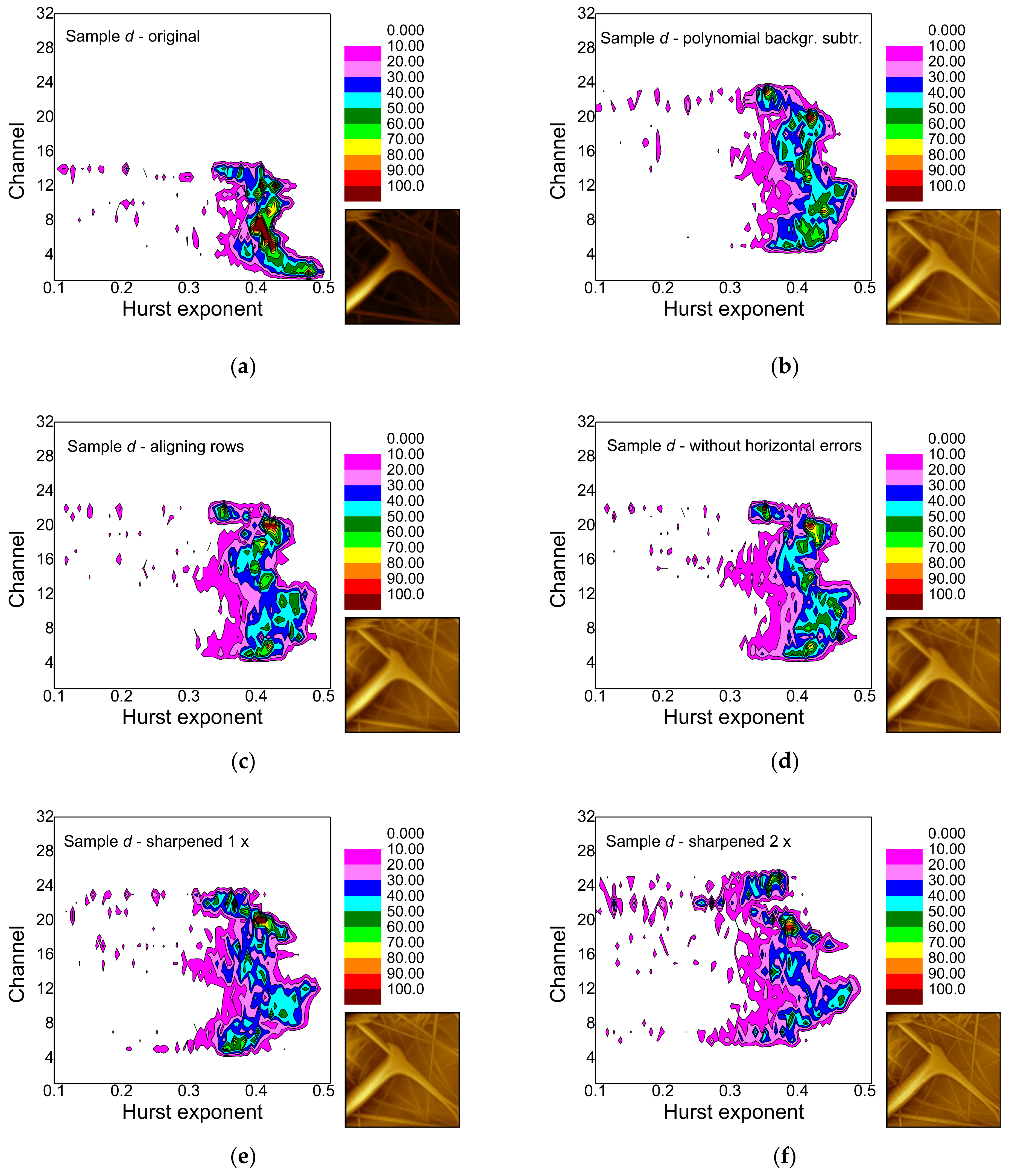
- False-color maps of gray-scale-resolved Hurst exponent distributions enable distinguishing between different fiber distributions, especially between images with many and with only few fibers.
- -
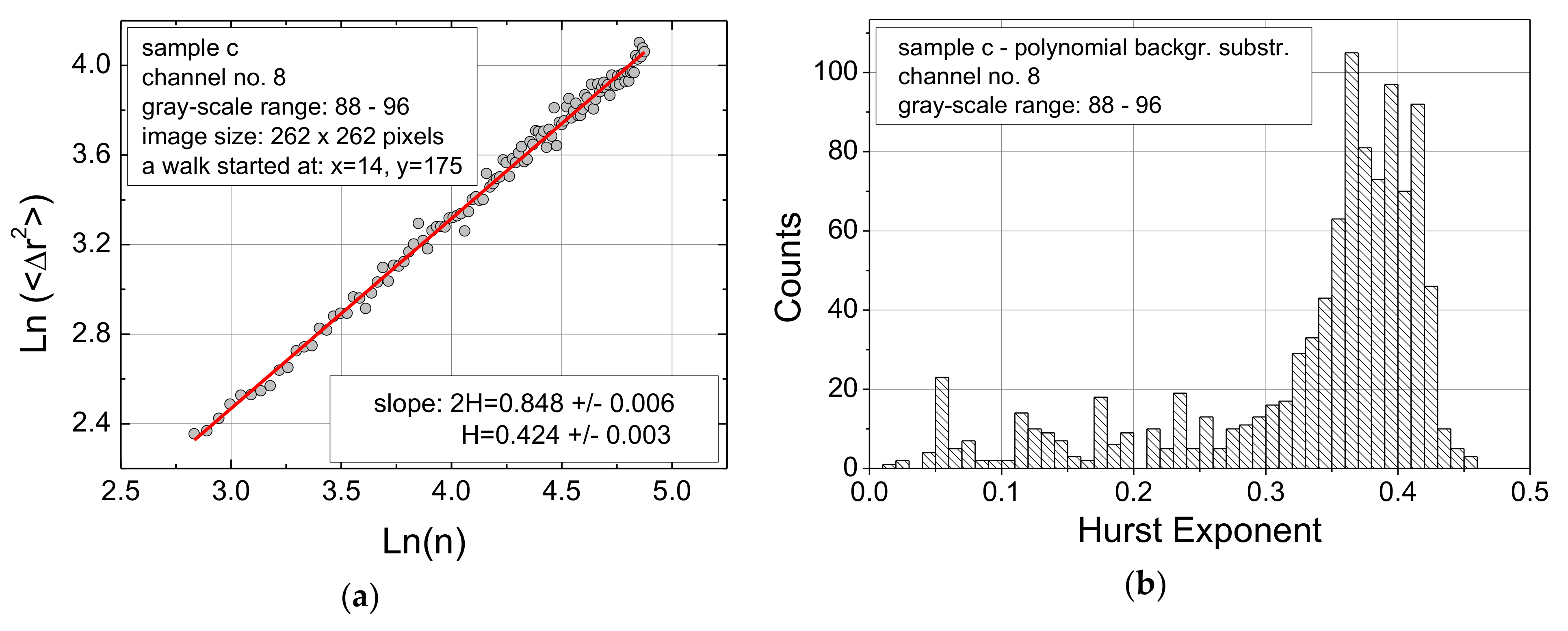
- Polynomial background subtraction levels out the upper channel numbers for which a signal occurs and should thus be performed, especially in order to avoid ignoring hidden features (cf. Figure 9a,b).
- -
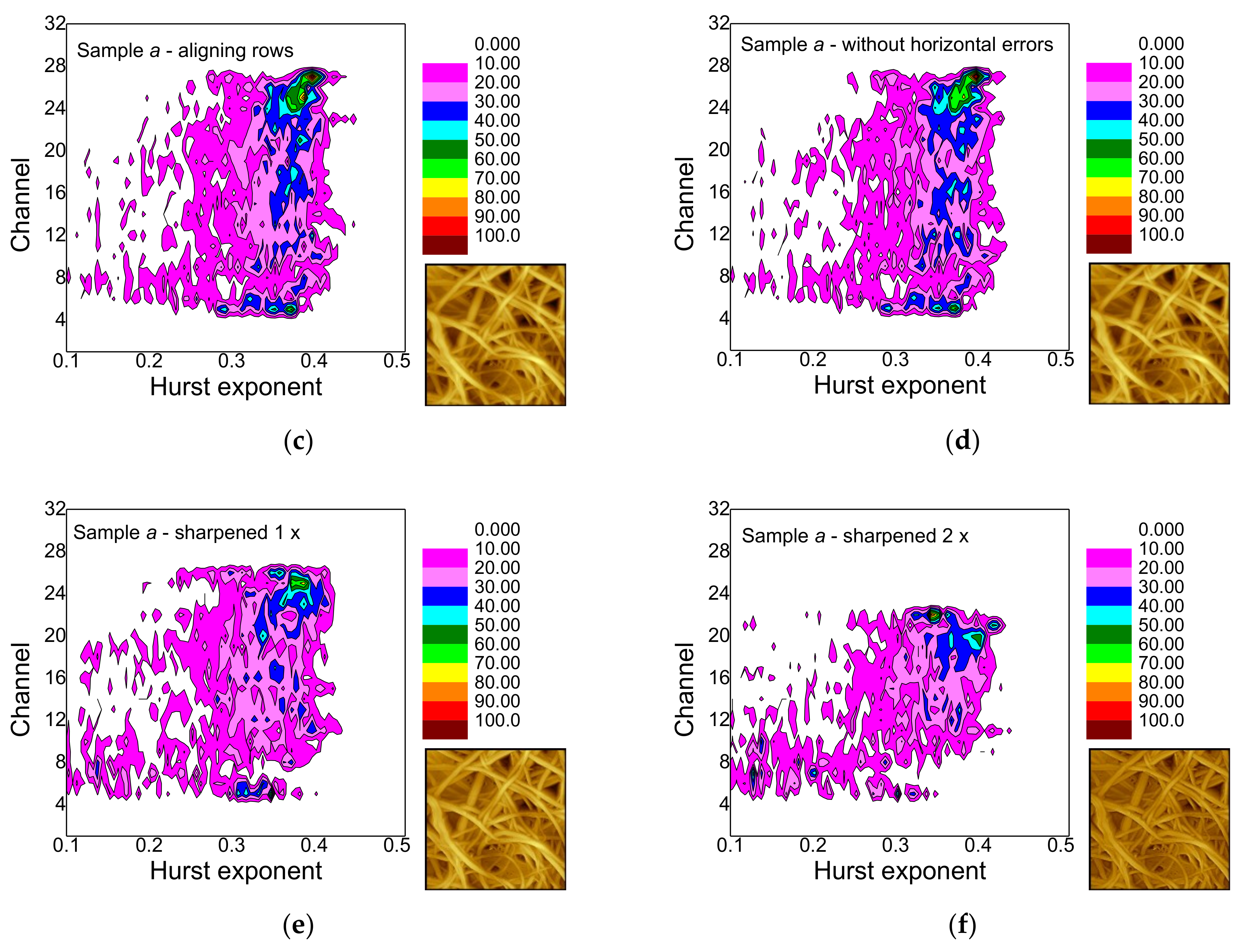
- Aligning rows and deleting horizontal errors leaves the images and thus, the false-color maps nearly unaltered.
- -
- The effect of sharpening once differs from sample to sample and must be investigated further in the next study.
- -
- Sharpening twice modifies not only the image in an unnaturally looking way, but also the false-color maps of the gray-scale-resolved Hurst exponent distributions and should thus be avoided.
- -
- What could not be performed yet, but has to be tested in the near future, is a comparison with a highly accurate AFM with increased quality of the original images, as reported in [36].
- -
- Generally, the meaning of the “noise” in the range of Hurst exponents values below approx. 0.25 needs further investigation to find out whether this range should be ignored since it is mostly based on errors in the images, or whether it can oppositely be used as part of the “fingerprint” of such AFM images. To explain the threshold value of 0.25, we can refer to the composition of two random processes in analogy to [37]. In our model the first random process would concern the formation of tiny features in textiles (or their maps) and the second one would be the random walk itself. Further referring to [25], such Hurst exponent values (being the inverse of the fractal dimension of the random walk therein) would be far below the outcome of the random walk on any percolation model in 2D.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Maver, T.; Kurecic, M.; Pivec, T.; Maver, U.; Gradisnik, L.; Gasparic, P.; Kaker, B.; Bratusa, A.; Hribernik, S.; Stana Kleinschek, K. Needleless electrospun carboxymethyl cellulose/polyethylene oxide mats with medicinal plant extracts for advanced wound care applications. Cellulose 2020, 27, 4487–4508. [Google Scholar] [CrossRef]
- Grothe, T.; Storck, J.L.; Dotter, M.; Ehrmann, A. Impact of solid content in the electrospinning solution on physical and chemical properties of polyacrylonitrile (PAN) nanofibrous mats. Tekstilec 2020, 63, 225–232. [Google Scholar]
- Roche, R.; Yalcinkaya, F. Electrospun polyacrylonitrile nanofibrous membranes for point-of-use water and air cleaning. ChemistryOpen 2019, 8, 97–103. [Google Scholar] [CrossRef]
- Grothe, T.; Großerhode, C.; Hauser, T.; Kern, P.; Stute, K.; Ehrmann, A. Needleless electrospinning of PEO nanofiber mats. Adv. Eng. Res. 2017, 102, 54–58. [Google Scholar]
- Reneker, D.H.; Chun, I.S. Nanometre diameter fibres of polymer, produced by electrospinning. Nanotechnology 1996, 7, 216–223. [Google Scholar] [CrossRef]
- Lemma, S.M.; Esposito, A.; Mason, M.; Brusetti, L.; Cesco, S.; Scampicchio, M. Removal of bacterial and yeast in water and beer by nylon nanofibrous membranes. J. Food Eng. 2015, 157, 1–6. [Google Scholar] [CrossRef]
- Boyraz, E.; Yalcinkaya, F.; Hruza, J.; Maryska, J. Surface-modified nanofibrous PVF membranes for liquid separation technology. Materials 2019, 12, 2702. [Google Scholar] [CrossRef] [PubMed]
- Lin, K.-Y.A.; Yang, M.-T.; Lin, J.-T.; Du, Y.C. Cobalt ferrite nanoparticles supported on electrospun carbon fiber as a magnetic heterogeneous catalyst for activating peroxymonosulfate. Chemosphere 2018, 208, 502–511. [Google Scholar] [CrossRef]
- García-Mateos, F.J.; Cordero-Lanzac, T.; Berenguer, R.; Morallón, E.; Cazorla-Amorós, D.; Rodríguez-Mirasol, J.; Cordero, T. Lignin-derived Pt supported carbon (submicron)fiber electro-catalysts for alcohol electro-oxidation. Appl. Catal. B Environ. 2017, 211, 18–30. [Google Scholar] [CrossRef]
- Dalton, P.D.; Klinkhammer, K.; Salber, J.; Klee, D.; Möller, M. Direct in vitro electrospinning with polymer melts. Biomacromolecules 2006, 7, 686–690. [Google Scholar] [CrossRef] [PubMed]
- Wehlage, D.; Blattner, H.; Sabantina, L.; Böttjer, R.; Grothe, T.; Rattenholl, A.; Gudermann, F.; Lütkemeyer, D.; Ehrmann, A. Sterilization of PAN/gelatin nanofibrous mats for cell growth. Tekstilec 2019, 62, 78–88. [Google Scholar] [CrossRef]
- Mamun, A. Review of possible applications of nanofibrous mats for wound dressing. Tekstilec 2019, 62, 89–100. [Google Scholar] [CrossRef]
- Wehlage, D.; Blattner, H.; Mamun, A.; Kutzli, I.; Diestelhorst, E.; Rattenholl, A.; Gudermann, F.; Lütkemeyer, D.; Ehrmann, A. Cell growth on electrospun nanofiber mats from polyacrylonitrile (PAN) blends. AIMS Bioeng. 2020, 7, 43–54. [Google Scholar] [CrossRef]
- Bian, Y.; Wang, S.J.; Zhang, L.; Chen, C. Influence of fiber diameter, filter thickness, and packing density on PM2.5 removal efficiency of electrospun nanofiber air filters for indoor applications. Build. Environ. 2020, 170, 106628. [Google Scholar] [CrossRef]
- Nikbakht, M.; Salehi, M.; Rezayat, S.M.; Majidi, R.F. Various parameters in the preparation of chitosan/polyethylene oxide electrospun nanofibers containing Aloe vera extract for medical applications. Nanomed. J. 2020, 7, 21–28. [Google Scholar]
- Storck, J.L.; Grothe, T.; Mamun, A.; Sabantina, L.; Klöcker, M.; Blachowicz, T.; Ehrmann, A. Orientation of electrospun magnetic nanofibers near conductive areas. Materials 2020, 13, 47. [Google Scholar] [CrossRef] [PubMed]
- Zheng, G.F.; Jiang, J.X.; Wang, X.; Li, W.W.; Liu, J.; Fu, G.; Lin, L.W. Nanofiber membranes by multi-jet electrospinning arranged as arc-array with sheath gas for electrodialysis applications. Mater. Des. 2020, 189, 108504. [Google Scholar] [CrossRef]
- Gaalova, J.; Yalcinkaya, F.; Curinova, P.; Kohout, M.; Yalcinkaya, B.; Kostejn, M.; Jirsak, J.; Stibor, I.; Bara, J.E.; van der Bruggen, B.; et al. Separation of racemic compound by nanofibrous composite membranes with chiral selector. J. Membr. Sci. 2020, 596, 117728. [Google Scholar] [CrossRef]
- Bu, H.G.; Huang, X.B. A novel multiple fractal features extraction framework and its application to the detection of fabric defects. J. Text. Inst. 2008, 99, 489–497. [Google Scholar] [CrossRef]
- Conci, A.; Proenca, C.B. A fractal image analysis system for fabric inspection system based on box counting method. Comput. Netw. Isdn Syst. 1998, 30, 1887–1895. [Google Scholar] [CrossRef]
- Giorgilli, A.; Casati, D.; Sironi, L.; Galgani, L. An efficient procedure to compute fractal dimensions by box counting. Phys. Lett. A 1986, 115, 202–206. [Google Scholar] [CrossRef]
- Valous, N.A.; Mendoza, F.; Sun, D.-W.; Allen, P. Texture appearance characterization of pre-sliced pork ham images using fractal metrics: Fourier analysis dimension and lacunarity. Food Res. Intern. 2009, 42, 353–362. [Google Scholar] [CrossRef]
- Plotnick, R.E.; Gardner, R.H.; Hargrove, W.W.; Prestegaard, K.; Perlmutter, M. Lacunarity analysis: A general technique for the analysis of spatial patterns. Phys. Rev. E 1996, 53, 5461–5468. [Google Scholar] [CrossRef]
- Grzybowski, J.; Blachowicz, T. Estimation of spatial distribution and symmetry of textile materials using numerical classification. Commun. Dev. Assem. Text. Prod. 2020, 1, 180–185. [Google Scholar] [CrossRef]
- Havlin, S.; Ben-Avraham, D. Diffusion in disordered media. Adv. Phys. 2002, 51, 187–292. [Google Scholar] [CrossRef]
- Haus, J.W.; Kehr, K.W. Diffusion in regular and disordered lattices. Phys. Rep. 1987, 150, 263–406. [Google Scholar] [CrossRef]
- Li, J.; Teng, H.L.; Liu, S.Q.; Xu, J.; Li, T.D. Three-dimensional spatial distribution analysis of fibre in wet-blue pig leather. J. Soc. Leather Technol. Chem. 2018, 102, 111–117. [Google Scholar]
- Blachowicz, T.; Ehrmann, A.; Domino, K. Statistical analysis of digital images of periodic fibrous structures using generalized Hurst exponent distributions. Phys. A Stat. Mech. Appl. 2016, 452, 167–177. [Google Scholar] [CrossRef]
- Ehrmann, A.; Blachowicz, T.; Domino, K.; Aumann, S.; Weber, M.O.; Zghidi, H. Examination of hairiness changes due to washing in knitted fabrics using a random walk approach. Text. Res. J. 2015, 85, 2147–2154. [Google Scholar] [CrossRef]
- Ehrmann, A.; Blachowicz, T.; Zghidi, H.; Weber, M.O. Reliability of statistic evaluation of microscopic pictures taken from knitted fabrics. J. Phys. Conf. Ser. 2015, 633, 012101. [Google Scholar] [CrossRef]
- Blachowicz, T.; Böhm, T.; Grzebowski, J.; Domino, K.; Ehrmann, A. Analysis of AFM images of nanofibre mats for automated processing. Tekstilec 2020, 63, 104–112. [Google Scholar] [CrossRef]
- Babič, M.; Kokol, P.; Guid, N.; Panjan, P. A new method for estimating the Hurst exponent H for 3D objects. Mater. Tehnol. 2014, 48, 203–208. [Google Scholar]
- Matej, B.; Miliaresis, G.C.; Matjaž, M.; Ambu, R.; Michele, C. New method for estimating fractal dimension in 3d space and its application to complex surfaces. Int. J. Adv. Sci. Eng. Inf. Technol. 2019, 9, 2154–2159. [Google Scholar]
- Blachowicz, T.; Andreychouk, V. Quantitative estimation of 3D cave networks complexity using random walk analysis. Landf. Anal. 2015, 29, 91–96. [Google Scholar] [CrossRef]
- Ehrmann, A.; Blachowicz, T. Image processing techniques for evaluation of textile materials. In Examination of Textiles with Mathematical and Physical Methods; Springer International Publishing AG: Cham, Switzerland, 2017; pp. 89–112. [Google Scholar]
- Mokrvenaite-Vilkonciene, I.; Virzonis, D.; Dzedzickis, A.; Bucinskas, V.; Rozene, J.; Vilkoncius, R.; Vaiciulis, D.; Ramanaviciene, A.; Ramanavicius, R. The improvement of the accuracy of electromagnetic actuator based atomic force microscope operating in contact mode and the development of a new methodology for the estimation of control parameters and the achievement of superior image quality. Sens. Act. A Phys. 2019, 287, 168–176. [Google Scholar] [CrossRef]
- Gadomski, A. Multilineal random patterns evolving subdiffusively in square lattice. Fractals 2003, 11, 233–241. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blachowicz, T.; Domino, K.; Koruszowic, M.; Grzybowski, J.; Böhm, T.; Ehrmann, A. Statistical Analysis of Nanofiber Mat AFM Images by Gray-Scale-Resolved Hurst Exponent Distributions. Appl. Sci. 2021, 11, 2436. https://doi.org/10.3390/app11052436
Blachowicz T, Domino K, Koruszowic M, Grzybowski J, Böhm T, Ehrmann A. Statistical Analysis of Nanofiber Mat AFM Images by Gray-Scale-Resolved Hurst Exponent Distributions. Applied Sciences. 2021; 11(5):2436. https://doi.org/10.3390/app11052436
Chicago/Turabian StyleBlachowicz, Tomasz, Krzysztof Domino, Michał Koruszowic, Jacek Grzybowski, Tobias Böhm, and Andrea Ehrmann. 2021. "Statistical Analysis of Nanofiber Mat AFM Images by Gray-Scale-Resolved Hurst Exponent Distributions" Applied Sciences 11, no. 5: 2436. https://doi.org/10.3390/app11052436
APA StyleBlachowicz, T., Domino, K., Koruszowic, M., Grzybowski, J., Böhm, T., & Ehrmann, A. (2021). Statistical Analysis of Nanofiber Mat AFM Images by Gray-Scale-Resolved Hurst Exponent Distributions. Applied Sciences, 11(5), 2436. https://doi.org/10.3390/app11052436








