Design and Modelling of an Amphibious Spherical Robot Attached with Assistant Fins
Abstract
1. Introduction
2. Mechanical Structure and Electrical Actuation and Control System
2.1. Design Objectives
- the ability to navigate on the water and on the land with exactly the same driving mechanism;
- a sealed structure, enclosing its vulnerable components to protect them from outside environments, e.g., water, sand and gas, so as to make it capable of surviving harsh environments;
- this robot can be remotely handled by an operator.
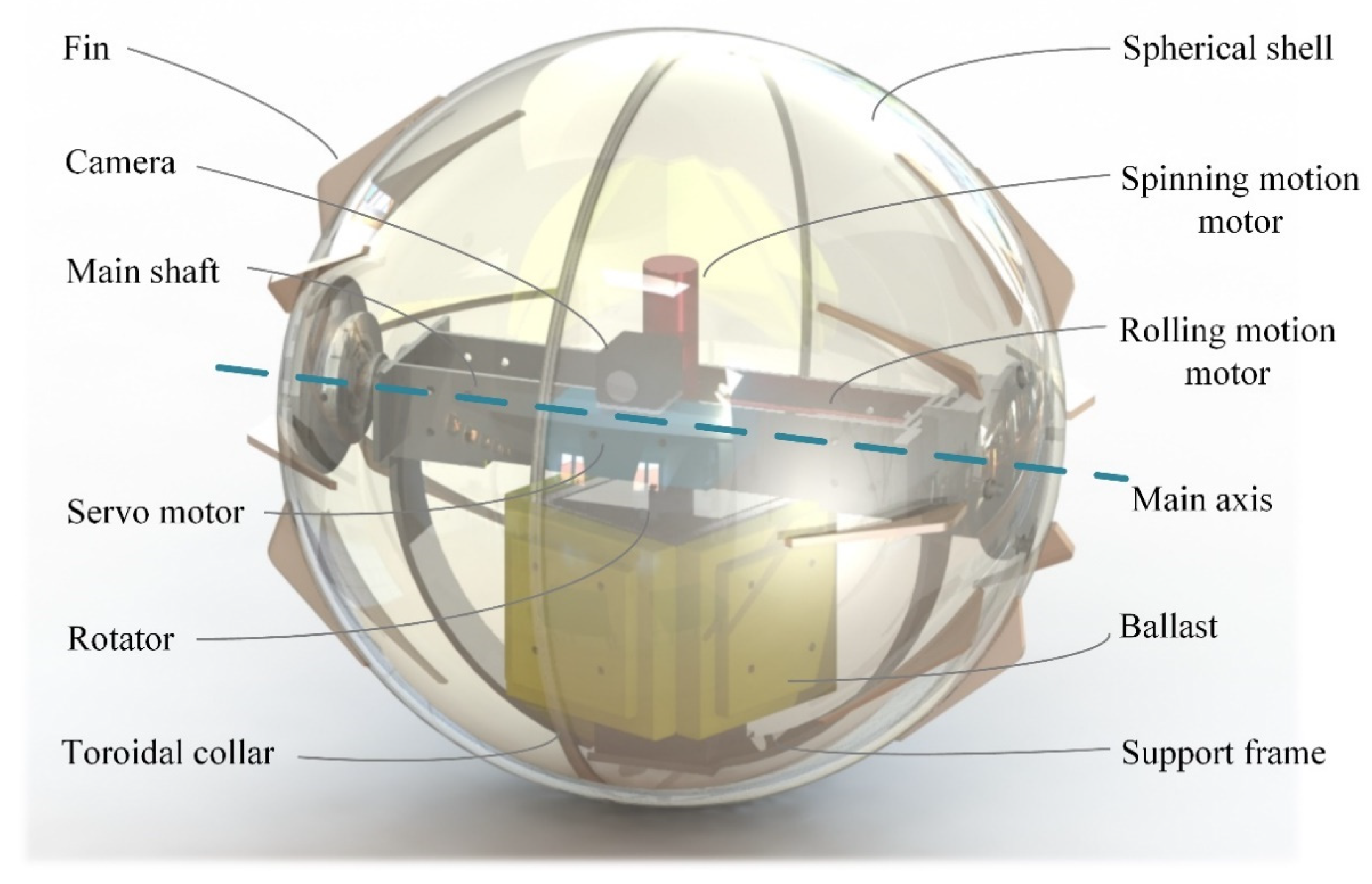
2.2. Introduction of the Developed Spherical Robot
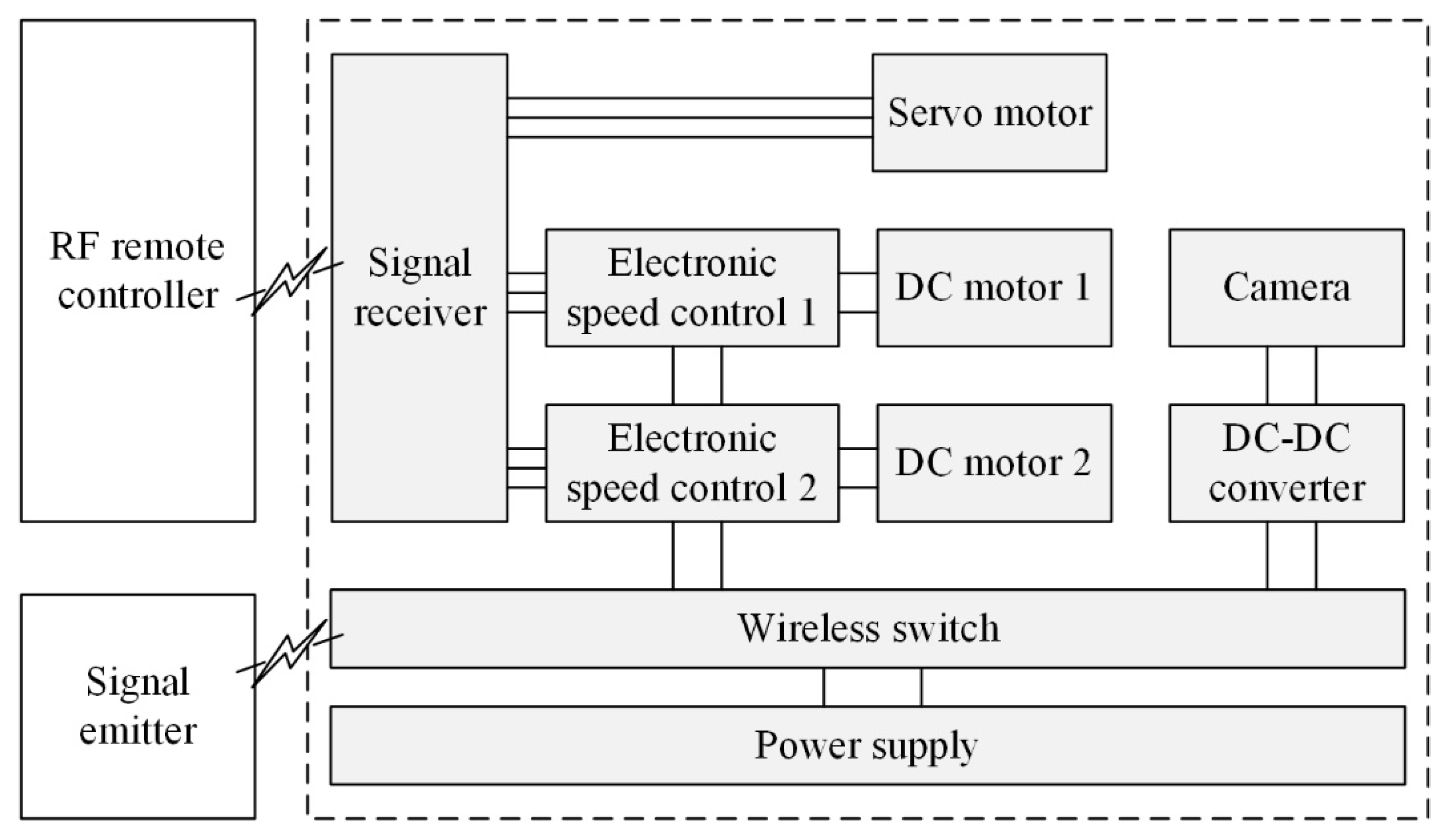
2.3. Electrical Actuation and Control System of the Robot
3. Dynamic Model of the Robot
3.1. Coordinate Frames
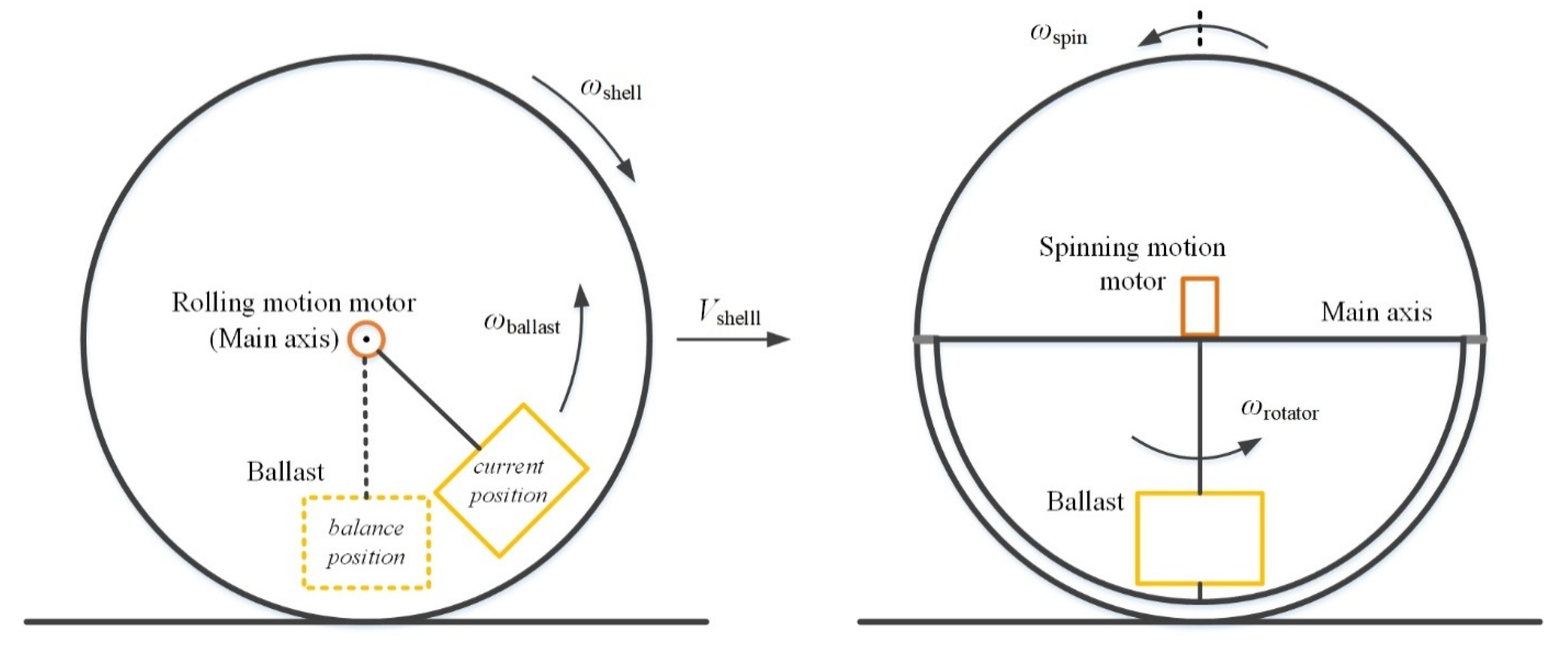
3.2. Kinematics
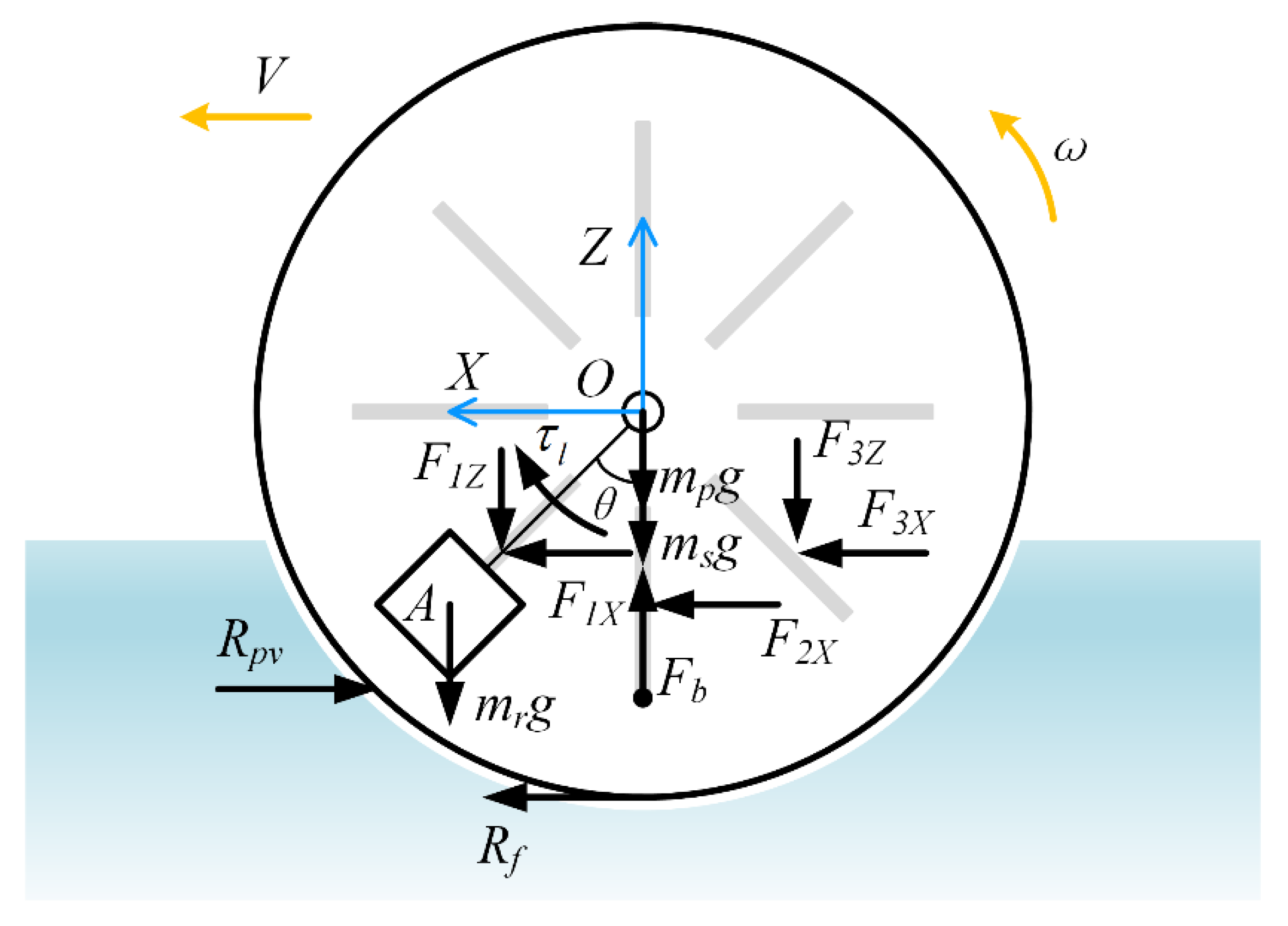
3.3. Generalized Forces
- (a)
- Buoyancy
- (b)
- Frictional Resistance
- (c)
- Pressure Resistance
- (d)
- Resultant Force Exerted on the Fins
3.4. Equations of Motion
3.5. Model Simplification
4. Simulation and Experiments
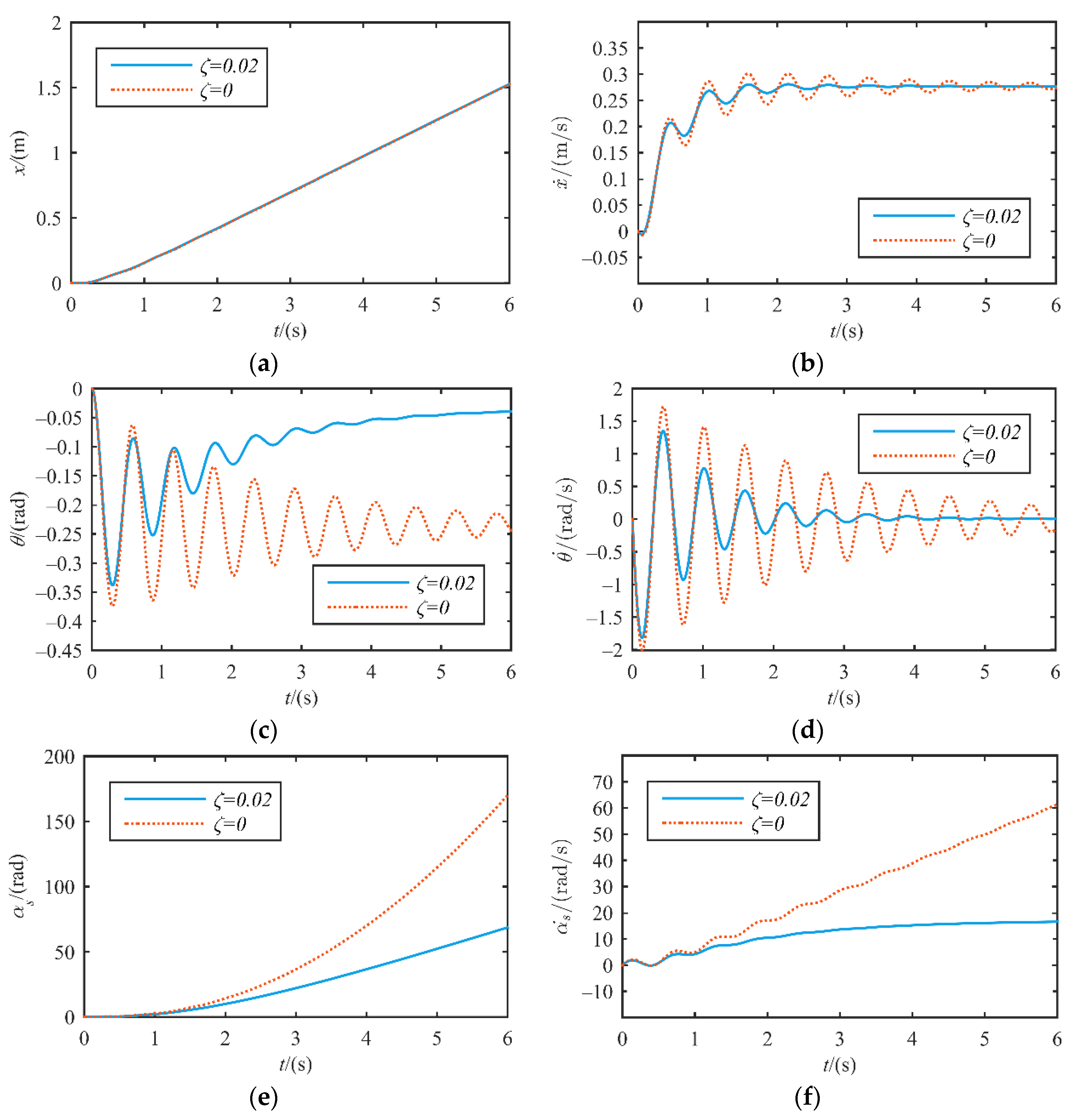
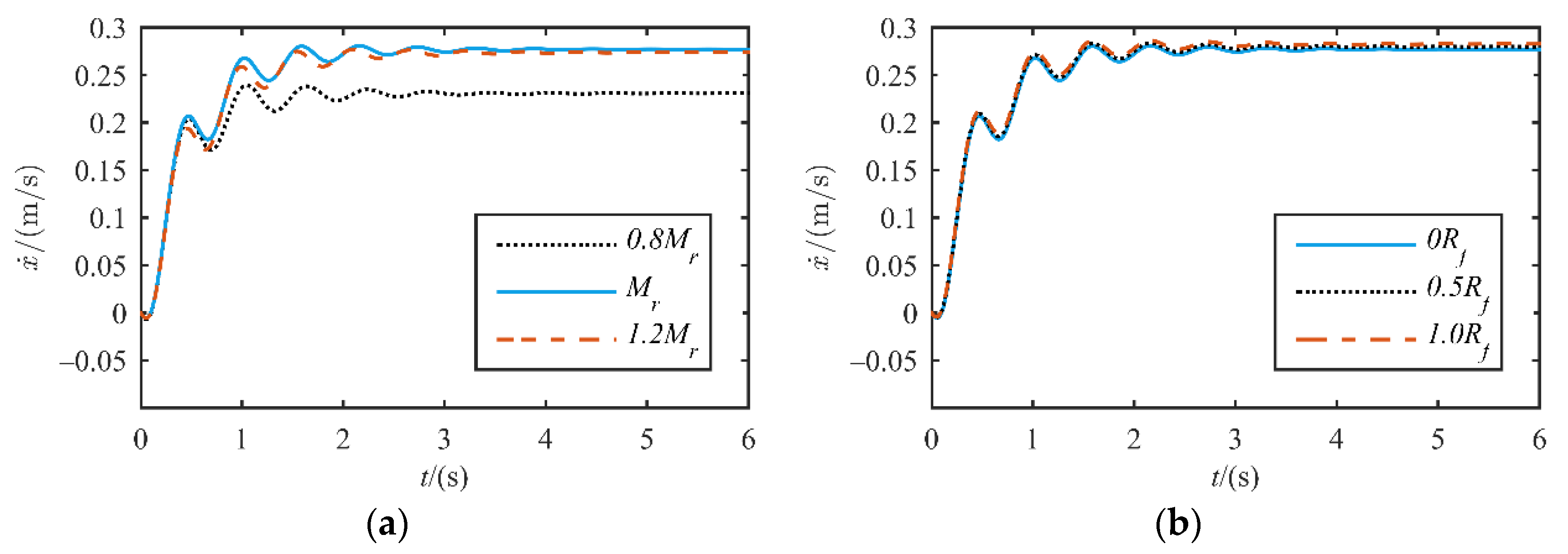
4.1. Simulation
4.2. Amphibious Spherical Robot Prototype
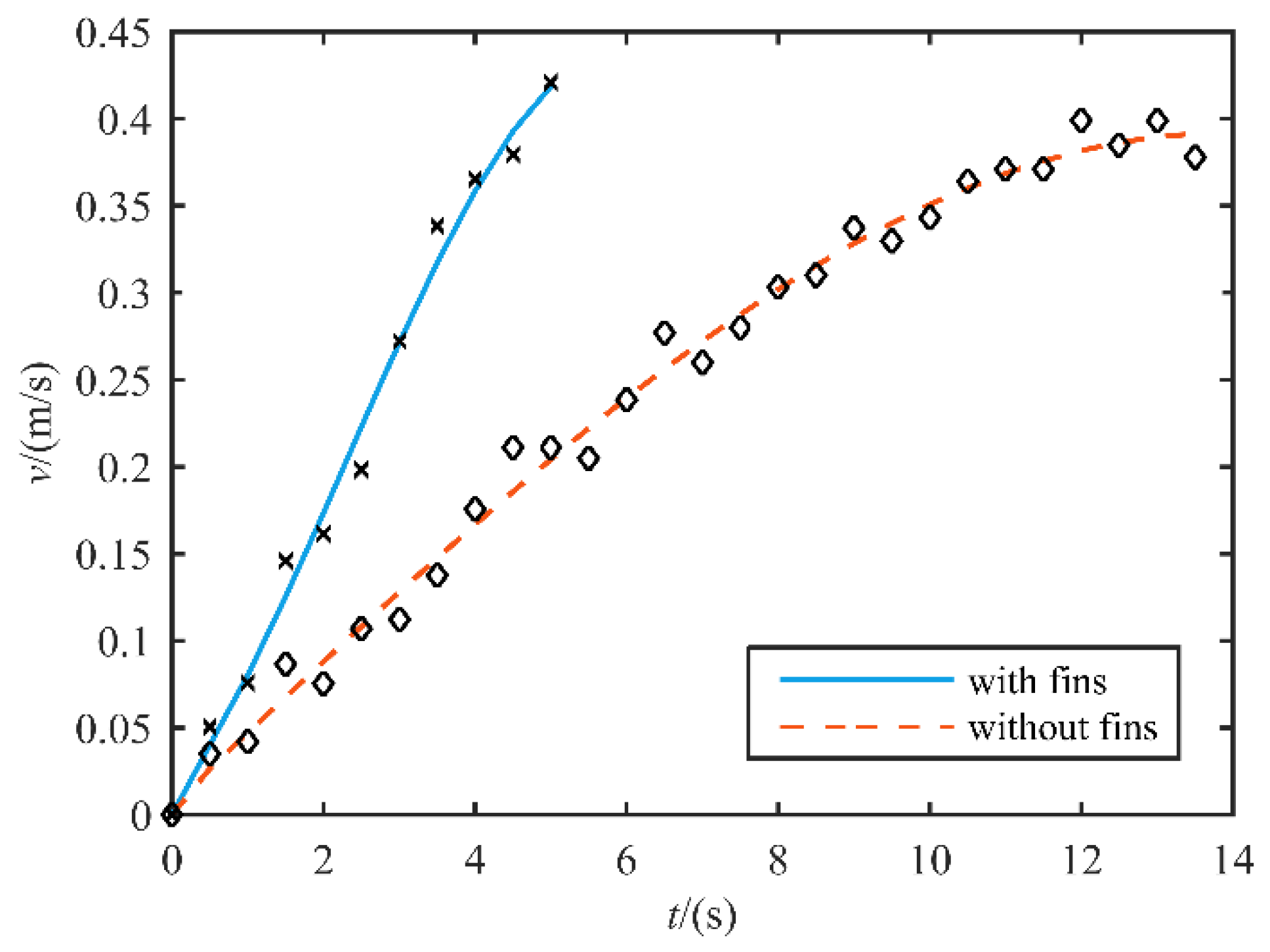
4.3. Movement Experiments
- (a)
- Movement on Land
- (b)
- Movement on the Water
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Prahacs, C.; Saudners, A.; Smith, M.K.; McMordie, D.; Buehler, M. Towards legged amphibious mobile robotics. In Proceedings of the Canadian Engineering Education Association (CEEA), Montreal, QC, Canada, 29–30 July 2004; pp. 2371–5243. [Google Scholar]
- Hirose, S.; Yamada, H. Snake-like robots [tutorial]. IEEE Rob. Autom. Mag. 2009, 16, 88–98. [Google Scholar] [CrossRef]
- Muthugala, M.A.V.J.; Le, A.V.; Cruz, E.S.; Elara, M.R.; Veerajagadheswar, P.; Kumar, M. A self-organizing fuzzy logic classifier for benchmarking robot-aided blasting of ship hulls. Sensors 2020, 20, 3215. [Google Scholar] [CrossRef] [PubMed]
- Takayama, T.; Hirose, S. Amphibious 3D active cord mechanism “HELIX” with helical swimming motion. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Lausanne, Switzerland, 30 September–4 October 2002; pp. 775–780. [Google Scholar]
- Yamada, H.; Hirose, S. Study of a 2-DOF joint for the small active cord mechanism. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Kobe, Japan, 12–17 May 2009; pp. 3827–3832. [Google Scholar]
- Crespi, A.; Badertscher, A.; Guignard, A.; Ijspeert, A.J. AmphiBot I: An amphibious snake-like robot. Robot. Auton. Syst. 2005, 50, 163–175. [Google Scholar] [CrossRef]
- Ijspeert, A.J.; Crespi, A.; Ryczko, D.; Cabelguen, J.-M. From swimming to walking with a salamander robot driven by a spinal cord model. Science 2007, 315, 1416–1420. [Google Scholar] [CrossRef] [PubMed]
- Crespi, A.; Ijspeert, A.J. Online optimization of swimming and crawling in an amphibious snake robot. IEEE Trans. Rob. 2008, 24, 75–87. [Google Scholar] [CrossRef]
- Crespi, A.; Karakasiliotis, K.; Guignard, A.; Ijspeert, A.J. Salamandra robotica II: An amphibious robot to study salamander-like swimming and walking gaits. IEEE Trans. Rob. 2013, 29, 308–320. [Google Scholar] [CrossRef]
- Kelasidi, E.; Liljeback, P.; Pettersen, K.Y.; Gravdahl, J.T. Innovation in underwater robots: Biologically inspired swimming snake robots. IEEE Rob. Autom. Mag. 2016, 23, 44–62. [Google Scholar] [CrossRef]
- Kelasidi, E.; Liljeback, P.; Pettersen, K.Y.; Gravdahl, J.T. Integral Line-of-Sight Guidance for Path Following Control of Underwater Snake Robots: Theory and Experiments. IEEE Trans. Rob. 2017, 33, 610–628. [Google Scholar] [CrossRef]
- Georgiades, C.; Nahon, M.; Buehler, M. Simulation of an underwater hexapod robot. Ocean Eng. 2009, 36, 39–47. [Google Scholar] [CrossRef]
- Meger, D.; Higuera, J.C.G.; Xu, A.; Giguere, P.; Dudek, G. Learning legged swimming gaits from experience. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 25–30 May 2015; pp. 2332–2338. [Google Scholar]
- Dudek, G.; Giguere, P.; Prahacs, C.; Saunderson, S.; Sattar, J.; Torres-Mendez, L.-A.; Jenkin, M.; German, A.; Hogue, A.; Ripsman, A.; et al. AQUA: An Amphibious Autonomous Robot. Computer 2007, 40, 46–53. [Google Scholar] [CrossRef]
- Sattar, J.; Giguère, P.; Dudek, G. Sensor-based behavior control for an autonomous underwater vehicle. Int. J. Rob. Res. 2009, 28, 701–713. [Google Scholar] [CrossRef]
- Boxerbaum, A.S.; Werk, P.; Quinn, R.D.; Vaidyanathan, R. Design of an autonomous amphibious robot for surf zone operation: Part I mechanical design for multi-mode mobility. In Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Monterey, CA, USA, 24–28 July 2005; pp. 1459–1464. [Google Scholar]
- Harkins, R.; Ward, J.; Vaidyanathan, R.; Boxerbaum, A.X.; Quinn, R.D. Design of an autonomous amphibious robot for surf zone operations: Part II-hardware, control implementation and simulation. In Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Monterey, CA, USA, 24–28 July 2005; pp. 1465–1470. [Google Scholar]
- Zhang, S.; Zhou, Y.; Xu, M.; Liang, X.; Liu, J.; Yang, J. AmphiHex-I: Locomotory Performance in Amphibious Environments with Specially Designed Transformable Flipper Legs. IEEE/ASME Trans. Mechatron. 2016, 21, 1720–1731. [Google Scholar] [CrossRef]
- Zhong, B.; Zhang, S.; Xu, M.; Zhou, Y.; Fang, T.; Li, W. On a CPG-based hexapod robot: AmphiHex-II with variable stiffness legs. IEEE/ASME Trans. Mechatron. 2018, 23, 542–551. [Google Scholar] [CrossRef]
- Chen, Y.; Doshi, N.; Goldberg, B.; Wang, H.; Wood, R.J. Controllable water surface to underwater transition through electrowetting in a hybrid terrestrial-aquatic microrobot. Nat. Commun. 2018, 9, 2495. [Google Scholar] [CrossRef] [PubMed]
- Kaznov, V.; Seeman, M. Outdoor navigation with a spherical amphibious robot. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Taipei, Taiwan, 18–22 October 2010; pp. 5113–5118. [Google Scholar]
- Li, M.; Guo, S.; Hirata, H.; Ishihara, H. Design and performance evaluation of an amphibious spherical robot. Robot. Auton. Syst. 2015, 64, 21–34. [Google Scholar] [CrossRef]
- He, Y.; Shi, L.; Guo, S.; Guo, P.; Xiao, R. Numerical simulation and hydrodynamic analysis of an amphibious spherical robot. In Proceedings of the IEEE International Conference on Mechatronics and Automation, Beijing, China, 2–5 August 2015; pp. 848–853. [Google Scholar]
- Li, Y.; Yang, M.; Sun, H.; Liu, Z.; Zhang, Y. A Novel Amphibious Spherical Robot Equipped with Flywheel, Pendulum, and Propeller. J. Intell. Rob. Syst. 2018, 89, 485–501. [Google Scholar] [CrossRef]
- Tadakuma, K.; Tadakuma, R.; Aigo, M.; Shimojo, M.; Higashimori, M.; Kaneko, M. “Omni-Paddle”: Amphibious spherical rotary paddle mechanism. In Proceedings of the IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 5056–5062. [Google Scholar]
- Zhan, Q.; Cai, Y.; Yan, C. Design, analysis and experiments of an omni-directional spherical robot. In Proceedings of the IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 4921–4926. [Google Scholar]
- Cai, Y.; Zhan, Q.; Xi, X. Path tracking control of a spherical mobile robot. Mech. Mach. Theory 2012, 51, 58–73. [Google Scholar] [CrossRef]
- Tupper, E.C. Introduction to Naval Architecture; Butterworth-Heinemann: Jersey City, NJ, USA, 2013. [Google Scholar]
- White, F.M. Fluid Mechanics, 4th ed.; McGraw-Hill Higher Education: Boston, MA, USA, 1998. [Google Scholar]
- Morsi, S.A.; Alexander, A.J. An investigation of particle trajectories in two-phase flow systems. J. Fluid Mech. 1972, 55, 193–208. [Google Scholar] [CrossRef]
- Cheng, C.M.; Fu, C.L. Characteristic of wind loads on a hemispherical dome in smooth flow and turbulent boundary layer flow. J. Wind Eng. Ind. Aerodyn. 2010, 98, 328–344. [Google Scholar] [CrossRef]
- Healey, A.J.; Rock, S.M.; Cody, S.; Miles, D.; Brown, J.P. Toward an improved understanding of thruster dynamics for underwater vehicles. IEEE J. Ocean Eng. 1995, 20, 354–361. [Google Scholar] [CrossRef]





| Items | Parameters |
|---|---|
| Diameter | 350 mm |
| Weight | 5.8 kg |
| Power supply voltage | 24 V |
| Duration time | 1 h |
| Speed (on ground) | 0.6 m/s |
| Speed (on the water) | 0.4 m/s(16 fins) |
| Control signal transmitting distance | 500 m |
| Camera signal transmitting distance | 60 m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chi, X.; Zhan, Q. Design and Modelling of an Amphibious Spherical Robot Attached with Assistant Fins. Appl. Sci. 2021, 11, 3739. https://doi.org/10.3390/app11093739
Chi X, Zhan Q. Design and Modelling of an Amphibious Spherical Robot Attached with Assistant Fins. Applied Sciences. 2021; 11(9):3739. https://doi.org/10.3390/app11093739
Chicago/Turabian StyleChi, Xing, and Qiang Zhan. 2021. "Design and Modelling of an Amphibious Spherical Robot Attached with Assistant Fins" Applied Sciences 11, no. 9: 3739. https://doi.org/10.3390/app11093739
APA StyleChi, X., & Zhan, Q. (2021). Design and Modelling of an Amphibious Spherical Robot Attached with Assistant Fins. Applied Sciences, 11(9), 3739. https://doi.org/10.3390/app11093739






