Fire Performance of Self-Tapping Screws in Tall Mass-Timber Buildings
Abstract
1. Introduction
2. Materials and Methods
2.1. Fasteners
2.2. Wood Products
2.3. Methodology
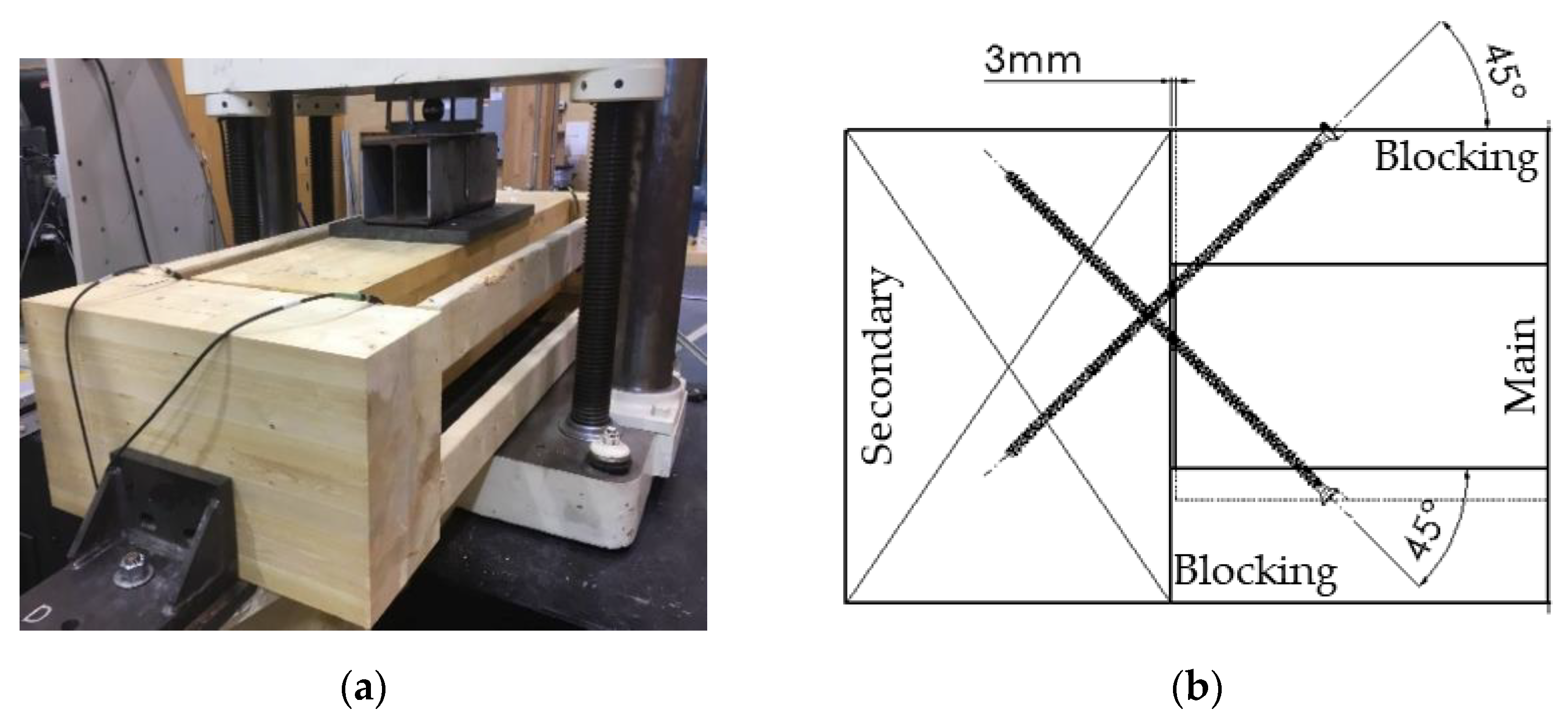
2.3.1. Small-Scale Fire Test
2.3.2. Vertical Load Test
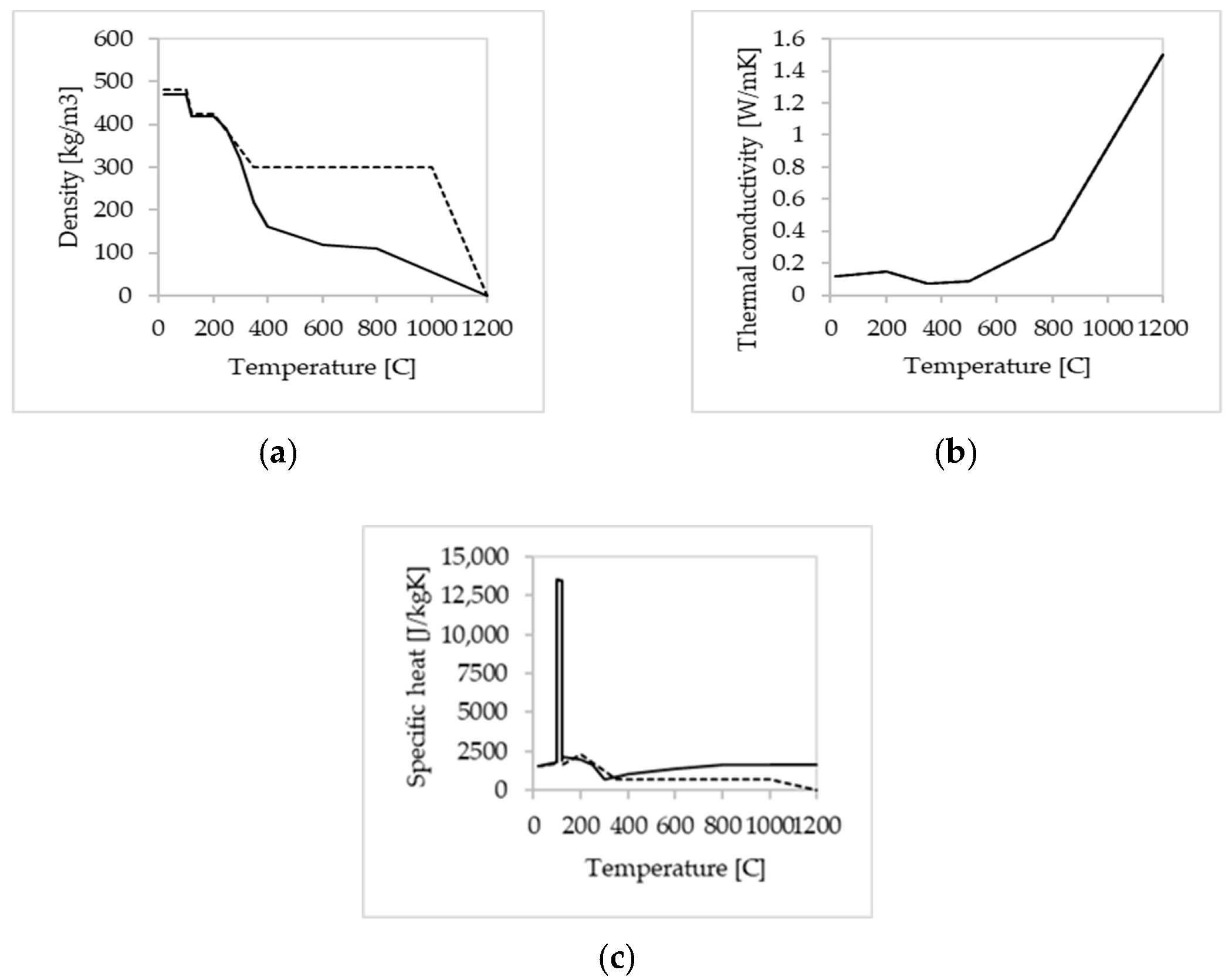
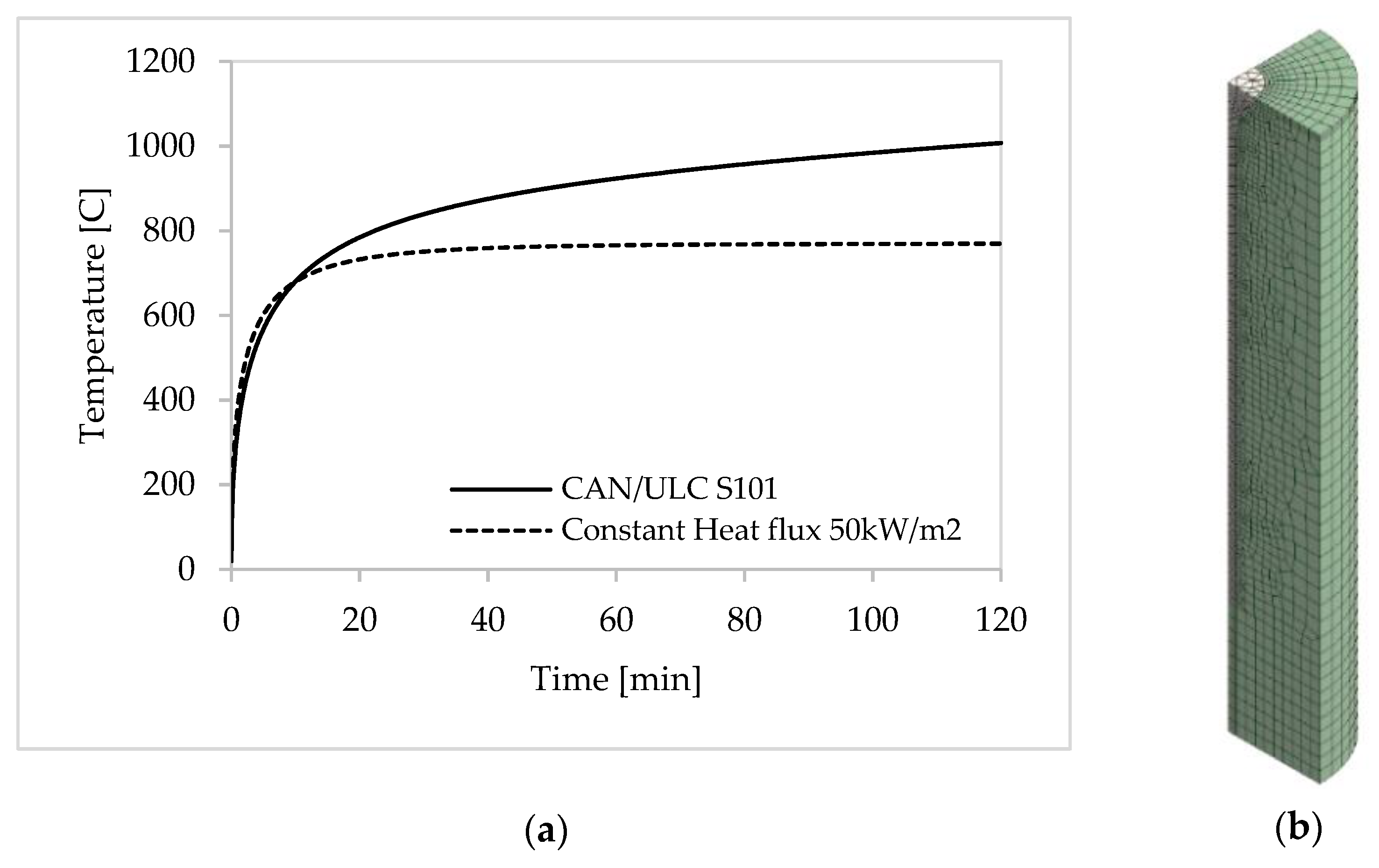
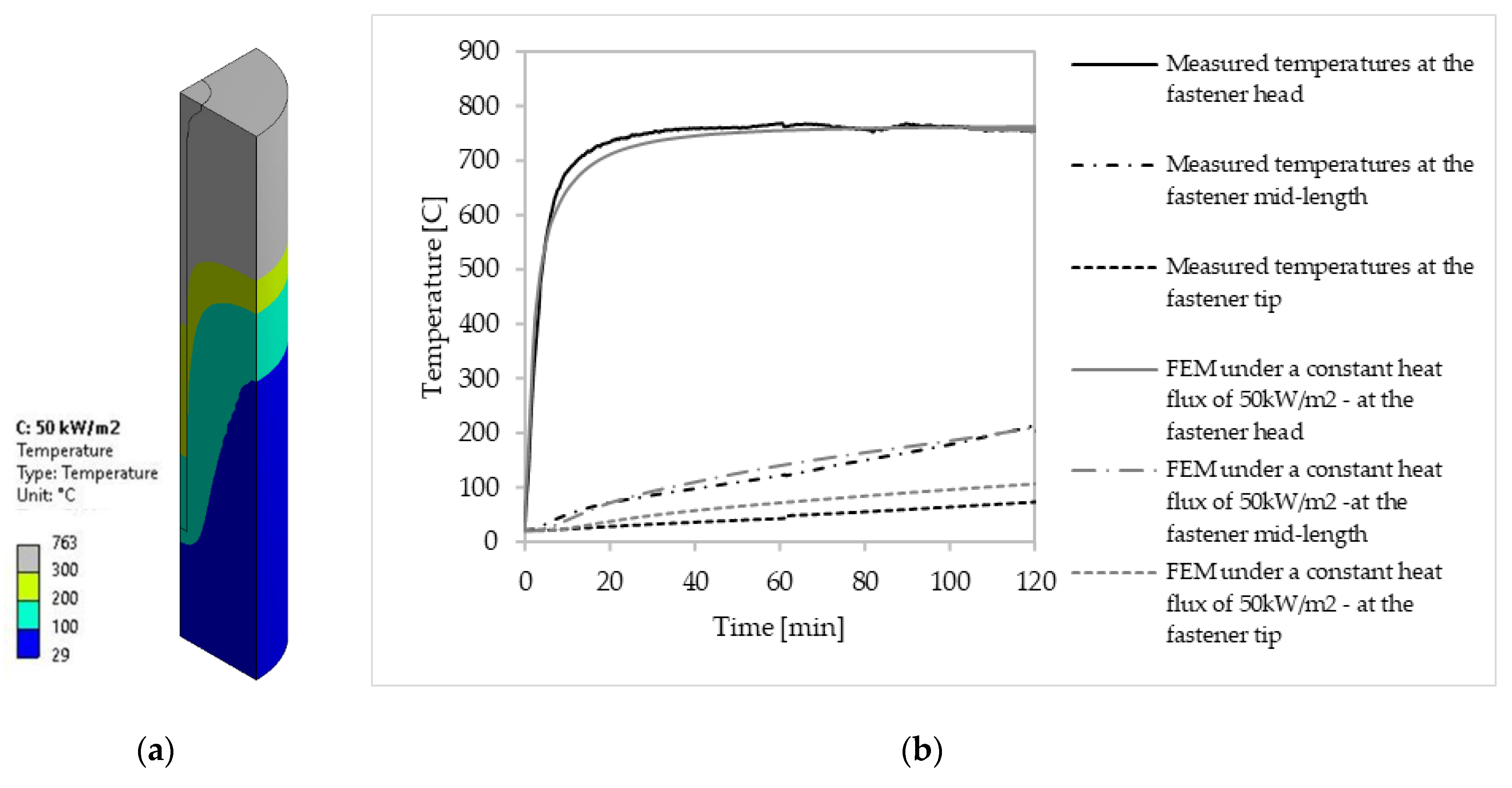
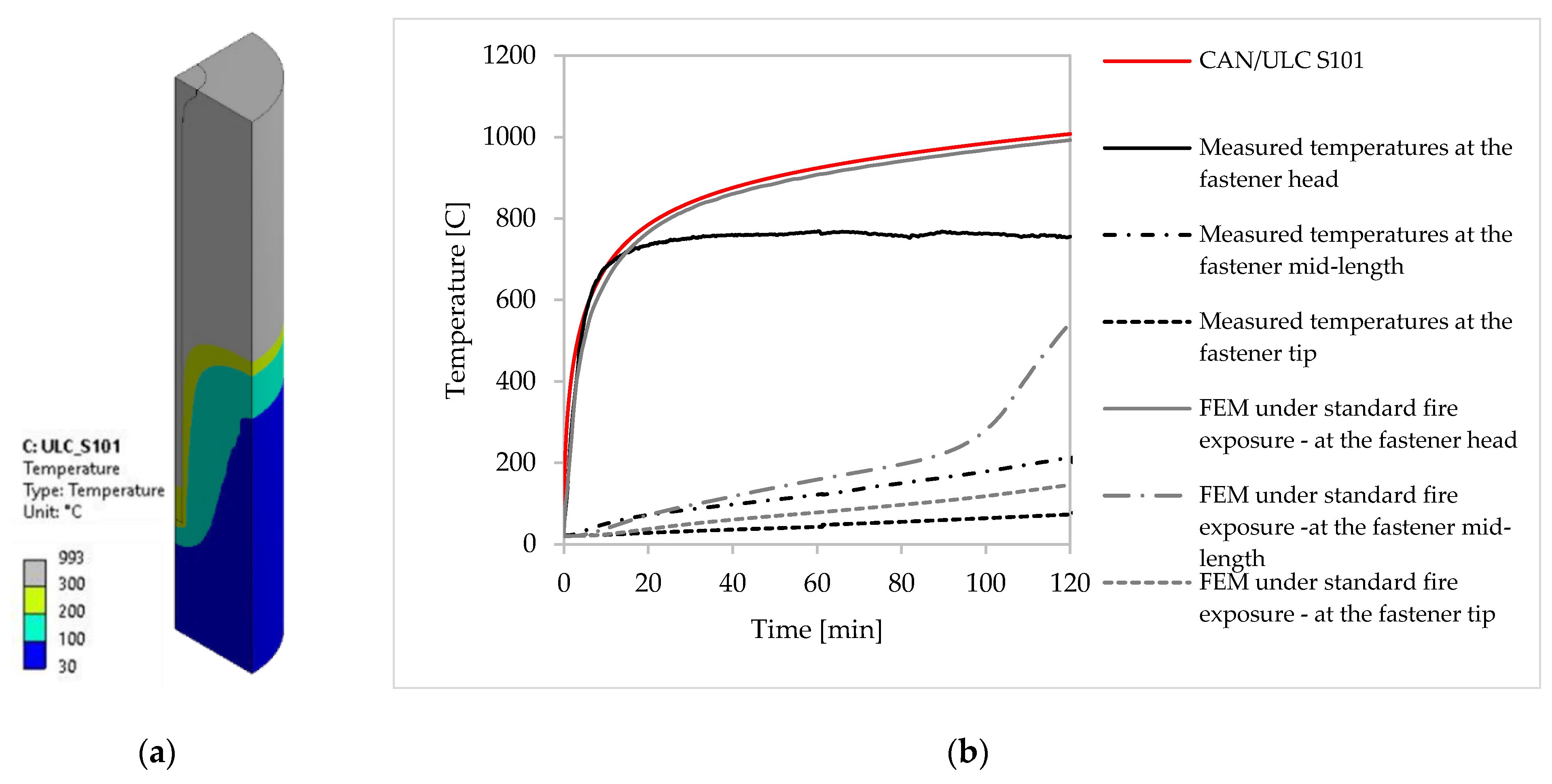
2.3.3. Numerical Modelling
3. Results and Discussion
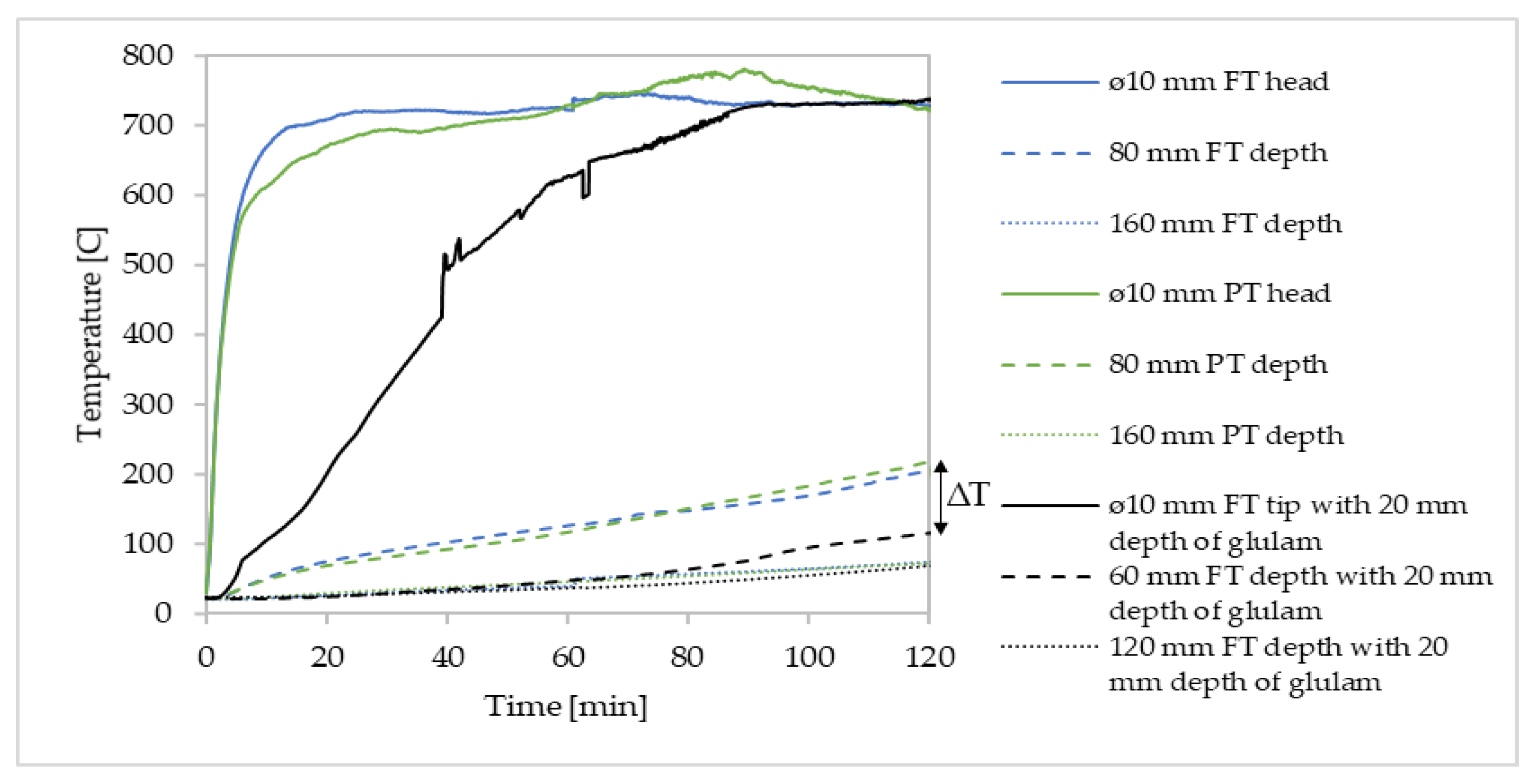
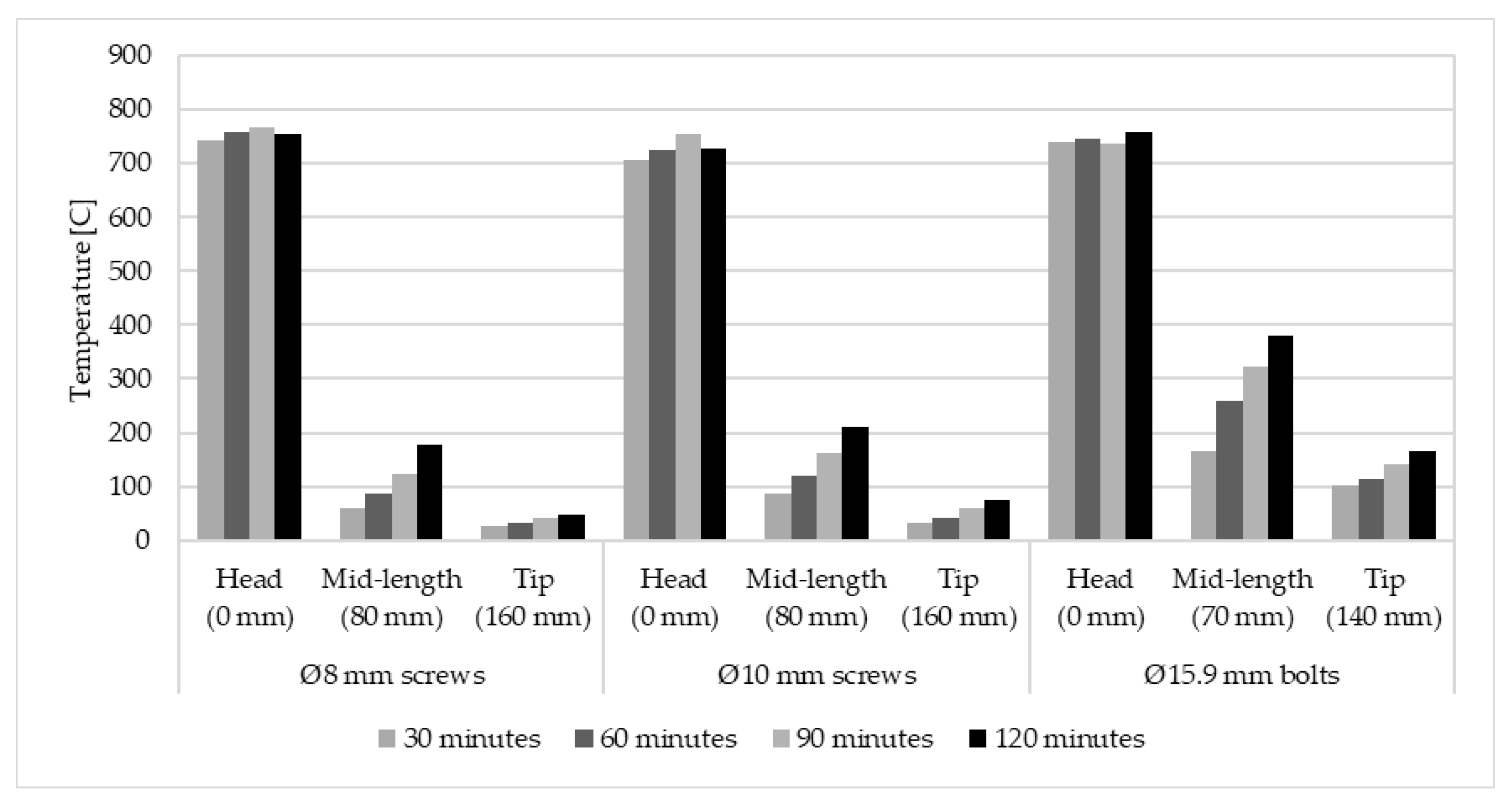
3.1. Effect of Temperature Distribution along the Fasteners
3.2. Effect of Fasteners on the Timber Charring Rate
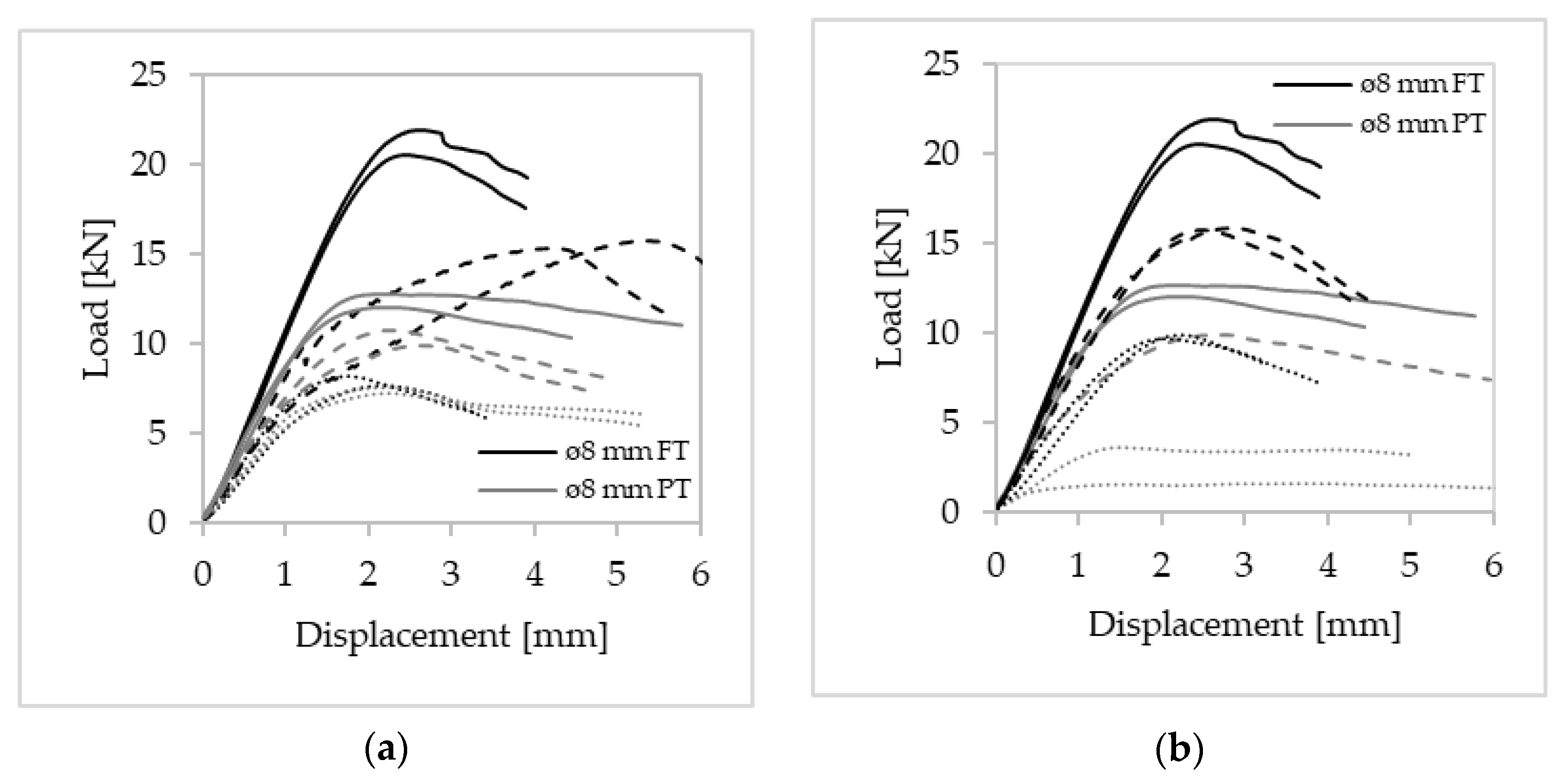
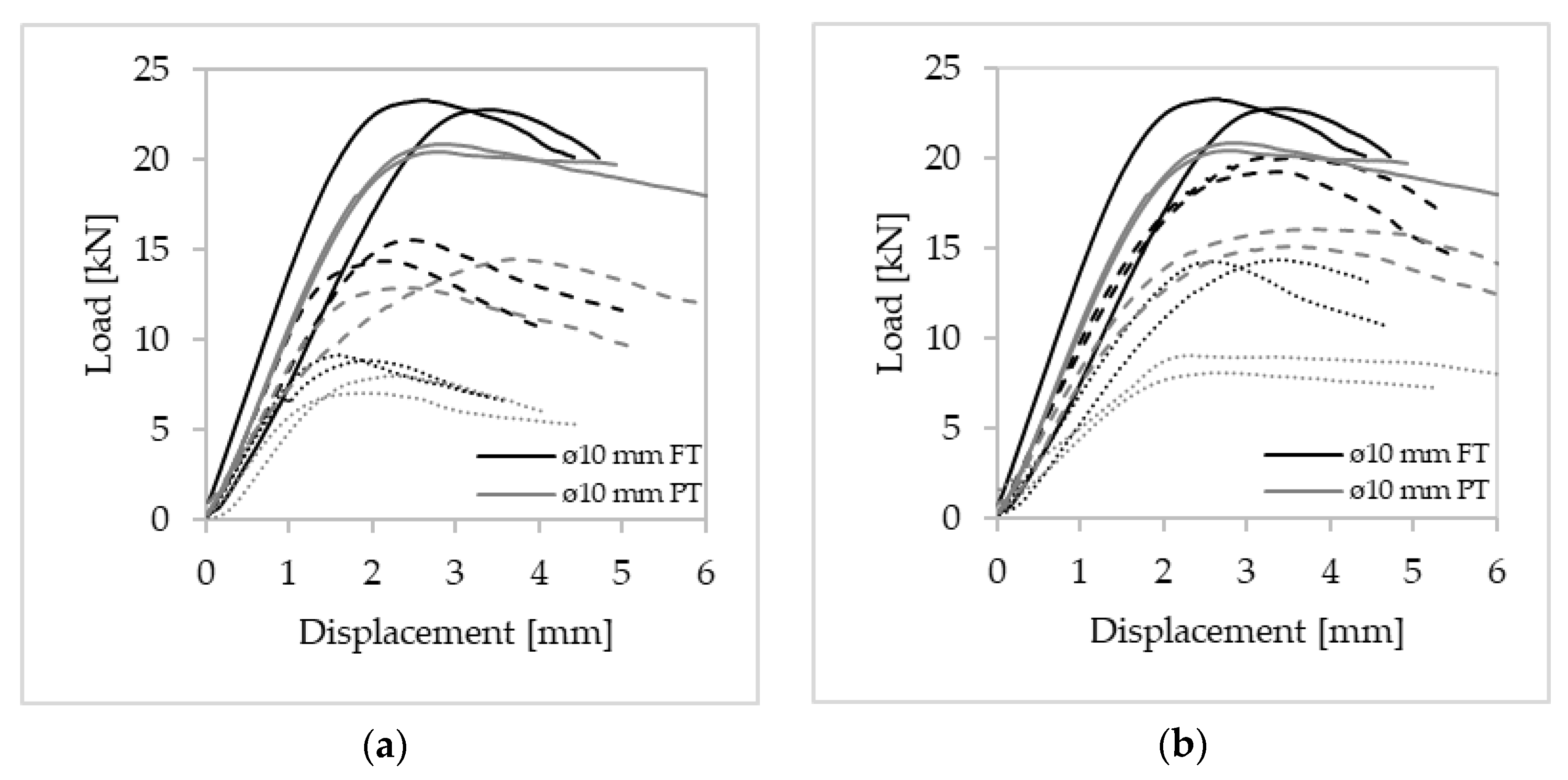
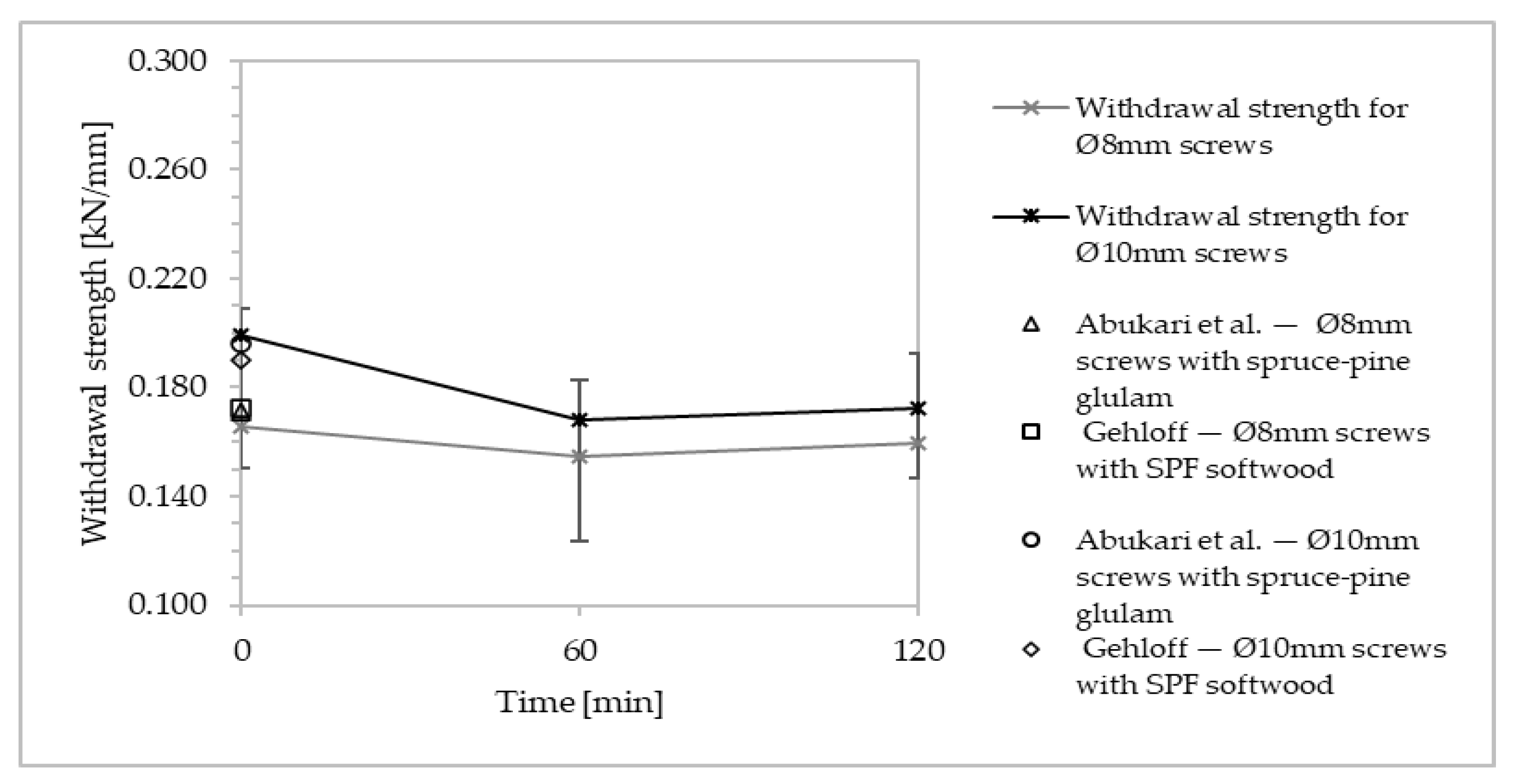
3.3. Effect of the Withdrawal Resistance on Self-Tapping Screws
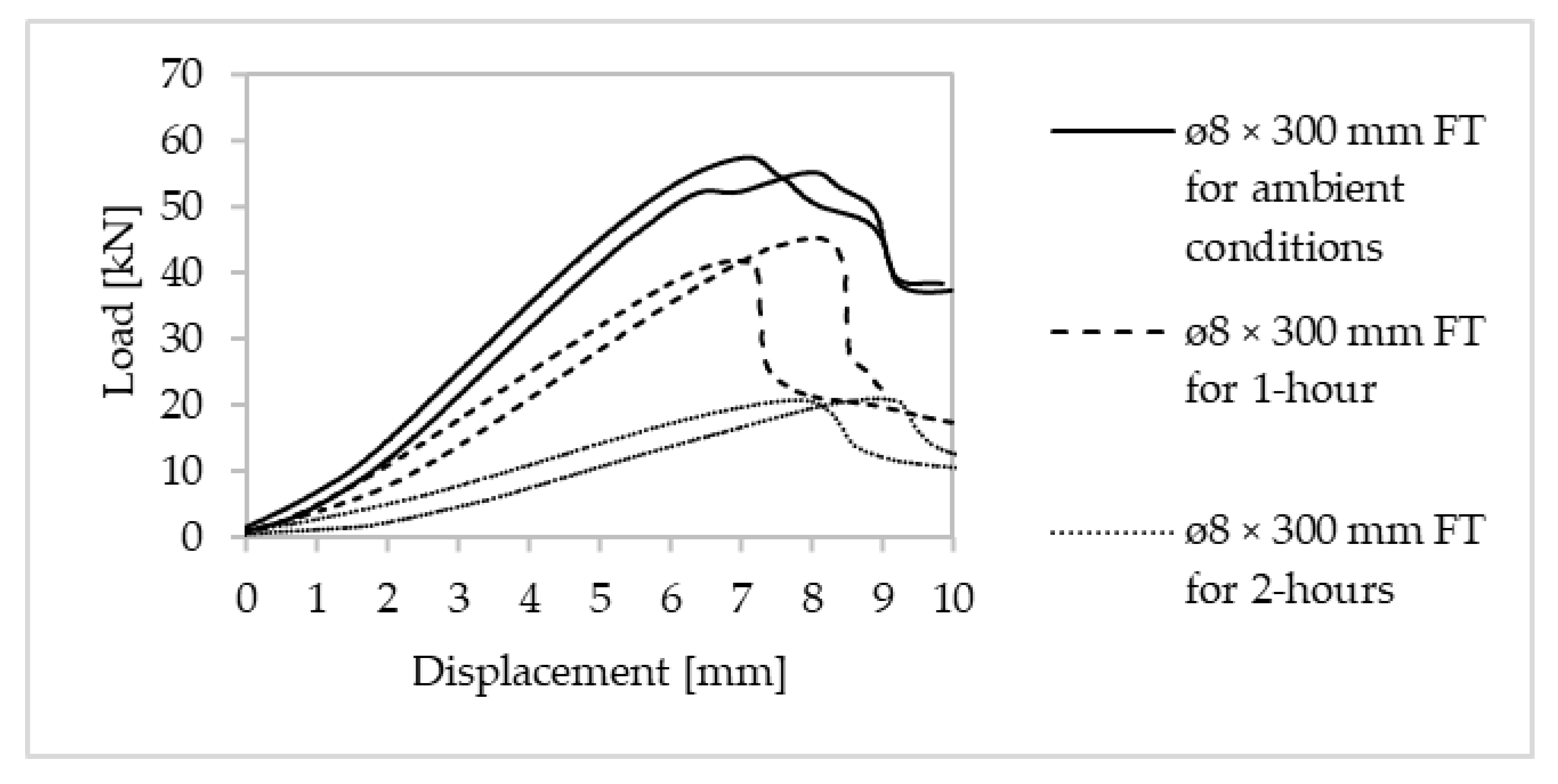
3.4. Effect of the Withdrawal Resistance on Self-Tapping Screws
4. Design Proposal
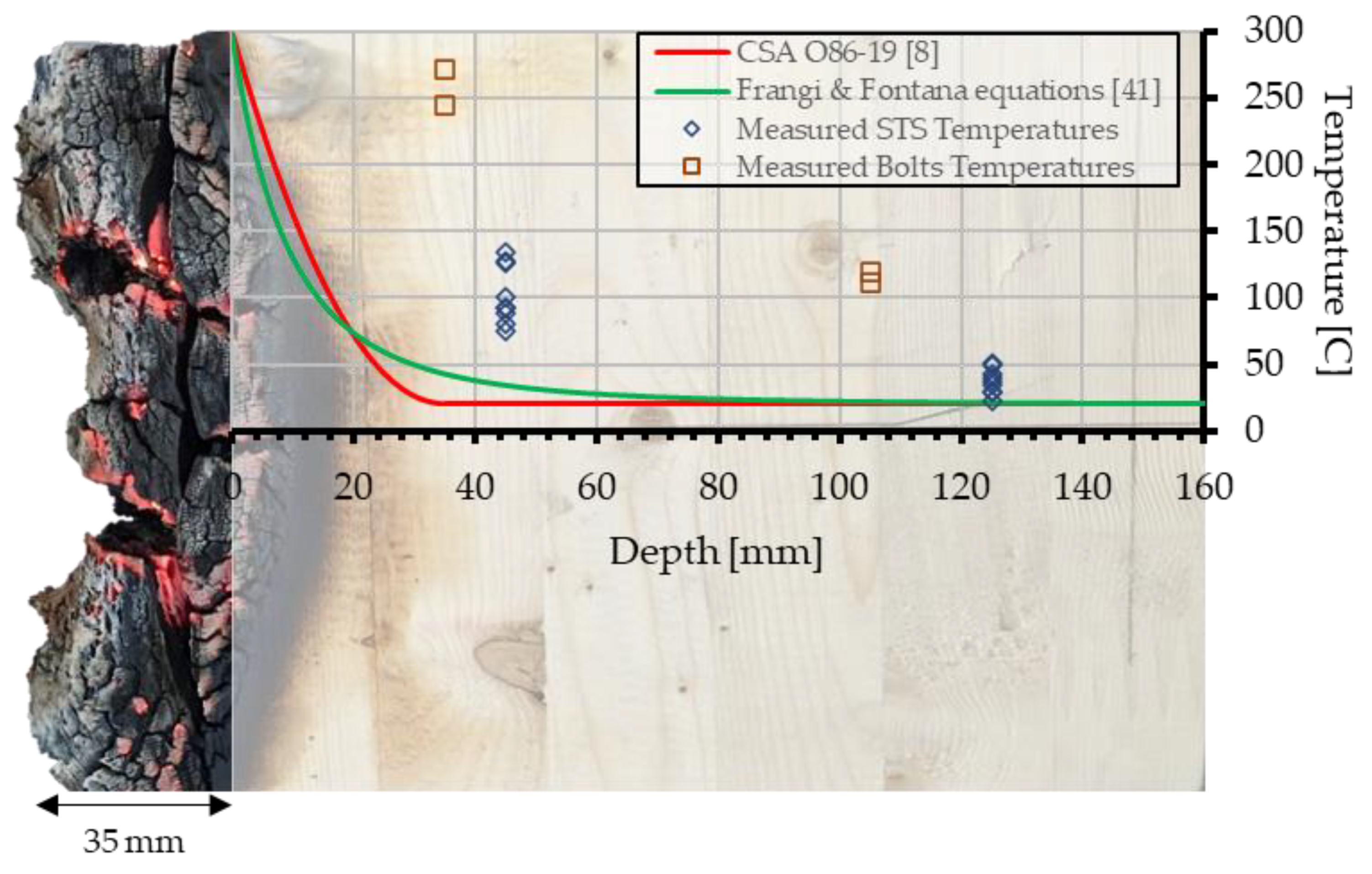
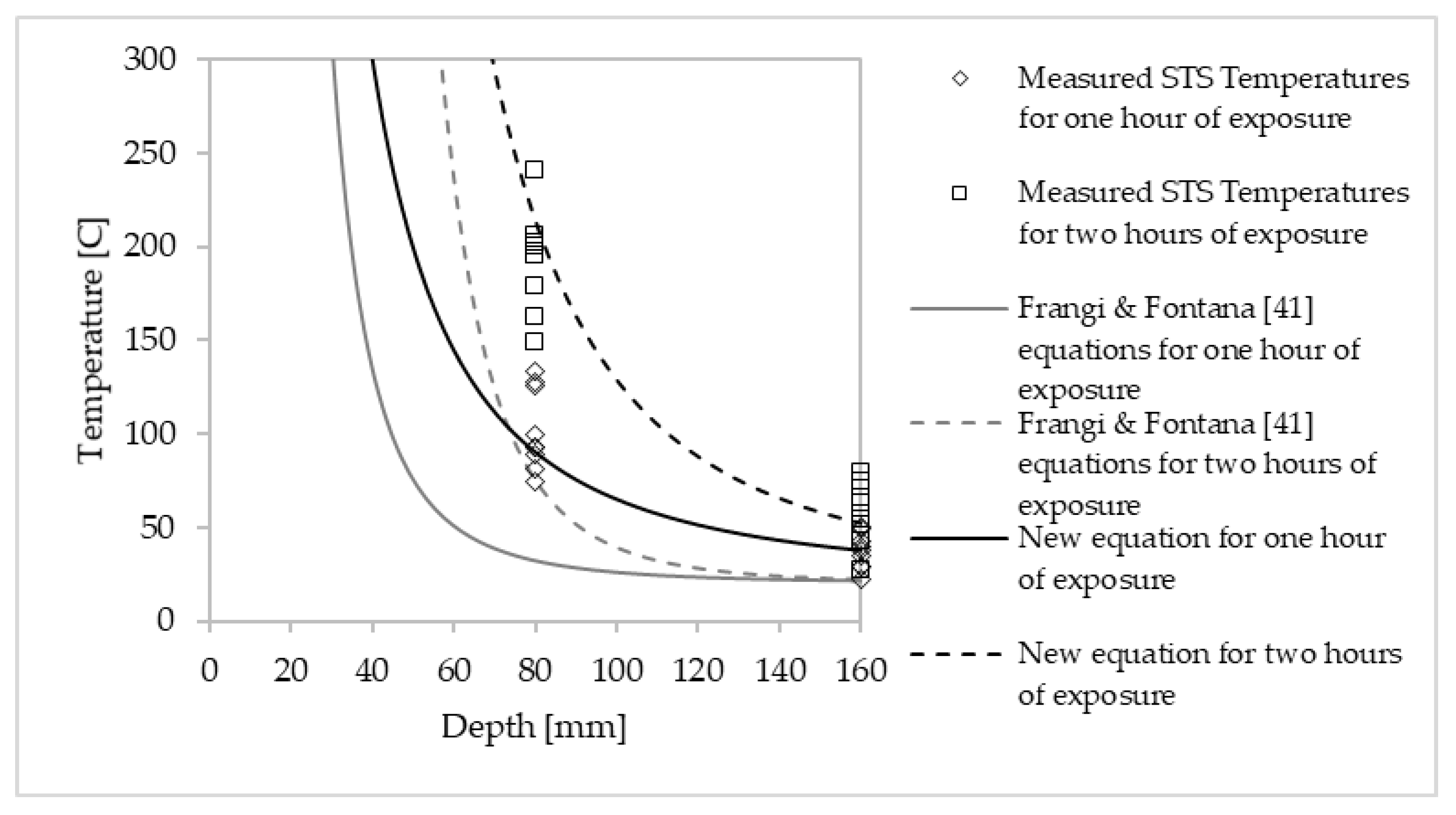
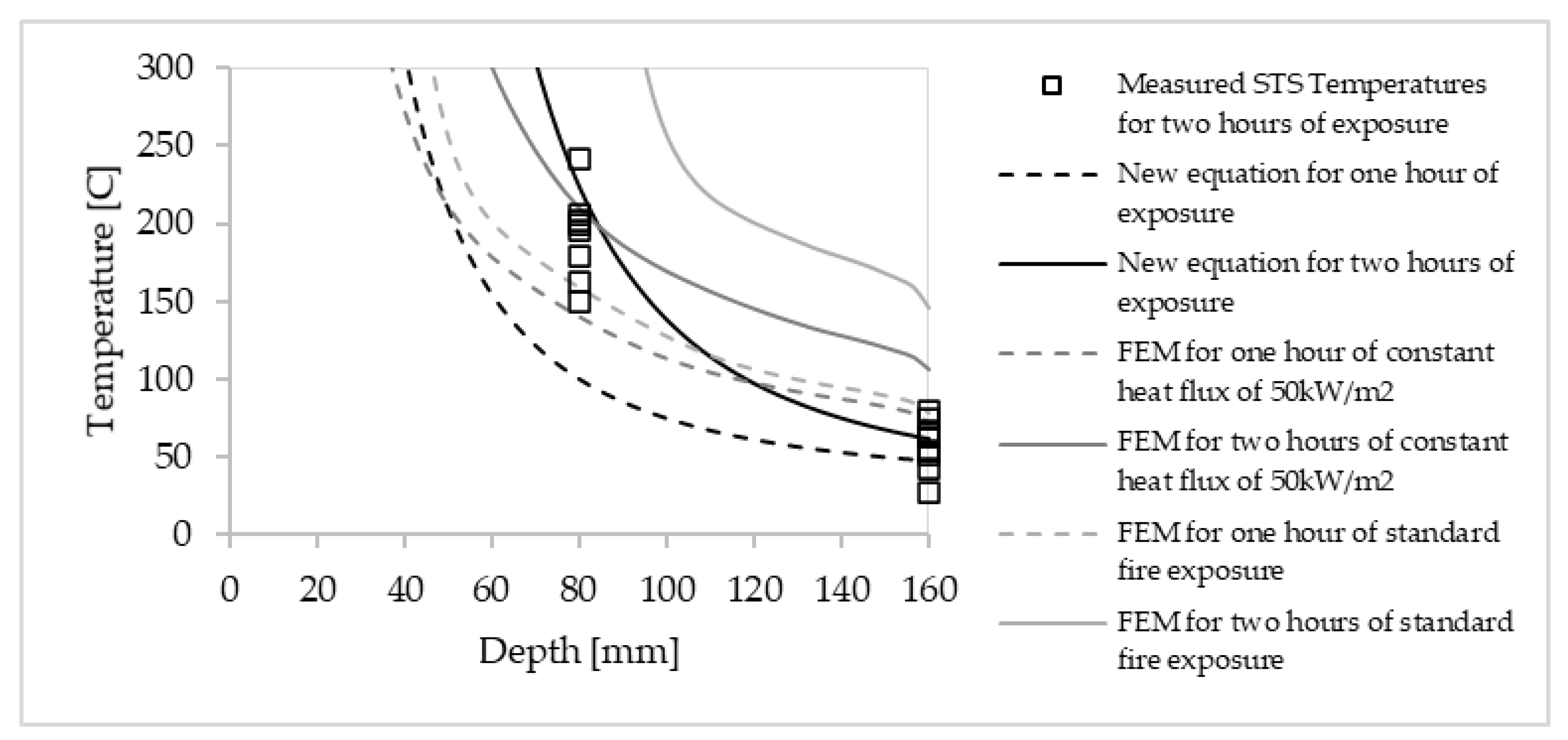
4.1. Charactization of the Heat-Affected Layer
4.2. Verification and Validation from Heat Transfer Modelling
4.3. Determination of the Withdrawal Resistance of Self-Tapping Screws
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Haaland, C.; van den Bosch, C.K. Challenges and strategies for urban green-space planning in cities undergoing densification: A review. Urban For. Urban Green. 2015, 14, 760–771. [Google Scholar] [CrossRef]
- Khorasani, Y. Feasibility Study of Hybrid Wood Steel Structures. Ph.D. Thesis, University of British Columbia, Vancouver, BC, Canada, 2011. [Google Scholar]
- National Research Council Canada. National Building Code of Canada; National Research Council Canada: Ottawa, ON, Canada, 2015. [Google Scholar]
- Buchanan, A.H.; Abu, A.K. Structural Design for Fire Safety, 2nd ed.; John Wiley & Sons Chichester: West Sussex, UK, 2017; p. 415. [Google Scholar]
- ASTM International. E119-20 Standard Test Methods for Fire Tests of Building Construction and Materials; ASTM International: West Conshohocken, PA, USA, 2020. [Google Scholar]
- Underwriters Laboratories of Canada. Standard Method of Fire Endurance Tests of Building Construction Materials (ULC-S101-07); Underwriters Laboratories of Canada: Toronto, ON, Canada, 2007. [Google Scholar]
- International Standard Organization. ISO 834-1: Fire-Resistance Test—Elements of Building Construction—Part 1: General Requirements; International Standard Organization: Geneva, Switzerland, 1999. [Google Scholar]
- Canadian Standards Association. CSA O86-19: Engineering Design in Wood; Canadian Standards Association: Mississauga, ON, Canada, 2019. [Google Scholar]
- International Code Council. 2018 International Building Code; International Code Council: Country Club Hills, IL, USA, 2017. [Google Scholar]
- European Committee for Standardization. CEN, Eurocode 5: Design of Timber Structures—Part 1–2: General—Structural Fire Design; European Committee for Standardization: Brussels, Belgium, 2004. [Google Scholar]
- Australian Building Codes Board. The National Construction Code; Australian Building Codes Board: Victoria, Australia, 2019.
- Barber, D. Determination of fire resistance ratings for glulam connectors within US high rise timber buildings. Fire Saf. J. 2017, 91, 579–585. [Google Scholar] [CrossRef]
- Audebert, M.; Dhima, D.; Bouchaïr, A.; Frangi, A. Review of experimental data for timber connections with dowel-type fasteners under standard fire exposure. Fire Saf. J. 2019, 107, 217–234. [Google Scholar] [CrossRef]
- Maraveas, C.; Miamis, K.; Matthaiou, C.E. Performance of Timber Connections Exposed to Fire: A Review. Fire Technol. 2013, 51, 1401–1432. [Google Scholar] [CrossRef]
- Peng, L.; Hadjisophocleous, G.; Mehaffey, J.; Mohammad, M. Fire Performance of Timber Connections, Part 1: Fire Resistance Tests on Bolted Wood-Steel-Wood and Steel-Wood-Steel Connections. J. Struct. Fire Eng. 2012, 3, 107–132. [Google Scholar] [CrossRef]
- Green, M. TALL WOOD-The Case for Tall Wood Buildings, 2nd ed.; Canadian Wood Council: Ottawa, ON, Canada, 2020. [Google Scholar]
- Salenikovich, A.; Moses, D.; Hong, M. Modern Wood Fasteners, Structural Connections. Struct. Mag. 2020. Available online: https://www.structuremag.org/?p=16285 (accessed on 12 April 2021).
- Hofmann, V.; Gräfe, M.; Werther, N.; Winter, S. Fire resistance of primary beam-secondary beam connections in timber structures. J. Struct. Fire Eng. 2016, 7, 126–141. [Google Scholar] [CrossRef]
- Petrycki, A.R.; Salem, O. (Sam) Structural fire performance of wood-steel-wood bolted connections with and without perpendicular-to-wood grain reinforcement. J. Struct. Fire Eng. 2019. ahead of print. [Google Scholar] [CrossRef]
- Canadian Construction Materials Centre. Evaluation Report CCMC 13677-R SWG Assy VG Plus and SWG ASSY 3.0 Self Tapping Wood Screws; Canadian Construction Materials Centre: Ottawa, ON, Canada, 2013. [Google Scholar]
- ICC Evaluation Service. ESR-3179: SWG ASSY 3.0 Wood Screws; ICC Evaluation Service: Country Club Hills, IL, USA, 2015. [Google Scholar]
- ETA. ETA 11/0190: Self-Tapping Screws for Use in Timber Constructions; Deutsches Institut für Bautechnik: Berlin, Germany, 2018. [Google Scholar]
- European Committee for Standardization. CEN, Eurocode 5: Design of Steel Structures, Part 1-1: General Rules and Rules for Buildings; European Committee for Standardization: Brussels, Belgium, 2004. [Google Scholar]
- Abukari, M.H. The Performance of Structural Screws in Canadian Glulam. Master’s Thesis, McGill University, Montreal, QC, Canada, 2012. [Google Scholar]
- Guo, J.; Shu, Z. Theoretical Evaluation of Moment Resistance for Bolted Timber Connections. MATEC Web Conf. 2019, 303, 03003. [Google Scholar] [CrossRef]
- Canadian Standards Association. CSA 0122-16 Structural Glued-Laminated Timber; Canadian Standards Association: Mississauga, ON, Canada, 2016. [Google Scholar]
- Canadian Standards Association. CSA O177-06 Qualification Code for Manufacturers of Structural Glued-Laminated Timber; Canadian Standards Association: Mississauga, ON, Canada, 2015. [Google Scholar]
- ASTM International. D1761-20 Standard Test Methods for Mechanical Fasteners in Wood and Wood-Based Materials; ASTM International: West Conshohocken, PA, USA, 2020. [Google Scholar]
- MTC Solutions. Structural Screw Design Guide. Available online: https://mtcsolutions.com/resource/structural-screw-design-guide/ (accessed on 25 February 2021).
- ASTM International. D7147-11(2018) Standard Specification for Testing and Establishing Allowable Loads of Joist Hangers; ASTM International: West Conshohocken, PA, USA, 2018. [Google Scholar]
- European Committee for Standardization. CEN, Eurocode 1: Actions on Structures—Part 1-2: General Actions—Actions on Structures Exposed to Fire; European Committee for Standardization: Brussels, Belgium, 2002. [Google Scholar]
- König, J.; Walleij, L. One-Dimensional Charring of Timber Exposed to Standard and Parametric Fires in Initially Unprotected and Postprotection Situations (Rapport I 9908029); Swedish Institute for Wood Technology Research: Stockholm, Sweden, 1999. [Google Scholar]
- European Committee for Standardization. CEN, Eurocode 3: Design of Steel Structures—Part 1-2: General—Structural Fire Design; European Committee for Standardization: Brussels, Belgium, 2005. [Google Scholar]
- Sultan, M.A. Incident heat flux measurements in floor and wall furnaces of different sizes. Fire Mater. 2006, 30, 383–396. [Google Scholar] [CrossRef][Green Version]
- Dagenais, C. Assessing the Fire Integrity Performance of Cross-Laminated Timber Floor Panel-to-Panel Joints. Ph.D. Thesis, Carleton University, Ottawa, ON, USA, 2016. [Google Scholar]
- Werther, N.; O’Neil, J.W.; Spellman, P.M.; Abu, A.K.; Moss, P.J.; Buchanan, A.H.; Winter, S. Parametric Study of Modelling Structural Timber in Fire with Different Software Packages. In Proceedings of the 7th International Conference on Structures in Fire, Zurich, Switzerland, 6–8 June 2012. [Google Scholar]
- Outinen, J.; Mäkeläinen, P. Mechanical properties of structural steel at elevated temperatures and after cooling down. Fire Mater. 2004, 28, 237–251. [Google Scholar] [CrossRef]
- Owusu, A. Fire Performance of Concealed Timber Connections with Varying Bolt Patterns. Master’s Thesis, Carleton University, Ottawa, ON, Canada, 2019. [Google Scholar]
- White, R.H.; Tran, H.C. Charring rate of wood exposed to a constant heat flux. Wood and fire safety. In Proceedings of the 3rd International Scientific Conference, The High Tatras, Slovak Republic, 6–9 May 1996; pp. 175–183. [Google Scholar]
- Yang, T.H.; Wang, S.Y.; Tsai, M.J.; Lin, C.Y. The charring depth and charring rate of glued laminated timber after a standard fire exposure test. Build. Environ. 2009, 44, 231–236. [Google Scholar] [CrossRef]
- Frangi, A.; Fontana, M. Charring rates and temperature profiles of wood sections. Fire Mater. 2003, 27, 91–102. [Google Scholar] [CrossRef]
- König, J. Structural fire design according to Eurocode 5: Design rules and their background. Fire Mater. 2005, 29, 147–163. [Google Scholar] [CrossRef]
- Gehloff, M. Pull-Out Resistance of Self-Tapping Wood Screws. Master’s Thesis, University of British Columbia, Vancouver, BC, USA, 2011. [Google Scholar]
- Robitaille, D.; (MTC Solutions, Montreal, QC, Canada). Personal communication, 2021.
- Pauli, J. The Behaviour of Steel Columns in Fire: Material-Cross-sectional Capacity-Column Buckling. IBK Ber. 2012, 343. [Google Scholar] [CrossRef]
- Kodur, V.; Dwaikat, M.; Fike, R. High-Temperature Properties of Steel for Fire Resistance Modeling of Structures. J. Mater. Civ. Eng. 2010, 22, 423–434. [Google Scholar] [CrossRef]
- Erchinger, C.; Frangi, A.; Fontana, M. Fire design of steel-to-timber dowelled connections. Eng. Struct. 2010, 32, 580–589. [Google Scholar] [CrossRef]
- Yang, T.H.; Wang, S.Y.; Tsai, M.J.; Lin, C.Y. Temperature distribution within glued laminated timber during a standard fire exposure test. Mater. Des. 2009, 30, 518–525. [Google Scholar] [CrossRef]
- Janssens, M.L.; White, R.H. Short communication: Temperature profiles in wood members exposed to fire. Fire Mater. 1994, 18, 263–265. [Google Scholar] [CrossRef]
- Aseeva, R.; Serkov, B.; Sivenkov, A. Fire Behavior and Fire Protection in Timber Buildings; Springer: New York, NY, USA, 2013. [Google Scholar]
- Norén, J. Load-bearing Capacity of Nailed Joints Exposed to Fire. Fire Mater. 1996, 20, 133–143. [Google Scholar] [CrossRef]




| Partial-(PT) or Full-Thread (FT) | Outside Thread Diameter (dF) (mm) | Shank Diameter (dmin) (mm) | Length (L)/Threaded Length (LF) (mm) | Penetration with Exposed Head (H) and with the Exposed Tip (T) (mm) |
|---|---|---|---|---|
| PT | 8 | 5 | 160/80 | 160 (H) |
| 120 (T) | ||||
| 10 | 6.3 | 160/100 | 160 (H) | |
| 120 (T) | ||||
| FT | 8 | 5 | 160/143 | 160 (H) |
| 120 (T) | ||||
| 10 | 6.2 | 160/145 | 160 (H) | |
| 120 (T) | ||||
| FT 1 | 8 | - | 300/283 | 300/230/171 |
| Fastener Head Diameter (dF) (mm) | Shank Diameter (dmin) (mm) | Length (L)/Threaded Length (LF) (mm) | Lead Hole Diameter (mm) | Penetration (mm) |
|---|---|---|---|---|
| 23.8 | 15.9 | 140/38 | 16.8 | 150 |
| Time Exposure | Fasteners | Exposed Side | Charring Depth | Charring Rate | ||
|---|---|---|---|---|---|---|
| Charred Layer (mm) | Local Charred (mm) | Charred Layer (mm/min) | Local Charred (mm/min) | |||
| One hour | Ø8 mm screws | Head | 34 | 18 | 0.57 | 0.30 |
| Tip | 28 | - | 0.46 | - | ||
| Ø10 mm screws | Head | 36 | 22 | 0.60 | 0.36 | |
| Tip | 28 | - | 0.47 | - | ||
| Two hours | Ø8 mm screws | Head | 62 | 21 | 0.52 | 0.18 |
| Tip | 61 | 17 | 0.51 | 0.14 | ||
| Ø10 mm screws | Head | 61 | 28 | 0.51 | 0.23 | |
| Tip | 57 | 13 | 0.42 | 0.11 | ||
| Ø15.9 mm bolts | Head | 74 | 140 | 0.62 | 1.17 | |
| Fastener Type | Withdrawal Resistance | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Ambient Conditions | Head Exposed | Tip Exposed | ||||||||
| One Hour of Exposure | Two Hours of Exposure | One Hour of Exposure | Two Hours of Exposure | |||||||
| Max Load (kN) | CoV | Max Load (kN) | CoV | Max Load (kN) | CoV | Max Load (kN) | CoV | Max Load (kN) | CoV | |
| Ø8 × 160 mm FT | 21.2 | 4.6% | 15.3 | 0.3% | 7.93 | 4.7% | 15.8 | 0.7% | 9.81 | 0.9% |
| Ø10 × 160 mm FT | 23.0 | 1.6% | 14.9 | 5.5% | 9.03 | 3.1% | 19.7 | 2.8% | 14.3 | 0.7% |
| Ø8 × 160 mm PT | 12.4 | 4.0% | 10.3 | 6.4% | 7.39 | 3.5% | 10.0 | 0.5% | 3.61 | - |
| Ø10 × 160 mm PT | 20.7 | 1.7% | 13.7 | 7.8% | 7.54 | 9.2% | 15.6 | 4.1% | 8.59 | 8.2% |
| Fastener Type | Load-Carrying Capacity | |||||
|---|---|---|---|---|---|---|
| Ambient Conditions | One Hour of Exposure | Two Hours of Exposure | ||||
| Max Load (kN) | CoV | Max Load (kN) | CoV | Max Load (kN) | CoV | |
| Ø8 × 300 mm FT | 56.3 | 2.8% | 43.6 | 5.7% | 20.8 | 0.7% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Létourneau-Gagnon, M.; Dagenais, C.; Blanchet, P. Fire Performance of Self-Tapping Screws in Tall Mass-Timber Buildings. Appl. Sci. 2021, 11, 3579. https://doi.org/10.3390/app11083579
Létourneau-Gagnon M, Dagenais C, Blanchet P. Fire Performance of Self-Tapping Screws in Tall Mass-Timber Buildings. Applied Sciences. 2021; 11(8):3579. https://doi.org/10.3390/app11083579
Chicago/Turabian StyleLétourneau-Gagnon, Mathieu, Christian Dagenais, and Pierre Blanchet. 2021. "Fire Performance of Self-Tapping Screws in Tall Mass-Timber Buildings" Applied Sciences 11, no. 8: 3579. https://doi.org/10.3390/app11083579
APA StyleLétourneau-Gagnon, M., Dagenais, C., & Blanchet, P. (2021). Fire Performance of Self-Tapping Screws in Tall Mass-Timber Buildings. Applied Sciences, 11(8), 3579. https://doi.org/10.3390/app11083579







