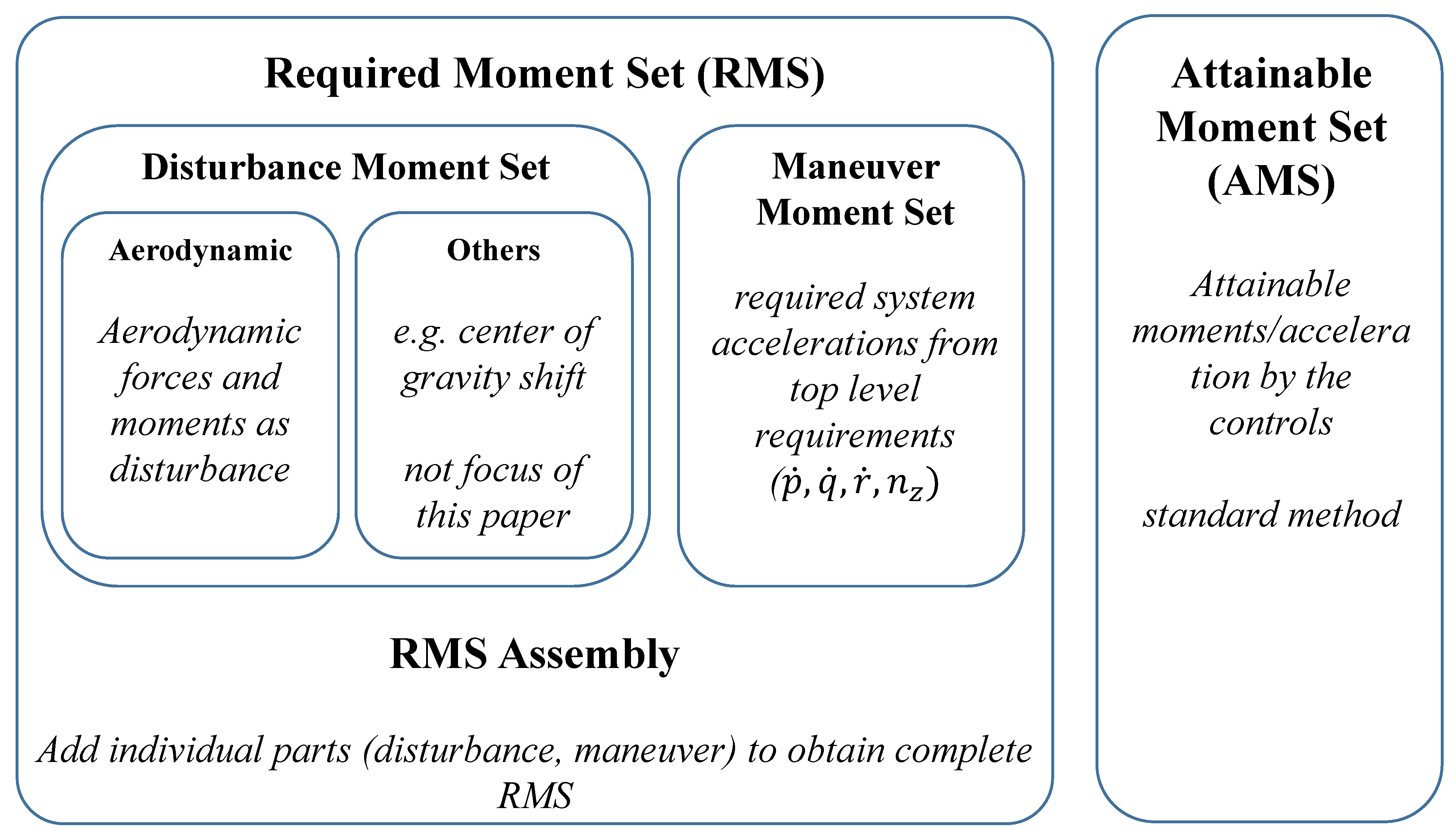
2.1. Separation Into Individual Required Control Subsets
In order to calculate the required moment set in a structured manner and in order to perform the proposed RMS-based controllability assessment in a traceable manner, the required forces and moments are split into individual subsets. We call the first part the disturbance part, which constitutes the required propulsive forces and moments that are required to counter disturbances. This paper focuses on the aerodynamic disturbance, as in hover mode the aerodynamic forces and moments have to be compensated for via the propulsive system and are not part of the flight control as they are for wingborne mode.
In order to determine the maximum possible aerodynamic disturbance that can act during the operation, the aircraft is first trimmed at the boundary points of the aerodynamic velocity envelope, as there the aerodynamic disturbance obtains the highest magnitudes. In all possible trimmed directions of flight, multiple attitude deviations from the trim points are used to evaluate aerodynamic forces and moments. With this approach we obtain a realistic set of possible aerodynamic forces and moments that need to be countered by the propulsive system.
For the sake of simplicity the calculation process and moment set approach include a configuration with a fixed direction of hover thrust (no tilt configuration); for this reason, the required moment set is defined by the three roll, pitch and yaw moments () or corresponding angular accelerations () and the total aircraft thrust in the body z-direction T or the corresponding body z load factor .
Figure 1 shows an overview of the different parts of the required moment set that is used throughout this paper. Besides countering aerodynamic disturbance, the propulsive system also needs to provide the desired maneuverability. The corresponding desired quantities are attainable accelerations (angular and translational), which from a kinematic point of view and provide sufficient dynamics for fulfilling higher level mission requirements. We use the angular body accelerations (
) and the inertial translational acceleration in the body z direction
as direct requirements. These acceleration limits again define a convex set (e.g., a four dimensional cube).
In order to sum up the disturbance and maneuverability parts of the required forces/ moments, we use query directions in the four-dimensional set space and find the cross sections with the convex hull of the corresponding sets. This procedure simplifies the summation process of disturbance and maneuverability sets, which finally yields the full set of required forces/moments.
In order to finally assess the controllability, the attainable and required control sets need to be compared. To evaluate this, first the AMS is calculated by applying all possible combinations of minimum or maximum propulsive inputs and assembling them in a convex set [
7,
8]. In a second step, the convex set intersections in the direction of the query directions are determined. Afterwards, attainable and required forces/moments are available in the same query directions and can be directly compared to assess the controllability margins and to identify critical directions/channels.
2.2. Underlying Aircraft Simulation Model
The use of a simulation model-based assessment can be applied already in early aircraft design and can help lower development costs. One of the main applications of aircraft simulation models is model-based control design as in [
9,
10]. In order to guarantee a close match to the real aircraft system, identification can be used to improve the accuracy of the models [
11,
12].
To demonstrate the RMS approach with the methods of this paper, a simulation model of a lift and cruise multirotor UAV is used. As the methods used in this paper do not require time simulation, this section only shows the force and moment balance parts of the equations of motion. The translational and rotational equations of motion read [
13].
where
denote the three velocity components,
K the kinematic nature,
G the center of gravity, the index
the inertial acceleration,
m the vehicle mass,
and
forces and moments due to aerodynamics
A or propulsion
P. The inertia around the center of gravity in the body frame is denoted with
.
In order to provide an aerodynamic model for flow from all possible directions, a multi-compartment aerodynamic model comparable to [
14] is used. Assembling all forces and moments in the center of gravity then yields
where
denotes the wing reference area,
s the wing span,
the chord,
the magnitude of the true airspeed and
the force/moment coefficients. The dependency of the coefficients with respect to the aerodynamic angle of attack
and angle of sideslip
are realized with lookup tables [
15].
The multirotor propulsion system is modeled independent of the aerodynamics; propulsion airframe interactions are neglected. For each propulsive unit, the propeller forces and moments are modelled as linear in the squares of the angular rates [
16,
17]
where
denotes the thrust of the
ith propeller,
the corresponding torque around the corresponding rotational axis,
the rotational rate in rad/s and
D the propeller diameter. As the aircraft only has propellers of the same type the thrust coefficient
and the torque coefficient
are the same for all propellers.
2.3. Trim-Based Calculation of Aerodynamic Disturbance Set
Now that an aircraft model is established, a very important next objective of this paper is to establish means to calculate different parts of required control sets. This section explains the proposed method of calculating the worst case aerodynamic disturbance throughout the aircraft mission.
The presented analysis is carried out for a given altitude
h and density of the atmosphere
. At this point the aircraft is required to be able to fly up to certain kinematic speeds in various directions. A convenient frame to describe the three-dimensional velocities is the control frame C as it is indifferent to the heading
but includes the down direction [
18].
Figure 2 shows the axes of the C-frame.
Besides the kinematic speed requirement, there can also be requirements for environmental conditions such as wind speeds. Combining both requirements yields a total airspeed envelope that the vehicle must be able to cover. For the sake of simplicity let us assume a cuboidal envelope of the shape
with
denoting the components of the aerodynamic velocity given in the C frame
.
For all points within this airspeed envelope the aircraft must be able to obtain steady state operation. In order for the aircraft to be in steady state attitude, the body rates (
) and the corresponding accelerations (
) need to be zero. The translational motion of the aircraft is then defined by the velocity point in the envelope
. The total hover thrust of the aircraft
T tilted by the attitude (
) needs to offset the aerodynamic and gravitational forces in order to reach no translational acceleration and steady state velocities in the C frame. For the sake of simplicity it is assumed that the hover thrust direction coincides with the negative body z direction which yields the force trim balance equation
Note that for applying this method an aerodynamic model defining
over the full envelope of angles of attack and angles of sideslip is required. As these models are nonlinear, Equation (
10) needs to be solved numerically, e.g., via Matlab’s fsolve() [
19] or more aircraft tailored trim solutions [
20].
In order to determine the maximum possible aerodynamic disturbance hull, only the boundary of the aerodynamic velocity envelope is considered, as the dynamic pressure and therefore also possible disturbance forces/moments reach their highest values here, see
Figure 3. As individual points are required for the moment set and assembly to a convex hull, we selected a number of query points that represents our envelope boundary. Unlike for simplified approaches when calculating an AMS where the number of set points is finite, for this nonlinear aerodynamic disturbance set the number of points can be chosen to be arbitrarily large. Higher resolution in the query points on the envelope boundary will increase the accuracy of the obtained RMS but also increase the amount of points that need to be analyzed. The later Results section will show the results for different chosen resolutions of the RMS.
As the mission hover envelope in most cases follows simple geometrical shapes (e.g., cuboid or ellipsoid) in the control frame, the points can be chosen as linearly spaced on the boundary. Let
denote the number of representative points on the boundary of the airspeed envelope.
Figure 3 shows exemplary representative query points in 2D for an ellipsoidal required aerodynamic velocity envelope.
As the operation of the aircraft is considered around a steady trim state and during the transition from one trim state to another trim state, the aircraft is trimmed at all
query points using Equation (
10). The aerodynamic forces and moments in these trim points already constitute one part of the disturbance moment set. However, as we are also interested in transitions/maneuvers from one trim state to another (e.g., acceleration or deceleration in the lateral direction), the disturbance for these maneuvers is calculated as well.
In order to account for these maneuvers, we assume that, at each trim point, the attitude of the aircraft can vary from the trim point while the airspeed is kept constant. In order to model the transition phases and the obtained aerodynamic inflow angles realistically without being too conservative, a range of attitude deviation from the trim point obtainable via maneuvers is determined. For this, minimum and maximum allowed attitude angles for maneuvers can be derived from system requirements. Additionally, an overshoot over the trim pitch/roll angles is allowed in order to make the disturbances more realistic.
Figure 4 shows the idea of the attitude variation for an exemplary 2D model. In the range of the minimum and maximum pitch and roll angles, different attitude deviations/combinations from the trim point are calculated. The allowed attitude region follows
As for the query points on the boundary of the velocity envelope, query points in the bounded --plane are used to obtain set points for various inflow angles during maneuvers from one trim state to another. Let denote the total number of points in the attitude plane. Note that the maneuver disturbance here follows from attitude deviations and body rates are neglected for the sake of reducing computational complexity.
The corresponding required moments to counter the disturbances follow by evaluating the aerodynamic model at the
query attitude points with the query inflow
where the index
D denotes the disturbance part. The requirement for the total propulsive thrust to compensate for the disturbances depends on the desired behavior during the maneuver. We considered transitions in the horizontal plane, as these transitions change the attitude/inflow angles, and therefore there will be arbitrary accelerations depending on the attitude in the horizontal direction. In the vertical direction, however, the propulsive system needs to counter the disturbance (e.g., negative lift of the wing when hovering forward with negative pitch angle). This requires a total zero force in the z direction of the control frame. Transforming the force balance Equation (
10) into the C frame and taking the z component yields
Solving for the thrust leads to
In order to have a more scale-free and kinematic judgment of the controllability configuration we transform the forces/moments to resulting accelerations and assemble the moment set points in the acceleration space. The rotational accelerations follow from the rotational equations of motion
The translational equations of motion lead to
This yields all angular and translational accelerations at the total query points for different envelope boundary points as well as attitude deviations. The next section explains how to assemble these points and combine them with other required moments in a convex hull approach.
2.4. Convex Hull-Based Control Set Assembly
The last subsection contributed to the objective of calculating clearly traceable parts of the RMS. This subsection proposes a method to add these individual RMS subsets and to compare them to the AMS. After the query points for the disturbance set are assembled, the convex hull [
7] of the set can be computed in order to obtain a worst case estimation of the aerodynamic disturbance. Note that this convex hull-based approach is chosen here as it can be performed generically for any set of points regardless of the physical origin. An efficient algorithm for determining the convex hull of an arbitrary set of points is the quickhull algorithm [
8], which is implemented in the Matlab function convhulln(). It is important to mention here that, due to the nonlinearities in the aerodynamic coefficients, the aerodynamic disturbance set is in general no convex set. The goal of this paper, however, is a comparison of the RMS with the AMS. For this reason, assembling the RMS as a convex set does not produce overly conservative results. Any convex AMS that contains a non-convex RMS will also contain a more conservative convex version of the RMS.
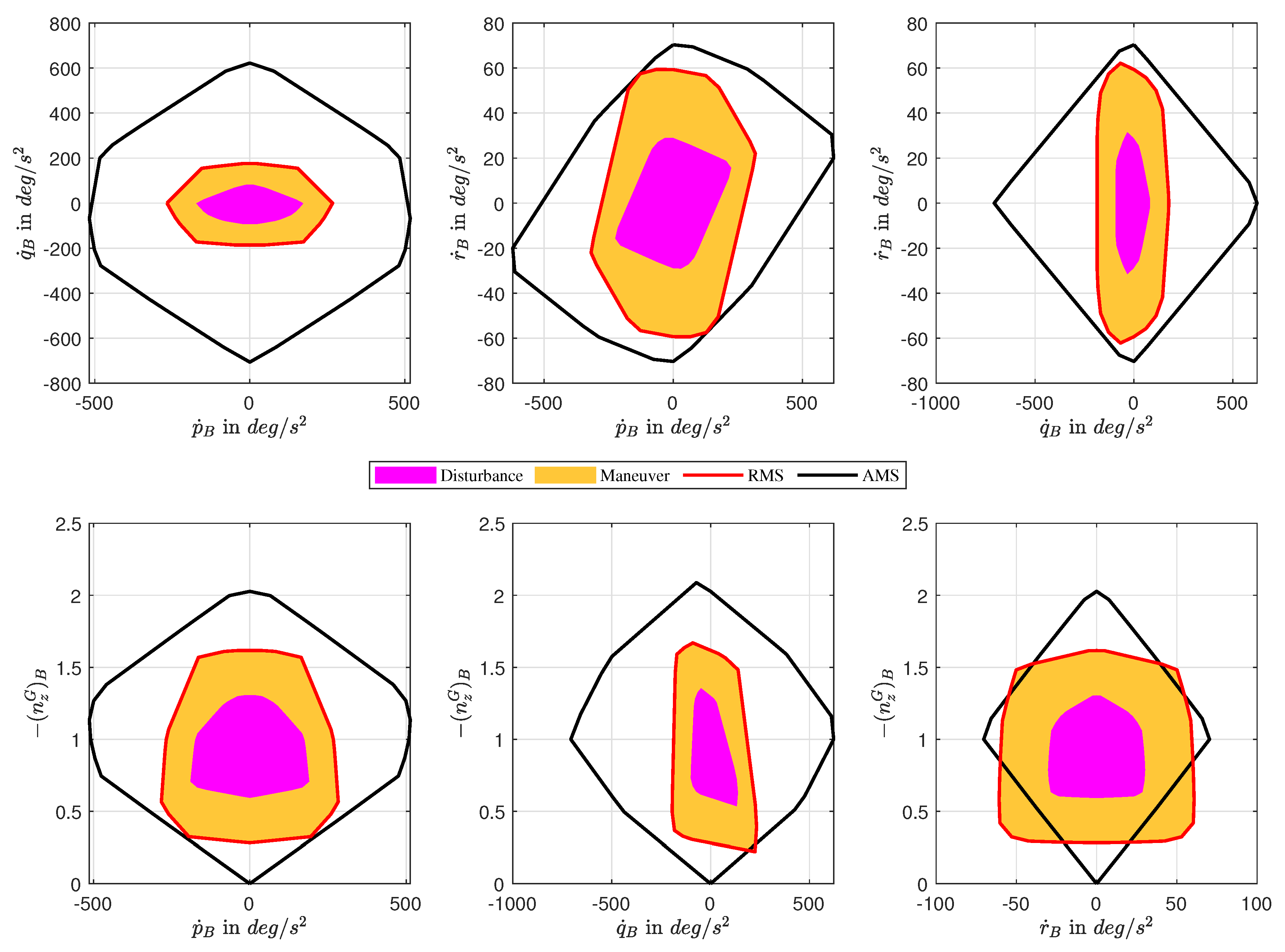
In order to be able to sum up the different independent elements of the RMS (disturbance and maneuverability parts) and compare them to the AMS, we propose to calculate the maximum attainable acceleration in the query directions of the four-dimensional acceleration space. This reduces computational effort and produces magnitudes in predefined directions that do not depend on the configuration but are chosen by the user. This approach also allows comparison of different configurations with respect to each other very easily. A disadvantage of this method is that for small numbers of query directions, the actual set might not be resolved accurately enough. In order to resolve the moment set with higher accuracy, the number of query directions increases very fast as the moment set is four-dimensional.
The maximum of the accelerations in the query directions is determined by the points in the query direction that lie on the convex hull. An efficient algorithm to determine the cross sections with the convex is presented in [
21].
To parameterize the four-dimensional directions, we use an n-spherical coordinate system [
22] which, for the four-dimensional case, requires three angles for the parameterization. Including a scaling along the four-dimensions which leads to
with the normalized query direction
and the three parameterization angles
and
. As for the velocity envelope and the attitude deviation, we again use linearly spaced parameterization angles. Let
denote the number of the corresponding angles for the linear spacing, then
is the total number of query directions. Finally, all directions are assembled in a direction matrix
.
Applying this query direction approach to the convex hull obtained from the aerodynamic disturbance moments in all directions contained in and assembling the results in a row vector yields the required acceleration magnitudes for disturbance rejection .
2.5. Calculation of Required Maneuver Set and Assembly of Total Required Set
The last subsection yielded a query direction-based control set interface which can be used to easily add and compare control sets. This section will focus on the required control set to maneuver the aircraft in order to complete the total required moment set.
The required moment set for maneuvering can be expressed in terms of maximum accelerations that are used by the system to fulfill higher level missions/maneuvers. In a possible controller architecture, these maximum accelerations could be implemented as limitations/protections. In the case of an individual channel limitation a cuboidal convex set is obtained, defined by
For the required maneuverability set above, the cross sections in the acceleration directions can directly be obtained via first finding the critical surface of the cuboid by applying an elementwise division of the direction
and the critical limits in the corresponding channels and taking the maximum value. Scaling up the direction vector
by the inverse of this value will lead to hitting the boundary of the cuboid; therefore, the inverse of the value is the cross section magnitude in this direction
where ⊘ and
denote the elementwise division and absolute value, respectively. Applying Equation (
29) to all directions in
and assembling the results in a row vector yields the required acceleration magnitudes for maneuverability
. To obtain the total required accelerations we now can simply add maneuver and disturbance accelerations
2.5.1. Evaluation of Attainable Moment Set
In order to finally perform a control set-based controllability analysis, the attainable control set needs to be calculated and transformed to the query direction-based control set interface. There are methods for evaluating the attainable moments for nonlinear control effector models [
5]. For the exemplary multirotor electric vertical take off vehicle (eVTOL) configurations that are the focus of this paper, simplified propellers with thrust and propeller torque that is linear in the squares of the angular propeller rates are used. For this reason the attainable set can be obtained by evaluating the angular and translational accelerations of all combinations of minimum and maximum propeller angular rates. The corresponding convex hull can again be found by using the quickhull algorithm [
8].
In general, the proposed approach allows more complex nonlinear propeller models for calculating the AMS as well. It is important to mention here that the comparison with the RMS does not allow an inflow dependent AMS, as the RMS is chosen for the worst case inflow in the envelope. A possible solution to this problem is to also choose the worst case AMS via intersecting multiple AMSs that were calculated at different points in the aerodynamic velocity envelope.
After the convex hull is calculated, the same approach as for the required moments is used to assemble the intersections in the query directions in the vector .
2.5.2. Controllability Evaluation
Now that attainable and required acceleration sets are determined, the easiest way to assess the controllability is just to check if, in any direction, the required moment set exceeds what is attainable:
According to this definition, Equation (
31) is a condition for fulfilling the controllability requirements. Note that this simple comparison contributes to two major objectives of this paper. First of all, a very simple final evaluation of controllability is possible. Second of all, the RMS is obtained from a simple sum of individual sets, therefore it is always traceable what the corresponding contributions of individual sets are.
In order to obtain continuous instead of binary controllability measures we can assemble a margin vector, which contains the differences of attainable and required accelerations. In order to obtain a more relative controllability measure, the margin can be normalized by the required moment set that obtains a relative margin vector
.
In order to assess the overall controllability, various norms can be used to transform the vector margin to a scalar controllability measure.