Featured Application
The research proposes a control methodology and analysis methods that could be applied to the trajectory tracking control of uncertain industrial robots such as serial robots, parallel robots, and hybrid robots as well as other uncertain nonlinear second-order systems in the industrial fields. It is beneficial to improve the robustness and active adaption ability to different industrial technological requirements for uncertain nonlinear systems.
Abstract
Some challenging issues exist in trajectory tracking control of an uncertain bilaterally symmetrical hybrid robot (UBSHR) with variational desired trajectories, mainly the uncertainty problem of UBSHR, the synchronization problem of UBSHR’s active joints and bilateral symmetrical hybrid mechanisms, and the flexible control problem of active adaption to different technological requirements without artificially adjusting the control parameters or switching the hardware system. To solve these problems, an adaptive fuzzy neural network in conjunction with subtractive clustering algorithm (SC-AFNN) for UBSHR is proposed. More specifically, a novel composite error is incorporated into the second-order sliding mode control method to generate ideal training data samples and to improve the uncertain system robustness and synchronization performance simultaneously. Furthermore, the SC-AFNN is introduced to realize self-learning and self-adjusting of control rules and control parameters and to enhance the flexible control performance of UBSHR with variational desired trajectories. Strict theoretical proof of the defined errors’ relationship and the stability of the poposed control method is given. Ultimately, simulations and experiments for the prototype system of an UBSHR are conducted to verify the effectiveness of the proposed control method.
1. Introduction
Serial and parallel robots have been used to implement complex tasks in industrial fields, such as the automobile manufacturing industry. The available automobile electrophoretic coating conveyers exhibit disadvantages such as poor carrying capacity and flexibility due to the use of a cantilever beam series structure [1]. By designing a mechanical configuration, compared with the traditional serial robot, the uncertain bilaterally symmetrical hybrid robot (UBSHR) has the potential advantage of being flexible without switching or changing the hardware system, owing to the introduction of a parallel mechanism and the ingenious combination of serial and parallel mechanisms [2]. Nevertheless, the research on a control method for UBSHRs that could satisfy the flexibility requirements has not attracted much attention.
To obtain high control performance of a UBSHR, three crucial problems are considered in the paper: (1) the uncertainty problem, (2) the synchronization problem, and (3) the flexible control problem of active adaption to different technological requirements without artificially adjusting the control parameters or switching the hardware system. Firstly, analyzed from the closed-chain structure of UBSHR and the actual operation environment, system uncertainties exist in UBSHR, i.e., modeling errors, and the internal friction and external disturbances. These uncertainties may influence the trajectory tracking control performance of a UBSHR. Moreover, the control security, dependability, and precision are influenced by the synchronization performance among active joints and the synchronization performance between UBSHR’s bilateral symmetrical hybrid mechanisms due to multiple active joints of UBSHR. Thus, the trajectory tracking performance under system uncertainties and the synchronization performance should be considered simultaneously. In addition, the controller parameters need to be adjusted artificially to satisfy the actual control requirements due to variational desired trajectories caused by different technological requirements in practice. As a result, the flexibility superiority of the mechanical structure cannot be exerted, which makes it difficult to realize the flexible control performance of active adaption to different technological requirements.
For the uncertainty problem existing in a robot system, robust control methods have been presented, i.e., H∞ control [3], backstepping control [4], and sliding mode control (SMC) [5]. The SMC method is insensitive to parameter changes and external disturbances. Hence, it has superiorities to dispose of the uncertainty problem for hybrid robots [6,7]. In a previous study by our research group, problems of system uncertainties and synchronization performance have been handled by combining the SMC algorithm and synchronous control strategy [8,9,10]. Nevertheless, for the researched UBSHR, the defined synchronization errors in [8,9,10] could only guarantee the synchronization performance of active joints. The synchronization performance of an UBSHR’s end-effector could not be considered. Therefore, a novel composite error was defined by considering synchronization errors and by tracking errors of the UBSHR’s end-effector. Combined with the second-order nonsingular fast terminal SMC (SOSMC) method [11,12,13], the composite error-based SOSMC (CE-SOSMC) for a hybrid robot was realized. Compared with the synchronization error in [8,9,10], the defined composite error could ensure the synchronization performance not only of active joints but also of the end-effector. Compared with the existing SMC method based on linear sliding mode surface, the designed SOSMC method possesses superiorities such as small chattering, non-singularity, and fast convergence rate. Therefore, the presented CE-SOSMC algorithm can improve the trajectory tracking performance under system uncertainties and synchronization performance simultaneously.
For the flexible control problem of active adaption to different technological requirements without constantly adjusting the control parameters or switching the hardware system, the existing related research achievements are few, and existing control methods are mostly suitable for systems with definite desired trajectories [14,15]. For example, due to the condition limitations of sliding mode existence, the SMC could not satisfy the flexible control requirements of active adaption to different desired trajectories caused by different technological requirements. Recently, intelligent control theory has been introduced to track different desired trajectories for robot systems [16,17]. In [16], for the KUKA industrial robot system, a learning from demonstration method was addressed to track different desired trajectories under unseen situations. The learning control method has strong nonlinear fitting ability and learning ability, but it needs a mass of training samples and does not possess the inferential and inductive capacity [18,19]. In [17], for a 3-RPR parallel robot system with physical uncertainties, such as the mass of a robot end-effector and the inertia of robot cylinders, a robust optimal fuzzy controller was presented to track step-type trajectories with different heights as well as sinusoidal trajectories with different frequencies and phases. The fuzzy control method exhibits merits such as strong nonlinearity, self-adaptability, and better stability under time-varying system parameters. However, it needs to establish a mass of rules and could not obtain the rules that are used to make corresponding control decisions automatically [20,21]. Consequently, the adaptive fuzzy neural network (AFNN) was introduced. Subtractive clustering in conjunction with evolutionary algorithm were applied to construct the fuzzy rule base with fewer rules automatically to avoid the rule base explosion problem for fuzzy control of the multivariable nonlinear hybrid robot system [22]. Furthermore, the Takagi–Sugeno model-based adaptive neural network (TSANN) based on the above fuzzy rules was constructed to realize self-learning and self-adjusting of control rules and control parameters [23,24,25]. Therefore, an adaptive fuzzy neural network in conjunction with subtractive clustering algorithm (SC-AFNN) for hybrid robot was constructed to improve the tracking performance under system uncertainties, synchronization performance, and flexible control performance of active adaption to variational desired trajectories caused by different technological requirements simultaneously.
The main contributions of this paper are (1) combining the defined novel composite error of hybrid robot with SOSMC; (2) constructing an AFNN in conjunction with subtractive clustering algorithm for UBSHR; (3) realizing self-learning and self-adjusting of control rules and control parameters for the proposed control method; and (4) improving the trajectory tracking performance under system uncertainties, the synchronization performance, and the flexible control performance of active adaption to variational desired trajectories simultaneously.
This paper is divided into five sections. A dynamic model of UBSHR and the problem formulation are covered in Section 2. In Section 3, the design and stability proofs of the developed control methods are presented. On the basis of a UBSHR prototype system, simulation and experimental research are carried out to further validate the validity of SC-AFNN in Section 4 and Section 5. Finally, Section 6 summarizes the research conclusions.
2. Dynamic Modeling and Problem Formulation
2.1. Robot Description
The UBSHR combines serial and parallel mechanisms ingeniously, and the flexibility of the UBSHR is improved without switching or changing the hardware system by designing the mechanical configuration. The structure of UBSHR’s lifting-turning mechanism is complex, which directly affects the electro-coating conveying performance. In Figure 1, the unilateral structure of the UBSHR is presented.
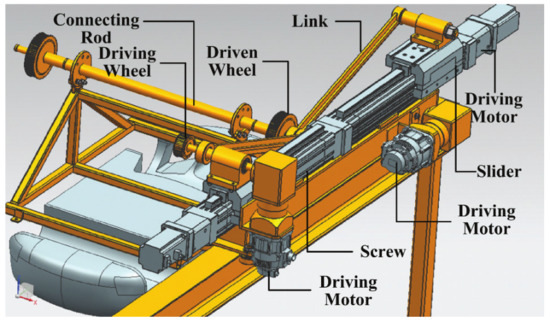
Figure 1.
The unilateral structure of the uncertain bilaterally symmetrical hybrid robot (UBSHR).
2.2. Dynamic Modeling
The virtual work principle was used to build the mathematical model of UBSHR. Considering the friction influence on every joints, the mathematical model of UBSHR was established [26]:
where denotes the generalized equivalent force, denotes the actual pose of UBSHR’s end-effector, is the Jacobian matrix, is the pseudo-inverse of , and .
The dynamic model of UBSHR in Cartesian space could be converted to a joint space as follows:
where , , and are the actual pose, velocity, and acceleration of UBSHR’s active joints, respectively; denotes the inertia matrix; denotes the Coriolis and centrifugal item; denotes the gravity item; and denotes the friction item. According to [27], , in which is the coulomb friction matrix and is the viscosity coefficient matrix; denotes the driving torque of UBSHR’s active joints.
2.3. Problem Formulation
The UBSHR is comprised of six active joints. To ensure the tracking performance, synchronization performance, and flexible control performance for the hybrid robot with uncertainties simultaneously, when different desired trajectories are given, the actual pose should approach the desired pose of active joints and the actual pose should approach the desired pose , that is, and ; meanwhile, the tracking errors of active joints , and tracking errors of the end-effector should satisfy control objectives A and B, respectively.
- A.
- The tracking errors of UBSHR’s active joints are defined as follows:in which and , and and are, respectively, the desired position and actual position for the hybrid robot’s ith slider and jth driving wheel. To guarantee the synchronization performance of UBSHR’s active joints, the tracking errors of the active joints should meet synchronous control theory as follows:
- B.
- The tracking errors of UBSHR’s end-effector are defined as follows:where , (i = 1, 2) and ,(i = 1, 2) denote the desired and actual pose. To improve the synchronization performance of UBSHR’s end-effector, the control objective can be described as follows:
Toward this end, the control objective is to investigate the control method that could improve the trajectory tracking performance under system uncertainties, synchronization performance, and flexible control performance. The hybrid robot system should satisfy , , and as well as be stable when different desired trajectories are given.
Figure 2 presents the control schematic diagram.
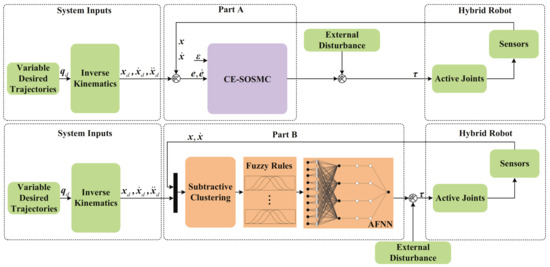
Figure 2.
The control schematic diagram.
As shown in Figure 2, and are, respectively, the tracking error and the synchronization error of UBSHR’s end-effector; and are the desired pose and the actual pose of active joints, respectively; and output data is the control torque of UBSHR.
Firstly, the hybrid robot is well-controlled under the designed CE-SOSMC controller (Part A) to generate ideal training data samples and to improve the uncertain system robustness and synchronization performance simultaneously. Then, a subtractive clustering algorithm is introduced to avoid the explosion phenomenon of fuzzy rules. Based on this, the SC-AFNN controller (Part B) is constructed to completely replace the CE-SOSMC controller (Part A).
3. Controller Design
3.1. The Design of CE-SOSMC
The synchronization error of each active joint is defined by (4):
in which is the tracking errors of UBSHR’s active joints and is the transfer matrix.
According to (6), the synchronization error of UBSHR’s end-effector could be defined as follows:
where , is the slider position for the hybrid robot in the -axis direction, denotes the position of the hybrid robot end-effector in the -axis, and and are the radius of the driving wheel and driven wheel, respectively.
In order to achieve precise tracking control for the hybrid robot and to ensure synchronization performance of the active joints and end-effector, by further combining with of UBSHR’s end-effector, a novel composite error is designed as follows:
in which .
On the basis of the novel composite error , the sliding surface of CE-SOSMC is constructed as follows:
where , ; , ; , ; and p,q are odd numbers. The non-singularity of is guaranteed in theory due to .
Then, the CE-SOSMC law for a hybrid robot is
in which ; ; ; and .
The first result is provided below.
Theorem 1.
For the nonlinear system (1), if the CE-SOSMC algorithm presented in (11) with , ; , ; and is adopted, the stabilization of sliding variable will be guaranteed in a finite time. Moreover, the tracking error and the synchronization error of hybrid robot end-effector as well as the synchronization error among active joints will asymptotically approach zero.
Proof.
Choose an appropriate Lyapunov function candidate as follows:
where , .
Note that is positive definite if , :
where is the Euclidean norm of . By differentiating (12), can be obtained as follows:
in which . is negative definite if . Combining (13) and (14) and the fact that , it follows that
where .
Considering that the differential equation , is given by
it follows from the comparison principle that when . From (16), one obtains that and converge to zero in finite time. Hence, the stabilization of sliding variable will be guaranteed in a finite time , i.e., .
Additionally, and will converge to 0 as when the sliding surface at time . Taking the derivative of (9), we have , where is given by (8) and , that is, the differential equation as . Thus, and while , that is, and of the UBSHR’s end-effector converge to 0 asymptotically. Moreover, from (7) and (8), and of the active joints converge to 0 asymptotically as as well. □
3.2. The Design of SC-AFNN
To solve the problem of active adaption to variational desired trajectories, SC-AFNN is introduced to entirely replace the CE-SOSMC designed in Section 3.1. Firstly, the hybrid robot is operated under the control of CE-SOSMC, and the ideal training data samples are generated. Then, the fuzzy rule base is built automatically by subtractive clustering algorithm. Finally, the SC-AFNN is constructed from the fuzzy rule base to entirely replace the CE-SOSMC. The input and output of the SC-AFNN controller are, respectively, the desired pose , the actual pose , and the control torque .
3.2.1. Fuzzy Rules Generation
The ideal training data samples, i.e., input data and and output data , are obtained under the control of CE-SOSMC for hybrid robot. Subtractive clustering in conjunction with the evolutionary algorithm is applied for constructing the fuzzy rule base with fewer rules automatically to avoid the rule base explosion problem for fuzzy control of the multivariable nonlinear hybrid robot system. In the algorithm, each point is seen as a potential cluster center . Then, the selected cluster center is reduced to search for the next cluster center. According to the number of cluster centers, the number of fuzzy rules and the membership functions of each input variable are determined and the position of the membership functions on the domain of discourse is defined [28]. After applying the subtractive clustering method for the data samples, four fuzzy rules are produced. Figure 3 gives the membership functions of the input variables.
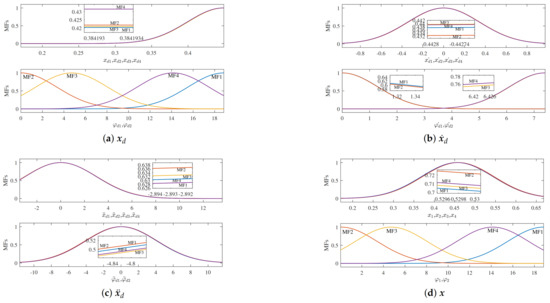
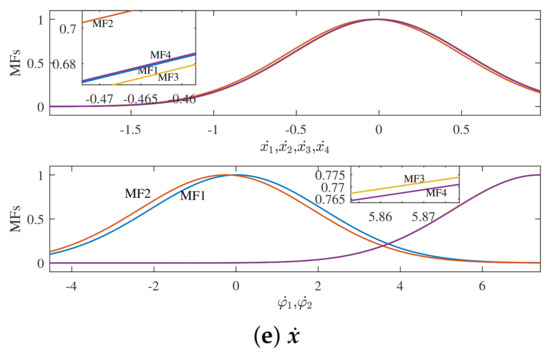
Figure 3.
Membership functions generated by subtractive clustering. (a) Membership functions of xd; (b) Membership
functions of ; (c) Membership functions of ; (d) Membership functions of x; (e) Membership functions of .
3.2.2. SC-AFNN Construction
Based on the fuzzy rule base, the SC-AFNN is further constructed to realize self-learning and self-adjusting of control rules and control parameters. Therefore, SC-AFNN could adapt variational desired trajectories caused by different technological requirements actively.
The SC-AFNN consists of an input layer, fuzzification layer, rule layer, normalization layer, defuzzification layer, and output layer. The first layer is the input layer, in which each neuron transmits the input signal to the next layer. The second layer is the fuzzification layer, in which the neurons receive the input layer signals and use Gaussian function as a membership function to divide the distribution of input signals. The third layer is the rule layer, where each neuron represents a fuzzy rule and the firing strength of each rule can be calculated. The fourth layer is the normalization layer, in which each neuron receives the input of all neurons in the rule layer and calculates the normalized firing strength of the given rule. The firing strength of the normalized layer is the ratio of the firing strength of a given rule to the sum of the firing strength of all rules. The fifth layer is the defuzzification layer, in which each neuron is connected to its own normalized layer neuron and receives the initial input. The sixth layer is the output layer, which calculates the sum of the outputs of all neurons in the defuzzification layer. Figure 4 presents the structure of SC-AFNN. The number of input layer neurons is ; the input comprises , and ; and the output is . The membership functions are defined by the Gaussian functions as follows:
where and , respectively, denotes the center and width of the membership functions; , n is the number of fuzzy rules; and , m is the number of input layer neurons.
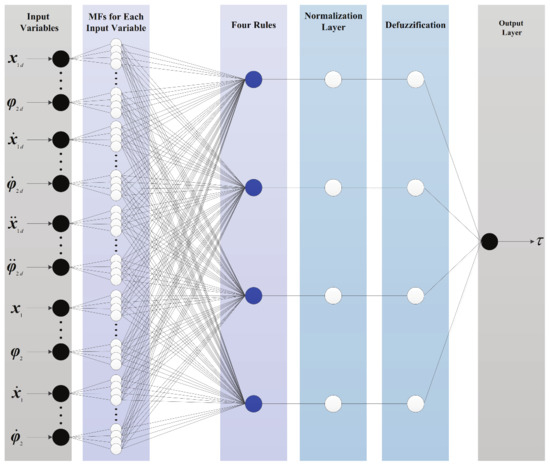
Figure 4.
The structure of Takagi–Sugeno model-based adaptive neural network (TSANN).
Then, the output layer of SC-AFNN, that is, the control torque of each active joint of the hybrid robot, is
where ; indicates the firing strength of a rule; represents parameters of the consequent part; and is the initial input of SC-AFNN.
According to (18), the SC-AFNN model of the hybrid robot is
in which , , .
Lemma 1.
For the fuzzy system (19), is a stable and nonsingular matrix. If there is a common positive definite matrix , for , , then for , is the stable matrix (the eigenvalues of the stable matrix are in the left half plane).
Proof.
According to the condition of Lemma 1, for , we have
Combine (20) and (21)
Namely, for , is the stable matrix. □
The steps to finding the common positive definite matrix are as follows.
(1) Find a positive definite matrix that makes . Suppose a positive definite matrix , which satisfies the Lyapunov equation . If is stable, will be obtained.
(2) Verify the existence of , which makes for . If exists, ; if not, return to step (1).
Assumption 1.
There exists a common positive definite matrix that enables .
The second result is provided below.
Theorem 2.
For the hybrid robot system (1), under Assumption 1 [29], when the SC-AFNN model in (19) is applied, the system asymptotic stability will be ensured.
Proof.
Select an appropriate Lyapunov function candidate as follows:
Equation (23) satisfies
- (1)
- ;
- (2)
- , when ;
- (3)
- , when .
Taking the derivative of (23):
Due to and the conditions of Theorem 2, for , and, thus,
According to Lyapunov stability theorem, the asymptotic stability of the SC-AFNN system is guaranteed. □
4. Simulations
MATLAB simulation of the proposed control methods for a UBSHR was divided into (1) Case 1, in which the tracking performance and synchronization performance of SC-AFNN were compared with the control method merely considering synchronization errors of active joints (SE-SOSMC) and the control method combining the composite error with first-order SMC (CE-SMC), and (2) Case 2, in which the flexible control performance of SC-AFNN is contrasted with CE-SOSMC method. Set the initial pose as . After debugging, the optimal parameters are , , , , , , , , , and .
4.1. Case 1
The desired trajectories of UBSHR’s end-effector are defined in (26)–(28). To verify the tracking performance of CE-SMC and SC-AFNN, the tracking results are exhibited in Figure 5 and the numerical values of the steady-state performance are shown in Table 1. Due to the symmetrical characteristic of UBSHR, this article only provides three unilateral active joints of UBSHR. Figure 6 exhibits the output torque curves. Moreover, to verify the synchronization performance of SE-SOSMC and SC-AFNN, the synchronization error curves of each component of UBSHR’s end-effector are shown in Figure 7.
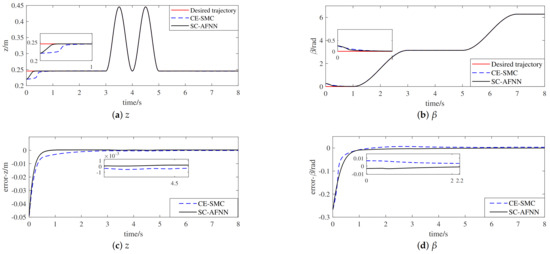
Figure 5.
The tracking results of the UBSHR’s end-effector (desired trajectory 1). (a) z, (b) , (c) error-z and (d) error-.

Table 1.
The numerical values of the steady-state performance.
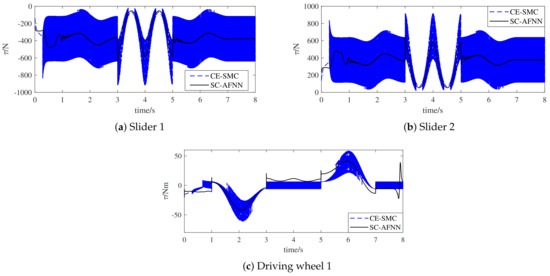
Figure 6.
The output torque curves. (a) Driving torque of slider 1; (b) Driving torque of slider 2; (c) Driving torque of driving wheel 1.
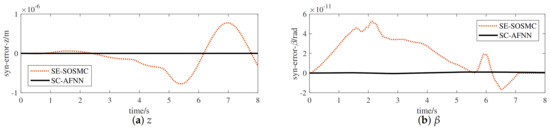
Figure 7.
The synchronization error curves of each component of the UBSHR’s end-effector. (a) Synchronization error in z-direction; (b) Synchronization error of .
Analyzed from Figure 5 and Figure 6 and Table 1, the reaching time of CE-SMC is about 2 times that of SC-AFNN, the maximum tracking error of SC-AFNN is nearly 1/2 of CE-SMC, and the chattering of the output torque is weakened under the control of SC-AFNN. The chief reason for this is the introduction of SOSMC. The switching term of SOSMC acts on the continuous higher-order derivative of the control input, which makes the input signal of the system continuous, thus showing the obvious superiority of alleviating chattering for the SMC system. Therefore, the proposed control method could enhance the tracking accuracy and convergence rate. Meanwhile, it is an effective way to alleviate chattering. As shown in Figure 7, the synchronization error of SC-AFNN is effectively reduced by combining tracking errors with synchronization errors. It is concluded that the SC-AFNN for a hybrid robot could improve the tracking control performance and synchronization performance at the same time.
4.2. Case 2
To verify the flexible control performance under different desired trajectories, the velocity v of the walking motion and the amplitude A of the lifting and turning motion, i.e., , , in the desired trajectory were determined by industrial application requirements. Within the above range of velocity of the walking motion and amplitude of the lifting and turning motion, different desired trajectories were defined by combining different velocities with different amplitudes randomly. Then, the steady-state response performance of the control algorithm for different desired trajectories was verified. Furthermore, it affected the steady-state reaching time and tracking accuracy of UBSHR when v and A of the desired trajectory were at maximum. Owing to space constraints, the parameters of a typical desired trajectory were selected as the maximum, i.e., m/s, m. The desired trajectory of a UBSHR’s end-effector is defined in (29)–(31) to verify the steady-state response performance of the developed control method for the typical desired trajectory. The simulation results for tracking the desired trajectory 2 under CE-SOSMC and SC-AFNN are depicted in Figure 8. Table 2 shows the numerical values of the steady-state performance and root mean square error (RMSE) for tracking the desired trajectory 2.
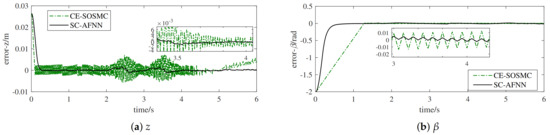
Figure 8.
The tracking error curves of the UBSHR’s end-effector (desired trajectory 2). (a) Tracking error curves in z-direction (6 s); (b) Tracking error curves of (6 s).

Table 2.
The numerical values of the steady-state performance and root mean square error (RMSE) (desired trajectory 2).
Analyzed from Figure 8 and Table 2, the reaching time and maximum tracking error and RMSE of SC-AFNN are smaller than that of CE-SOSMC. Thus, SC-AFNN possesses better tracking performance. The chief reason for this is that the control parameters of CE-SOSMC are obtained under optimal performance for desired trajectory 1. It is difficult to track different desired trajectories actively for CE-SOSMC. Nevertheless, the proposed SC-AFNN method can satisfy the flexible control of active adaption to variational desired trajectories caused by different technological requirements due to the capacity to self-learn and self-adjust control rules and control parameters.
In conclusion, the proposed SC-AFNN method can improve the tracking performance under system uncertainties, synchronization performance, and flexible control performance of active adaption to variational desired trajectories caused by different technological requirements simultaneously.
5. System Experiments
5.1. Control System Construction
Figure 9 presents the prototype of the UBSHR system. It consists of the ‘‘PC’’ and the “UMAC’’. The PC is fitted with an Intel Core i7 series and win7-32-bit processor to complete the functions of the human–computer interaction, code initialization and compilation, and condition monitoring. The UMAC is used to accomplish data calculation, digital to analog conversion, and motion control. The servo driving system consists of MR-J4-70A and MR-J4-100A servo drivers, and HG-SR102BJ and HG-KR73BJ AC servo motors. System experiments are implemented on the UBSHR’s prototype system to verify the effectiveness of the proposed SC-AFNN method.

Figure 9.
The prototype of the UBSHR system.
5.2. Experimental Results
Under the control of CE-SOSMC and SC-AFNN, the PMAC Plot software of UMAC was applied to obtain experimental results for tracking two different desired trajectories, as depicted in Figure 10 and Figure 11. Table 3 presents the experimental numerical values of the steady-state performance and RMSE for tracking two different desired trajectories. The experimental results further verify the validity of SC-AFNN, which could improve the tracking control performance under system uncertainties, synchronization performance, and flexible control performance of active adaption to variational desired trajectories caused by different technological requirements simultaneously.
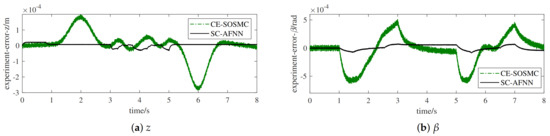
Figure 10.
The experimental tracking error curves of the UBSHR’s end-effector (desired trajectory 1). (a) Experimental tracking error curves in z-direction (8 s); (b) Experimental tracking error curves of (8 s).
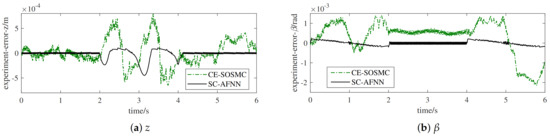
Figure 11.
The experimental tracking error curves of the UBSHR’s end-effector (desired trajectory 2). (a) Experimental tracking error curves in z-direction (6 s); (b) Experimental tracking error curves of (6 s).

Table 3.
The experimental numerical values of the steady-state performance and RMSE for tracking different desired trajectories.
6. Conclusions
For a UBSHR control system, SC-AFNN is presented to improve the tracking control performance under system uncertainties, synchronization performance, and flexible control performance.
- (1)
- A novel composite error considering the synchronization errors and tracking errors of a UBSHR’s end-effector was defined. The CE-SOSMC was realized combined with the SOSMC method to solve the uncertainty problem and the synchronization problem simultaneously. The relationship of asymptotic convergence among the novel composite error, tracking errors, and synchronization errors was stated. Strict theoretical proof of the stability of CE-SOSMC was presented.
- (2)
- AFNN was introduced, and subtractive clustering in conjunction with evolutionary algorithm was applied for constructing fuzzy rule base with fewer rules automatically. Based on the fuzzy rule base, the SC-AFNN was further constructed to realize self-learning and self-adjusting of control rules and control parameters to conquer the flexible control problem of active adaption to different technological requirements without artificially adjusting the control parameters or switching the hardware system. The asymptotic stability of SC-AFNN was analyzed.
- (3)
- Compared with the existing synchronization error, the defined composite error could ensure the synchronization performance not only of active joints but also of the end-effector. Compared with the existing SMC method based on linear sliding mode surface, the presented SOSMC method possesses superiorities such as small chattering, non-singularity, and fast convergence rate. Compared with the existing control methods for systems with definite desired trajectories, the proposed SC-AFNN can track variational desired trajectories for hybrid robots.
- (4)
- Simulation and experimental researches were carried out to further validate the validity of the developed SC-AFNN method.
Author Contributions
Conceptualization, Q.Q. and G.G.; methodology, Q.Q.; software, Q.Q.; validation, Q.Q.; formal analysis, Q.Q. and G.G.; investigation, Q.Q.; resources, G.G.; data curation, Q.Q.; writing—original draft preparation, Q.Q.; writing—review and editing, Q.Q. and G.G.; supervision, G.G.; funding acquisition, Q.Q. and G.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (grant No. 51375210), by the Zhenjiang Municipal Key Research and Development Program (grant No. GZ2018004), by the Graduate Research and Innovation Projects of Jiangsu Province (grant No. SJKY19_2564), and by the Priority Academic Program Development of Jiangsu Higher Education Institutions (grant No. PAPD-2018-87).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wu, J.; Chen, X.L.; Wang, L.P.; Liu, X.J. Dynamic load-carrying capacity of a novel redundantly actuated parallel conveyor. Nonlinear Dyn. 2014, 78, 241–250. [Google Scholar] [CrossRef]
- Xie, F.G.; Liu, X.J.; You, Z.; Wang, J.S. Type synthesis of 2T1R-type parallel kinematic mechanisms and the application in manufacturing. Robot. CIM-Int. Manuf. 2014, 30, 1–10. [Google Scholar] [CrossRef]
- Xu, F.X.; Liu, X.H.; Chen, W.; Zhou, C.; Cao, B.W. Improving handling stability performance of four-wheel steering vehicle based on the H2/H infinity robust control. Appl. Sci. 2019, 9, 857. [Google Scholar]
- Jagannathan, S.; Lewis, F.L. Robust backstepping control of robotic systems using neural networks. J. Intell. Robot. Syst. 1998, 23, 105–128. [Google Scholar] [CrossRef]
- Doan, Q.V.; Le, T.D.; Vo, A.T. Synchronization full-order terminal sliding mode control for an uncertain 3-DOF planar parallel robotic manipulator. Appl. Sci. 2019, 9, 1756. [Google Scholar] [CrossRef]
- Ding, S.H.; Liu, L.; Zheng, W.X. Sliding mode direct yaw-moment control design for in-wheel electric vehicles. IEEE Trans. Ind. Electron. 2017, 64, 6752–6762. [Google Scholar] [CrossRef]
- Wang, Y.Y.; Gu, L.Y.; Xu, Y.H.; Cao, X.X. Practical tracking control of robot manipulators with continuous fractional-order nonsingular terminal sliding mode. IEEE Trans. Ind. Electron. 2016, 63, 6194–6204. [Google Scholar] [CrossRef]
- Gao, G.Q.; Wu, X.T.; Cao, Y.Y.; Fang, Z.M. Synchronized sliding mode control of a hybrid mechanism for automobile electro-coating conveying. Electr. Mach. Control 2017, 21, 113–120. [Google Scholar]
- Gao, G.Q.; Zhang, M.C. Control of a novel hybrid conveying mechanism for electro-coating of automobile bodies. In Proceedings of the 2017 36th Chinese Control Conference, Dalian, China, 26–28 July 2017; pp. 4841–4846. [Google Scholar]
- Gao, G.Q.; Ye, M.Y.; Zhang, M.C. Synchronous robust sliding mode control of a parallel robot for automobile electro-coating conveying. IEEE Access 2019, 7, 85838–85847. [Google Scholar] [CrossRef]
- Feng, Y.; Han, X.; Wang, Y.; Yu, X. Second-order terminal sliding mode control of uncertain multivariable systems. Int. J. Control 2007, 80, 856–862. [Google Scholar] [CrossRef]
- Yi, S.C.; Zhai, J.Y. Adaptive second-order fast nonsingular terminal sliding mode control for robotic manipulators. ISA Trans. 2019, 90, 41–51. [Google Scholar] [CrossRef]
- Wang, Y.Y.; Zhu, K.W.; Yan, F.; Chen, B. Adaptive super-twisting nonsingular fast terminal sliding mode control for cable-driven manipulators using time-delay estimation. Adv. Eng. Softw. 2019, 128, 113–124. [Google Scholar] [CrossRef]
- Liang, Y.W.; Xu, S.D.; Liaw, D.C. A study of T-S model-based SMC scheme with application to robot control. IEEE Trans. Ind. Electron. 2008, 55, 3964–3971. [Google Scholar] [CrossRef]
- Lu, X.G.; Liu, M.; Liu, J.X. Design and optimization of interval type-2 fuzzy logic controller for delta parallel robot trajectory control. Int. J. Fuzzy Syst. 2017, 19, 120–206. [Google Scholar] [CrossRef]
- Xu, S.; Ou, Y.S.; Duan, J.H.; Wu, X.Y.; Feng, W.; Liu, M. Robot trajectory tracking control using learning from demonstration method. Neurocomputing 2019, 338, 249–261. [Google Scholar] [CrossRef]
- Moezi, S.A.; Rafeeyan, M.; Zakeri, E.; Zare, A. Simulation and experimental control of a 3-RPR parallel robot using optimal fuzzy controller and fast on/off solenoid valves based on the PWM wave. ISA Trans. 2016, 61, 265–286. [Google Scholar] [CrossRef]
- Rong, H.J.; Zhao, G.S. Direct adaptive neural control of nonlinear systems with extreme learning machine. Neural Comput. Appl. 2013, 22, 577–586. [Google Scholar] [CrossRef]
- Wu, Y.X.; Huang, R.; Li, X.; Liu, S. Adaptive neural network control of uncertain robotic manipulators with external disturbance and time-varying output constraints. Neurocomputing 2019, 323, 108–116. [Google Scholar] [CrossRef]
- Wu, L.L.; Zhao, P.Y.; Li, Y.Y.; Chen, Y.H. Optimal design of adaptive robust control for the delta robot with uncertainty: Fuzzy set-based approach. Appl. Sci. 2020, 10, 3472. [Google Scholar] [CrossRef]
- Yoo, B.K.; Ham, W.C. Adaptive control of robot manipulator using fuzzy compensator. IEEE Trans. Fuzzy Syst. 2000, 8, 186–199. [Google Scholar]
- Chiu, S.L. Fuzzy model identification based on cluster estimation. J. Intell. Robot. Syst. 1994, 2, 267–278. [Google Scholar] [CrossRef]
- ATakagi, T.; Sugeno, M. Fuzzy identification of systems and its applications to modeling and control. IEEE Trans. Syst. Man. Cybern. 1985, 15, 116–132. [Google Scholar] [CrossRef]
- Jang, J.S.R.; Sun, C.T.; Mizutani, E. Neuro-fuzzy and soft computing, a computational approach to learning and machine intelligence. IEEE Trans. Automat. Contr. 1997, 42, 1482–1484. [Google Scholar] [CrossRef]
- Gao, Y.; Er, M.J.; Yang, S. Adaptive control of robot manipulators using fuzzy neural networks. IEEE Trans. Ind. Electron. 2001, 48, 1274–1278. [Google Scholar]
- Gao, G.Q.; Chen, T.P.; Fang, Z.M. Dynamic modeling of a novel mechanism for automobile electro-coating conveying. J. Mech. Eng. 2016, 52, 8–16. [Google Scholar] [CrossRef]
- Shang, W.W.; Cong, S.; Zhang, Y.X.; Liang, Y.Y. Active joint synchronization control for a 2-DOF redundantly actuated parallel manipulator. IEEE Trans. Contr. Syst. Technol. 2009, 17, 416–423. [Google Scholar] [CrossRef]
- Yang, H.; Fu, Y.T.; Zhang, K.P.; Li, Z.Q. Speed tracking control using an ANFIS model for high-speed electric multiple unit. Control Eng. Pract. 2014, 23, 57–65. [Google Scholar] [CrossRef]
- Sun, Z.Q. Fuzzy-neural network and its application to system modeling and controls. J. Nanjing Univ. Chem. Technol. 2000, 22, 1–6. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).