Advances in High-Precision NO2 Measurement by Quantum Cascade Laser Absorption Spectroscopy
Abstract
1. Introduction
2. Materials and Methods
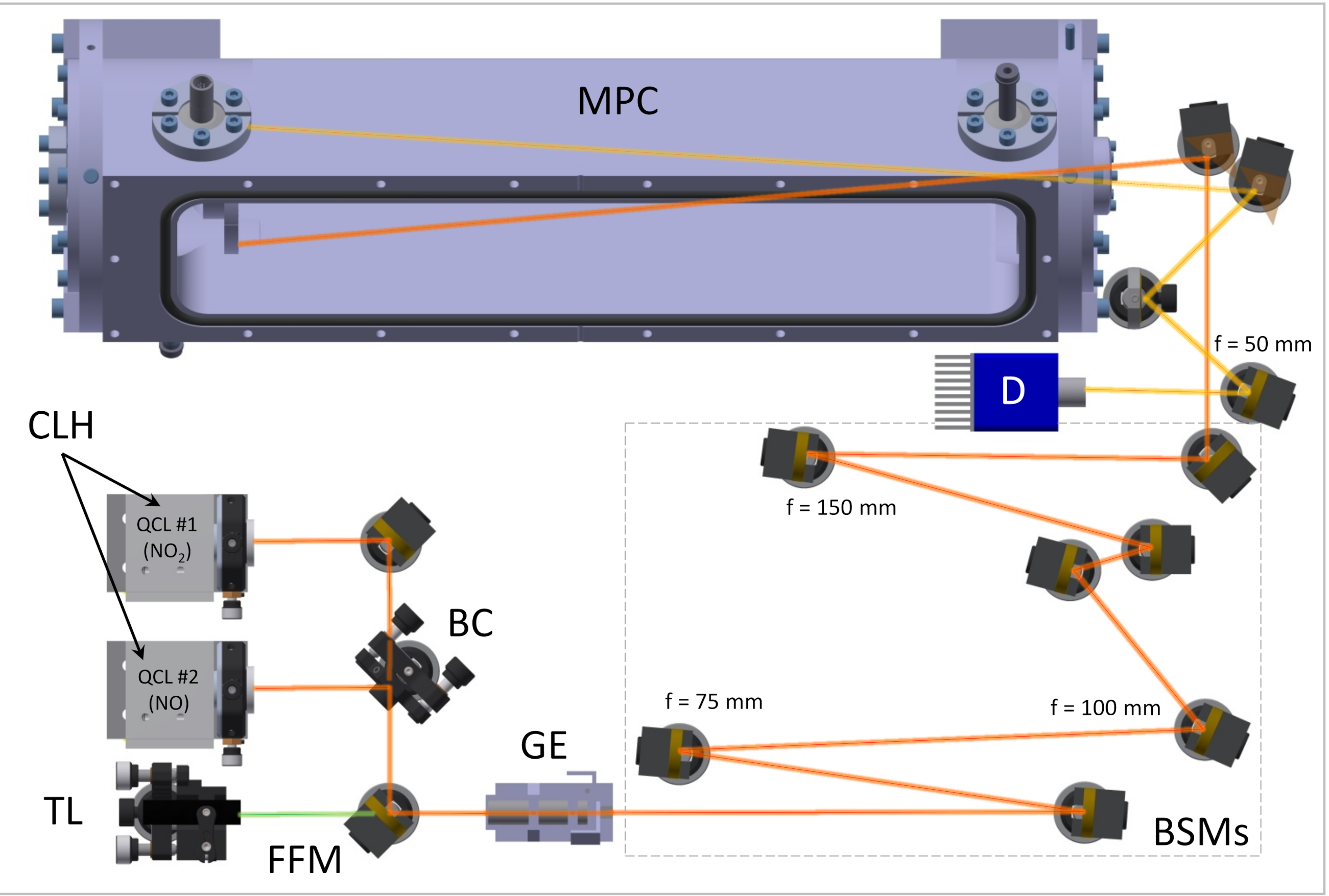
2.1. Description of the Dual-Laser Spectrometer
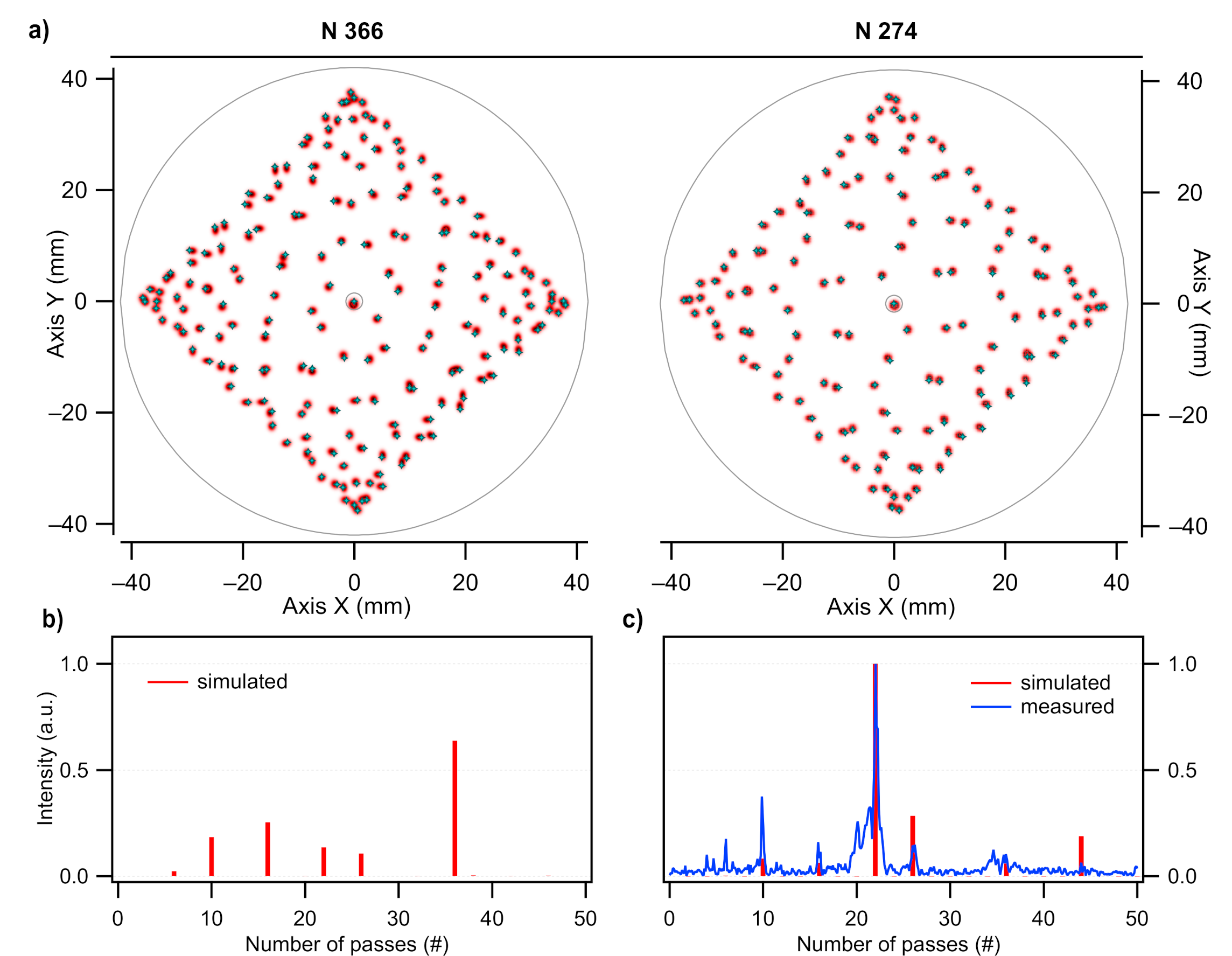
2.1.1. Instrument Inlet and Custom-Made Multipass Cell
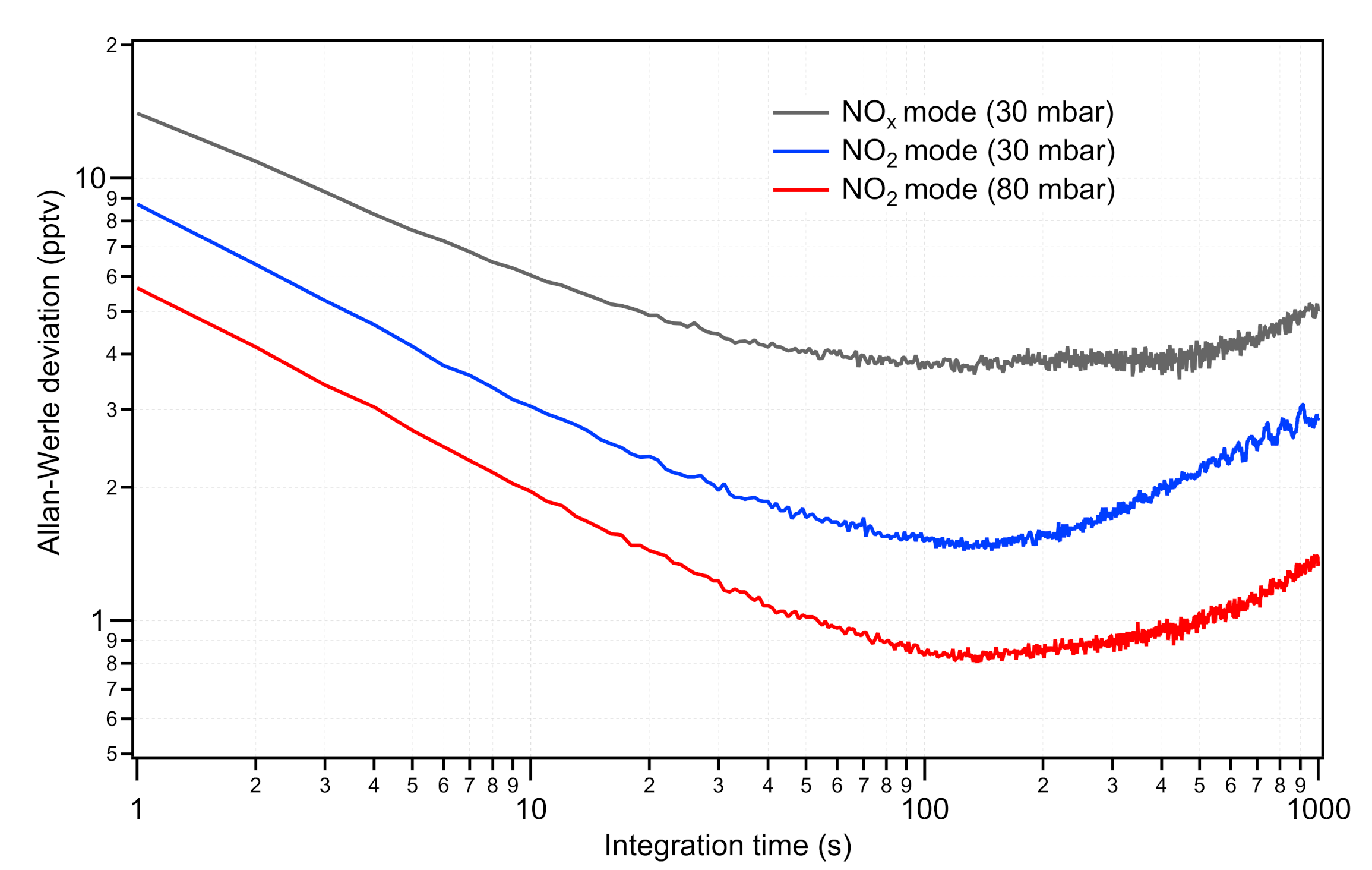
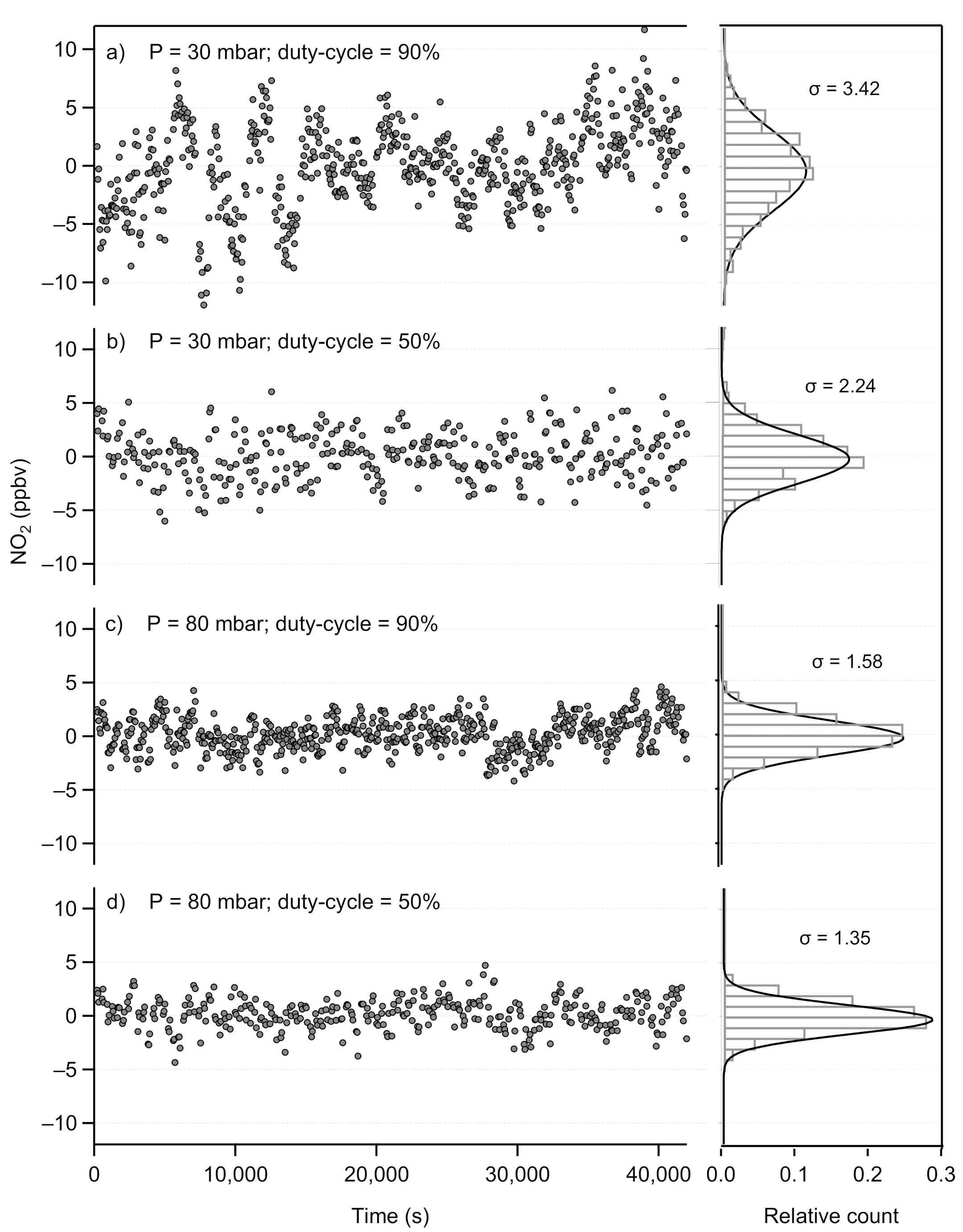
2.1.2. Performance Assessment
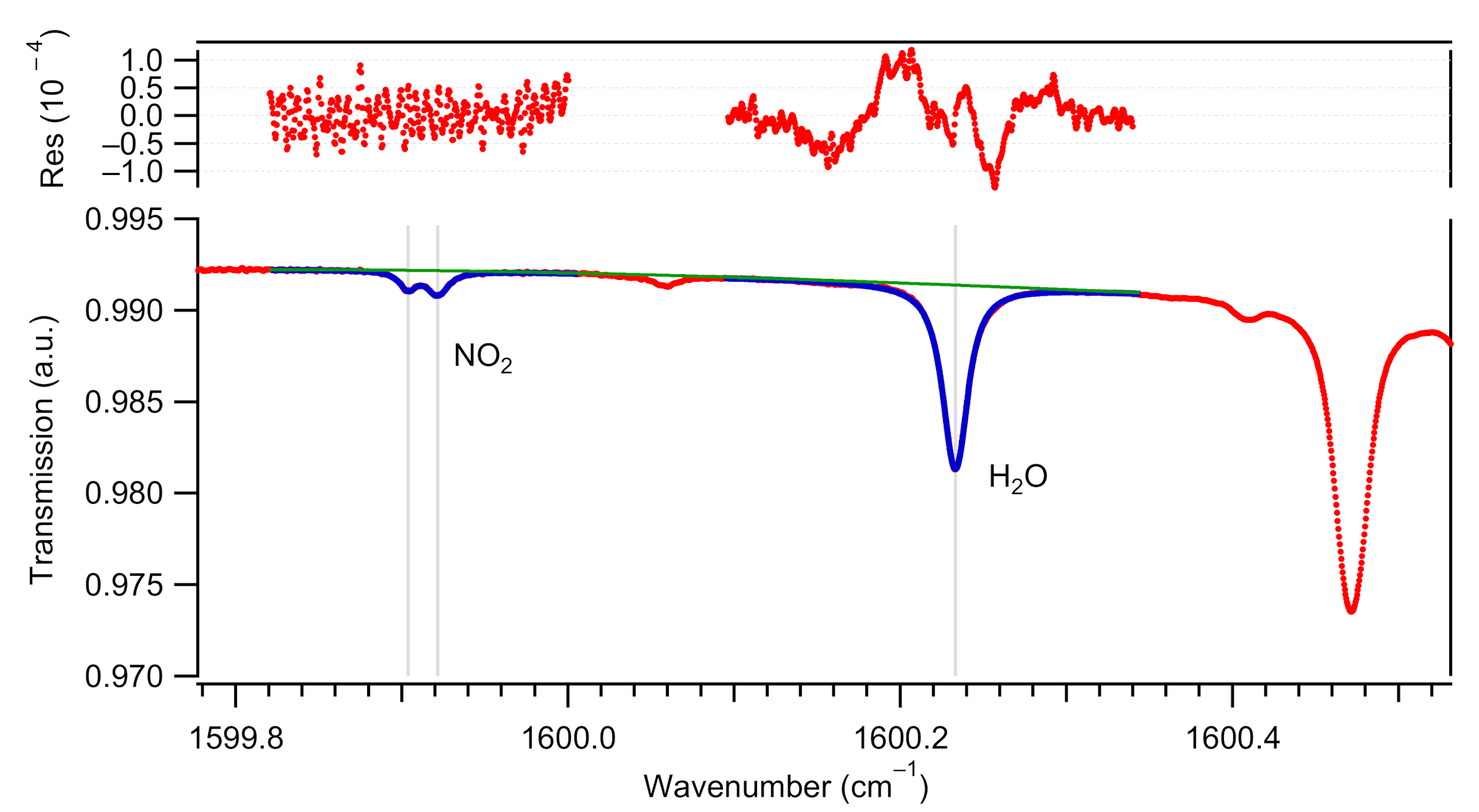
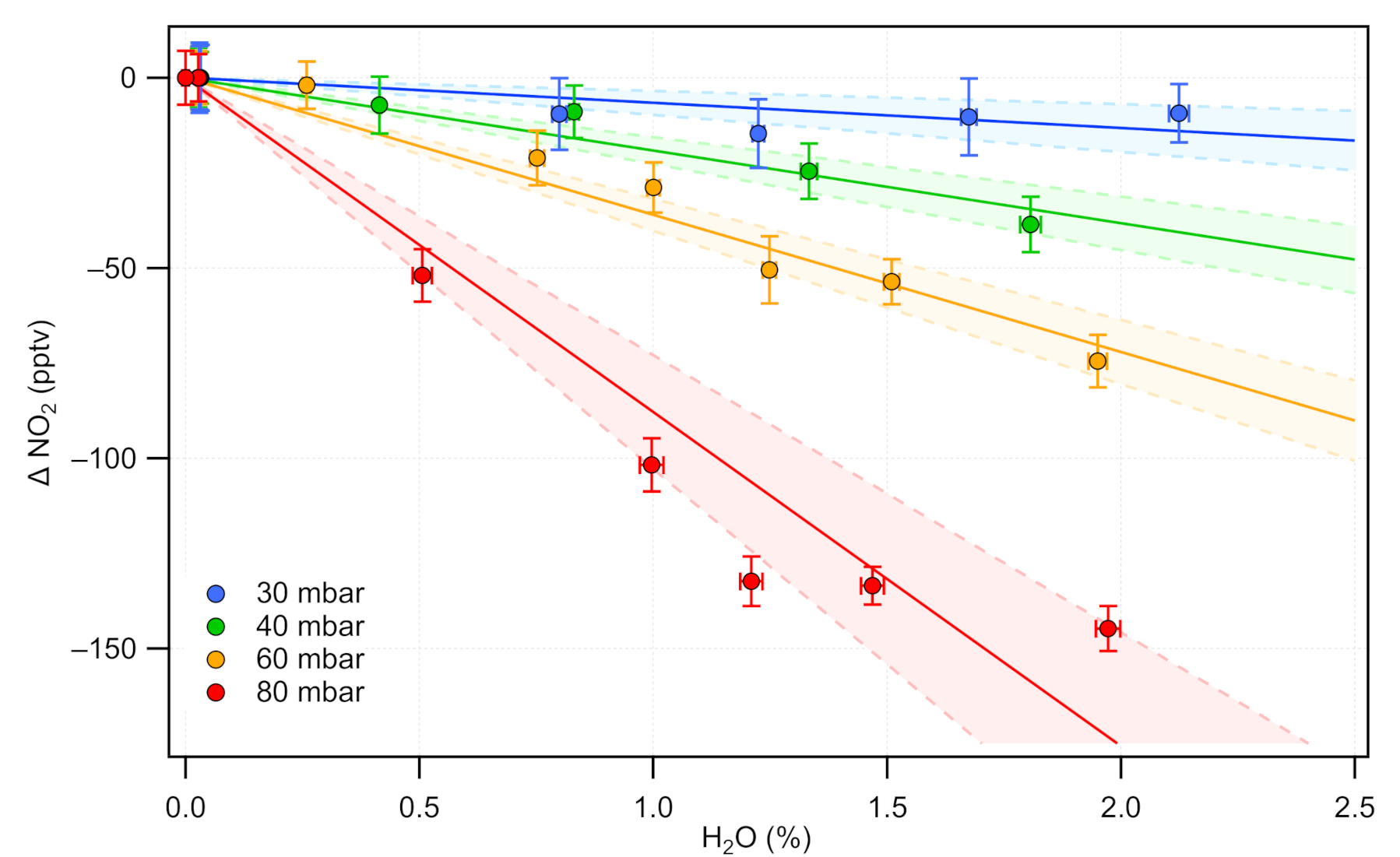
2.1.3. Spectral Interferences Induced by Water Vapor
2.2. Field Inter-Comparison Setup and Instrumentation
2.2.1. Commercial NO Instruments
2.2.2. Calibration Methods
3. Results and Discussion
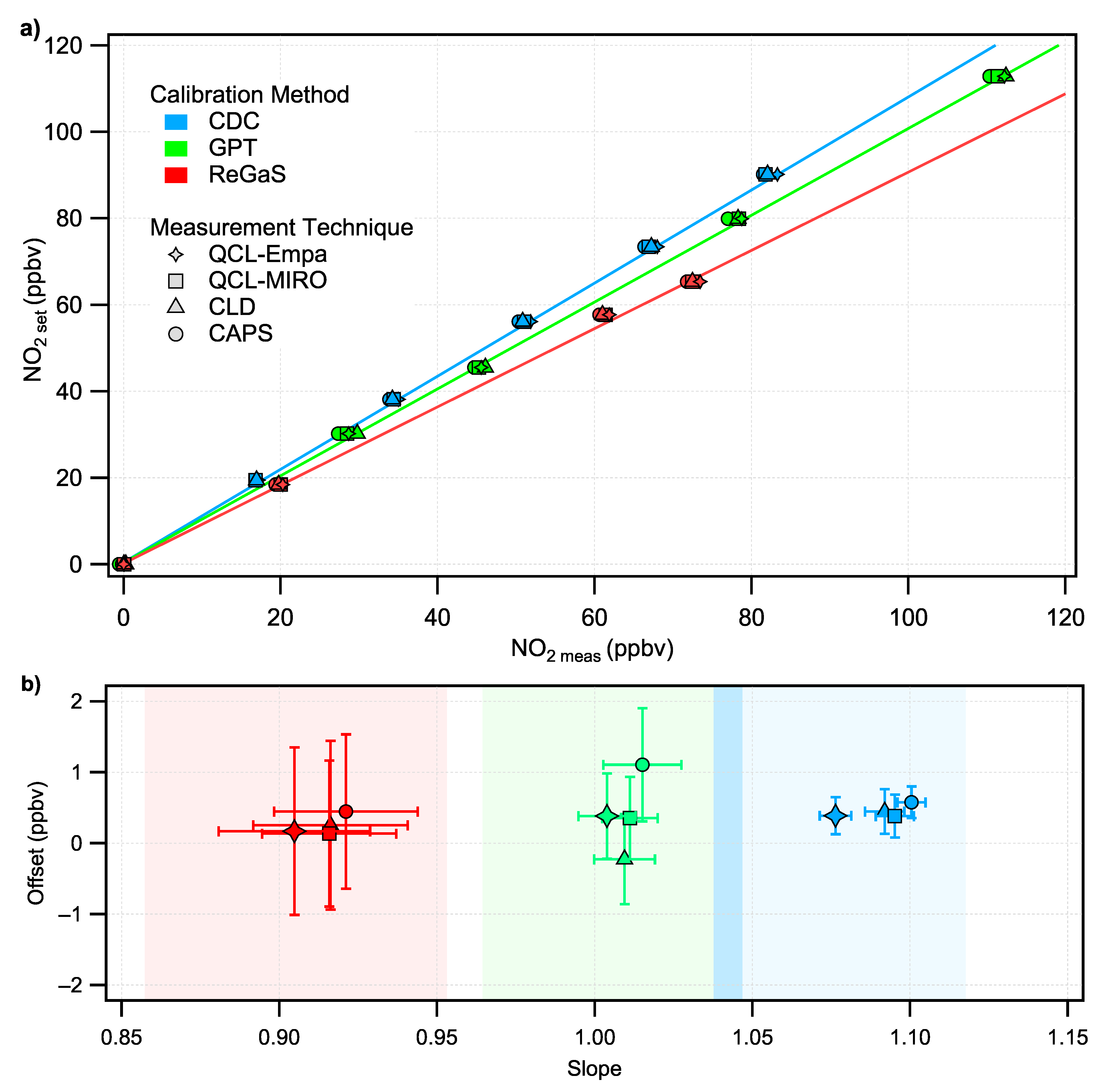
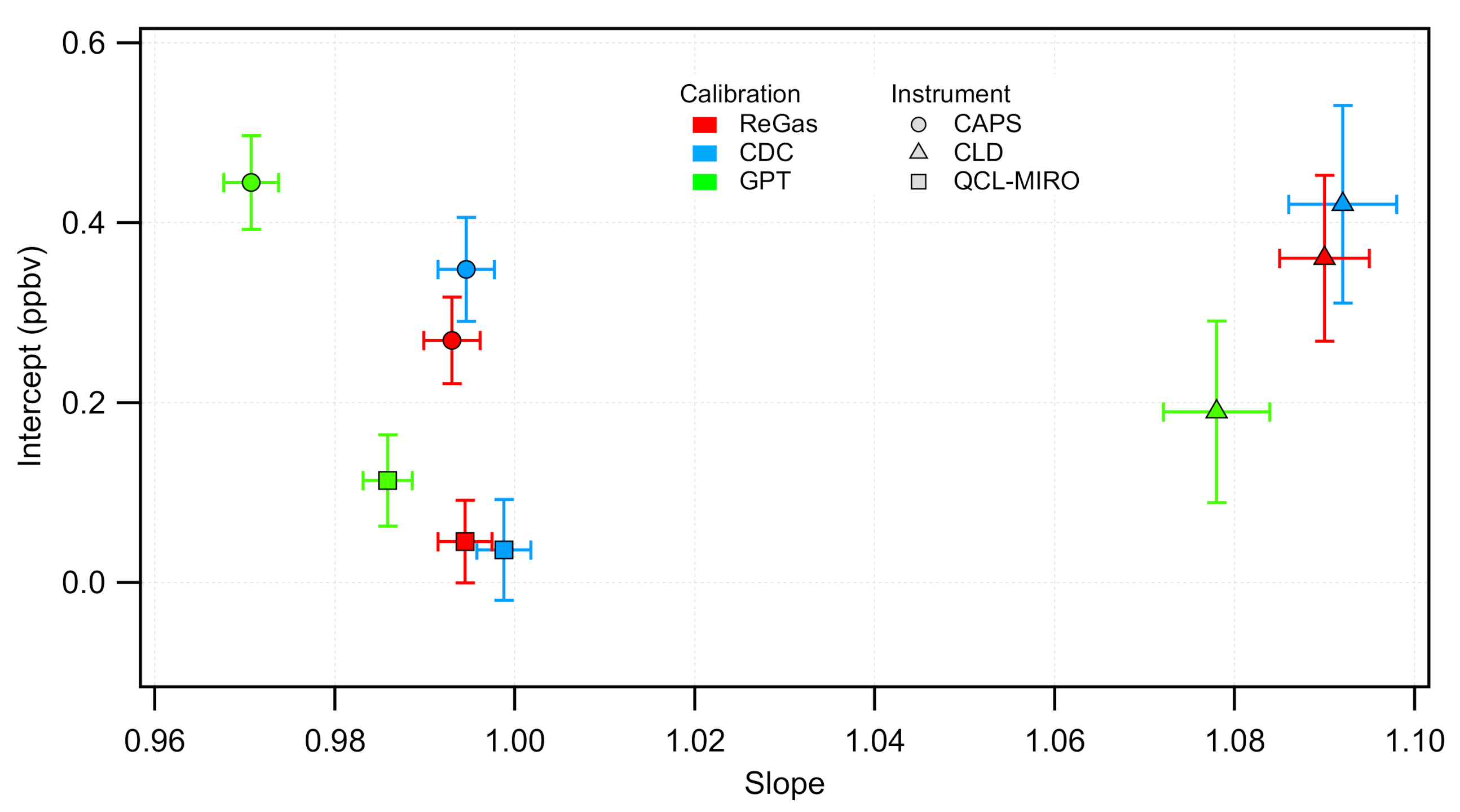
3.1. Calibrations of the NO Instruments
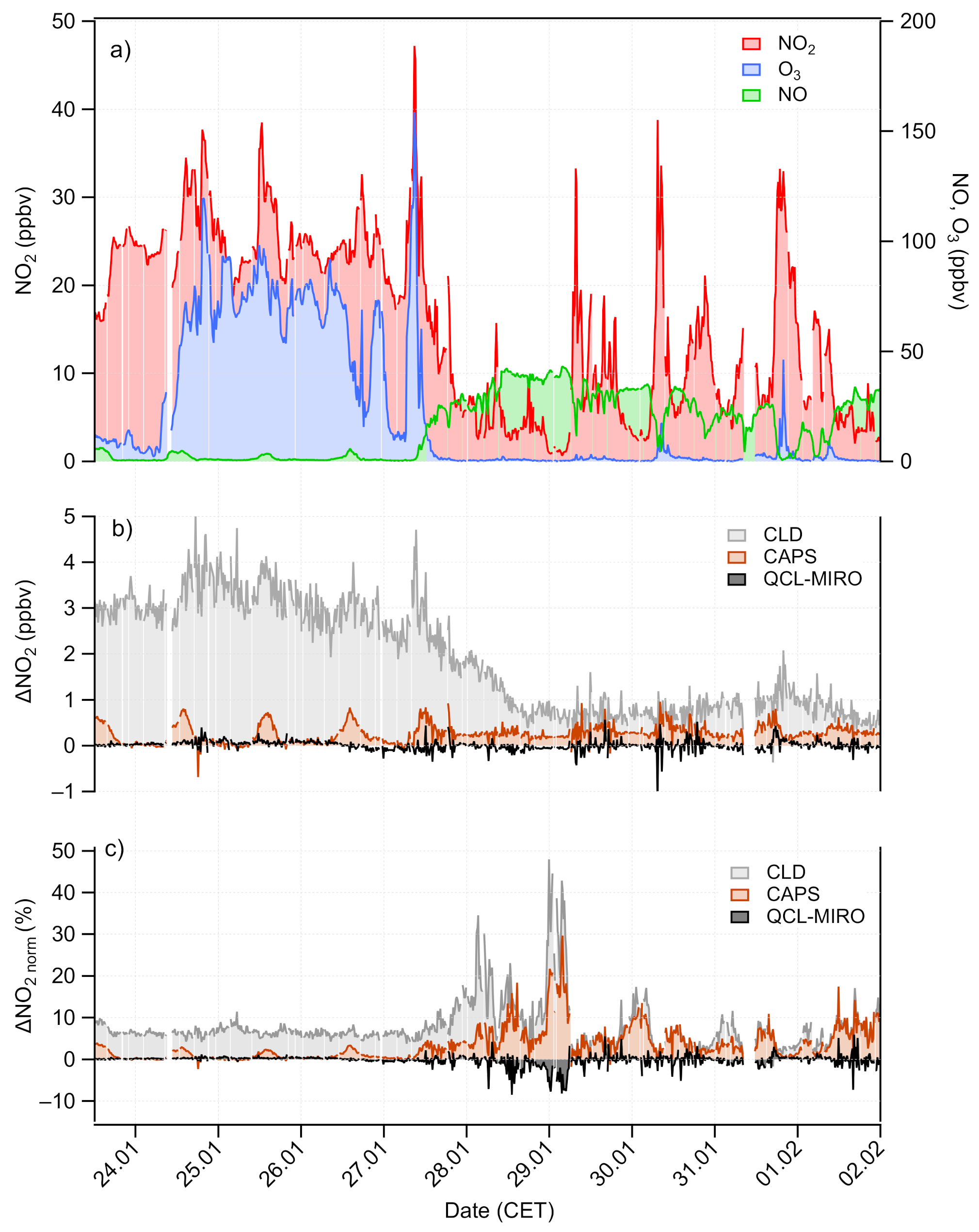
3.2. Ambient Air Measurements
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ADC | analog-to-digital converter |
| AR | anti-reflection |
| BRAM | block random access memory |
| CAPS | cavity attenuated phase shift spectrometer/spectroscopy |
| CES | cavity enhanced spectroscopy |
| CDC | cylinder dilution calibration |
| CLD | chemiluminescence detector/detection |
| CLH | compact laser housing |
| CRDS | cavity ring down spectroscopy |
| CW | continuous-wave |
| DAC | digital-to-analog converter |
| DAQ | data acquisition |
| DFB-QCL | distributed feedback quantum cascade laser |
| DIO | digital input/output |
| DSP | digital signal processors |
| FPGA | field-programmable gate array |
| FSR | free spectral range |
| GAW | Global Atmospheric Watch |
| GPT | gas phase titration |
| iCW | intermittent continuous-wave |
| LAS | laser absorption spectroscopy |
| LOD | limit of detection |
| MIR | mid-infrared |
| MPC | multipass cell |
| OPL | optical path length |
| PCB | printed circuit board |
| PFA | perfluoroalkoxy alkane |
| ppbv | part-per-billion by volume |
| pptv | part-per-trillion by volume |
| PTFE | polytetrafluoroethylene |
| QCLAS | quantum cascade laser absorption spectrometer/spectroscopy |
| SNR | signal-to-noise ratio |
| TDLAS | tunable diode laser absorption spectroscopy |
| TEC | thermoelectric cooling |
| VIS | visible range |
| WMO | World Meteorological Organisation |
References
- Crutzen, P.J. Role of NO and NO2 in the Chemistry of the Troposphere and Stratosphere. Annu. Rev. Earth Planet. Sci. 1979, 7, 443–472. [Google Scholar] [CrossRef]
- Monks, P.S.; Archibald, A.T.; Colette, A.; Cooper, O.; Coyle, M.; Derwent, R.; Fowler, D.; Granier, C.; Law, K.S.; Mills, G.E.; et al. Tropospheric ozone and its precursors from the urban to the global scale from air quality to short-lived climate forcer. Atmos. Chem. Phys. 2015, 15, 8889–8973. [Google Scholar] [CrossRef]
- Lelieveld, J.; Gromov, S.; Pozzer, A.; Taraborrelli, D. Global tropospheric hydroxyl distribution, budget and reactivity. Atmos. Chem. Phys. 2016, 16, 12477–12493. [Google Scholar] [CrossRef]
- Wayne, R.P.; Barnes, I.; Biggs, P.; Burrows, J.P.; Canosamas, C.E.; Hjorth, J.; Lebras, G.; Moortgat, G.K.; Perner, D.; Poulet, G.; et al. The Nitrate Radical - Physics, Chemistry, and the Atmosphere. Atmos. Environ. Part Gen. Top. 1991, 25, 1–203. [Google Scholar] [CrossRef]
- Matsumaru, T.; Yoneyama, T.; Totsuka, T.; Shiratori, K. Absorption of Atmospheric NO2 by Plants and Soils. 1. Quantitative Estimation of Absorbed NO2 in Plants by N-15 Method. Soil Sci. Plant Nutr. 1979, 25, 255–265. [Google Scholar] [CrossRef]
- Yoneyama, T.; Hashimoto, A.; Totsuka, T. Absorption of Atmospheric NO2 by Plants and Soils. 4. 2 Routes of Nitrogen Uptake by Plants from Atmospheric NO2 - Direct Incorporation into Aerial Plant-Parts and Uptake by Roots after Absorption into the Soil. Soil Sci. Plant Nutr. 1979, 26, 1–7. [Google Scholar] [CrossRef]
- Schindler, C.; Ackermann-Liebrich, U.; Leuenberger, P.; Monn, C.; Rapp, R.; Bolognini, G.; Bongard, J.P.; Brandli, O.; Domenighetti, G.; Karrer, W.; et al. Associations between lung function and estimated average exposure to NO2 in eight areas of Switzerland. Epidemiology 1998, 9, 405–411. [Google Scholar] [CrossRef]
- Barck, C.; Sandstrom, T.; Lundahl, J.; Hallden, G.; Svartengren, M.; Strand, V.; Rak, S.; Bylin, G. Ambient level of NO2 augments the inflammatory response to inhaled allergen in asthmatics. Respir. Med. 2002, 96, 907–917. [Google Scholar] [CrossRef]
- Weinmayr, G.; Romeo, E.; De Sario, M.; Weiland, S.K.; Forastiere, F. Short-Term Effects of PM10 and NO2 on Respiratory Health among Children with Asthma or Asthma-like Symptoms: A Systematic Review and Meta-Analysis. Environ. Health Perspect. 2010, 118, 449–457. [Google Scholar] [CrossRef]
- Reed, C.; Evans, M.J.; Di Carlo, P.; Lee, J.D.; Carpenter, L.J. Interferences in photolytic NO2 measurements: explanation for an apparent missing oxidant? Atmos. Chem. Phys. 2016, 16, 4707–4724. [Google Scholar] [CrossRef]
- Saiz-Lopez, A.; Notario, A.; Albaladejo, J.; McFiggans, G. Seasonal variation of NOx loss processes coupled to the HNO3 formation in a daytime urban atmosphere: A model study. Water Air Soil Pollut. 2007, 182, 197–206. [Google Scholar] [CrossRef]
- Li, J.Y.; Mao, J.Q.; Fiore, A.M.; Cohen, R.C.; Crounse, J.D.; Teng, A.P.; Wennberg, P.O.; Lee, B.H.; Lopez-Hilfiker, F.D.; Thornton, J.A.; et al. Decadal changes in summertime reactive oxidized nitrogen and surface ozone over the Southeast United States. Atmos. Chem. Phys. 2018, 18, 2341–2361. [Google Scholar] [CrossRef]
- Stohl, A.; Trainer, M.; Ryerson, T.B.; Holloway, J.S.; Parrish, D.D. Export of NOy from the North American boundary layer during 1996 and 1997 North Atlantic Regional Experiments. J. Geophys. Res. Atmos. 2002, 107, 4131–4140. [Google Scholar] [CrossRef]
- Parrish, D.D.; Ryerson, T.B.; Holloway, J.S.; Neuman, J.A.; Roberts, J.M.; Williams, J.; Stroud, C.A.; Frost, G.J.; Trainer, M.; Hubler, G.; et al. Fraction and composition of NOy transported in air masses lofted from the North American continental boundary layer. J. Geophys. Res. Atmos. 2004, 109, D09302–D09320. [Google Scholar] [CrossRef]
- Gilge, S.; Plass-Duelmer, C.; Galbally, I.; Brough, N.; Bottenheim, J.; Flocke, F.; Gerwig, H.; Lee, J.; Milton, M.; Rohrer, F.; et al. WMO/GAW Expert Workshop on Global Long-term Measurements of Nitrogen Oxides and Recommendations for GAW Nitrogen Oxides Network; World Meteorological Organization (WMO): Geneva, Switzerland, 2011. [Google Scholar]
- Fontijn, A.; Sabadell, A.J.; Ronco, R.J. Homogeneous Chemiluminescent Measurement of Nitric Oxide with Ozone-Implications for Continuous Selective Monitoring of Gaseous Air Pollutants. Anal. Chem. 1970, 42, 575. [Google Scholar] [CrossRef]
- Miller, C.C. Chemiluminescence Analysis and Nitrogen-Dioxide Measurement. Lancet 1994, 343, 300–301. [Google Scholar] [CrossRef]
- Winer, A.M.; Peters, J.W.; Smith, J.P.; Pitts, J.N. Response of Commercial Chemiluminescent NO-NO2 Analyzers to Other Nitrogen-Containing Compounds. Environ. Sci. Technol. 1974, 8, 1118–1121. [Google Scholar] [CrossRef]
- Steinbacher, M.; Zellweger, C.; Schwarzenbach, B.; Bugmann, S.; Buchmann, B.; Ordonez, C.; Prevot, A.S.H.; Hueglin, C. Nitrogen oxide measurements at rural sites in Switzerland: Bias of conventional measurement techniques. J. Geophys. Res. Atmos. 2007, 112, D11307–D11320. [Google Scholar] [CrossRef]
- Villena, G.; Bejan, I.; Kurtenbach, R.; Wiesen, P.; Kleffmann, J. Interferences of commercial NO2 instruments in the urban atmosphere and in a smog chamber. Atmos. Meas. Tech. 2012, 5, 149–159. [Google Scholar] [CrossRef]
- Fuchs, H.; Ball, S.M.; Bohn, B.; Brauers, T.; Cohen, R.C.; Dorn, H.P.; Dube, W.P.; Fry, J.L.; Haseler, R.; Heitmann, U.; et al. Intercomparison of measurements of NO2 concentrations in the atmosphere simulation chamber SAPHIR during the NO3Comp campaign. Atmos. Meas. Tech. 2010, 3, 21–37. [Google Scholar] [CrossRef]
- Rohrer, F.; Bruning, D. Surface NO and NO2 Mixing Ratios Measured between 30° N and 30° S in the Atlantic Region. J. Atmos. Chem. 1992, 15, 253–267. [Google Scholar] [CrossRef]
- Mazurenka, M.I.; Fawcett, B.L.; Elks, J.M.F.; Shallcross, D.E.; Orr-Ewing, A.J. 410-nm diode laser cavity ring-down spectroscopy for trace detection of NO2. Chem. Phys. Lett. 2003, 367, 1–9. [Google Scholar] [CrossRef]
- Kebabian, P.L.; Herndon, S.C.; Freedman, A. Detection of nitrogen dioxide by cavity attenuated phase shift spectroscopy. Anal. Chem. 2005, 77, 724–728. [Google Scholar] [CrossRef] [PubMed]
- Osthoff, H.D.; Brown, S.S.; Ryerson, T.B.; Fortin, T.J.; Lerner, B.M.; Williams, E.J.; Pettersson, A.; Baynard, T.; Dube, W.P.; Ciciora, S.J.; et al. Measurement of atmospheric NO2 by pulsed cavity ring-down spectroscopy. J. Geophys.-Res.-Atmos. 2006, 111. [Google Scholar] [CrossRef]
- Dhiman, C.; Khan, M.S.; Reddy, M.N. Phase-shift Cavity Ring Down Spectroscopy Set-up for NO2 Sensing: Design and Fabrication. Def. Sci. J. 2015, 65, 25–30. [Google Scholar] [CrossRef][Green Version]
- Kebabian, P.L.; Wood, E.C.; Herndon, S.C.; Freedman, A. A practical alternative to chemiluminescence-based detection of nitrogen dioxide: Cavity attenuated phase shift spectroscopy. Environ. Sci. Technol. 2008, 42, 6040–6045. [Google Scholar] [CrossRef]
- Fuchs, H.; Dube, W.P.; Lerner, B.M.; Wagner, N.L.; Williams, E.J.; Brown, S.S. A Sensitive and Versatile Detector for Atmospheric NO2 and NOx Based on Blue Diode Laser Cavity Ring-Down Spectroscopy. Environ. Sci. Technol. 2009, 43, 7831–7836. [Google Scholar] [CrossRef]
- Thieser, J.; Schuster, G.; Schuladen, J.; Phillips, G.J.; Reiffs, A.; Parchatka, U.; Pohler, D.; Lelieveld, J.; Crowley, J.N. A two-channel thermal dissociation cavity ring-down spectrometer for the detection of ambient NO2, RO2NO2 and RONO2. Atmos. Meas. Tech. 2016, 9, 553–576. [Google Scholar] [CrossRef]
- Horii, C.V.; Zahniser, M.S.; Nelson, D.D.; McManus, J.B.; Wofsy, S.C. Nitric acid and nitrogen dioxide flux measurements: A new application of tunable diode laser absorption spectroscopy. Appl. Tunable Diode Other Infrared Sources Atmos. Stud. Ind. Process. Monit. 1999, 152–161. [Google Scholar] [CrossRef]
- Sauer, C.G.; Pisano, J.T.; Fitz, D.R. Tunable diode laser absorption spectrometer measurements of ambient nitrogen dioxide, nitric acid, formaldehyde, and hydrogen peroxide in Parlier, California. Atmos. Environ. 2003, 37, 1583–1591. [Google Scholar] [CrossRef]
- McManus, J.B.; Zahniser, M.S.; Nelson, D.D.; Shorter, J.H.; Herndon, S.; Wood, E.; Wehr, R. Application of quantum cascade lasers to high-precision atmospheric trace gas measurements. Opt. Eng. 2010, 49(11), 111124–111135. [Google Scholar] [CrossRef]
- Lee, B.H.; Wood, E.C.; Zahniser, M.S.; McManus, J.B.; Nelson, D.D.; Herndon, S.C.; Santoni, G.W.; Wofsy, S.C.; Munger, J.W. Simultaneous measurements of atmospheric HONO and NO2 via absorption spectroscopy using tunable mid-infrared continuous-wave quantum cascade lasers. Appl. Phys. Lasers Opt. 2011, 102, 417–423. [Google Scholar] [CrossRef]
- Tuzson, B.; Zeyer, K.; Steinbacher, M.; McManus, J.B.; Nelson, D.D.; Zahniser, M.S.; Emmenegger, L. Selective measurements of NO, NO2 and NOy in the free troposphere using quantum cascade laser spectroscopy. Atmos. Meas. Tech. 2013, 6, 927–936. [Google Scholar] [CrossRef]
- Fehsenfeld, F.C.; Drummond, J.W.; Roychowdhury, U.K.; Galvin, P.J.; Williams, E.J.; Buhr, M.P.; Parrish, D.D.; Hubler, G.; Langford, A.O.; Calvert, J.G.; et al. Intercomparison of NO2 Measurement Techniques. J. Geophys. Res. Atmos. 1990, 95, 3579–3597. [Google Scholar] [CrossRef]
- Zenker, T.; Fischer, H.; Nikitas, C.; Parchatka, U.; Harris, G.W.; Mihelcic, D.; Musgen, P.; Patz, H.W.; Schultz, M.; Volz-Thomas, A.; et al. Intercomparison of NO, NO2, NOy, O3, and ROx measurements during the oxidizing capacity of the tropospheric atmosphere (OCTA) campaign 1993 at Izana. J. Geophys. Res. Atmos. 1998, 103, 13615–13634. [Google Scholar] [CrossRef]
- McManus, J.B.; Zahniser, M.S.; Nelson, D.D. Dual quantum cascade laser trace gas instrument with astigmatic Herriott cell at high pass number. Appl. Opt. 2011, 50, A74–A85. [Google Scholar] [CrossRef]
- Fischer, M.; Tuzson, B.; Hugi, A.; Bronnimann, R.; Kunz, A.; Blaser, S.; Rochat, M.; Landry, O.; Muller, A.; Emmenegger, L. Intermittent operation of QC-lasers for mid-IR spectroscopy with low heat dissipation: tuning characteristics and driving electronics. Opt. Express 2014, 22, 7014–7027. [Google Scholar] [CrossRef]
- Liu, C.; Tuzson, B.; Scheidegger, P.; Looser, H.; Bereiter, B.; Graf, M.; Hundt, M.; Aseev, O.; Maas, D.; Emmenegger, L. Laser driving and data processing concept for mobile trace gas sensing: Design and implementation. Rev. Sci. Instruments 2018, 89. [Google Scholar] [CrossRef]
- Hundt, P.M.; Tuzson, B.; Aseev, O.; Liu, C.; Scheidegger, P.; Looser, H.; Kapsalidis, F.; Shahmohammadi, M.; Faist, J.; Emmenegger, L. Multi-species trace gas sensing with dual-wavelength QCLs. Appl. Phys. Lasers Opt. 2018, 124. [Google Scholar] [CrossRef]
- McManus, J.B. Paraxial matrix description of astigmatic and cylindrical mirror resonators with twisted axes for laser spectroscopy. Appl. Opt. 2007, 46, 472–482. [Google Scholar] [CrossRef]
- Gordon, I.E.; Rothman, L.S.; Hill, C.; Kochanov, R.V.; Tan, Y.; Bernath, P.F.; Birk, M.; Boudon, V.; Campargue, A.; Chance, K.V.; et al. The HITRAN2016 molecular spectroscopic database. J. Quant. Spectrosc. Radiat. Transf. 2017, 203, 3–69. [Google Scholar] [CrossRef]
- McManus, J.B.; Nelson, D.D.; Herndon, S.C.; Shorter, J.H.; Zahniser, M.S.; Blaser, S.; Hvozdara, L.; Muller, A.; Giovannini, M.; Faist, J. Comparison of cw and pulsed operation with a TE-cooled quantum cascade infrared laser for detection of nitric oxide at 1900 cm-1. Appl. Phys. -Lasers Opt. 2006, 85, 235–241. [Google Scholar] [CrossRef]
- Werle, P.; Mucke, R.; Slemr, F. The Limits of Signal Averaging in Atmospheric Trace-Gas Monitoring by Tunable Diode-Laser Absorption-Spectroscopy (TDLAS). Appl. Phys. -Photophys. Laser Chem. 1993, 57, 131–139. [Google Scholar] [CrossRef]
- Li, Y.Q.; Demerjian, K.L.; Zahniser, M.S.; Nelson, D.D.; McManus, J.B.; Herndon, S.C. Measurement of formaldehyde, nitrogen dioxide, and sulfur dioxide at Whiteface Mountain using a dual tunable diode laser system. J. Geophys.-Res.-Atmos. 2004, 109, D16S08–D16S19. [Google Scholar] [CrossRef]
- Hundt, P.M.; Muller, M.; Mangold, M.; Tuzson, B.; Scheidegger, P.; Looser, H.; Huglin, C.; Emmenegger, L. Mid-IR spectrometer for mobile, real-time urban NO2 measurements. Atmos. Meas. Tech. 2018, 11, 2669–2681. [Google Scholar] [CrossRef]
- Pascale, C.; Guillevic, M.; Ackermann, A.; Leuenberger, D.; Niederhauser, B. Two generators to produce SI-traceable reference gas mixtures for reactive compounds at atmospheric levels. Meas. Sci. Technol. 2017, 28. [Google Scholar] [CrossRef]
- Liu, J.W.; Li, X.; Yang, Y.M.; Wang, H.C.; Wu, Y.S.; Lu, X.W.; Chen, M.D.; Hu, J.L.; Fan, X.B.; Zeng, L.M.; et al. An IBBCEAS system for atmospheric measurements of glyoxal and methylglyoxal in the presence of high NO2 concentrations. Atmos. Meas. Tech. 2019, 12, 4439–4453. [Google Scholar] [CrossRef]
- Min, K.E.; Washenfelder, R.A.; Dube, W.P.; Langford, A.O.; Edwards, P.M.; Zarzana, K.J.; Stutz, J.; Lu, K.; Rohrer, F.; Zhang, Y.; et al. A broadband cavity enhanced absorption spectrometer for aircraft measurements of glyoxal, methylglyoxal, nitrous acid, nitrogen dioxide, and water vapor. Atmos. Meas. Tech. 2016, 9, 423–440. [Google Scholar] [CrossRef]
- Miller, C.C.; Jacob, D.J.; Marais, E.A.; Yu, K.R.; Travis, K.R.; Kim, P.S.; Fisher, J.A.; Zhu, L.; Wolfe, G.M.; Hanisco, T.F.; et al. Glyoxal yield from isoprene oxidation and relation to formaldehyde: chemical mechanism, constraints from SENEX aircraft observations, and interpretation of OMI satellite data. Atmos. Chem. Phys. 2017, 17, 8725–8738. [Google Scholar] [CrossRef]
- Volkamer, R.; Molina, L.T.; Molina, M.J.; Shirley, T.; Brune, W.H. DOAS measurement of glyoxal as an indicator for fast VOC chemistry in urban air. Geophys. Res. Lett. 2005, 32, L08806–L08810. [Google Scholar] [CrossRef]
| Reference | OPL (m) / N / D (cm) | Lasers | P (mbar) | (pptv) | (pptv) / Time (s) |
|---|---|---|---|---|---|
| [34] | 204/434/47 | dual | 50 | 20 | 3/180 |
| [33] | 210/238/88 | dual | 53 | 10 | 1.7/60 |
| [45] | 153/174/88 | dual | 33 | 30 | 7/60 |
| this work | 110/274/40 | single | 80 | 5.5 | 0.8/150 |
| this work | 110/274/40 | single | 30 | 9 | 1.6/150 |
| this work | 110/274/40 | dual | 30 | 15 | 4/150 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sobanski, N.; Tuzson, B.; Scheidegger, P.; Looser, H.; Kupferschmid, A.; Iturrate, M.; Pascale, C.; Hüglin, C.; Emmenegger, L. Advances in High-Precision NO2 Measurement by Quantum Cascade Laser Absorption Spectroscopy. Appl. Sci. 2021, 11, 1222. https://doi.org/10.3390/app11031222
Sobanski N, Tuzson B, Scheidegger P, Looser H, Kupferschmid A, Iturrate M, Pascale C, Hüglin C, Emmenegger L. Advances in High-Precision NO2 Measurement by Quantum Cascade Laser Absorption Spectroscopy. Applied Sciences. 2021; 11(3):1222. https://doi.org/10.3390/app11031222
Chicago/Turabian StyleSobanski, Nicolas, Béla Tuzson, Philipp Scheidegger, Herbert Looser, André Kupferschmid, Maitane Iturrate, Céline Pascale, Christoph Hüglin, and Lukas Emmenegger. 2021. "Advances in High-Precision NO2 Measurement by Quantum Cascade Laser Absorption Spectroscopy" Applied Sciences 11, no. 3: 1222. https://doi.org/10.3390/app11031222
APA StyleSobanski, N., Tuzson, B., Scheidegger, P., Looser, H., Kupferschmid, A., Iturrate, M., Pascale, C., Hüglin, C., & Emmenegger, L. (2021). Advances in High-Precision NO2 Measurement by Quantum Cascade Laser Absorption Spectroscopy. Applied Sciences, 11(3), 1222. https://doi.org/10.3390/app11031222






