Recovery and Characterization of Orbital Angular Momentum Modes with Ghost Diffraction Holography
Abstract
:1. Introduction
2. Principle and Methods
2.1. Generation and Recovery of OAM Modes
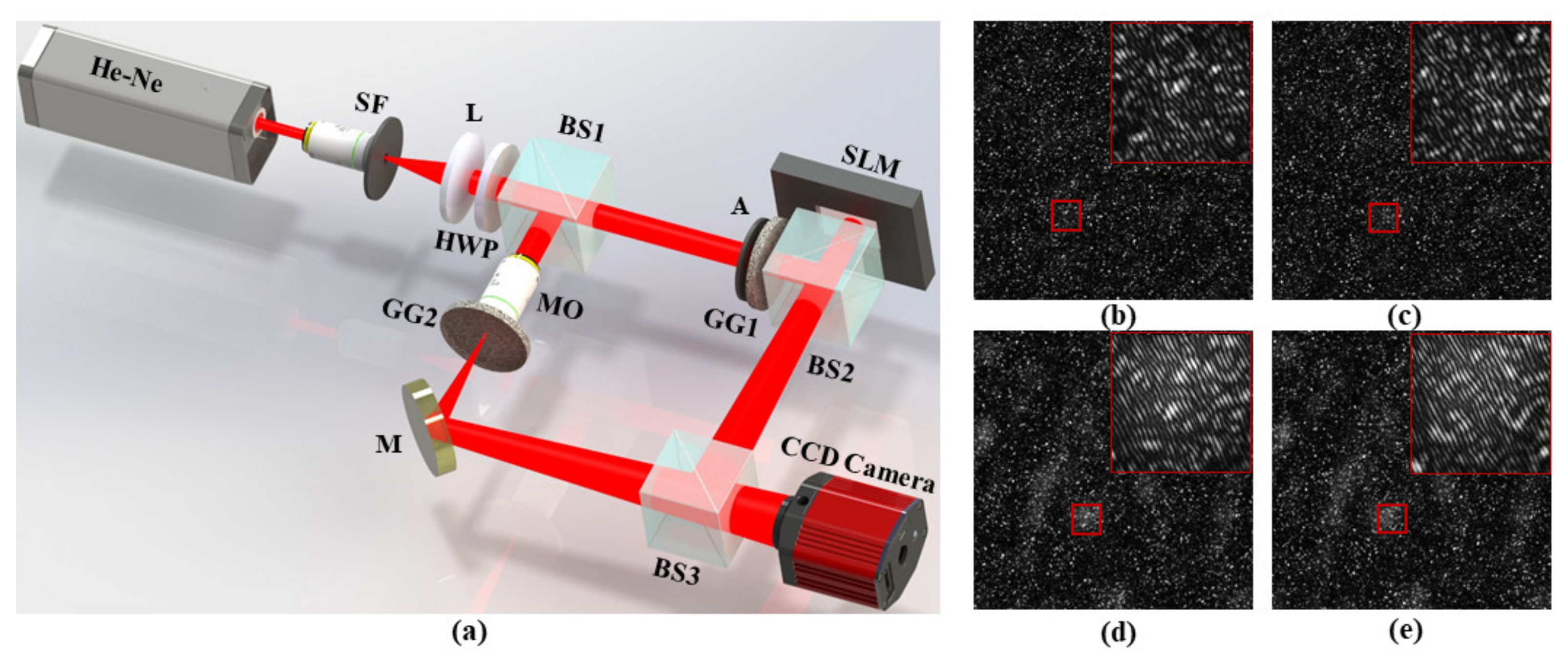
2.2. Experimental Design and Recovery Scheme
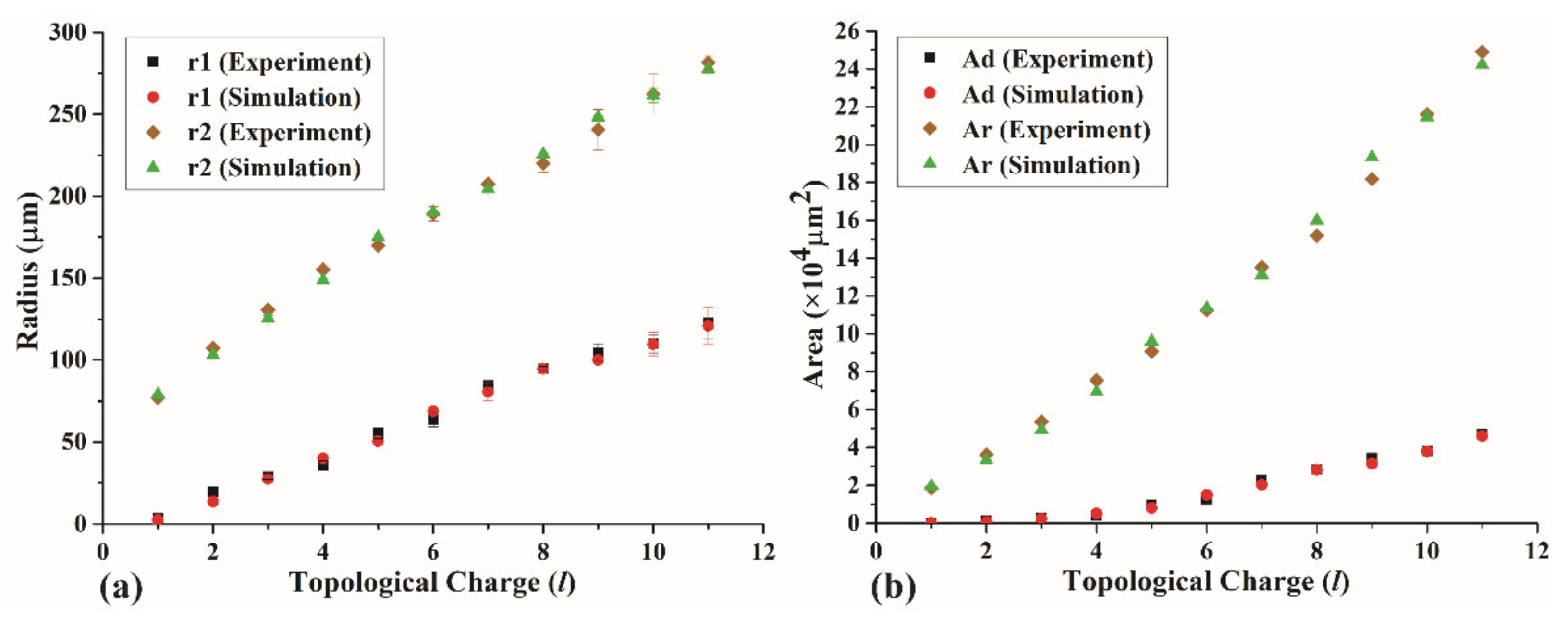
3. Results and Discussion
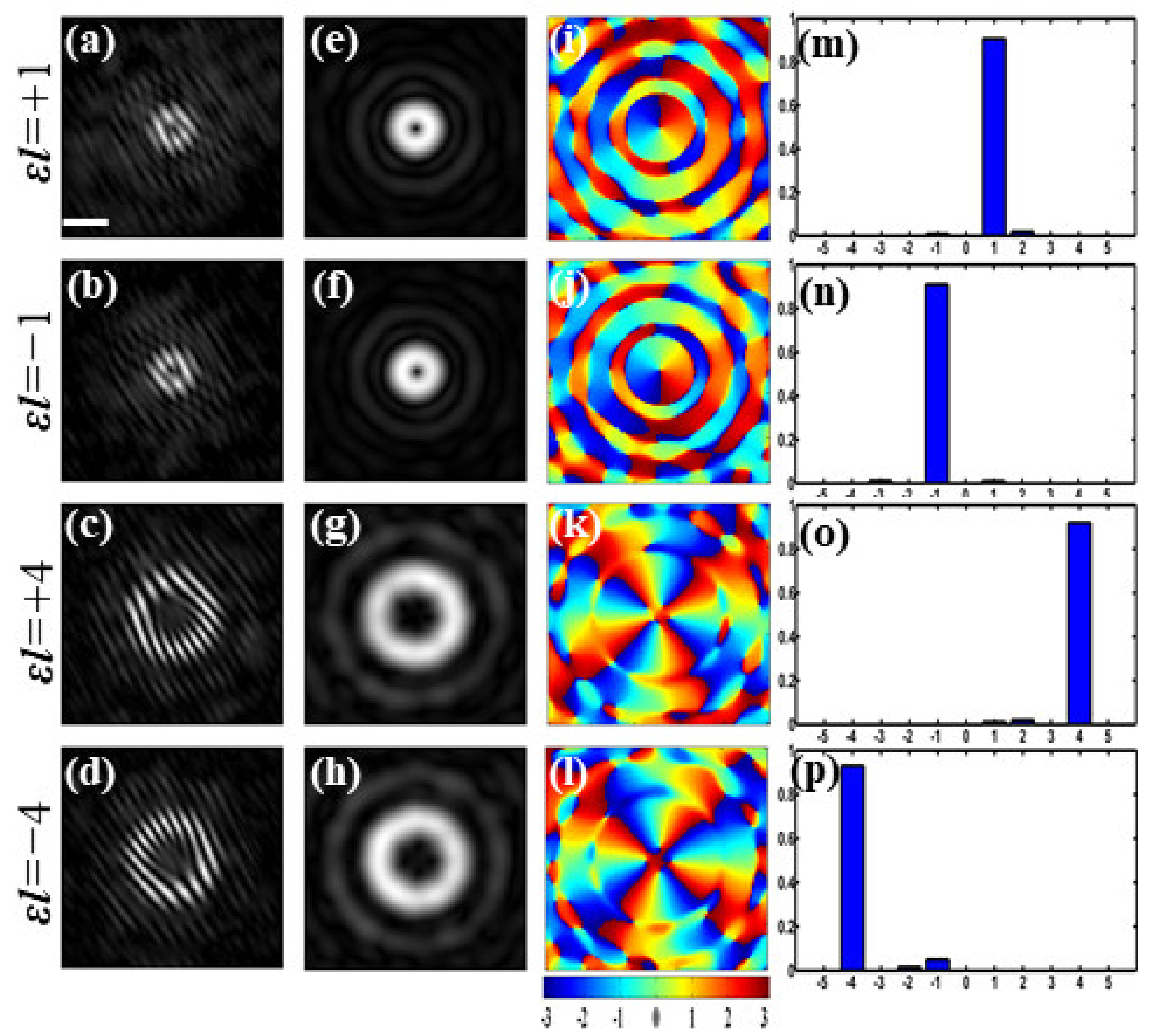
3.1. Simulation Results
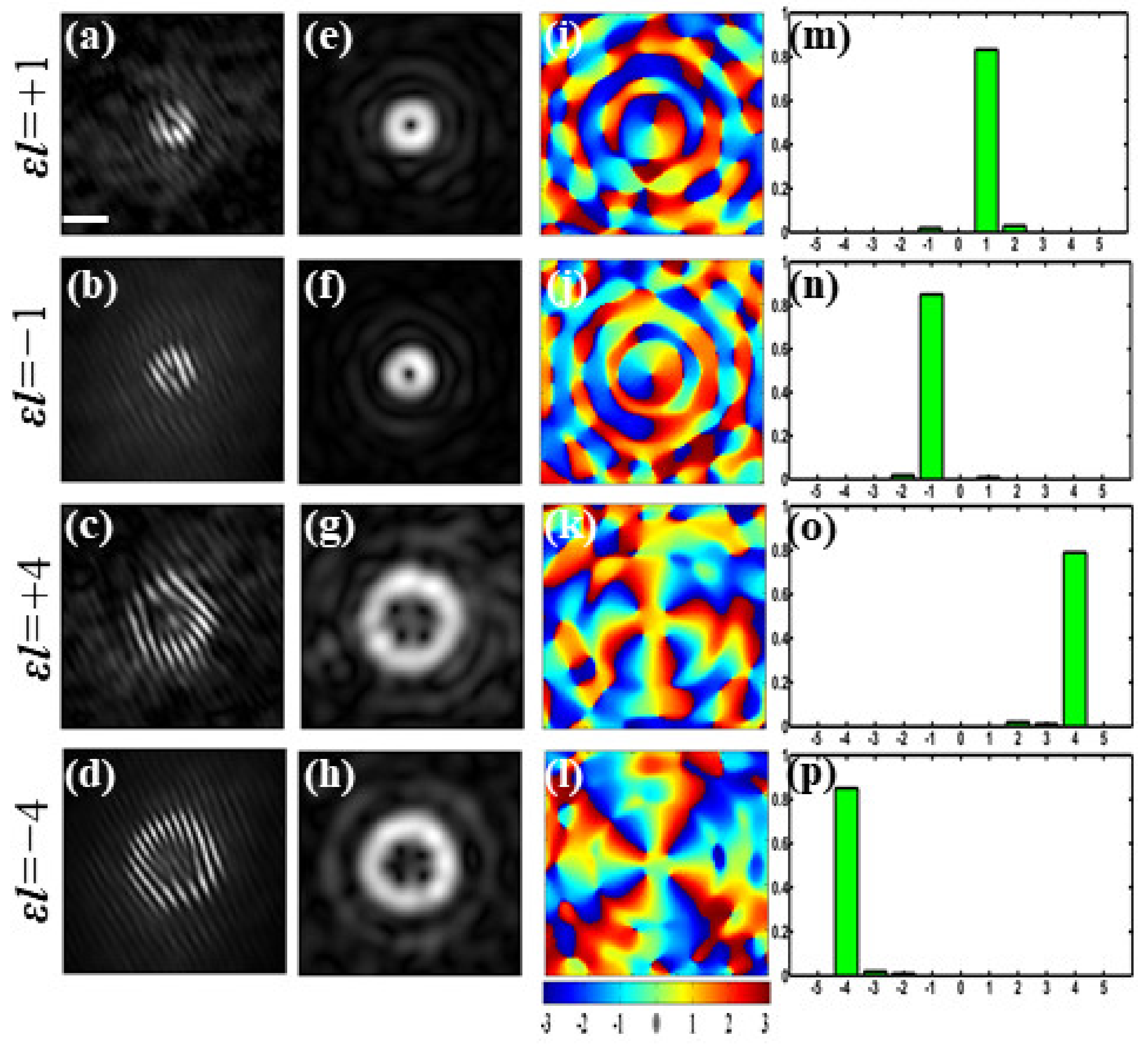
3.2. Experimental Results
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yao, A.M.; Padgett, M.J. Orbital Angular Momentum: Origins, Behavior and Applications. Adv. Opt. Photonics 2011, 3, 161. [Google Scholar] [CrossRef] [Green Version]
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.C.; Woerdman, J.P. Orbital Angular Momentum of Light and the Transformation of Laguerre-Gaussian Laser Modes. Phys. Rev. A 1992, 45, 8185–8189. [Google Scholar] [CrossRef] [PubMed]
- GBUR, G.J. Singular optics. Prog. Opt. 2021, 42, 219–276. [Google Scholar]
- Chen, R.; Zhou, H.; Moretti, M.; Wang, X.; Li, J. Orbital Angular Momentum Waves: Generation, Detection, and Emerging Applications. IEEE Commun. Surv. Tutor. 2020, 22, 840–868. [Google Scholar] [CrossRef] [Green Version]
- Willner, A.E.; Ren, Y.; Xie, G.; Yan, Y.; Li, L.; Zhao, Z.; Wang, J.; Tur, M.; Molisch, A.F.; Ashrafi, S. Recent Advances in High-Capacity Free-Space Optical and Radio-Frequency Communications Using Orbital Angular Momentum Multiplexing. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2017, 375, 20150439. [Google Scholar] [CrossRef] [PubMed]
- Gori, F.; Santarsiero, M.; Borghi, R.; Vicalvi, S. Partially Coherent Sources with Helicoidal Modes. J. Mod. Opt. 1998, 45, 539–554. [Google Scholar] [CrossRef]
- Gbur, G.; Visser, T.D. Phase Singularities and Coherence Vortices in Linear Optical Systems. Opt. Commun. 2006, 259, 428–435. [Google Scholar] [CrossRef]
- Zeng, J.; Lin, R.; Liu, X.; Zhao, C.; Cai, Y. Review on Partially Coherent Vortex Beams. Front. Optoelectron. 2019, 12, 229–248. [Google Scholar] [CrossRef]
- Bogatyryova, G.V.; Fel’de, C.V.; Polyanskii, P.V.; Ponomarenko, S.A.; Soskin, M.S.; Wolf, E. Partially Coherent Vortex Beams with a Separable Phase. Opt. Lett. 2003, 28, 878. [Google Scholar] [CrossRef]
- Palacios, D.M.; Maleev, I.D.; Marathay, A.S.; Swartzlander, G.A. Spatial Correlation Singularity of a Vortex Field. Phys. Rev. Lett. 2004, 92, 143905. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Duan, Z.; Hanson, S.G.; Miyamoto, Y.; Takeda, M. Experimental Study of Coherence Vortices: Local Properties of Phase Singularities in a Spatial Coherence Function. Phys. Rev. Lett. 2006, 96, 073902. [Google Scholar] [CrossRef]
- Perez-Garcia, B.; Yepiz, A.; Hernandez-Aranda, R.I.; Forbes, A.; Swartzlander, G.A. Digital Generation of Partially Coherent Vortex Beams. Opt. Lett. 2016, 41, 3471. [Google Scholar] [CrossRef]
- Liu, M.-J.; Chen, J.; Zhang, Y.; Shi, Y.; Zhao, C.-L.; Jin, S.-Z. Generation of Coherence Vortex by Modulating the Correlation Structure of Random Lights. Photonics Res. 2019, 7, 1485. [Google Scholar] [CrossRef]
- Singh, R.K.; Sharma, A.M.; Senthilkumaran, P. Vortex Array Embedded in a Partially Coherent Beam. Opt. Lett. 2015, 40, 2751. [Google Scholar] [CrossRef]
- Jesus-Silva, A.J.; Hickmann, J.M.; Fonseca, E.J.S. Strong Correlations between Incoherent Vortices. Opt. Express 2012, 20, 19708. [Google Scholar] [CrossRef]
- Reddy, S.G.; Prabhakar, S.; Kumar, A.; Banerji, J.; Singh, R.P. Higher Order Optical Vortices and Formation of Speckles. Opt. Lett. 2014, 39, 4364. [Google Scholar] [CrossRef] [Green Version]
- Salla, G.R.; Perumangattu, C.; Prabhakar, S.; Anwar, A.; Singh, R.P. Recovering the Vorticity of a Light Beam after Scattering. Appl. Phys. Lett. 2015, 107, 021104. [Google Scholar] [CrossRef]
- Vinu, R.V.; Singh, R.K. Determining Helicity and Topological Structure of Coherent Vortex Beam from Laser Speckle. Appl. Phys. Lett. 2016, 109, 111108. [Google Scholar] [CrossRef]
- Sarkar, T.; Parvin, R.; Brundavanam, M.M.; Singh, R.K. Higher-Order Stokes-Parameter Correlation to Restore the Twisted Wave Front Propagating through a Scattering Medium. Phys. Rev. A 2021, 104, 013525. [Google Scholar] [CrossRef]
- Yang, Y.; Mazilu, M.; Dholakia, K. Measuring the Orbital Angular Momentum of Partially Coherent Optical Vortices through Singularities in Their Cross-Spectral Density Functions. Opt. Lett. 2012, 37, 4949. [Google Scholar] [CrossRef] [Green Version]
- Ding, P.F.; Pu, J. The Cross Correlation Function of Partially Coherent Vortex Beam. Opt. Express 2014, 22, 1350. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.; Zhao, C.; Shao, Y.; Zeng, J.; Konijnenberg, S.; Zhu, X.; Popov, S.; Urbach, H.P.; Cai, Y. Phase Detection of Coherence Singularities and Determination of the Topological Charge of a Partially Coherent Vortex Beam. Appl. Phys. Lett. 2019, 114, 201106. [Google Scholar] [CrossRef]
- Wang, T.; Pu, J.; Chen, Z. Propagation of Partially Coherent Vortex Beams in a Turbulent Atmosphere. Opt. Eng. 2008, 47, 036002. [Google Scholar] [CrossRef]
- Jesus-Silva, A.J.; Alves, C.R.; Fonseca, E.J.S. Robustness of a Coherence Vortex. Appl. Opt. 2016, 55, 7544–7549. [Google Scholar] [CrossRef]
- Chen, J.; Li, Y. Discrimination of Incoherent Vortex States of Light. Opt. Lett. 2018, 43, 5595. [Google Scholar] [CrossRef]
- Bezerra, D.O.; Amaral, J.P.; Fonseca, E.J.S.; Alves, C.R.; Jesus-Silva, A.J. Sorting of Spatially Incoherent Optical Vortex Modes. Sci. Rep. 2020, 10, 1–7. [Google Scholar] [CrossRef]
- Goodman, J.W. Introduction to Fourier Optics; McGraw-Hill: New York, NY, USA, 1996. [Google Scholar]
- Goodman, J.W. Speckle Phenomena in Optics: Theory and Applications; Roberts & Co.: Sydney, Australia, 2007. [Google Scholar]
- Borghi, R.; Gori, F.; Santarsiero, M. Phase and Amplitude Retrieval in Ghost Diffraction from Field-Correlation Measurements. Phys. Rev. Lett. 2006, 96, 183901. [Google Scholar] [CrossRef] [Green Version]
- Reed, I.S. On a Moment Theorem for Complex Gaussian Processes. IRE Trans. Inf. Theory 1962, 8, 194–195. [Google Scholar] [CrossRef]
- Singh, R.K.; Vinu, R.V.; Sharma, M.A. Recovery of Complex Valued Objects from Two-Point Intensity Correlation Measurement. Appl. Phys. Lett. 2014, 104, 111108. [Google Scholar] [CrossRef]
- Vinu, R.V.; Chen, Z.; Singh, R.K.; Pu, J. Ghost Diffraction Holographic Microscopy. Optica 2020, 7, 1697. [Google Scholar] [CrossRef]
- Takeda, M.; Wang, W.; Naik, D.N.; Singh, R.K. Spatial Statistical Optics and Spatial Correlation Holography: A Review. Opt. Rev. 2014, 21, 849–861. [Google Scholar] [CrossRef]
- Takeda, M. Spatial Stationarity of Statistical Optical Fields for Coherence Holography and Photon Correlation Holography. Opt. Lett. 2013, 38, 3452–3455. [Google Scholar] [CrossRef]
- Li, C.; Chen, Z.; Singh, R.K.; Vinu, R.V.; Pu, J. Increasing field of view and signal to noise ratio in the quantitative phase imaging with phase shifting holography based on the Hanbury Brown-Twiss approach. Opt. Lasers Eng. 2022, 148, 106771. [Google Scholar] [CrossRef]
- Kreis, T. Handbook of Holographic Interferometry; Wiley-VCH: Weinheim, Germany, 2005; ISBN 3527405461. [Google Scholar]
- Singh, R.K.; Vyas, S.; Miyamoto, Y. Lensless Fourier Transform Holography for Coherence Waves. J. Opt. 2017, 19, 115705. [Google Scholar] [CrossRef]
- Takeda, M.; Ina, H.; Kobayashi, S. Fourier-Transform Method of Fringe-Pattern Analysis for Computer-Based Topography and Interferometry. J. Opt. Soc. Am. 1982, 72, 156–160. [Google Scholar] [CrossRef]
- D’Errico, A.; Piccirillo, B.; Cardano, F.; Marrucci, L.; D’Amelio, R. Measuring the Complex Orbital Angular Momentum Spectrum and Spatial Mode Decomposition of Structured Light Beams. Optica 2017, 4, 1350–1357. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Huang, S.-J.; Zhu, F.-Q.; Shao, W.; Chen, M.-S. Dimensional properties of Laguerre-Gaussian vortex beams. Appl. Opt. 2017, 56, 3556. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; R.V., V.; Chen, Z.; Sarkar, T.; Singh, R.K.; Pu, J. Recovery and Characterization of Orbital Angular Momentum Modes with Ghost Diffraction Holography. Appl. Sci. 2021, 11, 12167. https://doi.org/10.3390/app112412167
Huang Y, R.V. V, Chen Z, Sarkar T, Singh RK, Pu J. Recovery and Characterization of Orbital Angular Momentum Modes with Ghost Diffraction Holography. Applied Sciences. 2021; 11(24):12167. https://doi.org/10.3390/app112412167
Chicago/Turabian StyleHuang, Yanyan, Vinu R.V., Ziyang Chen, Tushar Sarkar, Rakesh Kumar Singh, and Jixiong Pu. 2021. "Recovery and Characterization of Orbital Angular Momentum Modes with Ghost Diffraction Holography" Applied Sciences 11, no. 24: 12167. https://doi.org/10.3390/app112412167
APA StyleHuang, Y., R.V., V., Chen, Z., Sarkar, T., Singh, R. K., & Pu, J. (2021). Recovery and Characterization of Orbital Angular Momentum Modes with Ghost Diffraction Holography. Applied Sciences, 11(24), 12167. https://doi.org/10.3390/app112412167






