Estimation of the Tapered Gutenberg-Richter Distribution Parameters for Catalogs with Variable Completeness: An Application to the Atlantic Ridge Seismicity
Abstract
1. Introduction
2. Methods
2.1. Maximum Likelihood Estimation of the Parameters
2.2. Estimation of the Uncertainties
3. Data
4. Results
5. Discussion
6. Conclusions
- (1)
- We introduce a new method to estimate the parameters of the tapered Gutenberg-Richter distribution and their uncertainties in the case of catalogs with a variable through-time magnitude of completeness;
- (2)
- We apply this method to the Atlantic ridge seismicity, finding a clear distinct behavior both for the parameters and corner magnitude, depending on the faulting mechanism: larger and smaller corner magnitude for normal events, smaller and larger corner magnitude for strike-slip events.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Abbreviation | Meaning |
| Mmax | Maximum magnitude |
| MLE | Maximum likelihood estimation |
| Mmin | Magnitude of completeness |
| CMT | Centroid moment tensor catalog |
| CM | Corner magnitude |
References
- Gutenberg, B.; Richter, C.F. Frequency of earthquakes in California. Bull. Seismol. Soc. Am. 1944, 34, 185–188. [Google Scholar] [CrossRef]
- Aki, K. Maximum likelihood estimate of b in the formula logN = a − bM and its confidence limits. Bull. Earthq. Res. Inst. 1965, 43, 237–239. [Google Scholar]
- Kagan, Y.Y. Seismic moment distribution revisited: I. Statistical results. Geophys. J. Int. 2002, 148, 520–541. [Google Scholar] [CrossRef]
- Zöller, G.; Holschneider, M. The earthquake history in a fault zone tells us almost nothing about mmax. Seismol. Res. Lett. 2016, 87, 132–137. [Google Scholar] [CrossRef]
- Holschneider, M.; Zöller, G.; Hainzl, S. Estimation of the maximum possible magnitude in the framework of a doubly truncated Gutenberg–Richter model. Bull. Seismol. Soc. Am. 2011, 101, 1649–1659. [Google Scholar] [CrossRef]
- Zöller, G.; Holschneider, M.; Hainzl, S. The maximum earthquake magnitude in a time horizon: Theory and case studies. Bull. Seismol. Soc. Am. 2013, 103, 860–875. [Google Scholar] [CrossRef]
- Geist, E.L.; Parsons, T. Undersampling power-law size distributions: Effect on the assessment of extreme natural hazards. Nat. Hazards 2014, 72, 565–595. [Google Scholar] [CrossRef]
- Kagan, Y.Y.; Schoenberg, F. Estimation of the upper cutoff parameter for the tapered Pareto distribution. J. Appl. Probab. 2001, 38, 168–185. [Google Scholar] [CrossRef]
- Schoenberg, F.P.; Patel, R.D. Comparison of Pareto and tapered Pareto distributions for environmental phenomena. Eur. Phys. J. Spec. Top. 2012, 205, 159–166. [Google Scholar] [CrossRef]
- Kijko, A.; Sellevoll, M.A. Estimation of earthquake hazard parameters from incomplete data files. Part I. Utilization of extreme and complete catalogs with different threshold magnitudes. Bull. Seismol. Soc. Am. 1989, 79, 645–654. [Google Scholar] [CrossRef]
- Weichert, D.H. Estimation of the earthquake recurrence parameters for unequal observation periods for different magnitudes. Bull. Seismol. Soc. Am. 1980, 70, 1337–1346. [Google Scholar] [CrossRef]
- Taroni, M.; Selva, J. GR_EST: An OCTAVE/MATLAB Toolbox to Estimate Gutenberg–Richter Law Parameters and Their Uncertainties. Seismol. Res. Lett. 2021, 92, 508–516. [Google Scholar] [CrossRef]
- Kagan, Y.Y. Earthquake number forecasts testing. Geophys. J. Int. 2017, 211, 335–345. [Google Scholar] [CrossRef][Green Version]
- Taroni, M.; Akinci, A. Good practices in PSHA: Declustering, b-value estimation, foreshocks and aftershocks inclusion; a case study in Italy. Geophys. J. Int. 2021, 224, 1174–1187. [Google Scholar] [CrossRef]
- Bird, P.; Kagan, Y.Y.; Jackson D., D. Plate tectonics and earthquake potential of spreading ridges and oceanic transform faults. In Plate Boundary Zones; Stein, S., Freymueller, J.T., Eds.; AGU: Washington, DC, USA, 2002; Volume 30, pp. 203–218. [Google Scholar]
- Bird, P.; Kagan, Y.Y. Plate-tectonic analysis of shallow seismicity: Apparent boundary width, beta, corner magnitude, coupled lithosphere thickness, and coupling in seven tectonic settings. Bull. Seismol. Soc. Am. 2004, 94, 2380–2399. [Google Scholar] [CrossRef]
- Kanamori, H. The energy release in great earthquakes. J. Geophys. Res. 1977, 82, 2981–2987. [Google Scholar] [CrossRef]
- Vere-Jones, D.; Robinson, R.; Yang, W. Remarks on the accelerated moment release model: Problems of model formulation, simulation and estimation. Geophys. J. Int. 2001, 144, 517–531. [Google Scholar] [CrossRef]
- Kagan, Y.Y.; Bird, P.; Jackson, D.D. Earthquake patterns in diverse tectonic zones of the globe. Pure Appl. Geophys. 2010, 167, 721–741. [Google Scholar] [CrossRef]
- Wilks, S.S. Mathematical Statistics; Wiley: New York, NY, USA, 1962. [Google Scholar]
- Venzon, D.J.; Moolgavkar, S.H. A method for computing profile-likelihood-based confidence intervals. J. R. Stat. Soc. Ser. C Appl. Stat. 1988, 37, 87–94. [Google Scholar] [CrossRef]
- Dziewonski, A.M.; Chou, T.-A.; Woodhouse, J.H. Determination of earthquake source parameters from waveform data for studies of global and regional seismicity. J. Geophys. Res. 1981, 86, 2825–2852. [Google Scholar] [CrossRef]
- Ekström, G.; Nettles, M.; Dziewonski, A.M. The global CMT project 2004–2010: Centroid-moment tensors for 13,017 earthquakes. Phys. Earth Planet. Inter. 2012, 200–201, 1–9. [Google Scholar] [CrossRef]
- Mizrahi, L.; Nandan, S.; Wiemer, S. The effect of declustering on the size distribution of mainshocks. Seismol. Res. Lett. 2021, 92, 2333–2342. [Google Scholar] [CrossRef]
- Marzocchi, W.; Spassiani, I.; Stallone, A.; Taroni, M. How to be fooled searching for significant variations of the b-value. Geophys. J. Int. 2020, 220, 1845–1856. [Google Scholar] [CrossRef]
- Lilliefors, H.W. On the Kolmogorov-Smirnov test for the exponential distribution with mean unknown. J. Am. Stat. Assoc. 1969, 64, 387–389. [Google Scholar] [CrossRef]
- Taroni, M. Back to the future: Old methods for new estimation and test of the Gutenberg-Richter b-value for catalogs with variable completeness. Geophys. J. Int. 2021, 224, 337–339. [Google Scholar] [CrossRef]
- Zhuang, J.; Ogata, Y.; Wang, T. Data completeness of the Kumamoto earthquake sequence in the JMA catalog and its influence on the estimation of the ETAS parameters. Earth Planets Space 2017, 69, 1–12. [Google Scholar] [CrossRef]
- Schorlemmer, D.; Wiemer, S.; Wyss, M. Variations in earthquake-size distribution across different stress regimes. Nature 2005, 437, 539–542. [Google Scholar] [CrossRef] [PubMed]
- Douglas, J.; Edwards, B. Recent and future developments in earthquake ground motion estimation. Earth-Sci. Rev. 2016, 160, 203–219. [Google Scholar] [CrossRef]
- Grezio, A.; Babeyko, A.; Baptista, M.A.; Behrens, J.; Costa, A.; Davies, G.; Geist, E.; Glimsdal, S.; Gonzales, F.I.; Griffin, J.; et al. Probabilistic Tsunami Hazard Analysis: Multiple Sources and Global Applications. Rev. Geophys. 2017, 55. [Google Scholar] [CrossRef]
- Selva, J.; Tonini, R.; Molinari, I.; Tiberti, M.M.; Romano, F.; Grezio, A.; Melini, D.; Piatanesi, A.; Basili, R.; Lorito, S. Quantification of source uncertainties in Seismic Probabilistic Tsunami Hazard Analysis (SPTHA). Geophys. J. Int. 2016, 205, 1780–1803. [Google Scholar] [CrossRef]

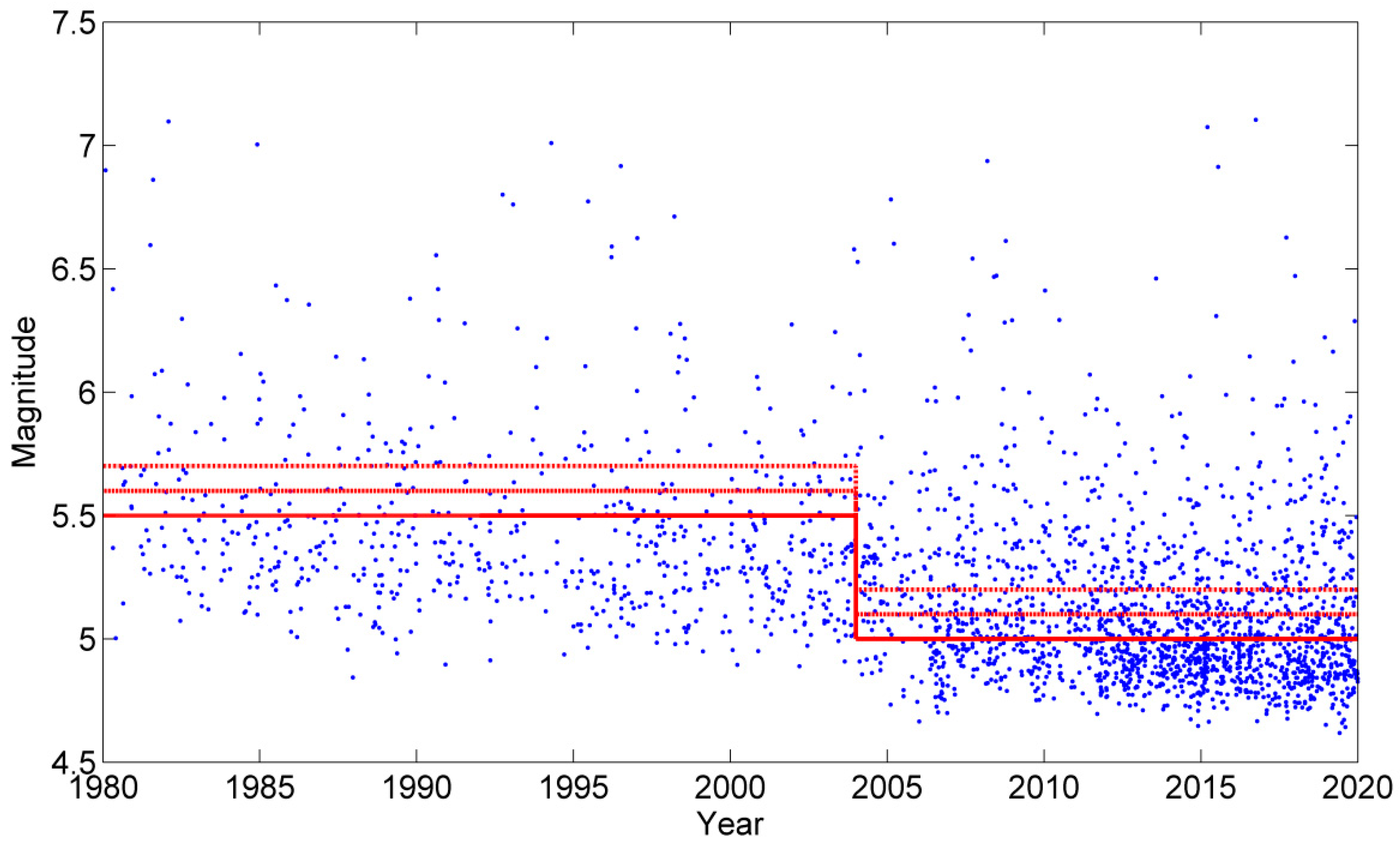

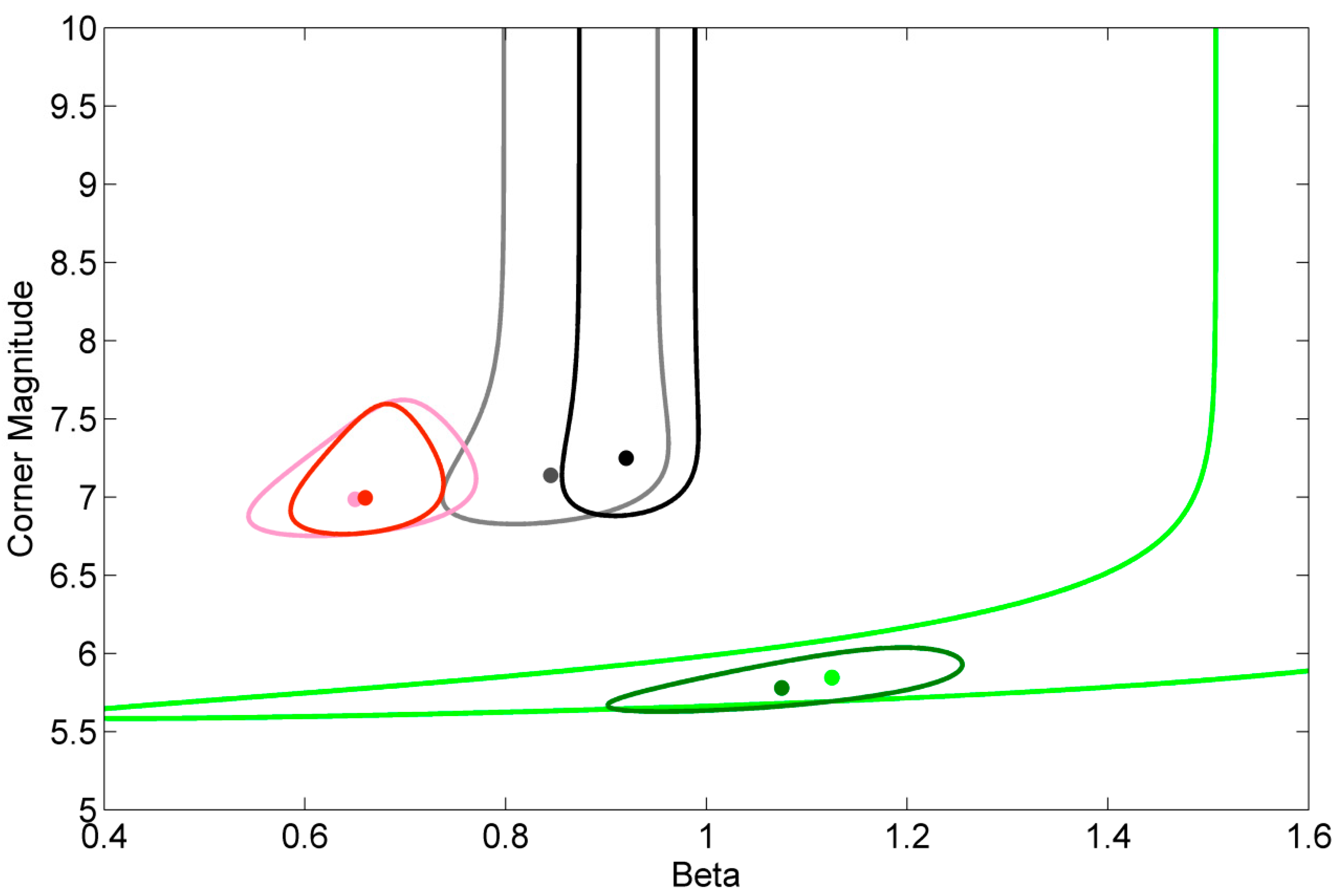
| Number of Simulated Events | Magnitude of Completeness Thresholds | Percentage of Events for Each Completeness | for the Simulations | Percentage of Confidence Regions Containing the Values Used in the Simulations | |||
|---|---|---|---|---|---|---|---|
| 100 | 5.5; 5.0 | 50%; 50% | 0.67 | 0.659 | 6.5 | 6.467 | 94.0% |
| 1000 | 5.5; 5.0 | 50%; 50% | 0.67 | 0.669 | 6.5 | 6.498 | 95.0% |
| 100 | 6.0; 5.0 | 25%; 75% | 0.80 | 0.785 | 7.5 | 7.232 | 93.1% |
| 1000 | 6.0; 5.0 | 25%; 75% | 0.80 | 0.798 | 7.5 | 7.459 | 95.2% |
| 100 | 6.5; 5.3 | 75%; 25% | 0.55 | 0.546 | 7.0 | 6.992 | 94.9% |
| 1000 | 6.5; 5.3 | 75%; 25% | 0.55 | 0.551 | 7.0 | 7.001 | 94.7% |
| Type | Number of Events | Percentage | Maximum Observed Magnitude |
|---|---|---|---|
| Whole catalog | 1168 | 100% | 7.10 |
| Normal events | 595 | 50.9% | 6.14 |
| Strike-slip events | 523 | 44.8% | 7.10 |
| Thrust events | 27 | 2.3% | 6.31 |
| Undefined | 23 | 2.0% | 5.83 |
| Type | Corner Magnitude (MLE) | (MLE) |
|---|---|---|
| Whole catalog | 7.25 | 0.92 |
| Normal events | 5.78 | 1.08 |
| Strike-slip events | 7.01 | 0.66 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taroni, M.; Selva, J.; Zhuang, J. Estimation of the Tapered Gutenberg-Richter Distribution Parameters for Catalogs with Variable Completeness: An Application to the Atlantic Ridge Seismicity. Appl. Sci. 2021, 11, 12166. https://doi.org/10.3390/app112412166
Taroni M, Selva J, Zhuang J. Estimation of the Tapered Gutenberg-Richter Distribution Parameters for Catalogs with Variable Completeness: An Application to the Atlantic Ridge Seismicity. Applied Sciences. 2021; 11(24):12166. https://doi.org/10.3390/app112412166
Chicago/Turabian StyleTaroni, Matteo, Jacopo Selva, and Jiancang Zhuang. 2021. "Estimation of the Tapered Gutenberg-Richter Distribution Parameters for Catalogs with Variable Completeness: An Application to the Atlantic Ridge Seismicity" Applied Sciences 11, no. 24: 12166. https://doi.org/10.3390/app112412166
APA StyleTaroni, M., Selva, J., & Zhuang, J. (2021). Estimation of the Tapered Gutenberg-Richter Distribution Parameters for Catalogs with Variable Completeness: An Application to the Atlantic Ridge Seismicity. Applied Sciences, 11(24), 12166. https://doi.org/10.3390/app112412166







