Electrochemical Characterization of Novel Polyantimonic-Acid-Based Proton Conductors for Low- and Intermediate-Temperature Fuel Cells
Abstract
:1. Introduction
2. Materials and Methods
2.1. PAA-Based Membrane Fabrication
2.2. Structure Characterization of Samples
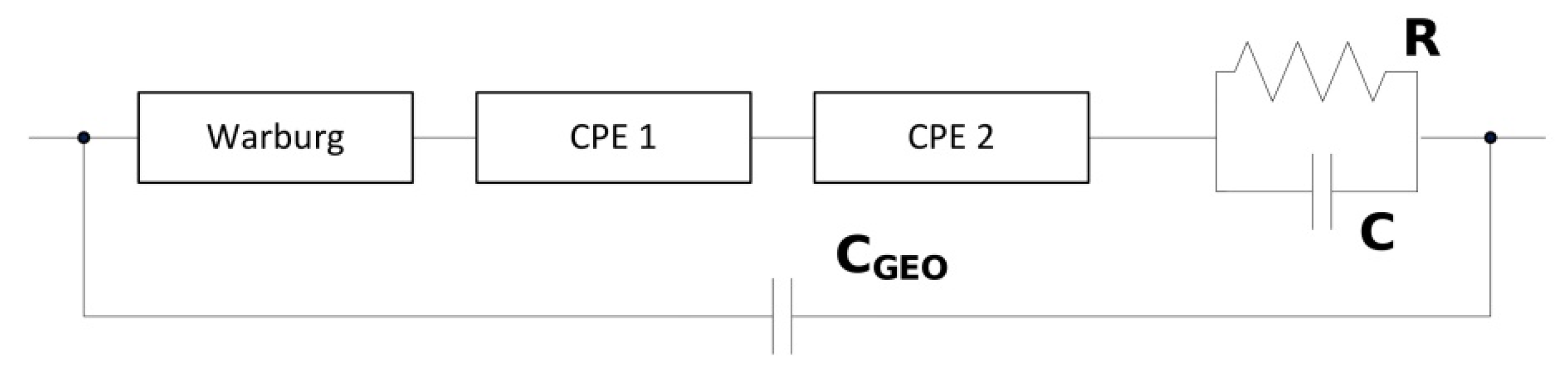
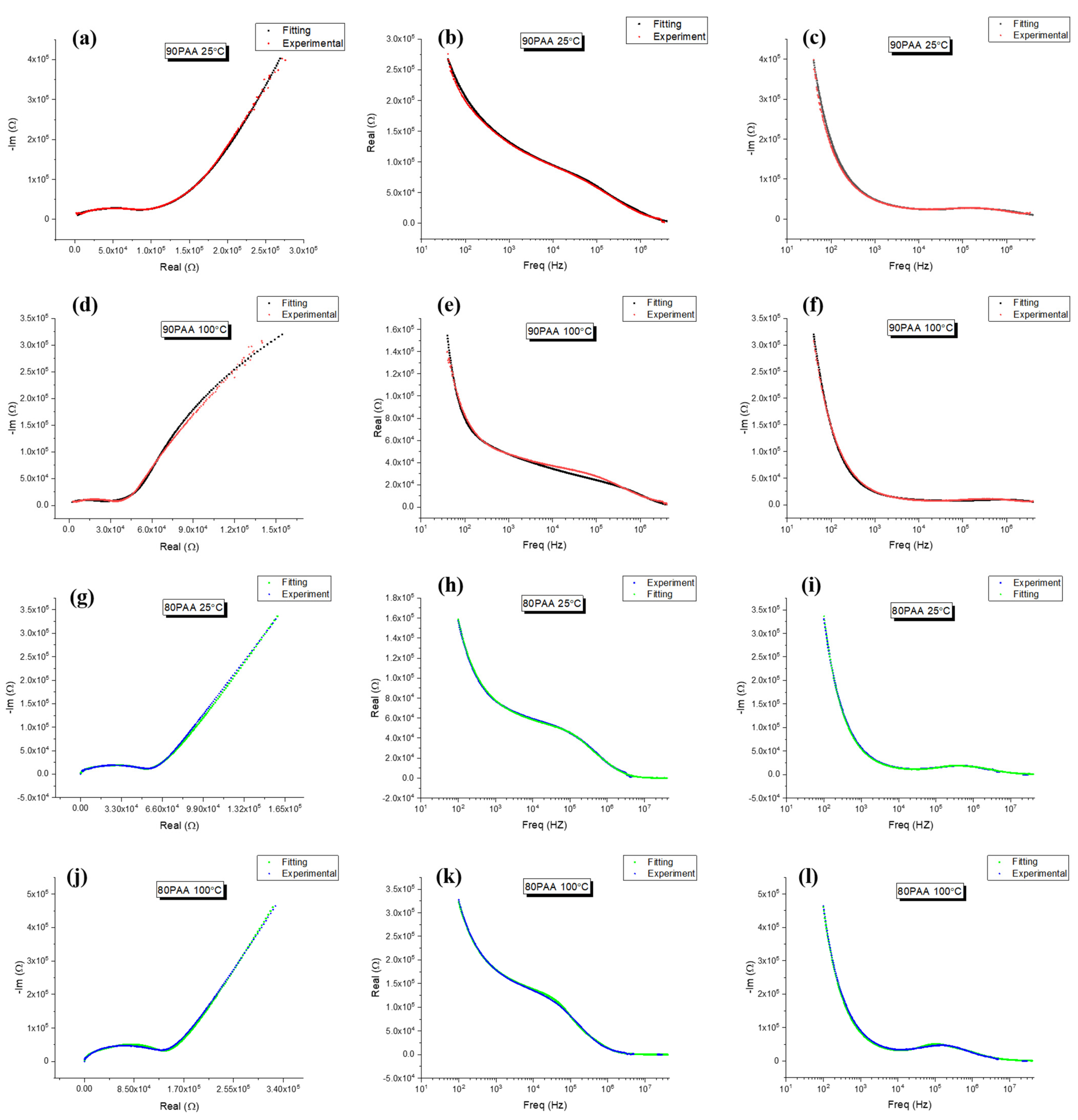
2.3. Electrical Response Measurements
3. Results
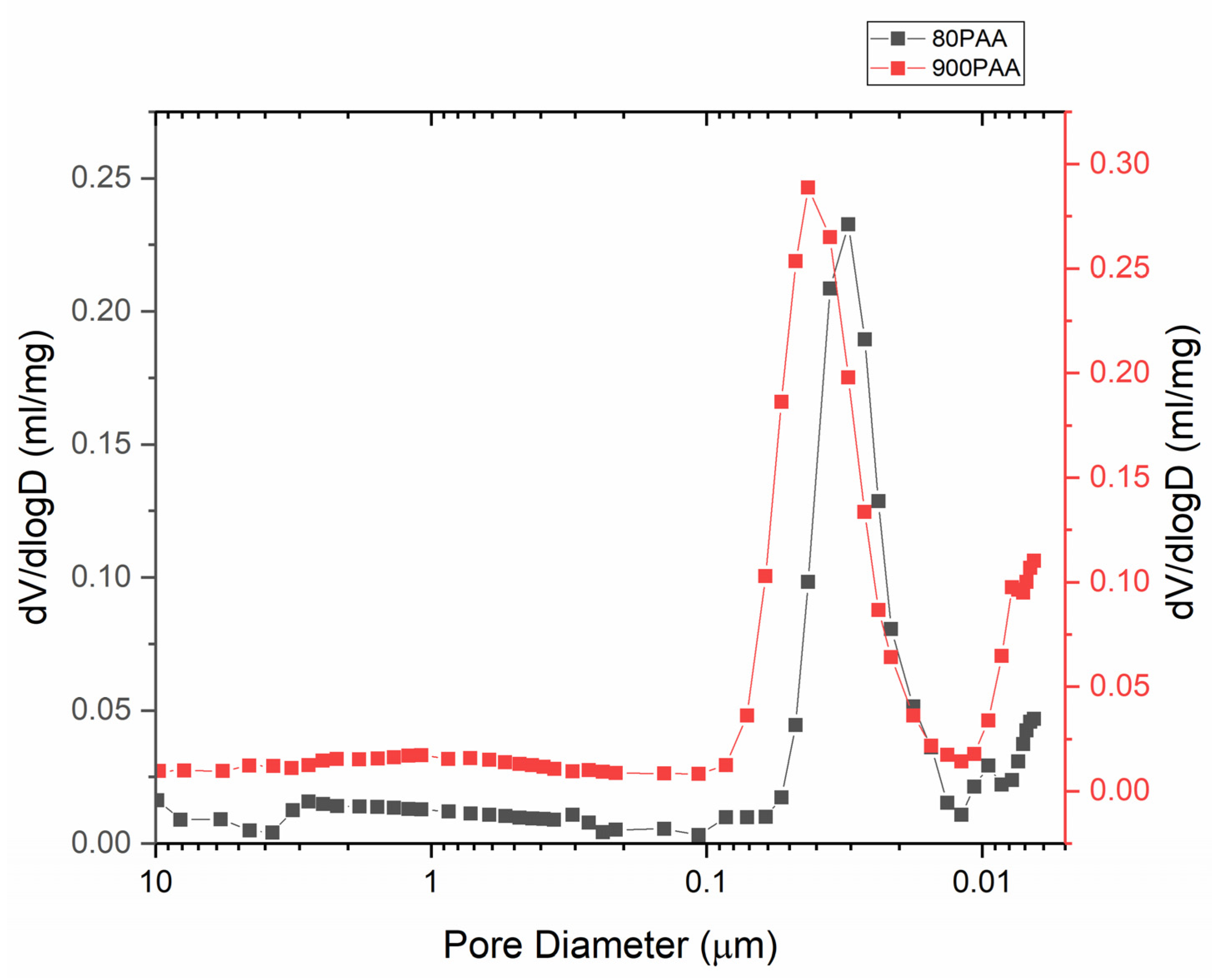
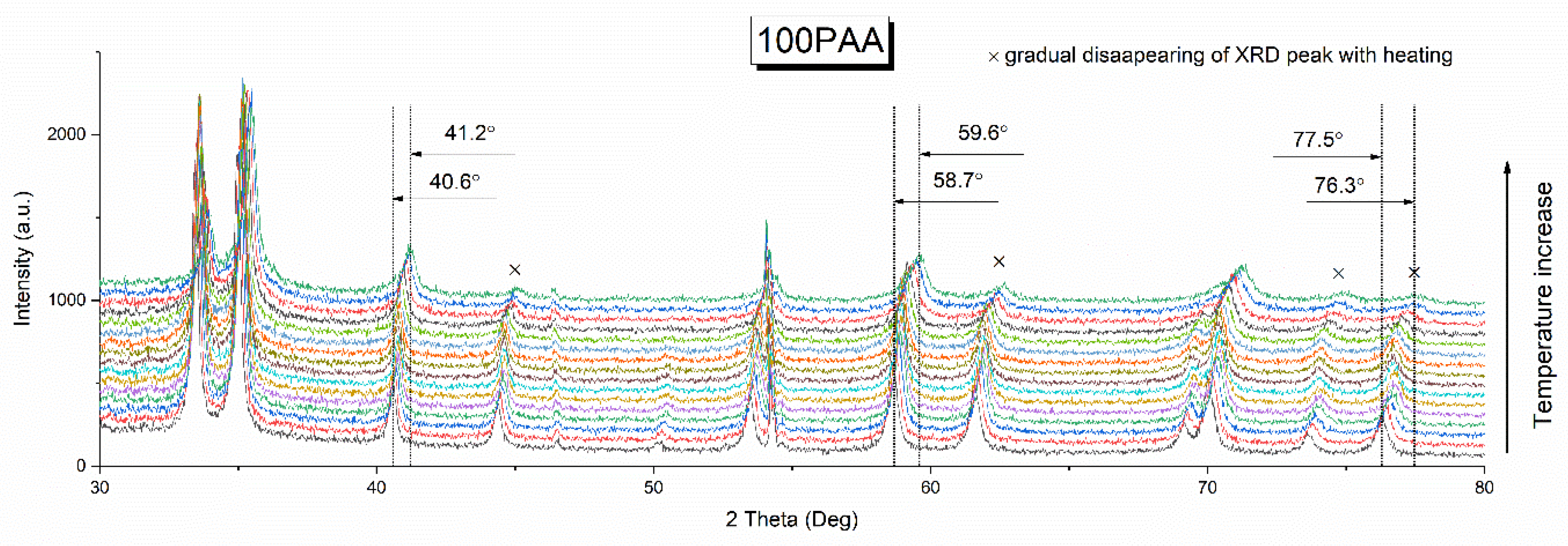
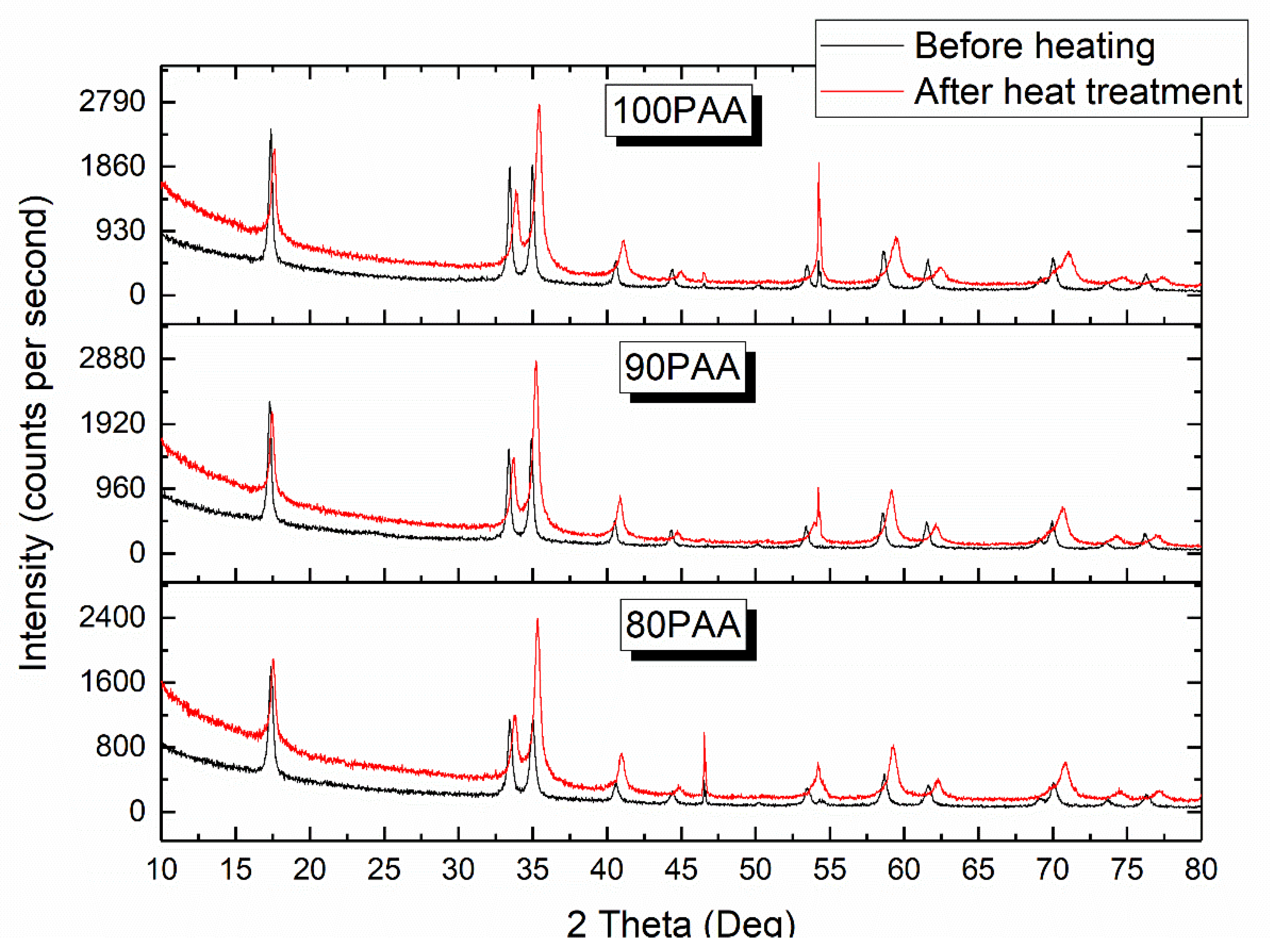
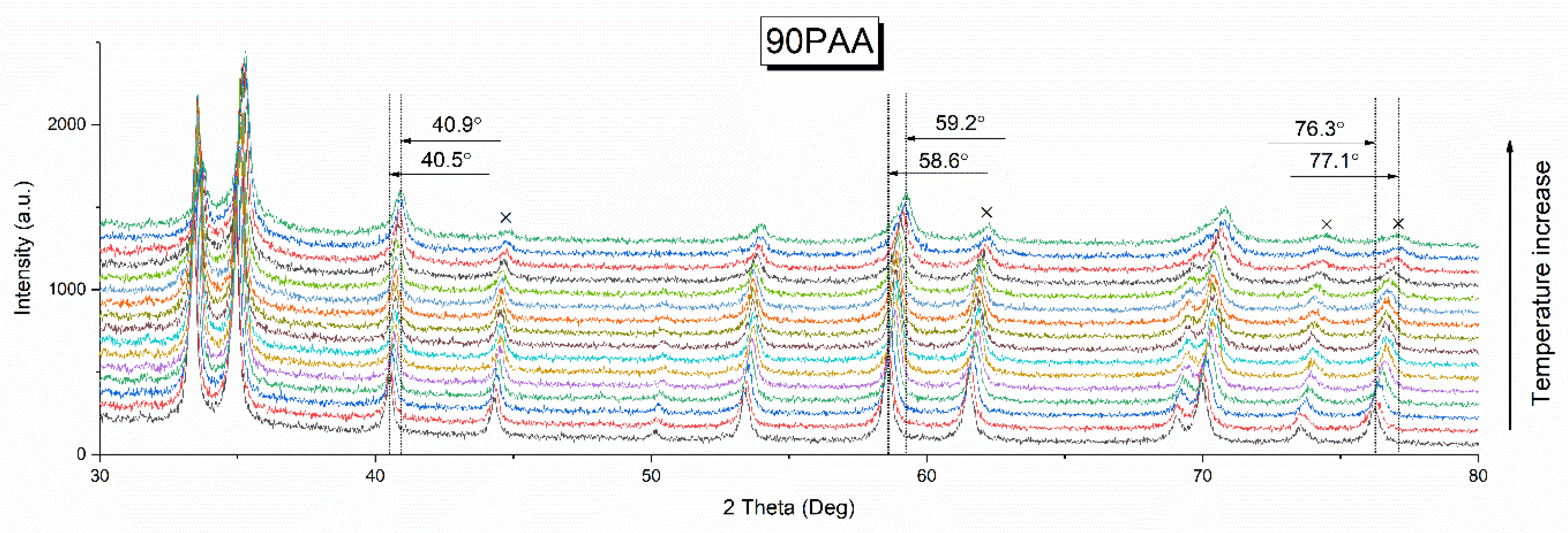
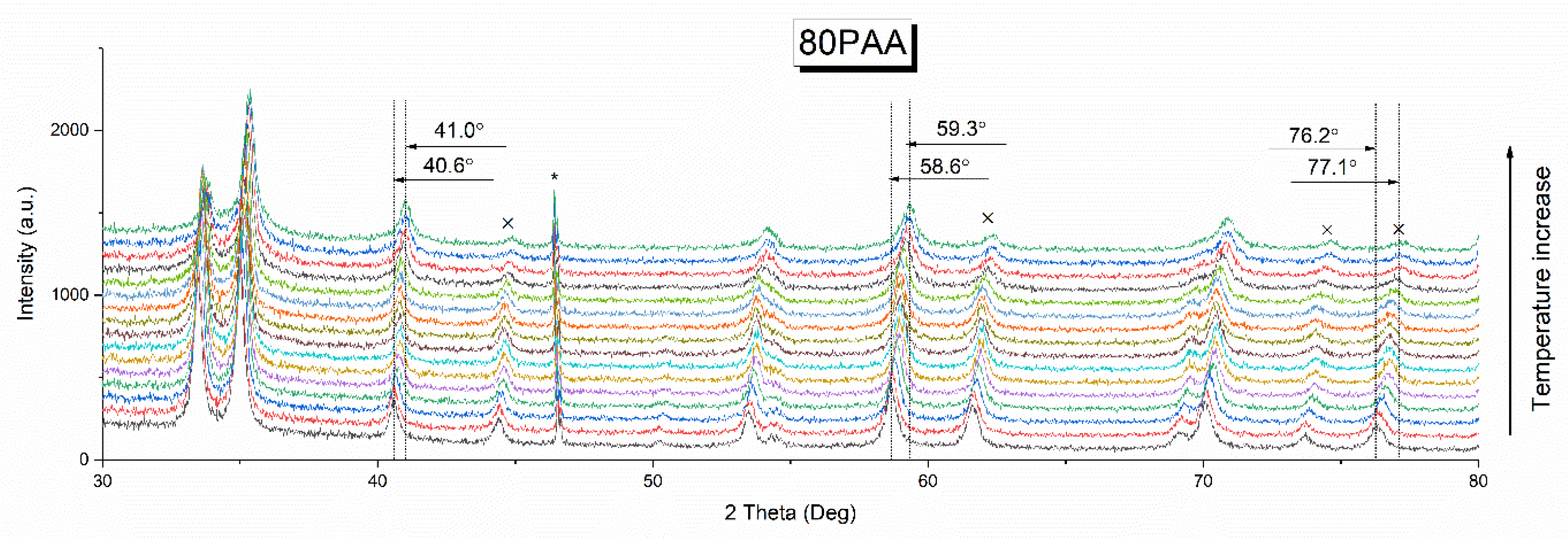
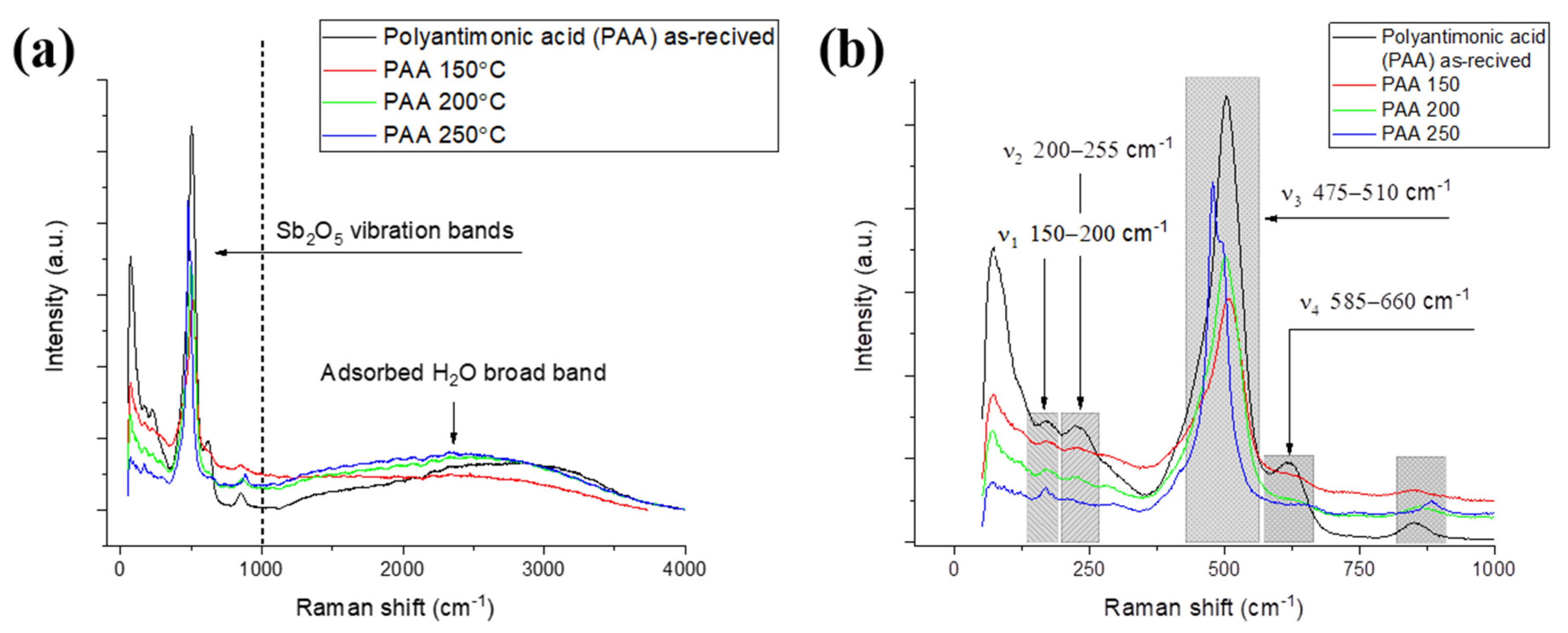
3.1. Effect of the Binder Concentration on the Thermal Evolution and Structure of Membranes
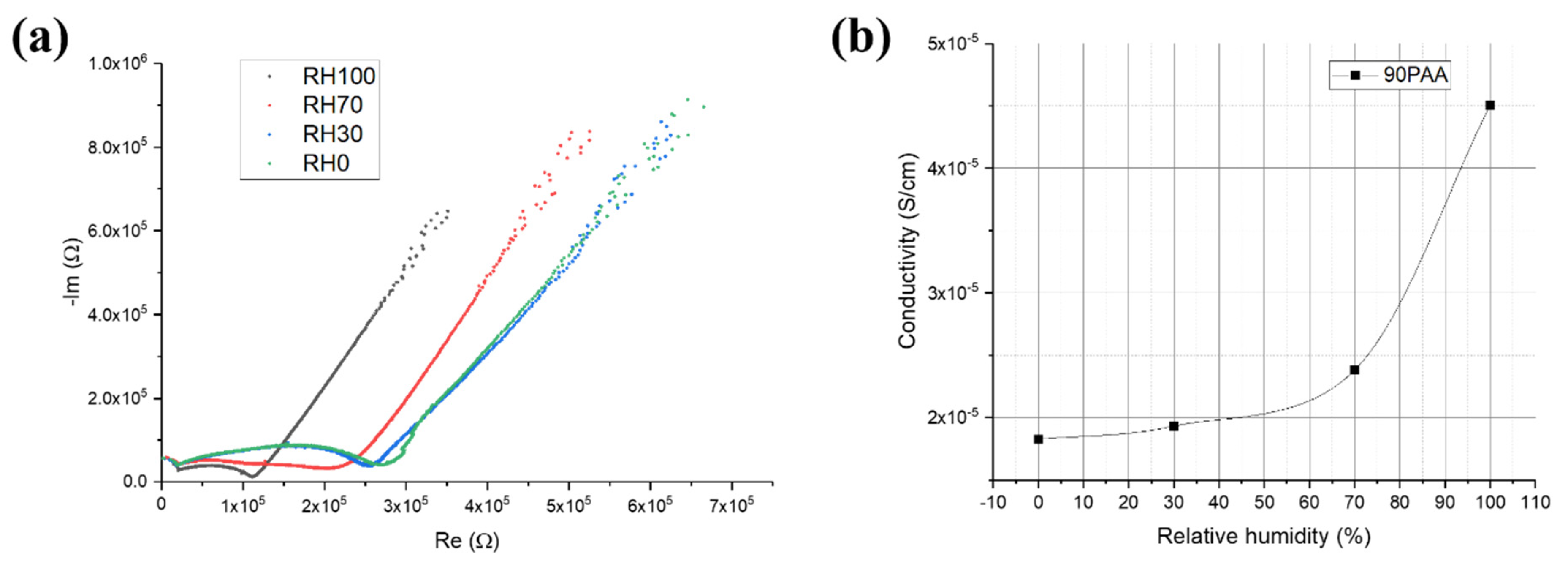
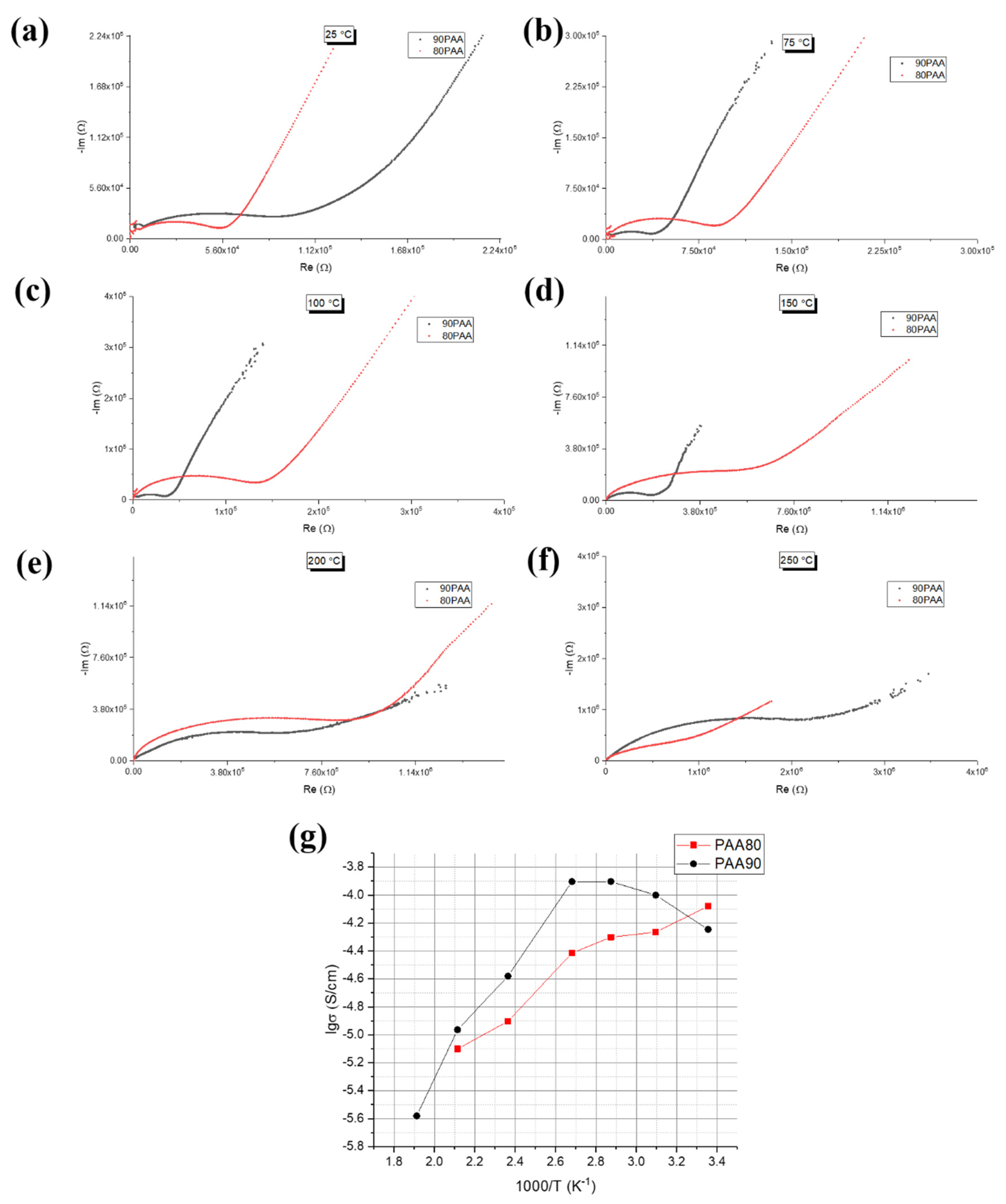
3.2. Moisture Influence on the Electrical Response
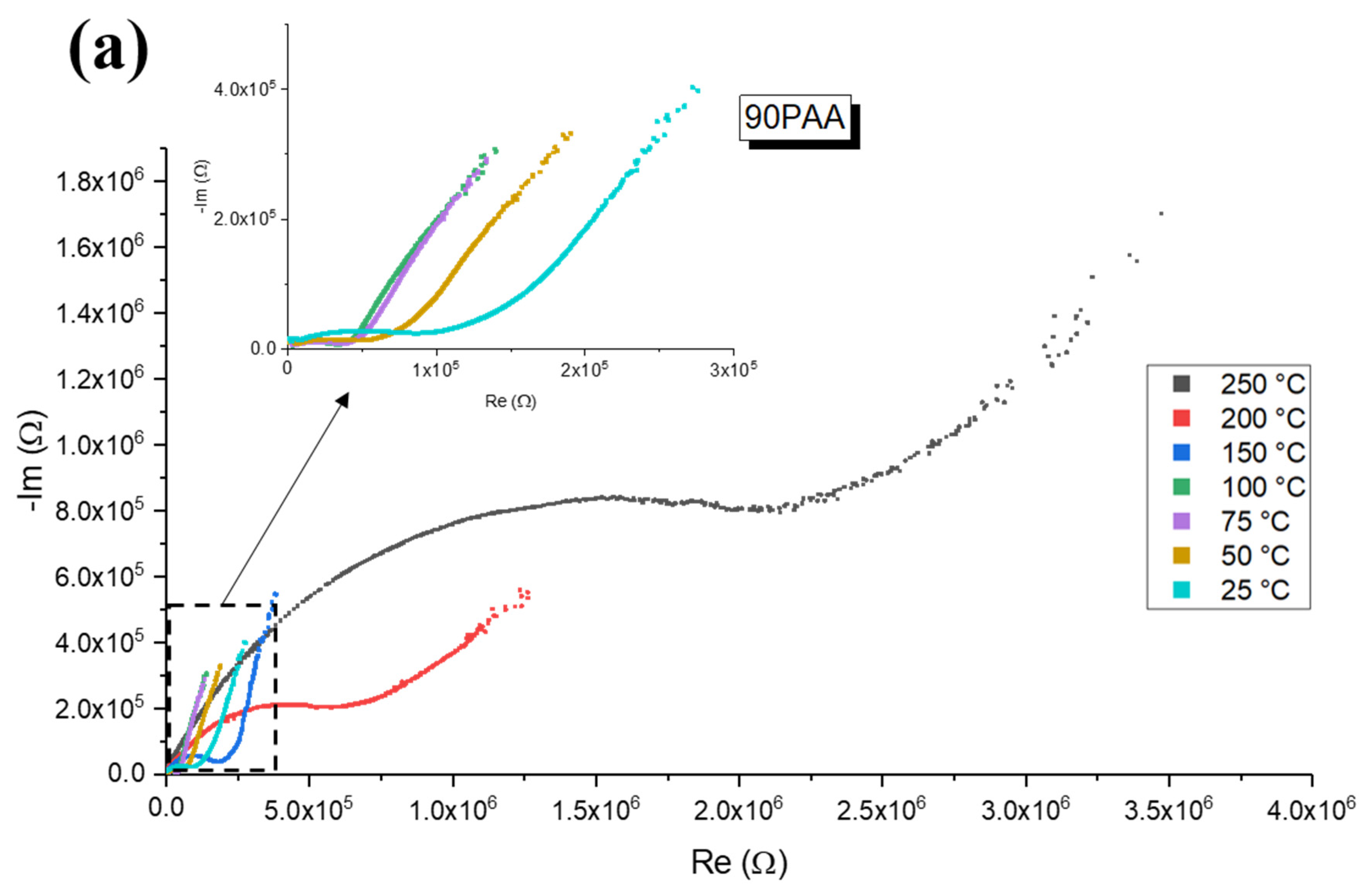
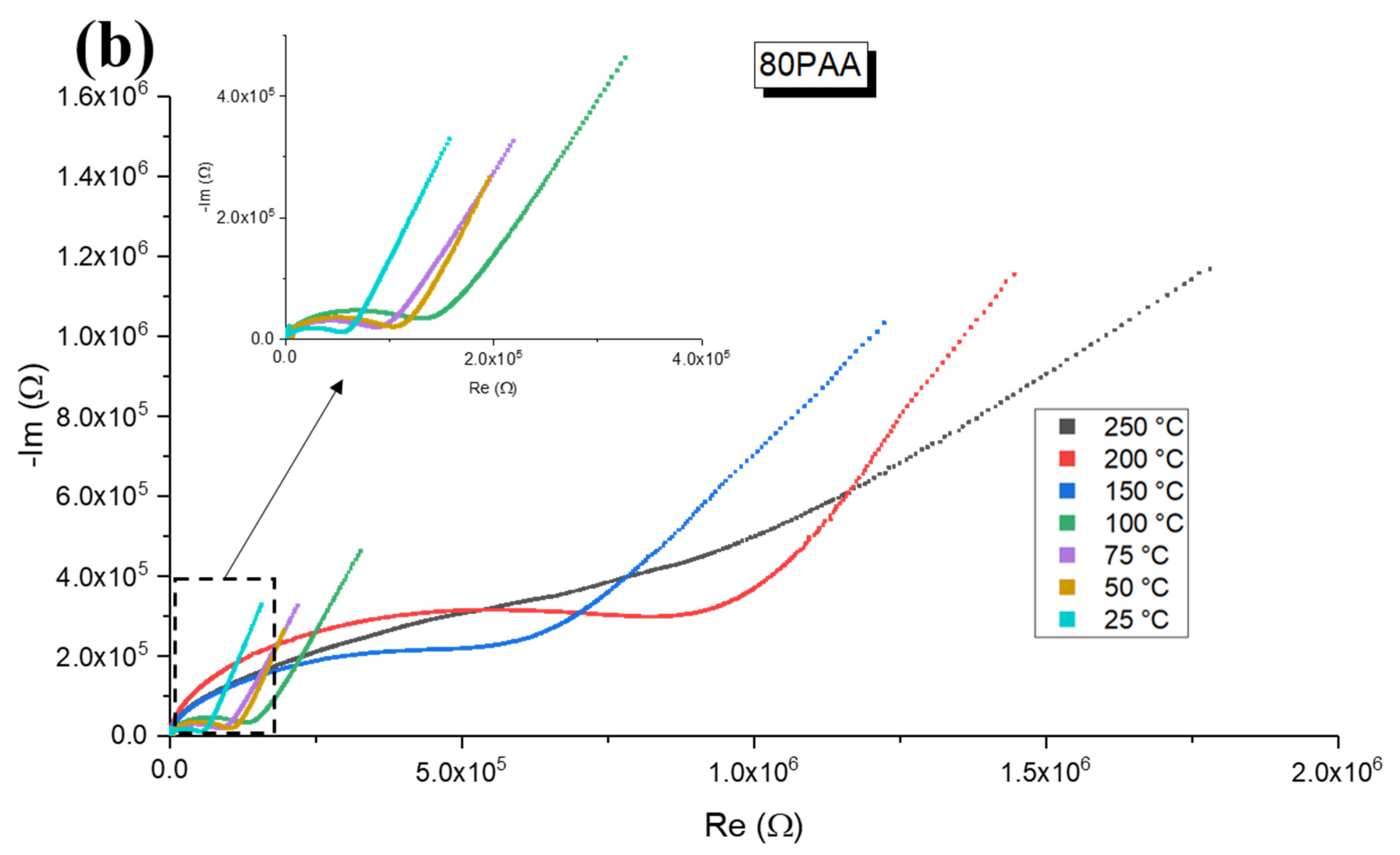
3.3. Influence of the Binder Concentration on the Electrical Response
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Acknowledgments
Conflicts of Interest
References
- Colomban, P. Proton conductors and their applications: A tentative historical overview of the early researches. Solid State Ion. 2019, 334, 125–144. [Google Scholar] [CrossRef]
- Abdelkareem, M.A.; Elsaid, K.; Wilberforce, T.; Kamil, M.; Sayed, E.T.; Olabi, A. Environmental aspects of fuel cells: A review. Sci. Total Environ. 2021, 752, 141803. [Google Scholar] [CrossRef] [PubMed]
- Mahato, N.; Banerjee, A.; Gupta, A.; Omar, S.; Balani, K. Progress in material selection for solid oxide fuel cell technology: A review. Prog. Mater. Sci. 2015, 72, 141–337. [Google Scholar] [CrossRef]
- Peighambardoust, S.J.; Rowshanzamir, S.; Amjadi, M. Review of the proton exchange membranes for fuel cell applications. Int. J. Hydrogen Energy 2010, 35, 9349–9384. [Google Scholar] [CrossRef]
- Norby, T. Proton Conduction in Solids: Bulk and Interfaces. MRS Bull. 2009, 34, 923–928. [Google Scholar] [CrossRef]
- Norby, T. Solid-state protonic conductors: Principles, properties, progress and prospects. Solid State Ion. 1999, 125, 1–11. [Google Scholar] [CrossRef]
- Yurko, Y.; Elbaz, L. The effect of membrane electrode assembly methods on the performance in fuel cells. Electrochim. Acta 2021, 389, 138676. [Google Scholar] [CrossRef]
- Chan, S.H.; Xia, Z.T. Polarization effects in electrolyte/electrode-supported solid oxide fuel cells. J. Appl. Electrochem. 2002, 32, 339–347. [Google Scholar] [CrossRef]
- Kreuer, K. On the development of proton conducting materials for technological applications. Solid State Ion. 1997, 97, 1–15. [Google Scholar] [CrossRef]
- Kreuer, K.D. On the development of proton conducting polymer membranes for hydrogen and methanol fuel cells. J. Memb. Sci. 2001, 185, 29–39. [Google Scholar] [CrossRef]
- Sun, X.; Simonsen, S.; Norby, T.; Chatzitakis, A. Composite Membranes for High Temperature PEM Fuel Cells and Electrolysers: A Critical Review. Membranes 2019, 9, 83. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Leysen, R.; Doyen, W.; Proost, R.; Vermeiren, P.; Adriansens, W.; Deknock, R. The use of Heterogeneous Membranes in Electrochemical Systems. In Synthetic Polymeric Membranes; Sedláček, B., Kahovec, J., Eds.; De Gruyter: Berlin, Germany, 1987; pp. 89–100. [Google Scholar]
- Leysen, R.; Doyen, W.; Vandenborre, H. On the Structure of Polyantimonic Acid-Polysulfone Membranes; Studiecentrum voor Kernenergie: Brussels, Belgium, 1985. [Google Scholar]
- Hickner, M.A.; Ghassemi, H.; Kim, Y.S.; Einsla, B.R.; McGrath, J.E. Alternative Polymer Systems for Proton Exchange Membranes (PEMs). Chem. Rev. 2004, 104, 4587–4612. [Google Scholar] [CrossRef] [PubMed]
- Weigelt, F.; Escorihuela, S.; Descalzo, A.; Tena, A.; Escolástico, S.; Shishatskiy, S.; Serra, J.M.; Brinkmann, T. Novel Polymeric Thin-Film Composite Membranes for High-Temperature Gas Separations. Membranes 2019, 9, 51. [Google Scholar] [CrossRef] [Green Version]
- Yu, J.; Pan, M.; Yuan, R. Nafion/Silicon oxide composite membrane for high temperature proton exchange membrane fuel cell. J. Wuhan Univ. Technol. Sci. Ed. 2007, 22, 478–481. [Google Scholar] [CrossRef]
- Tang, H.; Peikang, S.; Jiang, S.P.; Wang, F.; Pan, M. A degradation study of Nafion proton exchange membrane of PEM fuel cells. J. Power Sources 2007, 170, 85–92. [Google Scholar] [CrossRef]
- Mérida, W.; Harrington, D.A.; Le Canut, J.M.; McLean, G. Characterisation of proton exchange membrane fuel cell (PEMFC) failures via electrochemical impedance spectroscopy. J. Power Sources 2006, 161, 264–274. [Google Scholar] [CrossRef]
- Malavasi, L.; Fisher, C.A.J.; Islam, M.S. Oxide-ion and proton conducting electrolyte materials for clean energy applications: Structural and mechanistic features. Chem. Soc. Rev. 2010, 39, 4370–4387. [Google Scholar] [CrossRef]
- Slodczyk, A.; Colomban, P.; André, G.; Zaafrani, O.; Grasset, F.; Lacroix, O.; Sala, B. Structural modifications induced by free protons in proton conducting perovskite zirconate membrane. Solid State Ion. 2012, 225, 214–218. [Google Scholar] [CrossRef]
- Slodczyk, A.; Sharp, M.D.; Upasen, S.; Colomban, P.; Kilner, J.A. Combined bulk and surface analysis of the BaCe0.5Zr0.3Y0.16Zn0.04O3−δ (BCZYZ) ceramic proton-conducting electrolyte. Solid State Ion. 2014, 262, 870–874. [Google Scholar] [CrossRef]
- Baranov, A.; Grebenev, V.; Khodan, A.; Dolbinina, V.; Efremova, E. Optimization of superprotonic acid salts for fuel cell applications. Solid State Ion. 2005, 176, 2871–2874. [Google Scholar] [CrossRef]
- Ponomareva, V.G.; Lavrova, G.V. Effect of the excess protons on the electrotansport, structural and thermodynamic properties of CsH2PO4. Solid State Ion. 2017, 304, 90–95. [Google Scholar] [CrossRef]
- England, W.; Cross, M.; Hamnett, A.; Wiseman, P.; Goodenough, J. Fast proton conduction in inorganic ion-exchange compounds. Solid State Ion. 1980, 1, 231–249. [Google Scholar] [CrossRef]
- Zanchet, L.; da Trindade, L.G.; Trombetta, F.; Martins, A.D.; Martini, E.M.A.; Becker, M.R.; de Souza, M.O. Improving Nafion/zeolite nanocomposite with a SF-SO3 based ionic liquid for PEMFC application. Ionics 2021, 27, 2027–2036. [Google Scholar] [CrossRef]
- Shanmugam, S.; Ketpang, K.; Aziz, M.A.; Oh, K.; Lee, K.; Son, B.; Chanunpanich, N. Composite polymer electrolyte membrane decorated with porous titanium oxide nanotubes for fuel cell operating under low relative humidity. Electrochim. Acta 2021, 384, 138407. [Google Scholar] [CrossRef]
- Yaroshenko, F.A.; Burmistrov, V.A. Dielectric losses and proton conductivity of polyantimonic acid membranes. Russ. J. Electrochem. 2016, 52, 690–693. [Google Scholar] [CrossRef]
- Yaroslavtsev, A.B.; Dobrovolsky, Y.A.; Shaglaeva, N.S.; Frolova, L.A.; Gerasimova, E.V.; Sanginov, E.A. Nanostructured materials for low-temperature fuel cells. Russ. Chem. Rev. 2012, 81, 191–220. [Google Scholar] [CrossRef]
- Kovalenko, L.Y.; Burmistrov, V.A.; Lupitskaya, Y.A.; Yaroshenko, F.A.; Filonenko, E.M.; Bulaeva, E.A. Ion exchange of H+/Na+ in polyantimonic acid, doped with vanadium ions. Pure Appl. Chem. 2019, 92, 505–514. [Google Scholar] [CrossRef] [Green Version]
- Baetsle, L.H.; Huys, D. Structure and ion-exchange characteristics of polyantimonic acid. J. Inorg. Nucl. Chem. 1968, 30, 639–649. [Google Scholar] [CrossRef]
- Belinskaya, F.A.; Militsina, E.A.; Karmanova, L.A.; Grigorova, N.S. Antiradiation drugs on the basis of inorganic cationites. Vestn. St.-Peterbg. Univ. Seriya 4 Fiz. Khimiya 1992, 25, 36–41. [Google Scholar]
- Belinskaya, F.A.; Militsina, E.A. Inorganic Ion-exchange Materials Based on Insoluble Antimony(V) Compounds. Russ. Chem. Rev. 1980, 49, 933–952. [Google Scholar] [CrossRef]
- Yaroshenko, F.A.; Burmistrov, V.A. Proton conductivity of polyantimonic acid studied by impedance spectroscopy in the temperature range 370–480 K. Inorg. Mater. 2015, 51, 783–787. [Google Scholar] [CrossRef]
- Leysen, R.; Vandenborre, H. Synthesis and characterization of polyantimonic acid membranes. Mater. Res. Bull. 1980, 15, 437–450. [Google Scholar] [CrossRef]
- Yaroshenko, F.A.; Burmistrov, V.A. Dielectric relaxation and protonic conductivity of polyantimonic crystalline acid at low temperatures. Russ. J. Electrochem. 2015, 51, 391–396. [Google Scholar] [CrossRef]
- Yaroshenko, F.A.; Burmistrov, V.A. Synthesis of Hybrid Materials Based on MF-4SK Perfluorinated Sulfonated Cation-Exchange Membranes Modified with Polyantimonic Acid and Characterization of Their Proton Conductivity. Pet. Chem. 2018, 58, 770–773. [Google Scholar] [CrossRef]
- Leysen, R.; Vermeiren, P.; Baestle, L.; Spaepen, G.; Vanderborre, J.-B.H. Method of Preparing a Membrane Consisting of Polyantimonic Acid Powder and an Organic Binder. U.S. Patent 4253936, 3 March 1981. [Google Scholar]
- Ma, F.; Shi, W.; Meng, H.; Li, Z.; Zhou, W.; Zhang, L. Preparation, characterization and ion-exchange behavior of polyantimonic acid-polyacrylonitrile (PAA–PAN) composite beads for strontium(II). J. Radioanal. Nucl. Chem. 2016, 308, 155–163. [Google Scholar] [CrossRef]
- Kovalenko, L.Y.; Yaroshenko, F.A.; Burmistrov, V.A.; Isaeva, T.N.; Galimov, D.M. Thermolysis of Hydrated Antimony Pentoxide. Inorg. Mater. 2019, 55, 586–592. [Google Scholar] [CrossRef]
- Critchley, J.P.; Knight, G.J.; Wright, W.W. Fluorine-Containing Polymers. In Heat-Resistant Polymers; Springer US: Boston, MA, USA, 1983; pp. 87–123. [Google Scholar]
- Drobny, J.G. Technology of Fluoropolymers; CRC Press: Boca Raton, FL, USA, 2014; ISBN 9780429117251. [Google Scholar]
- Ostrovskii, D.; Valakh, M.; Karasiova, T.; Yaremko, A. The peculiarities of hydrogen bonds in raman spectra of solid superionic polyantimonic acids. Ferroelectrics 1997, 192, 93–99. [Google Scholar] [CrossRef]
- Cody, C.A.; DiCarlo, L.; Darlington, R.K. Vibrational and thermal study of antimony oxides. Inorg. Chem. 1979, 18, 1572–1576. [Google Scholar] [CrossRef]
- Nakamoto, K. Infrared and Raman Spectra of Inorganic and Coordination Compounds, 6th ed.; Wiley: Hoboken, NJ, USA, 2009; ISBN 978-0-471-74339-2. Available online: https://2lib.org/book/593471/6aaca8?id=593471&secret=6aaca8 (accessed on 22 April 2021).
- Burgard, M.; MacCordick, J. Isomorphism and spectral analogies in pairs of ionic and coordination complexes of SbCl5. Inorg. Nucl. Chem. Lett. 1970, 6, 599–602. [Google Scholar] [CrossRef]
- Janseen, M.; Pebler, J.; Dehsicke, K. 121Sb-Mosbauer-Spektrum und Schwingungsspektrum von Sb2O5. Z. Arnorg. Allg. Chem. 1982, 495, 120–126. [Google Scholar] [CrossRef]
- Dixit, A.; Majumder, S.B.; Dobal, P.S.; Katiyar, R.S.; Bhalla, A.S. Phase transition studies of sol–gel deposited barium zirconate titanate thin films. Thin Solid Film. 2004, 447–448, 284–288. [Google Scholar] [CrossRef]
- Bauerle, J.E. Study of solid electrolyte polarization by a complex admittance method. J. Phys. Chem. Solids 1969, 30, 2657–2670. [Google Scholar] [CrossRef]
- Peng, Z.; Huguet, P.; Deabate, S.; Morin, A.; Sutor, A.K. Depth-resolved micro-Raman spectroscopy of tri-layer PFSA membrane for PEM fuel cells: How to obtain reliable inner water contents. J. Raman Spectrosc. 2013, 44, 321–328. [Google Scholar] [CrossRef]
- Adjemian, K.T.; Lee, S.J.; Srinivasan, S.; Benziger, J.; Bocarsly, A.B. Silicon Oxide Nafion Composite Membranes for Proton-Exchange Membrane Fuel Cell Operation at 80–140°C. J. Electrochem. Soc. 2002, 149, A256. [Google Scholar] [CrossRef]
- Stoica, D.; Ogier, L.; Akrour, L.; Alloin, F.; Fauvarque, J.-F. Anionic membrane based on polyepichlorhydrin matrix for alkaline fuel cell: Synthesis, physical and electrochemical properties. Electrochim. Acta 2007, 53, 1596–1603. [Google Scholar] [CrossRef]
- Stoica, D.; Alloin, F.; Marais, S.; Langevin, D.; Chappey, C.; Judeinstein, P. Polyepichlorhydrin Membranes for Alkaline Fuel Cells: Sorption and Conduction Properties. J. Phys. Chem. B 2008, 112, 12338–12346. [Google Scholar] [CrossRef]
- Kumar, N.; Evaristo, M.; Trindade, B.; Faia, P. Humidity sensing properties of thin silicon-tin films prepared by magnetron sputtering. Sens. Actuators B Chem. 2020, 321, 128554. [Google Scholar] [CrossRef]
- Faia, P.M.; Libardi, J.; Barbosa, I.; Araújo, E.S.; de Oliveira, H.P. Preparation, Characterization, and Evaluation of Humidity-Dependent Electrical Properties of Undoped and Niobium Oxide-Doped TiO2: WO3 Mixed Powders. Adv. Mater. Sci. Eng. 2017, 2017, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Faia, P.M.; Libardi, J. Response to humidity of TiO2: WO3 sensors doped with V2O5: Influence of fabrication route. Sens. Actuators B Chem. 2016, 236, 682–700. [Google Scholar] [CrossRef]


| Temperature, °C | Δm, % | ||||
|---|---|---|---|---|---|
| Sample | Endo1- | Endo2- | Additional Endo Effects | Exo- | <300 °C |
| 100PAA | 57.1 | 126.3 | - | 369 | 14.8 |
| 90PAA | 100.5 | 123.8 | 190 232 | 303 | 14.7 |
| 80PAA | - | 127 | 166 211 | 302 | 14.5 |
| R | C | CGEO | QCPE1 | nCPE1 | QCPE2 | nCPE2 | Wcoeffi | |
|---|---|---|---|---|---|---|---|---|
| 10% bind., 25 °C | 1.56 × 104 | 6.79 × 10−9 | 3.07 × 10−12 | 2.23 × 10−6 | 0.15364 | 2.33 × 10−8 | 0.88312 | 5.35 × 10−9 |
| 10% bind., 50 °C | 8.35 × 105 | 2.45 × 10−8 | 4.85 × 10−12 | 3.97 × 10−6 | 0.13662 | 6.54 × 10−8 | 0.8229 | 4.97 × 10−9 |
| 10% bind., 75 °C | 1.23 × 106 | 1.44 × 10−8 | 6.70 × 10−12 | 1.05 × 10−5 | 9.18 × 10−2 | 7.56 × 10−6 | 0.29989 | 3.87 × 10−9 |
| 10% bind., 100 °C | 5.13 × 105 | 1.79 × 10−8 | 5.42 × 10−12 | 3.40 × 10−8 | 1 | 6.22 × 10−6 | 0.13678 | 3.72 × 10−9 |
| 10% bind., 150 °C | 6.72 × 105 | 2.01 × 10−8 | 6.23 × 10−12 | 1.26 × 10−8 | 0.99899 | 1.57 × 10−6 | 1.20 × 10−1 | 3.56 × 10−9 |
| 10% bind., 200 °C | 6.31 × 105 | 7.16 × 10−8 | 5.65 × 10−12 | 8.97 × 10−9 | 1 | 7.96 × 10−8 | 2.56 × 10−1 | 3.56 × 10−9 |
| 20% bind., 25 °C | 1.20 × 104 | 4.31 × 10−11 | 3.94 × 10−12 | 8.80 × 10−6 | 8.31 × 10−2 | 1.27 × 10−8 | 0.84565 | 2.71 × 10−10 |
| 20% bind., 50 °C | 2.20 × 104 | 5.31 × 10−11 | 3.94 × 10−12 | 4.80 × 10−6 | 8.41 × 10−2 | 1.37 × 10−8 | 0.86565 | 2.61 × 10−10 |
| 20% bind., 75 °C | 1.40 × 104 | 8.31 × 10−11 | 3.94 × 10−12 | 5.00 × 10−6 | 8.41 × 10−2 | 1.47 × 10−8 | 0.82565 | 2.73 × 10−10 |
| 20% bind., 100 °C | 4.45 × 104 | 3.01 × 10−11 | 4.14 × 10−12 | 4.00 × 10−6 | 8.91 × 10−2 | 1.20 × 10−8 | 0.80565 | 2.67 × 10−10 |
| 20% bind., 150 °C | 3.55 × 105 | 1.51 × 10−11 | 4.01 × 10−12 | 8.17 × 10−7 | 9.21 × 10−2 | 4.04 × 10−9 | 0.73565 | 2.77 × 10−10 |
| 20% bind., 200 °C | 2.85 × 105 | 2.51 × 10−11 | 4.01 × 10−12 | 6.27 × 10−7 | 1.61 × 10−1 | 5.04 × 10−9 | 0.71565 | 2.64 × 10−10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kurapova, O.Y.; Faia, P.M.; Zaripov, A.A.; Pazheltsev, V.V.; Glukharev, A.A.; Konakov, V.G. Electrochemical Characterization of Novel Polyantimonic-Acid-Based Proton Conductors for Low- and Intermediate-Temperature Fuel Cells. Appl. Sci. 2021, 11, 11877. https://doi.org/10.3390/app112411877
Kurapova OY, Faia PM, Zaripov AA, Pazheltsev VV, Glukharev AA, Konakov VG. Electrochemical Characterization of Novel Polyantimonic-Acid-Based Proton Conductors for Low- and Intermediate-Temperature Fuel Cells. Applied Sciences. 2021; 11(24):11877. https://doi.org/10.3390/app112411877
Chicago/Turabian StyleKurapova, Olga Yu., Pedro M. Faia, Artem A. Zaripov, Vasily V. Pazheltsev, Artem A. Glukharev, and Vladimir G. Konakov. 2021. "Electrochemical Characterization of Novel Polyantimonic-Acid-Based Proton Conductors for Low- and Intermediate-Temperature Fuel Cells" Applied Sciences 11, no. 24: 11877. https://doi.org/10.3390/app112411877
APA StyleKurapova, O. Y., Faia, P. M., Zaripov, A. A., Pazheltsev, V. V., Glukharev, A. A., & Konakov, V. G. (2021). Electrochemical Characterization of Novel Polyantimonic-Acid-Based Proton Conductors for Low- and Intermediate-Temperature Fuel Cells. Applied Sciences, 11(24), 11877. https://doi.org/10.3390/app112411877








