1. Introduction
Presently, the ever-increasing capabilities of measurement, generation, and storing of data have increased the scientific and industrial communities’ interest in what are known as functional data. In its most general form, the domain of functional data analysis deals with any object with the form of a function, regardless of its dimension. For example, the most basic form these objects can adopt is one-dimensional (i.e., univariate) real functions, which can represent the evolution of a physical parameter of interest over time (or another variable). These data normally originate through an empirical measurement system or a simulation code.
The great interest of the functional data analysis is that it allows consideration of the intrinsic nature of the data, i.e., the underlying process that generates them is supposed to have certain restrictions of domain, regularity, continuity and so on. As the functional data are infinite-dimensional by nature, functional data analysis methods always rely on a dimension reduction technique, whether implicitly or explicitly. More precisely, it is the case in the context of classification [
1], clustering [
2], landmark research and registration [
3] of functional data. By providing more synthetic descriptors of functional observations, functional data analysis methods allow a more practical treatment of data thanks to the available multivariate tools.
The domain of functional data analysis can be traced back to the works of Grenander [
4], but the term itself was coined by Ramsay, [
5]. Some of the most widely regarded references for the domain include the general works of [
6] or [
7], focused on non-parametric methods for functional data. Functional data can be found in a wide variety of contexts, among which we can mention: environmental sciences [
8,
9], medical sciences [
10], economy [
11] and others. In the context of this paper, our work is motivated using expensive simulation codes [
12,
13] that are commonly used in the nuclear industry to complement the nuclear safety assessment reports [
14], and which require specific statistical tools. These thermal-hydraulic simulators, such as the system code
CATHARE2 [
15], can simulate the evolution of the essential physical parameters during a nuclear transient, and they are expensive to evaluate (several hours per run) and analyze due to the complexity of the simulated phenomena (highly nonlinear interactions between its parameters).
In general, in the context of nuclear safety, the main analyzed parameters are the scalar values known as
Safety Parameters, which are representative of the severity of an accidental transient. However, the analysis of the whole evolution of the aforementioned physical parameters is a complex domain that has been subject to considerable research efforts in recent years, such as in the works of [
16] or [
17]. The detection and analysis of outlying transients in these sets of simulations are useful to detect unexpected physical phenomena, validate the simulations providing valuable descriptors of the functional outputs of interest, or quantify the extreme behavior or penalizing nature of specific subsets of those transients.
Despite the diversity of domains, there are several common points of interest between all of them. For example, in the most usual case of univariate functions, a typical difficulty that arises in the pre-treatment phase of the data are the subject of the discretization of the grid on which the data are observed. Univariate curves are not normally observed in their entirety (since they are intrinsically infinite-dimensional). Instead, they are indexed by some variable, usually the time in the univariate case, in a grid that can be homogeneous or not. Indeed, points are not necessarily equally spaced, as with biological measurements such as blood pressures, or with temporal data originated by a simulation code whose time step evolves accordingly with the convergence impositions of the numerical solver. Naturally, the representation of the underlying functional process is still a matter of discussion. It does not only depend on the spacing of each point in the time grid but also other notions such as the
density of data. This quantity can differ by several orders of magnitude in the case of numerical simulators depending on the restrictions imposed to time steps to guarantee the convergence, the presence or not of random noise, etc. For a more profound analysis on the importance of these subjects, the reader can refer to [
18].
This paper focuses on a functional outlier detection technique, which is an unsupervised problem, showing its sensitivity to both magnitude and shape outliers and its ranking capabilities. The importance of this work is closely related to the data quality domain, since the presence of anomalous behaviors that might have been originated by measurement errors, non-convergence of algorithms or the existence of non-physical values of numerical simulators may produce spurious results when treating a dataset. As explained in [
19], when the underlying process that creates the data
behaves unusually, it results in the creation of outliers. Therefore, it may contain useful information about
abnormal characteristics of the system. Finally, the particularities of functional data treatment with respect to multivariate ones require specific tools to have acceptable detection capabilities [
20].
The functional outlier detection domain has gained relevance in recent years, and the methods for detecting these outliers do not cease to improve. However, the techniques can differ significantly between them. Many of them rely on the notion of statistical depth [
9,
21,
22] or other measures (e.g., entropy [
23]). In contrast, others rely on other dimensionality reduction methods, clustering, or hypothesis testing on the coefficients of some functional decomposition [
24], as well as graphical tools [
25]. A simulation study comparing depth measurements to detect functional outliers can be found in [
26]. Naturally, all these techniques showcase different detection capabilities, and they can be more adapted to the detection of a particular type of outliers.
In our study, we consider that the data correspond to independent and identically distributed (i.i.d.) realizations of a random process
Z, taking its values in a functional space
. In practice, any realization
of the random variable
Z can only be observed in a limited number of points in the domain, i.e., it is observed as the random vector
, with
. This data representation is not itself appropriate to the detection of outlying functions.
Section 2 thus presents how to define and compute a modeling of data dedicated to the characterization of outliers, using Gaussian Mixture Models (GMM). The introduction of the measures and methods will be found in the
Supplementary Material of this paper. Based on this data representation,
Section 3 presents our functional outlier detection methodology.
Section 4 and
Section 5 provide some analytical and industrial application examples. The
Supplementary Material of this paper also contains complementary numerical tests. The properties, capabilities and limitations of the methodology are discussed in
Section 6.
2. Adapting Gaussian Mixture Models for Outlier Detection
As mentioned in the introduction, functional data are elements of a functional space, typically functions defined on a continuous interval of . Measuring, storing and analyzing these data is however realized using numerical devices and computers, and hence impose a digital representation of data. For this reason, the value of functions is available only on a finite-dimensional sub-domain of their theoretical definition domain, i.e., in a discretized version. When dealing with time-dependent physical quantities, this discretization basically consists of a projection on a time grid which can be regular or not. To achieve an efficient detection of outlying functions, a transformation of the dataset is required, which brings out the features of the data that discriminate outlying ones from the rest of the set.
The use of probabilistic models in lower-dimensional feature spaces is useful to detect anomalous points assuming that they provide a good fit for the data and are able of capturing the central trend of the data. In this context, the use of Gaussian Mixture Models (GMM) is a common approach [
20], since they can provide a good fit to the data if the number of components is not fixed, while providing an estimate of the generative probability of each point according to the model. However, their basic use suffers from well-known spurious effects in the outlier detection domain [
19]. The main problems are:
If the probabilistic model is adjusted including the potential outliers, they may bias the estimation of the underlying model. This is especially problematic if the outliers are assumed to be generated by a different distribution than the other data and are not only considered to be extreme realizations of the same underlying process as the others. On top of that, if the sample presents a high degree of contamination or the sample is small, this bias can greatly influence the detection.
If the multivariate sample can be classified in several different clusters but they number of components is not well-chosen, the possibility of overfitting the probabilistic model to the data becomes a real problem. In this case, some small-sized clusters may appear overly adjusted to the outliers, which will not be identified as such.
These reasons motivate the modifications of the Expectation Maximization (EM) algorithm used in order to fit the GMM to the sample of data in the considered feature space, , with being the set of features such that . The objective is to generate a probabilistic model appropriate for outlier detection.
Let
be an i.i.d. sample of functional data, with
being the set of associated features for each curve (for clarity,
), the objective is the estimation of the set of parameters of the GMM
. This optimization problem is usually solved by maximum likelihood estimation via the EM algorithm [
27]. The form of the problem is:
This well-known algorithm consists of maximizing the log-likelihood function of the Gaussian mixture when a certain amount of binary latent variables
such that
and
, and which allow the representation of the corresponding
kth gaussian component that is considered each time. This way, the conditional distribution of
and
. The last element required for the estimation of the GMM parameters in each step are the conditional probabilities of
given
(usually called
responsibility that component
k takes in explaining the observation). Their values are:
The estimation of the parameters is then performed in the following steps:
Initialize the values of the desired parameters ,
E-step: Evaluate the current responsibilities with the previous parameter values,
M-step: Re-estimate the parameters using the responsibilities,
Evaluate the log-likelihood function presented in Equation (
1).
The modifications of the algorithm consist of iteratively check and reinitialize the estimated parameters during the procedure to detect the undesired and spurious effects by adding two steps after the estimation of the likelihood function:
Check if
for any
. The appearance of these singularities may maximize the log-likelihood function to infinity, since it is unbounded, and cause an overfitting of the data to isolated points. This phenomenon is well described in [
28]. If this kind of anomaly is detected, the point is subtracted from the sample and the EM algorithm continues without it. Naturally, these points will be subject to close analysis since they are good candidates for potential outliers in the sample.
For each iteration step, can be viewed as the prior probability of , and can be seen as the posterior probability given the observed sample. If this posterior probability is considered too low (in our applications we shall take a value of as the minimum weight of the mixing coefficients), we will consider that the corresponding component is either overfitting the data, or that it has detected a small subset of points which is not representative of the central trend of the data. In this case, the other calculated parameters of the components are kept and the values of means and covariances of the small cluster are reinitialized to a random value in the space.
These modifications allow for the GMM that is fitted to the sample in the feature space to stay general, and provide good candidates of outliers during the construction of the model, all of that while avoiding overfitting.
3. Outlier Detection
3.1. Test for Outlyingness
Thanks to these elements, we can construct a hypothesis test by making use of the components of the GMM adjusted model. This way, for any
:
Under
,
, where
such that
. The set of data points less likely than
is composed by points
which verify:
And therefore, , where L follows a Chi-squared distribution, . By performing this test over all the points considered in the feature space, we obtain a unique criterion for outlier detection, such that the outlying points will be the ones presenting p-values under a certain threshold .
3.2. Ordering Score in the Feature Space
Once all the parameters are fixed at their estimated values, it is possible to quantify the extremal behavior of any point in the considered multivariate space through the notion of
Level Set [
29]. Formally, given an absolutely continuous probability measure
with density
p, the Minimum Level Set
is the set of minimal volume (according to the Lebesgue measure) whose measure is
:
where
is the Lebesgue measure in
. Due to the concave downward nature of the GMM [
30], the set
D is unique and
. This way, a probabilistic score of outlyingness for functional data can be obtained via the probability mass retained in the associated Level Set of each functional datum
:
where
is an indicator function, and
is the adjusted probability density function of the GMM with the estimated parameters:
This integral must be solved by numerical methods. For
, there exists efficient software able to solve it, whereas several algorithms based on the Cholesky decomposition have been developed for the higher-dimensional cases [
31]. In the applications presented here we will limit ourselves to two components, orienting each one of them to magnitude or shape outlier detection.
The above presented level set notion gives an unambiguous way of defining to what extend an observation is unlikely to be observed when assuming it was generated in accordance with the same probability law as the rest of the dataset. The GMM provides in turn the required underlying probabilistic model allowing this definition. With the resulting outlyingness scores , we have now available a properly constructed quantification tool for the degree of outlyingness of an observation. We can thus use common statistical approaches to implement an outlier detection procedure, such as considering the occurrence probability of a data point is too small when , where is a significance level.
Finally, let us consider the more realistic case where the availability of data is actually limited, and the sample of functional data is too small to generate the GMM with an acceptable level of reliability (the global convergence of the EM algorithm is not necessarily reached).This is for instance the case for expensive industrial simulation codes, such as mechanical or thermal-hydraulic simulators. In this case, a natural extension of this idea for outlier detection can be implemented via bootstrap resampling, [
32].
B groups are formed by successively drawn with replacement in the original sample. This way, the absence of data can be mitigated through the re-estimation of the GMM for each bootstrap group. If for
B bootstrap groups
represents the GMM of the
bth group, the form of the (bootstrap) estimator of outlyingness would then be:
Throughout this reasoning, the hyperparameter K (the number of components of the mixture model) has been supposed to be fixed, but in practice, this is yet another input parameter of the GMM that must be provided a priori to the EM algorithm. Indeed, the actual form of the model is significantly different depending on the number of components that are considered. If that is the case, the use of an oversimplified mixture when modeling complex multivariate distributions can induce incorrect conclusions about the distribution of data, whereas an unnecessary increase in the number of components may lead to overfitting problems, unacceptable computational costs or imprecise conclusions.
This issue can be treated as a model-selection problem, and several metrics are available to estimate an appropriate number of components depending on the sample. Some examples are the Bayesian Information Criterion (BIC) [
33] or the Integrated Completed Likelihood [
34]. In this paper, the selection of the number of components is performed by means of the Bayesian Information Criterion:
where
represents the log-likelihood function for the GMM,
k is the chosen number of components and
n is the sample size used for the estimation. The second term introduces a penalty which depends on the number of components to mitigate overfitting effects.
3.3. Proposed Detection Algorithm
The practical implementation of the detection algorithm is presented below, and several clarifications will be made. First, the approach does not include a projection of the considered functional data onto a functional expansion to homogenize the dataset. This preliminary step may be important in applications with heterogeneous time grids, if the data are observed with noise etc. Here, it will be supposed that the domain of the data is already uniform. Furthermore, this kind of projections are not necessary most times when estimating non-parametric features, such as norms.
Secondly, it is important to note that in the ideal case, the estimation of the GMM should be made based on a non-contaminated dataset, i.e., without outliers. These existent outliers should be separated before the estimation if the objective is to model the joint distribution of the desired features to avoid the introduction of a non-controlled bias. However, this knowledge is not available a priori, which justifies the trimming procedure of Algorithm 1. It is worth mentioning the iterative step. Even though it is not explicitly noted, the K components that are retained depend on the chosen sample for each bootstrap group. The task of reestimating the parameters for each GMM to optimize the number of components is not computationally expensive for small values of K, which is appropriate for datasets that do not present a high degree of multimodality and to avoid overfitting the data. In our simulations, .
Another important remark on the algorithm is the
extraction step, where the most outlying functions on the set according to the
are separated from the original dataset, and the procedure is re-applied to the remaining functions until a desired homogeneity level is reached. Naturally, in the case where many samples are available, some extreme data realizations are bound to appear. Therefore, regardless of the chosen value for
, these significant data might be separated from the set even though they do not actually contaminate the set since, although unlikely, these data appear due to the nature of the underlying generative process. Separating (trimming) all these data may introduce a bias in the estimation of the successive GMM. This is a known problem in the outlier detection domain. An example for the functional data case can be found in [
9].
| Algorithm 1: FOD algorithm |
![Applsci 11 11475 i001]() |
4. Analytical Test Cases
Following [
35,
36,
37] the detection capabilities of the algorithm can be assessed via controlled simulation examples. Such simulations make it possible to check whether a method succeeds in recognizing different kinds of outliers, when these are purposefully inserted in the dataset. Thus, inserted outliers are constructed to mimic typical outlying data engineers are facing in their daily practice. Some common notations for the analytical models are summarized in
Table 1.
4.1. Numerical Test Protocol
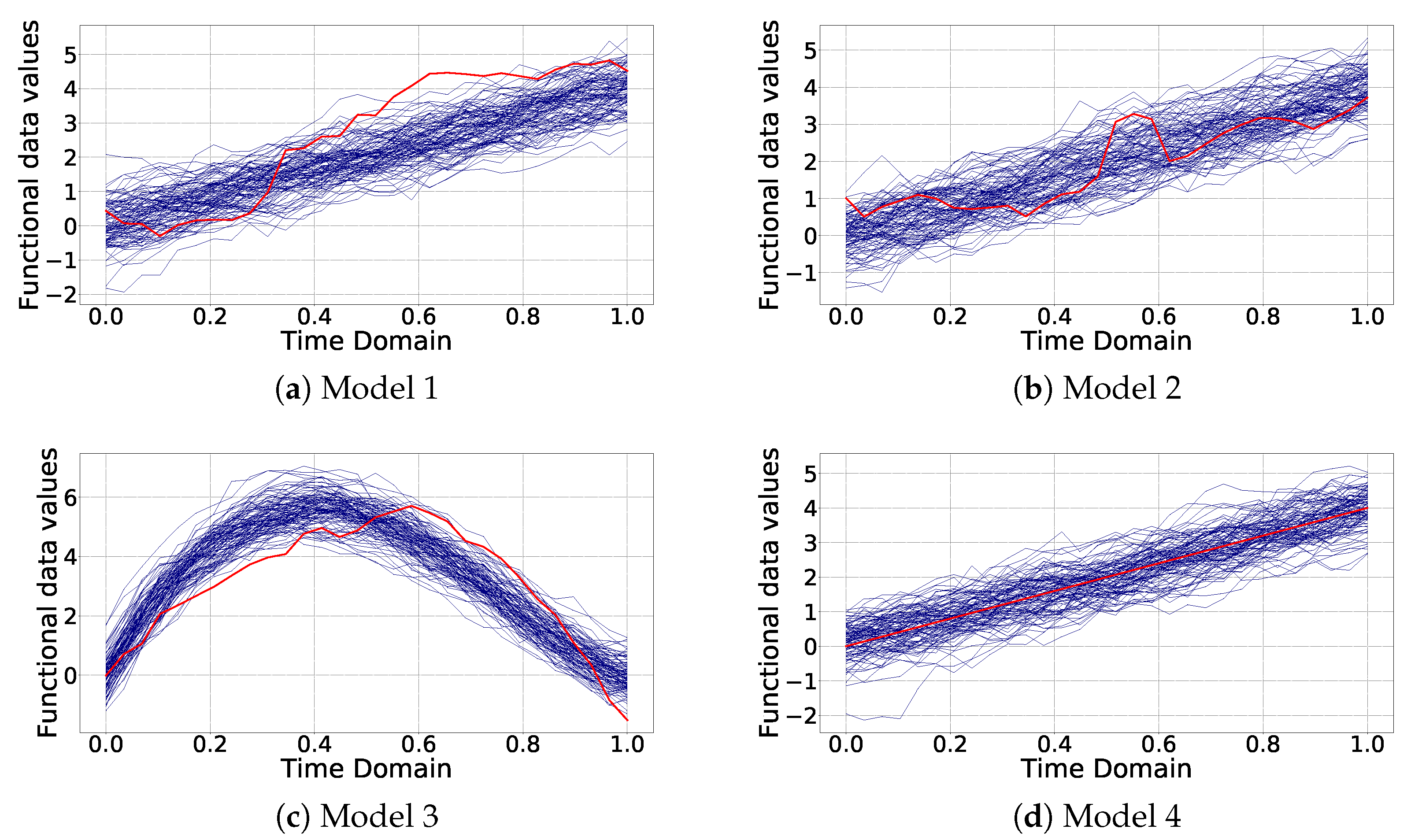
In all the simulation experiments, there will be a total number of curves, 49 of which are generated by a reference model, and one is the contaminating outlier. The functions are defined in the interval , with a grid of 30 equally spaced points and bootstrap groups. Using the previous notation for the DTW algorithm, points. The description of the models for these control simulation tests is as follows:
Model 1. is the function generator for the reference set of curves. In this case, the outliers follow the distribution .
Model 2. The reference model for the curve generation remains , whereas the outliers are now generated from the distribution .
Model 3. Here the reference model becomes . The outliers are generated from .
Model 4. For this last case, we keep the reference model as it is for Model 1 and Model 2, but the outliers simply consist of the sole deterministic part (the Gaussian component is removed).
Similar models to 1 and 2 can be found in [
35,
36,
37], although the multiplicative factor of the indicator function has been reduced to make the outliers less apparent. Model 3 was also considered in [
25,
35]. The fourth model was developed here to test the detection capabilities of pure shape outliers. These models (see
Figure 1) or similar ones have already been tested with existing methodologies, and they were therefore included here to facilitate the comparability with other detection methods.
In all cases, a bivariate Gaussian mixture model is adjusted to a pair of selected features and the outlier detection procedure is applied thereafter. Four commonly used features in the functional data analysis framework will be considered:
The detection procedure is applied to replications of each model. We shall use two scores to evaluate the quality of the detection procedure. The first one will naturally be the estimated values of the outlier in each model and replication. This parameter is directly linked to the probability of being more anomalous than the outliers if the model is correct. Therefore, the distribution of values of constitutes an indicator of the detected outlying nature of the function.
The second score is the average ranking of the outlier with respect to the total population of data. Since the score provides an ordering of the anomalous nature of each element in the set of curves, so it is possible to rank the data accordingly to said metric. In industrial applications, this ranking can be followed by the engineer to analyze particular data (e.g., numerical simulations) from the most suspicious (potentially interesting) datum to less suspicious ones.
Several tests evaluating the performance of the different couples of measures can be found in the
supplementary material of the paper. In particular, it can be seen that the use of the h-mode depth and the DTW seem appropriate for the detection of the considered types of outliers.
The use of the h-mode depth allows the detection of magnitude outliers taking into account the areas of the plane where the density of curves is less significant. This feature is useful since it allows the avoidance of problems derived from the consideration of multimodal distributions that may present several regions of high density and mask this type of outliers, a case which is not usually considered in the literature. Furthermore, the use of the normalized averaged version of the DTW that is considered in the paper allows the specific targeting of shape outliers. Its use allows the comparison of the functional data based on a pairwise comparison that only takes into account differences in shape, while being sensitive to shifts in the t-axis. In any case, their use has been tested against other similarity and depth measures, showcasing how the combination of these two measures provides the best identification grounds for outlier detection, both regarding the detection rates and the robustness.
Finally, we note that there exist similarities between the method presented here and in [
23], but with significant differences. First, in the construction of the model, our paper proposes modifications to the EM algorithm in order to solve some of the main difficulties in the use of probabilistic models for outlier detection. Secondly, the measures selected in the algorithm presented in our paper allow for a certain explainability of why specific samples have been identified as outliers of shape, magnitude, or a mixture of both, which was also one of the main objectives. Lastly, the algorithm presented in our paper also aims at providing an order of outlyingness of the functional data, without necessarily labeling them as outliers. This outlyingness score aims at being used in domains where a quantitative score is more useful, such as in the sensitivity analysis one. An industrial example is provided in
Section 5.
4.2. Comparison with State-of-the-Art Methodologies
The detection algorithm for the selected combination of features is performed to compare it to other detection methods. The selected methodologies are succinctly presented below.
4.2.1. Functional Boxplots
Given a sample of functional data
defined in a time domain
indexed by the variable
t, the
central region can be defined as:
This region can be interpreted as an analogous of the inter-quartile range for functional data, and it effectively corresponds to it pointwise. The whiskers of the functional boxplot can be computed by extending
times the pointwise extremes of the central region, such that the outliers are detected if they surpass the frontiers defined by these whiskers. The in-depth analysis of this method can be found in [
38].
4.2.2. High-Density Regions
Introduced by [
39], the method consists of regrouping the values of the functional data in the considered time steps in a matrix and performing the Karhunen-Loève decomposition, obtaining the corresponding coefficients in a lower-dimensional feature space where the density of the components is estimated via kernel density estimation. This way, the High-Density Regions (HDR) can be defined as the regions such that:
, and will correspond to the region with highest probability density function with a cumulative probability of
, which can impose a detection criterion.
4.2.3. Directional Detector
As described in [
40], let
X be a stochastic process,
, the Functional Directional Outlyingness is defined as:
where
is a weight function. This magnitude can be decomposed into two components, the Mean Directional Outlyingness (MO) and the Variation of Directional Outlyingness (VO). The detection algorithm is based on these quantities and the selection of cutoff values for inferred Mahalanobis distances based on standard boxplots.
4.2.4. Sequential Transformations
This algorithm from [
35] relies on the transformation of a wide diversity of shape outliers into magnitude outliers, much easier to detect through standard procedures. Given a sequence of operators defined in
(the functional space that generates the considered data)
, the method consists of sorting the raw and transformed data into vectors of ranks for each observation. The vectors of ranks are sorted according to a one-side depth notion, such as the
extreme rank depth for instance, and a global envelope is constructed, which allows the outlier identification.
4.2.5. Results
The results of the application of the algorithm are given for the previously used 4 models and different degrees of contamination. The experiments were simulated 500 times for a sample of curves of
, and three different degrees of contamination of outlying curves:
and
of outliers in the sample. The detection rates are summarized in
Table 2.
First, we must note that the identification capabilities and rates are clearly reduced when the size of the outlying sample is increased. This reduction of the performance of any detection algorithm is logical, since higher degrees of contamination naturally pollute the functional sample, which increases the bias of the score that is used for outlier detection. In the same line, if the size of the outlying sample is considerable (
of outliers for instance), an argument can be made to defend that this sample might not be outlying, and that it simply corresponds to another mode in a hypothetical multimodal functional sample. This kind of phenomenon, as well as masking effects, are described in detail in [
19].
Looking at the results, we can appreciate that the performance of the proposed algorithm is indeed competitive and on par with existent methods, even for complex sets of functional data, such as Model 4. In this case, we can clearly appreciate how the inclusion of a measure specifically dedicated to the detection of shape differences allows the consistent detection of the outlier. This capability is especially significant when we compare it with the other methods, which prove to be unable to detect this kind of shape outlier. In the case of the widely used Functional Boxplots, this is to be expected since they are intended to detect magnitude outliers. Regarding the HDR method, its low detection capabilities in this case are due to the fact that the low-dimensional representation through robust Functional Principal Component Analysis is not sufficiently precise to capture the outlying nature of the straight line. It is indeed possible that retaining a higher number of modes in this case could allow better detection capabilities, but this procedure greatly increases the curse of dimensionality problem (even if this subject is not treated in the paper by [
39]), and it does not allow visualization purposes.
It is clear that Model 3 (being the only pure magnitude outlier among the considered models) is the most simple and easy to detect and virtually any method can consistently detect this kind of outlier when the sample is not overly polluted. Methods which rely the most on the density of curves in the functional space and their trends is more vulnerable to the bias induced in the sample by the curves, as they tend to identify the proportion of curves that behave unusually as belonging to a different mode of curves instead of genuine outliers. In the case of the functional boxplots, this is to be expected since by construction they are dedicated to the detection of magnitude outliers, which is useful if the contamination of the sample is made by a wide variety of magnitude outliers, but not so much if those outliers have all been generated by a homogeneous family of curves. In the case of the HDR plots, the existence of a homogeneous sample of outliers generates a set of points in their two-dimensional feature space of principal component scores with a high density of data.
In Models 1 and 2 the conclusions are similar (both models present a combination of slight magnitude and shape outliers). Most methods do not showcase any robustness for such slight magnitude outliers, contrary to the presented algorithm. The main conclusion that can be extracted from these tests is that most methods struggle to find outliers when they are not apparent, as is the case of the models presented here.
Finally, it must be mentioned that the Directional Detector is the most robust method when it comes to detecting the pure magnitude outlier presented in Model 3, as is the least sensitive method to more contaminated samples. The main advantage of this methodology is its capability of finding outliers in multivariate functional data sets.
4.3. Ranking Results
Finally, another advantage of the methodology presented in this paper is the ability to provide a scalar ranking criterion (
) for a sample of functional data. This is not only useful from a clustering or outlying detection perspective, but also from an exploratory analysis one. In particular, this kind of score can be used to perform sensitivity analysis on the functional data (see an example in
Section 5).
Depth measures are widely used in this setting, but some advanced techniques that have developed in recent years, such as the method presented in
Section 4.2.4, which provides an efficient ordering of the data. Naturally, as it happened in the outlier detection setting, a good order measure should be capable of identifying a potential multimodality in the set of data, as well as handling the existence of magnitude, shape, or mixed outliers.
The ranking experiments are the same ones as the ones performed for outlier detection testing, with one outlier in the sample of 100 curves. The results are presented in
Table 3.
In this case, we can appreciate that more advanced ranking methods such as the one presented here and the one presented in [
35] provide a consistent ordering of the functional data. The results provided by these up-to-date methods show that for the sample of 100 curves, the introduced outlier is always found to belong to the
more outlying curves of the sample, and is frequently found to be the most outlying in simpler cases such as Model 3. Usual ranking techniques for functional data such as depth definitions fail to clearly identify the more outlying nature of the outlier in the sample, and cannot be reliably used as order measures in such homogeneous packages of univariate curves.
Finally, we can mention that the better ranking results provided by the Sequential Transformations algorithm for Model 4 with respect to the method presented in this paper can be explained due to the nature of the chosen transformations. In particular, the use of what they call transformation in their paper, which consists of taking the first-order derivative of the functional data (in their notation, ), is obviously appropriate in the case of Model 4, where the pure shape outlier differs mainly by the values of derivatives. This means that its superior ranking capabilities for this specific model cannot be generalized for any type of shape outlier, and both methods provide comparable ranking results.
5. Industrial Test-Case Study
5.1. Presentation
In this section, the outlier detection methodology is applied to a real industrial dataset of time-dependent numerical simulations. We consider an Intermediate Break Loss of Coolant Accident (commonly called IBLOCA or simply LOCA) in a nuclear power plant, simulated with the CATHARE2 code. CATHARE2 is a best estimate computer code capable of recreating the main physical phenomena that may occur in the different systems involved in nuclear reactors, in particular in the 900 MW French Pressurized Water Reactors. It embeds two-phase modeling to calculate the thermal-hydraulic behavior of the coolant fluid in the reactor.
A LOCA accident is originated by a breach in the primary circuit, which is designed to evacuate the heat generated by the nuclear core. The sudden loss of large quantities of coolant implies a fast increase of the water temperature nearby the nuclear fuel rods, due to the residual power generated by the core during the accidental transient. This power discharge and the subsequent temperature elevation must be compensated by the injection of water through a dedicated safety system. This is supposed to ensure that fuel rods temperature would remain below the fusion point at all times. Hence, the main safety criterion in LOCA regarding the confinement of the fuel concerns its Peak Cladding Temperature (PCT), i.e., its maximum cladding temperature over the duration of the LOCA (here, the time-dependent cladding temperature is the maximum cladding temperature for all the fuel rods, whatever its localization in the core).
The particular statistical model under study involves many scalar input parameters (), which specify all sorts of physical phenomena whose relative influences in the PCT are difficult to assess a priori. These input variables can be classified into various categories, such as (i) initial conditions and limit states for the system (Primary pressure, starting thermal power, the primary pumps inertia…), (ii) some parameters of specific physical models and correlations that are used (thermal exchanges between the components, friction between fluid phases or some geometric parameters of the installation), as well as (iii) some scenario variables (existence of blockages in the heat exchangers, fuel use in its life-cycle or initial temperature of the safety water injection).
All of these scalar inputs of the simulation code are uncertain, and are hence represented by the random vector , whereas the output of interest would be Y, which is normally a critical safety parameter in this case, such as the aforementioned PCT.
The total number of simulations that can be performed is relatively limited for such a high-dimensional input vector, since each run of the code takes around one hour to finish. For this reason, the use of classical multivariate statistical techniques is not straightforward. This explains the widely spread use of space-filling design methods to maximize the coverage of the input space [
42], as well as metamodeling techniques to better exploit the number of code runs available for the physical model. Briefly explained, space-filling designs try to optimally explore the space of input variables i.e., they establish criteria to better choose the analyzed points of this high-dimensional space (in the case of nuclear transients, there can easily exist more than a hundred input variables). In the case of metamodels, they are mathematical approximations of more complex physical models that, despite showing a higher precision in their calculations, take a much higher computation time. The use of metamodels helps to improve (increase) the total number of available simulations, so that the results that are finally obtained are more statistically relevant.
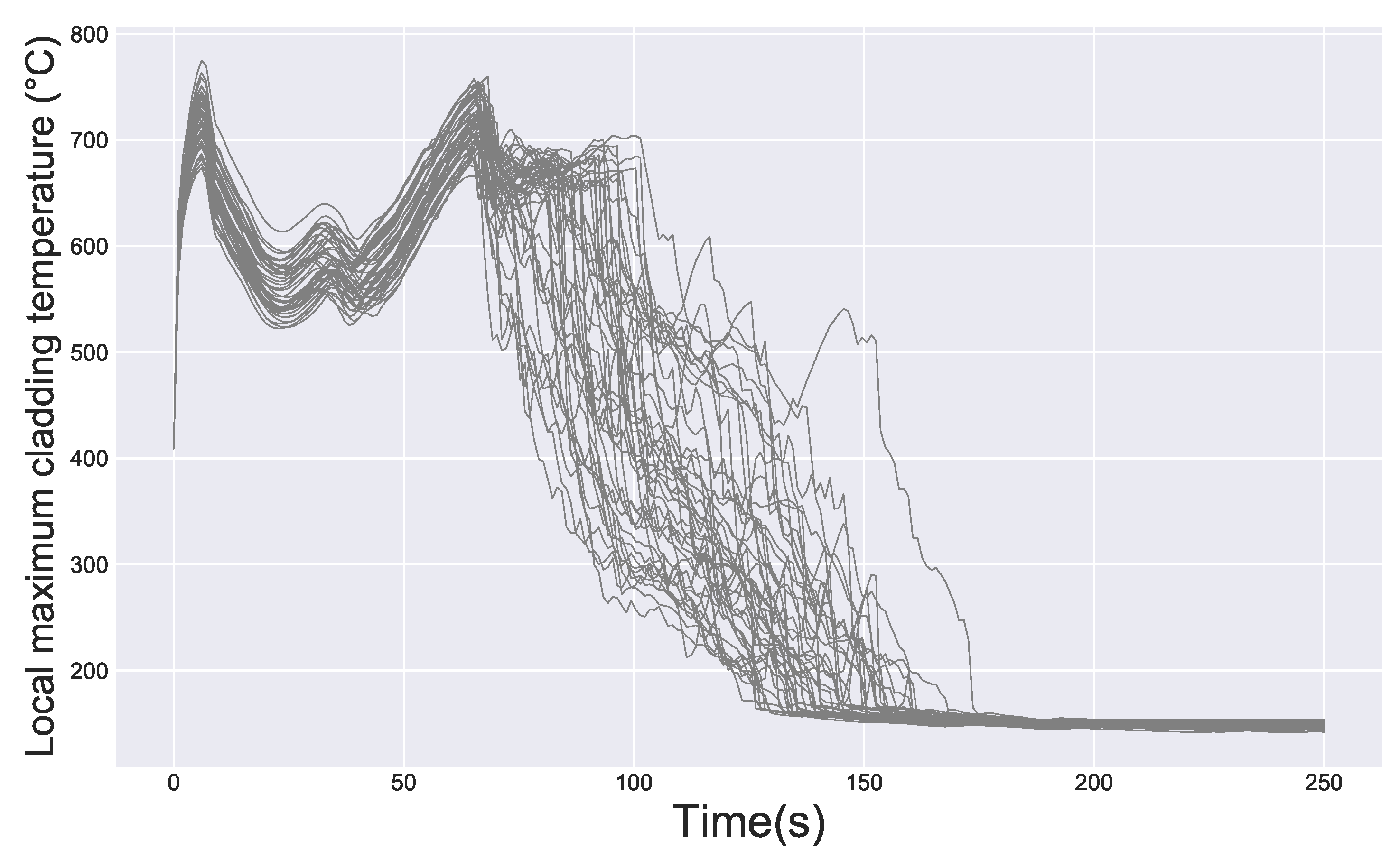
In this context, the consideration of the whole functional output (the evolution of the maximum cladding temperature, whatever its location) is expected to provide a better insight on the physical phenomena that govern in the transient than the scalar value of the PCT alone.In our case, 1000 Monte Carlo runs of the code were launched, generating the set of curves that is presented in
Figure 2 for the evolution of the maximum cladding temperature during the transient.
5.2. Functional Outlier Detection
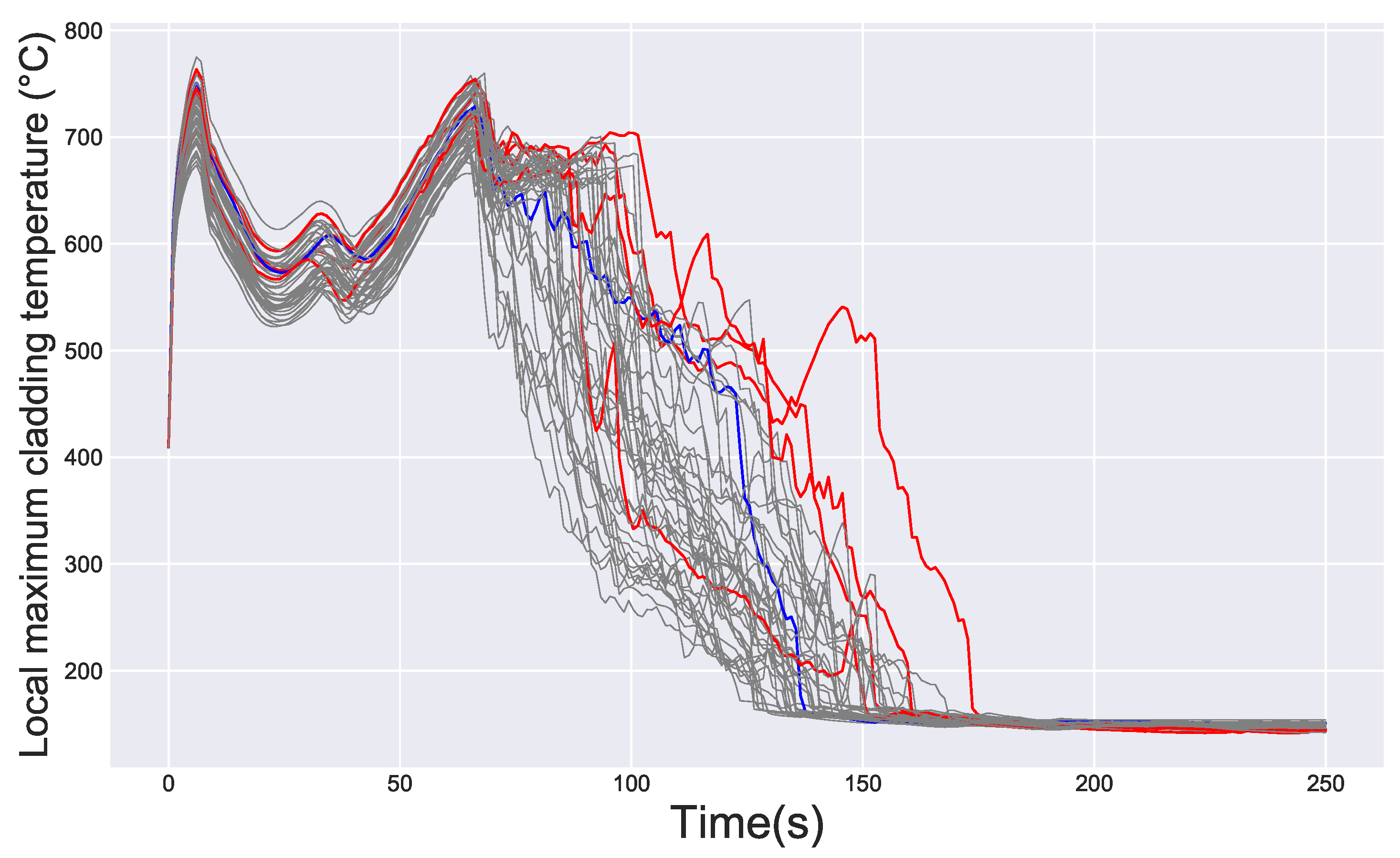
The previously presented outlier detection technique is applied to this set of curves. Both the h-mode depth and the DTW are the selected features to obtain the degree of outlyingness of each functional datum. The curves presenting a degree
of outlyingness over
are shown in
Figure 3.
The first apparent result is that the main magnitude outlier is easily detected, since the curve that acts as the upper envelope of temperature in most points of the domain is the one presenting the highest value of ( actually in this case). This curve is not only anomalous in the magnitude sense, but also in the shape one, similar to Model 4 that was presented in the previous section (these are sometimes called phase outliers).
Two other magnitude outliers have been identified, and one of them is also a shape outlier, presenting an anomalous peak of temperature after about 120 s of simulation (physical time). The final main outlier is a pure shape one, remaining zones with high density of data during the whole domain of simulation, but presenting two peaks of temperature. Especially notorious is the first peak, which occurs around the 100 s of transient, in a time interval that does not match most curves.
5.3. Sensitivity Analysis on Outliers
In this kind of numerical simulations, the detection of outputs that present a globally anomalous behavior is of critical importance, and characterizing what are the physical phenomena which have an actual influence on it can have the same importance, if not more. A way of performing this analysis is to establish some kind of dependence measure between the inputs of the simulation code and the outlying score
. However, the high dimensionality of the problem and the possible correlations between the input variables of the code can make this a difficult task. The Hilbert Schmidt Independence Criterion (HSIC) [
43] can be a useful tool in this context to test the dependence between the scalar input variables of the code and the outlying score. This is a first step to understand which physical variables are the ones that actually influence the anomalous behavior of the outputs.
By performing statistical tests on the HSIC values of the couples
in the design of experiments it is possible to quantify their dependence. Without going into the technical details of the procedure (see [
44] ), the HSIC represents a dependence measure between both variables, and can be used to build a statistical test with null hypothesis:
: the variable
and
Y are independent. The hypothesis is rejected if the associated
p-value of the test is inferior to a significance level threshold
. If
is rejected, then the existence of a dependence structure between the input variable
and the output exists.
In this case, we apply this measure to perform a Target Sensitivity Analysis, i.e., sensitivity analysis but quantifying the influence of the considered parameters in a restricted domain
of the possible output values (
such that
). This application to the set of input data and the obtained values of
yields several influential variables that are shown in
Table 4.
All these input variables can be considered to have an influence on the outlyingness of the resulting simulated curve, which represent the evolution of the maximum cladding temperature during the transient. Variable represents the friction between the injected water in the primary circuit by the accumulators and the injection line. This parameter has been found to be influential in other similar studies since the compensation of the lost water during the transient is mainly guaranteed by this system (the accumulators), and therefore the line connecting it to the primary is of crucial importance. If this value of friction increases, the water flow will be reduced, with the consequent increase in the average temperatures of the fuel.
Regarding variables and 64, they are representative of physical phenomena occurring in the reactor pressure vessel during the transient. They model respectively: the heat transfer coefficient between the nuclear fuel and the surrounding coolant; the increase in pressure drop due to the deformation of the nuclear fuel due to the thermal-mechanical stress, prevents the coolant from ascending easily to the top of the reactor pressure vessel; and the friction between the steam and water in the core during the reflood phase of the transient. These elements are relevant since their evolution greatly influences the rewetting dynamic of the fuel, and the heat extraction in the short-term phase of the transient.
Finally, variables and are representative of phenomena which occur between the steam and coolant water in the downcomer (the annular part which links the injection line of the accumulators and the nuclear core). This element is critical during the reflood process, which is why increases in the friction between the ascending steam and the descending water in this element are penalizing from a safety point of view. This is due to the fact that if the friction coefficient increases, it means that the momentum of the injected water will be reduced, and the core will take longer to be filled. Similar conclusions can be obtained for the heat exchange coefficient between both phases in the downcomer, since low values for this variable will imply lower heat extraction rates in the vessel.
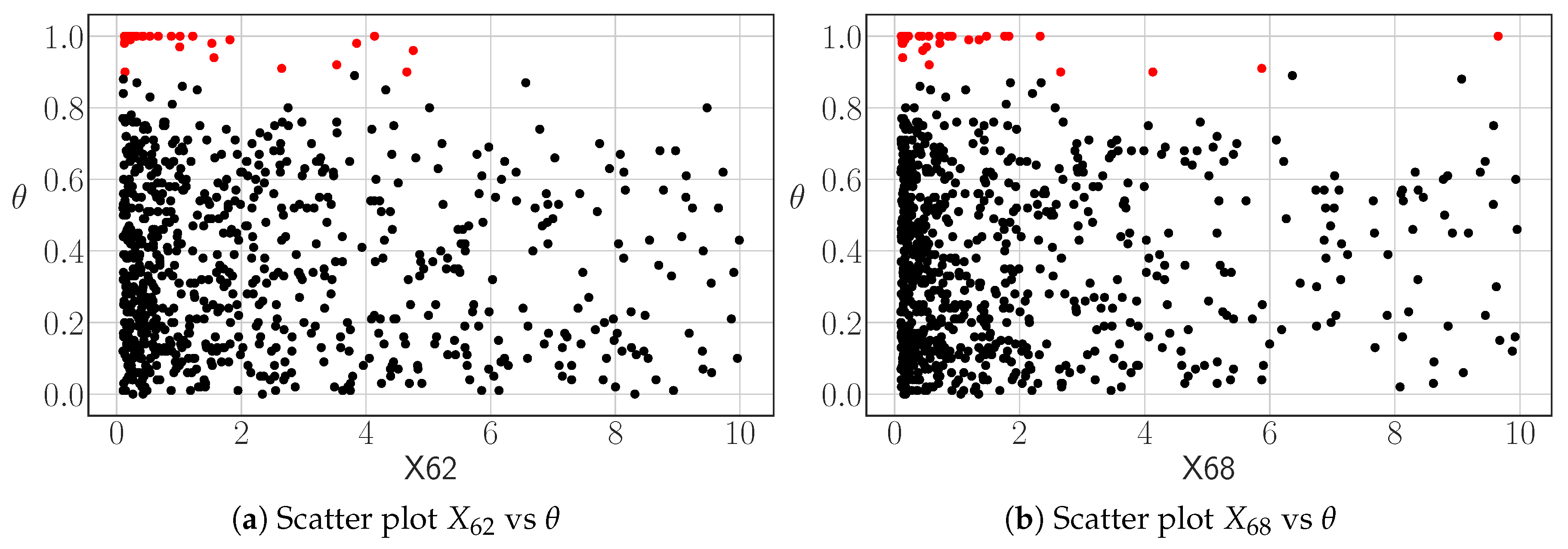
The study of two-dimensional scatter plots between these input parameters and the outlying score
could already prove to be useful to visualize how the inputs affect the outlying nature of the functional outputs. An example that illustrates the idea is presented in
Figure 4.
As it can be seen, outlying transient concentrate around specific subsets of the domain of the identified influential variables. These plots are useful to evaluate if the physical values that originate outlying simulations are physically coherent with their expected influence. In this particular case, for instance, lower values of friction should correspond to less penalizing and outlying configurations when the safety criterion is the Peak cladding temperature of the nuclear fuel. Therefore, the observed effect of this variable is actually not expected, and it corresponds to an anomalous effect in the coding of this particular transient that was later corrected by the engineers. In other words, the methodology and the analysis technique was capable of capturing not only extreme effects in the analyzed physical time-dependent variable (the Maximum Local Cladding temperature), but it was also capable of finding actual outliers, in the sense that those simulations showcase non-physical events in the particular modeling used in this study.
6. Discussion and Conclusions
This paper has dealt with a particular branch of unsupervised anomaly detection: the outlier detection problem in functional data. The main aspects to take into account when dealing with functional data or high-dimensional objects in general have also been developed, exposing its main challenges and advantages. A new time-dependent outlier detection methodology based on the use of non-parametric features has been proposed, assessed with synthetic data, and illustrated on thermal-hydraulic simulations, aiming at capturing the outlyingness of the elements of any considered functional dataset both in the magnitude and the shape senses. This is done via the joint use of the h-mode depth and the dynamic time warping, and by defining outliers as data which do not belong to the minimum volume set of a chosen probability. The underlying distribution in the feature space is modeled through a GMM whose estimation is adapted to the outlier detection framework by means of modifications of the EM algorithm. The maximal probability for which a datum is not regarded as an outlier anymore is used as a score of its outlyingness.
An original detection algorithm has been proposed, effectively allowing the trimming of functional data. This methodology, based on the use of two features, benefits from the notion of level set to treat real industrial problems based on time-dependent data even if the available data are scarce. Several features have been compared in this framework based on some toy examples and two scores related to the outlyingness of functional data. Based on the results of these application cases, both the notions of dynamic time warping, and the h-mode depth have proven their efficiency when compared to other features such as the norm and the Modified Band Depth.
Finally, the analysis of simulations of the thermal-hydraulic behavior of a nuclear reactor during a Loss Of Coolant Accident has been carried out to illustrate the benefits of the method. This was achieved thanks to the use of sensitivity analysis tools (HSIC-based) capable of accounting for the dependence of the input variables of the numerical simulator.
Regarding the perspectives of this work, a primary objective would be the in-depth quantification of the causes for the detected anomalous characteristics of certain functions in real physical cases. In the case of numerical simulators, the identification of the inputs of the code that actually present an influence on the anomalous outputs can help engineers to detect possible defects of the code or finding physical phenomena of interest. This is also relevant to ensure the quality of the datasets that are used in the assessment reports of critical systems such as nuclear power plants.