Artificial Neural Network-Based Model for Prediction of Frost Heave Behavior of Silty Soil Specimen
Abstract
1. Introduction

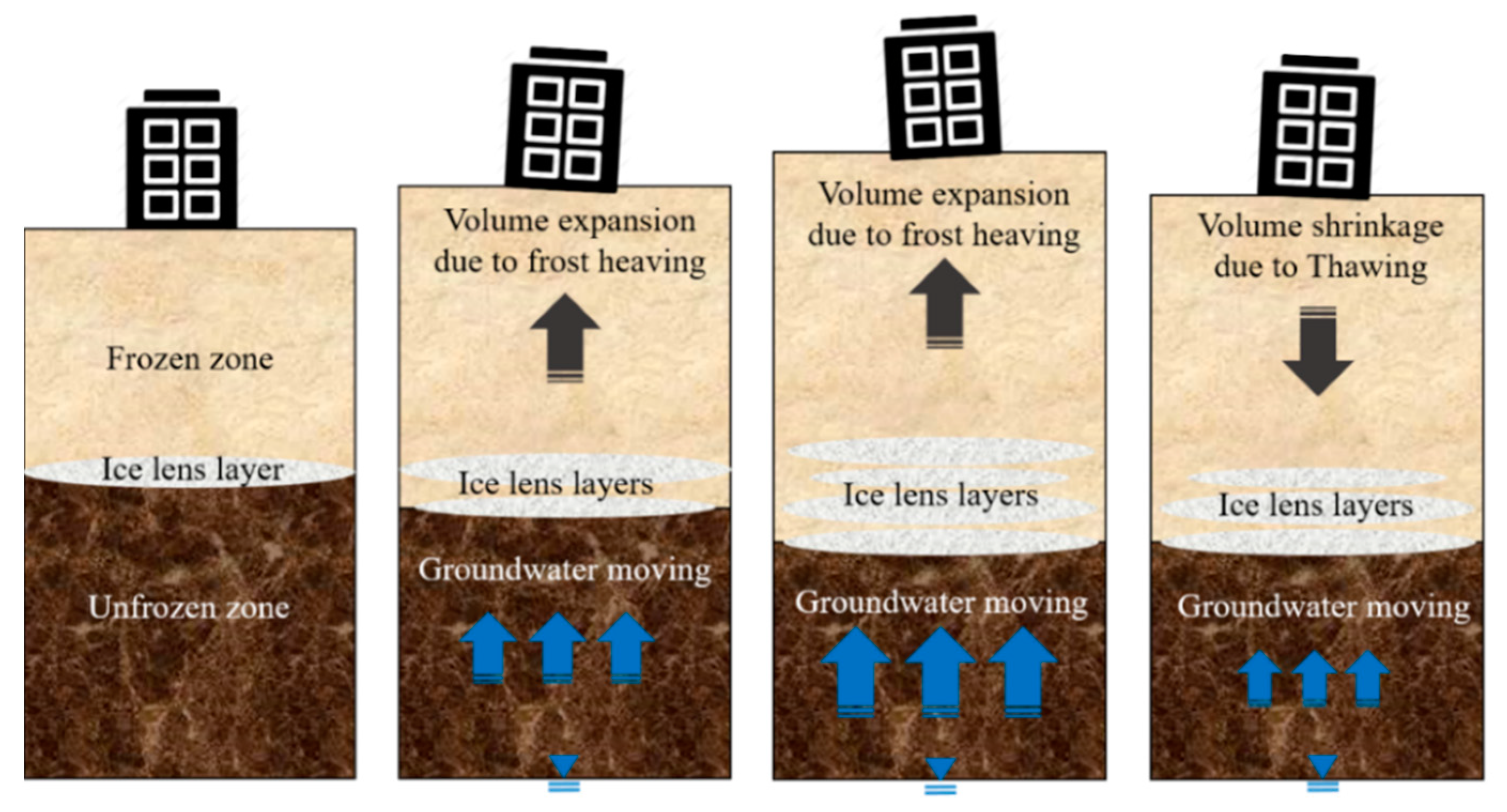
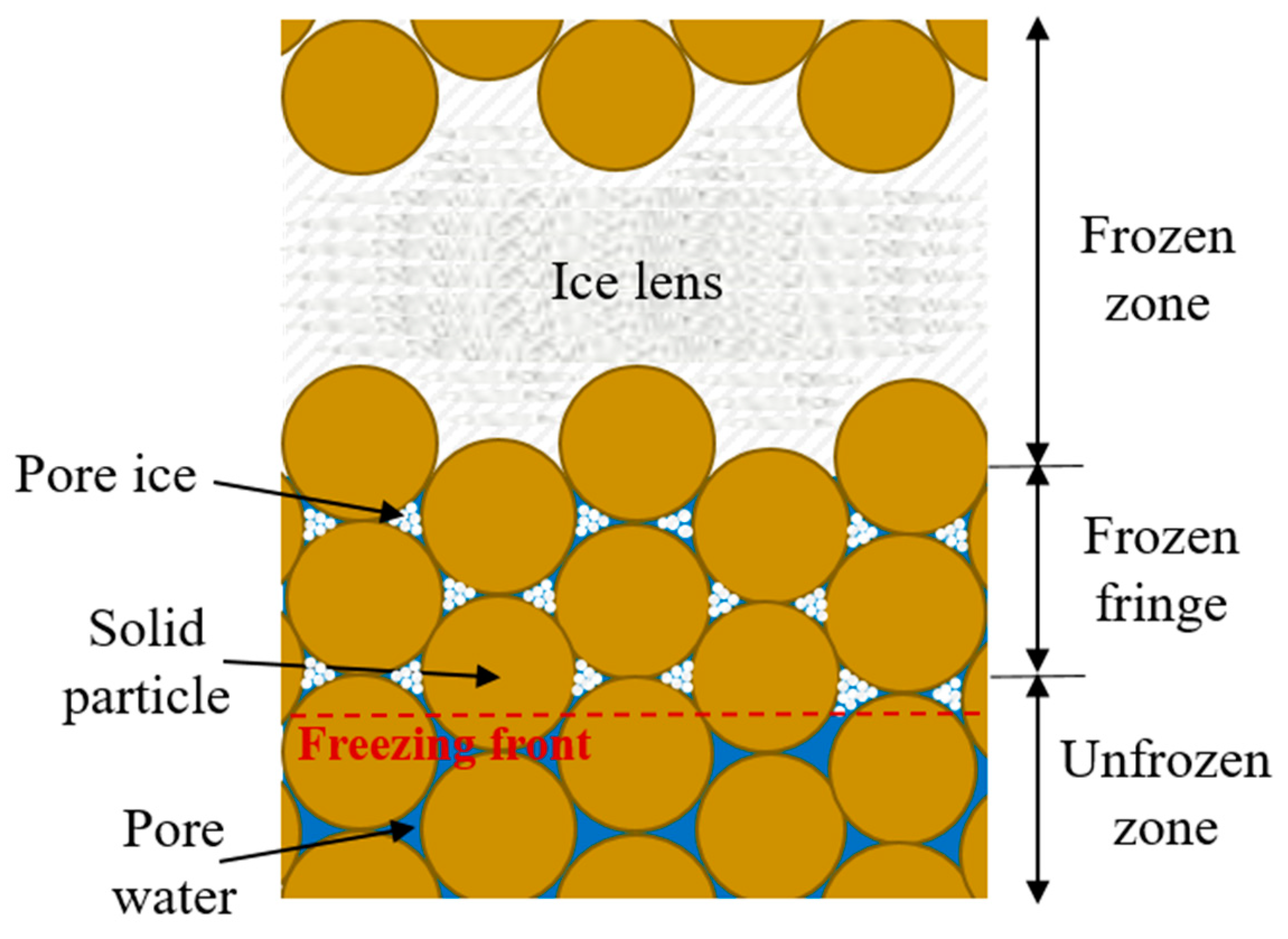
2. Materials and Methods
- The soil is isotropic and elastic.
- The soil is a fully saturated medium that is fully frozen, partially frozen, or unfrozen.
- The water migration that occurs in the frozen fringe and the unfrozen zone follows Darcy’s law.
- The soil particles, pore water, and ice are incompressible under the pressure and temperature conditions present in cold regions, and these three-phase soil materials satisfy the local thermal equilibrium.
2.1. Mass Balance Equation
2.2. Energy Conservation Equation
2.3. Force Equilibrium
2.4. Ice Lens Criteria
3. Evaluation of Frost Heave Ratio
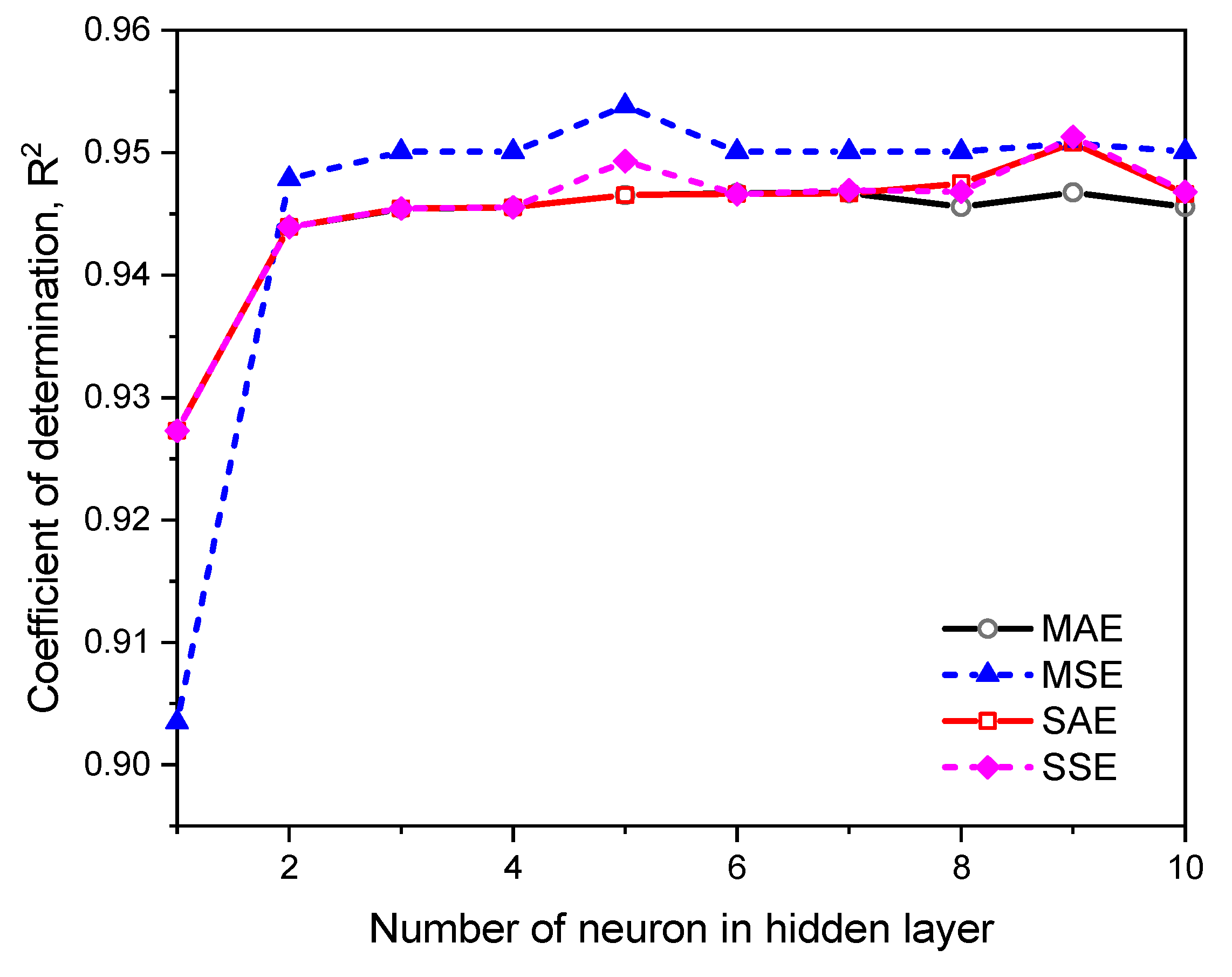
4. Prediction of Frost Heave Ratio Using the Artificial Neural Network Model
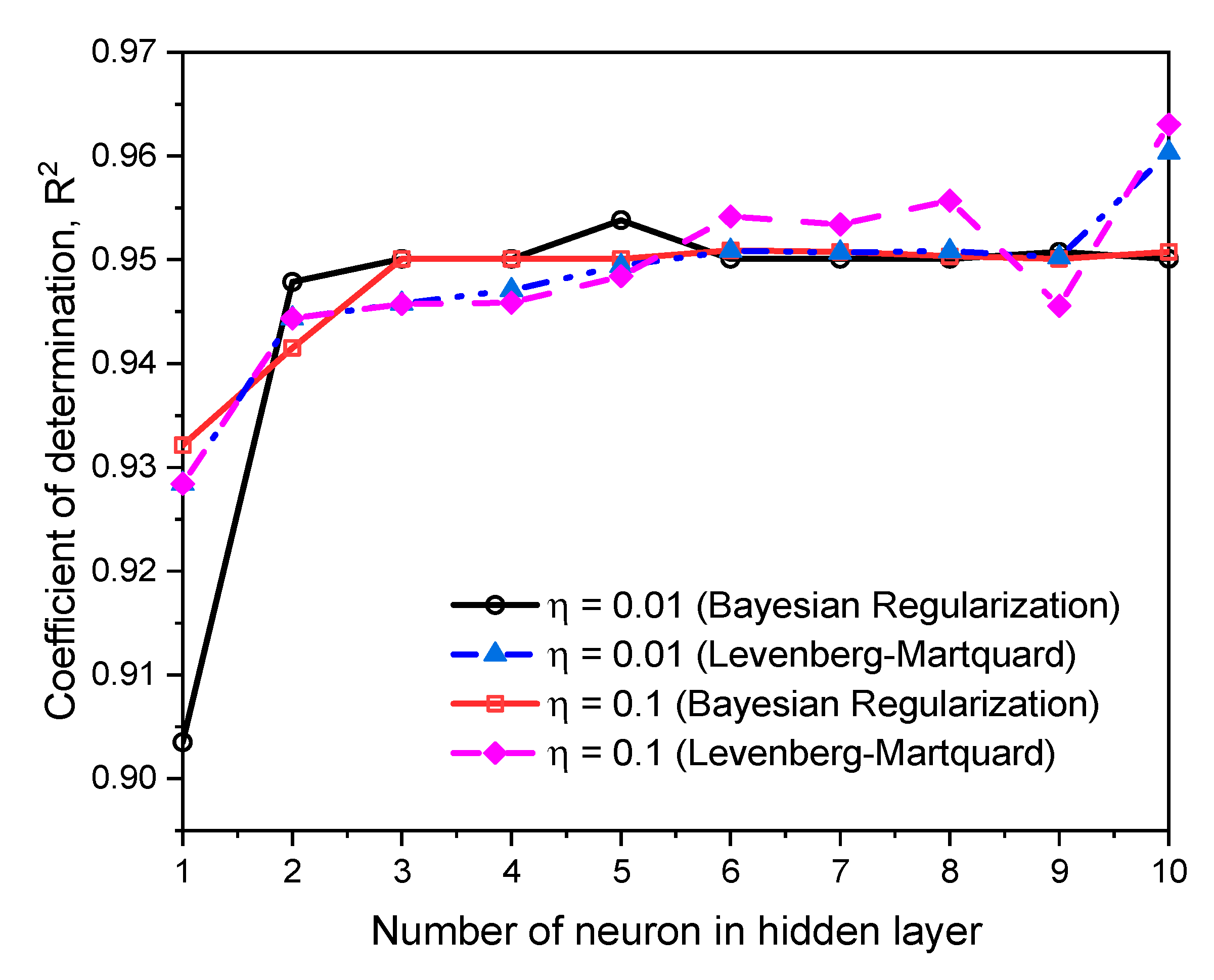
4.1. Establishment of an Artificial Neural Network
4.2. Application of an ANN to Frost Heave Ratio Predictions
5. Summary and Conclusions
- A fully coupled THM model numerically evaluated various physical phenomena that occur during one−dimensional freezing. During the freezing process, the freezing front propagated rapidly when freezing initially began but came to a halt as it approached thermal equilibrium. The amount of frost heave increased steadily until thermal equilibrium was achieved, after which the freezing front stopped and no further severe frost heave occurred.
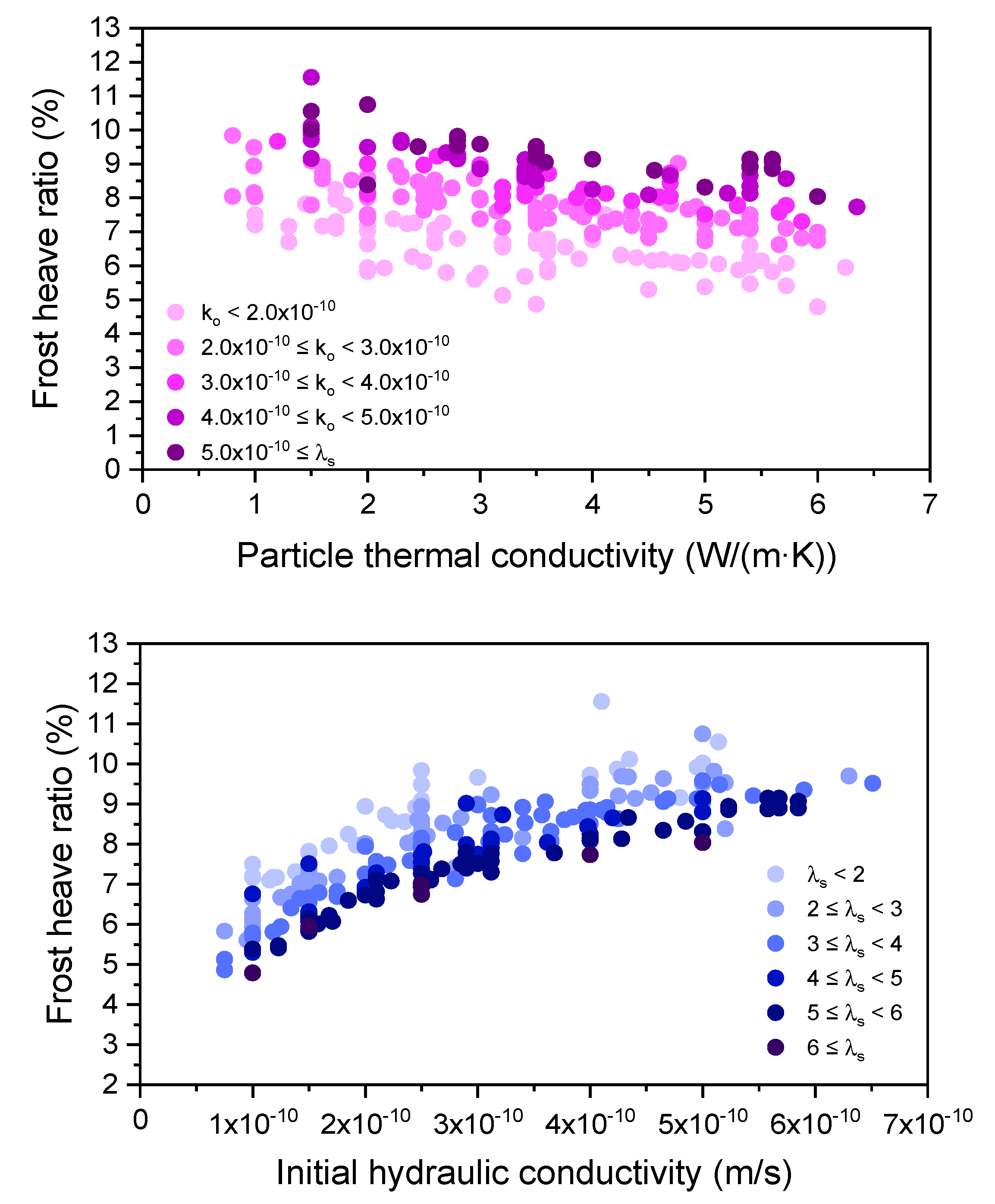
- According to the results of the parametric study, the overall patterns of the predictive model are explained by preconditions for frost heave action. The amount of heave tended to decrease as particle thermal conductivity increased. This may have something to do with thermal conditions that prevent a sufficient inflow of water from external sources due to a high freezing rate. Additionally, the frost heave ratio tended to increase as the initial hydraulic conductivity increased. If the thermal conditions are the same yet the hydraulic conditions are varied, it could be judged that higher soil hydraulic conductivity would result in a higher frost heave ratio.
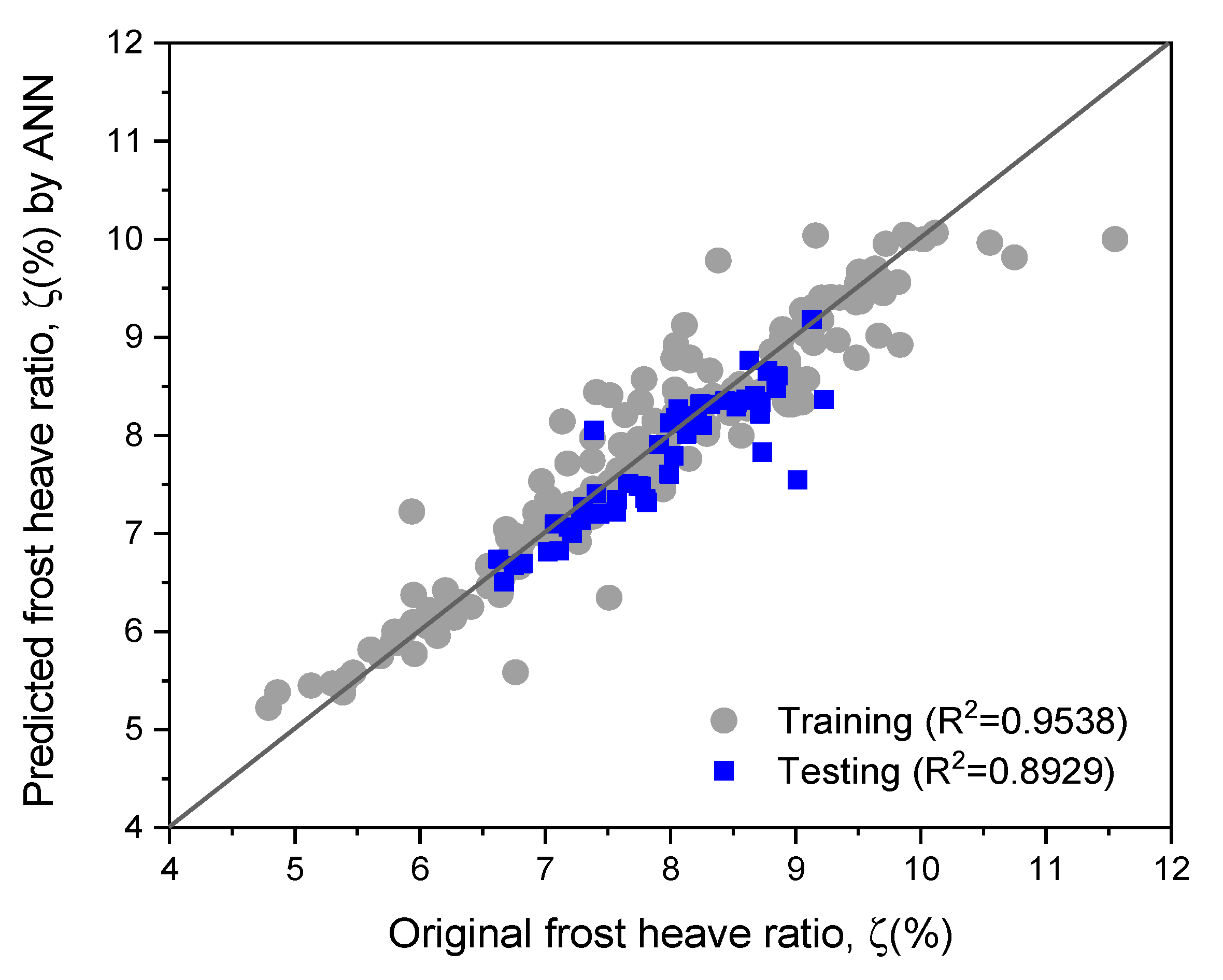
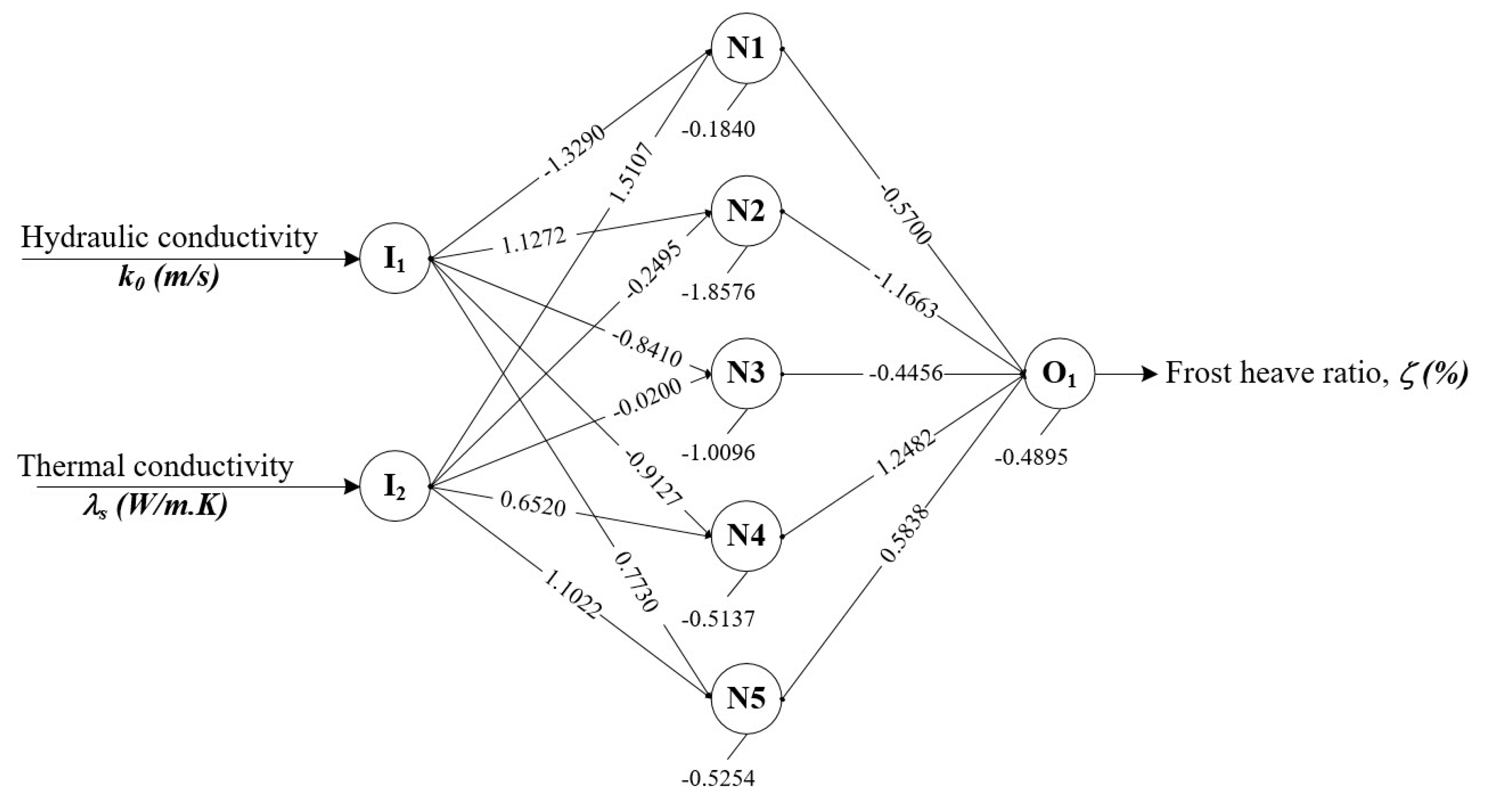
- After evaluating the sensitivity of each parameter to frost heave behavior through multiple statistical analyses, an artificial neural network model was proposed to practically estimate frost heave behavior. According to the interpreting connection weights, the hydraulic conductivity in the unfrozen zone (k0) was the most important input parameter that was a direct cause of the frost heave ratio ζ(%), and the thermal conductivity of the soil particle (λs) was lesser importance. In order to evaluate the applicability of the artificial neural network model, the model was tested with datasets that had not been introduced during the training stage. According to the verification results, the trained network model demonstrated a reliable accuracy (R2 = 0.893) in predicting frost heave ratio, even when the model used the test datasets that were not part of the training datasets. It is expected that this prediction model will be useful in many areas of research related to evaluating the frost heave behavior of saturated specimens.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- National Snow and Ice Data Center. All about Frozen Ground. Available online: https://nsidc.org/cryosphere/frozenground/index.html (accessed on 18 January 2018).
- Michalowski, R.L.; Zhu, M. Frost heave modelling using porosity rate function. Int. J. Numer. Anal. Meth. Geomech. 2006, 30, 703–722. [Google Scholar] [CrossRef]
- Zhang, Y. Thermal-Hydro-Mechanical Model for Freezing and Thawing of Soils. Ph.D. Thesis, Civil Engineering at University of Michigan, Ann Arbor, MI, USA, 2014. [Google Scholar]
- Konrad, J.M. Frost susceptibility related to soil index properties. Can. Geotech. J. 1999, 36, 403–417. [Google Scholar] [CrossRef]
- Wu, D.; Lai, Y.; Zhang, M. Heat and mass transfer effects of ice growth mechanisms in a fully saturated soil. Int. J. Heat Mass Transf. 2015, 86, 699–709. [Google Scholar] [CrossRef]
- Penner, E. Aspects of ice lens growth in soils. Cold Reg.Sci. Technol. 1986, 13, 91–100. [Google Scholar] [CrossRef]
- Harris, C.; Smith, J.S.; Davies, M.C.R.; Rea, B. An investigation of periglacial slope stability in relation to soil properties based on physical modelling in the geotechnical centrifuge. Geomorphology 2008, 93, 437–459. [Google Scholar] [CrossRef]
- Harris, C. Physical modelling of periglacial solifluction: Review and future strategy. Permafrost Periglac. Process. 1996, 7, 349–360. [Google Scholar] [CrossRef]
- Harris, C.; Luetschg, M.; Davies, M.C.R.; Smith, F.; Christiansen, H.H.; Isaksen, K. Field instrumentation for real-time monitoring of periglacial solifluction. Permafr. Periglac. Process. 2007, 18, 105–114. [Google Scholar] [CrossRef]
- Gilpin, R.R. A model for the prediction of ice lensing and frost heave in soils. Water Resour. Res. 1980, 16, 918–930. [Google Scholar] [CrossRef]
- Konrad, J.M.; Morgenstern, N.R. A mechanistic theory of ice lens formation in fine-grained foils. Can. Geotech. J. 1980, 17, 473–486. [Google Scholar] [CrossRef]
- O’Neill, K.; Miller, R.D. Exploration of a rigid ice model of frost heave. Water Resour. Res. 1985, 21, 281–296. [Google Scholar] [CrossRef]
- Nixon, J.F.D. Discrete ice lens theory for frost heave in soils. Can. Geotech. J. 1991, 28, 843–859. [Google Scholar] [CrossRef]
- Konrad, J.M.; Duquennoi, C. A model for water transport and ice lensing in freezing soils. Water Resour. Res. 1993, 29, 3109–3124. [Google Scholar] [CrossRef]
- Shin, H.S.; Kim, J.M.; Lee, J.; Lee, S.R. Mechanical Constitutive Model for Frozen Soil. J. Korean Geotech. Soc. 2012, 28, 85–94. [Google Scholar] [CrossRef][Green Version]
- Zheng, H.; Kanie, S.; Niu, F.; Akagawa, S.; Li, A. Application of practical one-dimensional frost heave estimation method in two-dimensional situation. Soils Found. 2016, 56, 904–914. [Google Scholar] [CrossRef]
- Ingeman-Nielsen, T. Lecture Notes—11854 Infrastructure Construction in the Arctic; ARTEK and DTU Byg: Kongens Lyngby, Denmark, 2017. [Google Scholar]
- Cicchetti, L. Thermo-Hydro-Mechanical Simulations of Artificial Ground Freezing. Master’s Thesis, Cold Climate Engineering, Departments of Civil and Environmental Engineering at NTNU and DTU, Trondheim, Norway, 2018. [Google Scholar]
- Thomas, H.R.; Cleall, P.; Li, Y.C.; Harris, C.; Kern-Luetschg, M. Modeling of cryogenic processes in permafrost and seasonally frozen soils. Geotechnique 2009, 59, 173–184. [Google Scholar] [CrossRef]
- Liu, Z.; Yu, X. Coupled thermo-hydro-mechanical model for porous materials under frost action: Theory and implementation. Acta Geotechnica 2011, 6, 51–65. [Google Scholar] [CrossRef]
- Zhou, J.; Li, D. Numerical analysis of coupled water, heat and stress in saturated freezing soil. Cold Reg. Sci. Technol. 2012, 72, 43–49. [Google Scholar] [CrossRef]
- Zhou, M.M. Computational Simulation of Soil Freezing: Multiphase Modeling and Strength Upscaling. Ph.D. Dissertation, Ruhr University Bochum, Bochum, Germany, 2013. [Google Scholar]
- Zhou, M.M.; Meschke, G. A three-phase thermo-hydro-mechanical finite element model for freezing soils. Int. J. Numer. Anal. Meth. Geomech. 2013, 37, 3173–3193. [Google Scholar] [CrossRef]
- Lai, Y.; Pei, W.; Zhang, M.; Zhou, J. Study on theory model of hydro-thermal–mechanical interaction process in saturated freezing silty soil. Int. J. Heat Mass Transfer. 2014, 78, 805–819. [Google Scholar] [CrossRef]
- Michalowski, R.L. A constitutive model of saturated soils for frost heave simulations. Cold Reg. Sci. Technol. 1993, 22, 47–63. [Google Scholar] [CrossRef]
- Zhang, Y.; Michalowski, R.L. Thermal-Hydro-Mechanical Analysis of Frost Heave and Thaw Settlement. J. Geotech. Geoenviron. Eng. 2015, 141, 04015027. [Google Scholar] [CrossRef]
- Liu, H.; Maghoul, P.; Shalaby, A.; Bahari, A. Thermo-Hydro-Mechanical Modeling of Frost Heave Using the Theory of Poroelasticity for Frost-Susceptible Soils in Double-Barrel Culvert Sites. Trans Geotech. 2019, 20, 100251. [Google Scholar] [CrossRef]
- Lee, Y.G.; Yoon, Y.W.; Kang, B.H. Prediction of undrained shear strength of normally consolidated clay with varying consolidation pressure ratios using artificial neural networks. J. KGS 2000, 16, 75–81. [Google Scholar]
- Min, T.K.; Hwang, K.M.; Jeon, H.W. Prediction of consolidation settlements at vertical drain using modular artificial neural networks. J. KGS 2000, 16, 71–77. [Google Scholar]
- Kim, Y.S. Development of neural network nodel for estimation of undrained shear strength of Korean soft soil based on UU triaxial test and piezocone test results. J. KGS 2005, 21, 73–84. [Google Scholar]
- Go, G.H.; Lee, S.R.; Kim, Y.S. A reliable model to predict thermal conductivity of unsaturated weathered granite soils. Int. Commun. Heat Mass Transf. 2016, 74, 82–90. [Google Scholar] [CrossRef]
- Yoon, S.; Jeon, J.S.; Kim, G.Y.; Seong, J.H.; Baik, M.H. Specific heat capacity model for compacted bentonite buffer materials. Ann. Nucl. Energy 2019, 125, 18–25. [Google Scholar] [CrossRef]
- Bragagnolo, L.; da Silva, R.V.; Grzybow, J.M.V. Artificial neural network ensembles applied to the mapping of landslide susceptibility. Catena 2020, 184, 104240. [Google Scholar] [CrossRef]
- Kim, C.Y.; Bae, G.J.; Hong, S.W.; Park, C.H.; Moon, H.K.; Shin, H.S. Neural network based prediction of ground surface settlements due to tunnelling. Compu. Geot. 2001, 28, 517–547. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Q.; Huo, Z.; Yu, T.; Wang, G.; Liu, T.; Wang, W. Prediction of Frost-Heaving Behavior of Saline Soil in Western Jilin Province, China, by Neural Network Methods. Math. Probl. Eng. 2017, 6, 1–10. [Google Scholar] [CrossRef]
- Tice, A.R.; Anderson, D.M.; Banin, A. The Prediction of Unfrozen Water Contents in Frozen Soils from Liquid Limit Determinations; Cold Regions Research & Engineering Laboratory, U.S. Army Corps of Engineers: Washington, DC, USA, 1976. [Google Scholar]
- Hoekstra, P. Moisture movement in soils under temperature gradients with the cold-side temperature below freezing. Water Resour. Res. 1966, 2, 241–250. [Google Scholar] [CrossRef]
- Mageau, D.W.; Morgenstern, N.R. Observations on moisture migration in frozen soils. Can. Geotech. J. 1980, 17, 54–60. [Google Scholar] [CrossRef]
- Kay, B.D.; Groenevelt, P.H. On the interaction of water and heat transport in frozen and unfrozen soils: I. Basic theory; The vapor phase. Soil Sci. Soc. Am. J. 1974, 38, 395–400. [Google Scholar] [CrossRef]
- Black, P.B. Applications of the Clapeyron Equation to Water and Ice in Porous Media; Cold Regions Research & Engineering Laboratory, U.S. Army Corps of Engineers: Washington, DC, USA, 1995. [Google Scholar]
- Henry, K.S. A review of the thermodynamics of frost heave. CRREL US Army Corps Eng. 2000, 1–26. [Google Scholar]
- Chen, F.X.; Song, Z.P.; Li, N. Study on moisture migrating force model of freezing soil base on adsorption-film moisture migration mechanism. J. Water Resour. Arch. Eng. 2006, 4, 1–4, (In Chinese with English Abstract). [Google Scholar]
- Nakano, Y. Quasi-steady problems in freezing soils. 1. Analysis on the steady growth of an ice layer. Cold Reg. Sci. Technol. 1990, 17, 207–226. [Google Scholar] [CrossRef]
- Everett, D.H. The thermodynamics of frost damage to porous solids. Trans. Faraday Soc. 1961, 57, 1541–1551. [Google Scholar] [CrossRef]
- Miller, R.D. Freezing and heaving of saturated and unsaturated soils. Highw. Res. Rec. 1972, 393, 1–11. [Google Scholar]
- O’Neill, K. The physics of mathematical frost heave models: A review. Cold Reg. Sci. Technol. 1983, 6, 275–291. [Google Scholar] [CrossRef]
- COMSOL Inc. Introduction to Comsol Multiphysics; COMSOL Inc.: Burlington, VT, USA, 2021. [Google Scholar]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences, 2nd ed.; Lawrence Erlbaum Associates: Hillsdale, NJ, USA, 1988. [Google Scholar]
- Lee, I.H. Easy Flow Regression Analysis; Hannarae Publishing Corporation: Seoul, Korea, 2014. [Google Scholar]
- Nguyen, D.; Widrow, B. Improving the learning speed of 2-layer neural networks by choosing initial values of the adaptive weights. In Proceedings of the International Joint Conference on Neural Networks, San Diego, CA, USA, 17–21 June 1990; Volume 3, pp. 21–26. [Google Scholar]
- Wilamowski, B.M.; Chen, Y.; Malinowski, A. Efficient algorithm for training neural networks with one hidden layer. In Proceedings of the IJCNN’99. International Joint Conference on Neural Networks, Washington, DC, USA, 10–16 July 1999; Volume 3, pp. 1725–1728. [Google Scholar] [CrossRef]
- Garson, G.D. Interpreting Neural Network Connection Weights. AI Expert. 1991, 6, 47–51. [Google Scholar] [CrossRef]



| Parameter | Value | Unit |
|---|---|---|
| Density of porewater, ρw | 1000 | kg/m3 |
| Density of ice ρi | 917 | kg/m3 |
| Density of solid particle, ρs | 2600 | kg/m3 |
| Heat capacity of water at constant pressure, Cw | 4180 | J/kg/K |
| Heat capacity of ice at constant pressure, Ci | 2044 | J/kg/K |
| Heat capacity of solid particle at constant pressure, Cs | 831 | J/kg/K |
| Latent heat of fusion, L | 334.5 | kJ/kg |
| Thermal conductivity of water, λw | 0.56 | W/m/K |
| Thermal conductivity of ice, λi | 2.24 | W/m/K |
| Melting point, T0 | 0 | °C |
| Young’s modulus, Es | 1.2 | MPa |
| λs | k0 | ζ | ||
|---|---|---|---|---|
| λs | Correlation coefficient | 1 | 0.114 | −0.330 ** |
| p-value (two sided) | >0.1 | 0.000 | ||
| k0 | Correlation coefficient | 0.114 | 1 | 0.805 ** |
| p-value (two sided) | >0.1 | 0.000 | ||
| ζ | Correlation coefficient | −0.330 ** | 0.805 ** | 1 |
| p-value (two sided) | 0.000 | 0.000 |
| B | Standard Error | t | p-Value | VIF | |
|---|---|---|---|---|---|
| Constant | 6.958 | 0.104 | 66.655 | ||
| Hydraulic conductivity | 7.68 × 109 | 2.41 × 108 | 31.963 | <0.01 | 1.013 |
| Thermal conductivity | −0.372 | 0.023 | −16.011 | <0.01 | 1.013 |
| R2 | 0.829 | ||||
| adjR2 | 0.827 |
| First Layer | Second Layer | |||||
|---|---|---|---|---|---|---|
| Weight | −1.3290 | 1.1272 | −0.8410 | −0.9127 | 0.7730 | −0.5700 |
| 1.5107 | −0.2495 | −0.0200 | 0.6520 | 1.1022 | −1.1663 | |
| −0.4456 | ||||||
| 1.2482 | ||||||
| 0.5838 | ||||||
| Bias | −0.1840 | −0.4895 | ||||
| −1.8576 | ||||||
| −1.0096 | ||||||
| −0.5137 | ||||||
| −0.5254 |
| Input Layer Connections | |||||
|---|---|---|---|---|---|
| k0 (m/s) FROM: | −1.3290 | 1.1272 | −0.8410 | −0.9127 | 0.7730 |
| λs (W/m.K) FROM: | 1.5107 | −0.2495 | −0.0200 | 0.6520 | 1.1022 |
| Hidden layer connections | |||||
| Hidden node #1 | |||||
| BIAS: | −0.1840 | ||||
| TO: | −1.3290 | 1.5107 | |||
| FROM: | −0.5700 | ||||
| Hidden node #2 | |||||
| BIAS: | −1.8576 | ||||
| TO: | 1.1272 | −0.2495 | |||
| FROM: | −1.1663 | ||||
| Hidden node #3 | |||||
| BIAS: | −1.0096 | ||||
| TO: | −0.8410 | −0.0200 | |||
| FROM: | −0.4456 | ||||
| Hidden node #4 | |||||
| BIAS: | −0.5137 | ||||
| TO: | −0.9127 | 0.6520 | |||
| FROM: | 1.2482 | ||||
| Hidden node #5 | |||||
| BIAS: | −0.5254 | ||||
| TO: | 0.7730 | 1.1022 | |||
| FROM: | 0.5838 | ||||
| Output layer connections | |||||
| Heavy ratio ζ (%) | |||||
| BIAS: | −0.4895 | ||||
| TO: | −0.5700 | −1.1663 | −0.4456 | 1.2482 | 0.5838 |
| Hidden Node | ||||
|---|---|---|---|---|
| V1 | V2 | OUT | ||
| Connection weights (Input to hidden) | ||||
| 1 | −1.3290 | 1.5107 | −0.5700 | |
| 2 | 1.1272 | −0.2495 | −1.1663 | |
| 3 | −0.8410 | −0.0200 | −0.4456 | |
| 4 | −0.9127 | 0.6520 | 1.2482 | |
| 5 | 0.7730 | 1.1022 | 0.5838 | |
| Absolute connection weights (input to hidden) | ||||
| 1 | 1.3290 | 1.5107 | 0.5700 | |
| 2 | 1.1272 | 0.2495 | 1.1663 | |
| 3 | 0.8410 | 0.0200 | 0.4456 | |
| 4 | 0.9127 | 0.6520 | 1.2482 | |
| 5 | 0.7730 | 1.1022 | 0.5838 | |
| Connection shares * hidden node input | ||||
| 1 | 0.2668 | 0.3032 | ||
| 2 | 0.9549 | 0.2114 | ||
| 3 | 0.4352 | 0.0104 | ||
| 4 | 0.7281 | 0.5201 | ||
| 5 | 0.2407 | 0.3431 | ||
| Sum: | 2.6257 | 1.3882 | ||
| Input node share of output layer connections, excluding bias ones | ||||
| 65.41% | 34.59% | |||
| k0 (m/s) | λs (W/M·K) | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoon, S.; Le, D.-V.; Go, G.-H. Artificial Neural Network-Based Model for Prediction of Frost Heave Behavior of Silty Soil Specimen. Appl. Sci. 2021, 11, 10834. https://doi.org/10.3390/app112210834
Yoon S, Le D-V, Go G-H. Artificial Neural Network-Based Model for Prediction of Frost Heave Behavior of Silty Soil Specimen. Applied Sciences. 2021; 11(22):10834. https://doi.org/10.3390/app112210834
Chicago/Turabian StyleYoon, Seok, Dinh-Viet Le, and Gyu-Hyun Go. 2021. "Artificial Neural Network-Based Model for Prediction of Frost Heave Behavior of Silty Soil Specimen" Applied Sciences 11, no. 22: 10834. https://doi.org/10.3390/app112210834
APA StyleYoon, S., Le, D.-V., & Go, G.-H. (2021). Artificial Neural Network-Based Model for Prediction of Frost Heave Behavior of Silty Soil Specimen. Applied Sciences, 11(22), 10834. https://doi.org/10.3390/app112210834





