Iterative Methods for the Biomechanical Evaluation of Corneal Response. A Case Study in the Measurement Phase
Abstract
:1. Introduction
2. Materials and Methods
2.1. Material Definition
2.2. Finite Element Model Definition
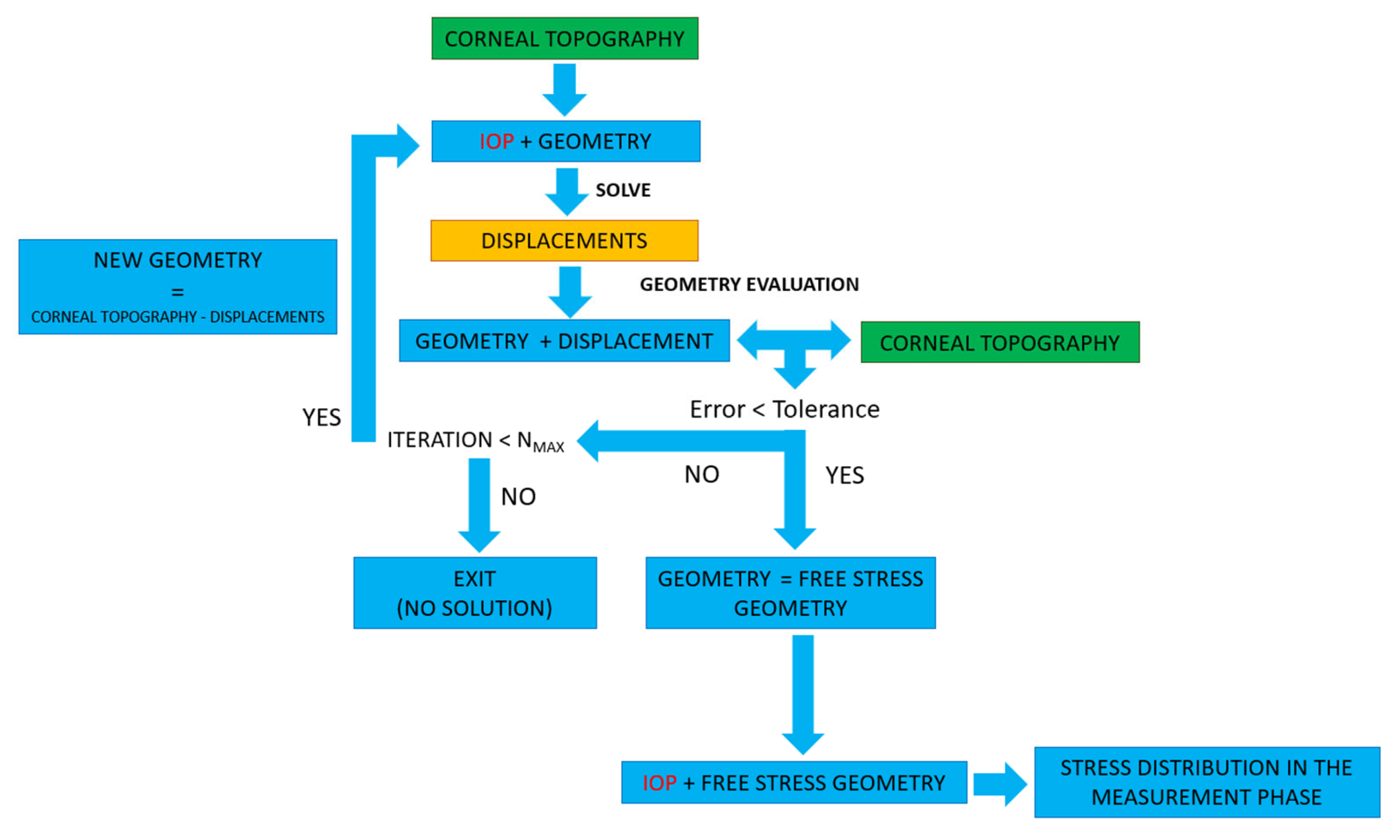
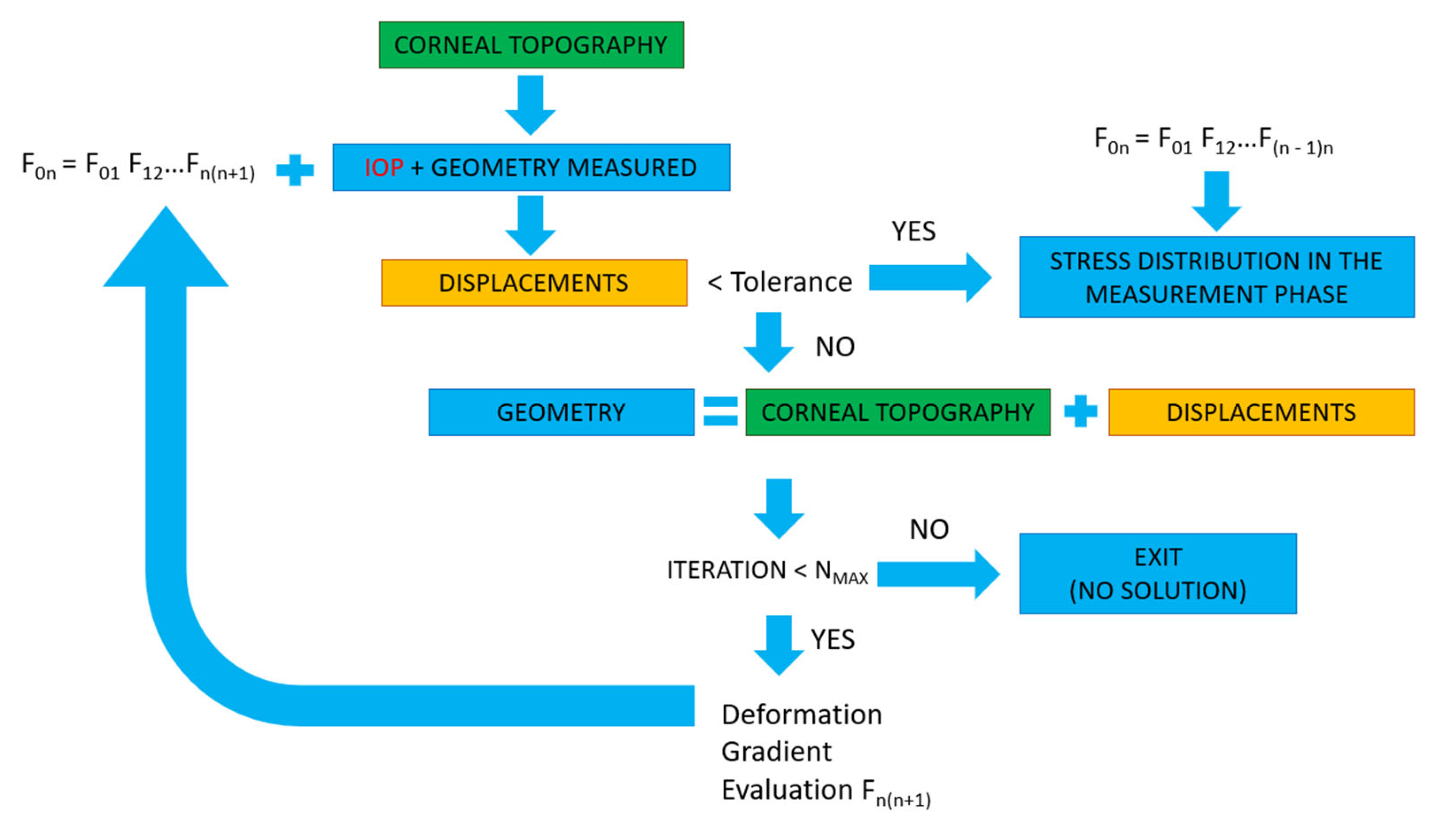
2.3. Calculation of the Stress Distribution in the Measurement Phase
2.3.1. Displacement Method
2.3.2. Prestress Method
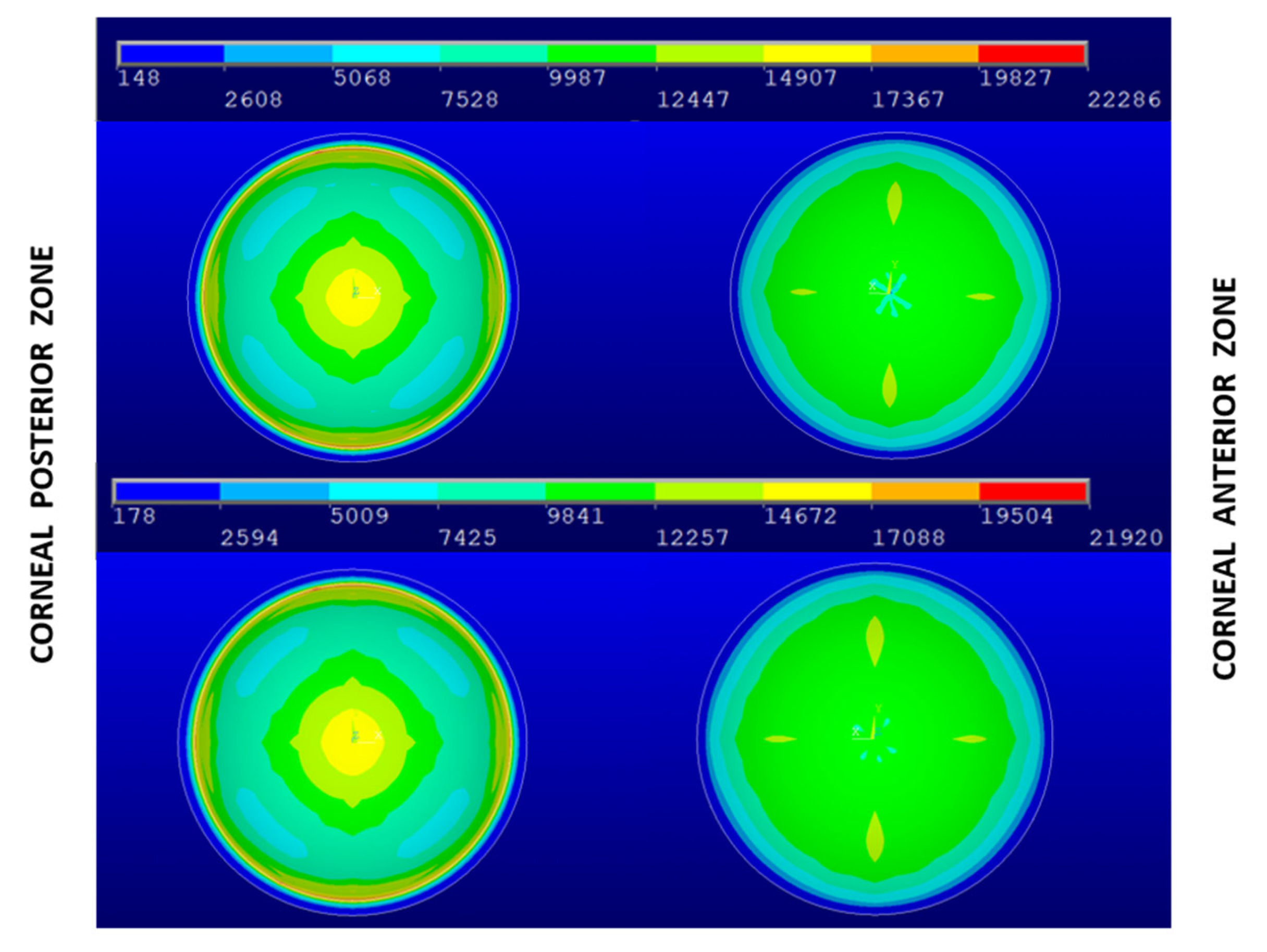
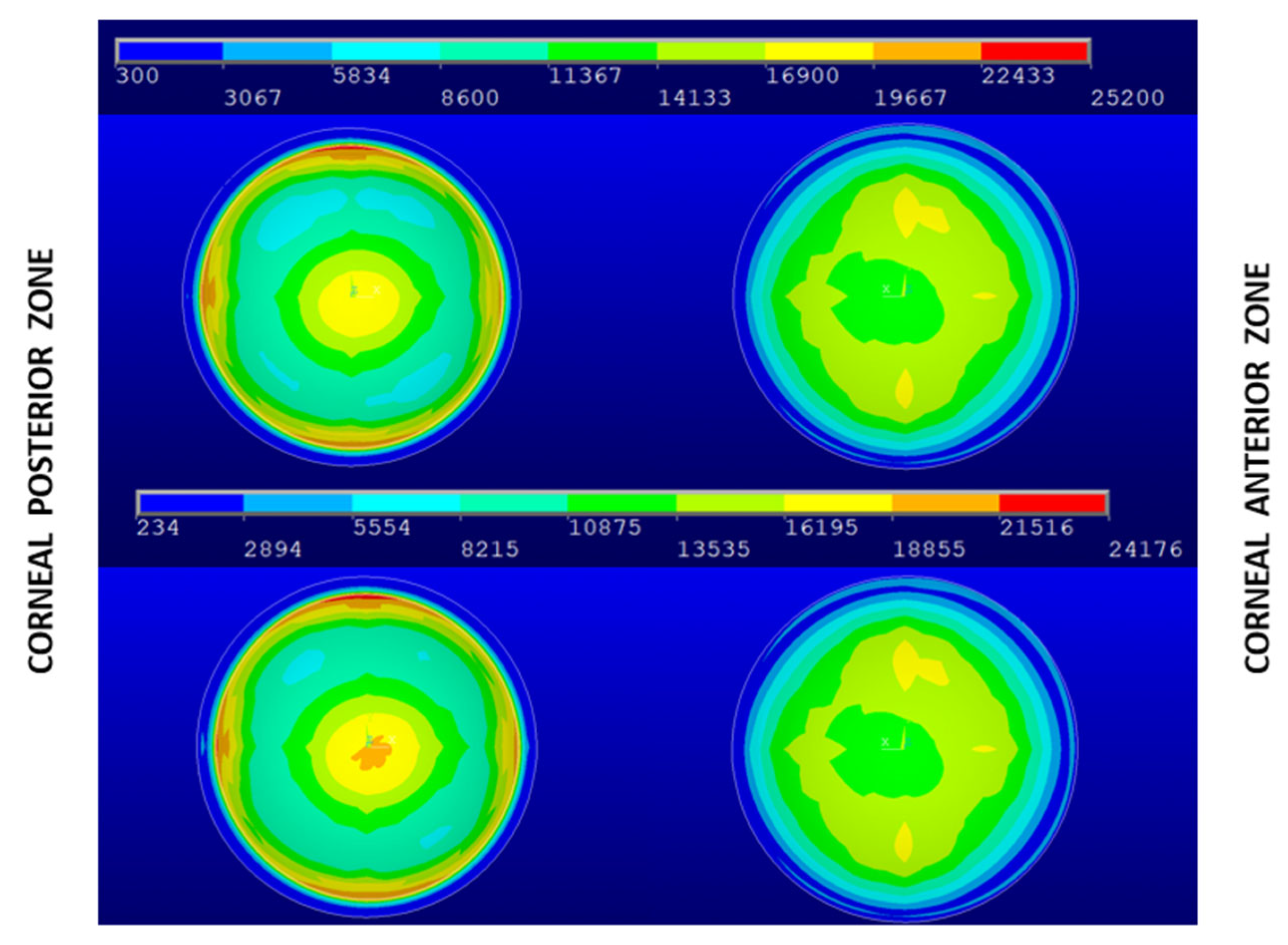
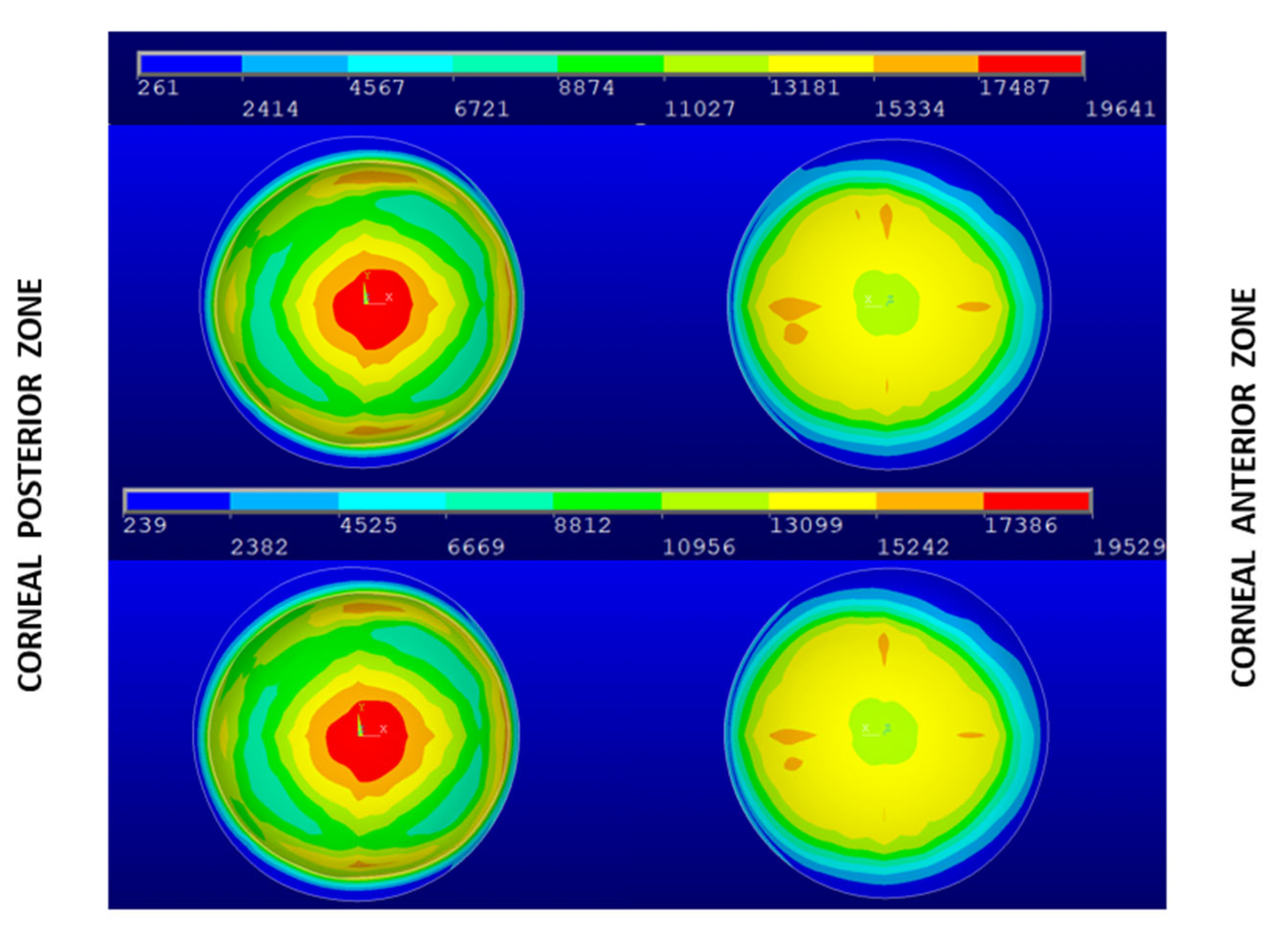
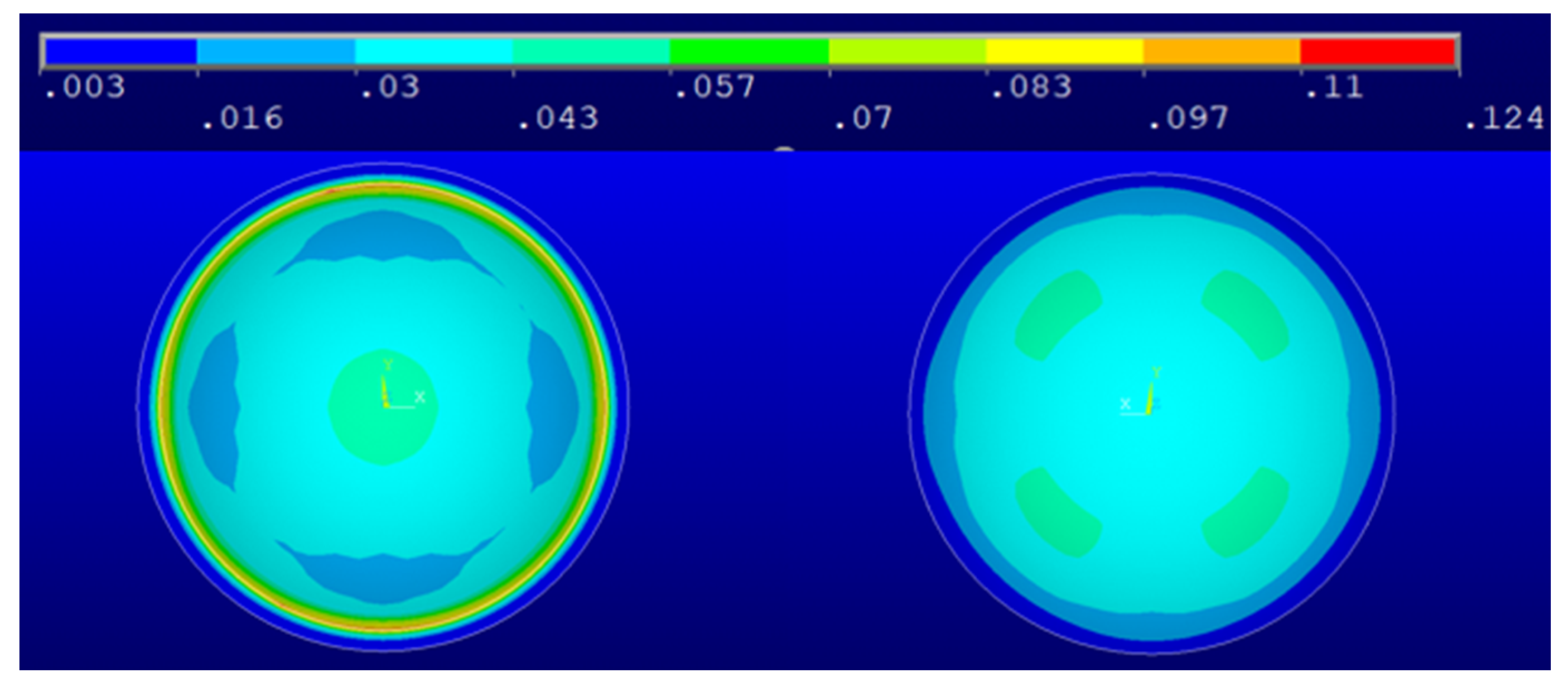
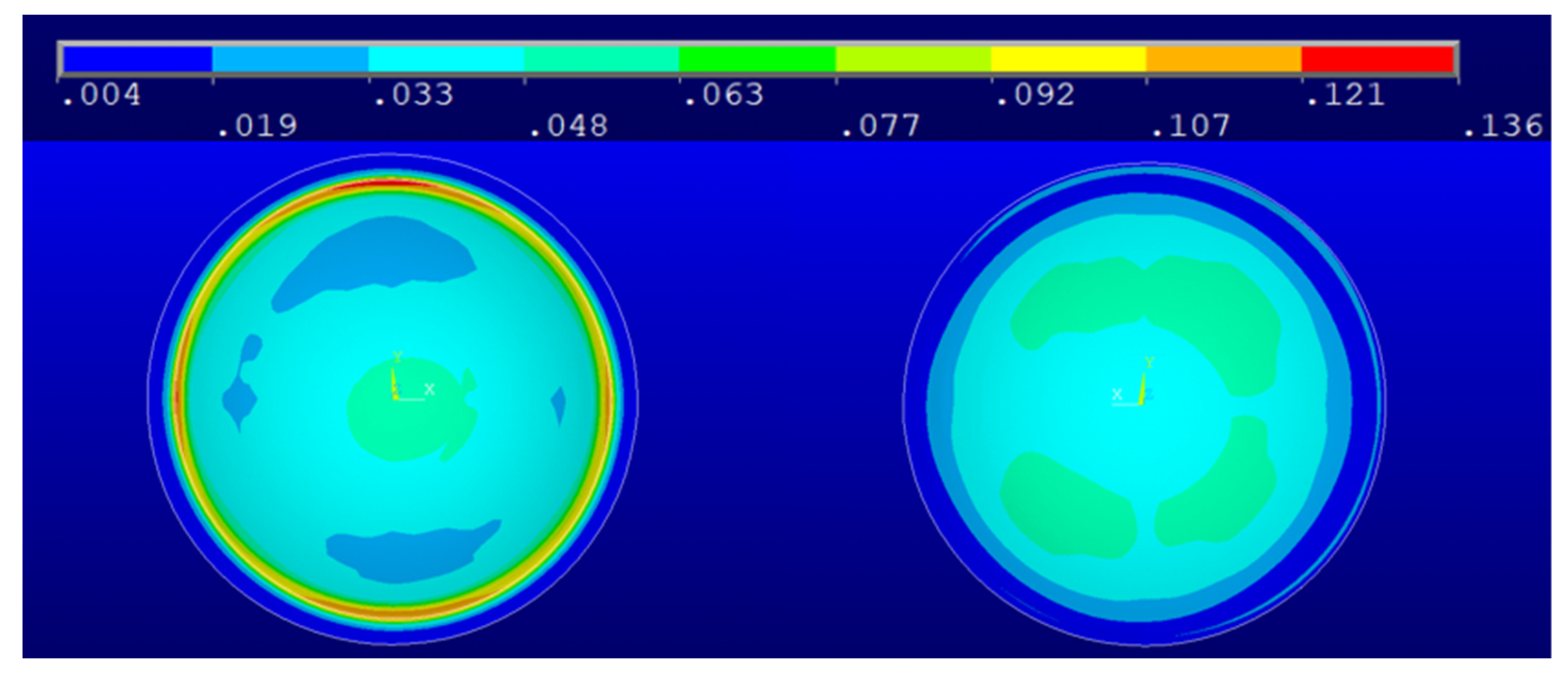
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Chagnon, G.; Rebouah, M.; Favier, D. Hyperelastic Energy Densities for Soft Biological Tissues: A Review. J. Elast. 2015, 120, 129–160. [Google Scholar] [CrossRef] [Green Version]
- Yousefi, A.A.K.; Nazari, M.A.; Perrier, P.; Panahi, M.S.; Payan, Y. A new model of passive muscle tissue integrating Collagen Fibers: Consequences for muscle behavior analysis. J. Mech. Behav. Biomed. Mater. 2018, 88, 29–40. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yousefi, A.A.K.; Nazari, M.A.; Perrier, P.; Panahi, M.S.; Payan, Y. A visco-hyperelastic constitutive model and its application in bovine tongue tissue. J. Biomech. 2018, 71, 190–198. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Martynenko, A.; Zozulya, V.V. Mathematical modeling of the cardiac tissue. Mech. Adv. Mater. Struct. 2021, 1–17. [Google Scholar] [CrossRef]
- Hurtado, D.E.; Zavala, P. Accelerating cardiac and vessel mechanics simulations: An energy-transform variational formulation for soft-tissue hyperelasticity. Comput. Methods Appl. Mech. Eng. 2021, 379, 113764. [Google Scholar] [CrossRef]
- Liber-Kneć, A.; Łagan, S. Experimental and Constitutive Approaches for a Study of Mechanical Properties of Animal Tendons. In Advances in Intelligent Systems and Computing; Springer: Cham, Switzerland, 2020; Volume 1033, pp. 288–297. [Google Scholar]
- Yousefsani, S.A.; Shamloo, A.; Farahmand, F. Micromechanics of brain white matter tissue: A fiber-reinforced hyperelastic model using embedded element technique. J. Mech. Behav. Biomed. Mater. 2018, 80, 194–202. [Google Scholar] [CrossRef]
- Feng, Y.; Okamoto, R.J.; Namani, R.; Genin, G.M.; Bayly, P.V. Measurements of mechanical anisotropy in brain tissue and implications for transversely isotropic material models of white matter. J. Mech. Behav. Biomed. Mater. 2013, 23, 117–132. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Benítez, J.M.; Montáns, F.J. The mechanical behavior of skin: Structures and models for the finite element analysis. Comput. Struct. 2017, 190, 75–107. [Google Scholar] [CrossRef]
- Karimi, A.; Faturechi, R.; Navidbakhsh, M.; Hashemi, S.A. A nonlinear hyperelastic behavior to identify the mechanical properties of rat skin under uniaxial loading. J. Mech. Med. Biol. 2014, 14, 1450075. [Google Scholar] [CrossRef]
- Hernández, Q.; Peña, E. Failure properties of vena cava tissue due to deep penetration during filter insertion. Biomech. Modeling Mechanobiol. 2016, 15, 845–856. [Google Scholar] [CrossRef] [PubMed]
- Veselý, J.; Horný, L.; Chlup, H.; Adámek, T.; Krajíček, M.; Žitný, R. Constitutive modeling of human saphenous veins at overloading pressures. J. Mech. Behav. Biomed. Mater. 2015, 45, 101–108. [Google Scholar] [CrossRef] [Green Version]
- Balzani, D.; Brinkhues, S.; Holzapfel, G.A. Constitutive framework for the modeling of damage in collagenous soft tissues with application to arterial walls. Comput. Methods Appl. Mech. Eng. 2012, 213, 139–151. [Google Scholar] [CrossRef]
- Kling, S.; Hafezi, F. Corneal biomechanics—A review. Ophthalmic Physiol. Opt. 2017, 37, 240–252. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nguyen, B.A.; Roberts, C.J.; Reilly, M.A. Biomechanical impact of the sclera on corneal deformation response to an air-puff: A finite-element study. Front. Bioeng. Biotechnol. 2019, 6, 210. [Google Scholar] [CrossRef]
- Jiang, Y.; Wang, Y.; Peng, X. A Visco-Hyperelastic Constitutive Model for Human Spine Ligaments. Cell Biochem. Biophys. 2015, 71, 1147–1156. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Liu, X.; Bao, F.; Lopes, B.T.; Wang, L.; Eliasy, A.; Abass, A.; Elsheikh, A. Review of ex-vivo characterisation of corneal biomechanics. Med. Nov. Technol. Devices 2021, 11, 100074. [Google Scholar] [CrossRef]
- Lopes, B.T.; Bao, F.; Wang, J.; Liu, X.; Wang, L.; Abass, A.; Eliasy, A.; Elsheikh, A. Review of in-vivo characterisation of corneal biomechanics. Med. Nov. Technol. Devices 2021, 11, 100073. [Google Scholar] [CrossRef]
- Navarro, R.; González, L.; Hernández, J.L. Optics of the average normal cornea from general and canonical representations of its surface topography. J. Opt. Soc. Am. A 2006, 23, 219–232. [Google Scholar] [CrossRef]
- Elsheikh, A.; Alhasso, D. Mechanical anisotropy of porcine cornea and correlation with stromal microstructure. Exp. Eye Res. 2009, 88, 1084–1091. [Google Scholar] [CrossRef]
- Pandolfi, A. Cornea modelling. Eye Vis. 2020, 7, 2. [Google Scholar] [CrossRef] [Green Version]
- Meek, K.M.; Boote, C. The use of X-ray scattering techniques to quantify the orientation and distribution of collagen in the corneal stroma. Prog. Retin. Eye Res. 2009, 28, 369–392. [Google Scholar] [CrossRef] [PubMed]
- Aghamohammadzadeh, H.; Newton, R.H.; Meek, K.M. X-Ray Scattering Used to Map the Preferred Collagen Orientation in the Human Cornea and Limbus. Structure 2004, 12, 249–256. [Google Scholar] [CrossRef] [PubMed]
- Daxer, A.; Fratzl, P. Collagen fibril orientation in the human corneal stroma and its implication in keratoconus. Investig. Ophthalmol. Vis. Sci. 1997, 38, 121–129. [Google Scholar]
- Wang, S.; Hatami-Marbini, H. Constitutive Modeling of Corneal Tissue: Influence of Three-Dimensional Collagen Fiber Microstructure. J. Biomech. Eng. 2021, 143, 031002. [Google Scholar] [CrossRef]
- Pandolfi, A.; Gizzi, A.; Vasta, M. A microstructural model of cross-link interaction between collagen fibrils in the human cornea. Philos. Trans. R. Soc. A 2019, 377, 20180079. [Google Scholar] [CrossRef] [Green Version]
- Kohlhaas, M. Iatrogenic Keratectasia: A Review. Klin. Mon. Fur Augenheilkd. 2015, 232, 765–772. [Google Scholar] [CrossRef]
- Ariza-Gracia, M.A.; Flecha-Lescún, J.; Rodríguez Matas, J.F.; Calzada, B.C. Personalized corneal biomechanics. In Advances in Biomechanics and Tissue Regeneration; Academic Press: London, UK, 2019; pp. 3–20. [Google Scholar] [CrossRef]
- Pandolfi, A.; Montanino, A. On the recovery of the stress-free configuration of the human cornea. Modeling Artif. Intell. Ophthalmol. 2020, 2, 11–33. [Google Scholar] [CrossRef]
- Toprak, I.; Cavas, F.; Velázquez, J.S.; Alio del Barrio, J.L.; Alio, J.L. Subclinical keratoconus detection with three-dimensional (3-D) morphogeometric and volumetric analysis. Acta Ophthalmol. 2020, 98, e933–e942. [Google Scholar] [CrossRef]
- Velázquez, J.S.; Cavas, F.; Piñero, D.P.; Cañavate, F.J.F.; Alio Del Barrio, J.; Alio, J.L. Morphogeometric analysis for characterization of keratoconus considering the spatial localization and projection of apex and minimum corneal thickness point. J. Adv. Res. 2020, 24, 261–271. [Google Scholar] [CrossRef]
- Cavas-Martínez, F.; Bataille, L.; Fernández-Pacheco, D.G.; Cañavate, F.J.F.; Alio, J.L. Keratoconus Detection Based on a New Corneal Volumetric Analysis. Sci. Rep. 2017, 7, 15837. [Google Scholar] [CrossRef] [Green Version]
- Alifa, R.; Piñero, D.; Velázquez, J.; Alió Del Barrio, J.L.; Cavas, F.; Alió, J.L. Changes in the 3D Corneal Structure and Morphogeometric Properties in Keratoconus after Corneal Collagen Crosslinking. Diagnostics 2020, 10, 397. [Google Scholar] [CrossRef] [PubMed]
- Lanchares, E.; Calvo, B.; Cristóbal, J.A.; Doblaré, M. Finite element simulation of arcuates for astigmatism correction. J. Biomech. 2008, 41, 797–805. [Google Scholar] [CrossRef] [PubMed]
- Pandolfi, A.; Holzapfel, G.A. Three-dimensional modeling and computational analysis of the human cornea considering distributed collagen fibril orientations. J. Biomech. Eng. 2008, 130, 061006. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pandolfi, A.; Manganiello, F. A model for the human cornea. Constitutive behavior and numerical analysis. Biomech. Modeling Mechanobiol. 2006, 5, 237–246. [Google Scholar] [CrossRef]
- Pitre, J.J.; Kirby, M.A.; Li, D.S.; Shen, T.T.; Wang, R.K.; O’Donnell, M.; Pelivanov, I. Nearly-incompressible transverse isotropy (NITI) of cornea elasticity: Model and experiments with acoustic micro-tapping OCE. Sci. Rep. 2020, 10, 12983. [Google Scholar] [CrossRef] [PubMed]
- Holzapfel, G.A.; Gasser, T.C.; Ogden, R.W. A new constitutive framework for arterial wall mechanics and a comparative study of material models. J. Elast. 2000, 61, 1–48. [Google Scholar] [CrossRef]
- Moore, J.; Shu, X.; Lopes, B.T.; Wu, R.; Abass, A. Limbus misrepresentation in parametric eye models. PLoS ONE 2020, 15, e0236096. [Google Scholar] [CrossRef]
- Ourselin, S.; Emberton, M.; Vercauteren, T. From computer-assisted intervention research to clinical impact: The need for a holistic approach. Med. Image Anal. 2016, 33, 72–78. [Google Scholar] [CrossRef]
- Zhang, J.; Zhong, Y.; Gu, C. Deformable Models for Surgical Simulation: A Survey. IEEE Rev. Biomed. Eng. 2018, 11, 143–164. [Google Scholar] [CrossRef] [Green Version]
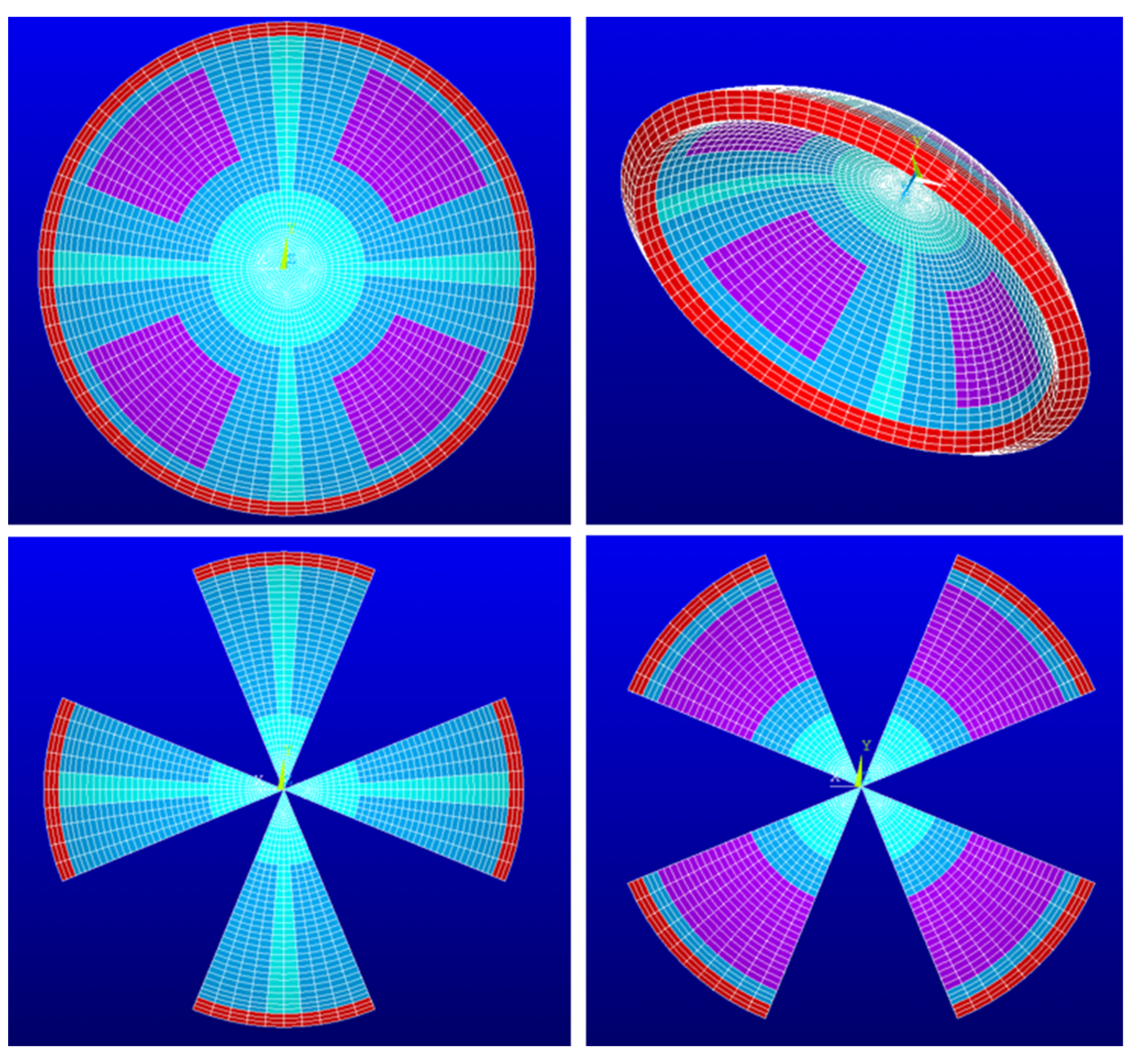

| Materials’ Constants | a1 (Pa) | a2 (Pa) | k1 (Pa) | k2 (-) |
|---|---|---|---|---|
| Central, N-T and S-I Zones | 40,000 | −10,000 | 50,000 | 200 |
| Transition Zones | 40,000 | −10,000 | 37,500 | 200 |
| Central Oblique Zones | 40,000 | −10,000 | 25,000 | 200 |
| Limbus | 40,000 | −10,000 | 50,000 | 200 |
| Geometry | Patient-Specific IOP (Pa) | Average Maximum von Mises Stress in the Central Zone (Pa) | IOP (Pa) | Average Maximum von Mises Stress in the Central Zone (Pa) |
|---|---|---|---|---|
| Navarro | 15 | 15,885 | 15 | 15,885 |
| G0 | 18 | 19,503 | 15 | 16,253 |
| G1 | 16 | 19,641 | 15 | 18,413 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gómez, C.; Piñero, D.P.; Paredes, M.; Alió, J.L.; Cavas, F. Iterative Methods for the Biomechanical Evaluation of Corneal Response. A Case Study in the Measurement Phase. Appl. Sci. 2021, 11, 10819. https://doi.org/10.3390/app112210819
Gómez C, Piñero DP, Paredes M, Alió JL, Cavas F. Iterative Methods for the Biomechanical Evaluation of Corneal Response. A Case Study in the Measurement Phase. Applied Sciences. 2021; 11(22):10819. https://doi.org/10.3390/app112210819
Chicago/Turabian StyleGómez, Carmelo, David P. Piñero, Manuel Paredes, Jorge L. Alió, and Francisco Cavas. 2021. "Iterative Methods for the Biomechanical Evaluation of Corneal Response. A Case Study in the Measurement Phase" Applied Sciences 11, no. 22: 10819. https://doi.org/10.3390/app112210819
APA StyleGómez, C., Piñero, D. P., Paredes, M., Alió, J. L., & Cavas, F. (2021). Iterative Methods for the Biomechanical Evaluation of Corneal Response. A Case Study in the Measurement Phase. Applied Sciences, 11(22), 10819. https://doi.org/10.3390/app112210819










