Abstract
Missing marker information is a common problem in Motion Capture (MoCap) systems. Commercial MoCap software provides several methods for reconstructing incomplete marker trajectories; however, these methods still rely on manual intervention. Current alternatives proposed in the literature still present drawbacks that prevent their widespread adoption. The lack of fully automated and universal solutions for gap filling is still a reality. We propose an automatic frame-wise gap filling routine that simultaneously explores restrictions between markers’ distance and markers’ dynamics in a least-squares minimization problem. This algorithm constitutes the main contribution of our work by simultaneously overcoming several limitations of previous methods that include not requiring manual intervention, prior training or training data; not requiring information about the skeleton or a dedicated calibration trial and by being able to reconstruct all gaps, even if these are located in the initial and final frames of a trajectory. We tested our approach in a set of artificially generated gaps, using the full body marker set, and compared the results with three methods available in commercial MoCap software: spline, pattern and rigid body fill. Our method achieved the best overall performance, presenting lower reconstruction errors in all tested conditions.
1. Introduction
Motion capture (MoCap) systems are used to digitally track and record human motion, with applications in clinical research, sports biomechanics, rehabilitation medicine, video game development, computer animation and others [1]. Optical MoCap systems use multiple cameras to estimate the three-dimensional (3D) position of a set of reflective markers that are strategically placed on the subject, allowing the quantitative analysis of human body kinematics [2,3] and the generation of realistic animations [4].
MoCap cameras and its proprietary software are used to calibrate 3D volume with relation to a fixed 3-axis referential. If a marker is inside the volume and can be captured by two or more cameras, its 3D coordinates will be continuously estimated at a fixed frame rate. Once an acquisition period is completed, these data can be exported to a single file that associates the coordinates of all markers available at a particular frame to that frame. However, if a marker is not detected by two or more cameras, the system will not estimate its coordinates. This phenomenon is quite frequent and translates into incomplete marker trajectories that can occur due to a marker falling off or due to temporary marker occlusion caused by other body segments, interaction with physical objects and overall non-optimal experimental setups. The resultant gaps impair data quality and compromise the accuracy of the analysis [5,6,7].
Several methods have been proposed to handle this problem. Some of them are available in commercial MoCap post-processing software such as those provided by leading MoCap companies, such as Qualysis (Qualysis AB, Gothernburg, Sweden) or Vicon (Oxford Metric, Limited, Oxford, England). Even though they provide satisfactory results in many situations, they still rely on manual intervention where the user needs to visually inspect each gap and decide how it should be filled [5]. This dependency on the user results in a time-consuming and cumbersome process.
Various techniques have been proposed to estimate trajectories of markers in frames where they are missing (i.e., missing markers). Basic methods, such as interpolation, are typically ineffective for long gaps [8], and more advanced methods have been proposed for this reason. Some of them require prior knowledge of skeleton constraints [9], while others rely on previously recorded data (training data) from which marker dynamics and inter-marker relationships can be learned [10,11]. Dynamic systems, e.g., Kalman filters [12,13], have also been proposed, but they are rejected by several authors on the grounds that they are extremely susceptible to unbounded errors and, therefore, are not suitable for longer gaps [9,14,15].
The literature suggests that each method has its own advantages, and in some specific situations unsatisfactory results may be obtained. Some methods, for instance, are not applicable when gaps occur at the beginning or end of the measurement [8,9]. Gap length, number of missing markers, motion speed and complexity and availability of training data and/or skeleton information are some of the factors that determine the choice of the method to use [7]. This means that a broader purpose solution for the problem of gap filling in MoCap sequences is still an open issue, as universal methods do not yet exist.
In this sense, we propose a fully automatic gap filling algorithm that does not require prior training or training data, information about the skeleton or a dedicated calibration trial. The method is framed as an optimization problem on which a set of empirical principles is considered and used to define a set of equations for frame-wise minimization. The method requires the correct labelling of all markers prior to the gap filling task.
We tested the algorithm in a set of artificially generated gaps featuring multiple activities captured using the full body marker set. We compared our approach with others available in commercial MoCap systems. We also demonstrate that the proposed method is able to correct the beginning and end of trajectories, which is currently a limitation of most approaches. The automation of this process avoids manual operation that is required in most commercial systems and does not need any user assistance to perform the task of gap filling. As such, by using this algorithm, the cost of post-processing of MoCap trajectories with respect to gap filling can be considered solely computational, which shall deeply decrease the number of man hours and overall cost of the post-processing task. This algorithm is, thus, the main contribution of this work.
Before introducing the automatic gap filling algorithm (Section 3), we present some related work (Section 2). Then, we detail the experiments performed under the scope of this work, including a description of the datasets used (Section 4). Finally, we present the results (Section 5), a critical discussion of the results (Section 6) and the conclusion of the work (Section 7).
2. Related Work
Recovering missing marker trajectories has been a recurring problem in the literature. Commercial software provides some solutions, yet in some cases they are insufficient. Gap filling methods found in literature can be broadly classified into (i) interpolation-based, (ii) skeleton-based, (iii) matrix-based, (iv) data-driven and (v) dynamical systems.
Interpolation methods are quite popular because they are fast and easy to implement. They predict missing trajectories using the information surrounding gap duration; the endpoints of the gap may be connected linearly or by using higher order polynomials, such as splines, to enhance curve fitting [8]. These methods assume the continuity of the trajectory without incorporating any information about skeleton or kinematic constraints. For this reason, they are ineffective for longer gaps (typically above 500 ms) [8]. Spline interpolation is available in Vicon Nexus, which is a data capture and processing software for clinical gait and biomechanics provided by Vicon [16].
Skeleton-based approaches, namely the pattern fill and the rigid body fill, are also available in Vicon Nexus [16]. These methods are grounded on the idea that some markers’ trajectories may be highly related due to bone length and motion range constraints. The pattern fill method uses a trajectory without gaps (the donor trajectory) to fill the selected gap, whereas the rigid body fill uses at least three donor trajectories that are assumed to be all part of the same rigid body [5,16]. A full description of these methods can be found in [5,17]. Skeleton-based methods require prior knowledge about skeleton constraints and are highly dependent on how accurately these constraints can be represented. As the human body presents some degree of flexibility, rigid body assumptions are not always true [9]. These methods may also fail when there is a large proportion of markers belonging to the same rigid body missing.
Several works approached this problem by incorporating information about movement dynamics. Using dynamical systems, e.g., Kalman filters, it is possible to estimate the next position of a marker based on its past positions and, simultaneously, preserve constraints imposed by neighbouring markers belonging to the same rigid body [12,13]. Kalman filters can be used in real-time, but they are vulnerable with respect to missing neighbours and longer gaps where the assumption of keeping the moving trend may not hold true [12,13,18]. These filters are also difficult to implement in practice: designing the filter to match data characteristics or correcting gaps that start from the beginning can be challenging tasks.
As an alternative, data may be modelled using data-driven approaches. Examples based on Principal Component Analysis (PCA) [10] or probabilistic model averaging [7] can be found in literature. More recently, methods based on deep neural networks and, more specifically, recurrent neural networks (e.g., [6,11,19]) have been proposed to model human motion sequences and recover missing markers’ trajectories. Although these methods achieve very good performance in general, they require training with a large and representative set of motions—using the same marker placement and similar movements—so that learned models can generalize well with respect to new data. However, obtaining clean and large datasets for training can be a challenge.
With matrix-based methods, models may be trained by using the motion sequence itself so that no additional data are required. These methods rely on the premise that human motion often exhibits low-dimensional local linearity; thus, they will represent the entire motion sequence as a matrix, they will learn linear relations between markers’ trajectories and they will use these relations to reconstruct gaps in the matrix. Matrix transformation techniques, such as PCA [14,20], singular value thresholding (SVT) [21] or non-negative matrix factorization (NMF) [22] have been employed. As shown in [21], skeleton constraints can also be incorporated. However, if the missing ratio is too high, unreasonable results may be obtained. According to [20], these algorithms may be less suitable for non-cyclic and less predictable movement patterns.
Existing methods cannot satisfy all requirements for a generic and universal gap filling approach. To overcome the need of manually selecting the most appropriate method, Camargo et al. [5] proposes an automatic pipeline, where spline interpolation, pattern fill and rigid body fill are iteratively selected. Despite replacing manual gap filling, the method may still fail when rigid body assumptions cannot be considered. The choice of the most appropriate method remains dependent on the characteristics of the data: length and number of missing trajectories, movement complexity, availability of training data and/or skeleton information are some of the dictating factors [7].
3. Proposed Method
This section introduces the automatic gap filling algorithm. The methods are framed in three subsections.
Section 3.1 (initialization) describes the structures that are defined a priori to enable the frame-wise gap filling routine. Unlike other approaches in the literature that rely on the definition of rigid-bodies, this step performs an automatic search of the set of markers with the potential to assist the reconstruction of the other markers, taking the entire set of markers in that trajectory as a possibility. This is a novel approach that addresses a major limitation of other skeleton-based methods that typically require prior knowledge about skeleton constraints.
The next subsection (Section 3.2) details the frame-wise gap filling routine. This is a two stage approach: first, we define the set of markers that will be used in a specific frame to reconstruct all markers that are missing in that frame; then, we estimate the coordinates of these markers by defining a set of equations that shall be simultaneously minimized using least squares minimization.
Finally, in Section 3.3, we introduce a mechanism of multiple initialization of the algorithm at different frames of a trajectory that is conceived to promote gains in both performance and efficiency.
The algorithm is designed to fill gaps in a fully labelled MoCap sequence; thus, correctly labeling the markers is a requirement of the algorithm.
3.1. Initialization
3.1.1. Auxiliary Markers
This initialization step intends to find a set of auxiliary markers () that posses semi-rigid behaviour with marker i, a property which the gap filling algorithm will later take advantage of. Markers placed on a rigid body (i.e., a body that will not deform or change shape) will ideally have their inter-marker distance unchanged during the course of the movement. In this paper, we refer to semi-rigid behaviour to define markers for which their inter-marker distance remains (roughly) constant, without requiring them to be placed on the same (previously defined) rigid body. The semi-rigid behaviour relaxes the assumption of markers being placed on the same rigid body but still presenting characteristics compatible with a rigid body movement assumption.
The auxiliary markers of a certain marker i will be defined by analysing how constant the distance between i and the other markers j are considering their trajectories over time. Every marker j for which the standard deviation of the distance between i and j over all frames is lower than cm will be considered as a potential auxiliary marker of i. Marker i can only have up to auxiliary markers. In the case where there are more potential auxiliary markers than , only the with lower standard deviation will be considered.
In order to find the auxiliary markers, the trajectories of the current sample (potentially with gaps) may be used. Alternatively, any other calibration trajectory (without gaps) that uses the same marker model may be used for initialization.
3.1.2. Unscented Kalman Filter
Every marker will be assigned an Unscented Kalman Filter (UKF) to keep track of its frame-by-frame movement state. We used the implementation of the FilterPy Python library (https://github.com/rlabbe/filterpy, accessed on 8 April 2021) which implements UKF as defined in [23] by using the formulation of [24]. The state vector (s) is defined by (1), where x, y and z correspond to the Cartesian coordinates of the marker’s position at a given frame; , and correspond to its instant velocity, and , and correspond to its acceleration in the motion capture system’s referential. Each marker’s filter is initialized with a state transition function (), a measurement function () and a measurement noise matrix (R) as depicted in (2)–(4), respectively:
where is the time between frames, is an error factor associated to the motion capture system and denotes the identity matrix. The error factor was defined with basis on the accuracy values commonly reported for MoCap systems under dynamic conditions [25].
Sigma points represent the state distribution and are required for the non-linear transformation in UKF [23,24]. In this work, sigma points were generated according to [26] by parameterizing alpha (), beta () and kappa (). According to [26], controls the spread of the sigma points and should be a small positive value between 0.01 and 1; is a secondary scaling parameter that can be set to 0.0; incorporates prior knowledge of the data distribution and, assuming a Gaussian distribution, the value of 2.0 should optimally define . In our experiments, we used , and .
At each new frame, each marker’s UKF is updated with a new position, velocity and acceleration measurement. This measurement can come straight from the marker’s coordinates provided by the motion capture system—if the marker is available—or from the coordinates estimated by the gap filling algorithm—if the marker is missing in the new frame.
3.2. Gap Filling Algorithm
3.2.1. Frame-Wise Selection of Markers for Reconstruction Assistance
In the previous subsection, we described the process of defining the set of auxiliary markers of each marker i. However, when a certain marker is missing at a given frame, it is possible that some of its auxiliary markers are also missing. As such, at each frame f and for each missing marker i, a selection of a subset of reconstruction-assistance markers will take place. If we consider that represents the set of auxiliary markers of marker i and that represents the set of markers that will be selected to reconstruct marker i at frame f, this means that .
Two conditions were defined in order to obtain and ascertain whether should include missing markers or not:
- If includes more than four non-missing markers in frame f, shall consist of the subset of non-missing markers of in f;
- Otherwise, , i.e., may include missing markers.
Table 1 illustrates this process in a hypothetical scenario where five markers—indexes 1, 2, 3, 4 and 5—are missing in a certain frame f and —the maximum number of auxiliary markers—is 6. The table shows the set of auxiliary markers identified during the initialization step, as well as the resulting reconstruction markers at frame f.

Table 1.
Markers selected to assist the reconstruction of missing markers in a certain frame (example scenario). Missing markers are presented in bold to facilitate the analysis.
Auxiliary sets , and fulfill condition one at frame f; therefore, the corresponding reconstruction sets , and do not include any missing marker—although missing markers were present in and at frame f. The auxiliary sets and fulfill condition two at frame f, as they solely contain three and four non-missing markers, respectively. For this reason, and include missing markers.
3.2.2. Least Squares Minimization of Systems of Equations
The optimal coordinates of each missing marker at a given frame will be estimated by translating a set of empirical principles into a nonlinear problem that is solved through least squares minimization. All empirical principles rely on the assumption that markers considered for the reconstruction of the other markers present a semi-rigid behaviour, i.e., their inter-markers’ distance and relative motion will remain (roughly) constant over the course of the trajectory.
In this problem, the independent variables consist of the the Cartesian coordinates of one or more missing markers, depending on whether the set of reconstruction markers of each of them may include (or not) other missing markers, i.e., whether they fulfilled condition two or one of Section 3.2.1. A marker that has fulfilled condition one is always considered alone: it will be reconstructed using a dedicated system of equations where the independent variable will solely consist of its coordinates. Taking marker one of Table 1 as an example, the independent variable (x) consists of an array that can be expressed as x , where , and represent the Cartesian coordinates of marker one. Markers that fulfill condition two are considered simultaneously if they can contribute towards each other’s reconstruction. Using the example of Table 1, this means that markers four and five will be considered in the same nonlinear problem, since they are included in each other’s set of reconstruction markers. Thus, in this case, the independent variable can be expressed as x .
Each nonlinear problem will aim to minimize a m-dimensional real function of the n-dimensional x with reference to the n variables. Let us consider, for each frame (where F corresponds to the total number of frames in the trajectory), the following representations:
- j: A reconstruction marker of marker i in frame f, where marker ;
- : Euclidean distance between markers i and j in frame f;
- : Average distance between markers i and j over the previous f-1 frames;
- : Standard deviation of the distance between markers i and j over the previous f-1 frames.
The first empirical principle assumes that the distance between markers i and j in f should follow a normal distribution with mean and standard deviation . This principle is inspired by the notion that there are markers that can maintain a (roughly) constant distance throughout the trajectory, as Figure 1 illustrates. Equation (5) translates this principle into a real function that shall be minimized, where is a function of the independent variable x. The concept behind this equation is also illustrated by Figure 2. We aim to find an optimal that minimizes the probability represented by the highlighted area, forcing a semi-rigid behaviour on the segment delimited by markers i and j, which favors the case where approximates .
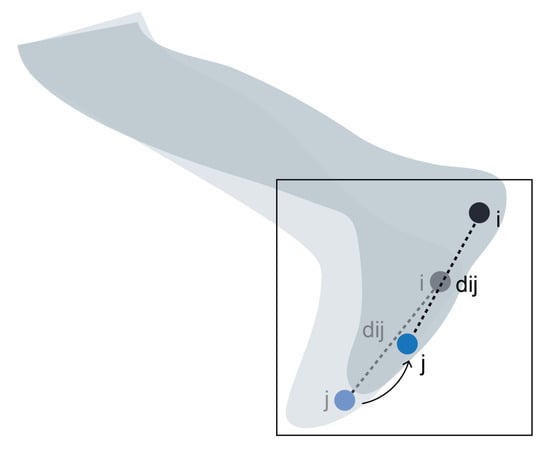
Figure 1.
Example of markers which maintain a (roughly) constant distance throughout a trajectory.
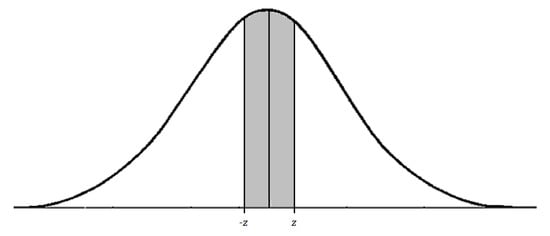
Figure 2.
Normal distribution curve. The probability to minimize using (5) is highlighted.
In order to explain the second empirical principle, let us also consider the following representations, where marker h is the marker in with the lowest :
- : coordinates of marker i in frame f;
- : instant velocity of marker i in f;
- : instant velocity of marker h in f;
- : average of the ratio between the instant velocity of markers i and h over the previous f-1 frames;
- : standard deviation of the ratio between the instant velocity of markers i and h over the previous f-1 frames.
The second empirical principle assumes that there are pairs of markers for which their relative movement is mostly constant over the course of the trajectory (Figure 3). This concept is depicted with the definition of marker h and the nature of its relationship with marker i. If the ratio between the velocity of markers i and h is mostly constant (i.e., is low), then can be obtained from (6); consequently, the direct application of the movement Equation (7) results in a possible position for a marker i in f, i.e., .
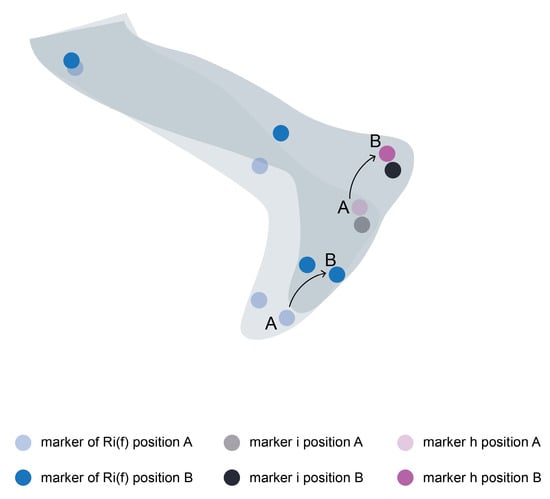
Figure 3.
Example of a pair of markers for which their relative movement is mostly constant over the course of the trajectory.
Then, we try to minimize the distance between and the coordinates of our missing marker i. Let us represent this distance by , which is a function of the independent variable x. We aim to find an optimal that minimizes the probability function represented by (8).
The last empirical principle consists of minimizing a new distance, , that is the distance between our missing marker i and its projection on the sphere centered in marker and with radius . This principle is illustrated by Figure 4, which shows how the optimal point should lay somewhere around these projections. We will represent the coordinates of each projection point as . This principle was implemented as described by (9) where both distances and are a function of the independent variable x. The normalization by the sphere’s radius confers less penalization of greater distances between and the missing marker i for larger spheres, since greater distances are likely associated with greater estimation errors.
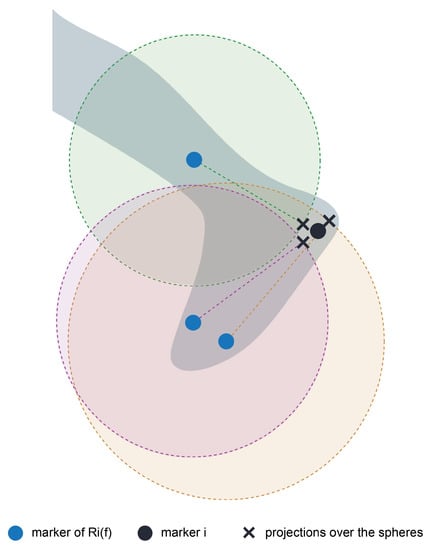
Figure 4.
Example of an optimal point in the surroundings of the projections over the spheres centered in marker and with radius .
These principles determine the number of functions to be simultaneously minimized by the least squares algorithm. As such, for each missing marker i from the first and third principles, (5) and (9), we will obtain one function per each marker j in ; from the second principle, in (8), only one function will be considered. The initial guess of the independent variable x will be provided by the UKF prediction of position for the missing marker(s) under consideration. Our implementation considered a smooth approximation relative to an absolute value as a loss function of the least squares minimization algorithm.
3.3. Multiple Initialization
Due to its sequential filling behaviour (i.e., the previous frame is used to estimate the next frame f), the algorithm shall be initialized in a fully filled frame, i.e., a frame where no markers are missing. It may be initialized at any frame of the trajectory, provided that at the selected frame all markers are present. This means that it can be initialized from different points of the trajectory and in any direction (i.e., forward or backwards), which can potentially increase performance both in terms of computational speed (e.g., split the full trajectory in chunks and fill them in parallel) and reconstruction error (e.g., fill the same gap in different directions and fuse the reconstructions to find a more robust solution).
By taking advantage of this feature, the algorithm is suitable for reconstructing even the first or last frames of the trajectory, overcoming a limitation of other approaches reported in the literature (e.g., in [5,8,9]).
4. Experiments
4.1. Datasets
We have selected four samples from two databases: the CMU Graphics Lab Motion Capture Database [27] and the Mocap Database HDM05 [28]. Each sample corresponds to a distinct activity, as shown in Table 2. In all sequences, the markers placement was defined based on the Full Body Model (http://mocap.cs.cmu.edu/markerPlacementGuide.pdf, accessed on 8 April 2021). All sequences were acquired at a sampling frequency of 120 Hz and had no gaps. Markers were fully labeled. Before processing the samples, we converted them from the C3D format to CSV using the data export functionality available in Vicon Nexus (Vicon Motion Systems Ltd., Oxford, UK, Version 2.10.1).

Table 2.
MoCap sequences used in the experiments.
4.2. Gap Generator
In order to test our gap filling approach, we needed to artificially generate gaps in the selected samples. To automatize this process, we created a script in Python. We have defined three parameters to influence the properties of the generated gaps: gap length, temporal location and number of missing markers. We have set the following possible values for each parameter:
- Gap length: varying from 0.5, 1 and 2 to 5 s, which corresponds to 60, 120, 240 and 600 frames;
- Temporal location: The temporal location of two non-overlapping gaps were randomly defined for each sample. These non-overlapping gaps could be located at any frame but they were explicitly not located on the initial and final frames of the samples to allow comparison with other methods that, by design, do not allow reconstructions on the initial and final frames of the sample (see Section 4.4). These generated samples are hereinafter referred to as samples with gaps in the middle. As an additional experiment, we also generated samples with gaps in the initial or in the final frames of the trajectories.
- Number of missing markers: The possible values of 1, 2, 4, 6, 8, 10, 12 and 14 missing markers were considered, where the markers that will be dropped were randomly selected. For each possible number of missing markers, we have randomly generated four combinations of markers to drop.
By combining all the possible values of each parameter, we generated 128 versions with gaps (4 gap lengths × 8 missing markers × 4 combinations), each including two non-overlapping gaps located in the middle of the sample. Additionally, we generated 128 samples with gaps in the initial or final frames of the trajectories. As such, a total of 1024 CSV files containing trajectories with gaps (4 MoCap sequences × 128 versions with gaps × 2 temporal locations) were used in the experiments.
4.3. Algorithm Initialization
The algorithm was initialized (to obtain the set of auxiliary markers required to assist the reconstruction of the gaps) by using samples with artificially generated gaps as calibration trajectories. We have also considered the original MoCap sequences (fully labeled and without gaps) as calibration trajectories in order to evaluate the influence of gaps on the estimation of auxiliary markers.
All subsequent experiments were reported using the original MoCap sequences as calibration trajectories to guarantee that the auxiliary markers’ sets were constant throughout the experiments using that sequence, despite the generated gaps. In this manner, we could guarantee that the selection of the markers to reconstruct a missing one was only dependent on conditions one and two presented in Section 3.2.1. Thus, the analysis of the performance of the algorithm in our experiments only depends of the variables that we aim to analyse, i.e., influence of the length of the gaps and number of missing markers.
In the experiments involving the reconstruction of files with gaps located in the middle of the sample, we considered two simultaneous initializations of the algorithm: (i) in the first frame of the trajectories, with forward filling direction; (ii) in the last frame of the trajectories, with backwards filling direction. The final reconstruction of each gap consisted of a fusion of the reconstructions in both directions by applying a sigmoid weighted average. This strategy ensured that more weight was provided for the reconstructions with the highest confidence, i.e., located in the first frames of the gap in forward filling direction and in the last frames of the gap in the backward filling direction.
In the experiments involving the analysis of samples with gaps located in the initial or final frames, we initialized the algorithm at the midpoint of the sample and filled gaps using the forward filling direction—in case the gap was located in the final frames of the sample—or the backward filling direction—in case the gap was located in the initial frames of the sample.
All experiments used cm and . These values were empirically chosen by using as a basis some exemplary samples from the dataset.
4.4. Trajectories Reconstruction
The trajectories of the 1024 files were reconstructed using our gap filling approach. For comparison, the samples with gaps in the middle—521 files—were also reconstructed using three methods available in Vicon Nexus: spline interpolation, rigid body fill and pattern fill (as described in [5,17]). To reconstruct the trajectories using these three methods, we built a Python script for Vicon Nexus that would recursively (i) load the file with the trajectories to reconstruct; (ii) select and run a pipeline with a gap filling method; and (iii) export the reconstructed trajectories to CSV.
4.5. Evaluation
We compared the original MoCap sequences (ground truth) with the reconstructions performed by each of the four methods employed. We calculated the Root Mean Squared Error (RMSE) for each frame’s pose, i.e., the sum of the squared error across the three axes of all missing markers in a MoCap sequence by considering only the frames with missing markers, following the same approach as described by [21].
The pattern fill method could not reconstruct some of the gaps; therefore, we decided to employ a data imputation method that would penalize those samples. For each file of the database, we calculated the maximum value for the squared error for each of the three axes, across all markers. Then, for the frames that were not filled with the pattern fill method, we have replaced the squared error with the maximum value of each axis. This approach allowed penalizing the frames that were not filled due to the limitations of the method.
5. Results
The comparison of the initialization strategies—i.e., using the sequences with artificially generated gaps and the original sequences without gaps—is shown in Table 3, where reconstruction performance results are presented per activity (i.e., boxing, reaching, walking and dancing). The performance obtained with both initialization strategies is very similar for all activities considered.

Table 3.
Summary of the performance of our method per activity using the sequences with gaps and the original sequences (without gaps) as calibration trajectories during initialization. Mean (standard deviation) of RMSE are presented in centimeters.
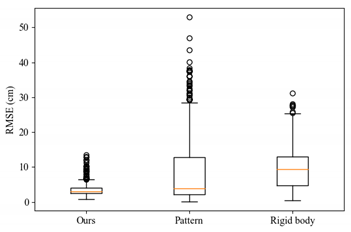
The summary statistics of the performance of the four gap filling methods—i.e., ours, pattern fill, rigid body fill and spline fill achieved in samples with gaps in the middle—is shown in Table 4, along with a boxplot representation that omitted spline fill results since its error can be up to three orders of magnitude superior to that of the remaining approaches. Our method achieved the lowest mean RMSE and the lowest dispersion of the errors, as evidenced by standard deviation (SD) and interquartile range (IQR) values. The minimum error was obtained with the pattern fill method, whereas the maximum error was obtained with spline.

Table 4.
Summary of the performance per method (RMSE values in cm).
The summary of the performance per activity (i.e., boxing, reaching, walking and dancing) is shown in Table 5, again, considering only the samples with gaps in the middle. The results show that our method is associated with lower errors than the remaining approaches for all activities under analysis. One can also observe more consistency of overall error across all activities for our method by verifying that the differences between average errors of each activity were no greater than 1.6 cm and that it systematically achieved the lowest standard deviation per activity when compared to the remaining methods.

Table 5.
Summary of the performance per activity. Mean (standard deviation) of RMSE are presented, in cm.
Table 6 shows the detailed performance of the four gap filling methods applied to the samples with gaps in the middle, where results are presented for each condition tested under the scope of this work—i.e., the four gap lengths and the eight numbers of missing markers. In this table, we can observe that our algorithm presents the most consistent performance (with regards to gap length and number of missing markers), with differences in errors no higher than 3 cm. In contrast, spline fill presents consistent results with regards to the number of missing markers, but errors tend to increase with the length of the gap, with errors approaching values in the order of meters for larger gaps. For this reason, spline fill was omitted from Figure 5, which shows a summary of the results achieved with each method in terms of gap length and number of missing markers, respectively.

Table 6.
Performance of the four gap filling methods (ours, pattern fill, rigid body fill and spline fill) in each tested condition. Mean (standard deviation) of RMSE is presented in cm.
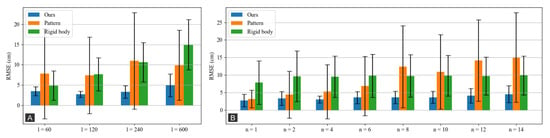
Figure 5.
Comparison of gap filling methods performance for each (A) gap length (l) and (B) number of missing markers (n). Vertical error bars represent standard deviation.
Figure 5A evidences an increase in error with the size of the gap on the rigid body fill method, but the same steady increase cannot be observed on the other methods (ours and pattern fill). In terms of number of missing markers (Figure 5B), we can observe that the increase in the number of missing markers affects mostly the pattern fill method, with errors increasing as the number of missing markers increase. Although our method and the rigid body fill present slightly higher errors when a higher number of markers is missing, the errors are much more consistent throughout the tested conditions.
Table 7 shows the detailed performance of our algorithm when applied to the reconstruction of the 512 samples with gaps located in the initial or final frames of the trajectories. In these experiments, only the performance of our algorithm could be reported, as the three methods used for the comparison—spline interpolation, rigid body fill and pattern fill—cannot fill gaps occurring at these positions [5,17]. The average error obtained in these samples is slightly above the error reported for our algorithm when reconstructing gaps in the middle, but it is considerably below the errors reported for Vicon Nexus’ methods (for gaps in the middle). The errors (average values) increase both with the number of missing markers and the length of the generated gaps. The dispersion of the errors (standard deviation) remains consistent throughout all tested conditions.

Table 7.
Performance of our algorithm when reconstructing samples with gaps located in the initial or final frames of the trajectories. Means (standard deviation) of RMSE are presented, in cm, per tested condition.
6. Discussion
In this work we proposed a fully automatic approach to the gap filling problem. We tested our approach in a set of artificially generated gaps and compared the results with three other methods available in Vicon Nexus software: spline interpolation, rigid body fill and pattern fill. For the comparison with these methods, only the samples with gaps in the middle were considered, as the methods in Vicon Nexus cannot reconstruct gaps in the initial and final frames [5,17]. We also generated samples with gaps in the initial or final frames and used our method to reconstruct them.
6.1. Comparison with Vicon Nexus’ Methods
In the experiments involving the reconstruction of gaps in the middle and in comparison with Vicon Nexus’ methods, our method achieved better and more consistent performance (Table 4), presenting lower reconstruction errors in all tested conditions, i.e., activity types (Table 5), gap lengths (Figure 5A) and number of missing markers (Figure 5B). Our method presented the lowest dispersion values, maintaining its consistency (in terms of central tendency and dispersion) irrespective of the size of the gaps (Figure 5A), activity type (Table 5) and number of missing markers (Figure 5B).
As expected, the spline fill method reveals acceptable performance for shorter gaps, but errors increase to the order of the meters as the size of the gap increases (Table 6). The errors on spline are theoretically independent of the number of missing markers, because it reconstructs the missing parts using only the trajectory of the missing marker. This observation can be confirmed by analysing Table 6. In Table 5, a notable difference between the reconstruction performance in boxing and reaching activities compared to walking and dancing can be observed. These results highlight another important characteristic of the spline fill method: When activities involve larger displacements in space (as is the case of walking and dancing), the reconstructions can approximate the larger displacements, ignoring the more granular movements occurring in between; when activities require less displacement in space (as is the case of boxing and reaching activities), interpolation will have more difficulties in reconstructing the performed trajectories, as most likely the information surrounding the gaps—used for the reconstruction—contain no valuable information concerning the behaviour of the markers in between. For this reason, the type of movement should also be considered a criteria in the selection of the method to use.
Contrarily to the spline fill method, the errors obtained with the pattern fill method increase as the number of missing markers increases (Figure 5B). The pattern fill method requires another marker that serves as a template (the donor trajectory) to fill in the missing data. In our experiments, the pattern fill method was not always able to reconstruct the missing trajectories, possibly due to the fact that the best template included invalid frames within the gap region [17], which happened more frequently when the number of missing markers was higher. When this happened, we chose to penalize the method by considering a maximum error value, which may justify the results.
The rigid body fill method resulted in errors that increased mostly with gap length (Figure 5A), but remained more or less constant with the increase in the number of missing markers (Figure 5B). The rigid body fill was able to reconstruct all missing parts; however, considering that the error increased with the length of the gaps, we can assume that it was not always able to use the best combination of donor trajectories—sometimes missing—with a higher impact on longer gaps. Contrary to the pattern fill method, the impact of using non-optimal donor trajectories in the rigid body fill method is attenuated by the fact that more than one donor trajectory is considered for the reconstruction. For this reason, the number of missing markers seems to have less impact on the rigid body fill reconstruction errors.
Although we present the results individually for each method available in Vicon Nexus, we know from the literature that iteratively selecting one method or another—always considering the method that would provide the best results at a given movement—would optimize the results [5]. However, to perform this process within Nexus, manual gap filling would be required.
By automatically selecting the best contributing markers at any moment, our algorithm can be considered more robust relative to increasingly challenging conditions: either relative to the length of the gaps (Figure 5A) or relative to the number of missing markers (Figure 5B). Even if the chosen contributing markers do not belong to the same rigid body (as required in rigid body and pattern fill methods in Vicon Nexus), they may still be considered good contributing markers depending on the movement being executed. Moreover, as it is based on an optimization process (that simultaneously explores the restrictions between markers’ distance and their movement dynamics), it always tries to find the best solution for the information available at each instant—without the need of manual intervention.
6.2. Filling Gaps in the Initial and Final Frames
Our method was able to fill all gaps generated in the initial and final frames of the samples, achieving an overall performance slightly worse than the one reported for our algorithm when reconstructing gaps in the middle. Although the results cannot be fairly compared (because gaps occur in different positions, possibly with different markers), the fact that the algorithm could not be initialized in two directions (as in the case of the samples with gaps in the middle) may have negatively affected the results. The bidirectional approach may bring some additional gains in performance (more stability and smoothness, particularly on the limits of the gap) due to the combination of the reconstructions in both directions, which is not possible when gaps occur in the initial and final frames of the samples. However, the results achieved in these cases are better than the results achieved for Vicon Nexus’ methods when filling gaps occurring in the middle of the sample.
The fact that the bidirectional approach could not be applied for reconstructing gaps in the initial and final frames may also justify the steady increase in the error with both the number of missing markers and the length of the gap, which is not observed when the bidirectional approach is applied. The bidirectional approach should be used whenever possible to ensure a better and more stable reconstruction of the missing markers.
6.3. Framing within State-of-the-Art
Compared to other approaches in literature, our algorithm presents some advantages. Unlike the approaches presented by [11], [7] or [6], our algorithm does not require any training with additional data prior to filling the gaps. As such, it is readily available to be employed for any trajectory without the need to collect prior data. Moreover, it does not require any manual input such as defining skeleton constraints or rigid bodies: Our approach will discover the best auxiliary and reconstructing markers automatically, based on the available data. Unlike the other approaches tested in this paper, our algorithm is able to fill gaps occurring in any part of the sample, including the beginning and end of the signal, although in these cases the method can only be initialized to run in one single direction. Contrary to the pattern fill method, our algorithm was able to reconstruct all generated gaps.
While rigid body, pattern fill and spline methods reconstruct a single missing marker at a time, our algorithm reconstructs missing markers simultaneously if they can contribute to each other’s reconstruction. The fact that missing markers are jointly optimized constitutes an advantage of our approach, as more information is available at the time of the reconstruction. In this reconstruction, multiple empirical principles are considered, which optimizes the results.
In this study, we reported the performance of our algorithm considering two simultaneous initializations, i.e., a forward and a backward filling direction, applied to the samples with gaps in the middle. The final reconstruction considered the fusion of the reconstructions performed in both directions, which should optimize the results. By using this approach, we required that the full sequence was available at the time of the gap filling, which is frequently the case for the purpose of motion analysis in health and sports. For filling gaps in the initial and final frames of the trajectory, only one filling direction should be considered. By using the forward gap filling direction, our method is theoretically compatible with the reconstruction of gaps in nearly real-time. In this scenario, the initialization of the algorithm could be performed with a calibration trajectory. Although theoretically feasible, the real-time reconstruction scenario was out of the scope of this work.
Similar to the rigid body and pattern fill methods, our method depends on a suitable set of auxiliary markers that will support the reconstructions. In rigid body and pattern fill methods, the definition of these markers—i.e., the donor trajectories—depends on the rigid bodies definition; in our algorithm, the definition of the auxiliary markers is more relaxed. In our experiments, the auxiliary markers were obtained from calibration trajectories (fully labelled and with no gaps) in order to ensure the reproducibility of our results. Alternatively, as supported by the results shown in Table 3, the samples with artificially generated gaps can be used to obtain auxiliary markers as the average and standard deviation of inter-markers distance should not differ when gaps are present. Unless the gap ratio is very high, the average and standard deviation of inter-markers distance should be maintained when gaps are present. Although it never occurred in our experiments, it may be possible that no suitable set of auxiliary markers is found in some situations. Considering that MoCap best practices require the inclusion of some redundant markers, if all guidelines are followed, it is very unlikely that auxiliary markers cannot be found. In case it happens, the algorithm can still rely on the predictions of the Kalman filter to reconstruct markers’ trajectories, considering only markers’ dynamics.
6.4. Limitations
In order to present the results, we have artificially generated gaps from fully available and fully labelled, trajectories. Gaps were randomly generated without controlling whether the missing markers would belong to the same rigid body or not or if they would occur in a more challenging part of the movement. This lack of control may justify the different results achieved in each activity type (Table 5)—except for the spline fill method that, as explained above, does not depend on the other markers. Nevertheless, the conditions were the same for all algorithms, enabling their comparison.
Another limitation of this study is that the generated gaps may hardly mimic what happens in reality when performing MoCap: Gaps may overlap and start asynchronously, and the number of missing markers may differ from frame to frame. Gaps may also occur due to imperfect system calibration conditions, which may result in markers’ positions being poorly estimated by the MoCap system. In these cases, the typical accuracy values reported for MoCap systems may not hold, creating additional challenges for the gap filling method. We account for non-ideal conditions by formulating the problem as an optimization problem, where the variance of inter-markers distance is considered as an input. In these situations, the errors obtained during system calibration could be taken into account to better adjust hyperparameters, e.g., the error factor in (4). Our experiments enable a comparison of the methods in a more controlled fashion, considering samples acquired in ideal conditions. However, the generalization of the performance to real scenarios must be performed with caution. The same is also true considering the performance achieved in different activities. In our study, only four different activities were considered and, as such, the impact of the different movement types on reconstructions’ performance could not be extensively studied.
The impact of using different marker sets could not be assessed, as only the full body marker set was considered in the experiments. For instance, the hyperparameters (thresholds and ) used to detect the auxiliary markers performed well in our experiments, but they were not recursively optimized considering their impact on the overall performance of the algorithm. The need for fine tuning the hyperparameters of the algorithm was dimmed due to the fact that only the full body marker set was used in this study. Further experiments with models with shorter distances between markers (e.g., the hand or the facial marker set) would be required to validate the method—and the thresholds—used to obtain auxiliary markers, as the standard deviations of the distances between markers are expected to be much smaller. Further experiments would need to be performed with different marker sets to ensure the generalization of the method regardless the scale of the marker sets used.
In this section, we also discuss some of the limitations of our method. We notice that our implementation is still very computationally expensive and should be optimized and tested for resource-consumption and execution time. Some solutions to decrease overall expensiveness should be proposed both at the algorithmic and implementation level. However, these experiments were not systematically performed yet and are out of the scope of this work. Moreover, we should assess the main reconstruction difficulties and try to notice patterns so that the reconstruction can be further improved (e.g., if movement speed affects reconstruction error, if markers placed in joints are more or less prone to error than the markers placed in rigid body segments, etc.). The conducted experiments do not allow us to draw conclusions about this later question, so there may still be unknown limitations of the method itself that should be further explored.
7. Conclusions
In this work, we proposed a fully automatic approach to the gap filling problem. The method was framed as an optimization problem that has simultaneously explored the restrictions between markers’ distance and their movement dynamics in a set of empirical principles and equations. We tested our approach in a set of artificially generated gaps using the full body marker set and compared the results with three other methods available in commercial software, achieving better performance in all tested conditions. The optimization approach ensured that the best solution could be found using the information available at each instant—without any restriction concerning length and number of missing markers or movement complexity. The method was designed to fully automate the task of the gap filling by assuming the prior labelling of the markers as part of the post-processing of MoCap sequences in motion analysis. The method finds applications in health or sports-related areas, requiring no pre-recorded data, no prior knowledge about skeleton constraints and rigid bodies and no manual intervention. The automation of this process avoids manual operation required in most commercial systems to perform the task of gap filling, reducing the number of man hours and the overall costs of the task.
In the future, we should test our algorithm in different marker sets and different movements, providing a more general understanding of its performance in different conditions. Hyperparameters defined empirically in this study—e.g., the thresholds used to identify auxiliary markers—should be further investigated and fine tuned considering their impact on the overall performance of the method when applied to the different conditions. Moreover, we should aim to test our approach in real scenarios, i.e., gaps occurring naturally when a MoCap sequence is collected. Since our approach requires no manual intervention, the time required to reconstruct trajectories is only computational—for gains in efficiency, the multiple initialization feature can be employed. Processing time should be thoroughly investigated and possibly improved in a future study. Real-time capabilities and performance under real-time requirements should also be investigated in order to support applications in computer animation-related areas.
Author Contributions
Conceptualization, D.G., V.G. and J.S.; methodology, D.G., V.G. and J.S.; software, D.G.; validation, D.G., V.G. and J.S.; formal analysis, V.G. and J.S.; investigation, D.G., V.G. and J.S.; resources, D.G.; writing—original draft preparation, D.G., V.G. and J.S.; writing—review and editing, D.G., V.G. and J.S.; visualization, D.G. and V.G.; project administration, V.G. and J.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was performed in the context of the project VITAAL (AAL-2017-066), funded under the AAL JP and co-funded by the European Commission and the National Funding Authorities of Portugal, Belgium and Switzerland, and in the context of the project IANVS (AAL-2018-5-116), funded under the AAL JP and co-funded by the European Commission and the National Funding Authorities of Portugal, Belgium and Switzerland.
Institutional Review Board Statement
Ethical review and approval were waived for this study since all data used in the experiments corresponded to publicly available datasets that were not collected by the authors.
Informed Consent Statement
Not applicable since all data used in the experiments corresponded to publicly available datasets that were not collected by the authors.
Data Availability Statement
Data used in this project were obtained from CMU’s motion capture database (mocap.cs.cmu.edu), which was created with funding from NSF EIA-0196217. Data were also obtained from the motion capture database HDM05.
Acknowledgments
The authors would like to acknowledge all authors of the public datasets used to conduct the experiments. The authors would also like to thank Elsa Oliveira for the design of the three principles’ images that illustrate the proposed method. We also thank Luís Francisco for his valuable experience with MoCap systems, which was crucial for identifying the current challenges of gap filling in MoCap software.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Menolotto, M.; Komaris, D.S.; Tedesco, S.; O’Flynn, B.; Walsh, M. Motion Capture Technology in Industrial Applications: A Systematic Review. Sensors 2020, 20, 5687. [Google Scholar] [CrossRef] [PubMed]
- Van der Kruk, E.; Reijne, M.M. Accuracy of human motion capture systems for sport applications; state-of-the-art review. Eur. J. Sport Sci. 2018, 18, 806–819. [Google Scholar] [CrossRef] [PubMed]
- Valevicius, A.M.; Jun, P.Y.; Hebert, J.S.; Vette, A.H. Use of optical motion capture for the analysis of normative upper body kinematics during functional upper limb tasks: A systematic review. J. Electromyogr. Kinesiol. 2018, 40, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Geng, W.; Yu, G. Reuse of Motion Capture Data in Animation: A Review. In Computational Science and Its Applications—ICCSA 2003; Goos, G., Hartmanis, J., van Leeuwen, J., Kumar, V., Gavrilova, M.L., Tan, C.J.K., L’Ecuyer, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; Volume 2669, pp. 620–629. [Google Scholar] [CrossRef]
- Camargo, J.; Ramanathan, A.; Csomay-Shanklin, N.; Young, A. Automated gap-filling for marker-based biomechanical motion capture data. Comput. Methods Biomech. Biomed. Eng. 2020, 23, 1180–1189. [Google Scholar] [CrossRef] [PubMed]
- Cui, Q.; Sun, H.; Li, Y.; Kong, Y. Efficient human motion recovery using bidirectional attention network. Neural Comput. Appl. 2020, 32, 10127–10142. [Google Scholar] [CrossRef]
- Tits, M.; Tilmanne, J.; Dutoit, T. Robust and automatic motion-capture data recovery using soft skeleton constraints and model averaging. PLoS ONE 2018, 13, e0199744. [Google Scholar] [CrossRef] [PubMed]
- Howarth, S.J.; Callaghan, J.P. Quantitative assessment of the accuracy for three interpolation techniques in kinematic analysis of human movement. Comput. Methods Biomech. Biomed. Eng. 2010, 13, 847–855. [Google Scholar] [CrossRef]
- Smolka, J.; Lukasik, E. The rigid body gap filling algorithm. In Proceedings of the 2016 9th International Conference on Human System Interactions (HSI), Portsmouth, UK, 6–8 July 2016; pp. 337–343. [Google Scholar] [CrossRef]
- Liu, G.; McMillan, L. Estimation of missing markers in human motion capture. Vis. Comput. 2006, 22, 721–728. [Google Scholar] [CrossRef]
- Kucherenko, T.; Beskow, J.; Kjellström, H. A Neural Network Approach to Missing Marker Reconstruction in Human Motion Capture. arXiv 2018, arXiv:1803.02665. [Google Scholar]
- Aristidou, A.; Cameron, J.; Lasenby, J. Predicting Missing Markers to Drive Real-Time Centre of Rotation Estimation. In Articulated Motion and Deformable Objects; Perales, F.J., Fisher, R.B., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 238–247. [Google Scholar]
- Li, L.; McCann, J.; Pollard, N.; Faloutsos, C. BoLeRO: A Principled Technique for Including Bone Length Constraints in Motion Capture Occlusion Filling. In Eurographics/ACM SIGGRAPH Symposium on Computer Animation; The Eurographics Association: Goslar, Germany, 2010; p. 10. ISBN 9783905674279. [Google Scholar]
- Federolf, P.A. A Novel Approach to Solve the “Missing Marker Problem” in Marker-Based Motion Analysis That Exploits the Segment Coordination Patterns in Multi-Limb Motion Data. PLoS ONE 2013, 8, e78689. [Google Scholar] [CrossRef] [Green Version]
- Xiao, J.; Feng, Y.; Hu, W. Predicting missing markers in human motion capture using l1-sparse representation. Comput. Animat. Virtual Worlds 2011, 22, 221–228. [Google Scholar] [CrossRef]
- Vicon Motion Systems Ltd. Vicon Nexus User Guide. Available online: https://docs.vicon.com/display/Nexus211 (accessed on 8 April 2021).
- Vicon Motion Systems Ltd. Technical Information—FAQs. Available online: https://www.vicon.com/software/nexus/ (accessed on 8 April 2021).
- Burke, M.; Lasenby, J. Estimating missing marker positions using low dimensional Kalman smoothing. J. Biomech. 2016, 49, 1854–1858. [Google Scholar] [CrossRef] [Green Version]
- Mall, U.; Lal, G.R.; Chaudhuri, S.; Chaudhuri, P. A Deep Recurrent Framework for Cleaning Motion Capture Data. arXiv 2017, arXiv:1712.03380. [Google Scholar]
- Gløersen, Ø.; Federolf, P. Predicting Missing Marker Trajectories in Human Motion Data Using Marker Intercorrelations. PLoS ONE 2016, 11, e0152616. [Google Scholar] [CrossRef] [PubMed]
- Tan, C.H.; Hou, J.; Chau, L.P. Motion capture data recovery using skeleton constrained singular value thresholding. Vis. Comput. 2015, 31, 1521–1532. [Google Scholar] [CrossRef]
- Peng, S.J.; He, G.F.; Liu, X.; Wang, H.Z. Hierarchical block-based incomplete human mocap data recovery using adaptive nonnegative matrix factorization. Comput. Graph. 2015, 49, 10–23. [Google Scholar] [CrossRef]
- Julier, S.J. The scaled unscented transformation. In Proceedings of the 2002 American Control Conference (IEEE Cat. No. CH37301), Anchorage, AK, USA, 8–10 May 2002; Volume 6, pp. 4555–4559. [Google Scholar]
- Wan, E.A.; Van Der Merwe, R. The unscented Kalman filter for nonlinear estimation. In Proceedings of the IEEE 2000 Adaptive Systems for Signal Processing, Communications, and Control Symposium (Cat. No. 00EX373), Lake Louise, AB, Canada, 4 October 2000; pp. 153–158. [Google Scholar]
- Merriaux, P.; Dupuis, Y.; Boutteau, R.; Vasseur, P.; Savatier, X. A Study of Vicon System Positioning Performance. Sensors 2017, 17, 1591. [Google Scholar] [CrossRef] [PubMed]
- Van Der Merwe, R.; Wan, E. Sigma-Point Kalman Filters for Probabilistic Inference in Dynamic State-Space Models. Ph.D. Thesis, OGI School of Science & Engineering at OHSU, Portland, OR, USA, 2004. [Google Scholar]
- Carnegie Mellon University. CMU Graphics Lab Motion Capture Database. Available online: http://mocap.cs.cmu.edu/ (accessed on 23 October 2020).
- Müller, M.; Röder, T.; Clausen, M.; Eberhardt, B.; Krüger, B.; Weber, A. Documentation Mocap Database HDM05; Technical Report CG-2007-2; Universität Bonn: Bonn, Germany, 2007; ISSN 1610-8892. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).