Abstract
Cross-frequency interactions, a form of oscillatory neural activity, are thought to play an essential role in the integration of distributed information in the brain. Indeed, phase-amplitude interactions are believed to allow for the transfer of information from large-scale brain networks, oscillating at low frequencies, to local, rapidly oscillating neural assemblies. A promising approach to estimating such interactions is the use of transfer entropy (TE), a non-linear, information-theory-based effective connectivity measure. The conventional method involves feeding instantaneous phase and amplitude time series, extracted at the target frequencies, to a TE estimator. In this work, we propose that the problem of directed phase-amplitude interaction detection is recast as a phase TE estimation problem, under the hypothesis that estimating TE from data of the same nature, i.e., two phase time series, will improve the robustness to the common confounding factors that affect connectivity measures, such as the presence of high noise levels. We implement our proposal using a kernel-based TE estimator, defined in terms of Renyi’s entropy, which has successfully been used to compute single-trial phase TE. We tested our approach on the synthetic data generated through a simulation model capable of producing a time series with directed phase-amplitude interactions at two given frequencies, and on EEG data from a cognitive task designed to activate working memory, a memory system whose underpinning mechanisms are thought to include phase–amplitude couplings. Our proposal detected statistically significant interactions between the simulated signals at the desired frequencies for the synthetic data, identifying the correct direction of the interaction. It also displayed higher robustness to noise than the alternative methods. The results attained for the working memory data showed that the proposed approach codes connectivity patterns based on directed phase–amplitude interactions, that allow for the different cognitive load levels of the working memory task to be differentiated.
1. Introduction
Biological neural systems exhibit rhythmic activity across many scales, from the spiking activity of individual neurons to the electric potentials generated by large populations of neurons, measurable from the scalp in the form of electroencephalographic (EEG) recordings [1]. Interactions between oscillations of different frequencies, known as cross-frequency couplings (CFCs), have been hypothesized to be directly related to the integration of distributed information in the brain [2] by regulating and synchronizing multi-scale communication within and across neural ensembles [3]. The most widely studied instance of CFC is the modulation of the amplitude envelope of high-frequency oscillations by the phase evolution of low-frequency activity, known as phase-amplitude coupling (PAC) [2,3,4]. These phase-amplitude interactions seem to be linked to normal and pathological brain processes in different mammalian species, including humans [5], and they were locally and interregionally observed across a wide range of cognitive tasks [6]. Theoretically, PAC allows for information transfer from large-scale brain networks associated with low-frequency oscillations to local, fast cortical processing areas exhibiting high-frequency activity [7].
Phase-amplitude interactions are commonly assessed using electrophysiological data through metrics of statistical dependency, such as the modulation index, mean vector length, and variations in the concept of mutual information [8,9,10]. However, they are unable to capture the directionality and delay of phase-amplitude interactions, quantities that are intrinsic to the concept of information being sent from one neural assembly to another [1,5,11]. A natural solution to this limitation, within the framework of information theory, would be to assess PACs using transfer entropy [3,9,11,12,13]. Transfer entropy (TE) is a model-free connectivity measure that estimates the directed interaction, or information flow, between two dynamical systems [14,15]. It is specially well-suited to exploratory analysis in neuroscience because of its ability to detect unknown non-linear interactions [16,17]. However, as a model-free information-theoretic measure, it does not capture the details of how the information transfer is carried out [1]. Standard TE will not reveal anything about the spectral characteristics of the interactions it detects. The most common approach explored in the literature to assess directed phase-amplitude interactions through TE involves bandpass-filtering the signals in the target frequency bands before the extraction of the instantaneous phase and amplitude time series, which are then fed to a TE analysis [5,18]. Nonetheless, it has been argued that filtering before TE computation negatively affects the results of TE [19,20], leading to false positives, and that it may not have the desired frequency-specific effects [1].
In this work, we reframe the problem of estimating directed phase-amplitude interactions through TE as the computation of TE between two instantaneous phase time series, known as phase TE [21], by borrowing the underlying premise of the cross-frequency directionality (CFD), a linear connectivity measure capable of estimating the PAC direction [11]. We previously addressed the problem of phase TE estimation from single trial data [22] and hypothesized that, for directed PAC, the proposed approach can correctly identify the interacting frequencies, as well as the direction of interaction, while being robust to common factors that degrade the performance of connectivity estimation methods, such as the presence of high levels of noise and volume conduction effects [23].
To test our proposal, we use a simulation model that allows generating synthetic data with unidirectionally phase-amplitude couplings at two target frequencies [11], and real EEG data from a change detection task with several difficulty levels designed to study visuospatial working memory [24,25]. Working memory (WM) is a memory system of limited capacity with the ability to store and manipulate information for a short period of time [26,27]. Current hypotheses for the mechanisms underpinning WM highlight the role of PAC [28], pointing to bidirectional interactions between the (4 Hz–7 Hz), (8 Hz–12 Hz), and bands (13 Hz–30 Hz) (particularly around 13.5 Hz to 16 Hz for the latter) linking the prefrontal cortex to parieto-occipital and medial temporal regions during the activation of WM [6,29]. Obtained results for the simulated data show that the proposed approach successfully captures statistically significant phase-amplitude interactions, correctly identifying the direction of interaction and the target frequencies under noisy and signal-mixing conditions. Furthermore, the results for the WM data reveal that our proposal captures discriminant phase-amplitude connectivity patterns that allow the cognitive load associated with a trial of the change-detection task to be detected.
The remainder of the paper is organized as follows: in Section 2, we present our proposal to estimate directed phase-amplitude interactions through a phase TE-based approach. Section 3 describes the two experiments we carried out to test the performance of our method. In Section 4, we present and discuss our results and, finally, we provide conclusions in Section 5.
2. Methods
2.1. Transfer Entropy
Transfer entropy (TE) is an information-theoretic measure of directed interactions between two dynamical systems [14,15]. Given two time-series and , with a discrete time index, , TE is defined as:
where are time-embedded versions of and , with the embedding dimension and delay, respectively; stands for the interaction delay between the two systems, and represents a probability density function [30]. The time embeddings are defined as [31,32]. TE, as in Equation (1), evaluates the statistical causality from to by measuring whether the information contained in the previous , alongside that of the previous , is better at predicting the future of than the information from the past of alone. If this is the case, then causes (in the sense of Wiener’s definition of causality [14]). For estimation convenience, we can also express TE as a linear combination of Shannon entropies:
where , X is a discrete random variable (), and , stand for joint and marginal entropies.
2.2. Transfer Entropy for Directed Phase-Amplitude Interactions
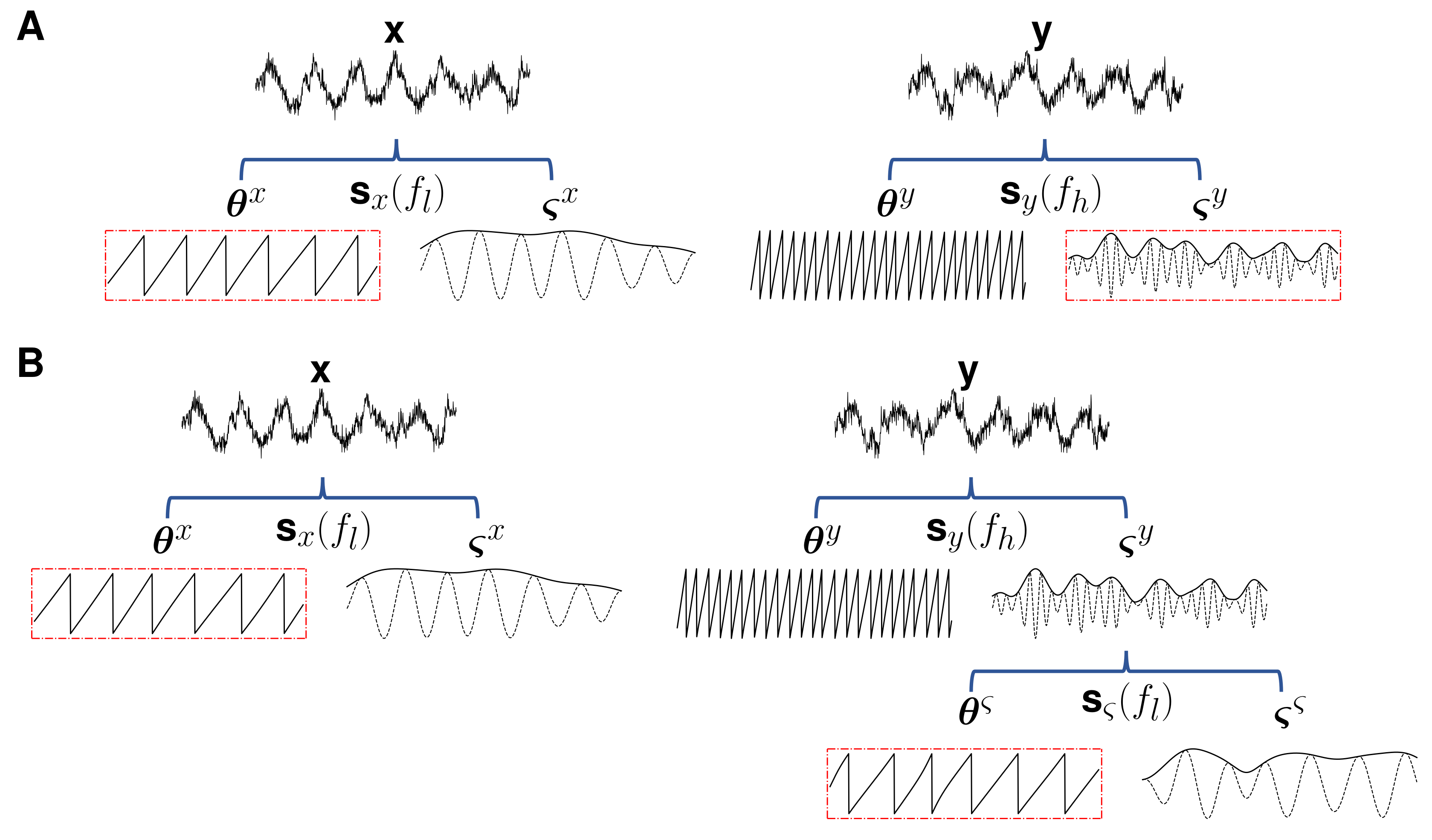
The conventional approach to estimate directed phase-amplitude interactions through TE consists of two stages. The first stage is a component extraction stage, which involves complex-filtering, or performing a phase/amplitude decomposition, to extract instantaneous phase and amplitude time series (see Figure 1A). Then, there is a TE computation stage that simply consists of estimating the information flow between the previously extracted data [5,18]. Formally, given two time series and , to estimate the TE from the phase of at a frequency (usually a low frequency) to the amplitude envelope of at a frequency (commonly a higher frequency than ), we obtain complex time series and , which contain the filtered values of and at and , respectively; where are instantaneous phase time series, and are amplitude envelopes [21]. Then, we compute the desired TE as:
where and are time-embedded versions of and .
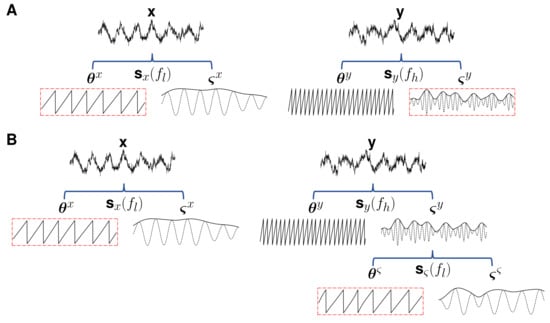
Figure 1.
(A) The conventional approach to capture directed phase-amplitude interactions through TE consists of estimating TE from the instantaneous phase and amplitude time series that were extracted at frequencies and , respectively. (B) Our approach implies a further step, comprising the extraction of the phase of the amplitude time series at frequency , to reformulate the problem as a phase TE estimation task.
2.3. Cross-Frequency Directionality
The cross-frequency directionality (CFD) estimates the direction of interaction between the phase of low-frequency () oscillations and the amplitude of faster, higher-frequency () oscillations [11]. This is based on the phase slope index (PSI), which measures the coupling directionality between two oscillatory signals of similar frequencies [33]. Given two time series and , the CFD from to is computed as the PSI between , the time series containing the slow oscillations of interest, and the amplitude envelope of at . Thus:
where is the complex coherence, is the cross-spectrum between and , are the auto-spectrums of and , corresponds to the frequency resolution, F indicates the frequency range over which the slope is summed, and ℑ stands for the fact that only the imaginary part of the sum is selected [33]. Therefore, the CDF estimates the slope of the phase difference, between the phases of and , as a function of frequency. That is to say, it translates the problem of estimating the direction of phase-amplitude interactions to estimating interaction between phases.
2.4. Phase Transfer Entropy and Directed Phase-Amplitude Interactions
We begin by noting that the conventional approach to estimate directed phase-amplitude interactions though TE, as expressed by Equation (3), implies the computation of TE from data of different properties, a phase time series , which represents a circular variable, and a smooth, continuous amplitude envelope . In this work, we reformulate the problem of directed phase-amplitude interaction detection using TE as a phase TE-estimation task [21]. We do this by applying the idea behind the CFD: obtaining the directionality of interactions between phase and amplitude time series can be redefined as estimating the direction of interaction between two-phase time series. We hypothesize that such a change can improve the robustness of phase-amplitude TE estimates to signal degradation by noise and volume conduction effects.
Given two time series and , we want to estimate the TE from the phase of at a frequency of to the amplitude envelope of at a frequency of . As before, and are the corresponding phase and amplitude time series, obtained at the adequate frequencies. However, before TE computation, we obtain a complex representation of at , , where is an instantaneous phase time series, and is an amplitude envelope (See Figure 1B). Next, we define:
where and are time-embedded versions of and .
The quantity in Equation (5) indicates the estimation of TE from two-phase time series extracted at the same frequency (). Thus, it corresponds to the definition of phase TE, a phase-specific, nonlinear directed connectivity measure introduced in [21]. In that sense, a robust, kernel-based approach to estimating phase TE from single-trial data was recently proposed by our group [22]. Following this approach, we can redefine Equation (5) as:
where stands for the kernel-based formulation of Renyi’s entropy introduced in [34], , are kernel matrices holding elements , with a positive, definite and infinitely divisible kernel function. For , contain the values of the time series at times i and j. While for and the vectors correspond to the time embedded versions of and , and , respectively, at times i and j, in accordance with the time indexing of TE. Renyi’s entropy is a parametric family of entropies [35]:
with and , and X a discrete random variable. This is a generalization of Shannon’s entropy, and tends towards it in the limiting case where . Its kernel-based formulation can bypass the need for direct probability estimation from the data, instead relying on the kernel matrices that capture similarity relationships [34]. It is defined as:
where is a kernel matrix containing elements , n is the number of realizations of X, and stands for the matrix trace. We used this formulation, along with its definition for joint probability distributions:
where is another kernel matrix, and the operator ∘ stands for the Hadamard product, to successfully and robustly estimate TE for real-valued and instantaneous phase time series [16,22]. In this study, we apply it in the context of directed phase-amplitude interaction estimation, following the TE estimation approach presented in Equation (6).
3. Experiments
3.1. Simulated Phase-Amplitude Interactions
3.1.1. Simulation Model
To evaluate the performance of our proposal, we generate simulated time series using a modified version of the PAC modeling strategy introduced in [11]. The model simulates a directed interaction from the phase of a time series , at a low frequency , to the amplitude of a time series , at a high frequency . We implement the model as follows: first, we build d time series segments corresponding to a sinusoidal signal period:
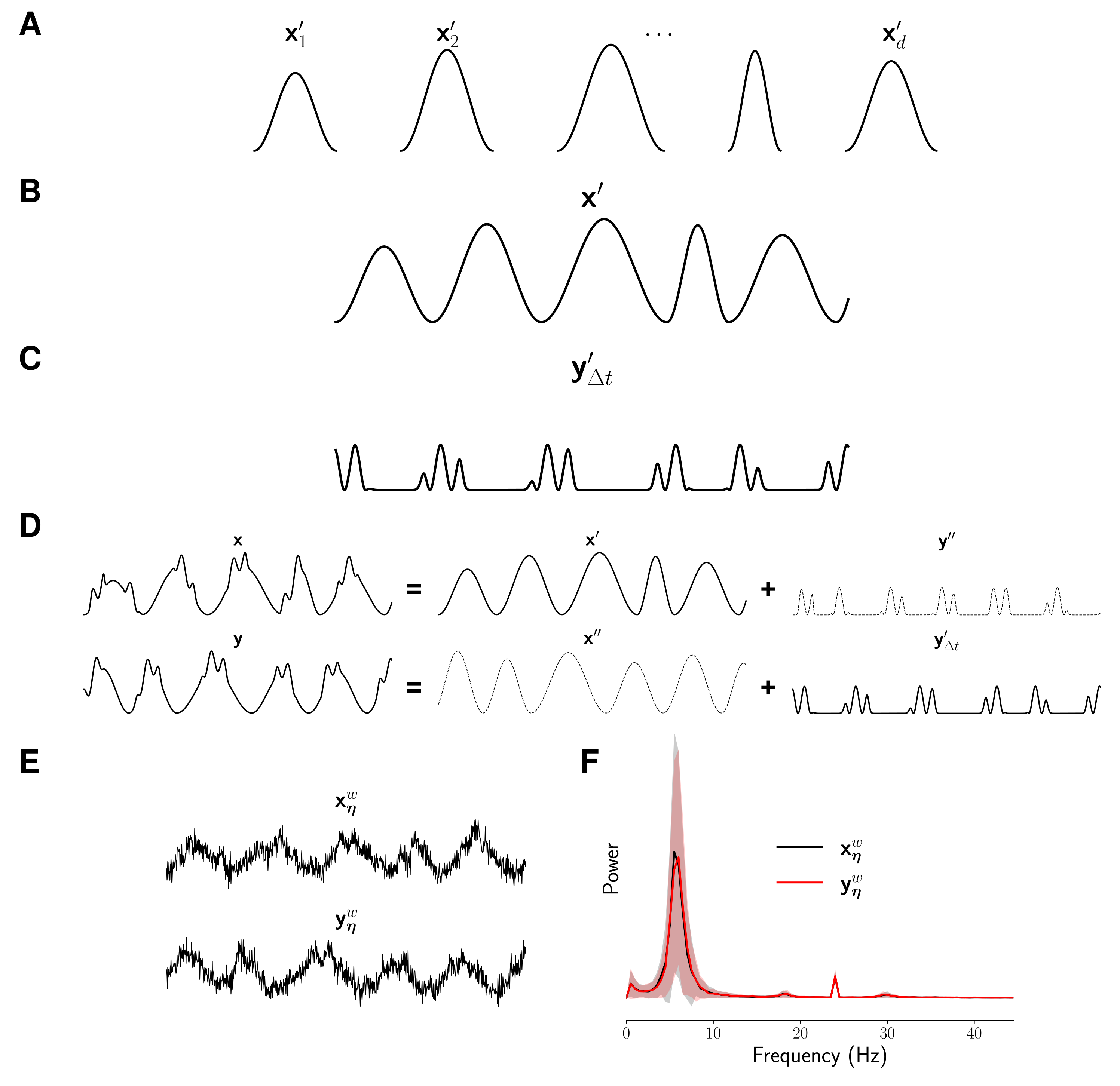
where , , and , with the sampling frequency in Hz; as shown in Figure 2A. For each segment i, the amplitude and the period are drawn from Gaussian distributions with means and and standard deviations of and , respectively. Then, we concatenated the d segments to obtain a continuous signal of varying amplitude, as depicted in Figure 2B, and with a power spectrum peaking at around . Next, we generate a signal oscillating at , whose amplitude is a function of , by defining:
where , , , and (see Figure 2C). The constant c represents a threshold value, so that when , the amplitude of increases, a controls the steepness of that increase. Next, we imposed a directionality of interaction from to by time-shifting by seconds Afterward, we construct two pairs of auxiliary signals following the steps described above. From one pair, we select the signal with low-frequency components, . From the remaining pair, we select the signal oscillating at the highest frequency, . Finally, we define and so that, by design, and have closely resembling power spectra (see Figure 2D–F).
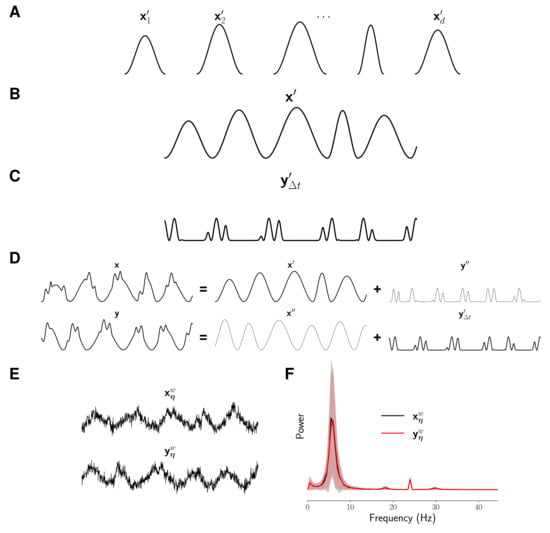
Figure 2.
Schematic representation of the simulation model used to obtain data with directed phase-amplitude interactions. (A) Sinusoidal signal segments of varying amplitude and period (). (B) A continuous, low-frequency signal () is obtained after concatenating the sinusoidal signal segments. (C) A high frequency signal () modulated by is computed through Equation (11). Then is time-shifted by seconds (). (D) and are combined with a pair of auxiliary, non-interacting signals and to generate signals and . (E) Signals and are contaminated with noise and linearly mixed. (F) The resulting signals, and , have very similar power spectra.
3.1.2. Experimental Setup
We simulate 100 pairs (trials) of 2 s long signals, sampled at 1000 Hz, with directed phase-amplitude interactions from the band ( Hz) to the band ( Hz), with a timeshift of 20 ms. We detrend and normalized the simulated signals, before contaminating them with normalized white () and pink () noise, as follows:
where the parameter SNR controls the signal to noise ratio. We vary this to simulate low (), moderate (), and high () noise conditions. For each scenario, we also mix the noisy signals, and , aiming to reproduce the effects of volume conduction, by defining , and , with the mixing strength. Then, we downsample and by a factor of 4 (we keep only every fourth sample) to 250 Hz, and estimate the directed phase-amplitude interactions present in the data for a square frequency grid ranging from 3 Hz to 45 Hz, in 3 Hz steps, using the three approaches described in Section 2. Finally, to determine whether the estimated interactions are statistically significant, we perform permutation tests based on randomized surrogate trials [19,36] for each evaluated condition and frequency pair. The Bonferroni-corrected significance level for the tests is set at .
3.2. Working Memory Data
3.2.1. Database
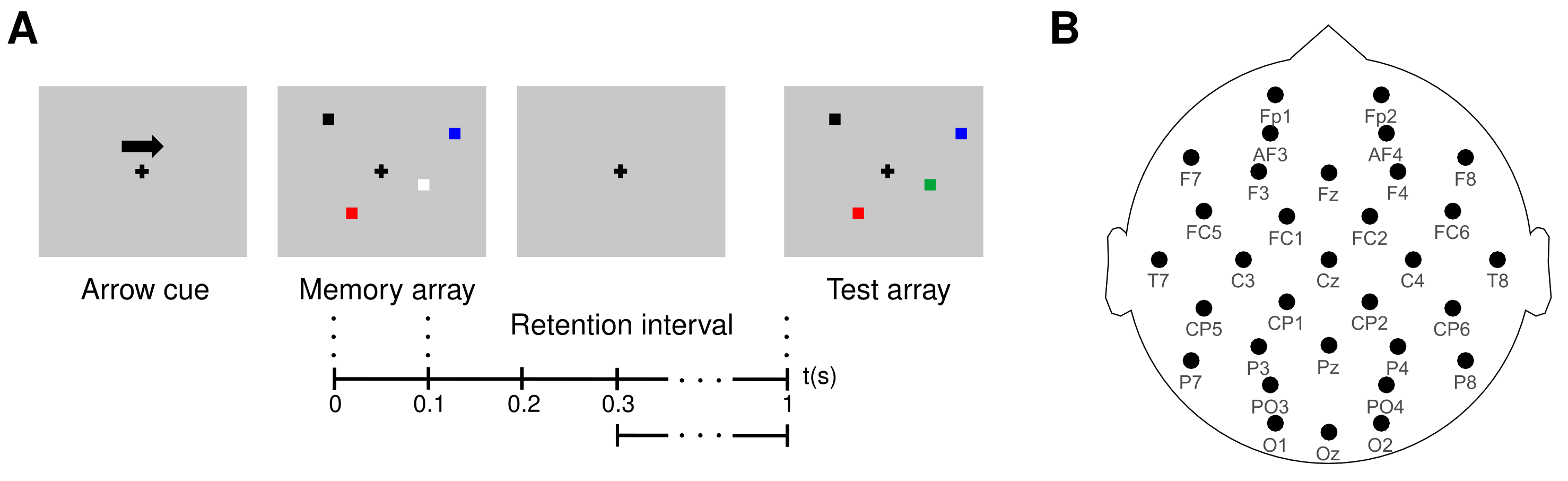
The database of brain activity during visual working memory [24] consists of the EEG data recorded from twenty-three subjects while they performed a change detection task [25] (https://data.mendeley.com/datasets/j2v7btchdy/2, accessed on 4 September 2021). The subjects had normal or corrected-to-normal vision, and did not have color-vision deficiency. The EEG data were acquired from 64 electrodes (Biosemi ActiveTwo), arranged according to the international 10/20 extended system, at a sampling rate of 2048 Hz. In addition to the EEG data, the database contains recordings from two external electrodes placed on the left and right mastoids, and four EOG channels. The goal of the change-detection task is to remember the colors of a set of squares (the memory array), and then compare them with the colors of a second set of squares (the test array), which appear in the same locations as the first set. The task has three levels: low-, medium-, and high-memory load. Each level has a different number of elements in the memory array: one square (low-memory load), two squares (medium-memory load), and four squares (high-memory load). At the beginning of each task trial, an arrow pointing to the left or right hemifield appears on the screen, signaling to the subject that they must remember only the stimuli that will be displayed on that side of the screen. Next, a memory array is presented for 0.1 s, followed by a retention period of 0.9 s. Afterward, a test array appears, and the subject reports whether the colors of the squares in the memory and test arrays are the same. Figure 3A depicts the task’s experimental paradigm. Each subject performed 96 trials (32 trials for each memory load level). The colors of the squares in the test and memory arrays were different in 50% of the trials.
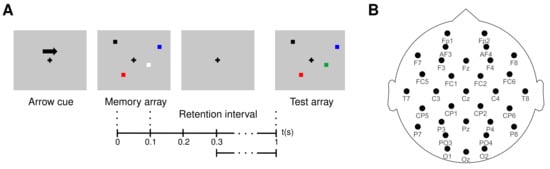
Figure 3.
(A) Graphical representation of the change detection task for WM. (B) EEG channels selected from the montage used for the acquisition of the WM database.
3.2.2. Preprocessing
First, the data were re-referenced to the average of the recordings from the electrodes located on the mastoids, bandpass-filtered between 0.01 Hz and 20 Hz using an order 2 Butterworth filter, and segmented using a 1.4 s squared window in order to extract the data corresponding to each trial. A trial segment started 0.2 s before the presentation of the memory array. Then, independent component analysis (ICA) was performed on the trial data to eliminate ocular artifacts using the fastICA algorithm, as implemented in the MNE python package, and the EOG information [24]. Next, all trials for which the subjects incorrectly matched the memory and test arrays were dropped from further analysis. Afterward, the 32 channels () depicted in Figure 3B were chosen from the 64 channels contained in the EEG data. Then, the trial data were downsampled by a factor of 2 (only every second sample is kept) to 1024 Hz, and underwent a final segmentation stage to select the part of the retention interval when the subject’s working memories held the stimulus information. To that end, a 0.7 s long time window () was used, starting 0.3 s after the onset of the memory array and ending before the test array appearsedon the screen, as schematized in Figure 3A. Finally, to reduce the effects of volume conduction, the surface Laplacian of each trial was computed through the spherical spline method for source current density estimation [37,38,39].
Subjects number 11 and 17 were discarded during preprocessing because their data contained strong artifacts in a very large number of trials. Subjects number 22 and 23 were reassigned as subjects 17 and 11, respectively.
3.2.3. Classification Setup
Our aim is to set up a subject-dependent classification system (one classifier per subject) that allows the different levels of the change detection task, to be differentiated using relevant directed phase-amplitude interactions captured through the proposed TE approach as inputs.
Feature Extraction
Let be the EEG set holding N trials from the WM dataset, recorded from a single subject, with C as the number of channels and M as the number of samples of each trial. Let be a set whose n-th element corresponds to a label assigned to the n-th trial . The elements of can take the values of 1, 2, and 3 to indicate low-, medium-, and high-memory loads, respectively. Our aim is to predict the label from the transfer entropy features that capture the directed phase-amplitude interactions present in .
Let be a TE measure between the phase of channel at frequency , and the amplitude envelope of at frequency , as defined in Equation (6). For all pairwise combinations of channels in , computing yields a connectivity matrix . When , then . The values of vary in the range from 4 Hz to 18 Hz, in 2 Hz steps, since activity in that frequency range has been associated with interactions between different brain regions during WM [6]. Then, three bandwidths are defined Hz, and the matrices are averaged within each pairwise combination of bandwidths (, , etc.). After that, each of the averaged matrices are normalized to the range , and stacked together. Therefore, each trial is characterized by a connectivity matrix . For the N trials, a set of connectivity matrices is used. Then, by applying vector concatenation to a vector is obtained. Finally, the N vectors are stacked together in order to obtain a single bi-dimensional matrix , , that characterizes in terms of phase-amplitude TE measures. In practice, for each subject, the training data have the following dimensions: N rows, which correspond to the number of trials of the task correctly performed by the subject (), and features, where accounts for the fact that the TE of a time series is not defined, and, therefore, the main diagonals of the matrices are empty (or all zeros, as in our case).
Feature Selection and Classification
In order to identify the TE features relevant to the discrimination between the cognitive load levels in the WM database, we rely on a relevance analysis methodology based on centered kernel alignment (CKA). CKA quantifies the similarity between two sample spaces by comparing two kernel functions that characterize each space [40]. This allows for a relevance vector index to be built, which can be used to rank the features in the characterizing matrix according to their discrimination ability. Each element in signals how relevant the p-th feature is regarding its usefulness in distinguishing between the class labels in , with higher values of indicating higher relevance [22]. However, estimating CKA from data with a very low number of trials per class leads to unstable results. Given the fact that, in the WM database, each subject’s dataset contains an average of less than 30 correct trials per class, we began by setting up an auxiliary cross-validation scheme to obtain an average per subject, termed . This auxiliary cross-validation scheme has 10 iterations. For each iteration, 80% of the trials were randomly assigned to a training set and the remaining 20% were assigned to a validation set (80/20). After the 10 iterations were performed, was obtained as the average of the vectors computed in each iteration. Then, we set up a 10 iteration, 80/20, cross-validation scheme for use in subject-dependent classification. In this study, we used a support vector classifier (SVC) with an RBF kernel [41]. All classification parameters were tuned through a grid search and selected according to the classification accuracy, which was used as the system performance evaluation metric. For each iteration, we used to rank the features in from the highest to lowest relevance. Then, we selected a percentage of the ranked features, raging from 5% to 100% in 5% increments, and input the chosen features to the classification algorithm, with the most relevant features being input first. The percentage of discriminant features was tuned along with the other classification parameters.
3.3. Parameter Selection
For the TE methods, all parameters were estimated before extracting the phase and amplitude time series, that is to say, from the initial, real-valued time series data. The value of the embedding delay was set to 1 autocorrelation time (ACT) [31]. The embedding dimension d was automatically selected using Cao’s criterion [36,42] from the range [22]. The parameter u was selected as the delay producing the largest TE from the following ranges: for the simulated data, and for the WM data. The parameter in Renyi’s entropy was set to 2, which is neutral to weighting, an a reasonable, a priori choice [16,34]. A radial basis function (RBF) kernel with Euclidean distance [43], defined as:
was employed as kernel function, where is a distance operator, and is the kernel’s bandwidth. The bandwidth was set in each case as the median distance of the data [44]. For CFD estimation, we used a sliding window 5 frequency bins long. Furthermore, for all measures, the required phase and amplitude decompositions we carried out by convolving the real-valued data with a Morlet wavelet, defined as:
where f is for the filter frequency, is the standard deviation of the wavelet in the time domain, and m controls the time/frequency resolution [21]. The parameter m was varied from 3 to 10 in a logarithmic scale, according to the selected frequency of the filter. Finally, all connectivity values were obtained through in-house implementations of the algorithms for the different measures studied. The Python implementation of the proposed approach is available at https://github.com/ide2704/Directed_PAC_through_kernel-based_Phase_Transfer_Entropy (accessed on 7 September 2021).
4. Results and Discussion
4.1. Simulated Data
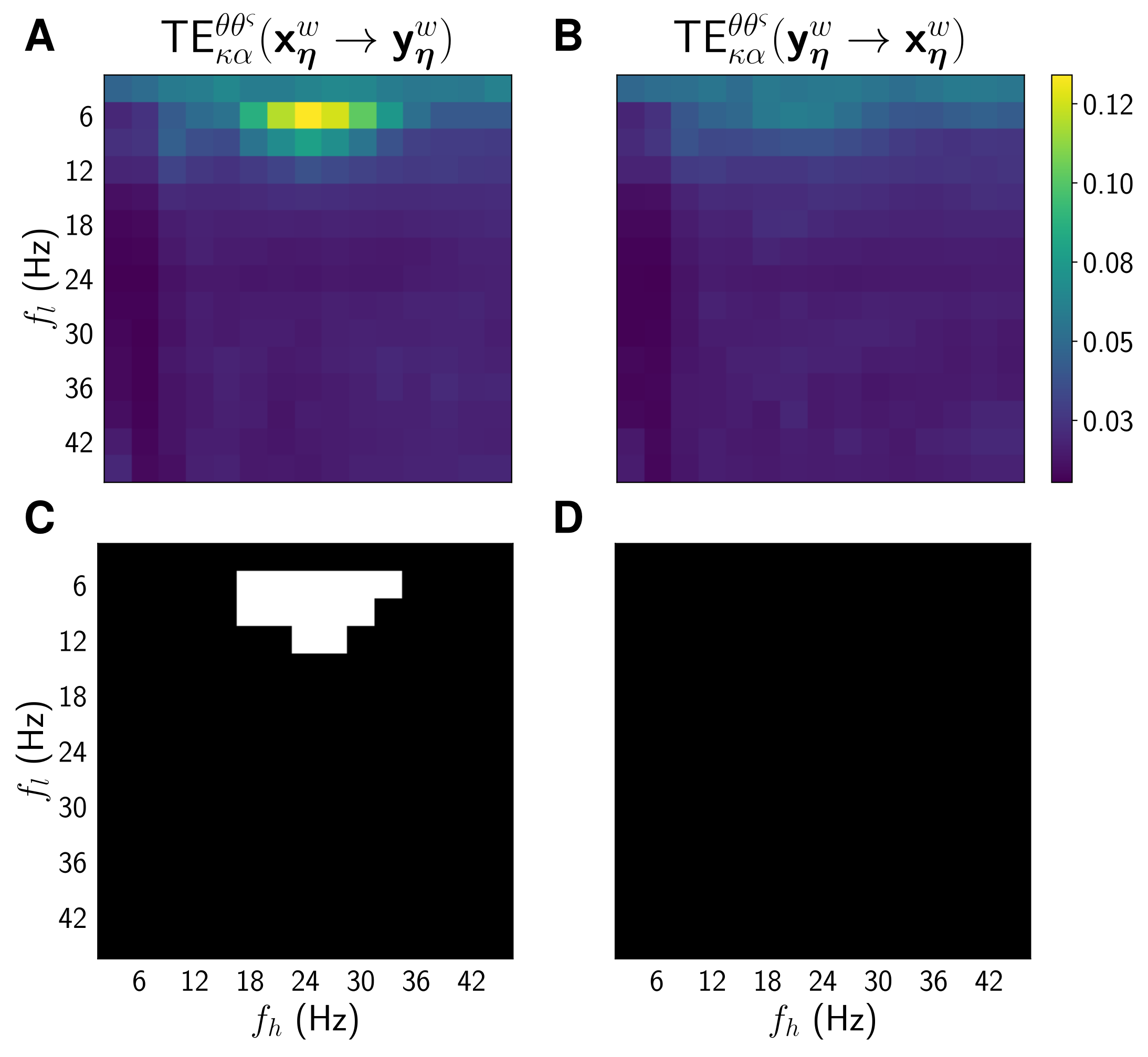
Figure 4 presents the results obtained through the proposed TE approach for the simulated data in the case where . Figure 4A shows the average values obtained for TE, with and varying in the range from 3 Hz to 45 Hz, in 3 Hz steps. That is to say, it shows the TE values that were computed following our proposal, assuming that the oscillation phases in drove the amplitude envelopes of the oscillations in . Similarly, Figure 4B shows the average obtained TE values, where the underlying assumption is that oscillation phases in are causal to the amplitude envelopes of the oscillations in . Figure 4C,D display the results returned by the permutation tests carried out over the TE data that were estimated for all the simulated trials, and whose average values are displayed in Figure 4A,B, respectively (statistically significant results are indicated in white). The results show that the proposed approach captures strong and statistically significant phase-amplitude-directed interactions around the target frequencies used to generate the simulated data. Statistically significant results were only obtained when TE was estimated from the phase of in the band, at around 6 Hz, to the amplitude of in the band, at around 24 Hz, and not when estimated assuming causality in the opposite direction.
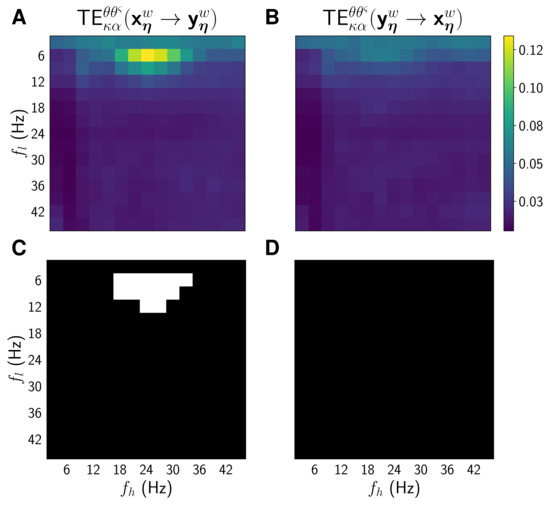
Figure 4.
TE results for the simulated data in the case when . (A) Average TE values. (B) average TE values. (C) Results of the permutation test performed on the TE values. Statistically significant connectivities are indicated in white. (D) Results of the permutation test performed on the TE values.
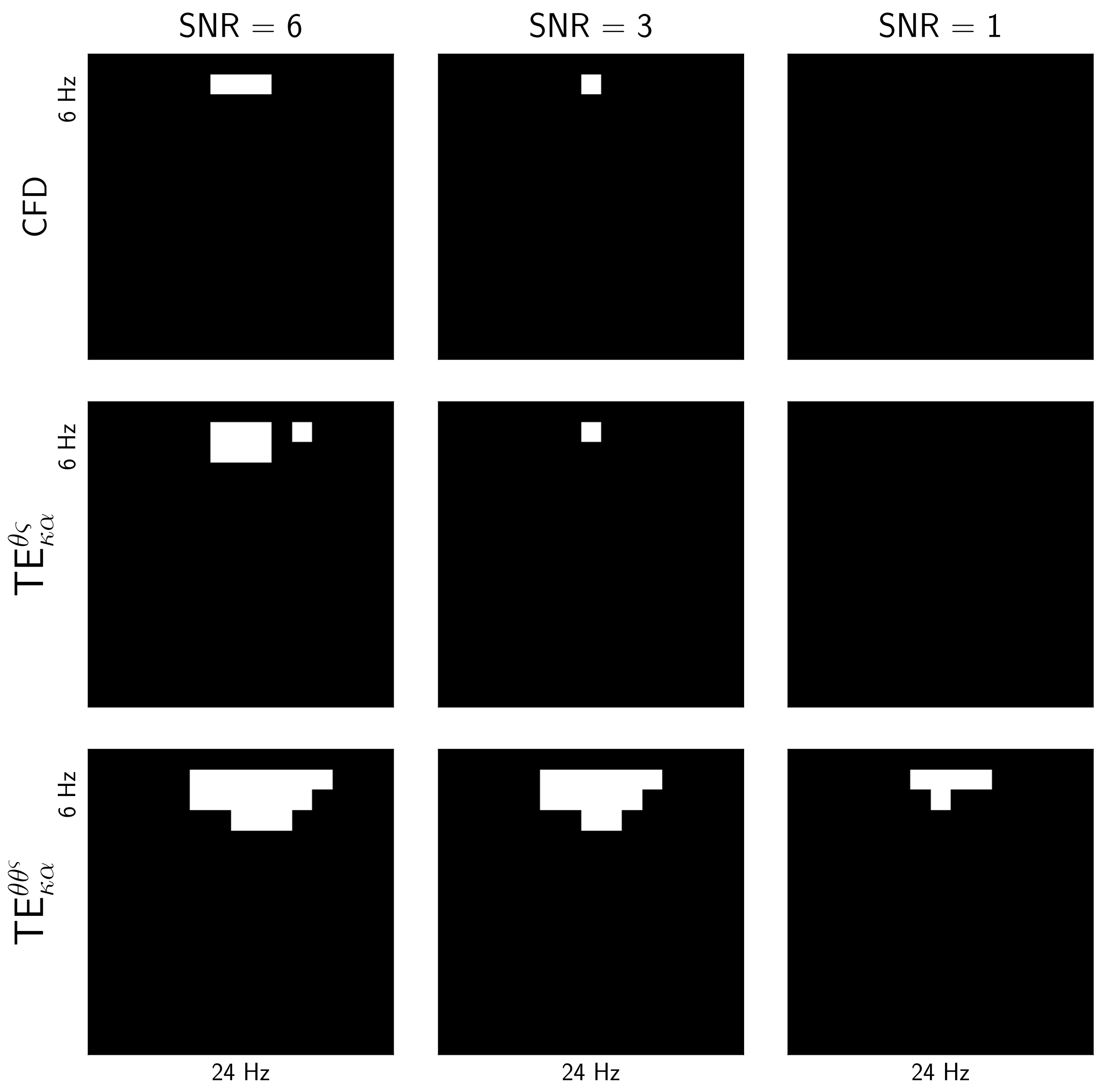
Figure 5 shows the results of the permutation tests carried out on the connectivity values estimated for all trials from the simulated data using, from top to bottom, CFD, TE (conventional approach to estimate directed phase-amplitude through TE, using the kernel-based Renyi’s TE estimator proposed in [16] ), and TE, under the three modeled noise conditions, from left to right, low (), moderate () and high () noise levels. In this case, all connectivity measures were obtained assuming the correct direction of causality, from to . As before, statistically significant results are displayed in white. For the low and moderate noise levels, the three connectivity estimation methods successfully capture statistically significant, phase-amplitude directed interactions around the target frequencies. Note that the CFD and TE display significant results on narrower frequency ranges around the interacting frequencies that were actually present in the data than TE. This is likely to be associated with the additional filtering stages involved in the computation of TE and, in the case of CFD, its high-frequency specificity is probably linked to its robustness against false positives [11]. However, unlike TE, both CFD and TE failed to capture any statistically significant interactions for the high-noise scenario. Therefore, our proposal exhibits higher robustness to the noise present in the data. Thus, from the results presented in Figure 4 and Figure 5, we can argue that the proposed TE approach allows for directed phase-amplitude interactions to be uncovered, capturing their strength and direction, even in the presence of high levels of noise and a confounding factor such as signal-mixing due to volume conduction.

Figure 5.
Results of the permutation tests carried out on the connectivity values estimated using CFD, TE and TE, for the three noise conditions modeled (), assuming interactions in the simulated data from the phase of to the amplitude of . Statistically significant results are shown in white.
4.2. Working Memory Data
The ability to store and manipulate information for short periods of time, provided by WM, plays a key role in complex cognitive tasks such as comprehension, reasoning, planning and learning [29,45]. WM consists of three distinct stages of information-processing: encoding, maintenance or retention, and retrieval [6], with the retention interval being considered as a defining component of WM, since it differentiates it from other memory types [27]. The most widely recognized model of WM [26] describes it as a several separate but interacting subsystems: a central component (central executive), two stimuli-dependent storage subsystems (the phonological loop and the visuo-spatial sketchpad), and a system of limited capacity that allows for interaction between the other components (episodic buffer) [46]. Moreover, multiple studies have found that neural oscillatory activity in a wide range of frequencies is modulated during WM [47]. High-frequency activity, in the and (>30 Hz) bands, seems to play a role in the encoding, retrieval, and maintenance of the stimulus; activity at lower frequencies, in the and ranges, especially in frontal areas, is associated with the coordination and integration of different cognitive processes during the execution of WM tasks [48]. This has led to hypotheses about the cross-frequency coupling mechanisms underpinning WM, with oscillatory activity in the central executive component interacting with oscillations at other frequencies in the peripheral storage systems [12,49]. PAC interactions are thought to play a crucial role in WM [28], with bidirectional interactions linking the prefrontal cortex to parieto-occipital and medial temporal regions [6,29].
In this study, we test the proposed TE approach for the estimation of directed phase-amplitude interactions in the context of an important topic in the study of WM: how the characteristics of brain activity are modulated by changes in memory loads, as induced by WM tasks with different difficulty levels [48]. This topic is closely related to the concept of WM capacity, the amount of information that can be maintained and manipulated in WM [45]. WM capacity is, in turn, linked to important abilities, including non-verbal reasoning and control of attention, among others, and can be altered in people with psychiatric disorders [50].
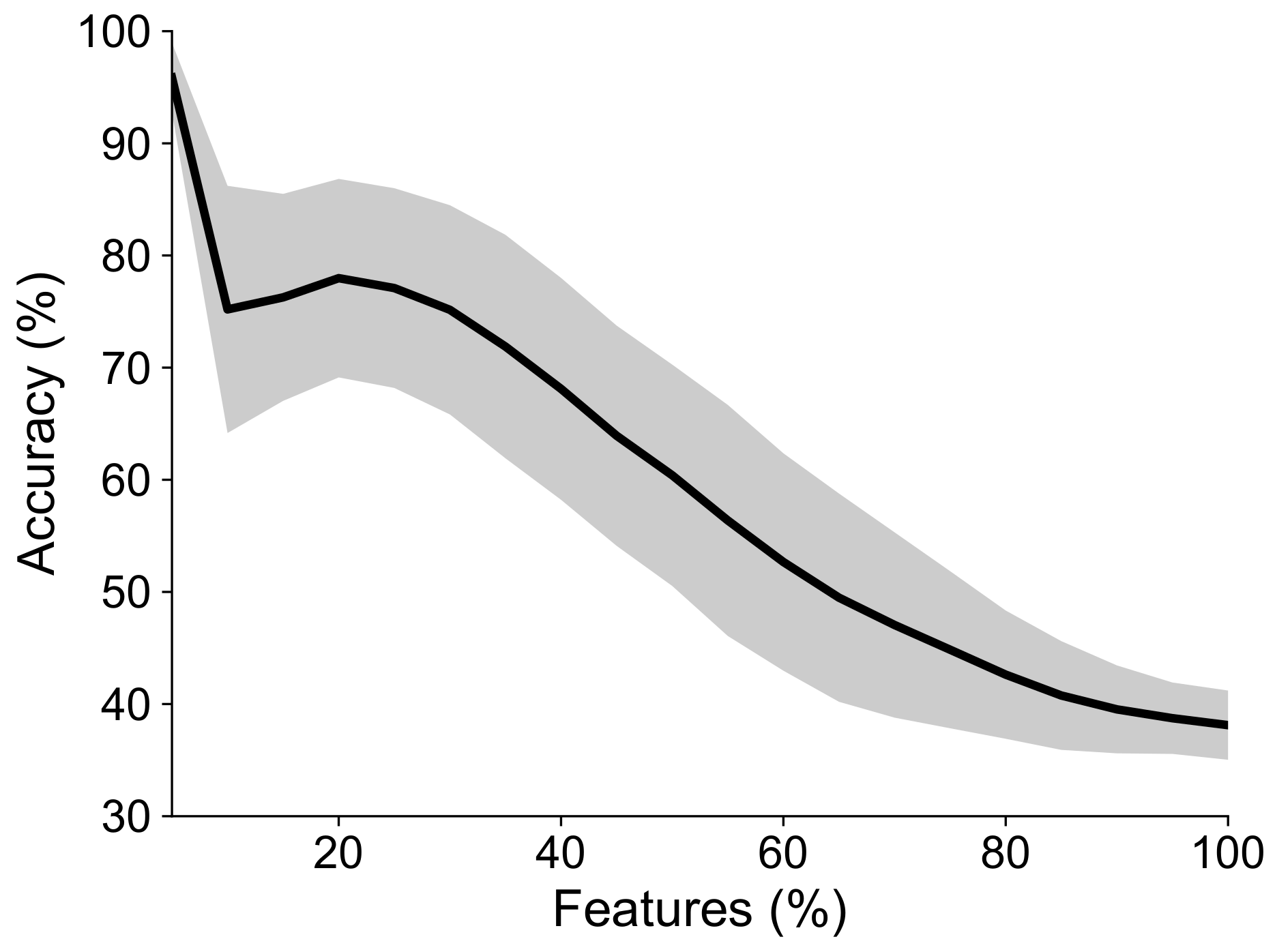
We built a subject-dependent classification system based on features extracted through the proposed TE method from the EEG data recorded during the retention interval of a change-detection task: a task designed to test visuospatial working memory capacity. The goal of the classifier is to assign a particular cognitive load (number of elements in the memory array) to EEG data from a task trial characterized using our proposal. Figure 6 presents the classification accuracy for all subjects in the WM database as a function of the percentage of features used to train the classifier. The best results are obtained when 5% of the features are selected. These are those with the with the highest relevance values according to the CKA-based relevance vector , achieving an average classification accuracy of for the three classes corresponding to each cognitive load level in the change detection task. Figure 7 shows the highest accuracy obtained for each subject in the WM database, as well as the precision, recall, and F1 score values. Although the subjects differ in performance, the proposed classification system exhibits accuracies well above what would be expected in a three-class classification task for all of them. The precision, recall and F1 score values indicate that the accuracies obtained by the classifiers for each subject are not the result of class imbalances in the data or biased class selection by the classifiers themselves. Additionally, all subjects, except subject 3, achieve peak performance when the classifier is trained with only 5% of the connectivity features (subject 3 does so when 10% of the features are selected). These results imply that our characterization strategy successfully captures the discriminant directed phase-amplitude interactions elicited during the change-detection task. Moreover, only a small fraction of those interactions are required to discriminate between the task’s levels. In fact, employing a higher percentage of features leads to a pronounced decrease in classification performance, as shown in Figure 6. This phenomenon can be explained because all channel connectivity analyses lead to datasets with a large number of features (see Section 3.2.3), which, in turn, leads to a well-known problem in machine learning: the curse of dimensionality. The larger the dimensionality of the data, the higher the chance that most training instances will be far away from each other, and that new instances will also be far away from those used to train the machine learning system. This makes it difficult to make good predictions [51]. In additiona, many of the obtained connectivity features will not provide useful information to discriminate between the conditions of the cognitive paradigm of interest [16], and will only add noise and complexity to the classification stage. Adequate feature selection reduces the dimensionality of the data by getting rid of non-relevant features (connectivity values), which can, as in our case, help with classification performance.
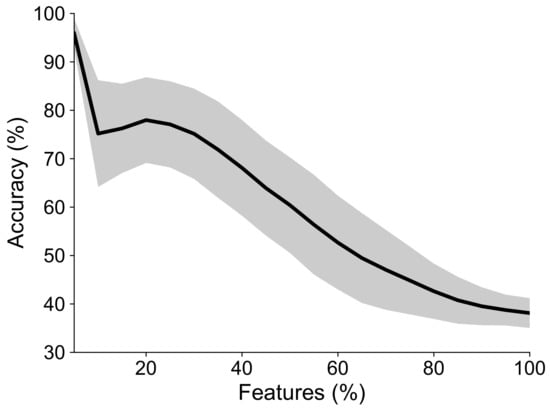
Figure 6.
Average classification accuracy for all subjects as a function of the percentage of selected TE features.
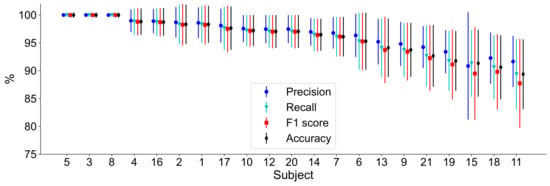
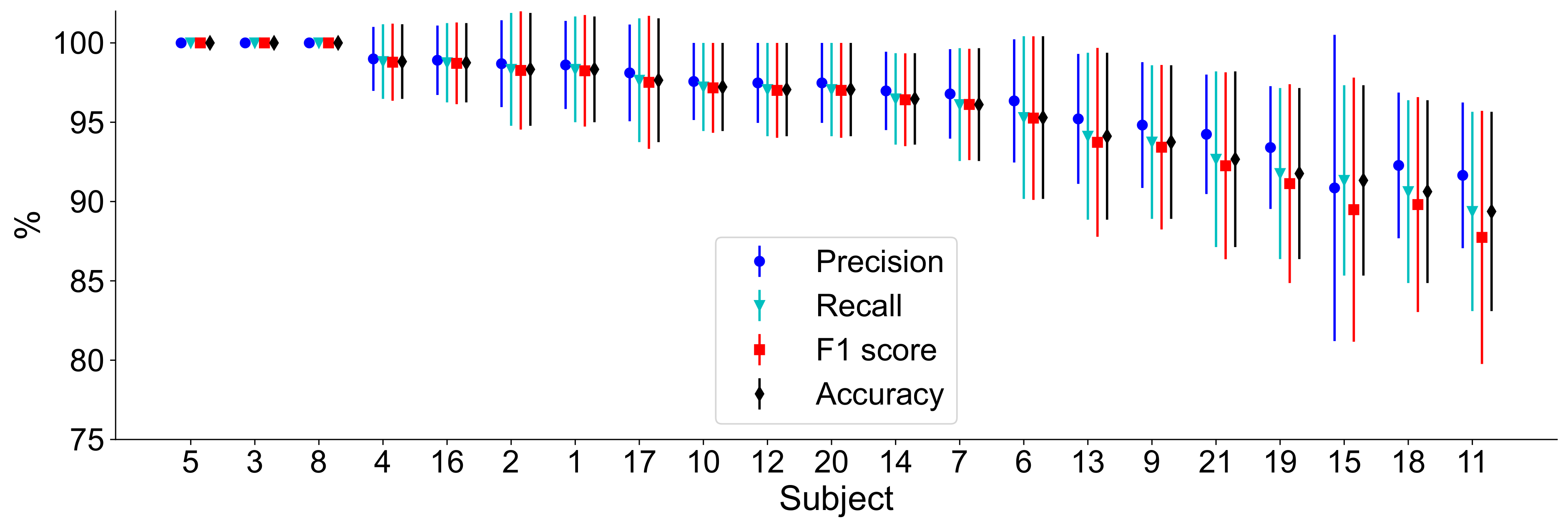
Figure 7.
Highest average classification performance for each subject in the WM database. Mean ± standard deviation values are displayed for four classification performance measures: precision, recall, F1 score and accuracy. The subjects are ordered from the highest to lowest accuracy.
At this point, it is worth noting that the vector , used to rank the features, is obtained as the average of the relevance vectors stemming from the different folds of an auxiliary cross-validation scheme, outside of the cross-validation process for classification. Therefore, our classification setup suffers from data leakage, and, as a consequence, the above results area is probably higher than that which could be obtained from a classification system suitable for real-world applications. Nonetheless, our results still show that relatively few connectivity values describing directed phase-amplitude interactions can successfully discriminate between the brain activity elicited at different levels of the change-detection task. Furthermore, the vector provides valuable insights regarding the directed phase-amplitude interactions that arise while the subjects perform the task. It does this by assigning a relevance value to each column, or feature, in the characterizing matrix . In the case of our analysis, indicates whether a particular connectivity between two channels, for a specific frequency-band pair (, , etc.), allows for discrimination of the different cognitive loads of the task. A feature’s discriminant ability is tantamount to its variation across classes. That is to say, the most relevant connectivities in are those that change consistently across trials as a function of the cognitive load, which points to the involvement of those directed phase-amplitude interactions in the underlying working memory systems activated during the task.
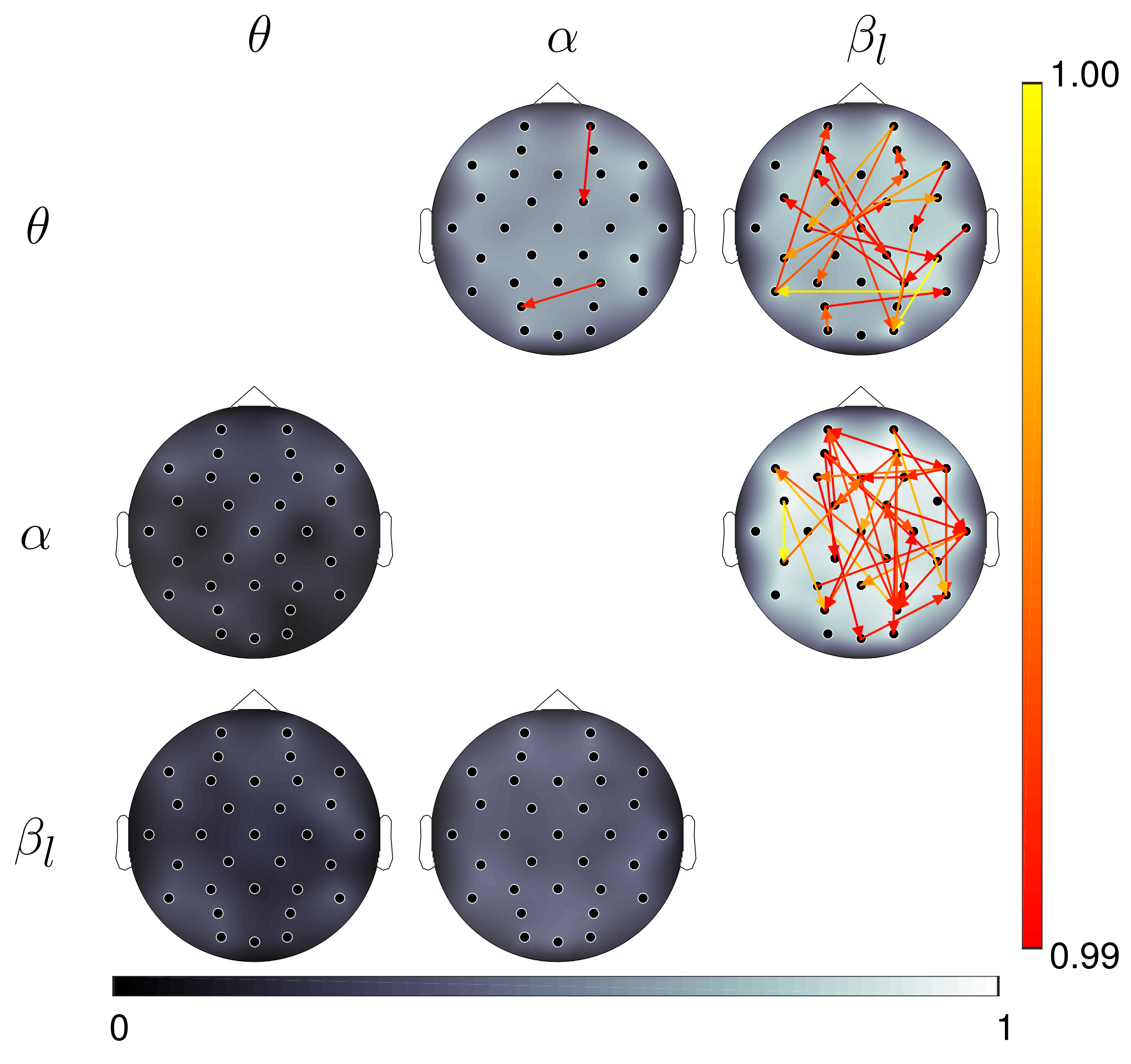
Figure 8 displays the most relevant connectivities (average for all subjects), according to the relevance vector , discriminated by the frequency band pair. The background topoplots show the average nodal relevance, which corresponds to the relevance of the total information flow of every node. This is defined as the sum of all the in associated with all directed interactions originating from and targeting a specific node or EEG channel [22]. We note that, in general, there is high nodal relevance for interactions where the phases of oscillations in the band drive the amplitudes of oscillations in the and bands. However, the highest nodal relevance is achieved by the phase-amplitude interactions from to band activity. As expected, the relevant connectivities are distributed in a similar way in terms of frequency. Spatially, they tend to involve long-range interactions linking frontal, temporal and parietal regions. In particular, for the phase-amplitude interactions from to , there are multiple bidirectional connections between channels on yhr frontal and prefrontal areas and channels on yhr parietal and parieto-occipital areas. There are also several relevant long-range connections targeting the right temporal region. These results coincide with those previously obtained from the within-frequency, phase-based connectivity analysis carried out on the same database [22], as well as with studies that identified the presence of fronto-parietal and fronto-temporal interactions during cognitive tasks that activate visuo-spatial working memory [6,29,49].
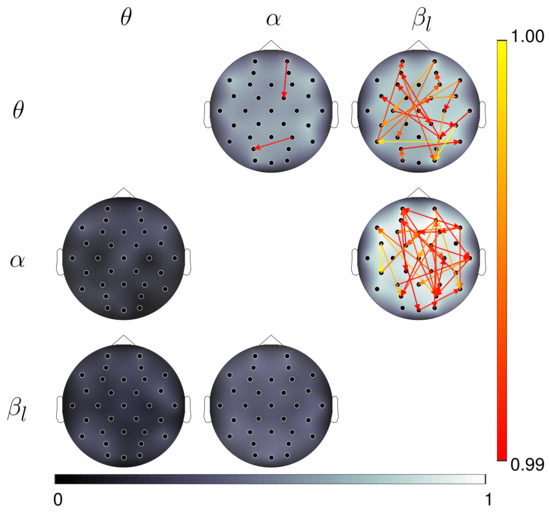
Figure 8.
Topoplots of the average nodal (channel) relevance for each tested frequency band pair. The arrows represent the most relevant connections. For visualization purposes, only the connections with the highest average relevance values are depicted (1% of all connections). The rows indicate the frequency band driving the phase-amplitude interactions, while the columns correspond to the frequency band of the driven oscillations (e.g., the topoplot in the top right corner shows the nodal relevance and relevant connections obtained when TE was computed, assuming directed interactions from the oscillations phases in the band to the amplitude envelope of oscillations in the band).
4.3. Limitations
The results obtained for the simulated data show that our proposal is, unlike the other tested approaches, able to detect statistically significant, directed phase-amplitude interactions in data with high levels of noise. However, it tends to be less frequency-specific than the CFD and the conventional approach for the estimation of directed phase-amplitude interactions through TE. Therefore, our method is well-suited to the analysis of noisy data, but care should be taken with results under more ideal conditions. The proposed approach also relies on the kernel-based, phase TE-estimation method introduced in [22]; therefore, it suffers from the same limitations, especially regarding the selection of the many parameters involved in TE computation. Here, we employed relatively simple parameter selection strategies, as described in Section 3.3, but it is possible that more elaborate strategies [52] may lead to better results. Additionally, the TE estimator used assumes stationary or weakly non-stationary data, and cannot distinguish direct interactions from those originating from unobserved common causes [16]. Finally, our proposal is strictly limited to the detection of directed phase-amplitude interactions. It is unable to capture any of the other types of cross-frequency interactions that arise in oscillatory neural activities (phase-phase coupling, phase-frequency coupling, etc.) [3]. it was also not designed to be full information-theoretic analysis that simultaneously accounts for the multiple rhythms that can interact at both the sender and receiver side of coupled dynamical systems [1].
5. Conclusions
In this work, we proposed a novel approach to estimate directed phase-amplitude interactions through TE. The central idea behind our proposal is to recast the problem of detecting directed PAC as that of estimating directed interactions between phase time series. Doing this allowed us to employ a single-trial, kernel-based phase TE-estimator to assess the cross-frequency interactions of interest. We tested the performance of our proposal on synthetic data containing directed phase-amplitude interactions and on an EEG database obtained under a WM paradigm. The obtained results for the synthetic data show that our approach successfully detects the direction of interaction and the interacting frequencies, while being more robust to noise than alternative methods. Additionally, for the WM data, our proposal revealed discriminant, directed, phase-amplitude interactions associated with the different cognitive loads of the task.
In future work, we will attempt to optimize the strategies for selecting the parameters involved in the filtering and time-embedding stages of the proposed approach and the kernel-based TE estimator.
Author Contributions
Conceptualization, I.D.L.P.P., V.G.-O. and A.Á.-M.; methodology, I.D.L.P.P., V.G.-O. and A.Á.-M.; software, I.D.L.P.P., A.Á.-M. and D.C.-P.; validation, I.D.L.P.P., A.Á.-M. and D.C.-P.; formal analysis, I.D.L.P.P., V.G.-O. and Á.O.-G.; investigation, I.D.L.P.P., V.G.-O. and A.Á.-M.; resources, I.D.L.P.P., A.Á.-M. and Á.O.-G.; data curation, I.D.L.P.P. and V.G.-O.; writing—original draft preparation, I.D.L.P.P., V.G.-O. and A.Á.-M.; writing—review and editing, A.Á.-M. and D.C.-P.; visualization, I.D.L.P.P.; supervision, Á.O.-G. and A.Á.-M.; project administration, Á.O.-G.; funding acquisition, I.D.L.P.P., V.G.-O. and A.Á.-M. All authors have read and agreed to the published version of the manuscript.
Funding
Authors Iván De La Pava Panche and Viviana Gómez-Orozco were supported by the program “Doctorado Nacional en Empresa—Convoctoria 758 de 2016”, funded by Minciencias. A.M. Álvarez-Meza thanks the project Prototipo de interfaz cerebro-computador multimodal para la detección de patrones relevantes relacionados con trastornos de impulsividad-HERMES 50835, funded by Universidad Nacional de Colombia.
Institutional Review Board Statement
In this study, we use a public-access EEG database introduced in a previously published work, and made freely available by its authors [24]. We did not collect any data from human participants ourselves.
Informed Consent Statement
This study uses an anonymized public database introduced in a previously published work by another group [24].
Data Availability Statement
The database used in this study is public and can be found at the following link: database from brain activity during visual working memory https://data.mendeley.com/datasets/j2v7btchdy/2 (accessed on 4 September 2021).
Conflicts of Interest
The authors declare that this research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Pinzuti, E.; Wollstadt, P.; Gutknecht, A.; Tüscher, O.; Wibral, M. Measuring spectrally-resolved information transfer. PLoS Comput. Biol. 2020, 16, e1008526. [Google Scholar] [CrossRef]
- Jirsa, V.; Müller, V. Cross-frequency coupling in real and virtual brain networks. Front. Comput. Neurosci. 2013, 7, 78. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- La Tour, T.D.; Tallot, L.; Grabot, L.; Doyère, V.; Van Wassenhove, V.; Grenier, Y.; Gramfort, A. Non-linear auto-regressive models for cross-frequency coupling in neural time series. PLoS Comput. Biol. 2017, 13, e1005893. [Google Scholar]
- Seymour, R.A.; Rippon, G.; Kessler, K. The detection of phase amplitude coupling during sensory processing. Front. Neurosci. 2017, 11, 487. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Martínez-Cancino, R.; Delorme, A.; Wagner, J.; Kreutz-Delgado, K.; Sotero, R.C.; Makeig, S. What can local transfer entropy tell us about phase-amplitude coupling in electrophysiological signals? Entropy 2020, 22, 1262. [Google Scholar] [CrossRef]
- Johnson, E.L.; Adams, J.N.; Solbakk, A.K.; Endestad, T.; Larsson, P.G.; Ivanovic, J.; Meling, T.R.; Lin, J.J.; Knight, R.T. Dynamic frontotemporal systems process space and time in working memory. PLoS Biol. 2018, 16, e2004274. [Google Scholar] [CrossRef] [Green Version]
- Shi, W.; Yeh, C.H.; Hong, Y. Cross-frequency transfer entropy characterize coupling of interacting nonlinear oscillators in complex systems. IEEE Trans. Biomed. Eng. 2018, 66, 521–529. [Google Scholar] [CrossRef]
- Cheng, N.; Li, Q.; Wang, S.; Wang, R.; Zhang, T. Permutation mutual information: A novel approach for measuring neuronal phase-amplitude coupling. Brain Topogr. 2018, 31, 186–201. [Google Scholar] [CrossRef]
- Martínez-Cancino, R.; Heng, J.; Delorme, A.; Kreutz-Delgado, K.; Sotero, R.C.; Makeig, S. Measuring transient phase-amplitude coupling using local mutual information. NeuroImage 2019, 185, 361–378. [Google Scholar] [CrossRef]
- Malladi, R.; Johnson, D.H.; Kalamangalam, G.P.; Tandon, N.; Aazhang, B. Mutual information in frequency and its application to measure cross-frequency coupling in epilepsy. IEEE Trans. Signal Process. 2018, 66, 3008–3023. [Google Scholar] [CrossRef]
- Jiang, H.; Bahramisharif, A.; van Gerven, M.A.; Jensen, O. Measuring directionality between neuronal oscillations of different frequencies. Neuroimage 2015, 118, 359–367. [Google Scholar] [CrossRef]
- Dimitriadis, S.I.; Sun, Y.; Thakor, N.V.; Bezerianos, A. Causal interactions between frontalθ–parieto-occipitalα2 predict performance on a mental arithmetic task. Front. Hum. Neurosci. 2016, 10, 454. [Google Scholar] [CrossRef]
- Shi, W.; Yeh, C.H.; An, J. Cross-Channel Phase-Amplitude Transfer Entropy Conceptualize Long-Range Transmission in sleep: A case study. In Proceedings of the 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 23–27 July 2019; pp. 4048–4051. [Google Scholar]
- Schreiber, T. Measuring information transfer. Phys. Rev. Lett. 2000, 85, 461. [Google Scholar] [CrossRef] [Green Version]
- Zhu, J.; Bellanger, J.J.; Shu, H.; Le Bouquin Jeannès, R. Contribution to transfer entropy estimation via the k-nearest-neighbors approach. Entropy 2015, 17, 4173–4201. [Google Scholar] [CrossRef] [Green Version]
- De La Pava Panche, I.; Alvarez-Meza, A.M.; Orozco-Gutierrez, A. A data-driven measure of effective connectivity based on Renyi’s α-entropy. Front. Neurosci. 2019, 13, 1277. [Google Scholar] [CrossRef]
- Ursino, M.; Ricci, G.; Magosso, E. Transfer Entropy as a Measure of Brain Connectivity: A Critical Analysis With the Help of Neural Mass Models. Front. Comput. Neurosci. 2020, 14, 45. [Google Scholar] [CrossRef]
- Besserve, M.; Schölkopf, B.; Logothetis, N.K.; Panzeri, S. Causal relationships between frequency bands of extracellular signals in visual cortex revealed by an information theoretic analysis. J. Comput. Neurosci. 2010, 29, 547–566. [Google Scholar] [CrossRef] [Green Version]
- Weber, I.; Florin, E.; Von Papen, M.; Timmermann, L. The influence of filtering and downsampling on the estimation of transfer entropy. PLoS ONE 2017, 12, e0188210. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Zhang, Y.; Cheng, S.; Xie, P. Transfer spectral entropy and application to functional corticomuscular coupling. IEEE Trans. Neural Syst. Rehabil. Eng. 2019, 27, 1092–1102. [Google Scholar] [CrossRef]
- Lobier, M.; Siebenhühner, F.; Palva, S.; Palva, J.M. Phase transfer entropy: A novel phase-based measure for directed connectivity in networks coupled by oscillatory interactions. Neuroimage 2014, 85, 853–872. [Google Scholar] [CrossRef]
- De La Pava Panche, I.; Álvarez-Meza, A.; Herrera Gómez, P.M.; Cárdenas-Peña, D.; Ríos Patiño, J.I.; Orozco-Gutiérrez, Á. Kernel-Based Phase Transfer Entropy with Enhanced Feature Relevance Analysis for Brain Computer Interfaces. Appl. Sci. 2021, 11, 6689. [Google Scholar] [CrossRef]
- Bastos, A.M.; Schoffelen, J.M. A tutorial review of functional connectivity analysis methods and their interpretational pitfalls. Front. Syst. Neurosci. 2016, 9, 175. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Villena-González, M.; Rubio-Venegas, I.; López, V. Data from brain activity during visual working memory replicates the correlation between contralateral delay activity and memory capacity. Data Brief 2020, 28, 105042. [Google Scholar] [CrossRef] [PubMed]
- Vogel, E.K.; Machizawa, M.G. Neural activity predicts individual differences in visual working memory capacity. Nature 2004, 428, 748–751. [Google Scholar] [CrossRef]
- Baddeley, A. Working memory: Theories, models, and controversies. Annu. Rev. Psychol. 2012, 63, 1–29. [Google Scholar] [CrossRef] [Green Version]
- Pavlov, Y.G.; Kotchoubey, B. Oscillatory brain activity and maintenance of verbal and visual working memory: A systematic review. Psychophysiology 2020, e13735. [Google Scholar] [CrossRef]
- Liang, W.K.; Tseng, P.; Yeh, J.R.; Huang, N.E.; Juan, C.H. Frontoparietal beta amplitude modulation and its interareal cross-frequency coupling in visual working memory. Neuroscience 2021, 460, 69–87. [Google Scholar] [CrossRef]
- Johnson, E.L.; King-Stephens, D.; Weber, P.B.; Laxer, K.D.; Lin, J.J.; Knight, R.T. Spectral imprints of working memory for everyday associations in the frontoparietal network. Front. Syst. Neurosci. 2019, 12, 65. [Google Scholar] [CrossRef] [Green Version]
- Wibral, M.; Pampu, N.; Priesemann, V.; Siebenhühner, F.; Seiwert, H.; Lindner, M.; Lizier, J.T.; Vicente, R. Measuring information-transfer delays. PLoS ONE 2013, 8, e55809. [Google Scholar] [CrossRef]
- Vicente, R.; Wibral, M.; Lindner, M.; Pipa, G. Transfer entropy—A model-free measure of effective connectivity for the neurosciences. J. Comput. Neurosci. 2011, 30, 45–67. [Google Scholar] [CrossRef] [Green Version]
- Takens, F. Detecting strange attractors in turbulence. In Dynamical Systems and Turbulence, Warwick 1980; Springer: Berlin/Heidelberg, Germany, 1981; pp. 366–381. [Google Scholar]
- Nolte, G.; Ziehe, A.; Nikulin, V.V.; Schlögl, A.; Krämer, N.; Brismar, T.; Müller, K.R. Robustly estimating the flow direction of information in complex physical systems. Phys. Rev. Lett. 2008, 100, 234101. [Google Scholar] [CrossRef] [Green Version]
- Giraldo, L.G.S.; Rao, M.; Principe, J.C. Measures of entropy from data using infinitely divisible kernels. IEEE Trans. Inf. Theory 2015, 61, 535–548. [Google Scholar] [CrossRef] [Green Version]
- Rényi, A. On measures of entropy and information. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Volume 1: Contributions to the Theory of Statistics; The Regents of the University of California: Oakland, CA, USA, 1961. [Google Scholar]
- Lindner, M.; Vicente, R.; Priesemann, V.; Wibral, M. TRENTOOL: A Matlab open source toolbox to analyse information flow in time series data with transfer entropy. BMC Neurosci. 2011, 12, 119. [Google Scholar] [CrossRef] [Green Version]
- Perrin, F.; Pernier, J.; Bertrand, O.; Echallier, J. Spherical splines for scalp potential and current density mapping. Electroencephalogr. Clin. Neurophysiol. 1989, 72, 184–187. [Google Scholar] [CrossRef]
- Cohen, M.X. Comparison of different spatial transformations applied to EEG data: A case study of error processing. Int. J. Psychophysiol. 2015, 97, 245–257. [Google Scholar] [CrossRef]
- Rathee, D.; Cecotti, H.; Prasad, G. Single-trial effective brain connectivity patterns enhance discriminability of mental imagery tasks. J. Neural Eng. 2017, 14, 056005. [Google Scholar] [CrossRef]
- Cortes, C.; Mohri, M.; Rostamizadeh, A. Algorithms for learning kernels based on centered alignment. J. Mach. Learn. Res. 2012, 13, 795–828. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Cao, L. Practical method for determining the minimum embedding dimension of a scalar time series. Phys. D Nonlinear Phenom. 1997, 110, 43–50. [Google Scholar] [CrossRef]
- Liu, W.; Principe, J.C.; Haykin, S. Kernel Adaptive Filtering: A Comprehensive Introduction; John Wiley & Sons: Hoboken, NJ, USA, 2011; Volume 57. [Google Scholar]
- Schölkopf, B.; Smola, A.J.; Bach, F. Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond; MIT Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Zhang, D.; Zhao, H.; Bai, W.; Tian, X. Functional connectivity among multi-channel EEGs when working memory load reaches the capacity. Brain Res. 2016, 1631, 101–112. [Google Scholar] [CrossRef]
- Toppi, J.; Astolfi, L.; Risetti, M.; Anzolin, A.; Kober, S.E.; Wood, G.; Mattia, D. Different topological properties of EEG-derived networks describe working memory phases as revealed by graph theoretical analysis. Front. Hum. Neurosci. 2018, 11, 637. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Daume, J.; Gruber, T.; Engel, A.K.; Friese, U. Phase-amplitude coupling and long-range phase synchronization reveal frontotemporal interactions during visual working memory. J. Neurosci. 2017, 37, 313–322. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dai, Z.; De Souza, J.; Lim, J.; Ho, P.M.; Chen, Y.; Li, J.; Thakor, N.; Bezerianos, A.; Sun, Y. EEG cortical connectivity analysis of working memory reveals topological reorganization in theta and alpha bands. Front. Hum. Neurosci. 2017, 11, 237. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dimitriadis, S.; Sun, Y.; Laskaris, N.; Thakor, N.; Bezerianos, A. Revealing cross-frequency causal interactions during a mental arithmetic task through symbolic transfer entropy: A novel vector-quantization approach. IEEE Trans. Neural Syst. Rehabil. Eng. 2016, 24, 1017–1028. [Google Scholar] [CrossRef]
- Constantinidis, C.; Klingberg, T. The neuroscience of working memory capacity and training. Nat. Rev. Neurosci. 2016, 17, 438–449. [Google Scholar] [CrossRef]
- Géron, A. Hands-on Machine Learning with Scikit-Learn, Keras, and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems; O’Reilly Media: Sebastopol, CA, USA, 2019. [Google Scholar]
- Zhou, S.; Xie, P.; Chen, X.; Wang, Y.; Zhang, Y.; Du, Y. Optimization of relative parameters in transfer entropy estimation and application to corticomuscular coupling in humans. J. Neurosci. Methods 2018, 308, 276–285. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).