A Many-Objective Simultaneous Feature Selection and Discretization for LCS-Based Gesture Recognition
Abstract
:1. Introduction
- 1.
- We propose a many-objective formulation to simultaneously deal with optimal feature subset selection, discretization, and parameter tuning for an LM-WLCSS classifier. This problem was resolved using the constrained many-objective evolutionary algorithm based on dominance (minimisation of the objectives) and decomposition (C-MOEA/DD) [40].
- 2.
- Unlike many discretization techniques requiring a prefixed number of discretization points, the proposed discretization subproblem exploits a variable-length representation [41].
- 3.
- To agree with the variable-length discretization structure, we adapted the recently proposed rand-length crossover to the random variable-length crossover differential evolution algorithm [42].
- 4.
- We refined the template construction phase of the microcontroller optimized Limited-Memory WarpingLCSS (LM-WLCSS) [21] using an improved algorithm for computing the longest common subsequence [43]. Moreover, we altered the recognition phase by reprocessing the samples contained in the sliding windows in charge of spotting a gesture in the steam.
- 5.
- To tackle multiclass gesture recognition, we propose a system encapsulating multiple LM-WLCSS and a light-weight classifier for resolving conflicts.
2. Preliminaries and Background
2.1. Constrained Many-Objective Optimization
2.2. C-MOEA/DD
2.3. Discretization
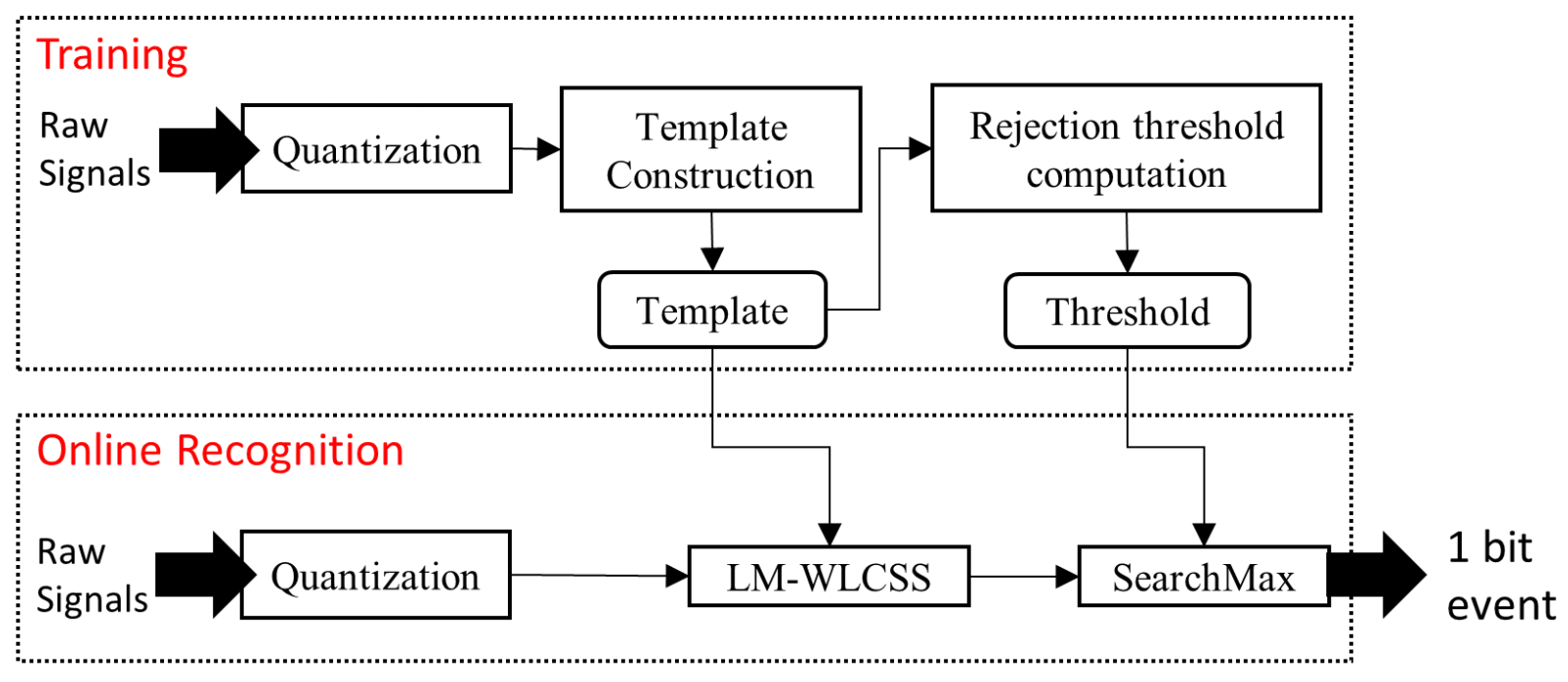
2.4. Limited-Memory Warping LCSS Gesture Recognition Method
2.4.1. Quantization Step (Training Phase)
2.4.2. Template Construction (Training Phase)
2.4.3. Limited-Memory Warping LCSS
2.4.4. Rejection Threshold (Training Phase)
2.4.5. Searchmax (Recognition Phase)
2.4.6. Backtracking (Recognition Phase)
2.5. Fusion Methods Using WarpingLCSS
3. Proposed Method
3.1. Solution Encoding and Population Initialization
- controls the latency of the recognition process, i.e., the required time to announce that a gesture peak is present in the matching score. is a positive integer uniformly chosen in the interval . By fixing the reward to 1, the penalty is a real number uniformly chosen in the range ; otherwise, gestures that are different from the selected template would be hardly recognizable.
- The coefficient of the threshold is strongly correlated to the reward and the discretization scheme . Since it cannot easily be bounded, its value is locally investigated for each solution.
- The backtracking variable length allows us to retrieve the start-time of a gesture. Although a too short length results in a decrease in recognition performance of the classifier, its choice could reduce the runtime and memory usage on a constrained sensor node. Since its length is not a major performance limiter in the learning process and it can easily be rectified by the decider during the deployment of the system, it was fixed to three times the length of the longest gesture occurrence in c in order to reduce the complexity of the search space.
3.2. Operators
3.2.1. Crossover Operation
3.2.2. Mutation Operation
| Algorithm 1: Rand-length crossover for discretization schemes. |
 |
3.3. Objective Functions
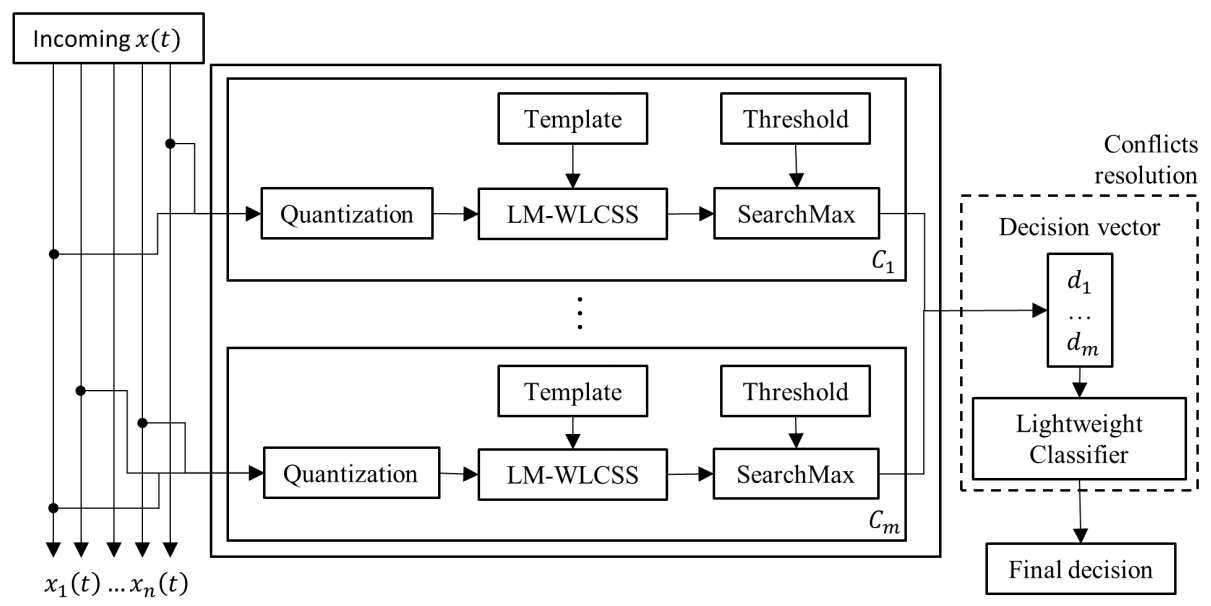
3.4. Multi-Class Gesture Recognition System
| Algorithm 2: Solution evaluation. |
 |
4. Experiments
4.1. Benchmark Dataset
4.2. Experimental Setup
4.3. Evaluation Metrics
- 1.
- Effectiveness: Work based on WarpingLCSS and its derivatives mainly use the weighted F1-score , and its variant , which excludes the null class, as primary evaluation metrics. can be estimated as follows:where and are, respectively, the number of samples contained in class c and the total number of samples. Additionally, we considered Cohen’s kappa. This accuracy measure, standardized to lie on a −1 to 1 scale, compares an observed accuracy with an expected accuracy , where 1 indicates the perfect agreement, and values below or equal to 0 represent poor agreement. It is computed as follows:
- 2.
- Reduction capabilities: Similar to Ramirez-Gallego et al. [60], a reduction in dimensionality is assessed using a reduction rate. For feature selection, it designates the amount of reduction in the feature set size (in percentage). For discretization, it denotes the number of generated discretization points.
5. Results and Discussion
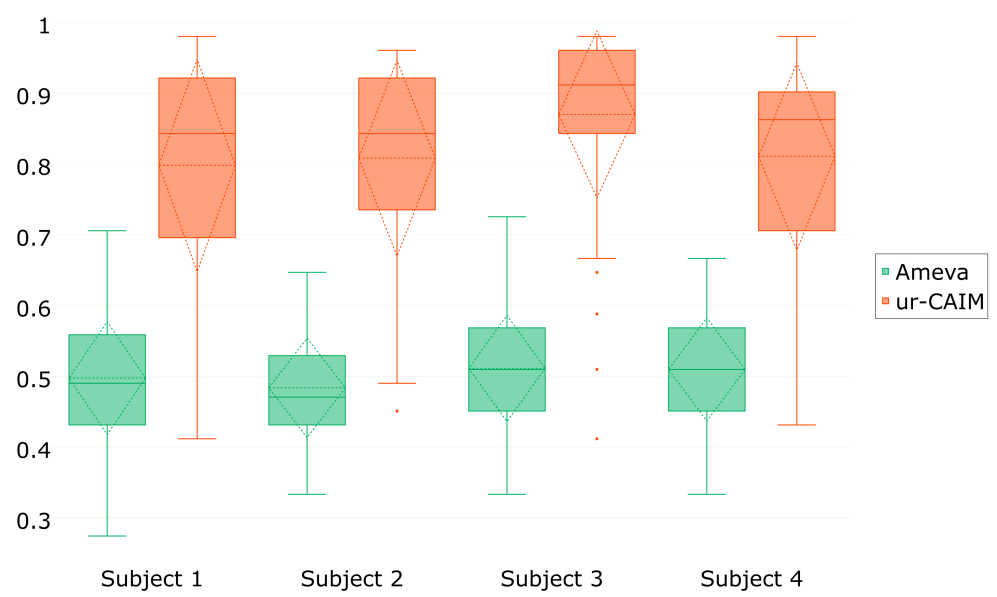
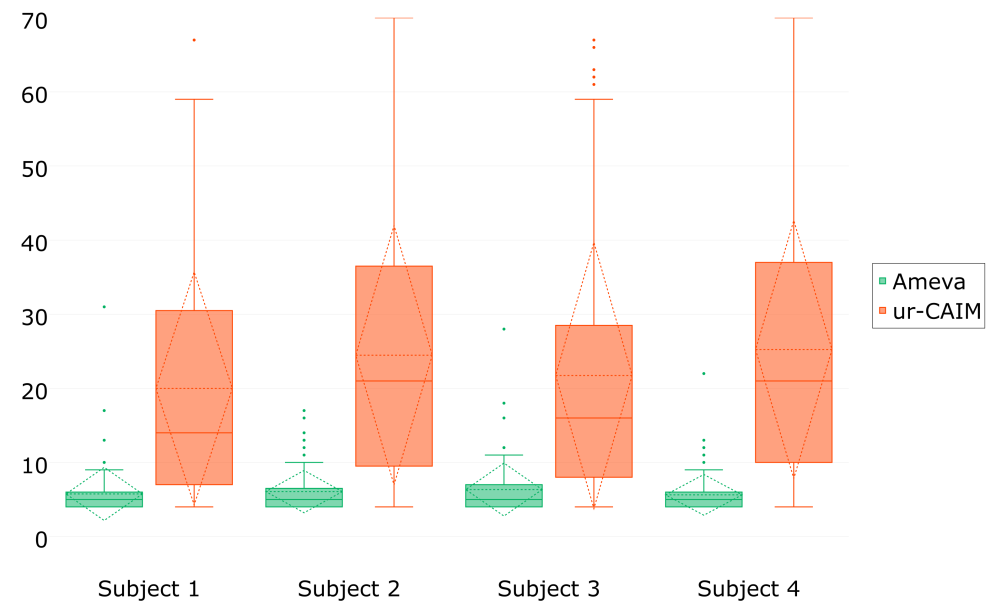
- 1.
- The ur-CAIM criterion consistently leads to a better reduction rate (close to 80% in mean). Therefore, from a design point of view, the effectiveness of sensors—and their ideal placements—to recognize a specific activity are more identified.
- 2.
- The Ameva criterion achieves a more stable standard deviation in the reduction rate across all subjects than the ur-CAIM criterion.
- 3.
- Since MOFSD-GR achieves a better recognition rate than the baseline, its implied reduction capabilities are still acceptable (>40%).
- (1)
- As intended by the nature of Ameva, MOFSD-GR yields a small number of cut points close to the constraint imposing that the template be made of at least three distinct discretization points (18). However, this advantage seems to limit the exploration capacity of C-MOEA/DD since only half of the original features are discarded.
- (2)
- In contrast, MOFSD-GR tends to generate larger discretization schemes than MOFSD-GR. Since the ur-CAIM criterion aggregates two conflicting objectives (CAIM aimed to generate a lower number of cut points, and the pair CAIR and CAIU advocates a larger number), compromises are made.
6. Limitation of the Study
7. Conclusions and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Byrne, R.W.; Cartmill, E.; Genty, E.; Graham, K.E.; Hobaiter, C.; Tanner, J. Great ape gestures: Intentional communication with a rich set of innate signals. Anim. Cogn. 2017, 20, 755–769. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yu, Z.; Chen, H.; Liu, J.; You, J.; Leung, H.; Han, G. Hybrid k -Nearest Neighbor Classifier. IEEE Trans. Cybern. 2016, 46, 1263–1275. [Google Scholar] [CrossRef] [PubMed]
- Amma, C.; Georgi, M.; Schultz, T. Airwriting: A wearable handwriting recognition system. Pers. Ubiquitous Comput. 2014, 18, 191–203. [Google Scholar] [CrossRef]
- Galka, J.; Masior, M.; Zaborski, M.; Barczewska, K. Inertial Motion Sensing Glove for Sign Language Gesture Acquisition and Recognition. IEEE Sens. J. 2016, 16, 6310–6316. [Google Scholar] [CrossRef]
- Lu, Z.; Chen, X.; Li, Q.; Zhang, X.; Zhou, P. A Hand Gesture Recognition Framework and Wearable Gesture-Based Interaction Prototype for Mobile Devices. IEEE Trans. Hum.-Mach. Syst. 2014, 44, 293–299. [Google Scholar] [CrossRef]
- Benatti, S.; Casamassima, F.; Milosevic, B.; Farella, E.; Schönle, P.; Fateh, S.; Burger, T.; Huang, Q.; Benini, L. A Versatile Embedded Platform for EMG Acquisition and Gesture Recognition. IEEE Trans. Biomed. Circuits Syst. 2015, 9, 620–630. [Google Scholar] [CrossRef]
- Geng, Y.; Chen, J.; Fu, R.; Bao, G.; Pahlavan, K. Enlighten Wearable Physiological Monitoring Systems: On-Body RF Characteristics Based Human Motion Classification Using a Support Vector Machine. IEEE Trans. Mob. Comput. 2016, 15, 656–671. [Google Scholar] [CrossRef]
- Fukui, R.; Watanabe, M.; Shimosaka, M.; Sato, T. Hand shape classification in various pronation angles using a wearable wrist contour sensor. Adv. Robot. 2015, 29, 3–11. [Google Scholar] [CrossRef]
- Cifuentes, J.; Boulanger, P.; Pham, M.T.; Prieto, F.; Moreau, R. Gesture Classification Using LSTM Recurrent Neural Networks. In Proceedings of the 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 23–27 July 2019; pp. 6864–6867. [Google Scholar]
- Wang, J.; Chen, Y.; Hao, S.; Peng, X.; Hu, L. Deep learning for sensor-based activity recognition: A survey. Pattern Recognit. Lett. 2019, 119, 3–11. [Google Scholar] [CrossRef] [Green Version]
- Shokoohi-Yekta, M.; Hu, B.; Jin, H.; Wang, J.; Keogh, E. Generalizing DTW to the multi-dimensional case requires an adaptive approach. Data Min. Knowl. Discov. 2017, 31, 1–31. [Google Scholar] [CrossRef] [Green Version]
- Dindo, H.; Presti, L.L.; Cascia, M.L.; Chella, A.; Dedić, R. Hankelet-based action classification for motor intention recognition. Robot. Auton. Syst. 2017, 94, 120–133. [Google Scholar] [CrossRef]
- Rakthanmanon, T.; Campana, B.; Mueen, A.; Batista, G.; Westover, B.; Zhu, Q.; Zakaria, J.; Keogh, E. Addressing Big Data Time Series: Mining Trillions of Time Series Subsequences Under Dynamic Time Warping. ACM Trans. Knowl. Discov. Data 2013, 7, 10:1–10:31. [Google Scholar] [CrossRef] [Green Version]
- Vlachos, M.; Kollios, G.; Gunopulos, D. Discovering similar multidimensional trajectories. In Proceedings of the 18th International Conference on Data Engineering, San Jose, CA, USA, 26 Feburary–1 March 2002; pp. 673–684. [Google Scholar] [CrossRef]
- Frolova, D.; Stern, H.; Berman, S. Most Probable Longest Common Subsequence for Recognition of Gesture Character Input. IEEE Trans. Cybern. 2013, 43, 871–880. [Google Scholar] [CrossRef]
- Stern, H.; Shmueli, M.; Berman, S. Most discriminating segment—Longest common subsequence (MDSLCS) algorithm for dynamic hand gesture classification. Pattern Recognit. Lett. 2013, 34, 1980–1989. [Google Scholar] [CrossRef]
- Nyirarugira, C.; Kim, T. Stratified gesture recognition using the normalized longest common subsequence with rough sets. Signal Process. Image Commun. 2015, 30, 178–189. [Google Scholar] [CrossRef]
- Nguyen-Dinh, L.V.; Calatroni, A.; Tröster, G. Robust Online Gesture Recognition with Crowdsourced Annotations. J. Mach. Learn. Res. 2014, 15, 3187–3220. [Google Scholar]
- Nguyen-Dinh, L.V.; Calatroni, A.; Troster, G. Towards a Unified System for Multimodal Activity Spotting: Challenges and a Proposal. In Proceedings of the 2014 ACM International Joint Conference on Pervasive and Ubiquitous Computing: Adjunct Publication, Seattle, WA, USA, 13–17 September 2014; ACM: New York, NY, USA, 2014; pp. 807–816. [Google Scholar] [CrossRef]
- Hardegger, M.; Roggen, D.; Calatroni, A.; Troster, G. S-SMART: A Unified Bayesian Framework for Simultaneous Semantic Mapping, Activity Recognition, and Tracking. ACM Trans. Intell. Syst. Technol. 2016, 7, 34:1–34:28. [Google Scholar] [CrossRef]
- Roggen, D.; Cuspinera, L.P.; Pombo, G.; Ali, F.; Nguyen-Dinh, L.V. Limited-Memory Warping LCSS for Real-Time Low-Power Pattern Recognition in Wireless Nodes. In Wireless Sensor Networks: 12th European Conference, EWSN, Proceedings; Springer International Publishing: Porto, Portugal, 2015; pp. 151–167. [Google Scholar] [CrossRef] [Green Version]
- Chan, M.; Estève, D.; Fourniols, J.Y.; Escriba, C.; Campo, E. Smart wearable systems: Current status and future challenges. Artif. Intell. Med. 2012, 56, 137–156. [Google Scholar] [CrossRef]
- Unler, A.; Murat, A. A discrete particle swarm optimization method for feature selection in binary classification problems. Eur. J. Oper. Res. 2010, 206, 528–539. [Google Scholar] [CrossRef]
- Xue, B.; Zhang, M.; Browne, W.N.; Yao, X. A Survey on Evolutionary Computation Approaches to Feature Selection. IEEE Trans. Evol. Comput. 2016, 20, 606–626. [Google Scholar] [CrossRef] [Green Version]
- Tahan, M.H.; Asadi, S. MEMOD: A novel multivariate evolutionary multi-objective discretization. Soft Comput. 2017, 22, 1–23. [Google Scholar] [CrossRef]
- Garcia, S.; Luengo, J.; Saez, J.A.; Lopez, V.; Herrera, F. A Survey of Discretization Techniques: Taxonomy and Empirical Analysis in Supervised Learning. IEEE Trans. Knowl. Data Eng. 2013, 25, 734–750. [Google Scholar] [CrossRef]
- Ramírez-Gallego, S.; García, S.; Benítez, J.M.; Herrera, F. Multivariate Discretization Based on Evolutionary Cut Points Selection for Classification. IEEE Trans. Cybern. 2016, 46, 595–608. [Google Scholar] [CrossRef]
- Wang, X.H.; Zhang, Y.; Sun, X.Y.; Wang, Y.L.; Du, C.H. Multi-objective feature selection based on artificial bee colony: An acceleration approach with variable sample size. Appl. Soft Comput. J. 2020, 88, 106041. [Google Scholar] [CrossRef]
- Yang, W.; Chen, L.; Wang, Y.; Zhang, M. Multi-Many-Objective Particle Swarm Optimization Algorithm Based on Competition Mechanism. Comput. Intell. Neurosci. 2020, 2020, 5132803. [Google Scholar] [CrossRef]
- Cano, A.; Nguyen, D.T.; Ventura, S.; Cios, K.J. ur-CAIM: Improved CAIM discretization for unbalanced and balanced data. Soft Comput. 2016, 20, 173–188. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Kang, J.; Kwong, S.; Wang, X.; Zhang, Q. An evolutionary multi-objective optimization framework of discretization-based feature selection for classification. Swarm Evol. Comput. 2021, 60, 100770. [Google Scholar] [CrossRef]
- Cheng, R.; Jin, Y. A competitive swarm optimizer for large scale optimization. IEEE Trans. Cybern. 2015, 45, 191–204. [Google Scholar] [CrossRef]
- Yu, X.; Zhang, X. Multiswarm comprehensive learning particle swarm optimization for solving multiobjective optimization problems. PLoS ONE 2017, 12, e0172033. [Google Scholar] [CrossRef]
- Zhou, Y.; Kang, J.; Guo, H. Many-objective optimization of feature selection based on two-level particle cooperation. Inf. Sci. 2020, 532, 91–109. [Google Scholar] [CrossRef]
- Sharmin, S.; Shoyaib, M.; Ali, A.A.; Khan, M.A.H.; Chae, O. Simultaneous feature selection and discretization based on mutual information. Pattern Recognit. 2019, 91, 162–174. [Google Scholar] [CrossRef]
- Roy, P.; Sharmin, S.; Ali, A.; Shoyaib, M. Discretization and Feature Selection Based on Bias Corrected Mutual Information Considering High-Order Dependencies; Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Singapore, 2020; Volume 12084, pp. 830–842. [Google Scholar] [CrossRef]
- Lu, H.Y.; Zhang, M.; Liu, Y.Q.; Ma, S.P. Convolution Neural Network Feature Importance Analysis and Feature Selection Enhanced Model. Ruan Jian Xue Bao/J. Softw. 2017, 28, 2879–2890. [Google Scholar] [CrossRef]
- Gong, M.; Liu, J.; Li, H.; Cai, Q.; Su, L. A multiobjective sparse feature learning model for deep neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 3263–3277. [Google Scholar] [CrossRef] [PubMed]
- Tsai, C.F.; Chen, Y.C. The optimal combination of feature selection and data discretization: An empirical study. Inf. Sci. 2019, 505, 282–293. [Google Scholar] [CrossRef]
- Li, K.; Deb, K.; Zhang, Q.; Kwong, S. An Evolutionary Many-Objective Optimization Algorithm Based on Dominance and Decomposition. IEEE Trans. Evol. Comput. 2015, 19, 694–716. [Google Scholar] [CrossRef]
- Ryerkerk, M.L.; Averill, R.C.; Deb, K.; Goodman, E.D. Solving metameric variable-length optimization problems using genetic algorithms. Genet. Program. Evolvable Mach. 2017, 18, 247–277. [Google Scholar] [CrossRef]
- Al-Dabbagh, M.D.; Al-Dabbagh, R.D.; Abdullah, R.R.; Hashim, F. A new modified differential evolution algorithm scheme-based linear frequency modulation radar signal de-noising. Eng. Optim. 2015, 47, 771–787. [Google Scholar] [CrossRef]
- Zhu, D.; Wang, L.; Wu, Y.; Wang, X. A Practical O(R∖log∖log n+n) time Algorithm for Computing the Longest Common Subsequence. CoRR 2015, 44, abs/1508.05553. [Google Scholar]
- Zhang, Q.; Li, H. MOEA/D: A Multiobjective Evolutionary Algorithm Based on Decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I: Solving Problems With Box Constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- García, S.; López, V.; Luengo, J.; Carmona, C.J.; Herrera, F. A Preliminary Study on Selecting the Optimal Cut Points in Discretization by Evolutionary Algorithms. ICPRAM 2012, 2012, 211–216. [Google Scholar]
- Eshelman, L.J. The CHC Adaptive Search Algorithm: How to Have Safe Search When Engaging in Nontraditional Genetic Recombination. In Foundations of Genetic Algorithms; Rawlins, G.J., Ed.; Elsevier: Amsterdam, The Netherlands, 1991; Volume 1, pp. 265–283. [Google Scholar] [CrossRef]
- Tsai, C.J.; Lee, C.I.; Yang, W.P. A discretization algorithm based on Class-Attribute Contingency Coefficient. Inf. Sci. 2008, 178, 714–731. [Google Scholar] [CrossRef]
- Gonzalez-Abril, L.; Cuberos, F.; Velasco, F.; Ortega, J. Ameva: An autonomous discretization algorithm. Expert Syst. Appl. 2009, 36, 5327–5332. [Google Scholar] [CrossRef]
- Soria Morillo, L.M.; Alvarez-Garcia, J.A.; Gonzalez-Abril, L.; Ortega Ramirez, J.A. Discrete classification technique applied to TV advertisements liking recognition system based on low-cost EEG headsets. Biomed. Eng. Online 2016, 15, 75. [Google Scholar] [CrossRef] [Green Version]
- Ángel Álvarez de la Concepción, M.; Morillo, L.M.S.; Álvarez García, J.A.; González-Abril, L. Mobile activity recognition and fall detection system for elderly people using Ameva algorithm. Pervasive Mob. Comput. 2017, 34, 3–13. [Google Scholar] [CrossRef] [Green Version]
- Wagner, R.A.; Fischer, M.J. The String-to-String Correction Problem. J. ACM 1974, 21, 168–173. [Google Scholar] [CrossRef]
- Iliopoulos, C.S.; Rahman, M.S. New efficient algorithms for the LCS and constrained LCS problems. Inf. Process. Lett. 2008, 106, 13–18. [Google Scholar] [CrossRef]
- Ladkany, G.S.; Trabia, M.B. A genetic algorithm with weighted average normally-distributed arithmetic crossover and twinkling. Appl. Math. 2012, 3, 1220–1235. [Google Scholar] [CrossRef] [Green Version]
- Ben-David, A. A lot of randomness is hiding in accuracy. Eng. Appl. Artif. Intell. 2007, 20, 875–885. [Google Scholar] [CrossRef]
- Roggen, D.; Calatroni, A.; Rossi, M.; Holleczek, T.; Förster, K.; Troster, G.; Lukowicz, P.; Bannach, D.; Pirkl, G.; Ferscha, A.; et al. Collecting complex activity datasets in highly rich networked sensor environments. In Proceedings of the 2010 Seventh International Conference on Networked Sensing Systems (INSS), Kassel, Germany, 15–18 June 2010; pp. 233–240. [Google Scholar] [CrossRef] [Green Version]
- Ordonez, F.J.; Roggen, D. Deep Convolutional and LSTM Recurrent Neural Networks for Multimodal Wearable Activity Recognition. Sensors 2016, 16, 115. [Google Scholar] [CrossRef] [Green Version]
- Chavarriaga, R.; Sagha, H.; Calatroni, A.; Digumarti, S.T.; Tröster, G.; del R. Millán, J.; Roggen, D. The Opportunity challenge: A benchmark database for on-body sensor-based activity recognition. Pattern Recognit. Lett. 2013, 34, 2033–2042. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.L.; Wu, X.; Li, T.; Cheng, J.; Ou, Y.; Xu, M. Dimensionality reduction of data sequences for human activity recognition. Neurocomputing 2016, 210, 294–302. [Google Scholar] [CrossRef]
- Ramirez-Gallego, S.; Krawczyk, B.; Garcia, S.; Wozniak, M.; Herrera, F. A survey on data preprocessing for data stream mining: Current status and future directions. Neurocomputing 2017, 239, 39–57. [Google Scholar] [CrossRef]
- Inoue, S.; Lago, P.; Takeda, S.; Shamma, A.; Faiz, F.; Mairittha, N.; Mairittha, T. Nurse Care Activity Recognition Challenge. IEEE Dataport 2019. [Google Scholar] [CrossRef]
- Lin, H.Y. Feature clustering and feature discretization assisting gene selection for molecular classification using fuzzy c-means and expectation–maximization algorithm. J. Supercomput. 2021, 77, 5381–5397. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, W.; Kang, J.; Zhang, X.; Wang, X. A problem-specific non-dominated sorting genetic algorithm for supervised feature selection. Inf. Sci. 2021, 547, 841–859. [Google Scholar] [CrossRef]
- Hu, Y.; Zhang, Y.; Gong, D. Multiobjective Particle Swarm Optimization for Feature Selection with Fuzzy Cost. IEEE Trans. Cybern. 2021, 51, 874–888. [Google Scholar] [CrossRef]
| Subject 1 | Subject 2 | Subject 3 | Subject 4 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Gesture Length | Gesture Length | Gesture Length | Gesture Length | |||||||||
| Gesture Names | #inst | avg | SD | #inst | avg | SD | #inst | avg | SD | #inst | avg | SD |
| CleanTable | 20 | 120.00 | 47.01 | 20 | 163.10 | 42.43 | 18 | 132.6 | 15.90 | 21 | 74.14 | 29.30 |
| CloseDishwasher | 20 | 86.85 | 11.03 | 19 | 89.05 | 11.44 | 18 | 85.67 | 7.86 | 21 | 59.57 | 15.15 |
| CloseDoor1 | 21 | 102.95 | 9.55 | 20 | 110.35 | 9.31 | 18 | 126 | 8.64 | 21 | 85.14 | 10.43 |
| CloseDoor2 | 20 | 101.70 | 20.54 | 20 | 121.05 | 10.47 | 18 | 135.8 | 7.43 | 21 | 83.00 | 9.17 |
| CloseDrawer1 | 20 | 61.80 | 4.43 | 20 | 42.05 | 6.84 | 18 | 68.83 | 5.71 | 21 | 38.67 | 10.60 |
| CloseDrawer2 | 20 | 63.35 | 5.05 | 20 | 43.60 | 7.60 | 18 | 75.44 | 7.40 | 21 | 43.86 | 9.38 |
| CloseDrawer3 | 20 | 76.50 | 8.04 | 20 | 73.40 | 9.33 | 18 | 78.28 | 5.72 | 21 | 55.10 | 10.04 |
| CloseFridge | 20 | 76.25 | 5.84 | 20 | 73.20 | 7.57 | 19 | 84.79 | 13.37 | 21 | 56.00 | 12.94 |
| DrinkfromCup | 40 | 189.05 | 19.57 | 40 | 209.20 | 29.33 | 36 | 186.4 | 18.22 | 40 | 159.00 | 44.08 |
| OpenDishwasher | 20 | 89.75 | 5.70 | 21 | 97.19 | 14.03 | 18 | 90.33 | 7.34 | 21 | 65.81 | 12.05 |
| OpenDoor1 | 20 | 91.75 | 11.09 | 20 | 101.55 | 14.72 | 18 | 130.6 | 10.86 | 21 | 79.81 | 10.94 |
| OpenDoor2 | 20 | 103.10 | 5.66 | 20 | 101.10 | 18.01 | 18 | 145.2 | 14.64 | 21 | 77.24 | 11.53 |
| OpenDrawer1 | 20 | 64.80 | 7.57 | 20 | 72.25 | 9.29 | 18 | 74.28 | 8.56 | 21 | 53.76 | 11.98 |
| OpenDrawer2 | 20 | 68.75 | 5.46 | 20 | 56.30 | 8.32 | 18 | 76.56 | 5.80 | 21 | 47.57 | 12.34 |
| OpenDrawer3 | 20 | 82.60 | 4.79 | 20 | 61.90 | 8.37 | 18 | 85.39 | 6.69 | 21 | 55.67 | 10.94 |
| OpenFridge | 20 | 75.50 | 6.43 | 20 | 82.50 | 11.28 | 19 | 100.2 | 11.19 | 21 | 57.71 | 6.69 |
| ToggleSwitch | 38 | 39.84 | 10.58 | 28 | 62.04 | 25.75 | 36 | 55.36 | 11.87 | 39 | 31.03 | 26.31 |
| [19] | MOFSD-GR | |||||||
|---|---|---|---|---|---|---|---|---|
| Ameva | ur-CAIM | |||||||
| Kappa | Kappa | |||||||
| Subject 1 | 0.82 | 0.83 | 0.84 | 0.83 | 0.81 | 0.90 | 0.91 | 0.88 |
| Subject 2 | 0.71 | 0.73 | 0.82 | 0.81 | 0.79 | 0.89 | 0.90 | 0.87 |
| Subject 3 | 0.87 | 0.85 | 0.89 | 0.87 | 0.85 | 0.93 | 0.93 | 0.91 |
| Subject 4 | 0.75 | 0.74 | 0.85 | 0.83 | 0.81 | 0.87 | 0.87 | 0.84 |
| Subject 1 | Subject 2 | Subject 3 | Subject 4 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Gesture Names | ||||||||||||||||
| CleanTable | 25.20 | 3.90 | 5.40 | 0.55 | 26.40 | 3.05 | 4.80 | 1.30 | 23.60 | 1.95 | 6.00 | 1.58 | 24.80 | 3.27 | 6.20 | 1.64 |
| CloseDishwasher | 27.00 | 6.67 | 5.20 | 1.79 | 24.60 | 5.08 | 4.60 | 0.89 | 21.60 | 5.13 | 5.20 | 1.64 | 22.20 | 3.56 | 5.80 | 1.30 |
| CloseDoor1 | 22.60 | 7.50 | 5.60 | 2.07 | 27.00 | 1.22 | 4.80 | 1.30 | 24.20 | 4.49 | 6.00 | 2.92 | 22.00 | 2.92 | 5.60 | 2.51 |
| CloseDoor2 | 24.60 | 2.41 | 4.00 | 0.00 | 28.20 | 2.59 | 4.60 | 0.89 | 22.20 | 1.92 | 6.20 | 1.92 | 25.80 | 4.60 | 4.20 | 0.45 |
| CloseDrawer1 | 28.80 | 2.28 | 6.40 | 2.30 | 27.40 | 4.83 | 9.40 | 3.21 | 24.00 | 4.18 | 6.40 | 1.52 | 21.80 | 4.55 | 8.60 | 2.79 |
| CloseDrawer2 | 25.00 | 2.65 | 7.60 | 3.21 | 28.80 | 3.03 | 6.20 | 1.48 | 23.60 | 2.61 | 6.00 | 2.35 | 21.60 | 3.71 | 7.00 | 3.74 |
| CloseDrawer3 | 27.20 | 3.27 | 4.40 | 0.55 | 25.20 | 4.15 | 5.00 | 1.00 | 26.00 | 4.12 | 4.40 | 0.55 | 25.40 | 3.44 | 4.20 | 0.45 |
| CloseFridge | 26.00 | 2.55 | 4.60 | 0.89 | 26.60 | 3.21 | 5.20 | 1.10 | 26.40 | 3.21 | 6.20 | 2.17 | 27.40 | 2.51 | 4.40 | 0.55 |
| DrinkfromCup | 24.40 | 3.44 | 4.00 | 0.00 | 24.80 | 3.96 | 4.40 | 0.89 | 25.00 | 4.00 | 5.00 | 1.00 | 26.20 | 5.02 | 4.60 | 1.34 |
| OpenDishwasher | 24.60 | 3.36 | 4.60 | 0.89 | 24.20 | 4.21 | 4.20 | 0.45 | 27.00 | 3.39 | 5.00 | 0.00 | 26.00 | 2.12 | 4.80 | 0.84 |
| OpenDoor1 | 27.80 | 5.26 | 7.20 | 5.54 | 28.80 | 2.77 | 7.60 | 5.27 | 23.20 | 3.56 | 5.60 | 1.82 | 25.20 | 1.10 | 4.60 | 0.89 |
| OpenDoor2 | 29.20 | 2.39 | 4.40 | 0.89 | 25.60 | 3.29 | 4.60 | 0.89 | 23.20 | 3.56 | 4.80 | 1.10 | 23.80 | 1.64 | 4.40 | 0.55 |
| OpenDrawer1 | 25.00 | 4.30 | 6.20 | 2.68 | 26.00 | 2.55 | 9.80 | 2.17 | 24.60 | 2.70 | 6.00 | 2.35 | 27.00 | 4.85 | 8.40 | 7.67 |
| OpenDrawer2 | 24.00 | 3.08 | 6.80 | 1.30 | 24.00 | 3.39 | 5.80 | 1.92 | 25.40 | 2.19 | 9.00 | 5.15 | 26.20 | 4.82 | 5.00 | 1.00 |
| OpenDrawer3 | 25.40 | 4.67 | 4.20 | 0.45 | 26.40 | 4.22 | 6.20 | 2.68 | 25.80 | 1.92 | 5.20 | 1.79 | 27.80 | 3.56 | 5.40 | 2.07 |
| OpenFridge | 25.20 | 4.09 | 5.40 | 0.89 | 27.20 | 4.87 | 8.80 | 5.72 | 27.00 | 4.69 | 8.80 | 5.07 | 27.00 | 1.41 | 5.20 | 2.17 |
| ToggleSwitch | 23.20 | 1.92 | 11.40 | 11.08 | 26.40 | 2.70 | 5.80 | 1.79 | 25.60 | 5.50 | 11.00 | 9.67 | 24.60 | 2.07 | 7.80 | 2.49 |
| Mean | 25.60 | 3.75 | 5.73 | 2.06 | 26.33 | 3.48 | 5.99 | 1.94 | 24.61 | 3.48 | 6.28 | 2.50 | 24.99 | 3.24 | 5.66 | 1.91 |
| Subject 1 | Subject 2 | Subject 3 | Subject 4 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Gesture Names | ||||||||||||||||
| CleanTable | 13.20 | 8.64 | 33.00 | 22.99 | 9.00 | 7.11 | 14.80 | 9.04 | 7.60 | 7.70 | 11.60 | 5.68 | 11.20 | 9.83 | 15.60 | 21.03 |
| CloseDishwasher | 6.80 | 4.76 | 17.20 | 15.67 | 13.60 | 7.64 | 10.40 | 5.22 | 2.20 | 1.30 | 7.00 | 5.10 | 6.20 | 5.67 | 22.00 | 12.75 |
| CloseDoor1 | 4.60 | 2.19 | 12.00 | 10.17 | 5.40 | 2.41 | 19.00 | 10.84 | 10.80 | 10.03 | 16.00 | 11.90 | 6.80 | 5.54 | 17.40 | 13.56 |
| CloseDoor2 | 6.60 | 4.62 | 10.20 | 9.12 | 6.20 | 5.07 | 15.40 | 7.44 | 7.40 | 6.19 | 20.00 | 24.03 | 3.40 | 2.30 | 10.80 | 6.06 |
| CloseDrawer1 | 22.40 | 5.98 | 30.60 | 16.47 | 16.80 | 9.26 | 36.60 | 25.17 | 14.00 | 4.85 | 41.40 | 19.05 | 14.20 | 7.40 | 46.80 | 15.51 |
| CloseDrawer2 | 16.60 | 3.21 | 36.80 | 25.97 | 15.40 | 4.34 | 37.80 | 13.81 | 4.60 | 1.52 | 31.60 | 18.73 | 14.40 | 5.77 | 27.20 | 7.50 |
| CloseDrawer3 | 5.40 | 4.51 | 7.40 | 4.77 | 4.20 | 1.48 | 23.40 | 23.20 | 5.80 | 4.97 | 14.00 | 11.64 | 10.60 | 10.33 | 22.40 | 18.19 |
| CloseFridge | 7.60 | 6.50 | 11.80 | 6.50 | 8.40 | 5.68 | 26.20 | 12.01 | 4.40 | 2.79 | 18.20 | 12.19 | 10.20 | 6.06 | 28.00 | 10.79 |
| DrinkfromCup | 6.80 | 4.44 | 12.40 | 5.86 | 8.80 | 10.13 | 10.40 | 10.26 | 3.60 | 1.52 | 13.20 | 5.54 | 14.00 | 8.15 | 13.80 | 19.16 |
| OpenDishwasher | 5.60 | 6.07 | 10.40 | 7.40 | 9.40 | 7.02 | 14.00 | 10.42 | 4.00 | 2.00 | 9.00 | 5.48 | 3.80 | 2.95 | 19.20 | 22.88 |
| OpenDoor1 | 3.60 | 1.52 | 8.60 | 2.41 | 7.20 | 5.12 | 23.80 | 18.03 | 5.00 | 3.94 | 9.40 | 4.93 | 7.60 | 4.88 | 7.40 | 2.07 |
| OpenDoor2 | 13.60 | 7.37 | 9.00 | 8.00 | 6.20 | 3.27 | 9.40 | 3.51 | 3.80 | 1.48 | 15.80 | 7.26 | 8.00 | 3.67 | 10.60 | 3.21 |
| OpenDrawer1 | 11.60 | 4.93 | 25.80 | 5.26 | 9.40 | 7.47 | 36.20 | 14.11 | 16.60 | 10.90 | 43.80 | 23.64 | 11.20 | 5.12 | 30.60 | 17.16 |
| OpenDrawer2 | 16.20 | 10.69 | 37.40 | 15.50 | 14.60 | 8.02 | 40.40 | 13.58 | 6.40 | 2.19 | 28.00 | 20.38 | 9.80 | 4.82 | 38.80 | 10.83 |
| OpenDrawer3 | 10.40 | 7.83 | 23.20 | 22.42 | 8.00 | 5.00 | 22.20 | 18.31 | 3.20 | 2.17 | 8.60 | 5.86 | 6.20 | 5.07 | 34.40 | 19.24 |
| OpenFridge | 13.20 | 9.39 | 35.20 | 8.20 | 5.00 | 2.45 | 37.20 | 25.02 | 2.20 | 0.45 | 36.20 | 16.13 | 8.40 | 7.30 | 38.60 | 21.61 |
| ToggleSwitch | 13.80 | 9.26 | 31.80 | 11.14 | 17.80 | 7.66 | 29.20 | 18.21 | 12.00 | 3.39 | 35.60 | 19.82 | 17.40 | 6.66 | 30.60 | 16.02 |
| Mean | 10.47 | 5.99 | 20.75 | 11.64 | 9.73 | 5.83 | 23.91 | 14.01 | 6.68 | 3.96 | 21.14 | 12.79 | 9.61 | 5.97 | 24.36 | 13.97 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Otis, M.J.-D.; Vandewynckel, J. A Many-Objective Simultaneous Feature Selection and Discretization for LCS-Based Gesture Recognition. Appl. Sci. 2021, 11, 9787. https://doi.org/10.3390/app11219787
Otis MJ-D, Vandewynckel J. A Many-Objective Simultaneous Feature Selection and Discretization for LCS-Based Gesture Recognition. Applied Sciences. 2021; 11(21):9787. https://doi.org/10.3390/app11219787
Chicago/Turabian StyleOtis, Martin J.-D., and Julien Vandewynckel. 2021. "A Many-Objective Simultaneous Feature Selection and Discretization for LCS-Based Gesture Recognition" Applied Sciences 11, no. 21: 9787. https://doi.org/10.3390/app11219787
APA StyleOtis, M. J.-D., & Vandewynckel, J. (2021). A Many-Objective Simultaneous Feature Selection and Discretization for LCS-Based Gesture Recognition. Applied Sciences, 11(21), 9787. https://doi.org/10.3390/app11219787







