A Statistical Approach for Modeling Individual Vertical Walking Forces
Abstract
:1. Introduction
2. Experimental Setup and Measurements
3. Walking Force Models
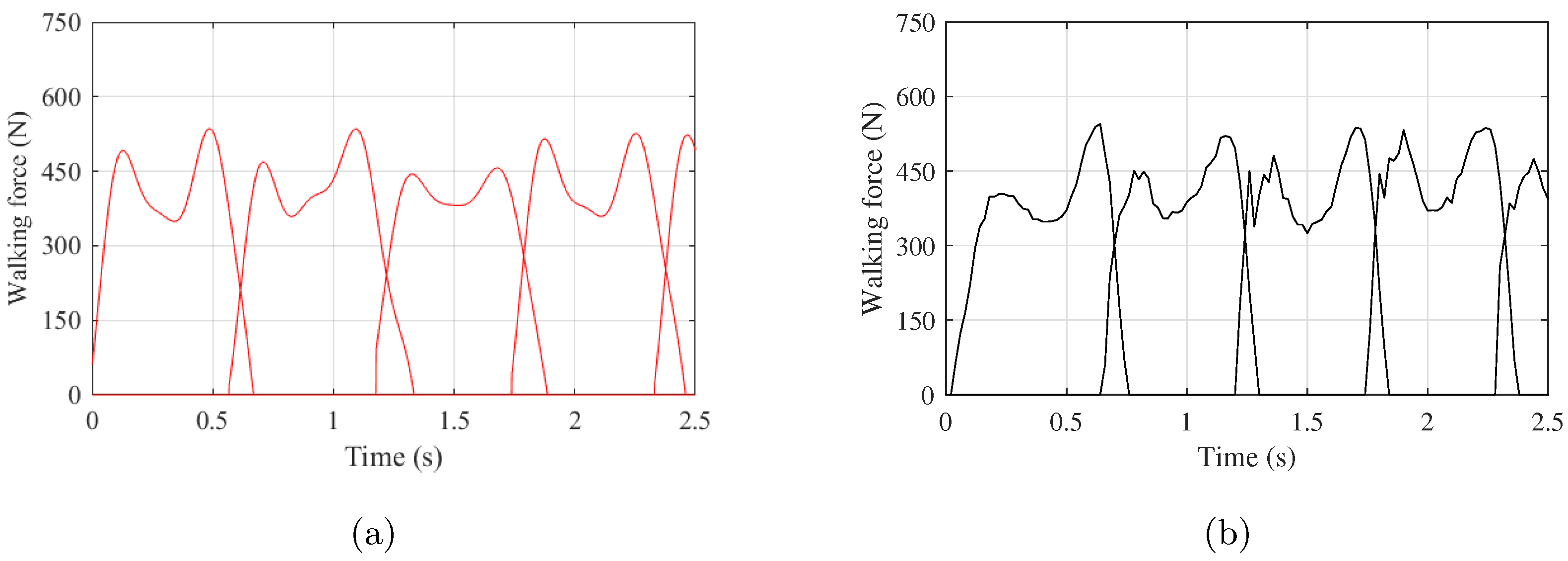
3.1. Proposed Force Model
3.2. Simplified Force Model
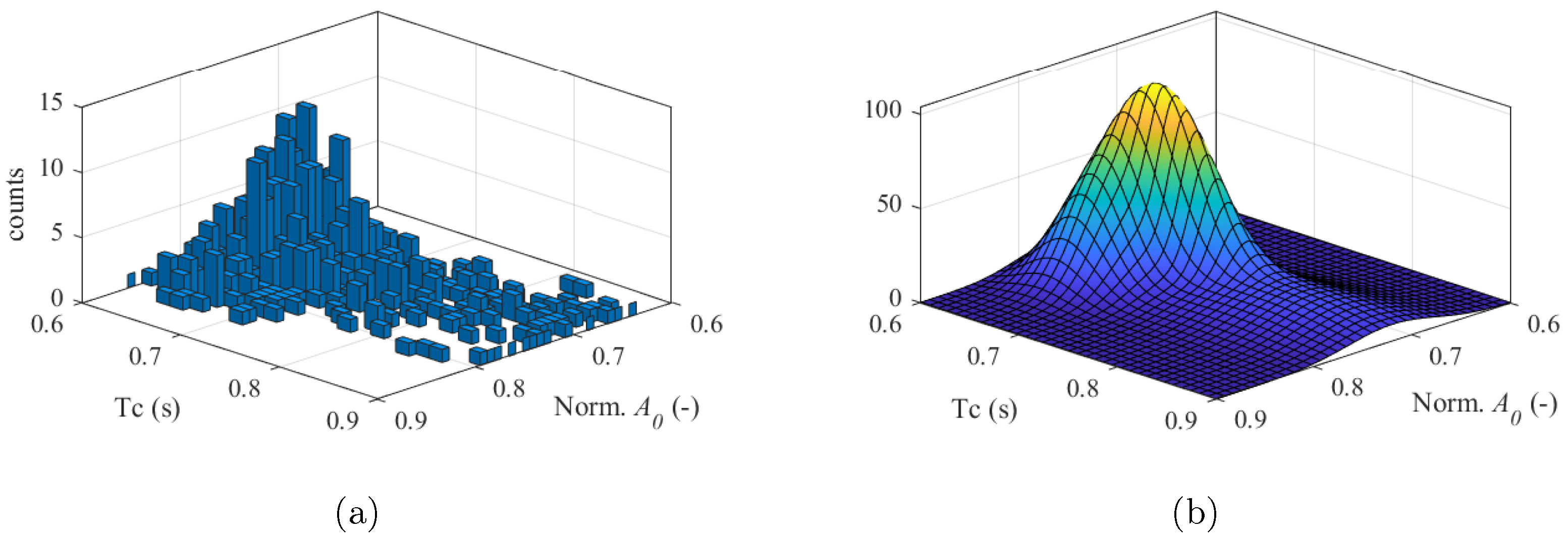
4. Statistical Characterization of the Walking Parameters
- For each TS, collect all the measured steps .
- For each step, evaluate the temporal and spatial parameters that characterize the force models of Section 3:
- –
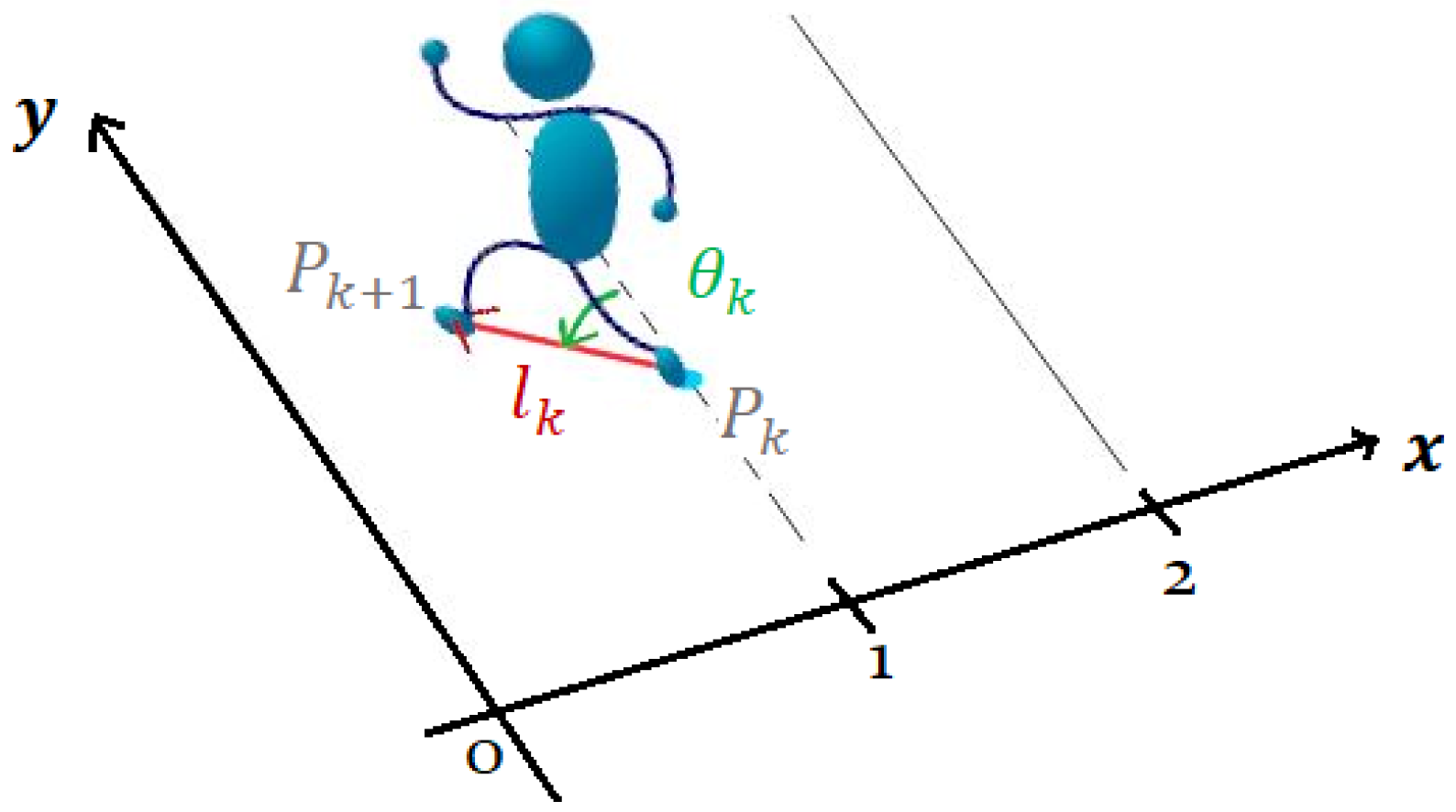
- For the proposed force model, the model parameters are: , , , , , , l, , and . In particular, the temporal feature is easily evaluated measuring the period during which the analyzed step overlaps the following one. The step frequency (equal to the frequency of the first harmonic), the amplitudes , , , and the phases , are evaluated based on a Fourier analysis of the measured step. Finally, the distance l and the direction from the step to the next one are evaluated considering the mid-position of the foot. These parameters are collected in three matrices, one for each TS, of dimensions .
- –
- For the simplified load model, the model parameters are: , , , l and . Besides the parameters previously described, the temporal parameter is evaluated measuring the total duration of the foot force while the amplitude of the constant footfall force is calculated so that the integrals of the experimental and simulated step forces over the step duration are the same. These parameters are collected in three matrices, one for each TS, of dimensions .
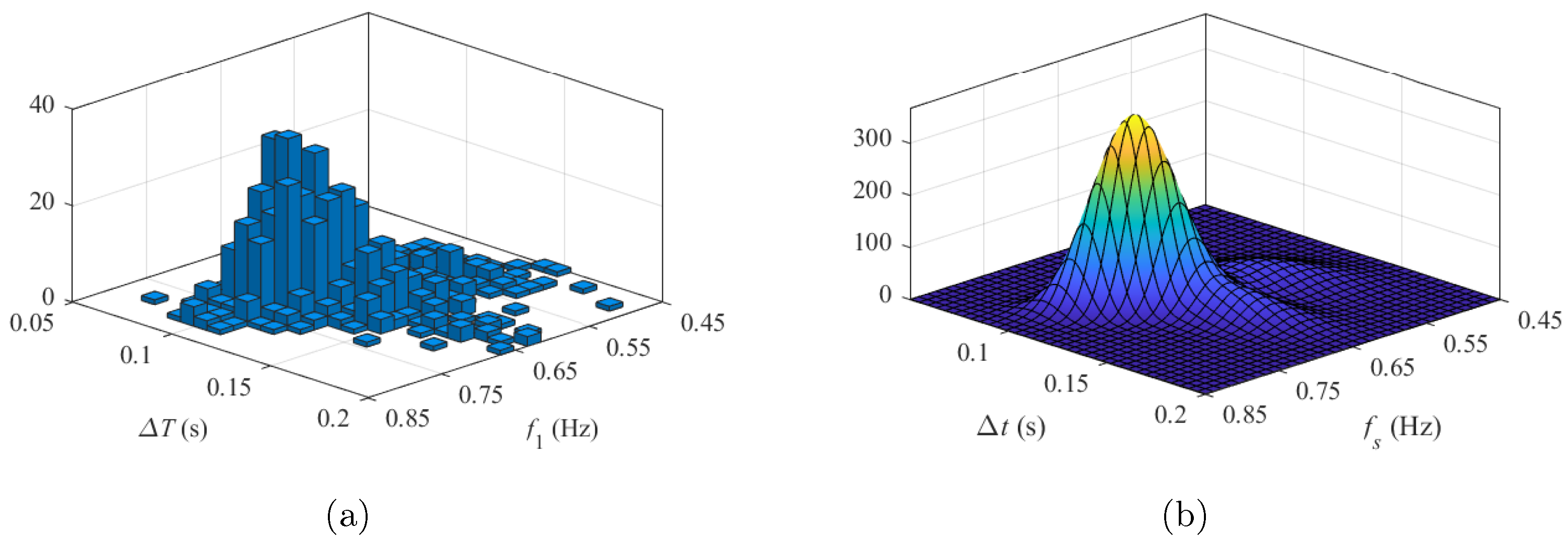
- For each TS, calculate the correlation matrices starting from the parameter matrices defined in the previous step. Correlation matrices collect the pairwise linear correlation coefficient between each pair of walking parameters. Depending on the considered force model (proposed or simplified), the resulting matrices have dimensions or .
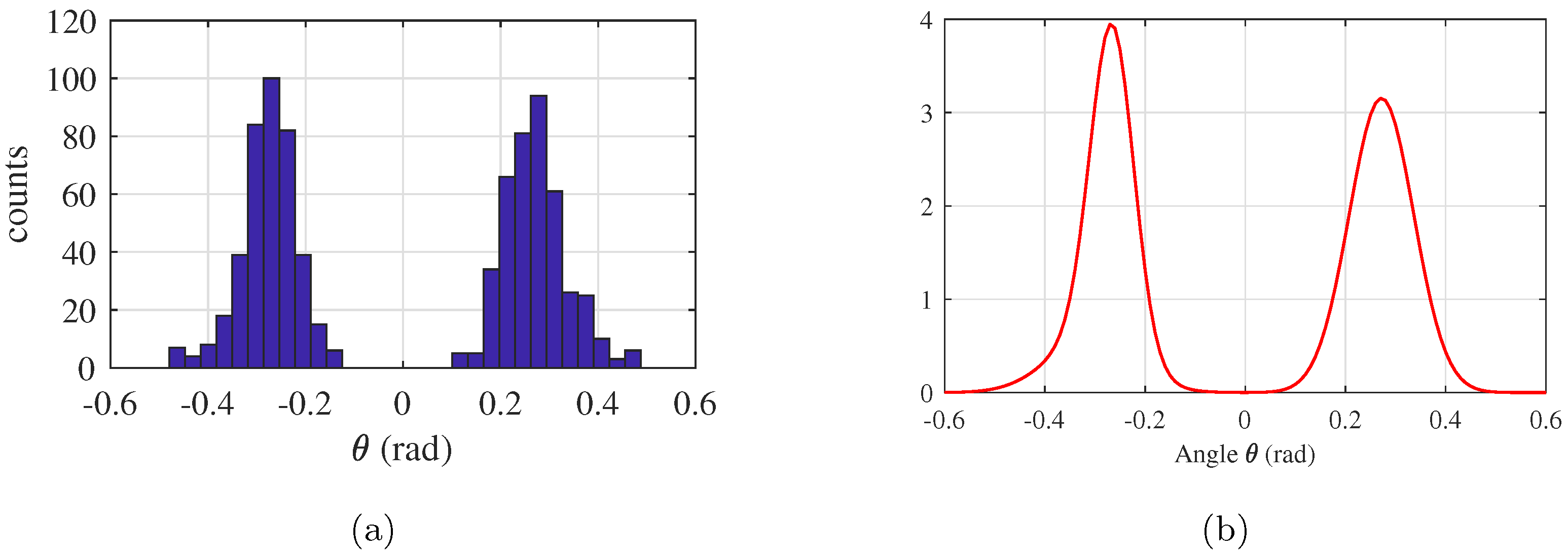
- Based on the average correlation matrices, evaluate which parameters are correlated and which are not. For both force models, results show that all model parameters are correlated except for the step direction .
- Assess the accuracy of the calibrated GM model through the Kolmogorov–Smirnov test [34].
4.1. Proposed Force Model
4.2. Simplified Force Model
5. Simulation of Human-Induced Vibrations
5.1. Footbridge Parameters
5.2. Footbridge Response Simulation
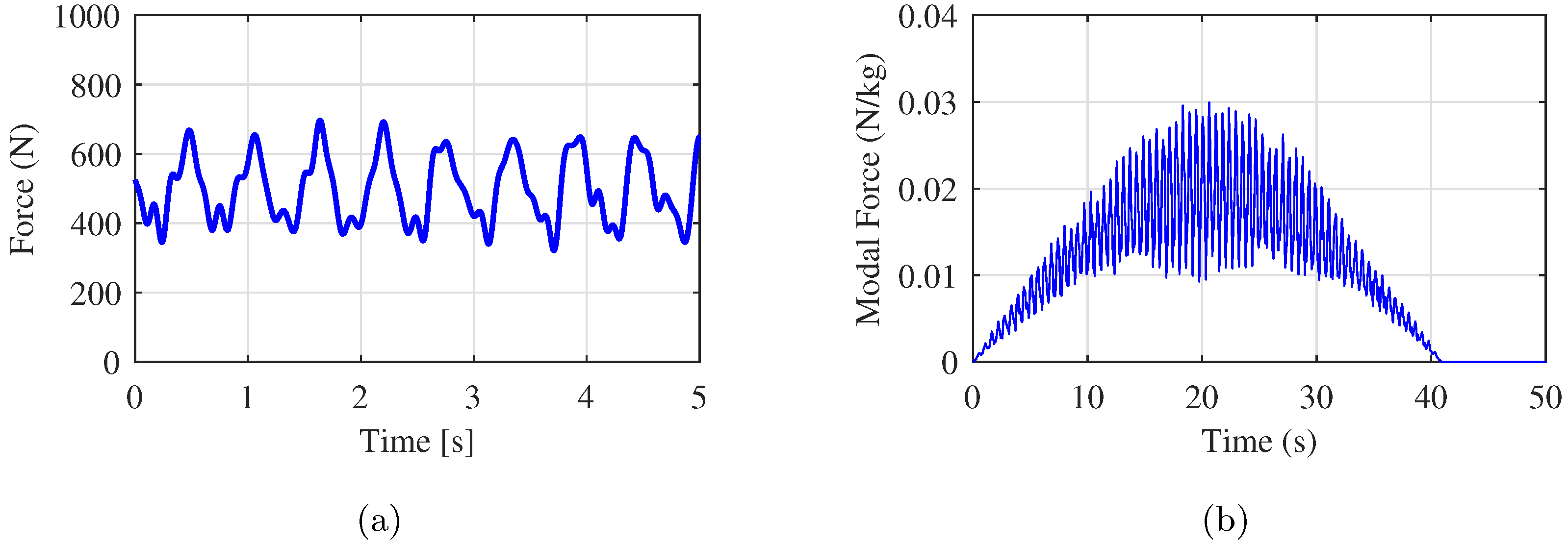
5.3. Simulation Procedure
5.4. Comparison with Existing Models
5.4.1. Single-Step Load Model
5.4.2. Multi-Harmonic Force Model
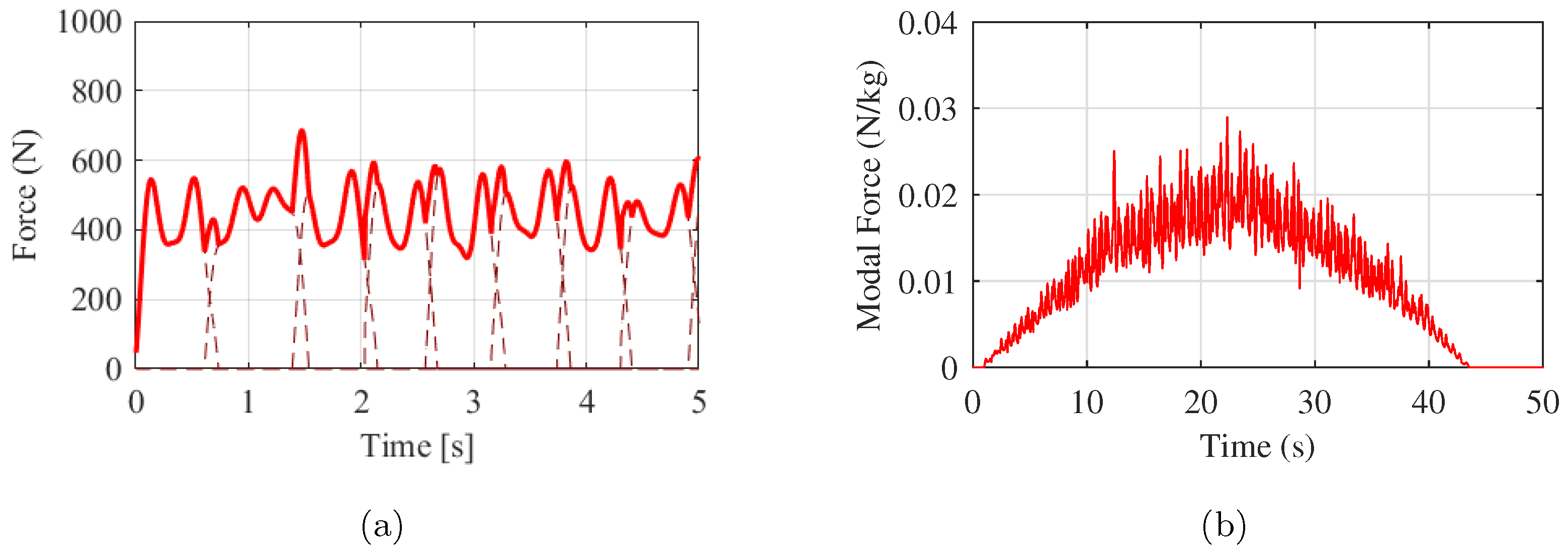
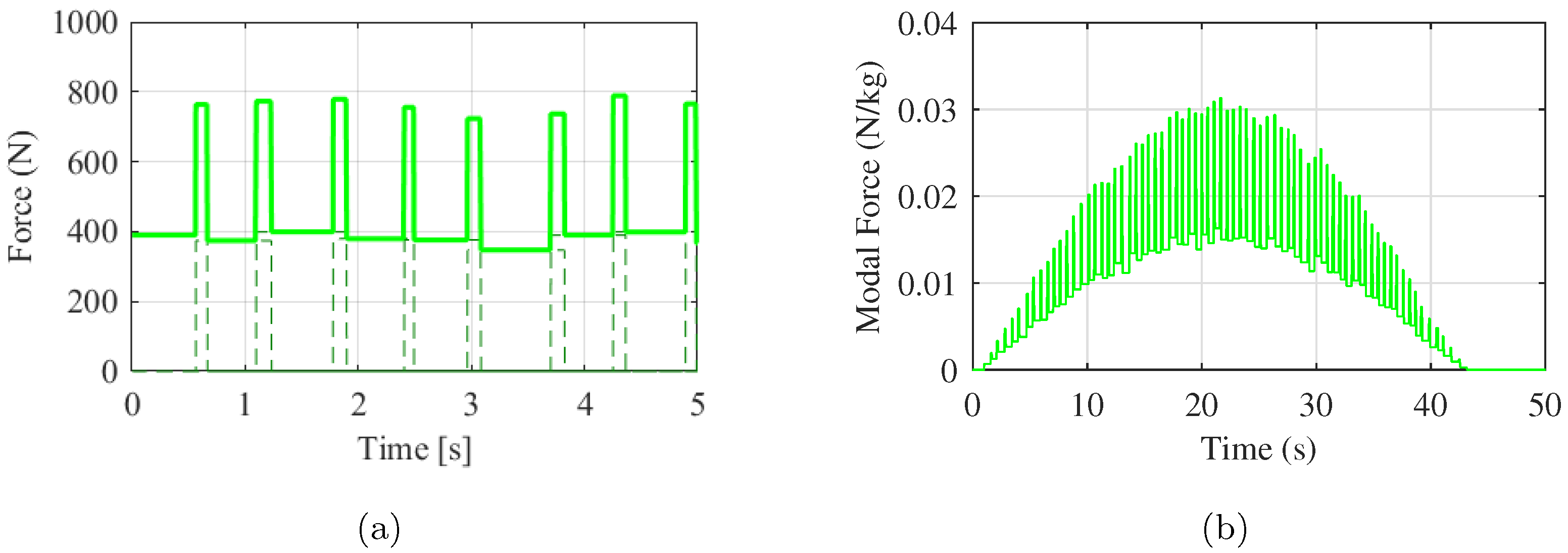
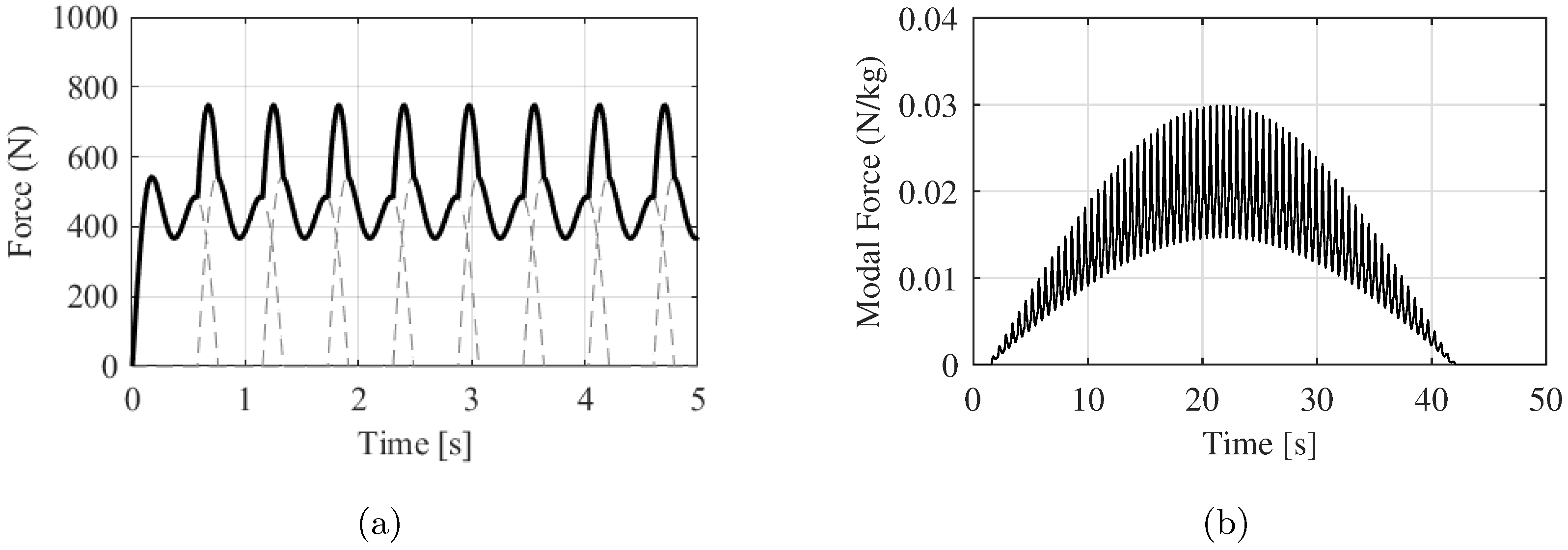
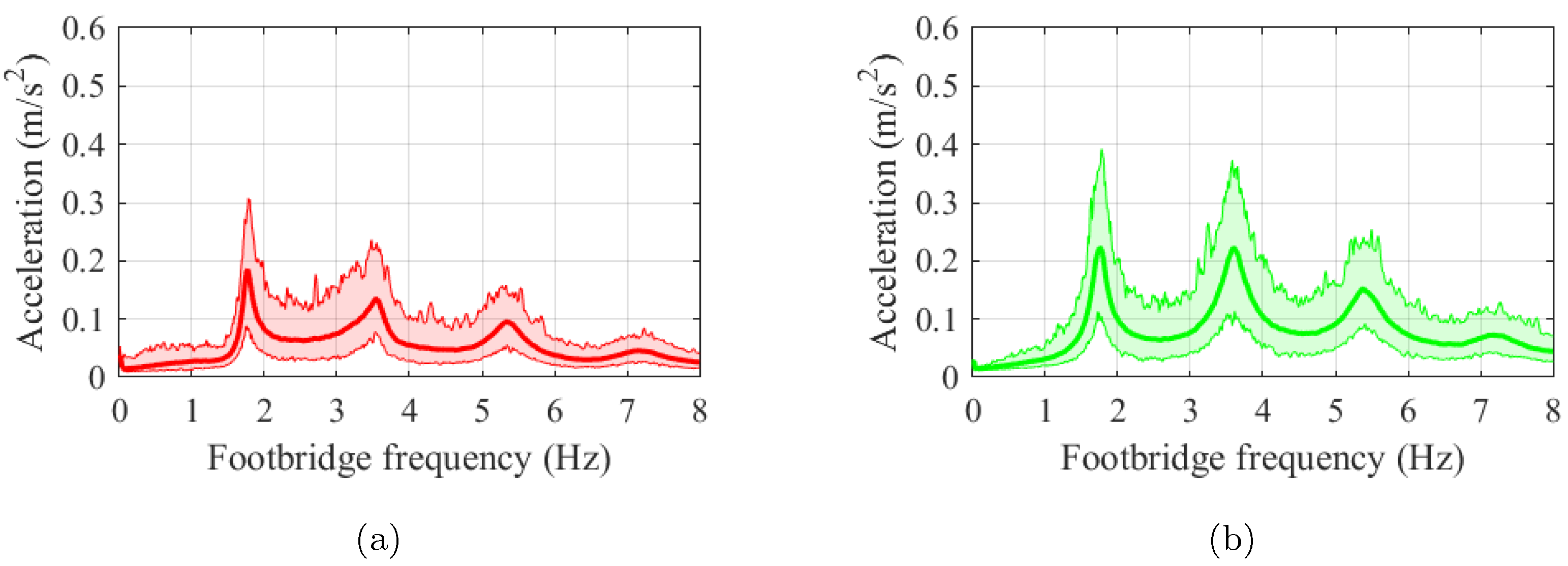
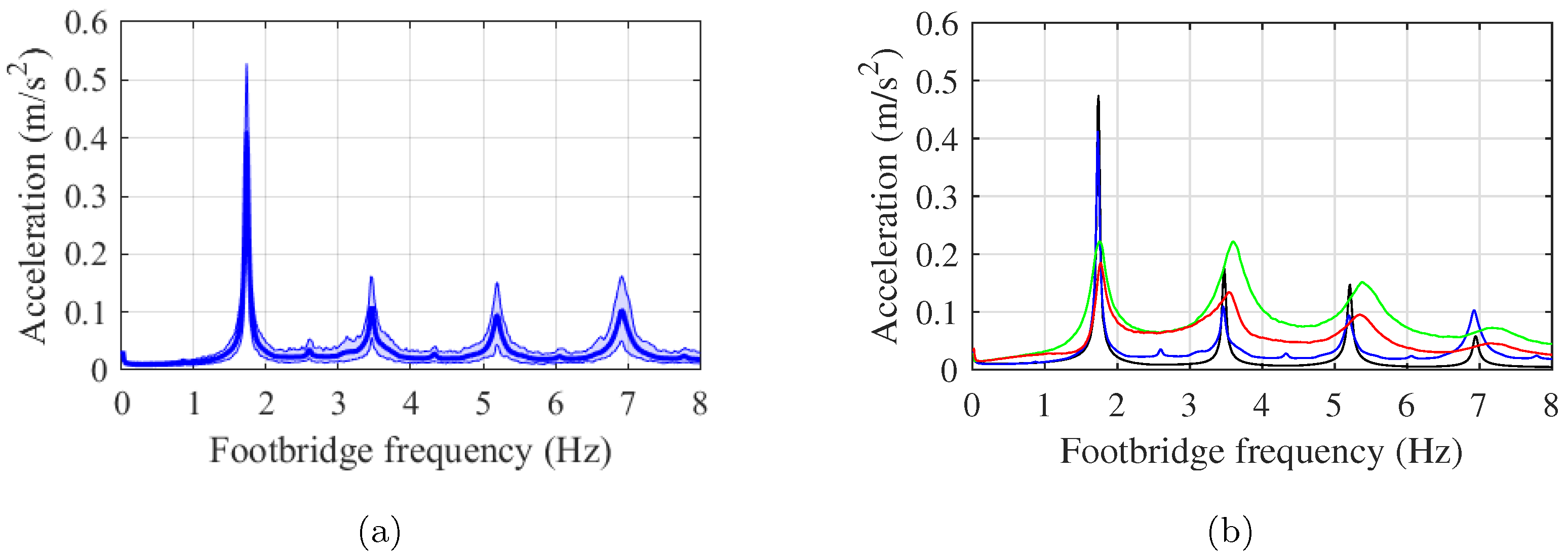
5.5. Results and Discussion
5.5.1. Comparison among the Force Models
5.5.2. Simulation Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Parameters of the Gaussian Mixture Models
| TS 1 | TS 2 | TS 3 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.147 | 0.281 | 0.175 | 0.035 | 0.363 | 0.017 | 0.281 | 0.181 | 0.271 | 0.251 | 0.211 | 0.053 | 0.156 | 0.092 | 0.490 |
| 0.5838 | 0.7207 | 0.6682 | 0.5546 | 0.7056 | 0.5369 | 0.5670 | 0.5635 | 0.5895 | 0.5581 | 0.6132 | 0.5558 | 0.5100 | 0.5877 | 0.5957 |
| 1.0391 | 1.0763 | 1.0221 | 0.9790 | 1.0158 | 1.1930 | 1.2624 | 1.1714 | 1.2260 | 1.1858 | 1.3953 | 1.3535 | 1.2904 | 1.3315 | 1.3009 |
| 0.2993 | 0.3785 | 0.3019 | 0.2256 | 0.3433 | 0.2450 | 0.3064 | 0.3042 | 0.2870 | 0.2338 | 0.3923 | 0.2746 | 0.2529 | 0.2893 | 0.3238 |
| 0.0878 | 0.0437 | 0.0498 | 0.1372 | 0.0549 | 0.0745 | 0.0492 | 0.0555 | 0.0330 | 0.0423 | 0.0497 | 0.0699 | 0.1399 | 0.0803 | 0.0500 |
| 0.0962 | 0.0511 | 0.0632 | 0.1070 | 0.0652 | 0.1193 | 0.0682 | 0.0862 | 0.0811 | 0.0762 | 0.0659 | 0.0865 | 0.0890 | 0.0632 | 0.0683 |
| −1.6275 | −1.5040 | −1.4590 | −1.6748 | −1.5174 | −1.4371 | −1.5002 | −1.5526 | −1.4864 | −1.4805 | −1.5018 | −1.4691 | −1.6193 | −1.5259 | −1.5065 |
| −1.5025 | −1.2197 | −1.1513 | −1.5505 | −1.2441 | −1.1708 | −1.3136 | −1.2883 | −1.2956 | −1.2894 | −1.2201 | −1.0979 | −1.5144 | −1.2318 | −1.2310 |
| 0.1233 | 0.1134 | 0.1424 | 0.1265 | 0.1109 | 0.2637 | 0.1762 | 0.1658 | 0.1730 | 0.2021 | 0.1538 | 0.2029 | 0.1717 | 0.1778 | 0.1603 |
| 0.6827 | 0.7251 | 0.6416 | 0.7028 | 0.6919 | 0.9140 | 0.7289 | 0.7141 | 0.7331 | 0.6025 | 0.7028 | 0.5952 | 0.7065 | 0.4844 | 0.6610 |
| TS 1 | TS 2 | TS 3 | |
|---|---|---|---|
| 0.509 | 0.505 | 0.493 | |
| 0.272 | 0.235 | 0.331 | |
| 4.137 | 3.475 | 4.415 | |
| 0.117 | 0.118 | 0.487 | |
| −0.311 | −0.316 | −0.333 | |
| 6.995 | 3.203 | 2.821 | |
| 0.375 | 0.377 | 0.019 | |
| −0.266 | −0.222 | −0.478 | |
| 1.857 | 1.253 | 0.199 |
| TS 1 | TS 2 | TS 3 | |
|---|---|---|---|
| 0.292 | 0.208 | 0.663 | |
| 0.220 | 0.708 | 0.168 | |
| 0.488 | 0.084 | 0.169 | |
References
- Živanović, S.; Pavić, A.; Reynolds, P. Vibration serviceability of footbridges under human-induced excitation: A literature review. J. Sound Vib. 2005, 279, 1–74. [Google Scholar] [CrossRef] [Green Version]
- Racic, V.; Pavic, A.; Brownjohn, J. Experimental identification and analytical modelling of human walking forces: Literature review. J. Sound Vib. 2009, 326, 1–49. [Google Scholar] [CrossRef]
- Van Nimmen, K.; Lombaert, G.; Jonkers, I.; De Roeck, G.; Van den Broeck, P. Characterisation of walking loads by 3D inertial motion tracking. J. Sound Vib. 2014, 333, 5212–5226. [Google Scholar] [CrossRef] [Green Version]
- Younis, A.; Avci, O.; Hussein, M.; Davis, B.; Reynolds, P. Dynamic Forces Induced by a Single Pedestrian: A Literature Review. Appl. Mech. Rev. 2017, 69, 020802. [Google Scholar] [CrossRef]
- Dang, H.V.; Živanović, S. Experimental characterisation of walking locomotion on rigid level surfaces using motion capture system. Eng. Struct. 2015, 91, 141–154. [Google Scholar] [CrossRef] [Green Version]
- Matsumoto, Y.; Nishioka, T.; Shiojiri, H.; Matsuzaki, K. Dynamic design of footbridges. IABSE Proceedings. 1978, pp. 1–15. Available online: https://www.e-periodica.ch/cntmng?pid=bse-pe-004:1978:2::30 (accessed on 30 September 2021).
- Kramer, H.; Kebe, H. Man-induced structural vibrations. Der Bauing. 1980, 54, 195–199. [Google Scholar]
- Kerr, S.; Bishop, N. Human induced loading on flexible staircases. Eng. Struct. 2001, 23, 37–45. [Google Scholar] [CrossRef]
- Pachi, A.; Ji, T. Frequency and velocity of people walking. Struct. Eng. 2005, 83, 36–40. [Google Scholar]
- Sahnaci, C.; Kasperski, M. Random loads induced by walking. In Proceedings of the 6th European Conference on Structural Dynamics, Paris, France, 4–7 September 2005. [Google Scholar]
- Živanović, S.; Pavić, A.; Reynolds, P. Probability-based prediction of multi-mode vibration response to walking excitation. Eng. Struct. 2007, 29, 942–954. [Google Scholar] [CrossRef]
- Živanović, S. Probability-Based Estimation of Vibration for Pedestrian Structure Due to Walking. Ph.D. Thesis, Departement of Civil and Structural Engineering, University of Sheffield, Sheffield, UK, 2006. [Google Scholar]
- Wheeler, J. Prediction and control of pedestrian-induced vibration in footbridges. ASCE J. Struct. Div. 1982, 108, 2045–2065. [Google Scholar] [CrossRef]
- Ellis, B. On the response of long-span floors to walking loads generated by individuals and crowds. Struct. Eng. Lond. 2000, 78, 17–25. [Google Scholar]
- Rainer, J.H.; Pernica, G.; Allen, D.E. Dynamic loading and response of footbridges. Can. J. Civ. Eng. 1988, 15, 66–71. [Google Scholar] [CrossRef] [Green Version]
- García-Diéguez, M.; Racic, V.; Zapico-Valle, J. Complete statistical approach to modelling variable pedestrian forces induced on rigid surfaces. Mech. Syst. Signal Process. 2021, 159, 107800. [Google Scholar] [CrossRef]
- Van Nimmen, K.; Zhao, G.; Seyfarth, A.; Van den Broeck, P. A Robust Methodology for the Reconstruction of the Vertical Pedestrian-Induced Load from the Registered Body Motion. Vibration 2018, 1, 18. [Google Scholar] [CrossRef] [Green Version]
- Rezende, F.; Brunet, O.; Diniz Varela, W.; Pereira, A.; Carvalho, E. Evaluation of TMD Performance in Footbridges Using Human Walking Probabilistic Models. Vibration 2021, 4, 21. [Google Scholar] [CrossRef]
- Ramos-Moreno, C.; Ruiz-Teran, A.M.; Stafford, P.J. Impact of stochastic representations of pedestrian actions on serviceability response. Proc. Inst. Civ. Eng. Bridge Eng. 2021, 174, 113–128. [Google Scholar] [CrossRef]
- Pedersen, L.; Frier, C. Sensitivity of footbridge vibrations to stochastic walking parameters. J. Sound Vib. 2010, 329, 2683–2701. [Google Scholar] [CrossRef]
- Brownjohn, J.; Pavić, A.; Omenzetter, P. A spectral density approach for modelling continuous vertical forces due to walking. Can. J. Civ. Eng. 2004, 31, 65–77. [Google Scholar] [CrossRef] [Green Version]
- Yamasaki, M.; Sasaki, T.; Torii, M. Sex difference in the pattern of lower limb movement during treadmill walking. Eur. J. Appl. Physiol. Occup. Physiol. 1991, 62, 99–103. [Google Scholar] [CrossRef]
- Racic, V.; Brownjohn, J. Stochastic model of near-periodic vertical loads due to humans walking. Adv. Eng. Inform. 2011, 25, 259–275. [Google Scholar] [CrossRef]
- Piccardo, G.; Tubino, F. Equivalent spectral model and maximum dynamic response for the serviceability analysis of footbridges. Eng. Struct. 2012, 40, 445–456. [Google Scholar] [CrossRef]
- Krenk, S. Dynamic response to pedestrian loads with statistical frequency distribution. J. Eng. Mech. 2012, 138, 1275–1281. [Google Scholar] [CrossRef]
- Caprani, C.C. Application of the pseudo-excitation method to assessment of walking variability on footbridge vibration. Comput. Struct. 2014, 132, 43–54. [Google Scholar] [CrossRef]
- Bassoli, E.; Van Nimmen, K.; Vincenzi, L.; Van den Broeck, P. A spectral load model for pedestrian excitation including vertical human-structure interaction. Eng. Struct. 2018, 156, 537–547. [Google Scholar] [CrossRef]
- Brownjohn, J.; Racic, V.; Chen, J. Universal response spectrum procedure for predicting walking-induced floor vibration. Mech. Syst. Signal Process. 2016, 70–71, 741–755. [Google Scholar] [CrossRef] [Green Version]
- Bocian, M.; Brownjohn, J.; Racic, V.; Hester, D.; Quattrone, A.; Gilbert, L.; Beasley, R. Time-dependent spectral analysis of interactions within groups of walking pedestrians and vertical structural motion using wavelets. Mech. Syst. Signal Process. 2018, 105, 502–523. [Google Scholar] [CrossRef]
- Papoulis, A.; Pillai, S.U. Probabiliy, Random Variables and Stochastic Processes, 4th ed.; McGraw-Hill: New York, NY, USA, 2002. [Google Scholar]
- Fontanili, L.; Milani, M.; Montorsi, L.; Valente, G. Gait Analysis for Muscular Forces Evaluation in Human Movement: Integration Protocol of Typical Measurement Methods. In Proceedings of the ASME 2018 International Mechanical Engineering Congress and Exposition, Pittsburgh, PA, USA, 9–15 November 2018; p. V003T04A084. [Google Scholar] [CrossRef]
- Reynolds, D. Gaussian Mixture Models. In Encyclopedia of Biometrics; Li, S.Z., Jain, A., Eds.; Springer: Boston, MA, USA, 2009; pp. 659–663. [Google Scholar] [CrossRef]
- Li, Q.; Fan, J.; Nie, J.; Li, Q.; Chen, Y. Crowd-induced random vibration of footbridge and vibration control using multiple tuned mass dampers. J. Sound Vib. 2010, 329, 4068–4092. [Google Scholar] [CrossRef]
- Massey, F.J. The Kolmogorov–Smirnov Test for Goodness of Fit. J. Am. Stat. Assoc. 1951, 46, 68–78. [Google Scholar] [CrossRef]
- Clough, R.; Penzien, J. Dynamics of Structures; McGraw-Hill: New York, NY, USA, 1993. [Google Scholar]
- Mancuso, M.; Ubertini, F. An efficient integration procedure for linear dynamics based on a time discontinuous Galerkin formulation. Comput. Mech. 2003, 32, 154–168. [Google Scholar] [CrossRef]
- Bassoli, E.; Gambarelli, P.; Vincenzi, L. Human-induced vibrations of a curved cable-stayed footbridge. J. Constr. Steel Res. 2018, 146, 84–96. [Google Scholar] [CrossRef]





| TS | Mass [kg] | Age [Years] | Gender |
|---|---|---|---|
| 1 | 45 | 25 | female |
| 2 | 54 | 25 | female |
| 3 | 55 | 22 | female |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pancaldi, F.; Bassoli, E.; Milani, M.; Vincenzi, L. A Statistical Approach for Modeling Individual Vertical Walking Forces. Appl. Sci. 2021, 11, 10207. https://doi.org/10.3390/app112110207
Pancaldi F, Bassoli E, Milani M, Vincenzi L. A Statistical Approach for Modeling Individual Vertical Walking Forces. Applied Sciences. 2021; 11(21):10207. https://doi.org/10.3390/app112110207
Chicago/Turabian StylePancaldi, Fabrizio, Elisa Bassoli, Massimo Milani, and Loris Vincenzi. 2021. "A Statistical Approach for Modeling Individual Vertical Walking Forces" Applied Sciences 11, no. 21: 10207. https://doi.org/10.3390/app112110207
APA StylePancaldi, F., Bassoli, E., Milani, M., & Vincenzi, L. (2021). A Statistical Approach for Modeling Individual Vertical Walking Forces. Applied Sciences, 11(21), 10207. https://doi.org/10.3390/app112110207






